Помехоустойчивое кодирование. Реализация кодирования

1. Помехоустойчивое кодирование

Реализация кодирования

2. Реализация кодирования циклических кодов

Кодирование циклического кода сводится к умножению
информационного многочлена a(x) на порождающий
многочлен g (x ) :
g ( x) a( x)
( g 0 g1 x ... g n k 1 x
n k 1
g n k x
(a0 a1 x ... ak 1 x
k 1
)
n k
)

3. Реализация кодирования циклических кодов

Кодирование циклического кода сводится к умножению
информационного многочлена a(x) на порождающий
многочлен g (x ) :
g 0 a0 (a0 g1 g 0 a1 ) x ...
(a0 g k 1 ... g 0 ak 1 ) x
k 1
(a0 g k ... g1 ak 1 ) x ...
k
g n k ak 1 x
n 1

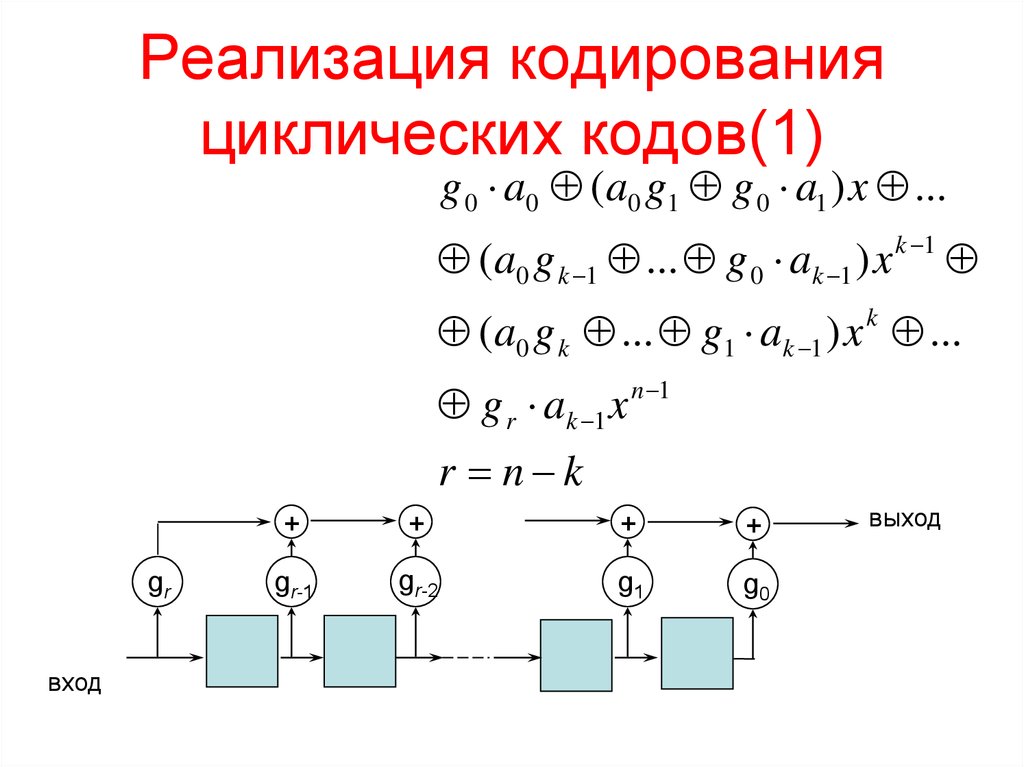
4. Реализация кодирования циклических кодов(1)

g 0 a0 (a0 g1 g 0 a1 ) x ...
(a0 g k 1 ... g 0 ak 1 ) x
k 1
(a0 g k ... g1 ak 1 ) x k ...
g r ak 1 x n 1
r n k
gr
вход
+
+
+
+
gr-1
gr-2
g1
g0
выход

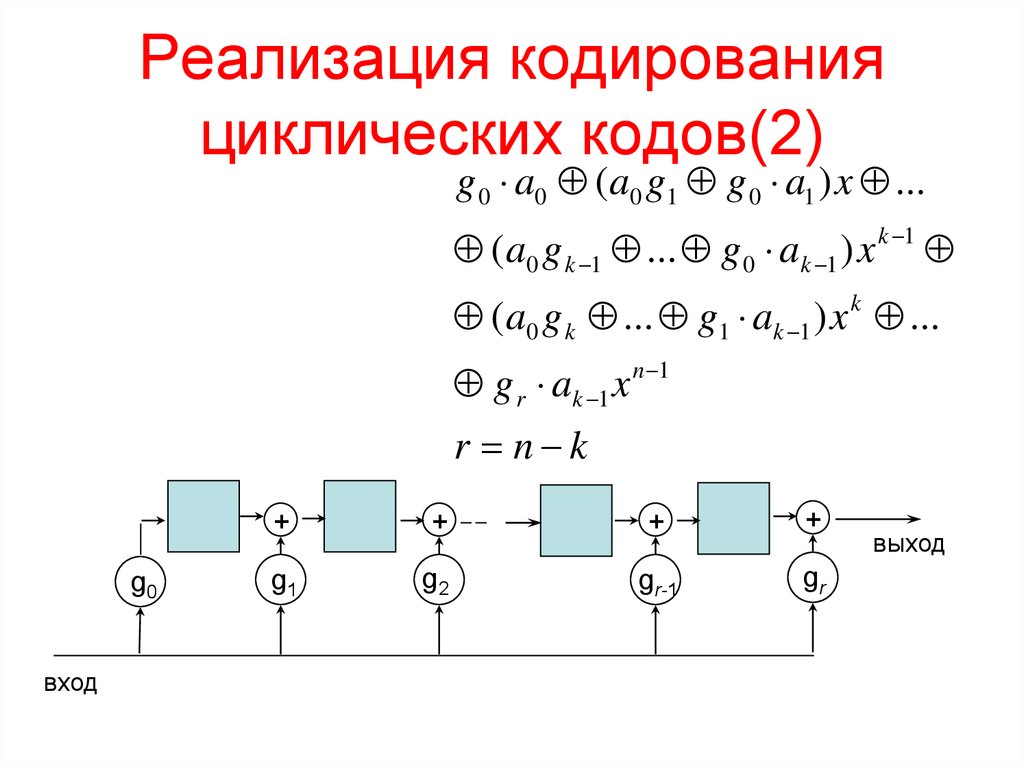
5. Реализация кодирования циклических кодов(2)

g 0 a0 (a0 g1 g 0 a1 ) x ...
(a0 g k 1 ... g 0 ak 1 ) x
k 1
(a0 g k ... g1 ak 1 ) x k ...
g r ak 1 x n 1
r n k
g0
вход
+
+
+
+
g1
g2
gr-1
gr
выход

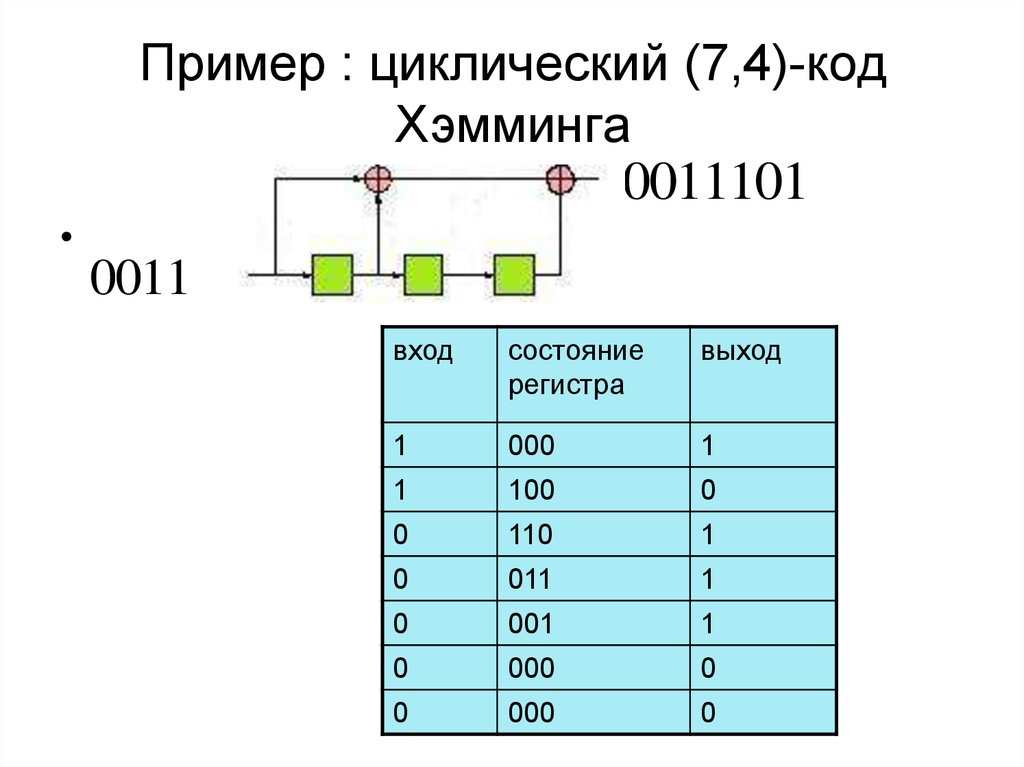
6. Пример : циклический (7,4)-код Хэмминга

• Порождающий многочлен
• информационный многочлен
g ( x) 1 x 2 x 3
а ( x) x 2 x 3
• тогда кодовый многочлен
с ( x ) а ( x) g ( x ) x 2 x 3 x 4 x 6

7. Пример : циклический (7,4)-код Хэмминга

0011101
0011
вход
состояние
регистра
выход
1
000
1
1
100
0
0
110
1
0
011
1
0
001
1
0
000
0
0
000
0

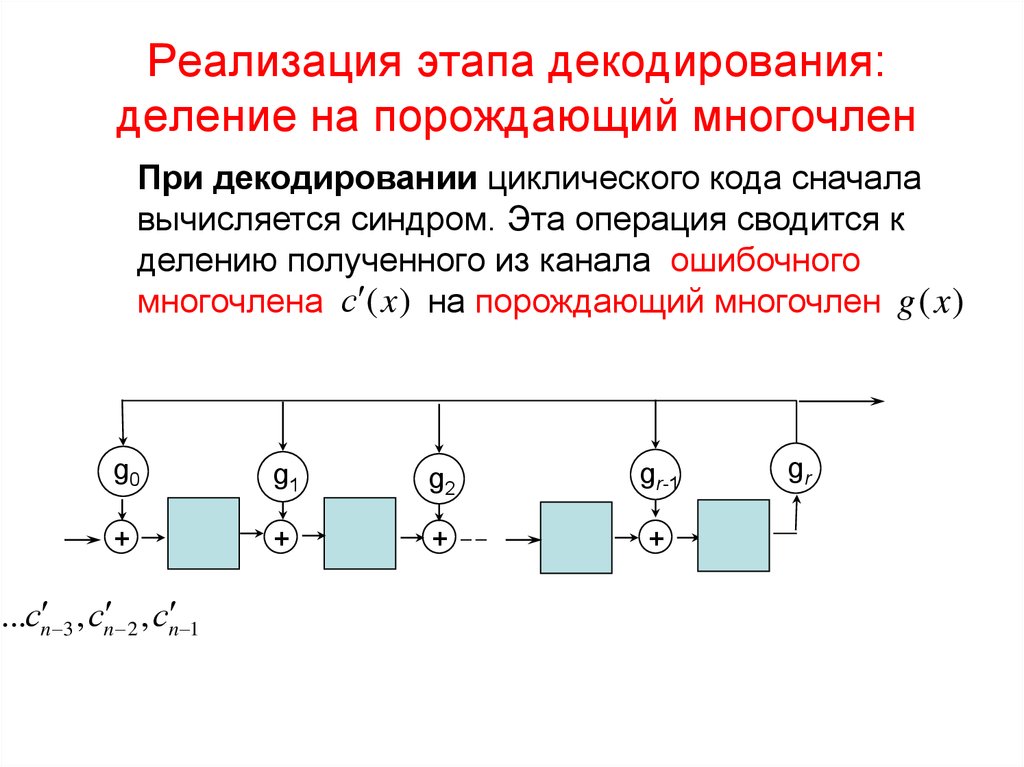
8. Реализация этапа декодирования: деление на порождающий многочлен

При декодировании циклического кода сначала
вычисляется синдром. Эта операция сводится к
делению полученного из канала ошибочного
многочлена с (x ) на порождающий многочлен g (x )
g0
g1
g2
gr-1
+
+
+
+
...сn 3 , сn 2 , сn 1
gr

9. Пример : циклический (7,4)-код Хэмминга

Пусть полученное слово 1110101
Регистр реализует процесс деления
1110101
1011
1011000 1100 частное
____________________
101101
101100
____________________
1 остаток

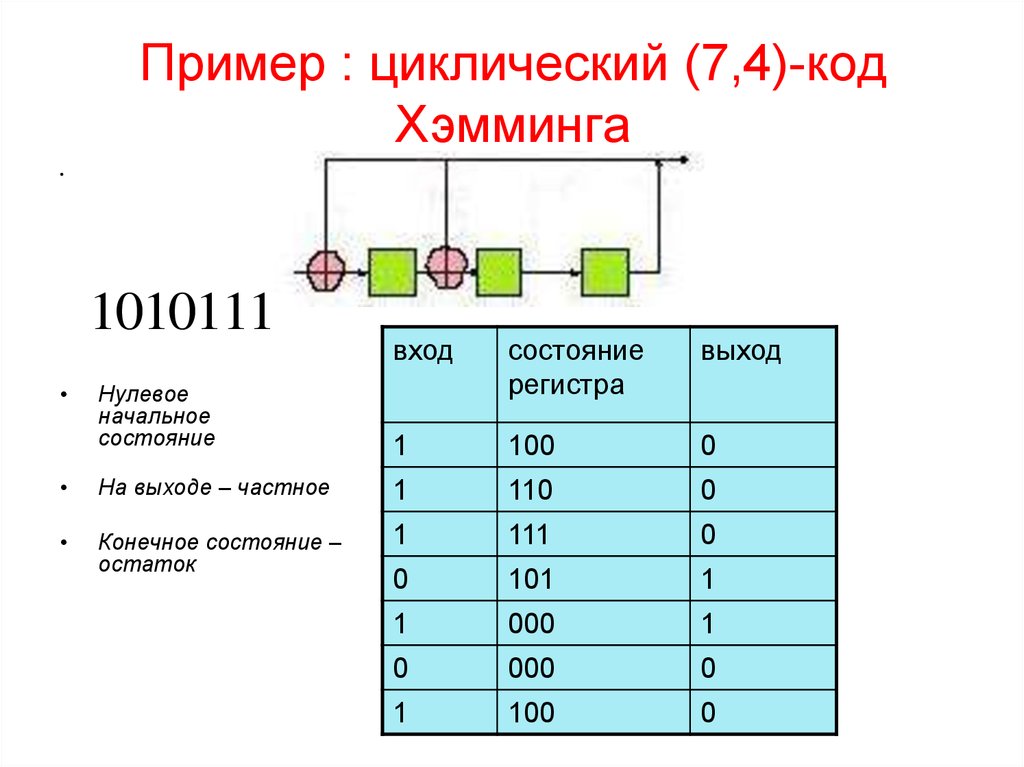
10. Пример : циклический (7,4)-код Хэмминга

1010111
вход
выход
Нулевое
начальное
состояние
состояние
регистра
1
100
0
На выходе – частное
1
110
0
Конечное состояние –
остаток
1
111
0
0
101
1
1
000
1
0
000
0
1
100
0