Похожие презентации:
Задача на тестирование ВР
1. Задача на тестирование ВР
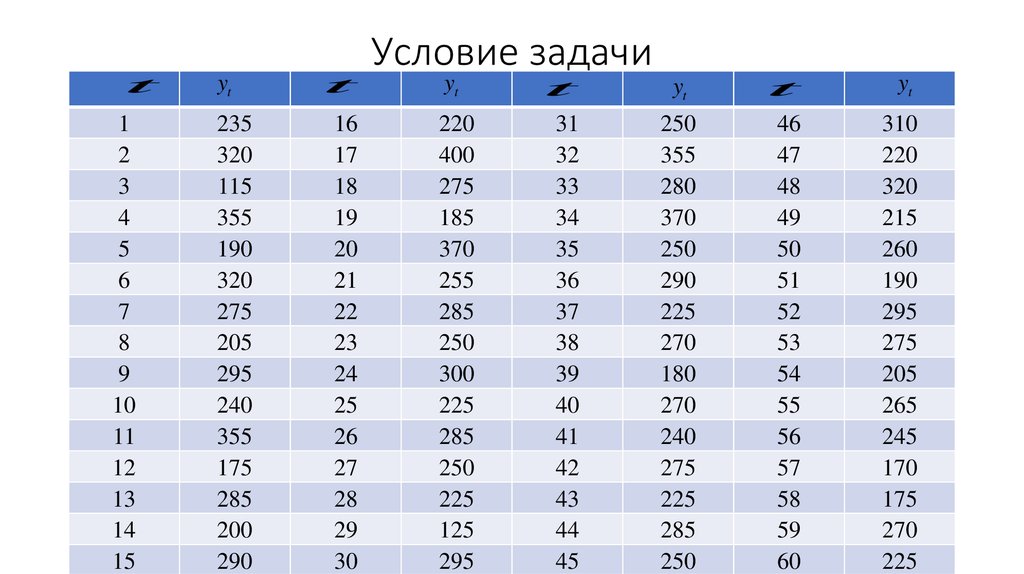
2. Условие задачи
t1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
yt
235
320
115
355
190
320
275
205
295
240
355
175
285
200
290
Условие задачи
t
yt
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
220
400
275
185
370
255
285
250
300
225
285
250
225
125
295
t
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
yt
t
yt
250
355
280
370
250
290
225
270
180
270
240
275
225
285
250
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
310
220
320
215
260
190
295
275
205
265
245
170
175
270
225
3.
Имеются данные о размерах запасов компании А.Требуется провести тестирование ряда на постоянство
математического
ожидания
и
дисперсии
с
помощью
параметрических тестов на основе:
• 1.
- критерия Стьюдента;
• 2.
- критерия Фишера;
• 3. критерия Кокрена, основанного на распределении Фишер;
• 4. критерия Бартлетта.
• и непараметрических тестов:
• 5. Манна-Уитни;
• 6. Сиджела – Тьюки;
4. Критерий Стьюдента
• Для тестирования ряда на постоянство математическогоожидания по критерию Стьюдента, разобьем ряд на 2 части, в
первую из которых войдут наблюдения с 1 по 35, а во вторую – с
36 по 60.
• Определим оценки математических ожиданий:
60
35
y1
y
t 1
35
t
265,8571
y
t
y2 t 36 246
25
5. Критерий Стьюдента
• Рассчитаем дисперсии:T1
2
1
y
t
t 1
y1
T1 1
T
2
2
y
t T1 1
t
35
2
y
t 1
y2
T2 1
t
265,8571
35 1
60
2
y
t 36
t
2
153674,2857
4519,8319
34
246
25 1
2
42400
1766,6667
24
6. Критерий Стьюдента
ty1 y2
2
1
T1
2
2
T2
265,8571 246
1,4048
4519,8319 1766,6667
35
25
• Сравнивая с критическим значением
t T 2 t 0,05; 58 2,0017
• приходим к выводу, что нельзя отклонить гипотезу, что
математическое ожидание постоянно, т.к. t t 0,05;58
7. Критерий Фишера
• Проверка гипотезы о постоянстве дисперсии временного ряда вслучае разбиения исходного интервала на две части
осуществляется с использованием двухстороннего критерия
Фишера. Расчетное значение критерия
Фишера определяется:
2
1
F 2
2
• Для нашего ряда:
4519,8319
F
2,5584
1766,6667
• Сравнивая его с табличным значением критерия Фишера с 34 и 24
степенями свободы: F 0,025;34;24 2,1797
• можно сделать вывод, о том, что гипотеза о постоянстве
дисперсии отвергается, так как F F 0,025;34;24
8. Критерий Кокрена
• При разбиение ряда на несколько частей для проверки гипотезыо постоянстве дисперсий может быть использован критерий
Кокрена, основанный на распределении Фишера. Он
применяется в предположении, что объемы этих частей равны
между собой. Расчетное значение этого критерия определяется:
K
2
max
...
2
1
2
n
,
где
2
max
max( )
i
2
i
• А критическое значение критерия рассчитывается по формуле:
F , 1 , 2
n
K ( , n, N 1)
(n 1) F , 1 , 2
n
9. Критерий Кокрена
• Где 1 N 1 и 2 ( n 1) 1Разобьем исходный ряд на 5 равных частей ( N 12 ).
Для каждой из подвыборок рассчитаем дисперсию по формуле:
Ti
y
i2 t 1 T
t
yi
2
i 1
12
2
1
yt y1
11
yt y3
32 t 25
11
24
2
t 1
36
N 1
63766,6667
5796,9697
11
2
2
yt y2
44716,6667
4065,1515
11
2
4
43456,25
3950,5682
11
t 13
11
48
2
2
y
t 37
t
y4
11
2
17891,6667
1626,5152
11
10. Критерий Кокрена
60y
52 t 49
K
2
max
n
2
i
t
y5
11
2
19225
1747,7273
11
2
max
max( i2 ) 12 5796,9697
i
5796,9697
0,3373
5796,9697 3950,5682 4065,1515 1626,5152 1747,7273
i 1
1 0,95
F
;11;44
5
2,6804 0,4012
K 0,05;5;11
1 0,95
4 2,6804
4 F
;11;44
5
Поскольку расчетное значение меньше критического значения,
то нельзя отвергнуть гипотезу о постоянстве дисперсии.
11. Критерий Бартлетта
• В нашем примере разобьем ряд на 3 части: первая – с 1 по 20,вторая – с 21 по 40, третья – 41 по 60. Рассчитаем дисперсии для
подвыборок:
40
20
2
2
y
y
t 2 55363,75
yt y1
2
1
2
107623,75
t 21
5664,4079
2
19
19
60
2
yt y3 34513,75
32 t 41
1816,5132
19
19
t 1
19
19
• Общая дисперсия для всей выборки:
3
2
2
i i
i 1
3
i 1
i
107623,75 55363,75 34513,75
3464,9342
57
2913,8816
12. Критерий Бартлетта
• Т.к. 1 2формуле:
Критерий Бартлетта
3 19
, то значение критерия находится по
n
1
1
1
2
2
i ln
n ln ln i
c i 1
c
n i 1
• где
n
2
i
2
1 n 1
1
n
c 1
3(n 1) i 1 i
i
i 1
или
n 1
c 1
3n
13. Критерий Бартлетта
• получаем, при3 1
c 1
1,0234
3 3 19
3 19
1 3
2
2
ln ln i
c
3 i 1
57
1
ln 3464,9342 ln 5664,4079 ln 2913,8816 ln1816,5132 6,0798
1,0234
3
0,05
;2 7,3778
2
6,0798
• так как
постоянстве дисперсии.
, нельзя отклонить гипотезу о
14.
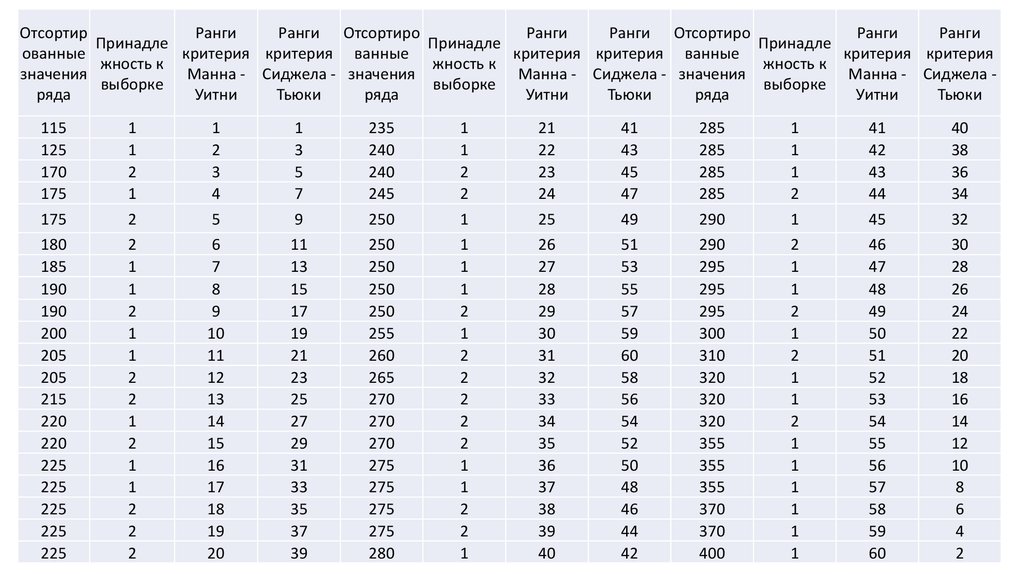
ОтсортирРанги
Ранги Отсортиро
Ранги
Ранги Отсортиро
Ранги
Ранги
Принадле
Принадле
Принадле
ованные
критерия критерия ванные
критерия критерия ванные
критерия критерия
жность к
жность к
жность к
значения
Манна - Сиджела - значения
Манна - Сиджела - значения
Манна - Сиджела выборке
выборке
выборке
ряда
Уитни
Тьюки
ряда
Уитни
Тьюки
ряда
Уитни
Тьюки
115
125
170
175
175
180
185
190
190
200
205
205
215
220
220
225
225
225
225
225
1
1
2
1
2
2
1
1
2
1
1
2
2
1
2
1
1
2
2
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
235
240
240
245
250
250
250
250
250
255
260
265
270
270
270
275
275
275
275
280
1
1
2
2
1
1
1
1
2
1
2
2
2
2
2
1
1
2
2
1
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
43
45
47
49
51
53
55
57
59
60
58
56
54
52
50
48
46
44
42
285
285
285
285
290
290
295
295
295
300
310
320
320
320
355
355
355
370
370
400
1
1
1
2
1
2
1
1
2
1
2
1
1
2
1
1
1
1
1
1
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
40
38
36
34
32
30
28
26
24
22
20
18
16
14
12
10
8
6
4
2
15. Критерий Манна - Уитни
• Сумма рангов для первой подвыборке равна:R1 1148
• Тогда стандартизованная переменная, рассчитанная по формуле:
T1 T1 T2 1
R1
2
z
T1 T2 T1 T2 1
12
• Будет равна:
35 35 25 1
1148
2
z
1,207
35 25 35 25 1
12
16. Критерий Манна - Уитни
• Статистика Манна – Уитни имеет стандартное нормальноераспределение.
• Так как ,
1,96 z 1,207 1,96
• то гипотеза о постоянстве математического ожидания принимается.
17. Критерий Cиджела - Тьюки
• Сумма рангов критерия Сиджела –Тьюки для первой подвыборкиравна:
R1 959
• Тогда стандартизованная переменная, рассчитанная по формуле:
T1 T1 T2 1
R1
2
z
T1 T2 T1 T2 1
12
• Будет равна:
35 35 25 1
959
2
z
1,627
35 25 35 25 1
12
18. Критерий Cиджела - Тьюки
• Статистика Cиджела – Тьюки, так же как и Манна - Уитни, имеетстандартное нормальное распределение.
• И так как ,
1,96 z 1,627 1,96
• то гипотеза о постоянстве дисперсии не отклоняется.
















 Математика
Математика








