Похожие презентации:
Небесная механика
1. Небесная МЕХАНИКА
5 лекция2.
2.1.5 Екі дене есебіндегі қозғалыстың классификациясыКруговое
и эллиптическое
– –финитные,
они происходят
Шеңберлік
және эллипстікдвижения
қозғалыстар
финитті қозғалыстар
(қозғалыс в
ограниченной
части плоскости,
полная
энергия
отрицательна
–
жазықтықтың шектеулі
аймағында болады),
жалпы
энергияның
мәні «-» болады
кинетической
энерги не
хватает для преодоления
– тартылыс центрдің
гравитациялық
әсерінен шығу гравитационного
үшін кинетикалық
действия
центра.
энергияныңпритягивающего
мәні жеткіліксіз болу
керек.
Параболическое
и гиперболическое
движения
– инфинитные,
полная
Параболалық және
гиперболалық қозғалыстар
– инфинитті
қозғалыстар,
энергия
не меньше
и движущаяся
точка преодолевает
силукүшіне
тяготения и
жалпы энергии
0-ден0,жоғары
және қозғалатын
нүкте тартылыс
уходит
в бесконечность.
қарамастан
шексізге кетеді.
Шеңберлік жылдамдық VC және параболалық жылдамдық
Шеңберлік жылдамдық VC r
және параболалық жылдамдық
r
V
Шеңберлік
жылдамдық
және
параболалық жылдамдық
C
2
r
VP
арқылы
бірінші және екінші ғарыштық жылдамдықтырын анықтауға
2
r
VP2
арқылы бірінші және екінші ғарыштық жылдамдықтырын анықтауға
r
V
арқылы
бірінші және екінші
ғарыштық
жылдамдықтырын
P
болады.
Егер
r арақашықтықты
R - орталық
дененің
радиусы жәнеанықтауға
Н - ұшу
r
болады.
Егер
r
арақашықтықты
R
орталық
дененің
радиусы
және
Н - ұшу
биіктігі
ал μ – гравитациялық
тұрақтысын
- дененің
радиусы
болады. арқылы,
Егер r арақашықтықты
R - орталық
дененің
радиусы
және мен
Н -оның
ұшу
биіктігі
арқылы,
ал μ –үдеуі
гравитациялық
тұрақтысын
- дененің радиусы мен оның
бетіндегі
ауырлық
күшінің
(g)
арқылы
ауыстырсақ
биіктігі арқылы, ал μ – гравитациялық тұрақтысын - дененің радиусы мен оның
бетіндегі ауырлық күшінің үдеуі (g) арқылы ауыстырсақ
бетіндегі ауырлық күшінің үдеуі (g) арқылы ауыстырсақ
gR2 қозғалысының
2 gR2 түрлері
6 сурет
–
Кеплер
2
(2.37)
VC
, VP
, 2
2 gR
22 gR
R
H
R
H
(2.37)
V
, V 2 gR
,
gR
(2.37)
VC C
VP P
R, H
R, H
R H
R H
сонда Н=0 жағдайда бірінші және екінші ғарыштық жылдамдықтары
сонда Н=0 жағдайда бірінші және екінші ғарыштық жылдамдықтары
сонда Н=0 жағдайда бірінші және екінші ғарыштық жылдамдықтары
(2.38)
V1 gR, V2 2 gR.
(2.38)
V gR, V 2 gR.
(2.38)
V1 1gR, V2 22 gR.
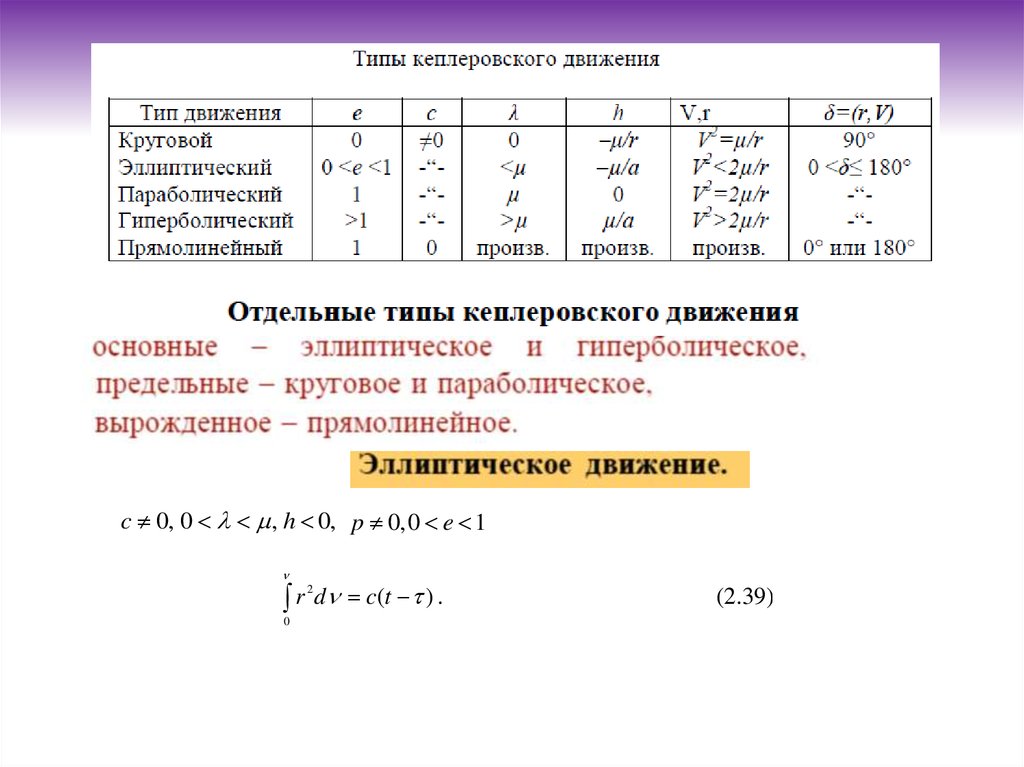
3.
2.2 Кеплер қозғалысының арнайы түрлері2.2 Кеплер қозғалысының арнайы түрлері
Екі дене есебінде қозғалыстың түрлері:
ері
Негізгі - эллипстік және гиперболалық;
Екі дене есебінде қозғалыстың түрлері:
Шектеулі – шеңберлік және параболалық;
Негізгі - эллипстік және гиперболалық;
Нұқсанды – түзусызықты қозғалыс. Шектеулі – шеңберлік және параболалық;
қ;
Нұқсанды – түзусызықты қозғалыс.
лық;
2.2.1 Эллипстік қозғалыс
2.2.1 Эллипстік қозғалыс
Егер бірінші интегралдардың тұрақтылары c 0, 0 , h 0,
Егер
бірінші
қозғалыс
болады.интегралдардың тұрақтылары c 0, 0
0, 0 e 1 мәндерге ие болса - эллипстік
қтылары
c 0,шешу
0
, h шын
0, pаномалиямен
болса - эллипстік
0, 0 e 1 мәндерге
Екі дене есебін
үшін
уақыттыңиебайланысы
осы қозғалыс болады.
грал арқылы
анықталады
озғалыс
болады.
Екі дене есебін шешу үшін шын аномалиямен уақыттың ба
интеграл арқылы анықталады
2
иямен уақыттың байланысы rосы
d c(t ) .
(2.39)
0
r d
2
0
c(t ) .
).
(2.39)
Интегралды шешу үшін тағы негізгі параметрлерді еңгізу қажет.
Интегралды шешу үшін тағы негізгі параметрлерді еңгізу қаж
метрлерді еңгізу қажет.
4.
Е- эксцентрическая аномалия6 сурет – Эксцентрлік аномалия
Егер
cos E e
1 e 2 sin E
cos
, sin
,
1 e cos E
1 e cos E
(2.43)
5.
арасындағыбұрышбұрыш(10
(10сурет).
сурет).
қозғалыс
бағытында
0ден
ден
360
арасында
o
арасындағы
бұрыш
(10 сурет).
Е360
қозғалыс
бағытында 0 де
арасындағы
Е Еқозғалыс
бағытында
0oдегеніміз
арасында
аномалия
анықталады.
Эксцентрлік
аномалия
Е
эллипстің
үлкен
жарты
осі
және
перпендикулярдың
шеңбермен
қиылысу
нүкте
бағыты
өлшенеді.
өлшенеді.
өлшенеді.
o
o
жарты бұрыш
осі және
перпендикулярдың
бағыты
арасындағы
(10 сурет).
Е қозғалыс шеңбермен
бағытында 0қиылысу
ден 360нүкте
арасында
Сонда
Сонда
Сонда
o
o
арасындағы бұрыш (10 сурет).
Е қозғалыс
өлшенеді.
.
a cos
E
ae
cos
r cos
бағытында
a0cosден
E 360
ae(2.40)
(2.40)
rарасында
cos .
.
a
cos
E
ae
r
өлшенеді.
Сонда
Сонда
(2.40)
a cos E
yc a a
yc 2 ae
a r cos .
2
y
Егер c және
және r sin
болса,
r sin
esin
E ae
sin
Егер
және
sin
a 1орбиталдық
орбиталдық
e sin E болса,
. дененің
(2.40) денен
a2 cos
E
r cosr дененің
Егер
болса,
a a1 1e
E
y
b
ye b
ye yce b a
y және
Егер
r sin координаттары:
a 1 e 2 sin E болса, дененің орбиталдық
координаттары:
a
координаттары:
ye b c
Егер
және r sin racos
дененің
E E болса,
1 e 2 asin
cos
e ,
r cos орбиталдық
a cos E e ,
r
cos
a
cos
E
e
,
y
b
e
координаттары:
(2.41) 2
2
(2.41)
2
rr sin
1e eEsin sin
r sin a 1 e sin E ,
координаттары:
r
sin
cos
e ,,E ,
a aa1 cos
E
(2.41)
r cos a аномалия
және
радиус-векторы
және
радиус-векторы
6 сурет
– Эксцентрлік
2cos E e ,
және
радиус-векторы
r sin a 1 e sin E ,
(2.41)
Егер
2
r sin a аномалия
1 e2 sin E ,
және радиус-векторы
6 сурет
– 1
Эксцентрлік
.
(2.42)
r
a
e
cos
E
cos
E .
cos
E
e
1
E . e sin E , r a 1 e(2.42)
, sin
(2.43)
Егеррадиус-векторы cos r a 1 e cos
және
1 e cos E
1 e cos E
(2.42)
rcos
aE 1
e e cos E . 1 e 2 sin E
cos
, sin
,
(2.43)(2.42)
.
r
a
1
e
cos
E
1
e
cos
E
1
e
cos
E
болса, шын және эксцентрлік аномалиялар арасындағы байланысы
(2.43) дифференциалдаған кезінде
болса, шын және эксцентрлік аномалиялар
байланысы
1 eарасындағы
e2 E
1
.
d tg 1 e tg dE
2 .
1 e 1cos
(2.43) дифференциалдаған кезінде
eE E
tg
tg .
2
1
e
2
1 e
d ескерген
dEкезде
.
(2.42) мен (2.45)-ті (2.39)-ші формулада
1 e cos E
кезде
(2.42) мен (2.45)-ті (2.39)-ші формулада
ескерген
1
e
cos
E
dE
3 (t )
0
a2
E
немесе
1
e
cos
E
dE
E e sin E 3n((tt ).)
(2.44)
(2.45)
(2.44)
(2.45)
E
(2.46)
(2.46)
(2.47)
6.
месеa
1
e
cos
E
dE
(t )
3
0
2
3
(2.46)
a
E e sin E n(t ).
E e sin E n(t ).
0
немесе
2
(2.47)
(2.47)
сында n 3 - эллипстік
орбита бойымен
дененің
орташа
средняя
угловая
скорость қозғалатын
движения по
эллиптической
орбите
2
aЕгер
–3 орташа
аномалия
болсабойымен
және
Осында
-среднее
эллипстік
орбита
қозғалатын дененің орташа
n М или
движение
2
рыштық жылдамдығы
немесе орташа қозғалыс деп аталады. (2.47) формула a
бұрыштық
орташа
деп аталады.
(2.47) формула
липстік
қозғалысжылдамдығы
кезіндегі екі немесе
дене есебінің
теңдеуі.
(2.48)
M шешімі
nқозғалыс
(t ), – Кеплер
эллипстік
қозғалыс кезіндегі екі дене есебінің шешімі – Кеплер теңдеуі.
сонда (2.47)
М – средняя аномалия.
(2.49)
E e sin E M .
Егер а радиусы бар шеңбер арқылы кез келген нүкте тұрақты
жылдамдылығымен қозғалса, және бір уақытта аспан денесімен бірге
Осыдан жалпыландырылған Кеплердің үшінші заңы
перицентр арқылы өтетін болса, сонда осы нүктенің радиус-векторы және
T
перицентр бағыты арасындағы бұрыш
М аспан
m mМ 4орташа
(2.52)
const. аномалия болады.
a 0o дан 360
G o өлшенеді.
денесінің қозғалыс бағытына қарай
Эллипстік қозғалысында энергия тұрақтысы
2
2
0
3
h
2 2
c2
e2 1
,
p
a
p
c2
,
e
.
(2.50)
Эллипстік орбита бойымен қозғалатын материалдық нүктенің айналу
периоды
T 2
a
3
3
a2
2
.
G (m0 m)
2
S – эллипстің фокусы, О – эллипстің центрі, Р - перицентр, А - апоцентр, ω =
(2.51)
7.
oo нүктенің радиус-векторы және
перицентрқозғалыс
арқылыбағытына
өтетін болса,
осы
денесінің
қарай
дан
(2.48)
M 0сонда
n
(t 360
), өлшенеді.
перицентр
бағыты
арасындағы
бұрыштұрақтысы
М- орташа аномалия болады. М аспан
Эллипстік
қозғалысында
энергия
сонда (2.47)
денесінің қозғалыс бағытына қарай 0o дан 360o өлшенеді.
(2.49)
E e sin E M .
Эллипстік қозғалысында
энергия
2 2
e 2 1 тұрақтысы
c2
(2.50)
h
,
p ,
e .
2
c
p
a
Егер а радиусы 2бар 2 шеңбер
арқылы кез 2келген нүкте тұрақты
e2 1
уақытта
c
денесімен бірге
жылдамдылығымен
және
бір
аспан
(2.50)
h қозғалса,
,
p
,
e
.
2
c бойымен
p қозғалатын
Эллипстік
орбита
материалдық
нүктенің
айналу
перицентр
арқылы
өтетін
болса,
сондаa осы нүктенің
радиус-векторы
және
периоды
перицентр бағыты арасындағы бұрыш М- орташа аномалия болады. М аспан
3
Эллипстік
орбита
бойымен
нүктенің айналу
2
денесінің
қозғалыс
бағытына
қарайaқозғалатын
03 2o дан 360o өлшенеді.
aматериалдық
T энергия
2
2
.
(2.51)
периоды
Эллипстік қозғалысында
тұрақтысы
G (m302 m)
3
a2
a
2
2 T 22
2
2
.
(2.51)
e
1
c
G
(
m
m
)
Осыдан жалпыландырылған
Кеплердің
үшінші
заңы
(2.50)
h
,
p 0 ,
e .
2
Сонда екі дене cесебінің
шешімі
орбита бойымен
p
aбойынша эллипстік
қозғалатын нүктенің координаттары
T 2 шешімі 4бойынша
2
Сонда екі дене есебінің
эллипстік орбита бойымен
(2.52)
m
m
const
.
0 қозғалатын материалдық нүктенің айналу
Эллипстік
орбита
бойымен
қозғалатын
нүктенің
координаттары
a3
G
Px
x
Qx
периоды
3
3
2
2
E e aQ
(2.53)
yx a PPyx a cos
Q2yx 1 e sin E
T
2
2
.
(2.51)
z
Q
) 1 e 2 sin E
(2.53)
y a PPzy cos E e G ( m
Q0 zy m
z
Q
Pz
z
және жылдамдық компоненттері
және жылдамдық компоненттері
P
x
Qx
na 2 x
2
P
sin
E
Q
1
e
cos
E
(2.54)
y x
P
Q
.
y
y
x
x
2
r
z na P
Q
y
P
sin
E
(2.54)
Qzy 1 e 2 cos E .
zy
r
P
Q кезіндегі жылдамдықтың
Энергия сақталу заңынан
қозғалыс
эллипстік
z
z
z
8.
Pxx
Q
na 22 Pxx
Qxx
na P sin E Q
yy
r
Pyy sin E Qyy
z
Q
r P
z
Qzz
Pzz
Энергия
Энергия сақталу
сақталу заңынан
заңынан эллипстік
эллипстік қозғалыс
қозғалыс
модулі
модулі
22 11
2
2
V
V r
a
r a
немесе
немесе
1 e cos E
2
2 1 e cos E .
V
V a 1 e cos E .
a 1 e cos E
2
11
(2.54)
ee 2 cos
cos E
E ..
(2.54)
кезіндегі
жылдамдықтың
кезіндегі жылдамдықтың
(2.55)
(2.55)
(2.56)
(2.56)
Эллипстік қозғалыс кезінде кейбір параметрлерді басқаларымен
Эллипстікперицентрлік
қозғалыс арақашықтықты
кезінде кейбір –параметрлерді
ауыстырады:
перицентрдің басқаларымен
бойлығымен
ауыстырады: перицентрлік арақашықтықты – перицентрдің бойлығымен
ауыстырады
ауыстырады
(2.57)
,
(2.57)
,
- перицентр арқылу өту моментін – t 0 - бастапқы дәуірдегі M 0 - орташа
өту моментін – t 0 - бастапқы дәуірдегі M 0 - орташа
- перицентрMарқылу
аномалиямен;
0 – бастапқы дәуірдегі орташа бойлығымен
аномалиямен; M 0 – бастапқы дәуірдегі орташа бойлығымен
M0 M0.
(2.58)
M0 M0.
(2.58)
Сонда эллипстік қозғалыс кезіндегі эллипстік кеплер эллементтері , , iСонда
, e, a, . эллипстік қозғалыс кезіндегі эллипстік кеплер эллементтері , , i, e, a, .
9.
Сонда эллипстік қозғалыс кезіндегі эллипстік кеплер эллементтері , , i, e, a, .- эллиптические кеплеровские элементы10.
11.
Егер бірінші интегралдардың тұрақтылары c 0, , h 0, p 0, e 1байқалады.
теңдеулерде
осындай
өзгерістер
Эллипстік
және Сондықтан
гиперболалық
қозғалыстардың
бір бірінен
айырмашылығы
мәндергеекенін
ие болса
гиперболалық
қозғалысэллипстік
болады.
еңгіземіз:
көп болса
да,гиперболалық
олардың қозғалысын
сипаттайтын
теңдеулердің
құрылымы ұқсас
Эллипстік
және
қозғалыстардың
бір бірінен
айырмашылығы
,
sin Eсипаттайтын
shHэллипстік
, cos Eтеңдеулердің
chH
, tgE
thHосындай
екенін
байқалады.
Сондықтан
теңдеулерде
өзгерістер
көп болса
да, олардың
қозғалысын
құрылымы
ұқсас
еңгіземіз: Сондықтан эллипстік теңдеулерде осындай өзгерістер
ыларыекенін
c 0, байқалады.
, h 0, p 0, e 1
, өзгереді. Сонда,
E shH ,шама,
cos E
chH
, tgE
осында
айнымалы
-ден
дейін
thH
H - өлшемі жоқsin
еңгіземіз:
болады.
шын аномалиямен
sin E H
шаманың
shH , cos Eбайланысы
chH , tgE thH ,
стардың бір бірінен айырмашылығы
осында H - өлшемі жоқ айнымалы шама, -ден дейін өзгереді. Сонда,
йтын теңдеулердің құрылымы
ұқсас
шын
аномалиямен
H шаманың
e 1 H
осында H осындай
- өлшемі жоқ
айнымалы
шама,байланысы
өзгереді. Сонда, (2.59)
теңдеулерде
өзгерістер
tg -ден th дейін
.
e 1 2
шын аномалиямен H шаманың байланысы
e 1 H
chH , tgE thH ,
tg
th .
(2.59)
e
1
2
e Кеплер
1 H теңдеуінің аналогы
Гиперболалық қозғалыс үшін
tg
th .
(2.59)
-ден дейін өзгереді. Сонда,
e 1 2
Орбиталдық координаттар
(ae Кеплер
– гиперболаның
осінің нақты мәні)
Гиперболалық
қозғалыс үшін
теңдеуінің
H
n(t жарты
).аналогы
(2.60)
Орбиталдық координаттар
(a –chH
гиперболаның
жарты
осінің нақты мәні)
Гиперболалық қозғалыс үшін Кеплер теңдеуінің аналогы
a(e HchH
1 H
e chH
n),
(2.60)
a
(
e
chH
),(t ).
th .
(2.59)
1 2
an(te 22 ).1 shH ,
e chH H
(2.60) (2.61)
a e 1 shH ,
(2.61)
r a(e chH 1).
r a(e chH 1).
еңдеуінің аналогы
Қозғалыс жылдамдығы
Қозғалыс жылдамдығы
n(t ).
(2.60)
2 1 e chH 1
V 22 2 1 e chH 1.
(2.62)
V r a a e chH 1 .
(2.62)
r a a e chH 1
Егер материалдық нүкте гипербола бойымен шексізге ұмтылса, оның
Егер материалдық нүкте гипербола бойымен шексізге ұмтылса, оның
жылдамдығы
жылдамдығы
12.
ra
a e chH 1
Егер материалдық нүкте гипербола бойымен шексізге ұмтылса, оның
жылдамдығы
V
(2.63)
a
Сонда жылдамдықтың
екі дене есебінің
шешімі бойынша
гиперболалық
бұл теңдеу
гиперболалық
артығы
деп аталады.орбита бойымен
қозғалатын нүктенің координаттары
Px
x
Qx
2
y
a
P
e
chH
Q
e
1
shH
y
y
.
z
Q
Pz
z
(2.64)
13.
2.2.3 Шеңберлікқозғалыс
Аспан денесі
шеңберлік орбита бойымен қозғалса ( r p a ), бастапқы
тікбұрышты координаттары
Егер c 0, 0, h 0, p 0, e 0 болса, сол кезде екі дене есебіндегі
денесі шеңберлік
орбита қозғалыс
бойымен қозғалса
( r шеңберлік
p a ), бастапқы
рапайым Аспан
қозғалыстың
түрі - xшеңберлік
болады.
Тек
a cos cos M sin sin M cosi ,
тікбұрышты
координаттары
зғалыс үшін қозғалыстағы дененің жылдамдығының координаттары мен
(2.65)
y a sin cos M cos sin M cosi ,
мпоненттері
айқын
уақыт
функцияларымен
анықталады.
Осы
қозғалыста
Аспан денесі шеңберлік орбита бойымен қозғалса ( r p a ), бастапқы
cosM sin
cos
sin sin Mсоңдықтан
cosi ,
zx aasin
i, Mболмайды,
рицентр
және апоцентр
сипаттамалары
тікбұрышты
координаттары
рицентрлік арақашықтықтың мағынасы
болмайды.
(2.65)
y a sin
cos M cos sin M cosi ,
мен орбиталдық
тікбұрышты
координаттары
Шеңберлік
орбитада
дененің
орбитаның
жоғары
cosM sin
asin
cos
M және
sin жылдамдық
sin
M cosi , компоненттері:
zx aорналасу
i,бұрышын
олтүстік) түйіннен есептеуге болады. Сол кезде - шын аномалия бір
(2.65)
sinжағынан
y aacos
,cos M Е
cos
sin
M
cos
i, ,
ағынан u - еңдік аргументімен, екінші
- эксцентрлік
аномалиямен
M
an
sin
M
мен орбиталдық тікбұрышты координаттары және жылдамдық компоненттері:
(2.66)
z
a
sin
M
sin
i
,
әне М - орташа аномалиямен
сәйкес
келеді.
Орбитаның
векторлық
a sin M ,
an cos M ,
ементтерінің мағынасы болмайды.
an sin M ,
осында
төрт
a cosэлементтерімен
M,
Шеңберлік
қозғалыс
орбитаның
мен орбиталдық тікбұрышты координаттары және анықталады:
жылдамдық компоненттері:
(2.66)
ansin
cosnM
r - орбитаның радиусы,
M
(t M
), n(t t0 ) Man
(2.67)
,
3
0,
Ω осында
- бұрыштың бойлығы,
a cos M ,
an sin M , a 2
(2.66)
i - орбита еңкеюі,
ansin
Man
M
(tтүйін
M
), арқылы
n(t t0 )
, cosn M
, (немесе
3
0мерзімі
t 0 - (2.67)
нүктеніңбұрыштық
жоғары
өту
n- -материалдық
қозғалыстың тұрақты
жылдамдық.
осында
a2
(2.67) формула
стапқы дәуіріндегі
М0 - арқылы
орташа шеңберлік
аномалия).қозғалыс үшін Кеплердің үшінші заңын
және қозғалыстың сызықты жылдамдығын
анықтауға
болады
M
n
(
t
)
n
(
t
t
)
M
,
(2.67)
n
3
0
0
n - қозғалыстың тұрақты бұрыштық жылдамдық.
2
(2.67) формула арқылы шеңберлік қозғалыс үшін Кеплердіңaүшінші заңын
2 3 2 анықтауға
болады
және қозғалыстың сызықты жылдамдығын
(2.68)
T
r , V
жылдамдық. r
n - қозғалыстың тұрақты бұрыштық
(2.67) формула арқылы шеңберлік қозғалыс үшін Кеплердің үшінші заңын
2 3 2
14.
2.2.4 Параболалық қозғалысЕгер бірінші интегралдардың тұрақтылары c 0, , h 0, p 0, e 1
Егер ие
бірінші
тұрақтылары
мәндерге
болса интегралдардың
параболалық
қозғалыс
болады. cc 00,, ,, hh 00,,pp 00,,ee 11
Егер бірінші
интегралдардың
тұрақтылары
Қозғалыс
заңы
мәндерге
ие болса
параболалық қозғалыс болады.
мәндерге ие болса параболалық қозғалыс болады.
Қозғалыс
заңы
ылары Қозғалыс
c 0,
, h 0, p 0, e 1
заңы
d
лады.
(2.69)
t .
2 p 3 2
0 1 dcos
d 2 3 t .
(2.69)
0 1 cos
(2.69)
t
.
2
2 p 32
Егер
1
cos
0
p
Егер
(2.69)
2
t .
Егер
3
1
tg
2
p
(2.70)
cos 1 tg 22 2 ,
1 tg 22v
(2.70)
cos 1 tg 2,
2
,
(2.70)
cos
v
2
2
v
1
tg
2
2,
1 tg 2
(2.70)
болса
v
2
2
болса
2
болса
2
(2.71)
sec2 dv 3 t .
1 tg
2
2 2
2 2
0
p3 t .
(2.71)
11 tg
2 sec 2 dv
(2.71)
tg
sec
dv
t
.
2
2
2
3
0
p
2
2
2
2
(2.71) 0
ec dv 3 t .
p
2
2
p - орбита
p параметрінің орнына 2q ( q – параболаның төбесінен фокусқа дейін
- орбита параметрінің
орнына 2qүшін
( q – параболаның төбесінен
фокусқа дейін
pарақашықтық
немесе парабола
арақашықтық)
және
орбита
параметрінің
орнына
параболаның
төбесінен
фокусқа
дейін
p
2q ( q – перицентрлік
раболаның
фокусқа
дейін үшін перицентрлік арақашықтық)
төбесінен
арақашықтық
немесе
парабола
және
tg
теңдеуге
енгізгенде,
интегралдын
шешімі – Баркер
теңдеуі
арақашықтық
немесе
парабола
үшін
перицентрлік
арақашықтық)
және
2
ицентрлік
және
tg 2 арақашықтық)
теңдеуге енгізгенде,
интегралдын шешімі – Баркер теңдеуі
tg – 2Баркер
теңдеуге
енгізгенде, интегралдын шешімі – Баркер теңдеуі
шешімі
теңдеуі
(2.72)
3 3 3n(t ) 0 ,
Уравнение Баркера
3
(2.72)
3 3n(t ) 0 ,
(2.72) 3 3 3n(t ) 0 ,
t осында
) 0 ,
(2.72)
осында
3
2
осында
(2.73)
n
q 3 .
3 2
(2.73)
n 2q 322.
(2.73)
q .
15.
r q 112 tgtg22 ,
2
және егер
sin r q 1 2 2 ,,
болса, және
орбиталды
2
егер координаттар:
1 2tg
r cos tg
q 12 2 2 ,
2tg ,
(2.74)
болса, орбиталды координаттар: sin
2. ,
2
r sin
sin 1 2tgq
r cos 1q 1tg 22 2 ,
(2.74)
2
болса,
орбиталды
координаттар:
және бастапқы
тікбұрышты
координат
жүйесінің
координаттары
r sin 2q .
болса, орбиталды координаттар:
2
r cos
q
1
r cos q 1 2 ,,
(2.74)
(2.74)
Q
x P
және бастапқы тікбұрышты координат
жүйесінің
координаттары
r
sin
2
q
.
x
x
r sin 2q .
2
(2.75)
y q Py 1 2 Qy .
және бастапқы
тікбұрышты
жүйесініңкоординаттары
Q
PPx жүйесінің
және бастапқы
тікбұрышты
xzкоординат
координат
координаттары
x
Q
z
z
2
(2.75)
y xq P y P 1 2 QQy .
Qxx модулі
x
zxкезіндегі
PP x жылдамдықтың
Q
Параболалық қозғалыс
2
y q z Py 1 2 2 Qz y .
(2.75)
(2.75)
y q P y 1 2 Qy .
Qz
z z 2 P 2 P z
Q
z .
V жылдамдықтың
zмодулі
Параболалық қозғалыс кезіндегі
(2.76)
r
Параболалық қозғалыс кезіндегі жылдамдықтың модулі
Параболалық қозғалыс кезіндегі
модулі
2жылдамдықтың
V 2 2. параболалық қозғалыс болу мүмкін
(2.76)
Табиғатта ұйытқулар болғандықтан,
2
r
V
. қозғалыс кезінде эксцентриситетің
(2.76)
емес. Бірақ эллипстік және гиперболалық
r
2
V2
.
(2.76)
мәні 1-ге жақындаса осы қозғалысты
қарастырады.
Мысалы кометалардың
Табиғатта
ұйытқулар
болғандықтан,
параболалық
қозғалыс
болу
мүмкін
r
қозғалысы.Табиғатта ұйытқулар болғандықтан,
параболалық қозғалыс болу мүмкін
емес. Бірақ
эллипстік
және
гиперболалық
қозғалыс
эксцентриситетің
емес. Бірақ эллипстік және гиперболалық қозғалыс кезінде
кезінде эксцентриситетің
Табиғатта
болғандықтан,
параболалық
қозғалыс
болу мүмкін
мәні 1-ге
осы осы
қозғалысты
қарастырады.
Мысалы
кометалардың
мәніжақындаса
1-ге ұйытқулар
жақындаса
қозғалысты
қарастырады.
Мысалы
кометалардың
емес. Бірақ
эллипстік және гиперболалық қозғалыс кезінде эксцентриситетің
қозғалысы.
қозғалысы.
мәні 1-ге жақындаса осы қозғалысты қарастырады. Мысалы кометалардың
Орбита тендеуіне енгізгенде
16.
(2.77)ерге ие болса түзусызықты қозғалыс
болады.
rx0
r y 0 , z .
0
0
0
Орбитаның
сызығы
координат басы нүктесінен өтеді, өйткені r r .
және
скалярлық
теңдеулер
онда
r
ттау векторы ретінде бастапқы вектор
x
y
z
0 алынады.
(2.77)
V2
r 2 .
Осы жағдайда
лары
c 0, векторлық
, h 0, p теңдеу
0, e 1 x 0 y0 z0
r0 r 0 ,
олады.
Сонда
әне
энергия интегралын табу
арқылы
осы траекторияның қозғалыс заңын
2
скалярлық
теңдеулер
нүктесінен
өтеді,
өйткені r r . V r 2
ықтауға
болады.
x
y жолымен
z
алынады.
Интегралдың шешімін қарапайым
анықтау үшін берілген
(2.77)
.
және
энергия
интегралын
табу
арқылы
осы
траекторияның
қозғалыс
заңын
x0 y0 z0
амаларды басқа шамаларымен ауыстырамыз
болады.
0нықтауға
,
да
Интегралдың шешімін қарапайым
жолымен анықтау үшін берілген
2
2
V
r
h dt
dt rd ,
(2.78)
шамаларды
басқа шамаларымен ауыстырамыз
z
a
(2.77)
.
z
ында
0
энергия
интегралын табу арқылы осы траекторияның қозғалыс заңын
dt rd ,
h
dt
(2.78)
тауға болады.
a
,a
h
Интегралдың
шешімін
қарапайым
жолымен
анықтау үшін берілген
осында
аларды басқа шамаларымен ауыстырамыз
,
ы
траекторияның
қозғалыс
заңын
a Сонда
- жаңа
өлшемі жоқ
айнымалы
шама.
h
олымен анықтау үшін берілгенh dt dt rd ,
(2.78)
a
dr
з - жаңа өлшемі жоқ айнымалы шама.
Сонда
.
(2.79)
2
нда
2ar sign(h) r
,
a
dr
dt rd ,
(2.78) h
(2.79)
a
2ar sign(h) r 2 .
аңа өлшемі жоқ айнымалы шама. Сонда
17.
0a
r 2,
h 0,
(2.80)
2
a (1 cos ),
h 0,
a (ch 1),
h 0.
a
ы анықтауға болады
r 2,
h 0,
(2.80)
2
Осы жағдайда t уақыт аргументімен осындай байланыста болады
a (ch 1),
h 0.
a (1 cos ),
h 0,
sin ,
h 0,
a 2
rОсы
жағдайда
,
h
0
,
(2.80) байланыста болады
t уақыт аргументімен
осындай
3
2
(2.81)
3 (t t 0 ), h 0,
a (ch 1),
h 0.
2
6
sina ,
h 0,
sh3
h 0.
ентімен осындай байланыста болады (t t ), h 0,
(2.81)
3
0
2
6
Егер e 1, a const болса -a эксцентрлік аномалияның және оның
sin ,
h 0,
sh мәні
болады. (2.81)-дің
h 0.
гиперболалық
аналогының
шектеулі
бірінші және үшінші
3
қатынастары
Кеплер
теңдеуінің және
оның гиперболалық аналогының
Егер
t0
), –1h, a
0
,
(2.81)
3 (t e
const болса
- эксцентрлік аномалияның және оның
6шектеулі
a 2 формалары. a - эллипстің үлкен жартылай осінің немесе гиперболаның
гиперболалық
аналогының
шектеулі мәні
бірінші
және үшінші
0 болса,
a max(r
) . Осы
нақты
шектеулі
мәні.болады.
Егер h(2.81)-дің
sh
жартылай
h осінің
0.
қатынастары
– Кеплер теңдеуінің
оның бір
гиперболалық
аналогының
теңдеулер Ньютонның
тартылыс және
өрісіндегі
материалдық
нүктенің
шектеулі формалары.
- эллипстің үлкен жартылай
осінің немесе гиперболаның
a
жәнеаномалияның
сфера-симметриялық
са қозғалысын
- эксцентрлік
және оның шаңды бұлттың эволюциясын
нақты
жартылай осінің шектеулі мәні. Егер h 0 болса, a max(r ) . Осы
сипаттайды.
теулі мәні болады. (2.81)-дің бірінші және үшінші
теңдеулер Ньютонның тартылыс өрісіндегі бір материалдық нүктенің
уінің және оның гиперболалық аналогының
қозғалысын және сфера-симметриялық шаңды бұлттың эволюциясын
стің үлкен жартылай осінің немесе гиперболаның
сипаттайды.
еулі мәні. Егер h 0 болса, a max(r ) . Осы
ылыс өрісіндегі бір материалдық нүктенің
мметриялық шаңды бұлттың эволюциясын















 Физика
Физика








