Похожие презентации:
Кривые линии. Комплексный чертеж поверхности
1.
2.
содержание лекциикривые линии
поверхности
способы задания поверхности на чертеже
классификация поверхностей
поверхности вращения
условия принадлежности точки и линии поверхности
точки на цилиндре вращения
точки на сфере
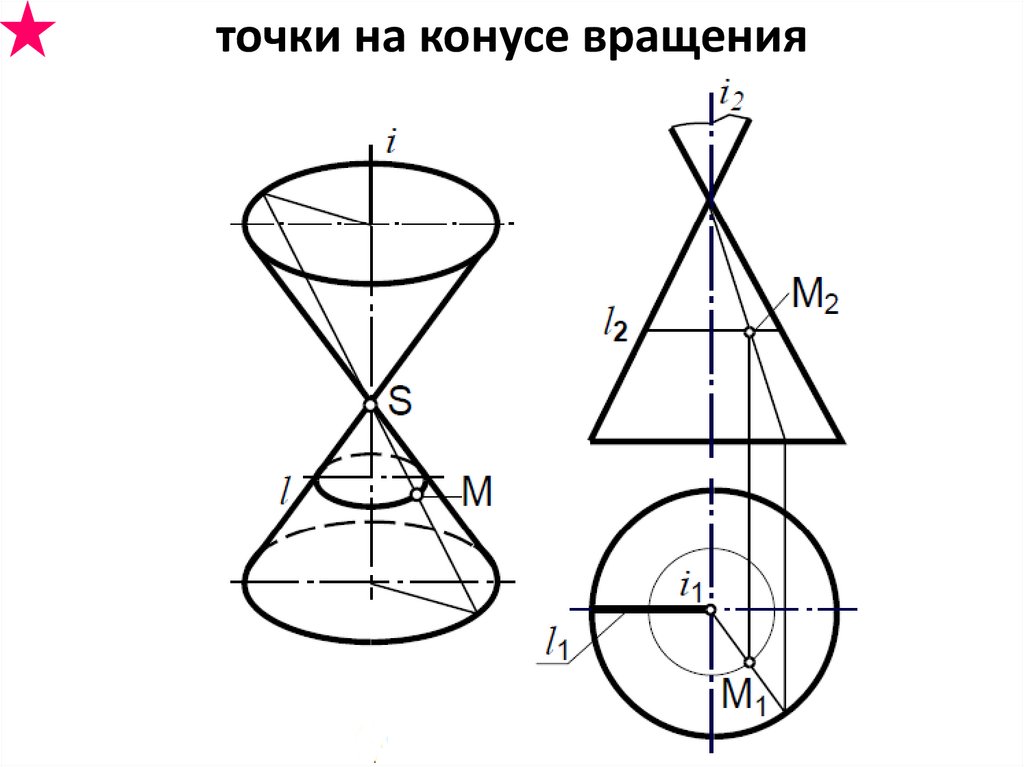
точки на конусе вращения
построение линий на поверхностях
3.
4.
кривая линиямножество точек пространства,
координаты которых – функции одной переменной
кривая линия
траектория, описанная движущейся точкой
проекция другой кривой
линия пересечения двух поверхностей
множество точек с общим для всех их свойством
5.
способы задания кривых линийаналитический
математическим уравнением
графический
визуально
табличный
координатами
последовательного ряда точек
r=aφ
6.
плоские кривые линиипарабола
гипербола
эллипс
окружность
(частный случай эллипса)
синусоида
все точки линии
принадлежат одной
плоскости
7.
пространственные кривые линиицилиндрическая
винтовая линия
коническая
винтовая линия
8.
проецирование окружностиокружность
на плоскости уровня
проецируется
в виде
окружности
на проецирующей
или
плоскости общего
положения
проецируется
в виде
эллипса
9.
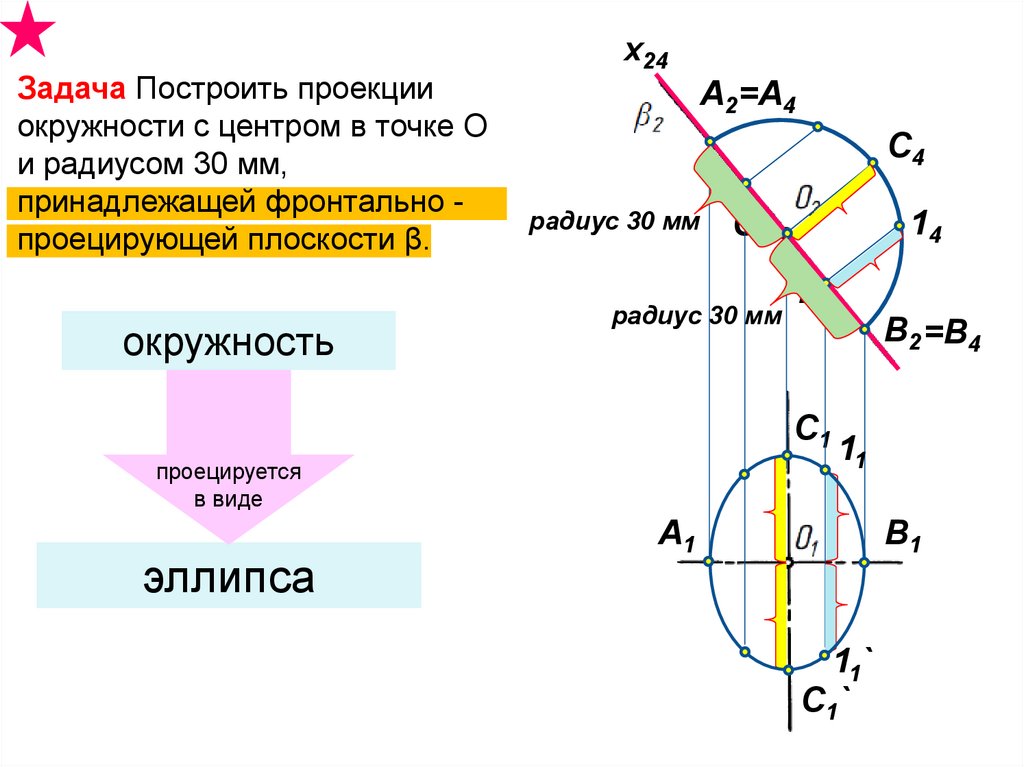
Задача Построить проекцииокружности с центром в точке О
и радиусом 30 мм,
принадлежащей фронтально проецирующей плоскости β.
окружность
x24
А2=А4
C4
радиус 30 мм
14
C2
радиус 30 мм
12
B2 =B4
C1
проецируется
в виде
эллипса
11
А1
B1
11`
C1`
10.
11.
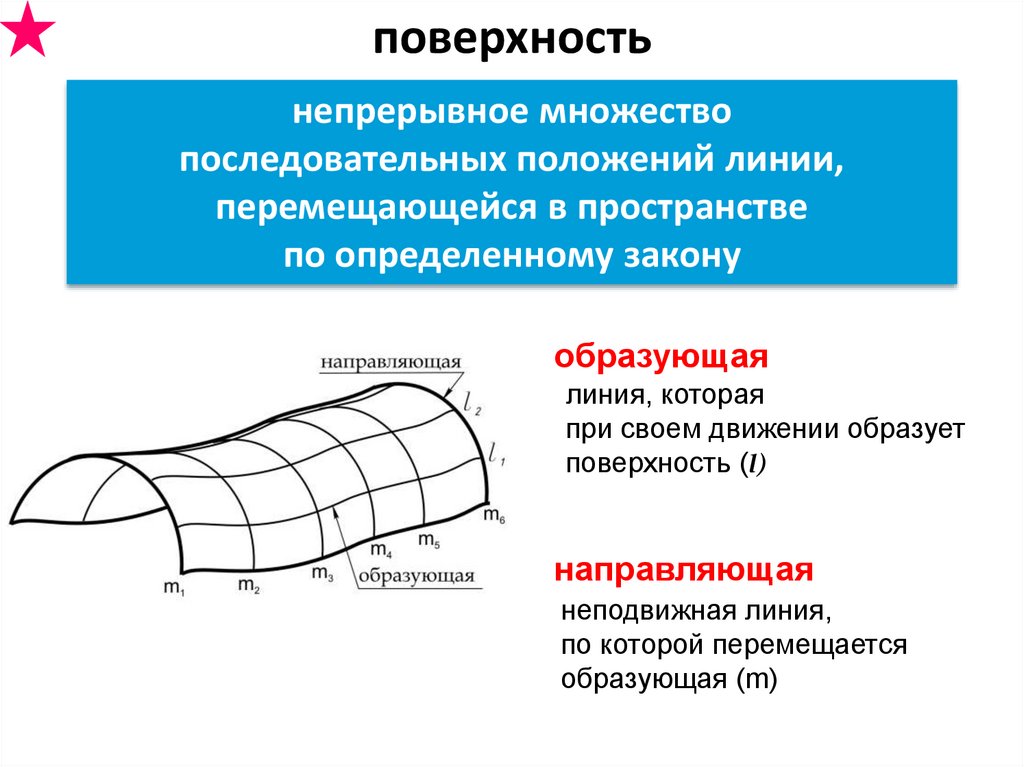
поверхностьнепрерывное множество
последовательных положений линии,
перемещающейся в пространстве
по определенному закону
образующая
линия, которая
при своем движении образует
поверхность (l)
направляющая
неподвижная линия,
по которой перемещается
образующая (m)
12.
способы задания поверхности на чертеже1. каркас
2. определитель
3. очерк
13.
способы задания поверхности на чертеже1. каркас – сеть линий, состоящая из двух семейств:
семейства образующих l1, l2, …
и семействами направляющих m1, m2…
каждая линия одного семейства пересекает все линии
второго семейства
14.
способы задания поверхности на чертеже2. определитель (∆) – совокупность геометрических
элементов и условий, необходимых и достаточных
для однозначного задания поверхности в пространстве
и на чертеже
определитель содержит две части – геометрическую и
алгоритмическую
геометрическая часть –
совокупность геометрических фигур,
с помощью которых можно образовать
поверхность.
алгоритмическая часть – алгоритм
формирования поверхности
при помощи фигур, входящих в
геометрическую часть определителя.
например, определитель
цилиндрической поверхности:
∆ (l, а); l || S; l ∩ а
15.
способы задания поверхности на чертеже3. очерк – проекция линии контура поверхности
контур поверхности – линия, точки которой являются
точками касания к поверхности проецирующих лучей
16.
способы задания поверхности на чертеже3. очерк – проекция линии контура поверхности
никакая точка
поверхности не может
спроецироваться
за пределы очерка
проекция контурной линии (очерк) = линия видимости
= линия видимого контура
поверхности
разделяет поверхность на две части –
видимую - обращенную к наблюдателю, и
невидимую
17.
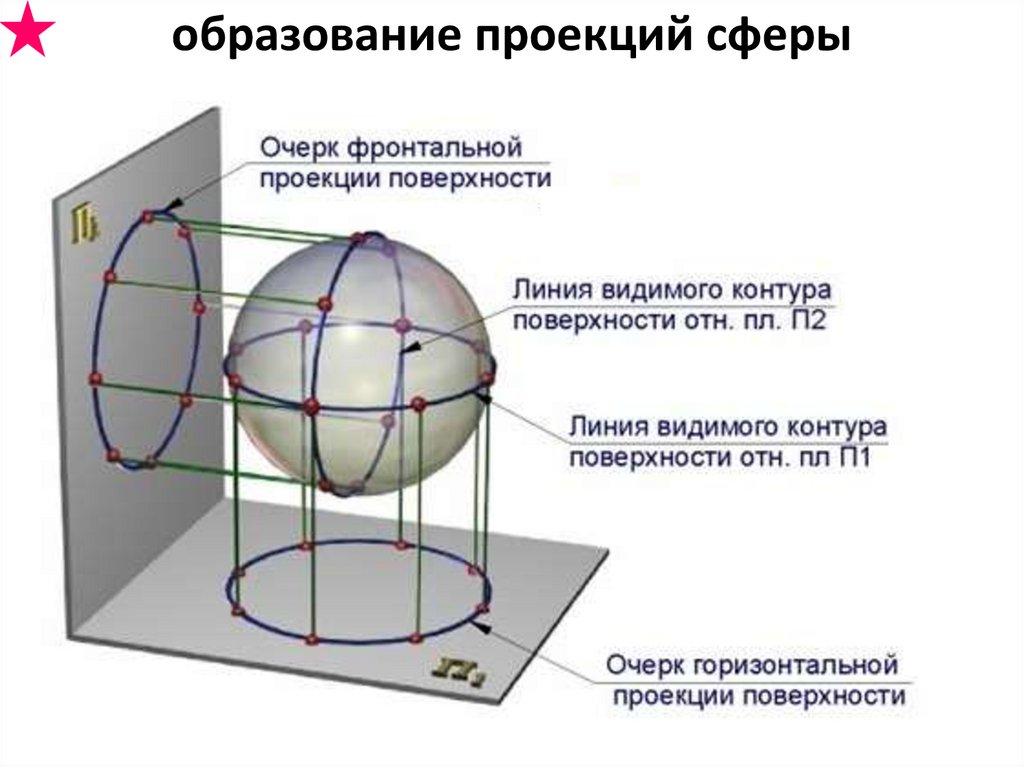
образование проекций сферы18.
классификация поверхностейпо виду образующей:
1. линейчатые поверхности – с прямолинейной образующей
2. нелинейчатые – с криволинейной образующей
по закону движения образующей: (т. е. по направляющей)
1. поверхности вращения
2. винтовые поверхности
3. поверхности с плоскостью параллелизма (поверхности
Каталана)
19.
классификация поверхностейпо виду образующей
развертываемые
неразвертываемые
линейчатые
криволинейные
цилиндр
конус
пирамида
призма
образованы движением
прямолинейной
образующей
образующая
плоская
Образующая
пространственная
сфера
эллипсоид
тор
образованы движением
криволинейной
образующей
20.
классификация поверхностейпо закону движения образующей
коноид
с плоскостью
параллелизма
цилиндроид
вращения
гиперболический
параболоид
винтовые
тор
сфера
цилиндр
конус
геликоид
21.
22.
поверхность вращенияповерхность созданная при вращении
образующей m вокруг оси
(неподвижной прямой) i
23.
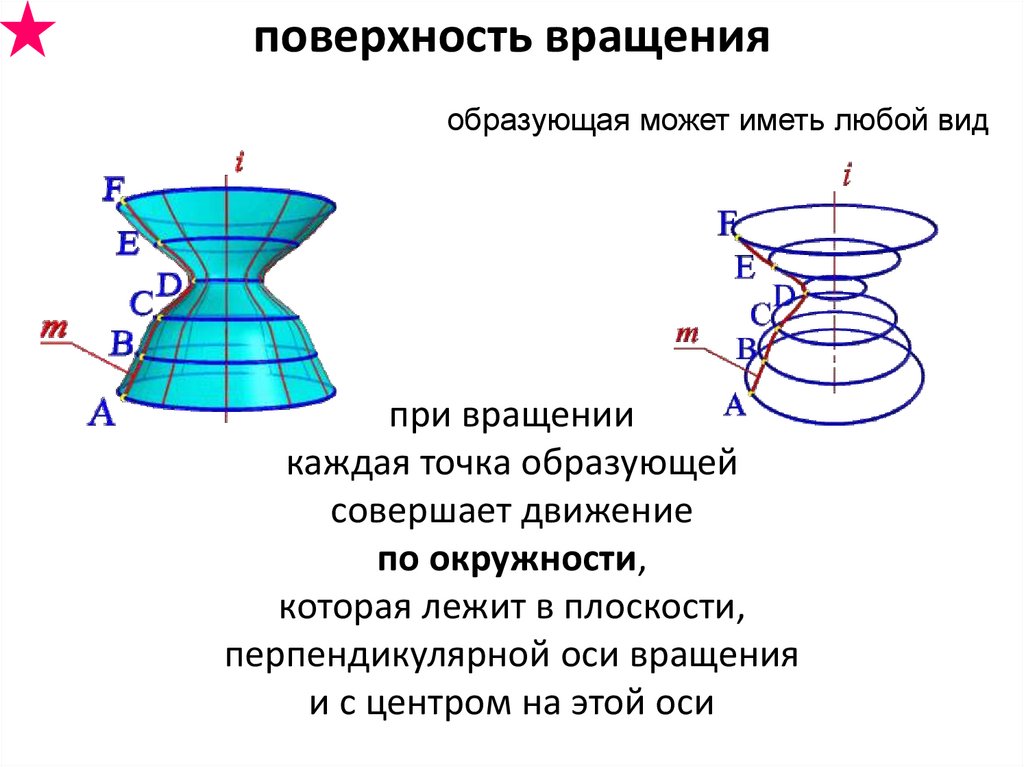
поверхность вращенияобразующая может иметь любой вид
при вращении
каждая точка образующей
совершает движение
по окружности,
которая лежит в плоскости,
перпендикулярной оси вращения
и с центром на этой оси
24.
примеры поверхностей вращениятор
сфера
однополостной
параболоид вращения
двуполостной
гиперболоид вращения
25.
поверхность вращения26.
поверхность вращениямеридиан
линия по которой плоскость,
проходящая через ось вращения,
пересекает поверхность
главный меридиан
расположен в плоскости,
параллельной плоскости проекций
и проецируется на эту плоскость
проекций очерком поверхности
27.
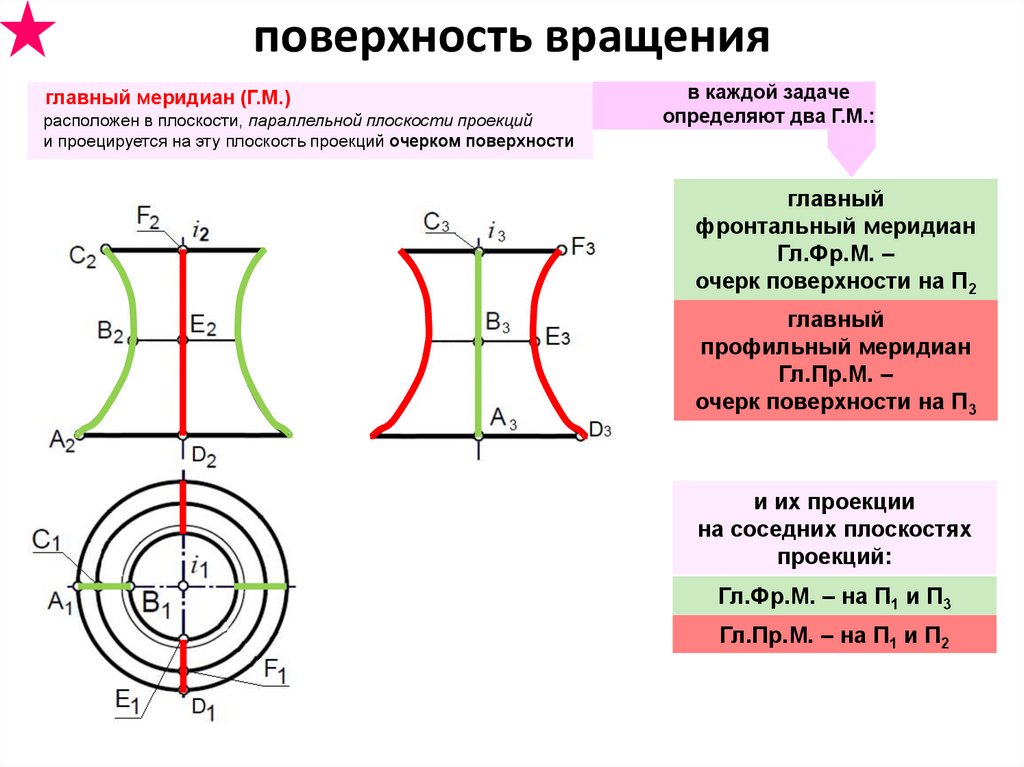
поверхность вращенияглавный меридиан (Г.М.)
расположен в плоскости, параллельной плоскости проекций
и проецируется на эту плоскость проекций очерком поверхности
в каждой задаче
определяют два Г.М.:
главный
фронтальный меридиан
Гл.Фр.М. –
очерк поверхности на П2
главный
профильный меридиан
Гл.Пр.М. –
очерк поверхности на П3
и их проекции
на соседних плоскостях
проекций:
Гл.Фр.М. – на П1 и П3
Гл.Пр.М. – на П1 и П2
28.
поверхность вращенияпараллели
окружности, по которым перемещаются все точки образующей
экватор
наибольшая параллель
горловина (горло)
наименьшая параллель
29.
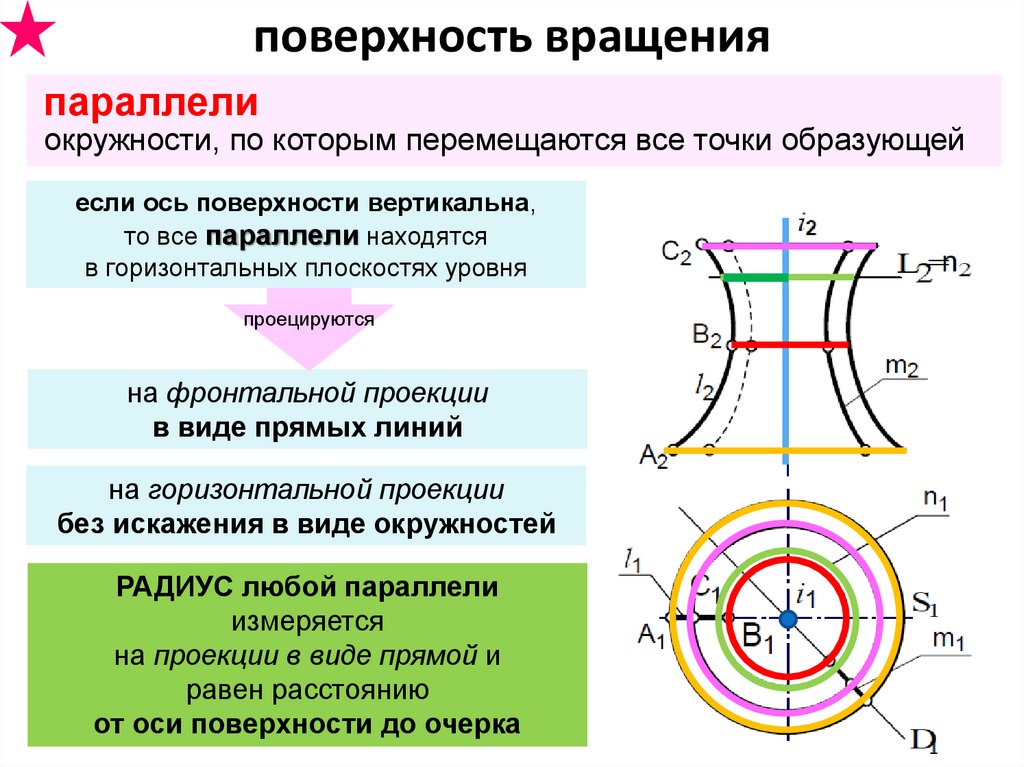
поверхность вращенияпараллели
окружности, по которым перемещаются все точки образующей
если ось поверхности вертикальна,
то все параллели находятся
в горизонтальных плоскостях уровня
проецируются
на фронтальной проекции
в виде прямых линий
на горизонтальной проекции
без искажения в виде окружностей
РАДИУС любой параллели
измеряется
на проекции в виде прямой и
равен расстоянию
от оси поверхности до очерка
30.
цилиндр вращениянаглядное
изображение
комплексный чертеж
31.
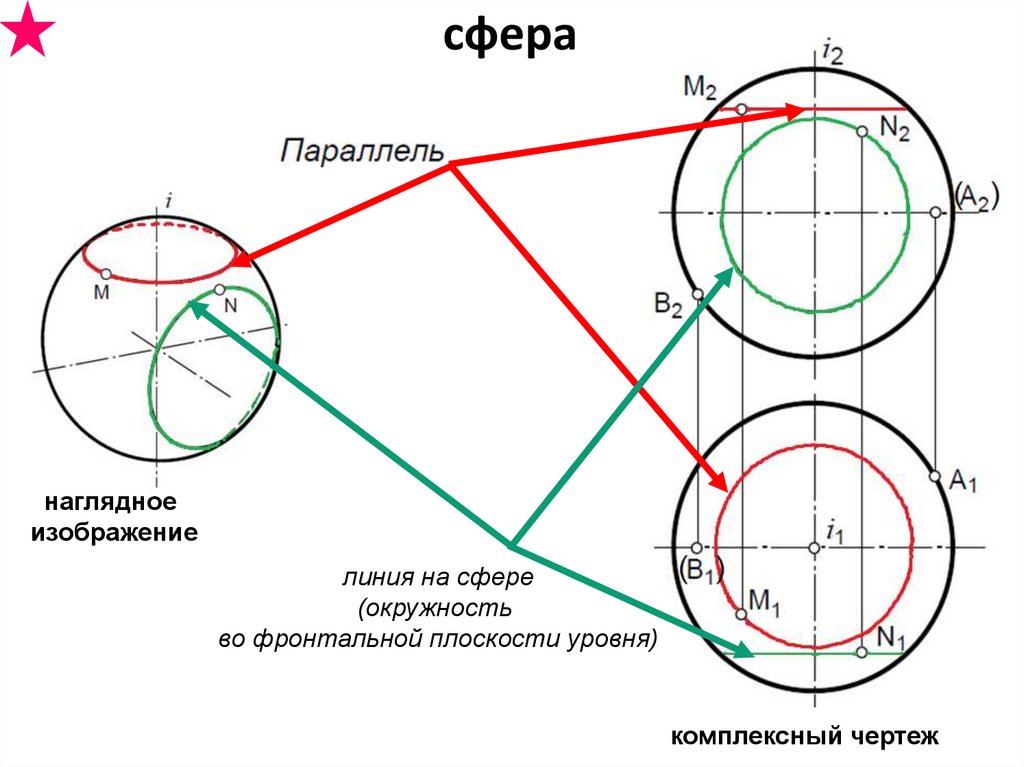
сферанаглядное
изображение
линия на сфере
(окружность
во фронтальной плоскости уровня)
комплексный чертеж
32.
конус вращения33.
поверхность вращенияв каждой задаче
определяют:
ГРАНИЦЫ ВИДИМОСТИ ТОЧЕК И ЛИНИЙ
необходимы для определения видимости и положения точек
на плоскостях проекций
граница
видимости
на п3
границы видимости на
плоскости П2 –
линии, которые проходят
по Гл.Фр.М.
отмечают на П1 и П3
граница
видимости
на п2
границы видимости на
плоскости П3 –
линии, которые проходят
по Гл.Пр.М.
отмечают на П1 и П2
со стороны знака «+» точки в видимой зоне поверхности
со стороны знака «–» точки в невидимой зоне поверхности
граница
видимости
на п2
граница видимости
на п3
стрелка показывает направление взгляда наблюдателя
НА указанную плоскость проекций
34.
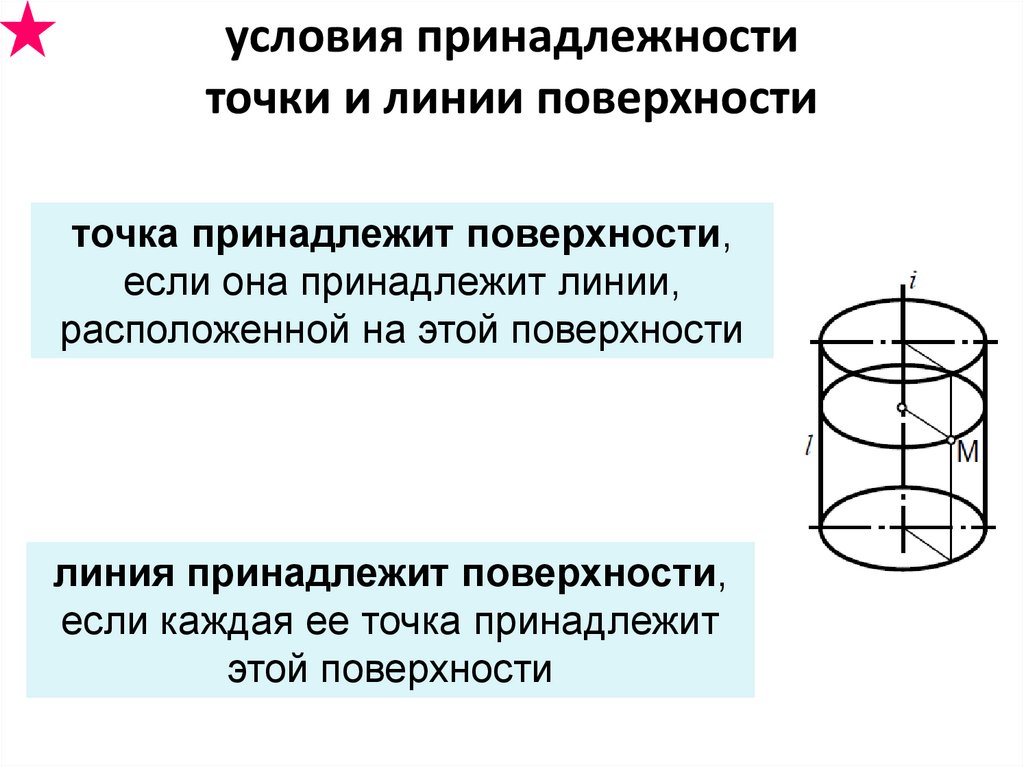
условия принадлежноститочки и линии поверхности
точка принадлежит поверхности,
если она принадлежит линии,
расположенной на этой поверхности
линия принадлежит поверхности,
если каждая ее точка принадлежит
этой поверхности
35.
точки на цилиндре вращения36.
построение точки на поверхности цилиндраглавный
профильный
меридиан
граница видимости на п3
i2
i3
главный
фронтальный
меридиан
M2
yM
M3)
(M
граница
видимости
на п2
i1
граница
видимости
на п2
yM
M1
на п3 отложить координату
точки
М
(циркулем)
главные
меридианы
т.Y на
М
не
видна
на
п3
провести
линию
связи
п
отмерить
1
вправоточки
от оси
т.к. «-»
провести
линию
связи
(проекции
М в–зоне
вниз
на
п
до
координату
Y
точки
1 п
границ
видимости
т.вправо
М видна
на
на
п3 2 М
(указанное
расстояние
пересечения
сточки)
очерком
границы
в пвысоте
и пвидимости
п3)
(зона
«+»
видимости
1границ
2 - на
(по
(в в
виде
окружности)
пциркулем)
3 и п1 - на п2)
37.
точки на сфере(
(
)
)
38.
построение точки на поверхности сферыграница видимости на п3
главный
фронтальный
меридиан
на п1
главный
профильный
меридиан
провести через точку
линию // горизонтальной
оси сферы – параллель
(// П1)
1
на п1
(N3)
N2
10
8
2
измерить циркулем
радиус параллели = R
9
YN 4
3
вычертить параллель
радиусом = R
Экватор
граница
видимости
на п2
YN
граница
видимости
на п2
построение проекций
Главные
меридианы
Границы
видимости
точки
N1
6
5
7
39.
точки на конусе вращения40.
построение точки на поверхности конусачерез образующую
S2 i2
через параллель
S2 i2
m2
А2
ℓ2
(B2)
R
B1
i1
i1
S1
ℓ1
S1
А1
m1
41.
алгоритм построения линий на поверхностях1
построить опорные точки
экстремальные точки –
высшая и низшая,
крайняя левая и крайняя правая,
самая далекая и самая ближняя точки кривой
граничные точки видимости кривой,
лежат на очерках поверхности
отделяют видимую часть поверхности от ее невидимой части
2
дополнительные точки
промежуточные точки между опорными
3
соединить найденные точки
4
определить видимость линии
































 Математика
Математика Инженерная графика
Инженерная графика








