Похожие презентации:
Модель поверхности
1. МОДЕЛЬ ПОВЕРХНОСТИ
2. Очерк - Проекция линии касания проецирующей поверхности, которая ограничивает ее изображение .
• Модель поверхности –• Две проекции вершин и ребер
(многогранники)
• Проекции двух очерков (все
остальные поверхности )
3.
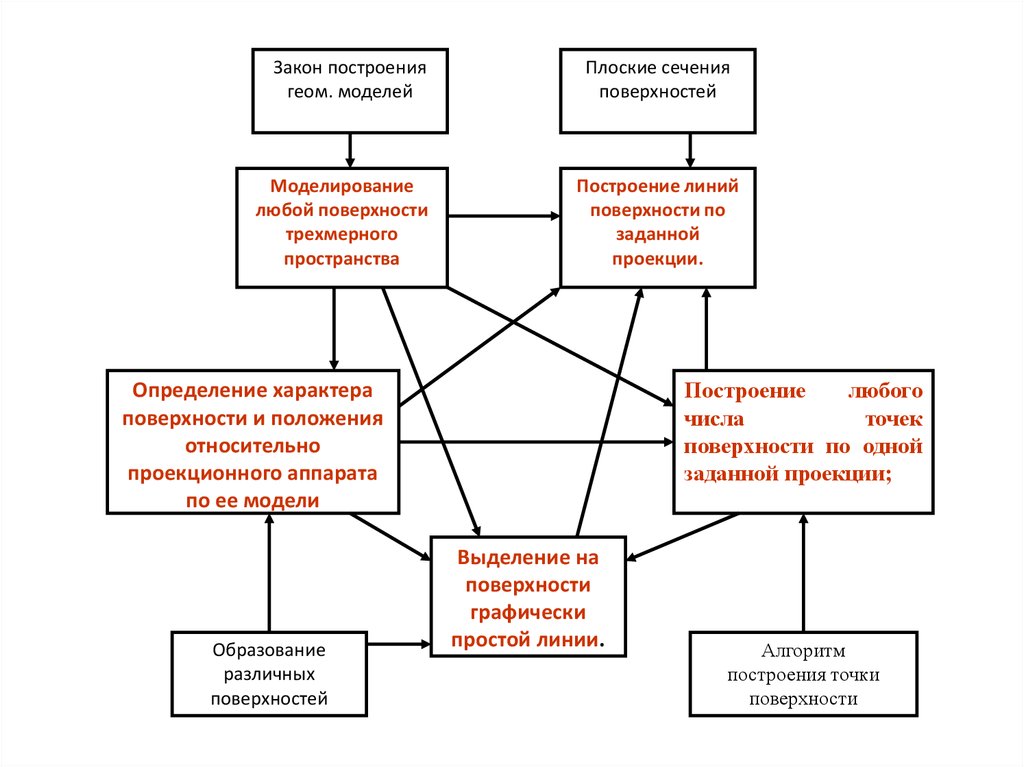
Закон построениягеом. моделей
Моделирование
любой поверхности
трехмерного
пространства
Плоские сечения
поверхностей
Построение линий
поверхности по
заданной
проекции.
Построение
любого
числа
точек
поверхности по одной
заданной проекции;
Определение характера
поверхности и положения
относительно
проекционного аппарата
по ее модели
Образование
различных
поверхностей
Выделение на
поверхности
графически
простой линии.
Алгоритм
построения точки
поверхности
4. Работа с их моделями складывается из решения следующих задач
• 1)моделирование любой поверхности трехмерного
пространства с помощью метода двух изображений;
2) определение характера поверхности и положения
относительно проекционного аппарата по ее модели;
3)
выделение на поверхности графически простых
линий (прямых, окружностей);
4)
построение любого числа точек поверхности по
одной заданной проекции;
5)
построение линий поверхности по заданной
проекции.
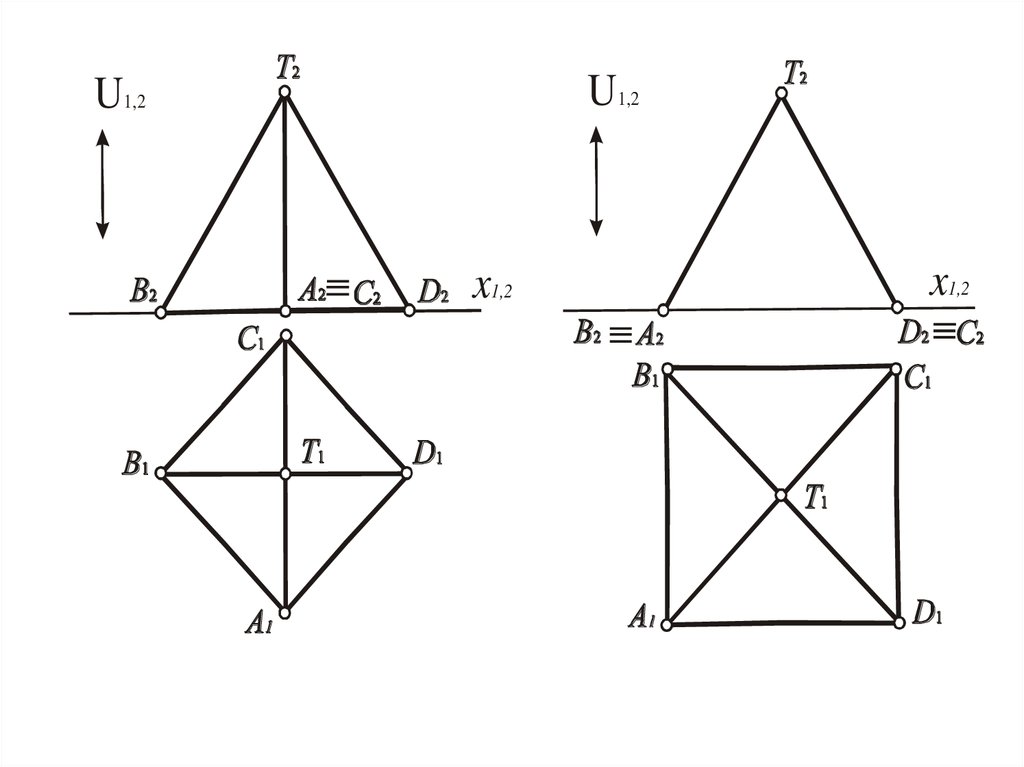
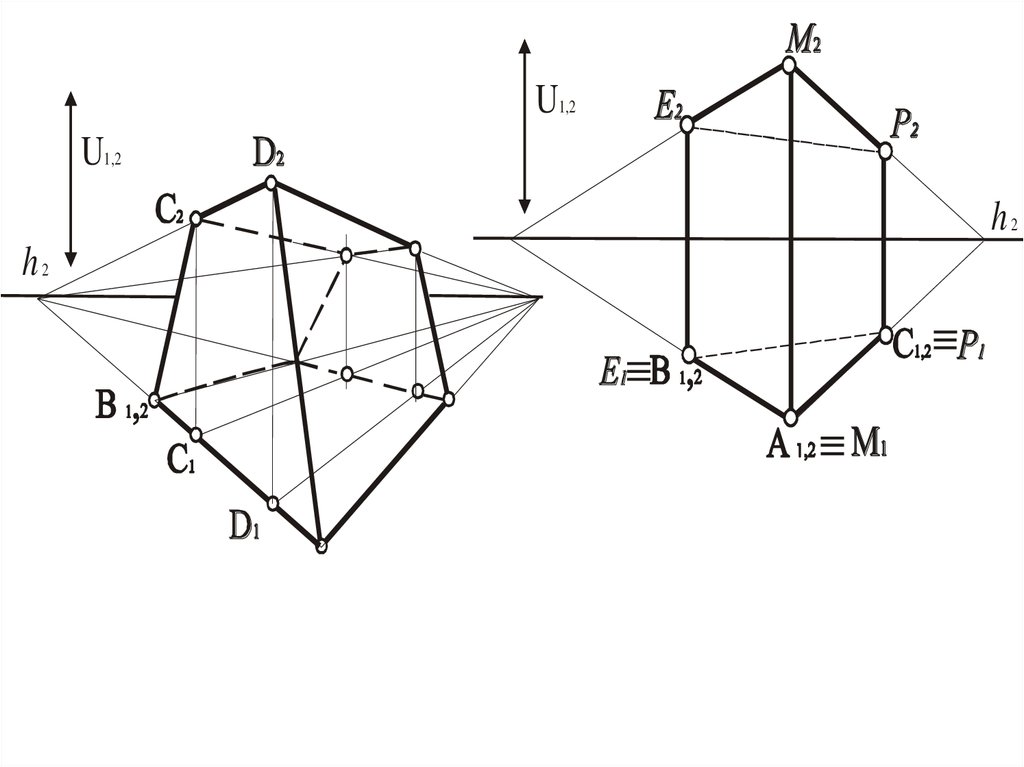
5. Классификация
• 1. Поверхности частного положенияих
вершины
тождественно
совпадают с одним из центров
проецирования.
• 2. Поверхности общего положения –
все остальные.
6. Задачи
Дана поверхность в трехмерномпространстве. Построить ее модель.
• 2. Дана модель поверхности.
Определит характера поверхности и
ее положение относительно
проекционного аппарата.
• 1.
7.
8.
rU 1,2
r
f1
9.
rf
r
f
10.
rr
11.
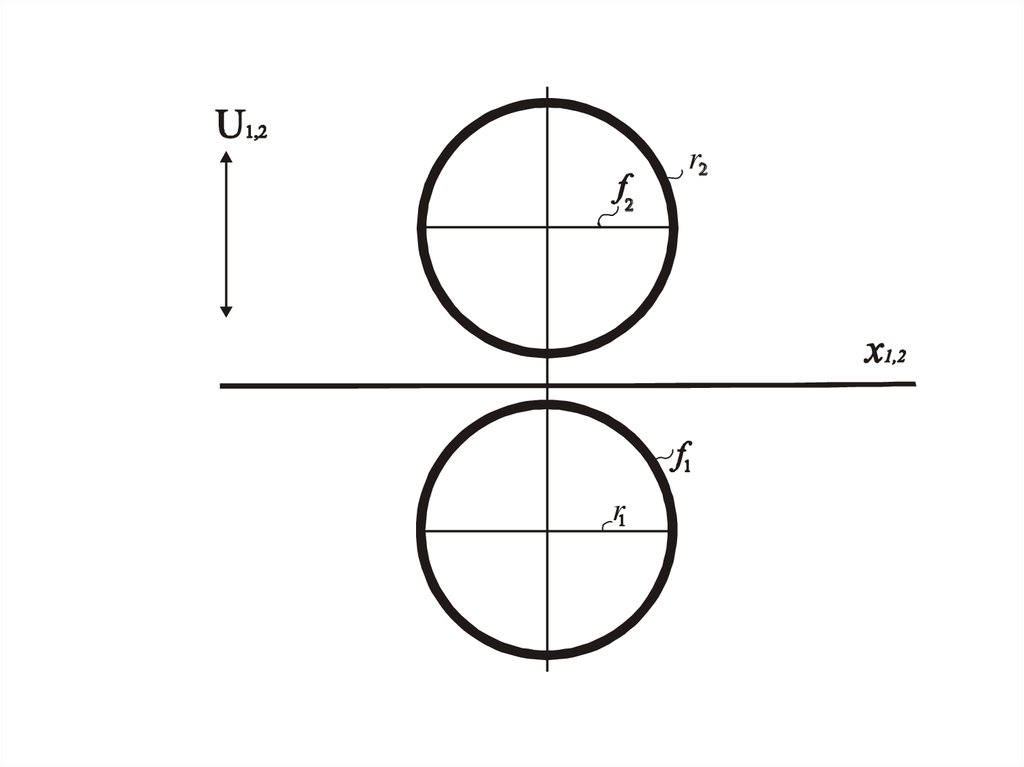
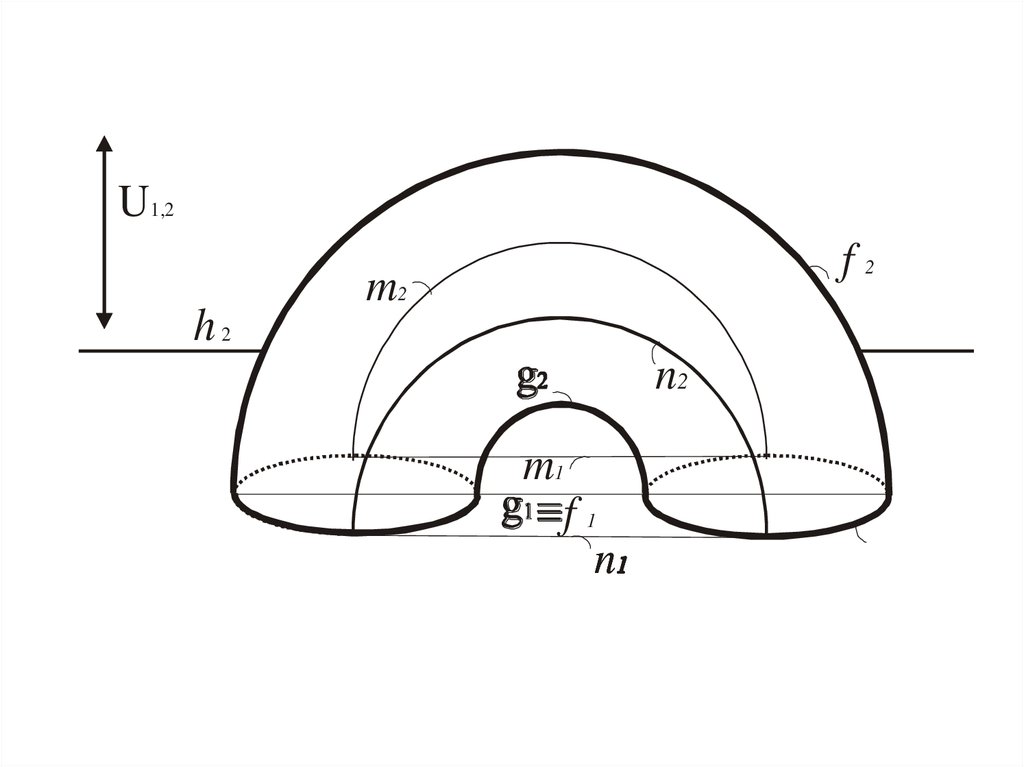
U1,2h2
f2
m2
n2
m1
f1
n
12.
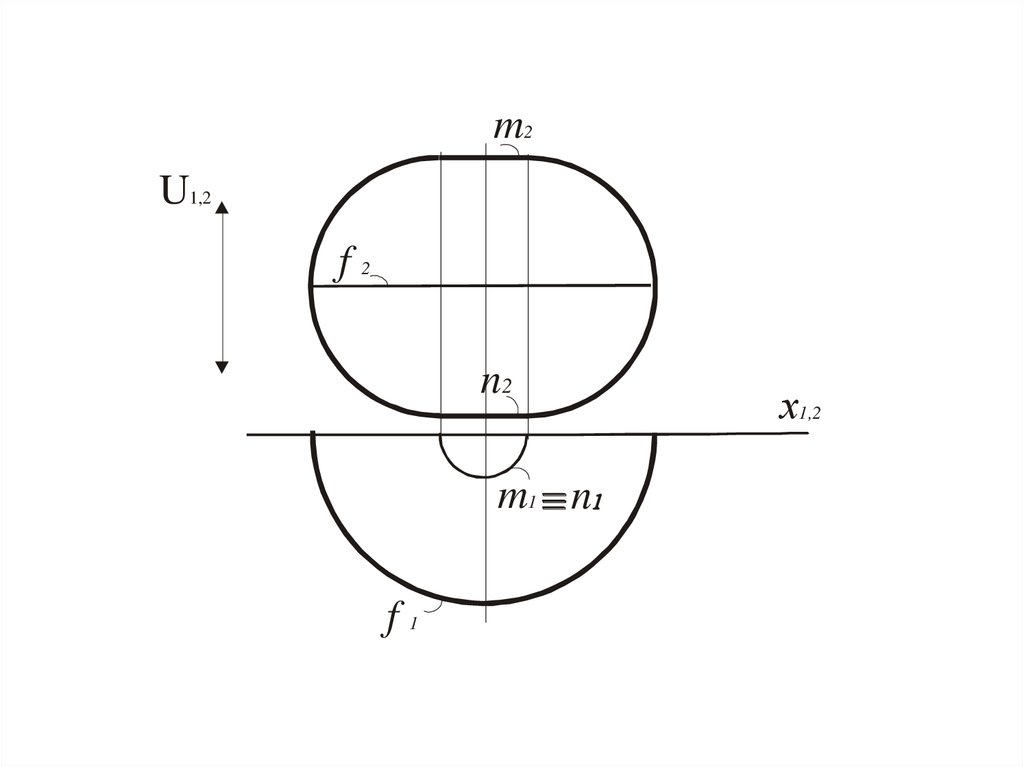
m2U1,2
f2
n2
m1 n
f1
х1,2
13.
nn
m1
m1
n
n
14.
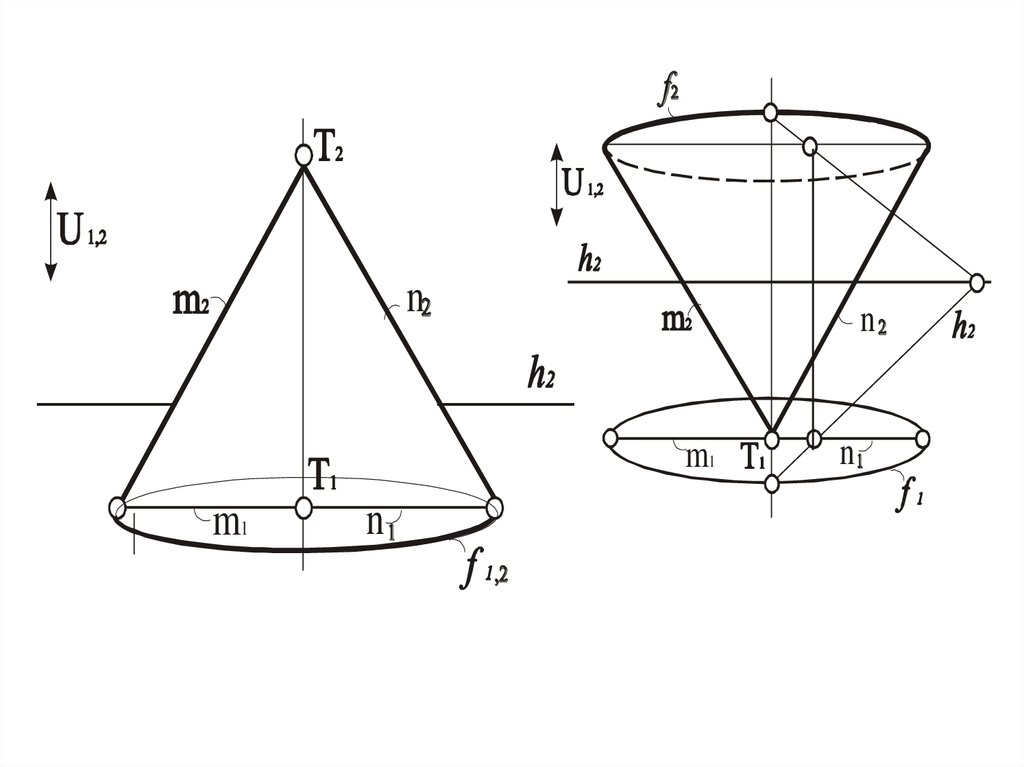
fT
T
n
n
n
U1,2
U1,2
U1,2
T
f
m1
f
T
T
T
m1
n
f
n
m1
f
n
f
15.
U1,2m2
h2
U1,2
n2
n2
h2
m2
16.
U1,2U1,2
m2
n2
х1,2
х1,2
m1
17.
U1,2h2
U1,2
h2
B1
B1
18.
U1,2U1,2
x1,2
x1,2
19.
U1,2U1,2
h2
h2
20.
21.
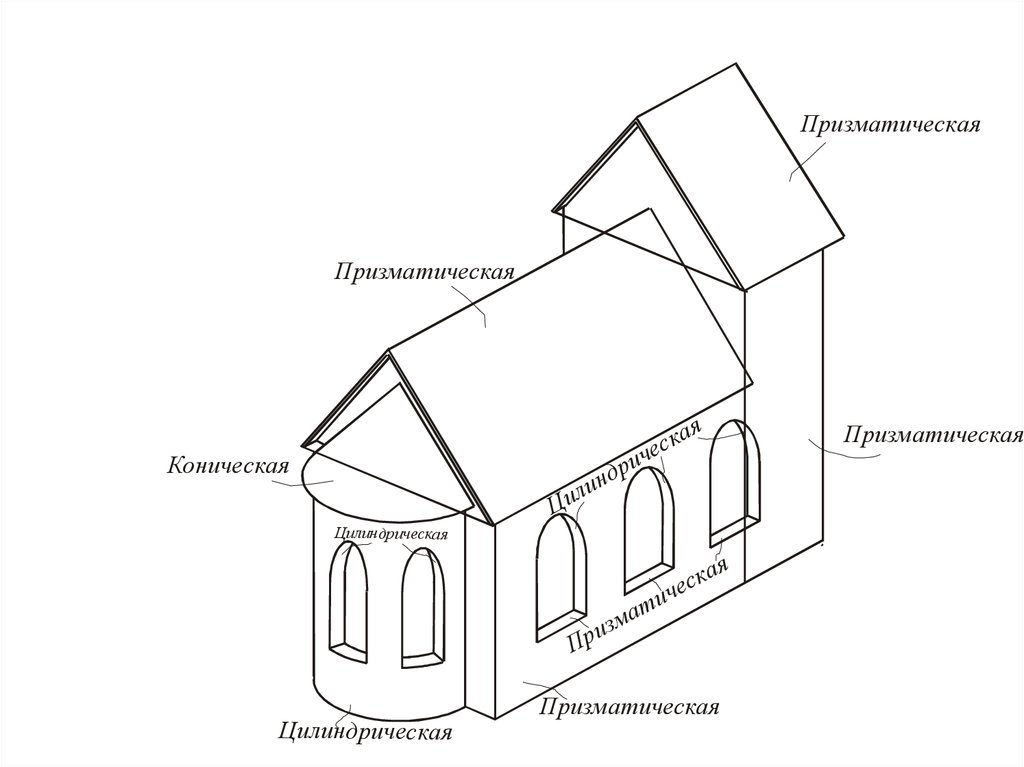
ПризматическаяПризматическая
Коническая
Ц
нд
и
л
и
ая
к
с
е
ри ч
Цилиндрическая
ат
м
з
и
Пр
Цилиндрическая
ая
к
с
иче
Призматическая
Призматическая
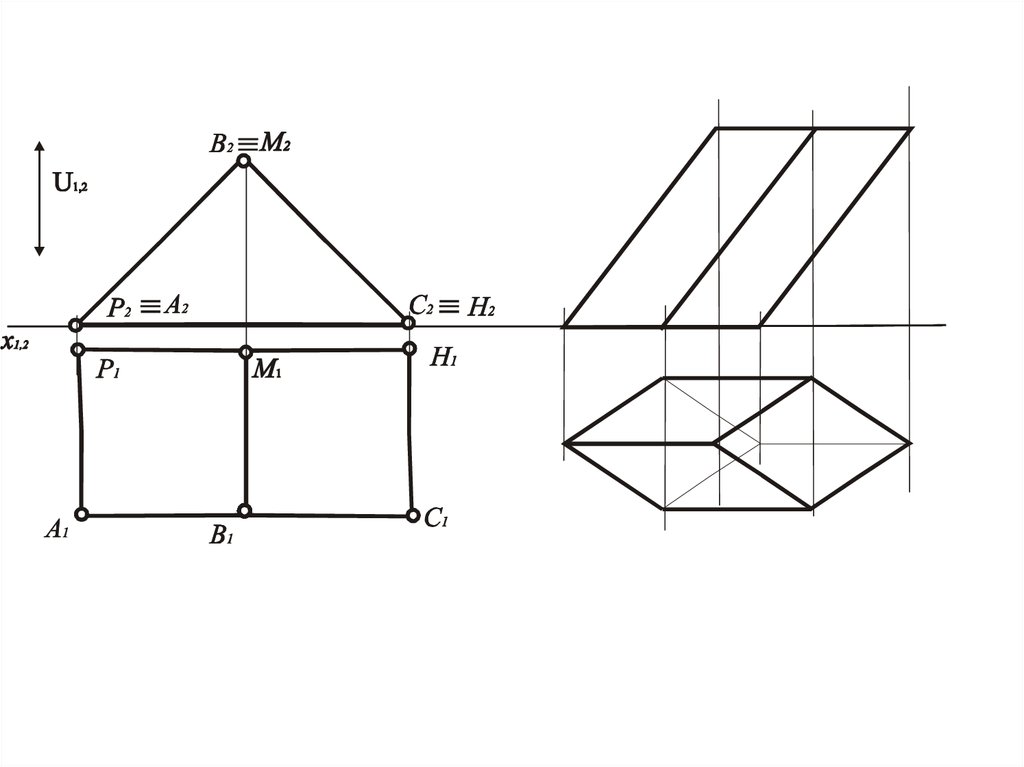
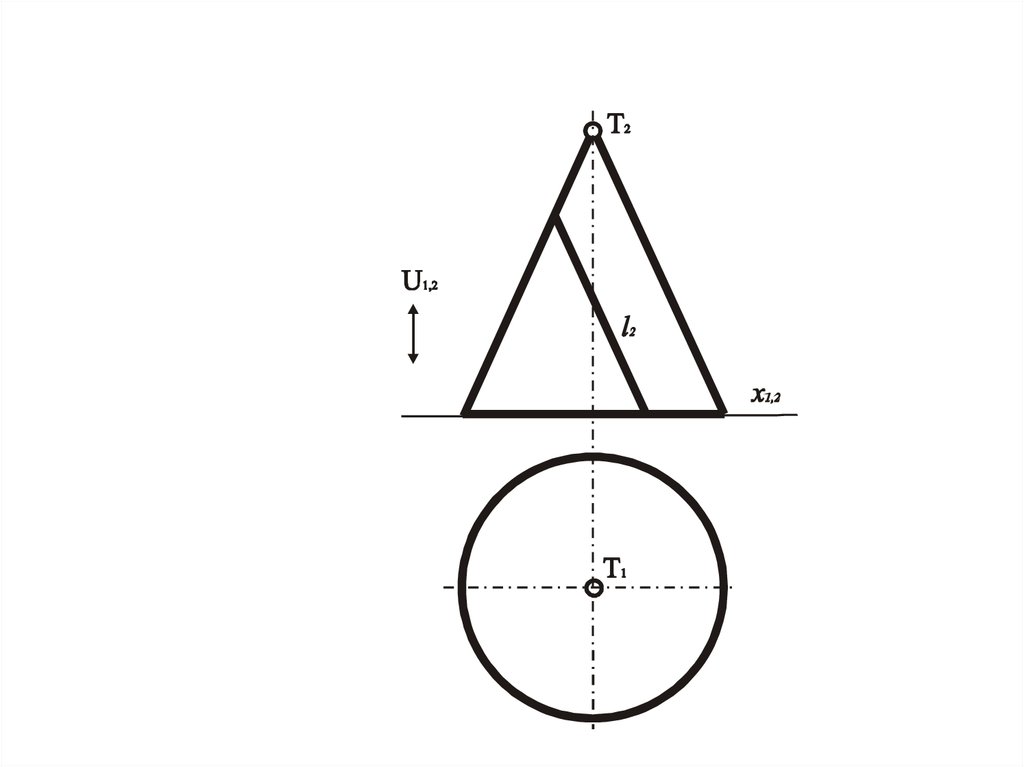
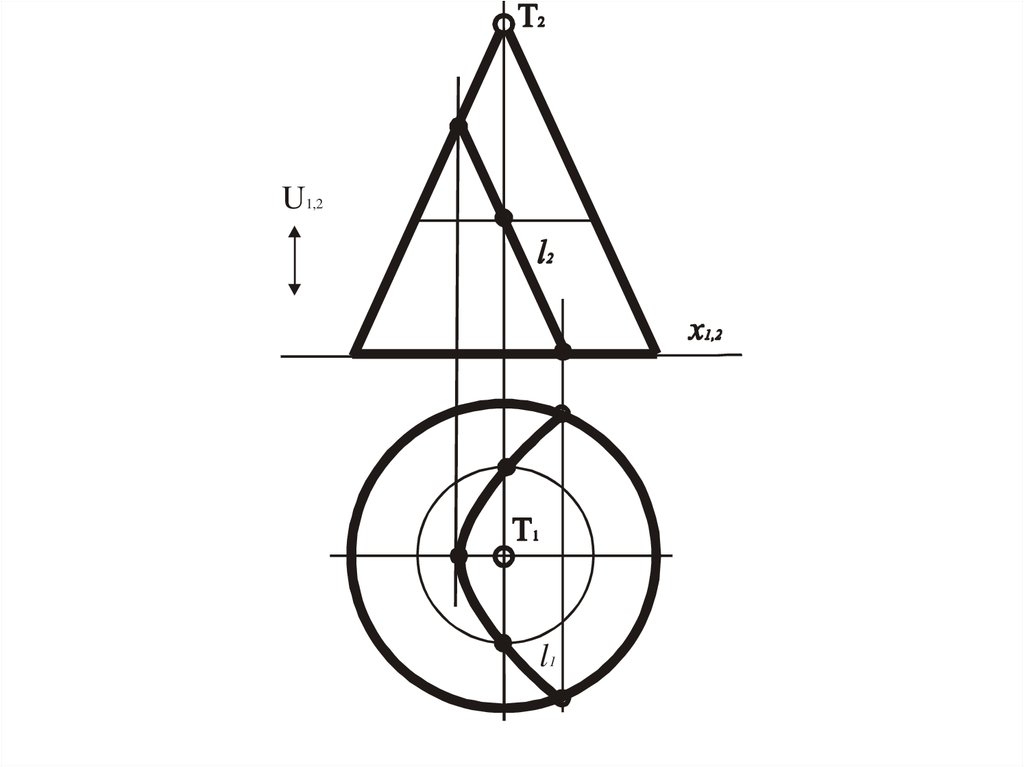
22. Задача 3
• Дана модель поверхности. Выделить наней графически простую линию.
• Графически простой линией называются
прямые или окружности, которые
проецируются в прямые или
окружности.
23.
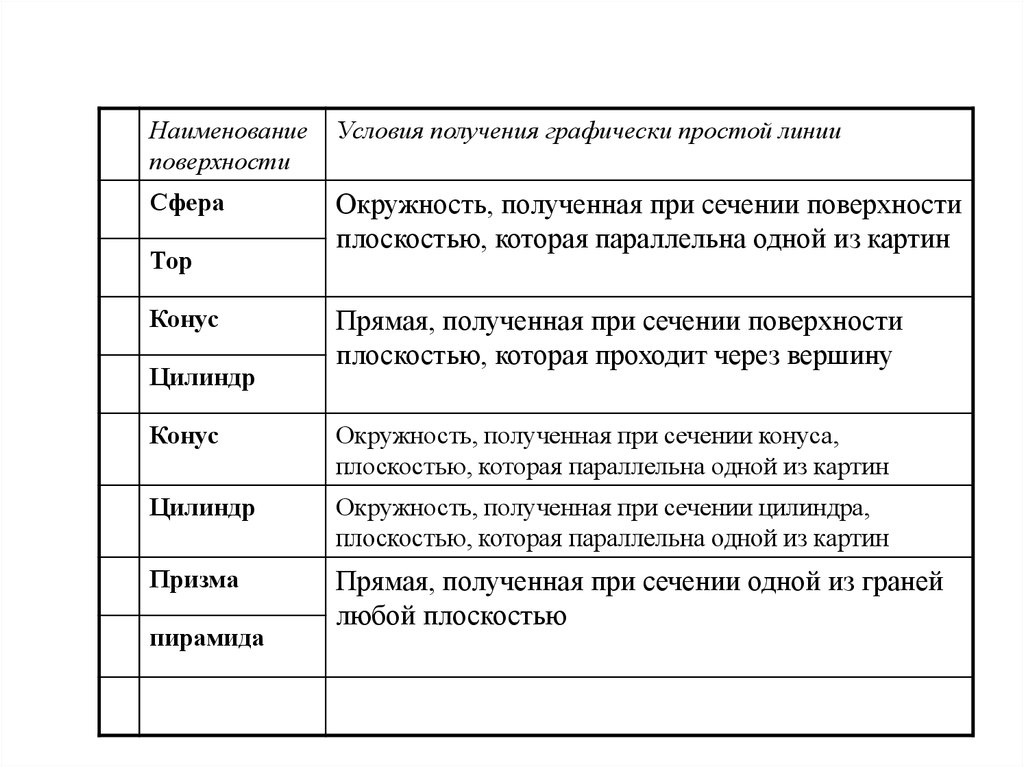
Наименованиеповерхности
Условия получения графически простой линии
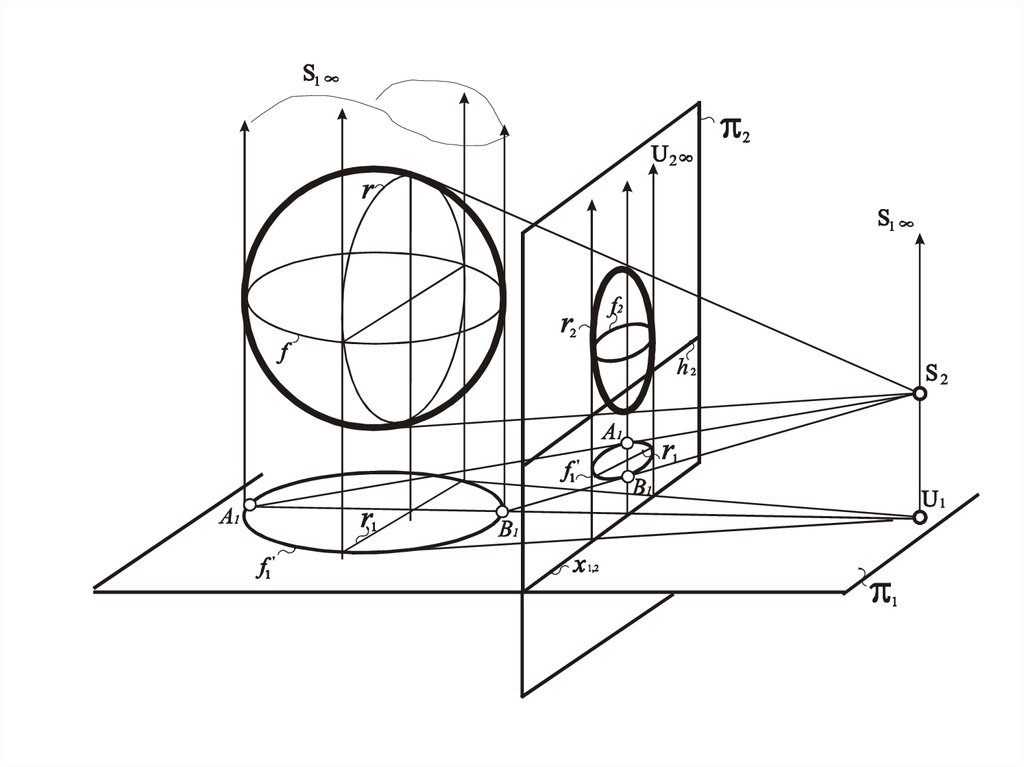
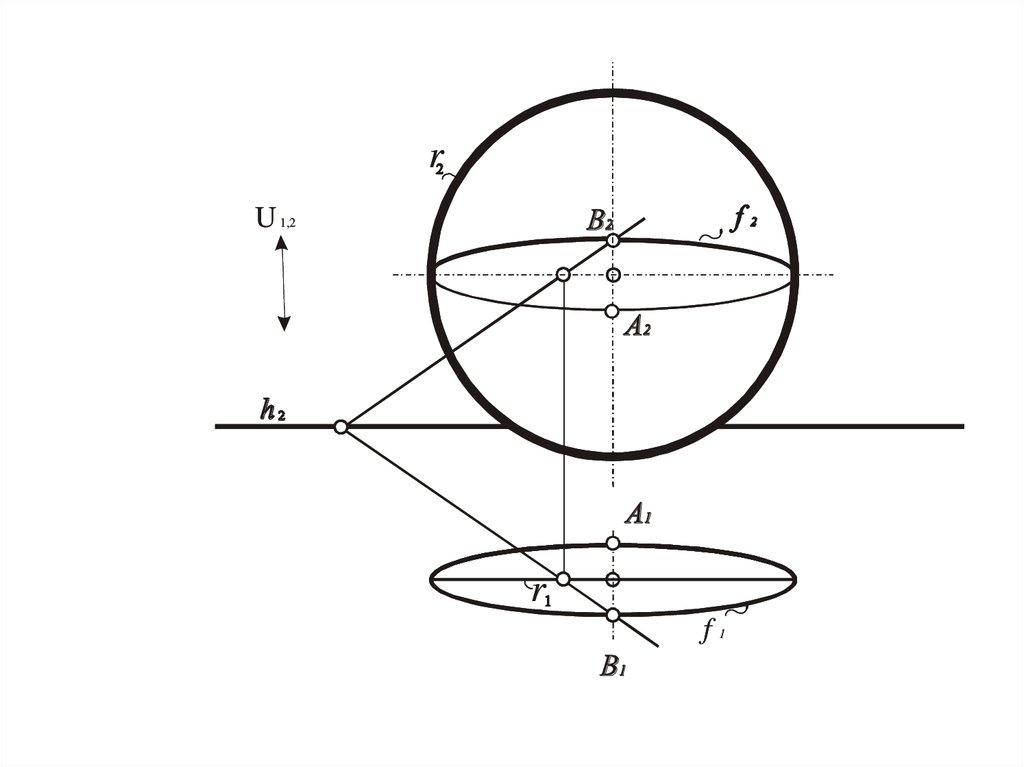
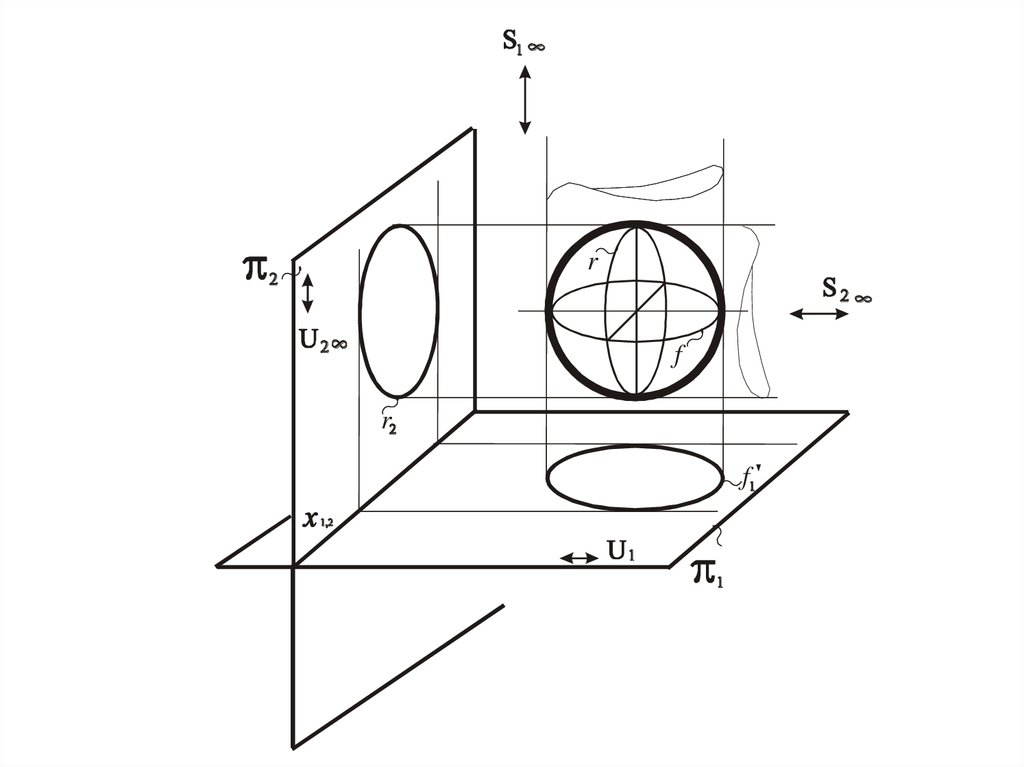
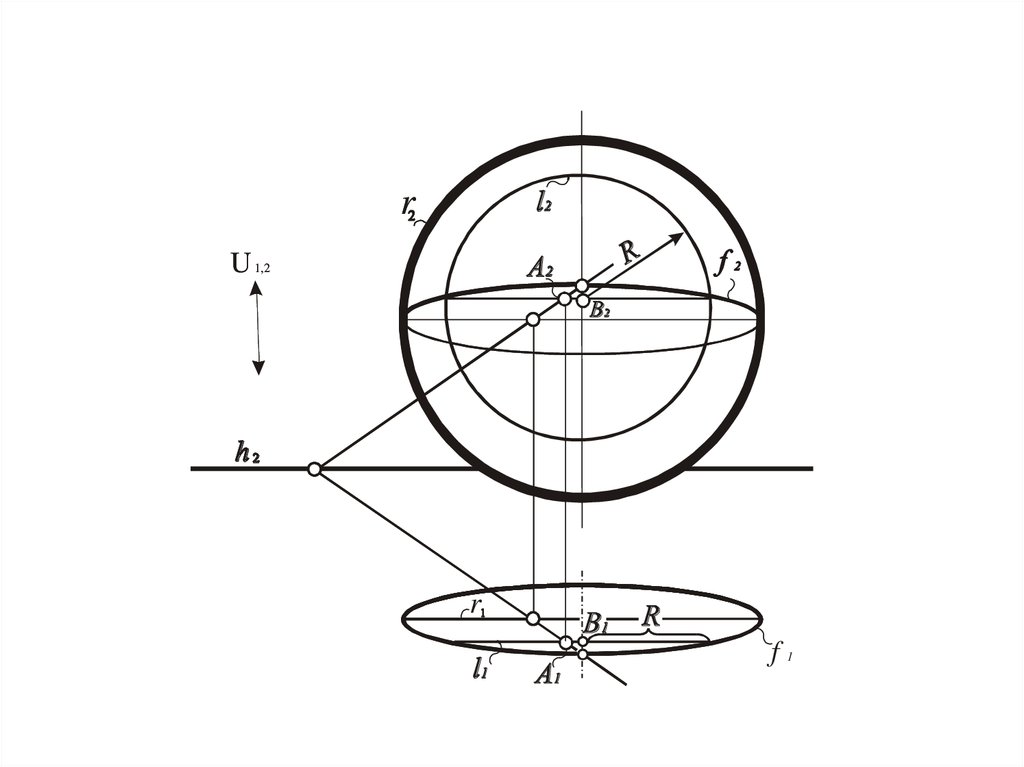
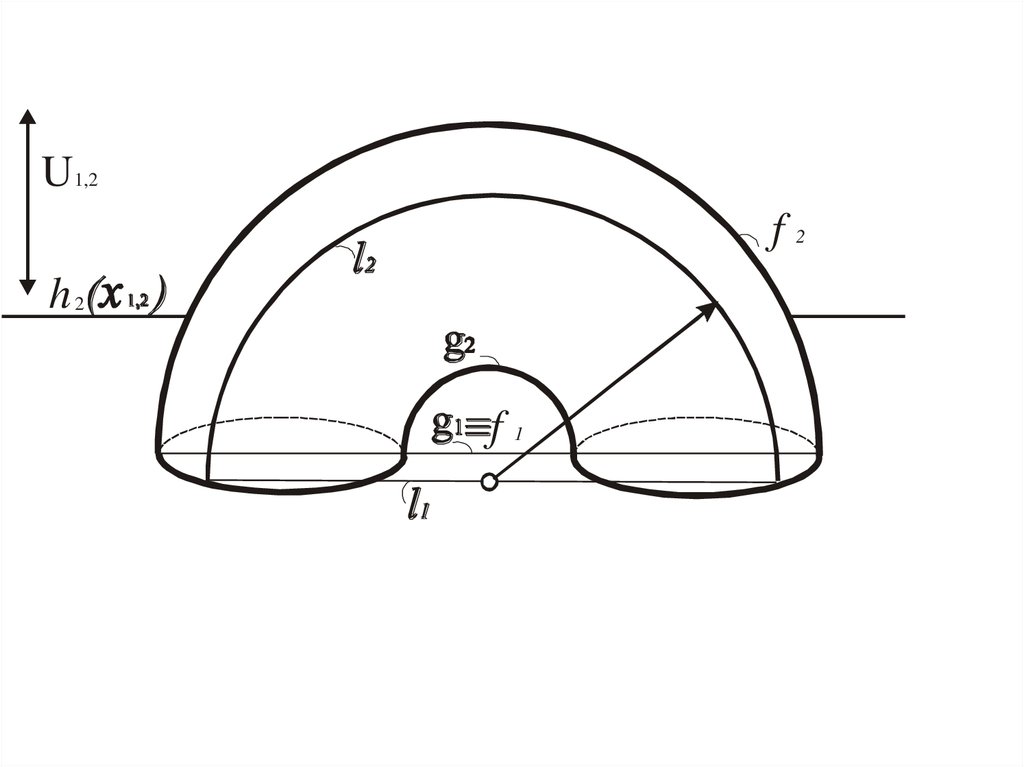
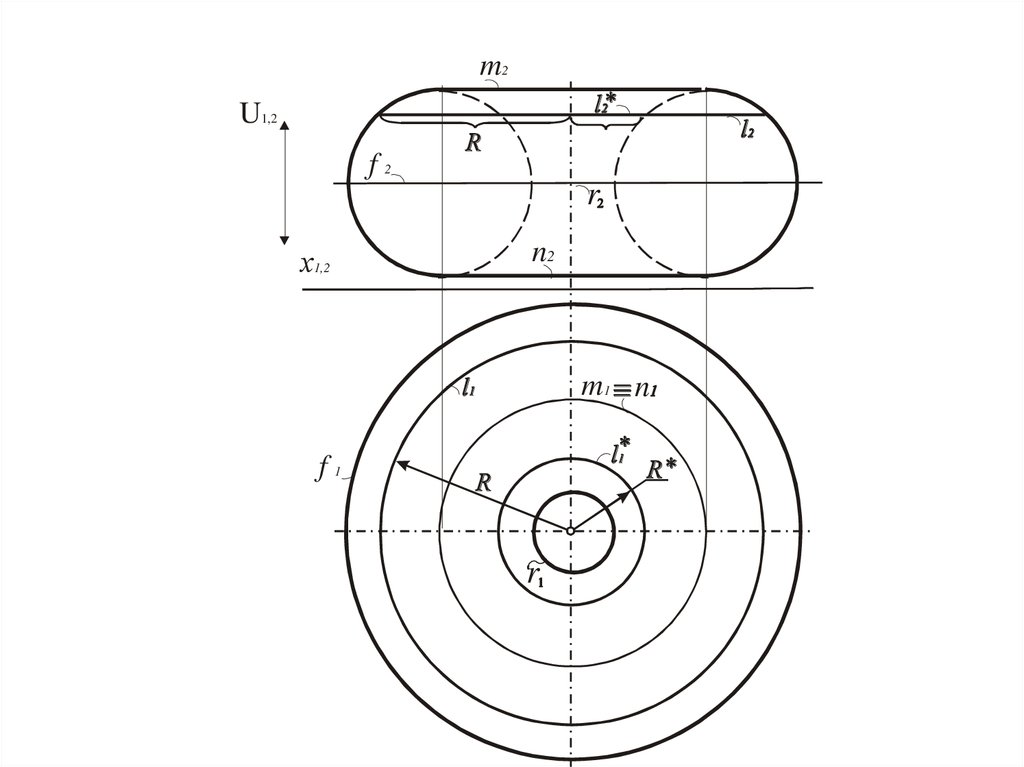
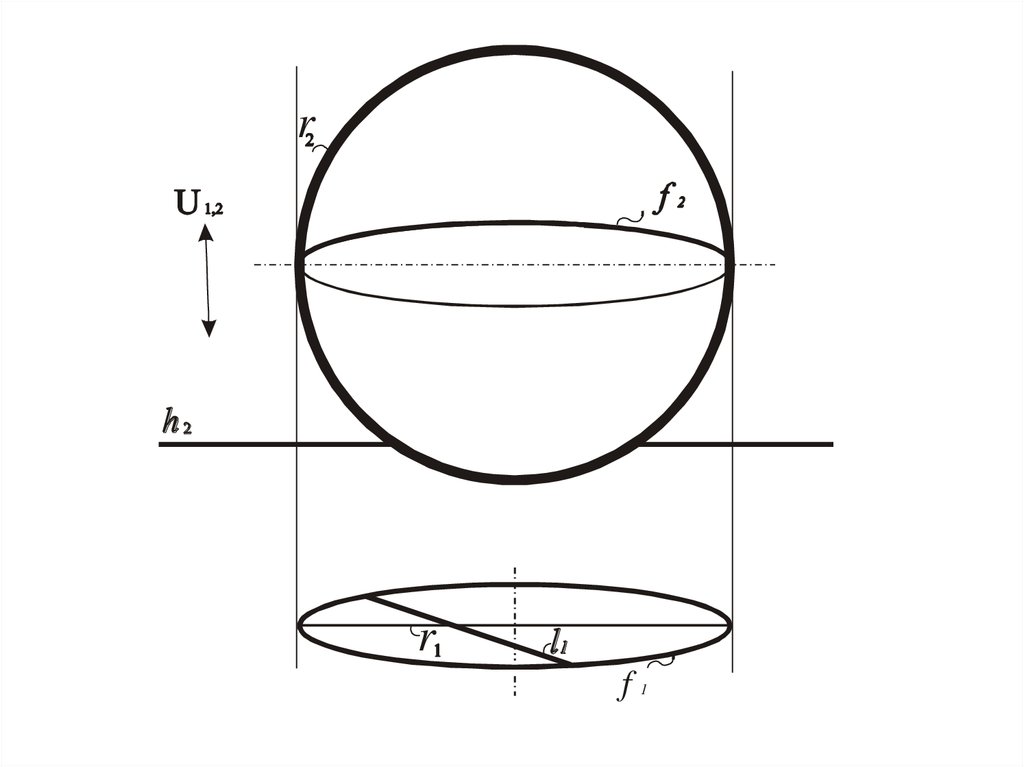
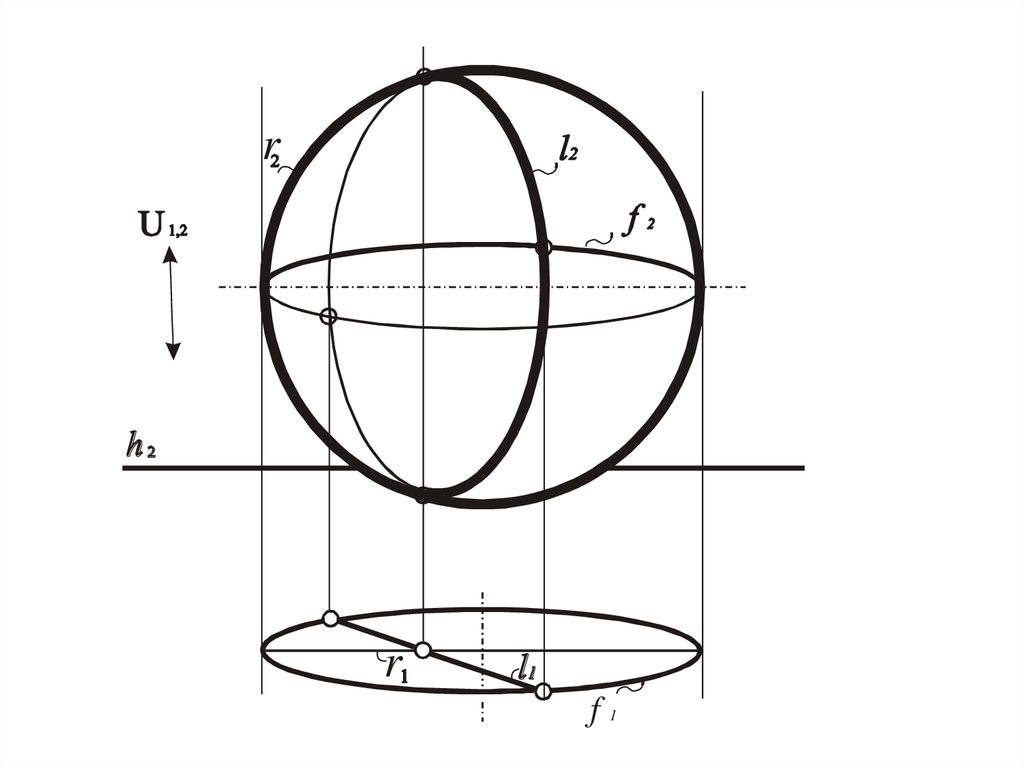
Сфера
Окружность, полученная при сечении поверхности
плоскостью, которая параллельна одной из картин
Тор
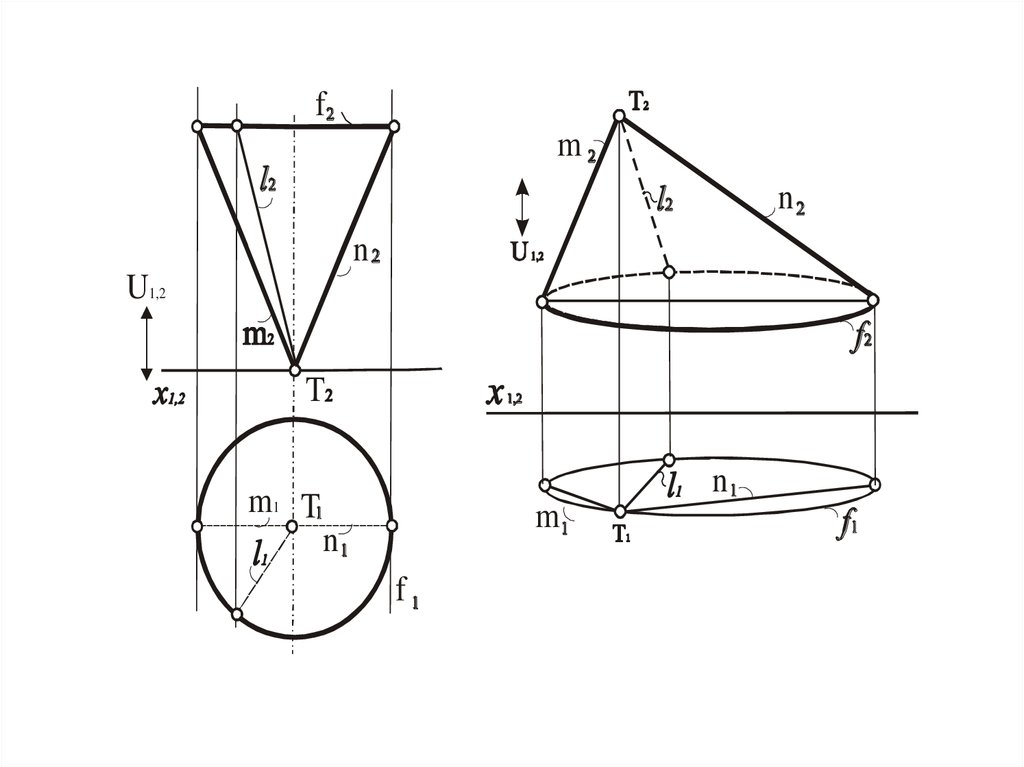
Конус
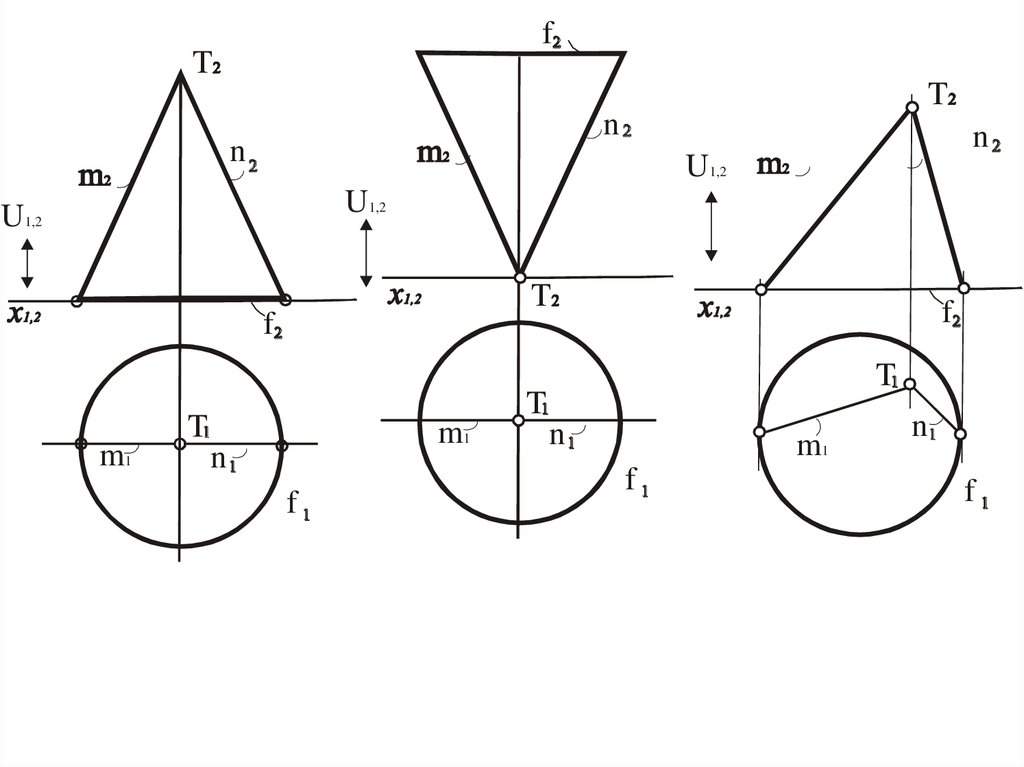
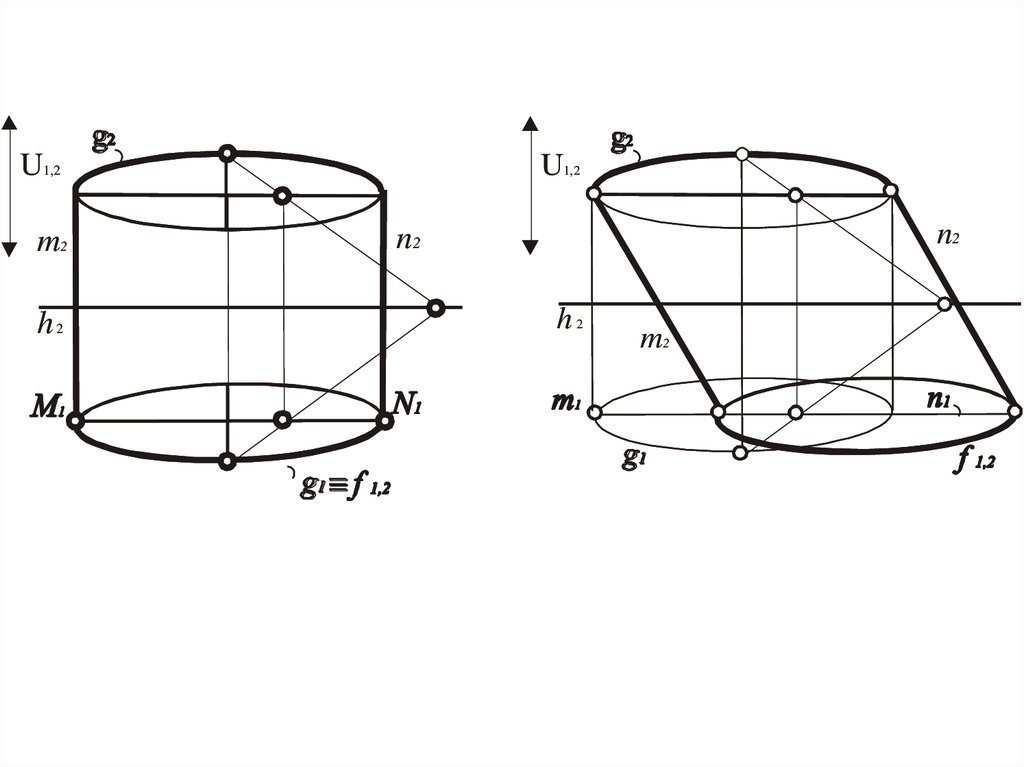
Цилиндр
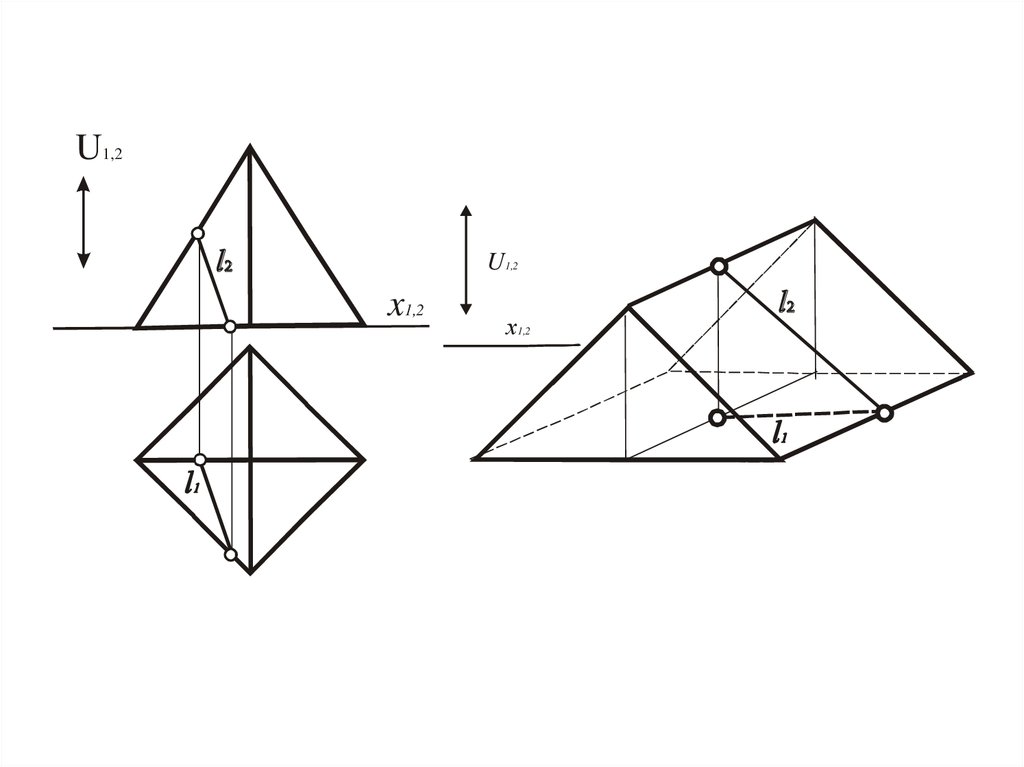
Прямая, полученная при сечении поверхности
плоскостью, которая проходит через вершину
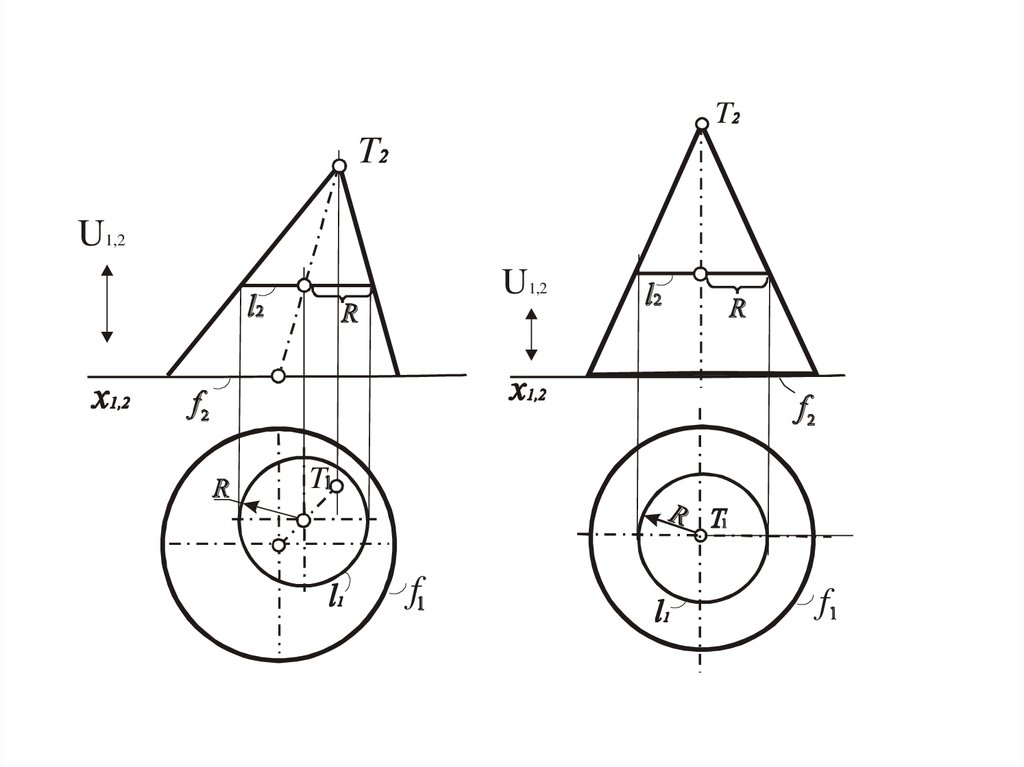
Конус
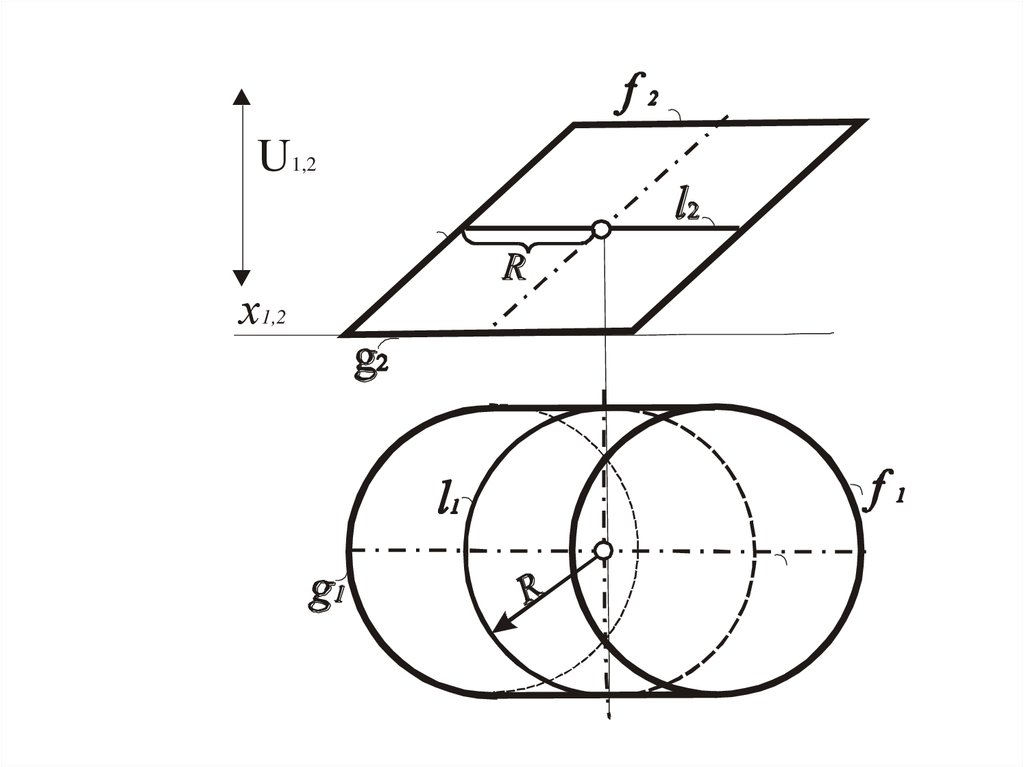
Окружность, полученная при сечении конуса,
плоскостью, которая параллельна одной из картин
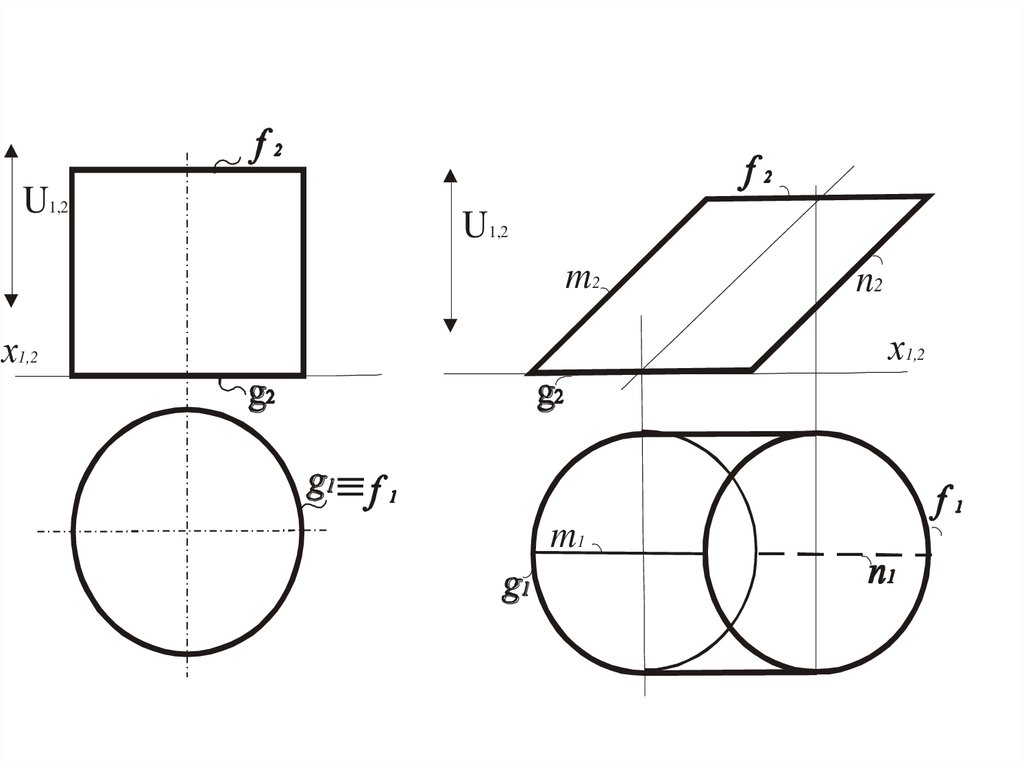
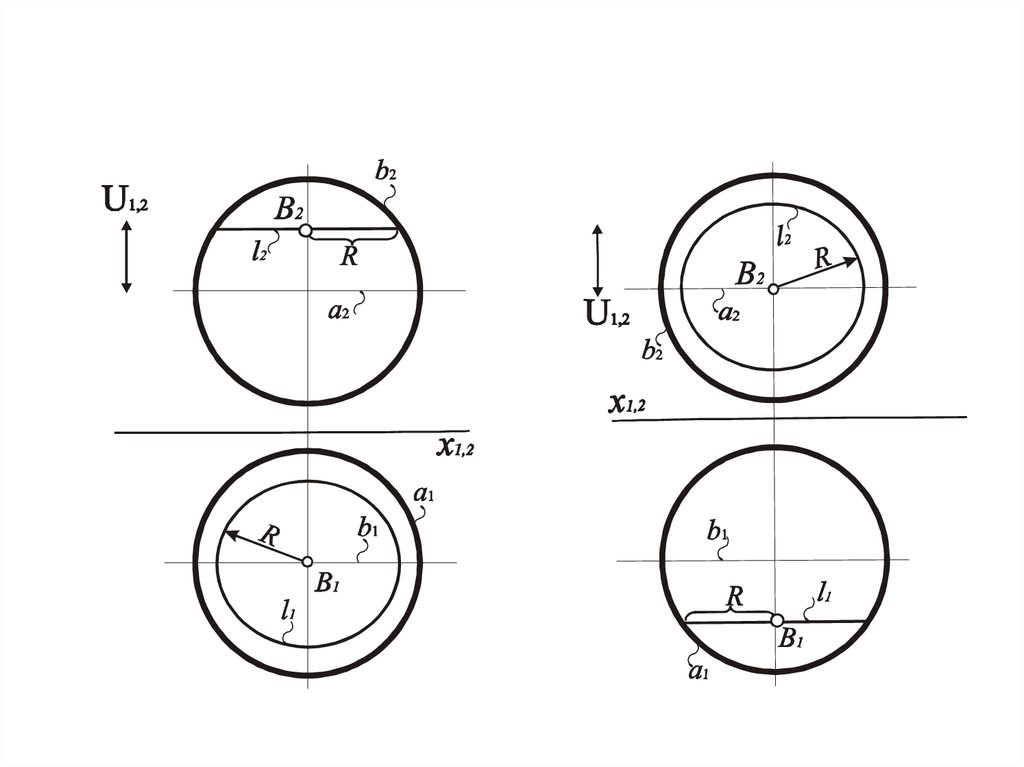
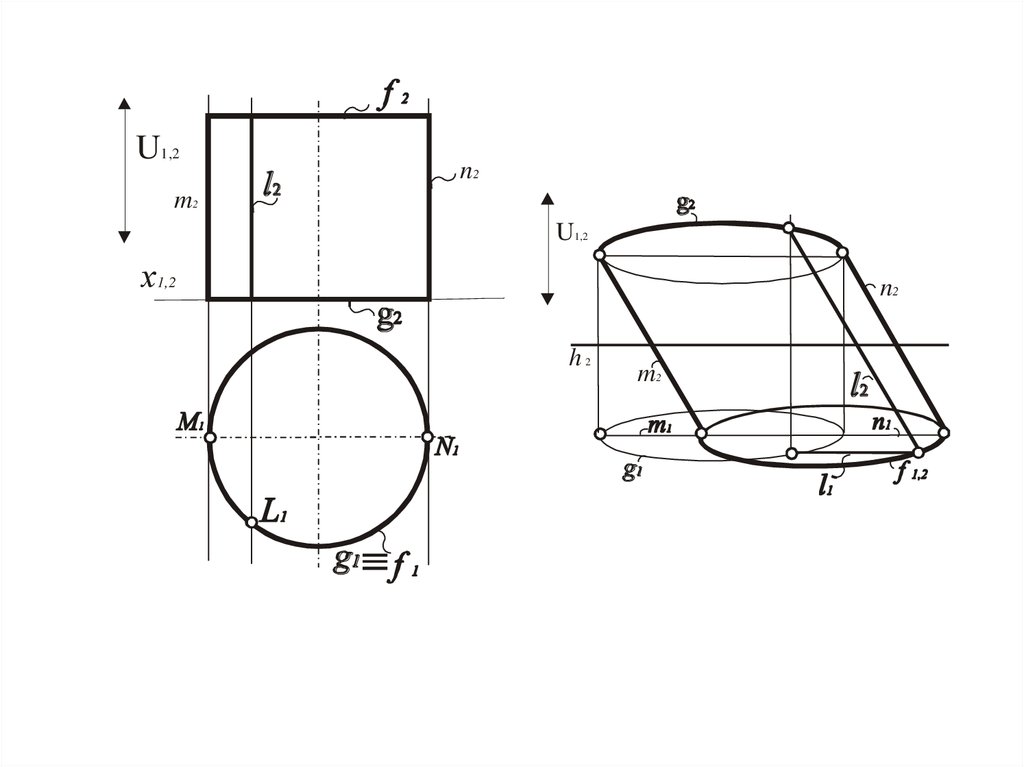
Цилиндр
Окружность, полученная при сечении цилиндра,
плоскостью, которая параллельна одной из картин
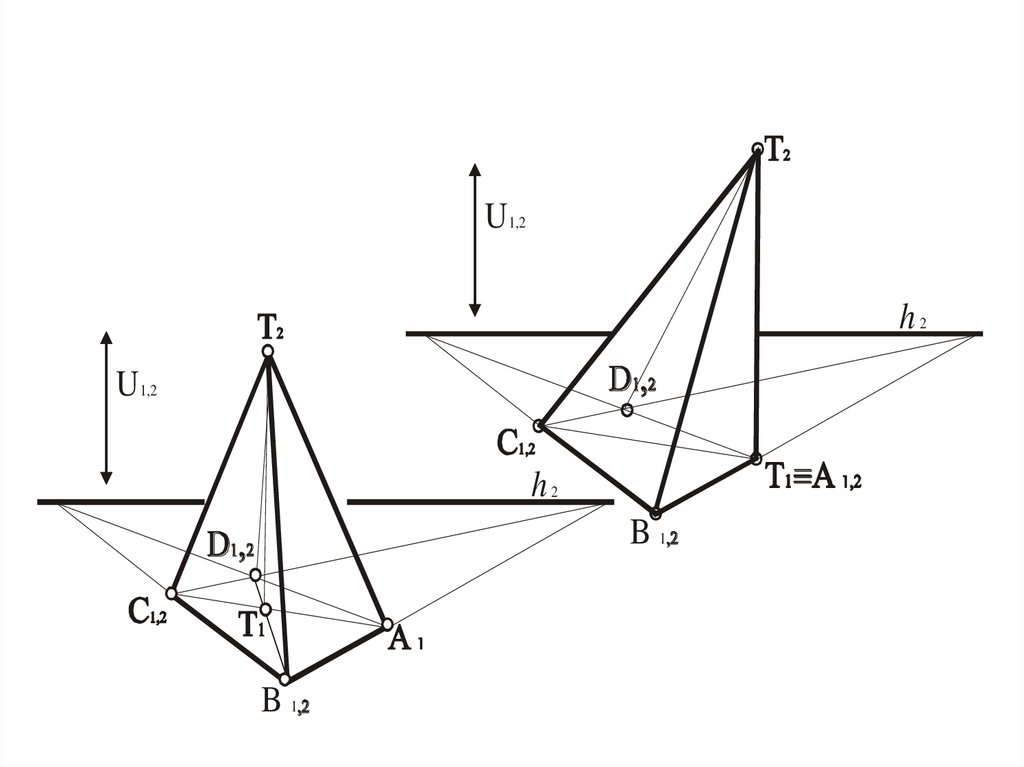
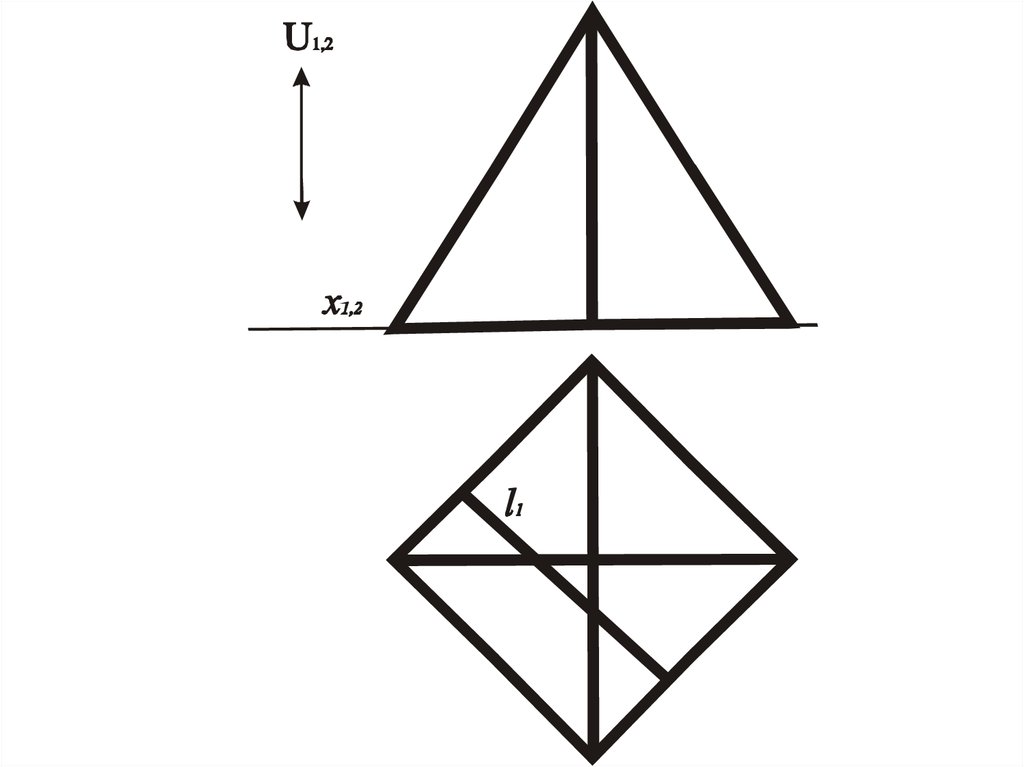
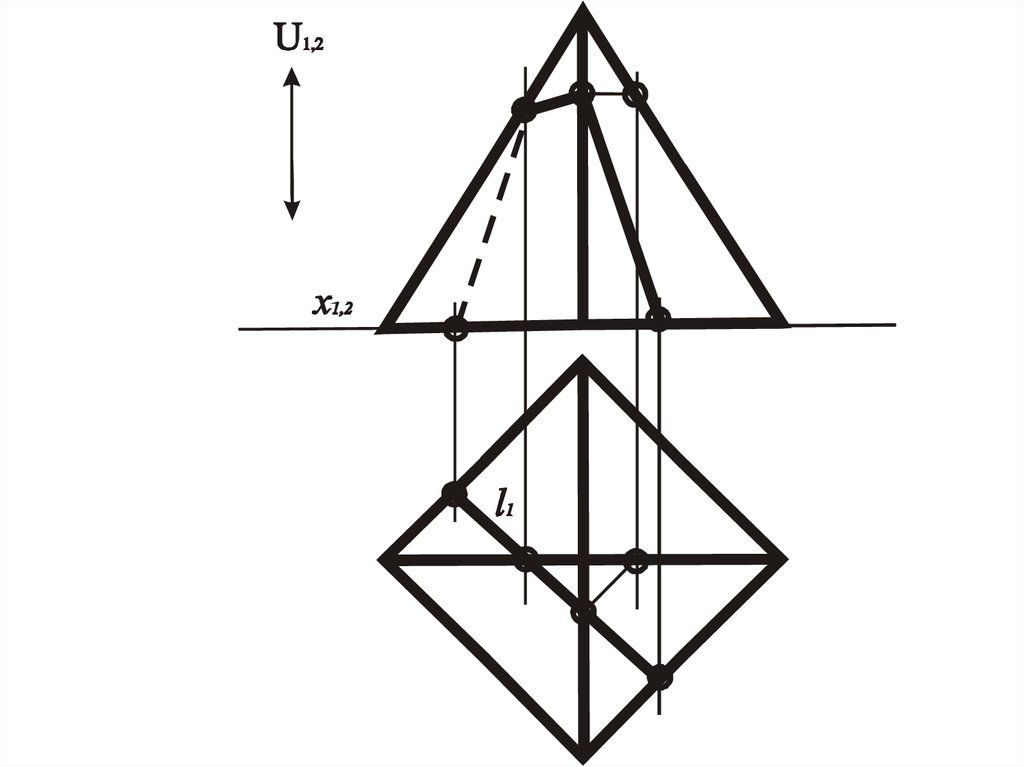
Призма
Прямая, полученная при сечении одной из граней
любой плоскостью
пирамида
24.
rU 1,2
r
f1
25.
26.
U1,2f2
h2
f1
27.
m2U1,2
f2
r
х1,2
n2
m1 n
f1
r
28.
fm
n
n
U1,2
T
n
m1 T
m
n
f
29.
U1,2n2
m2
U1,2
х1,2
n2
h2
m2
30.
TT
U1,2
U1,2
T
f
f
31.
U1,2х1,2
32.
U1,2U1,2
x1,2
х1,2
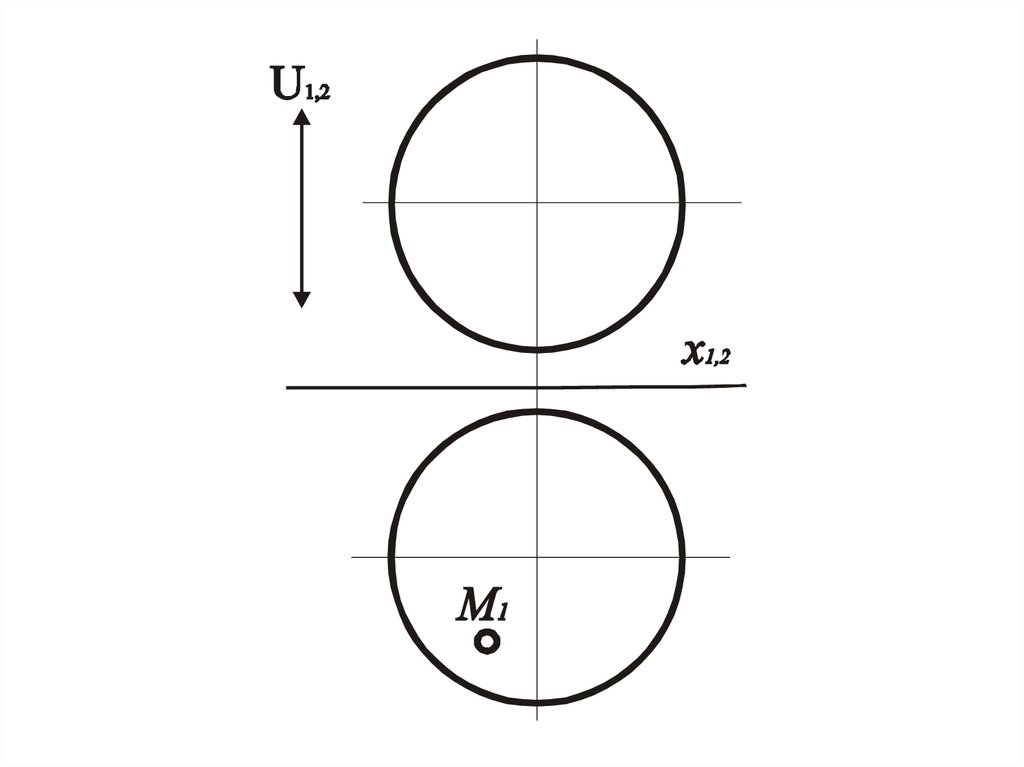
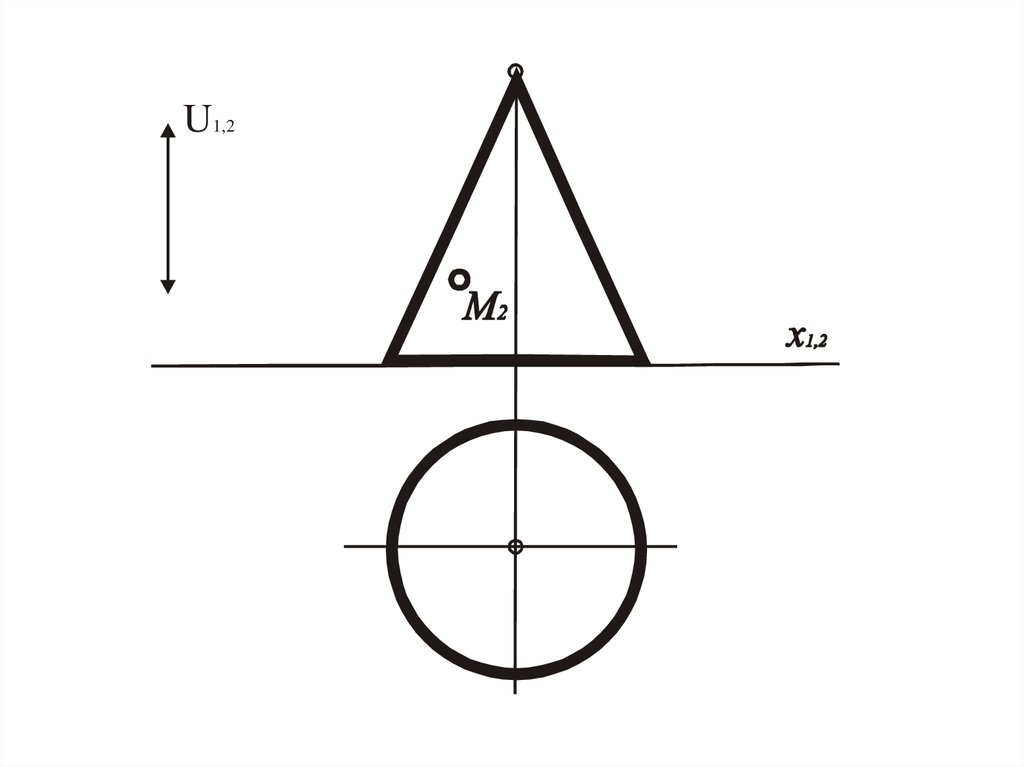
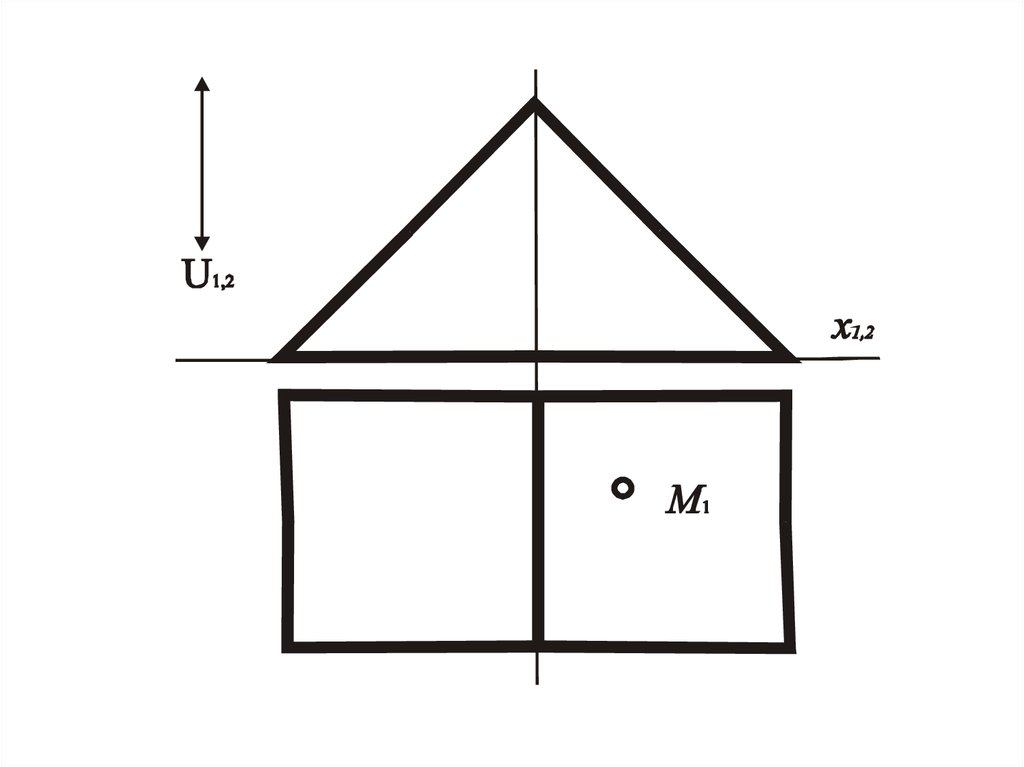
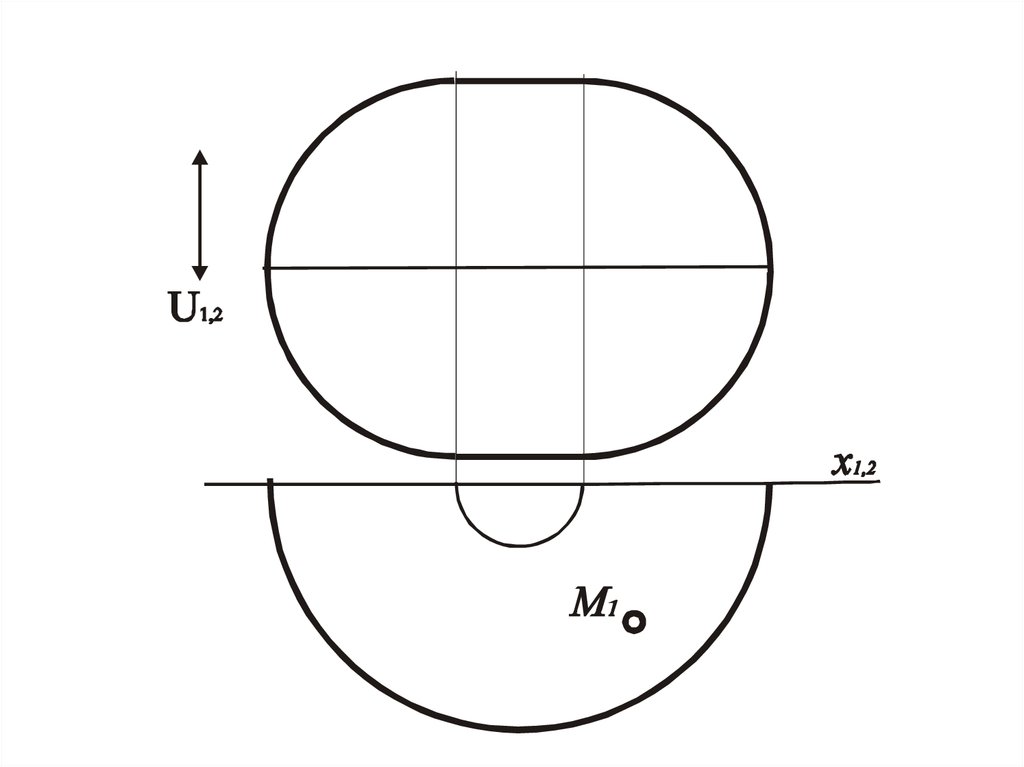
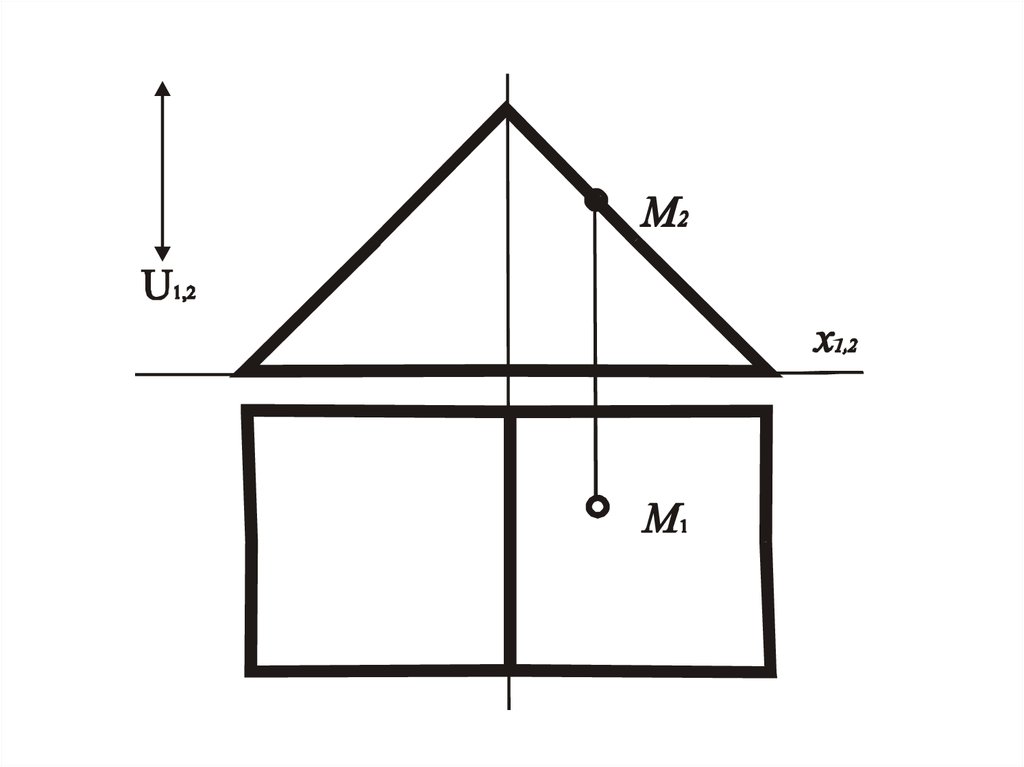
33. Задача.4.
• Дана одна проекция точки, котораялежит на поверхности построить другую
проекцию этой точки.
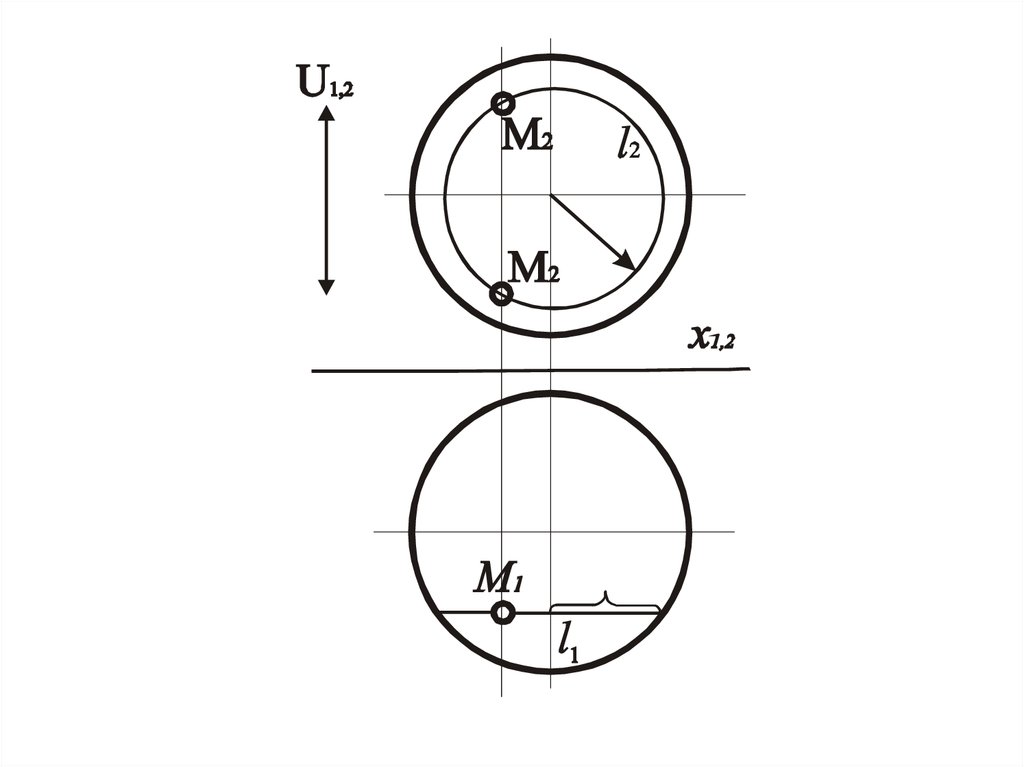
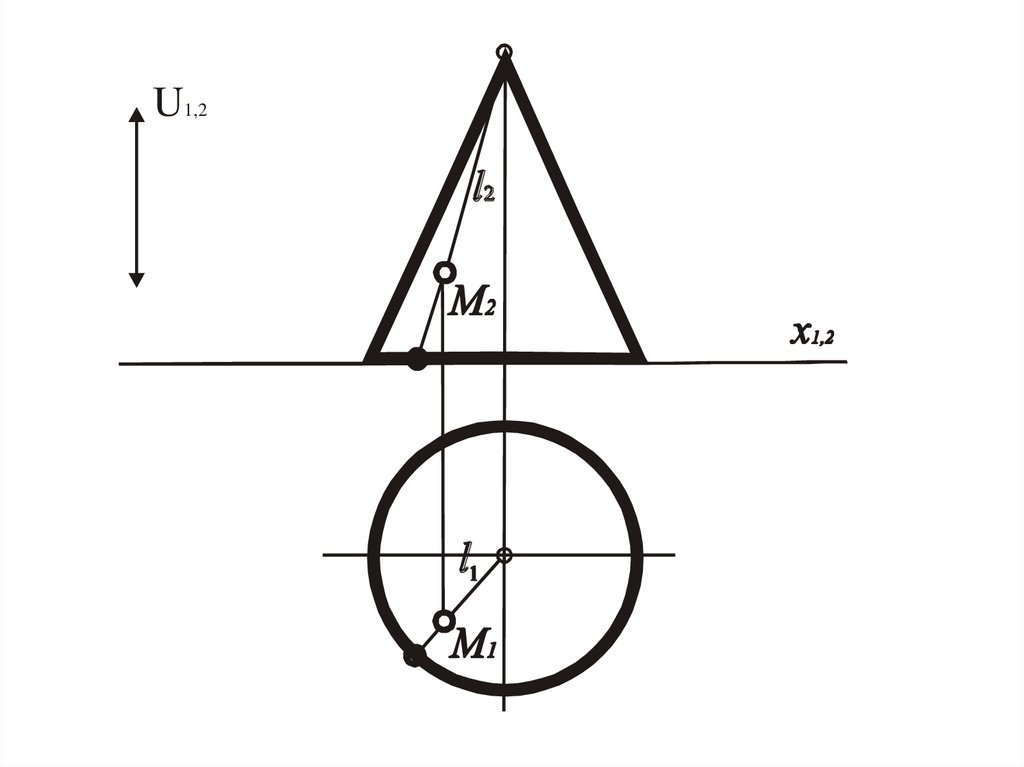
34. Алгоритм решения
• 1. Через заданную проекцию точки Мпровести графически простую линию
поверхности.
• 2. Построить другую проекцию этой
линии.
• 3. Определить на ней положение искомой
проекции точки М.
35.
36.
37.
U1,238.
U1,239.
40.
41.
42.
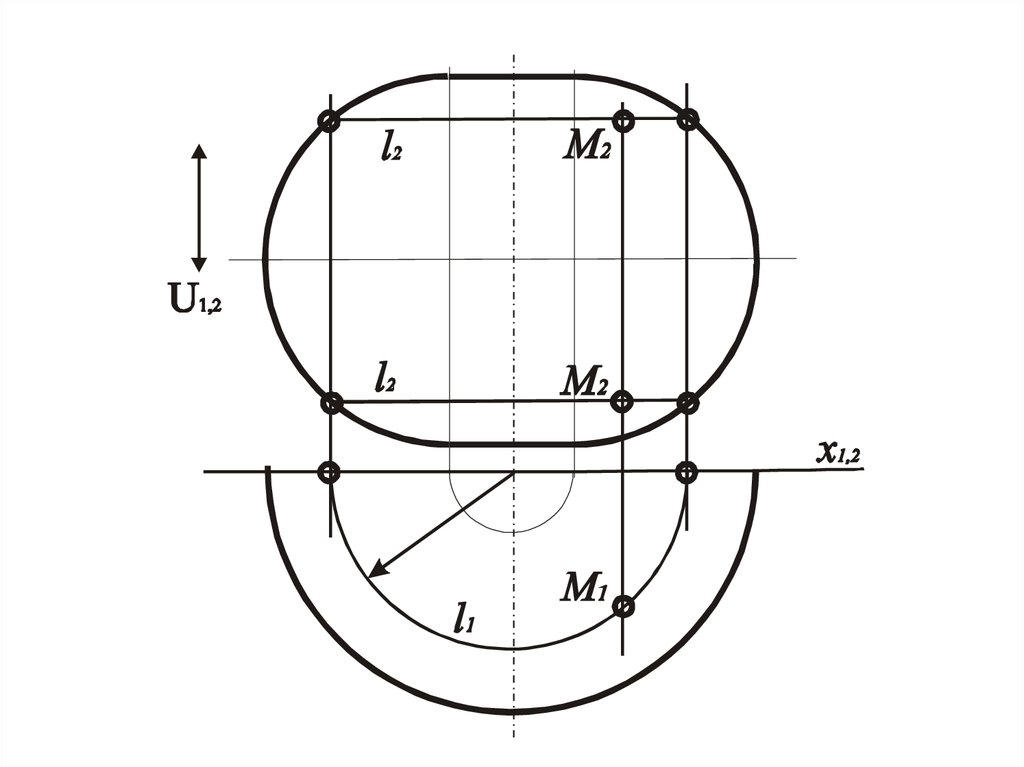
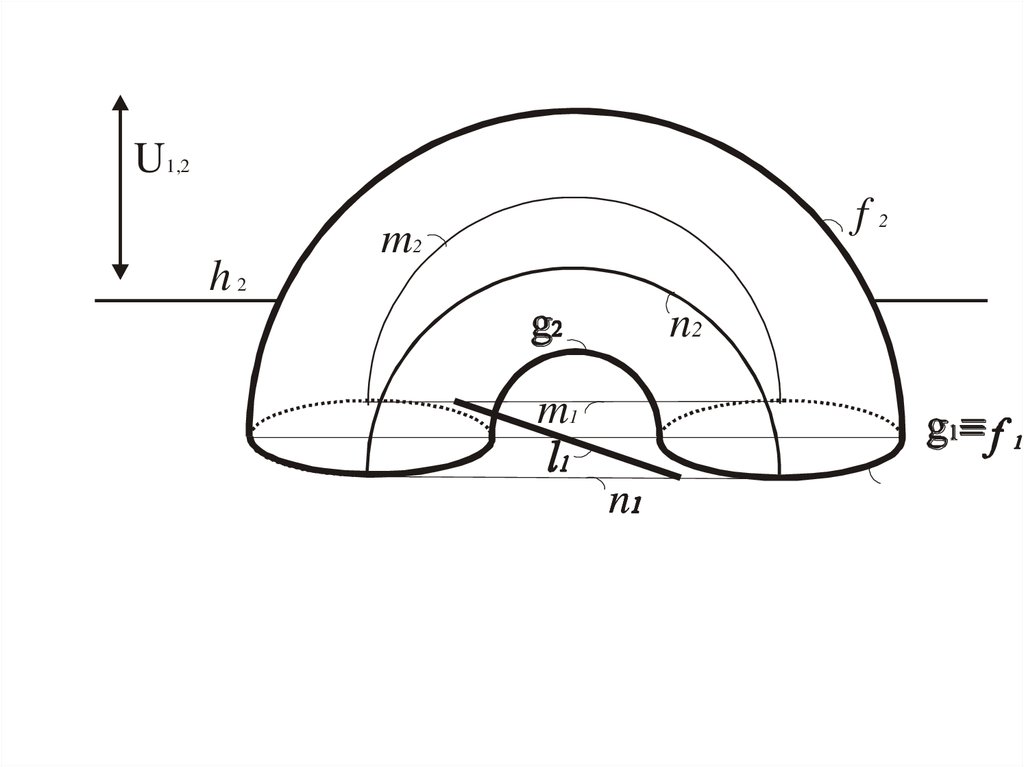
43. Задача. 5
• Дана одна проекция линии,которая лежит на поверхности.
Построить другую проекцию
этой линии
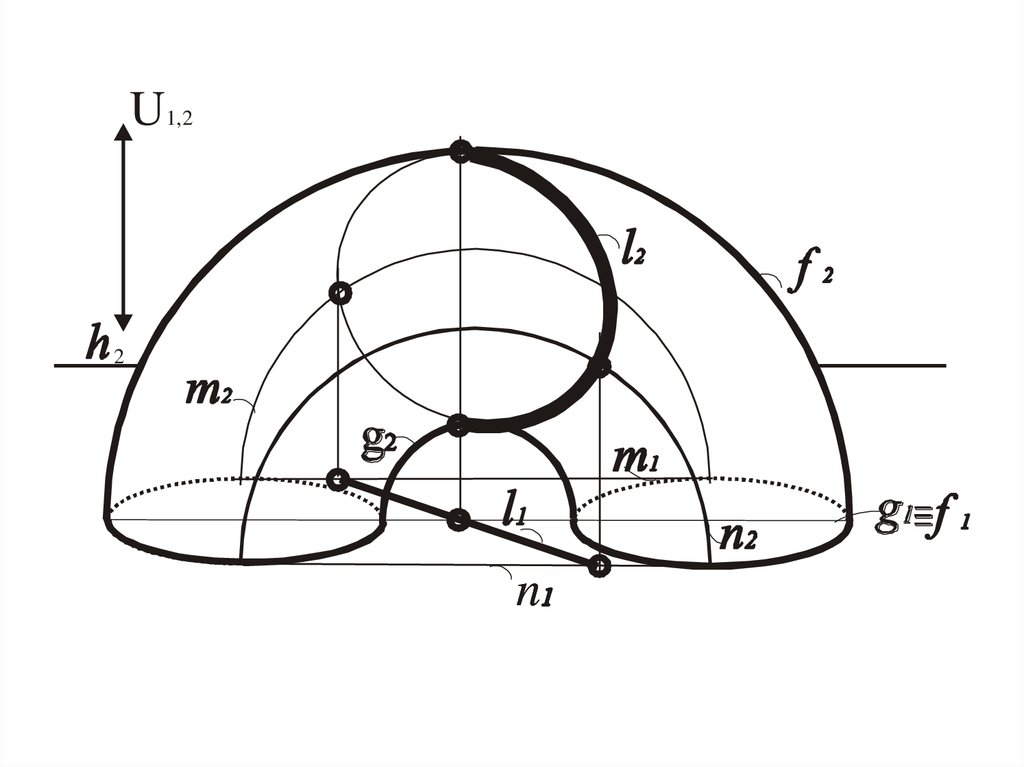
44. Алгоритм решения
• 1. Определить характер линии.• 2. Выделить на заданной проекции
линии опорные точки, если необходимо
еще и случайные точки.
• 3.Построить другие проекции
выделенных точек.
• 4. Соединить построенные проекции
точек с учетом характера заданной
линии.
45.
46.
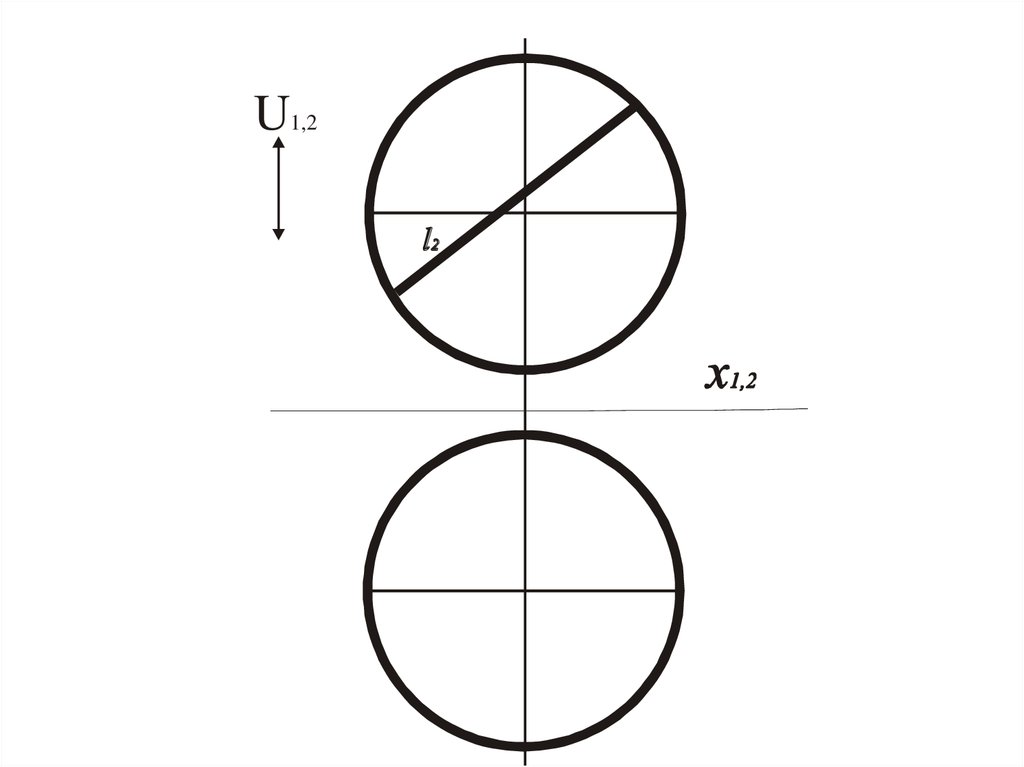
U1,2l1
47.
U1,2h2
f2
m2
n2
m1
n
48.
U1,22
n
49.
U1,250.
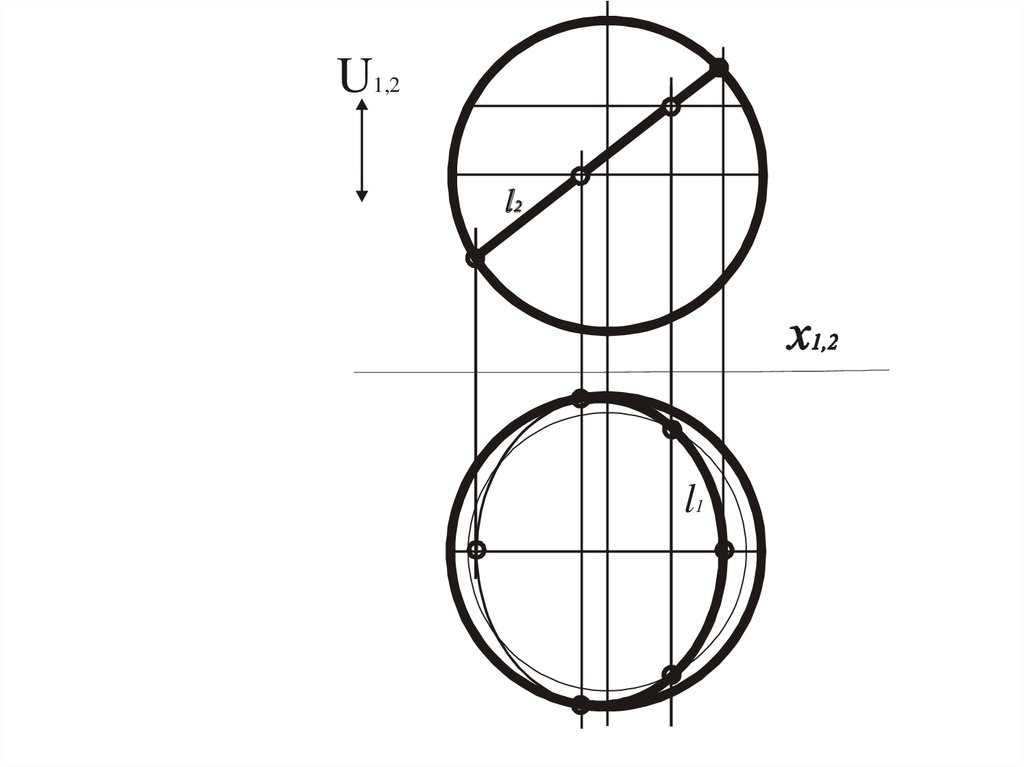
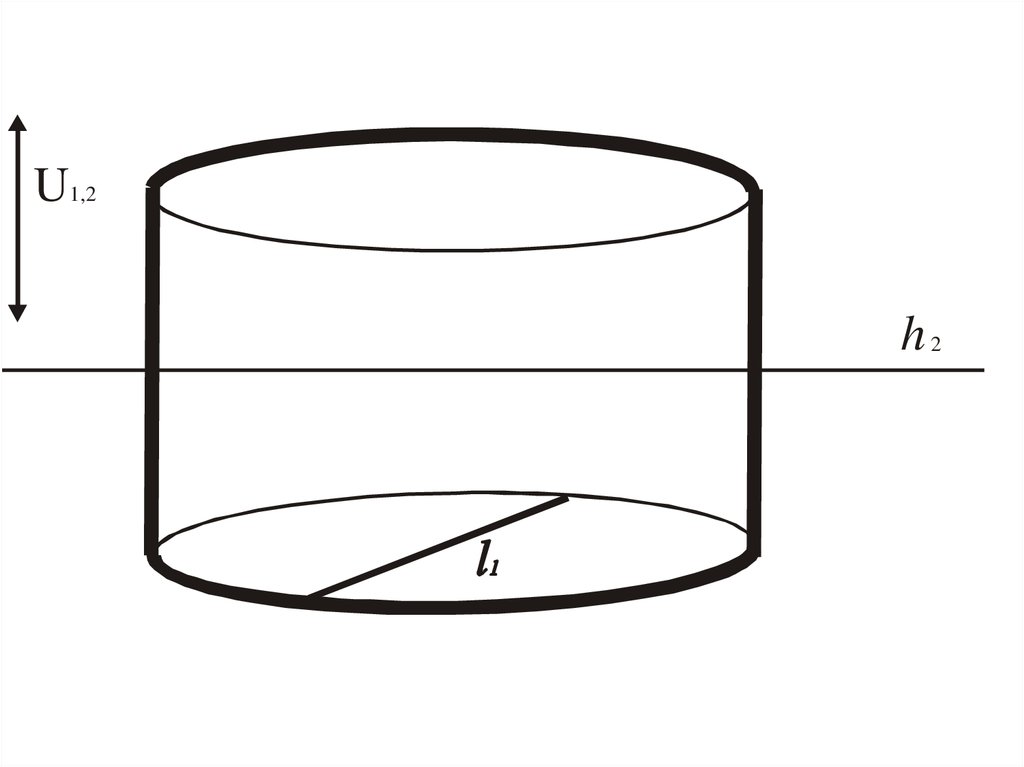
U1,2l1
51.
rr
f1
52.
rr
f1
53.
54.
55.
U1,2h2










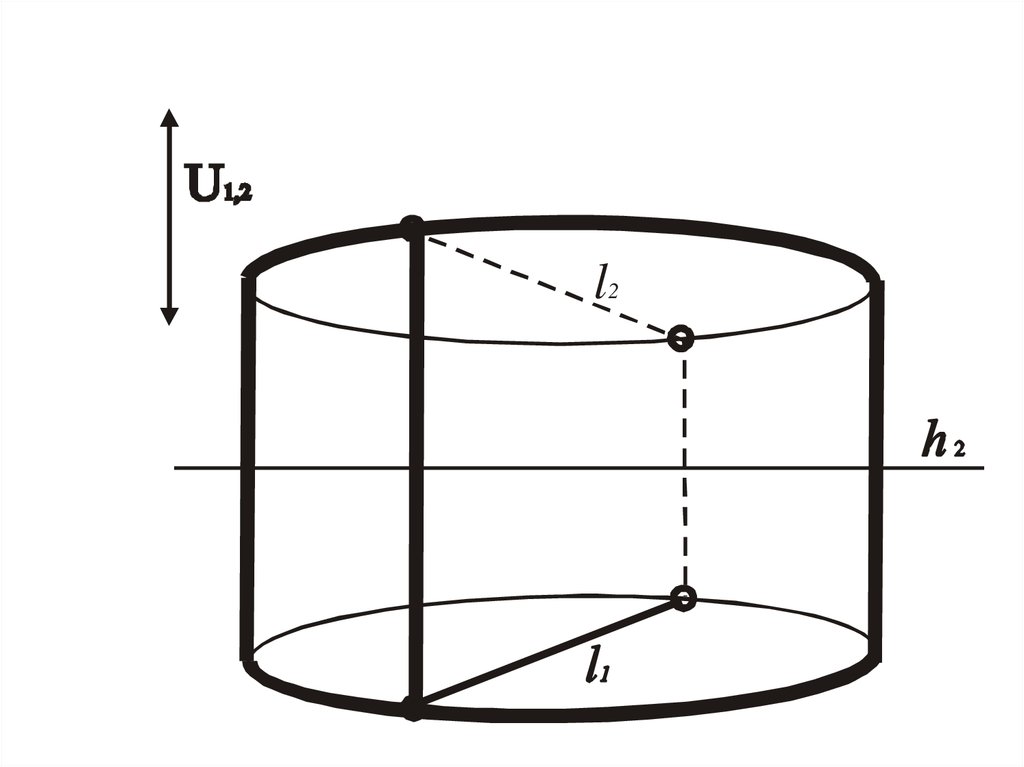
 Инженерная графика
Инженерная графика








