Похожие презентации:
Позиционные задачи. Лекция №2
1. Позиционные задачи
ИФ МГТУ ГАЛекция №2
Позиционные задачи
1. Точка и прямая;
2. Взаимное положение двух прямых;
3. Прямая и плоскость
4. Точка и плоскость;
5. Взаимное положение двух плоскостей.
2. Позиционные задачи
Позиционными называются задачи при решении которыхвыясняется взаимное расположение геометрических элементов
При этом возможны случаи:
1. Полной принадлежности, например, точка, принадлежит
прямой, прямая принадлежит плоскости (прямая есть
подмножество плоскости);
2. Пересечения, например, прямая пересекается с плоскостью
(прямая не является подмножеством плоскости), одна
плоскость пересекается с другой;
3. Отсутствия принадлежности, на пример, у двух
скрещивающихся прямых.
3. Прямая и точка
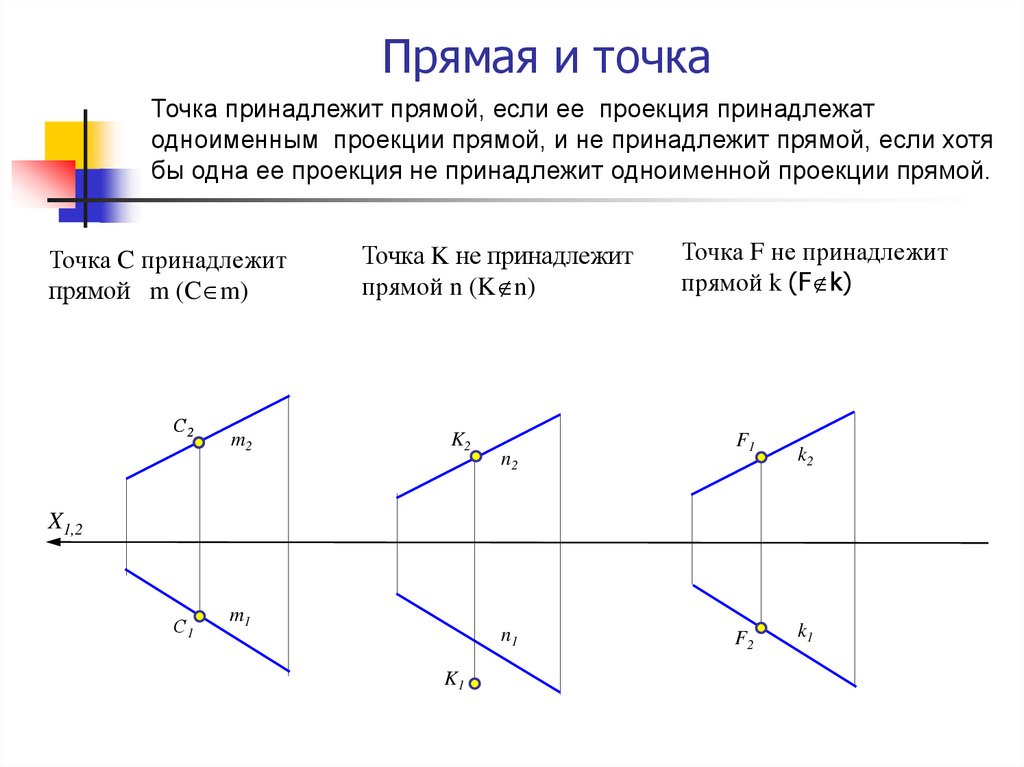
Точка принадлежит прямой, если ее проекция принадлежатодноименным проекции прямой, и не принадлежит прямой, если хотя
бы одна ее проекция не принадлежит одноименной проекции прямой.
Точка C принадлежит
прямой m (C m)
С2
m2
Точка K не принадлежит
прямой n (K n)
K2
n2
Точка F не принадлежит
прямой k (F k)
F1
k2
X1,2
С1
m1
n1
K1
F2
k1
4. Прямая и точка
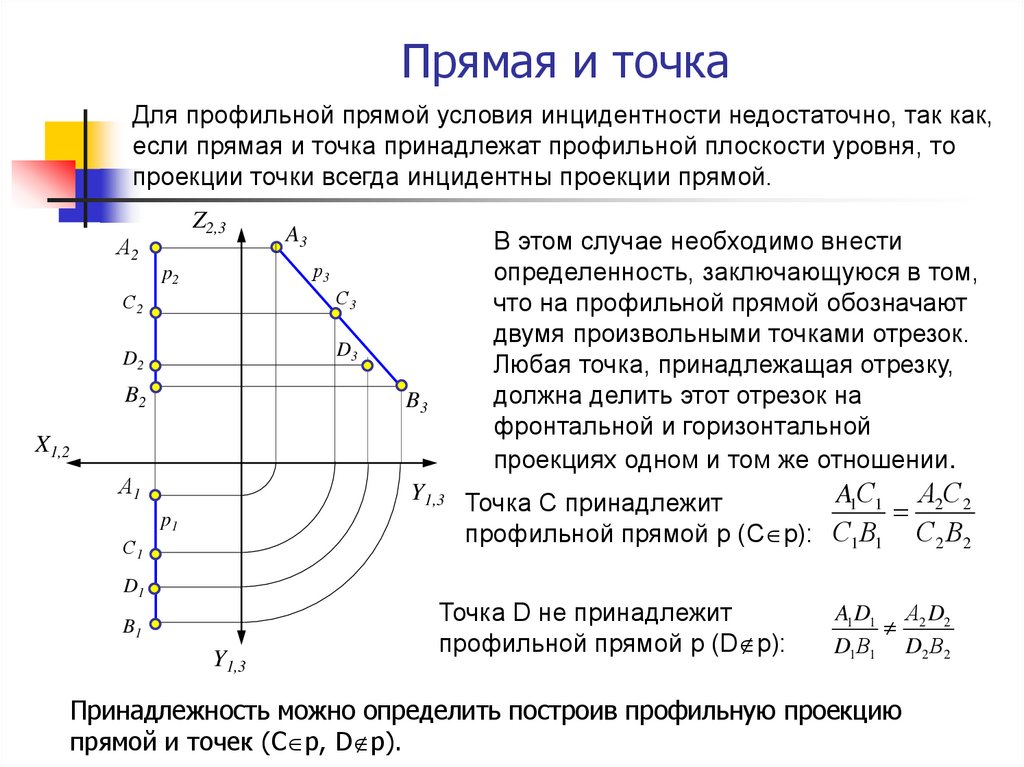
Для профильной прямой условия инцидентности недостаточно, так как,если прямая и точка принадлежат профильной плоскости уровня, то
проекции точки всегда инцидентны проекции прямой.
Z2,3
А2
A3
р3
p2
С2
С3
D2
D3
В этом случае необходимо внести
определенность, заключающуюся в том,
что на профильной прямой обозначают
двумя произвольными точками отрезок.
Любая точка, принадлежащая отрезку,
должна делить этот отрезок на
фронтальной и горизонтальной
проекциях одном и том же отношении.
B2
B3
А1
Y1,3 Точка C принадлежит
X1,2
A1С1 А2С2
профильной прямой p (C p): С1 В1 С2 В2
p1
С1
D1
B1
Y1,3
Точка D не принадлежит
профильной прямой p (D p):
A1 D1 А2 D2
D1 В1 D2 В2
Принадлежность можно определить построив профильную проекцию
прямой и точек (C p, D p).
5. Две прямые
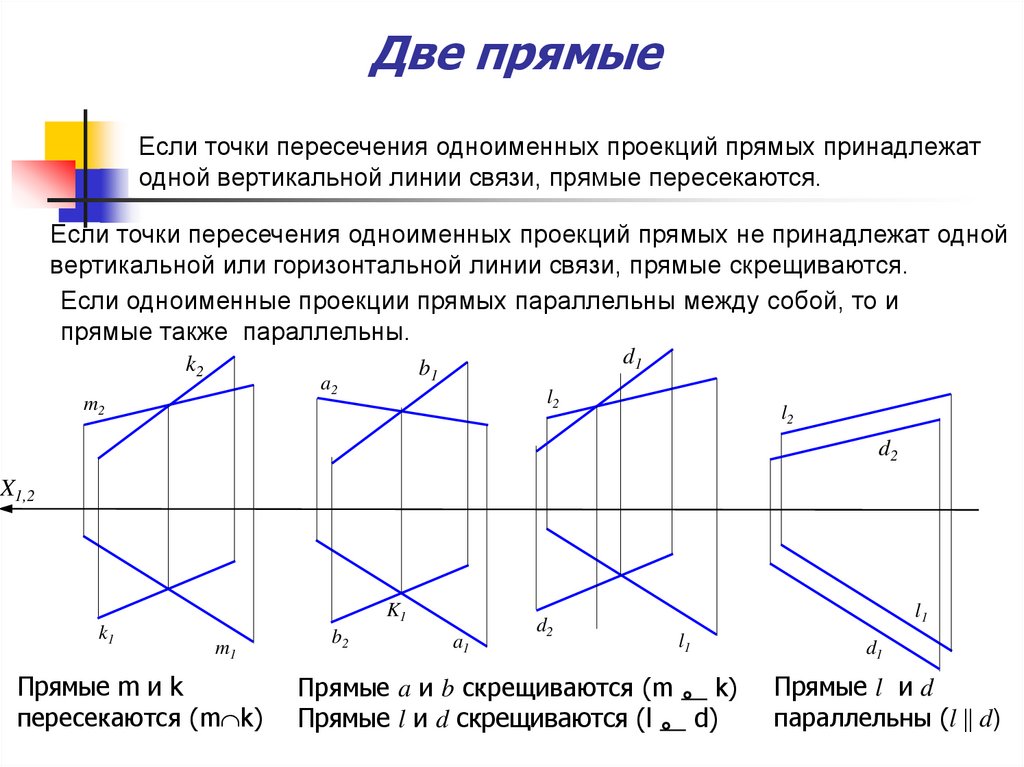
Если точки пересечения одноименных проекций прямых принадлежатодной вертикальной линии связи, прямые пересекаются.
Если точки пересечения одноименных проекций прямых не принадлежат одной
вертикальной или горизонтальной линии связи, прямые скрещиваются.
Если одноименные проекции прямых параллельны между собой, то и
прямые также параллельны.
k2
a2
m2
d1
b1
l2
l2
d2
X1,2
K1
k1
m1
Прямые m и k
пересекаются (m k)
b2
a1
d2
l1
l1
Прямые a и b скрещиваются (m 。 k)
Прямые l и d скрещиваются (l 。 d)
d1
Прямые l и d
параллельны (l d)
6. Две прямые
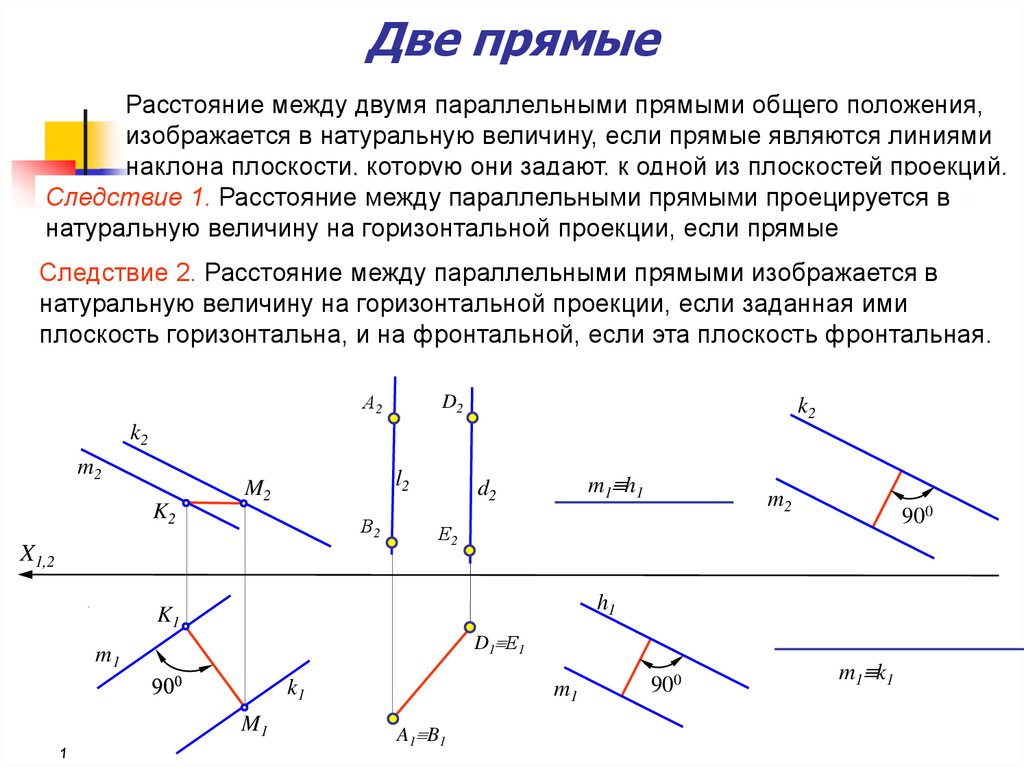
Расстояние между двумя параллельными прямыми общего положения,изображается в натуральную величину, если прямые являются линиями
наклона плоскости, которую они задают, к одной из плоскостей проекций.
Следствие 1. Расстояние между параллельными прямыми проецируется в
натуральную величину на горизонтальной проекции, если прямые
вертикальны,
и фронтальной,
прямые фронтально
Следствие
2. Расстояние
междуесли
параллельными
прямымипроецирующие
изображается.в
натуральную величину на горизонтальной проекции, если заданная ими
плоскость горизонтальна, и на фронтальной, если эта плоскость фронтальная.
А2
D2
k2
k2
m2
K2
l2
M2
В2
X1,2
m1 h1
d2
m2
900
Е2
h1
K1
D1 Е1
m1
k1
M1
m1
A1 B1
900
m1 k1
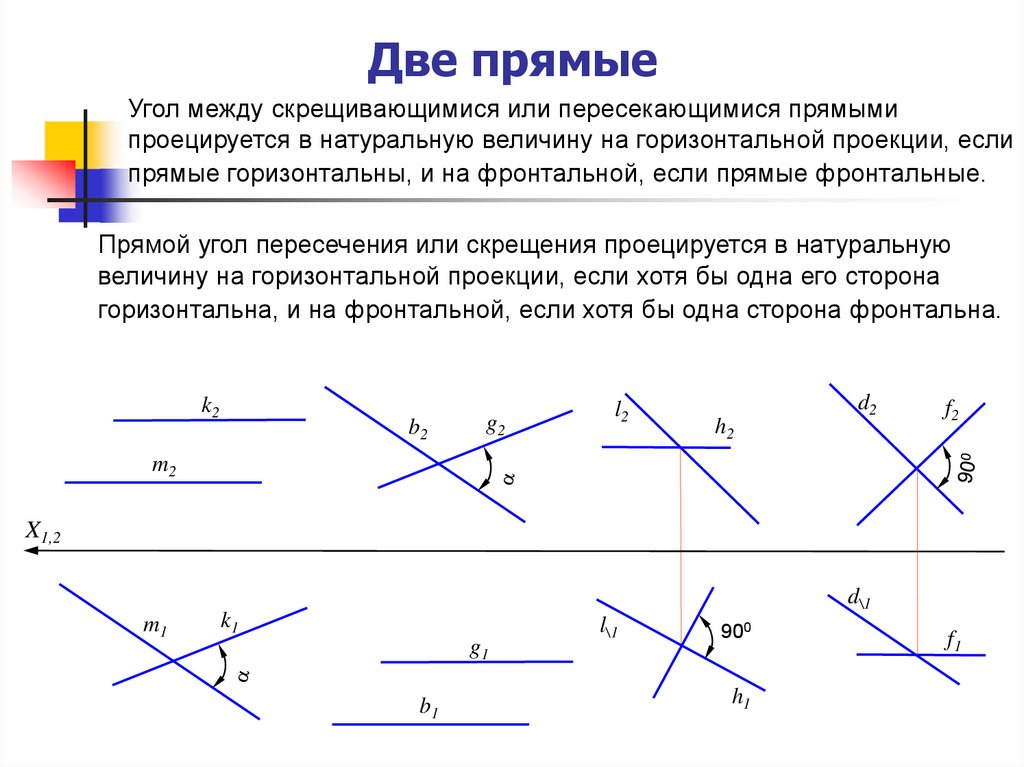
7. Две прямые
Угол между скрещивающимися или пересекающимися прямымипроецируется в натуральную величину на горизонтальной проекции, если
прямые горизонтальны, и на фронтальной, если прямые фронтальные.
Прямой угол пересечения или скрещения проецируется в натуральную
величину на горизонтальной проекции, если хотя бы одна его сторона
горизонтальна, и на фронтальной, если хотя бы одна сторона фронтальна.
k2
b2
g2
l2
h2
d2
f2
m2
X1,2
m1
d\1
k1
g1
b1
l\1
900
h1
f1
8. Прямая и плоскость
Взаимное положение прямой и плоскости определяют используяследующий алгоритм (способом сечения):
• прямая заключается во вспомогательную плоскость;
• определяется линия пересечения заданной плоскости со
вспомогательной плоскостью;
• выясняется взаимное положение двух прямых: заданной и линии
пересечения.
При этом возможны три случая
•две прямые пересекаются в одной точке, значит прямая пересекается с
плоскостью в этой точке.
•две прямые параллельны, значит, прямая параллельна плоскости
•две прямые совпадают, значит прямая, есть подмножество плоскости.
Определение точки встречи прямой с плоскостью — основная
позиционная задача курса инженерной графики, к ней можно свести
большинство позиционных задач.
9.
Основная позиционная задачаm2
D2
42
B2
D2
42
B2
m2
R2
32
32
C2
C2
x1,2
C1
C1
31
31
R1
D1
41
B1
m1
D1
41
B1
m1
1
1
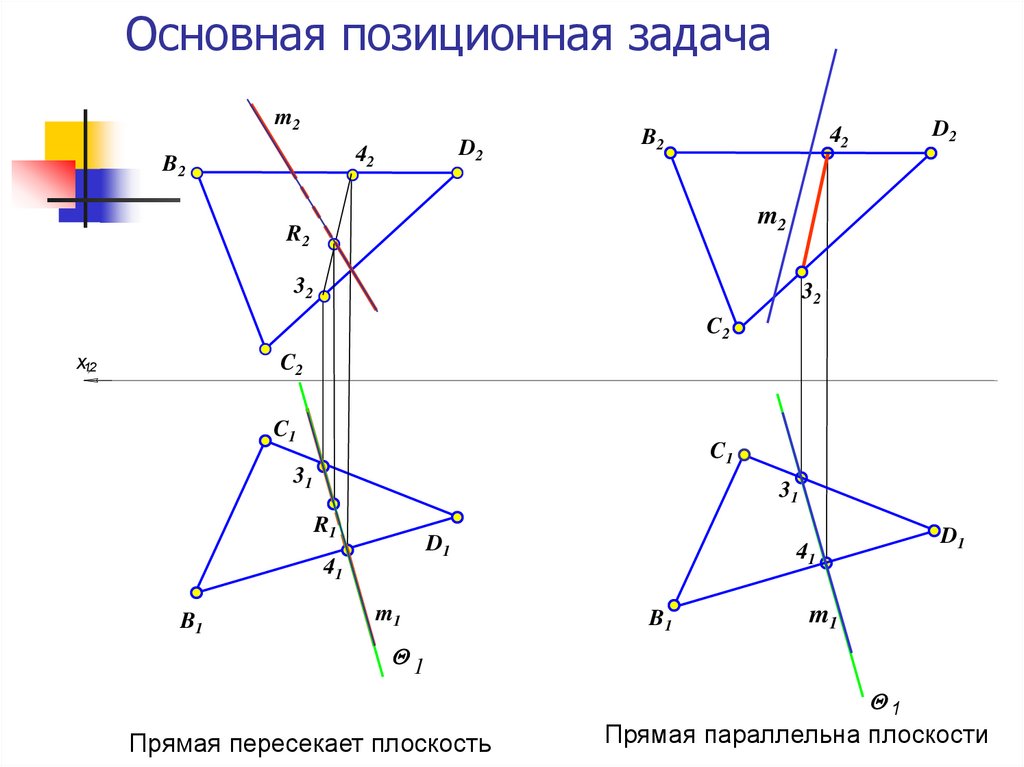
Прямая пересекает плоскость
Прямая параллельна плоскости
10. Основная позиционная задача
k242
B2
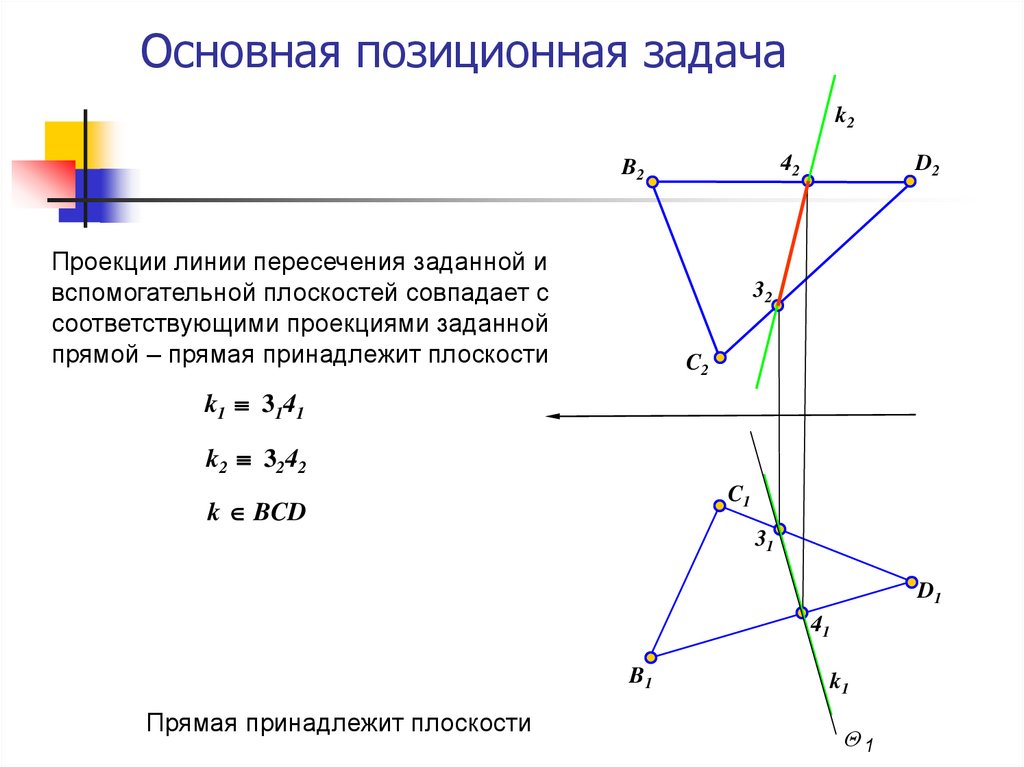
Проекции линии пересечения заданной и
вспомогательной плоскостей совпадает с
соответствующими проекциями заданной
прямой – прямая принадлежит плоскости
D2
32
C2
k1 3141
k2 3242
C1
k BCD
31
D1
41
B1
Прямая принадлежит плоскости
k1
1
11. Основная позиционная задача
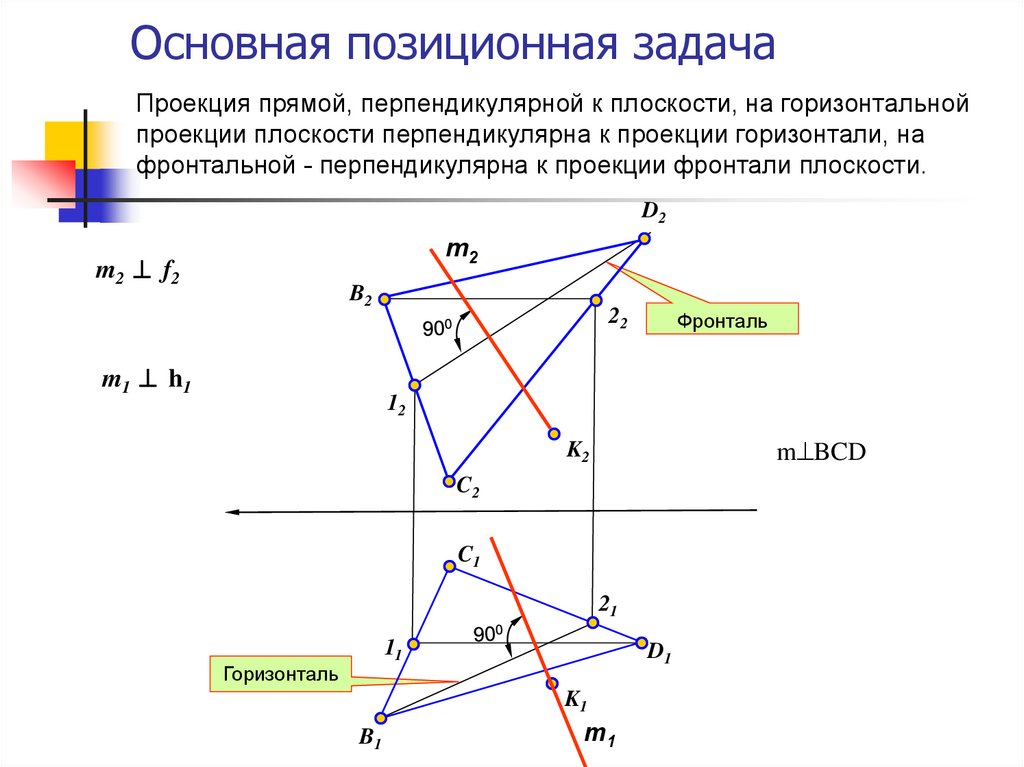
Проекция прямой, перпендикулярной к плоскости, на горизонтальнойпроекции плоскости перпендикулярна к проекции горизонтали, на
фронтальной - перпендикулярна к проекции фронтали плоскости.
D2
m2
m 2 f2
B2
m1 h1
22
Фронталь
12
K2
m BCD
C2
C1
21
11
Горизонталь
D1
K1
B1
m1
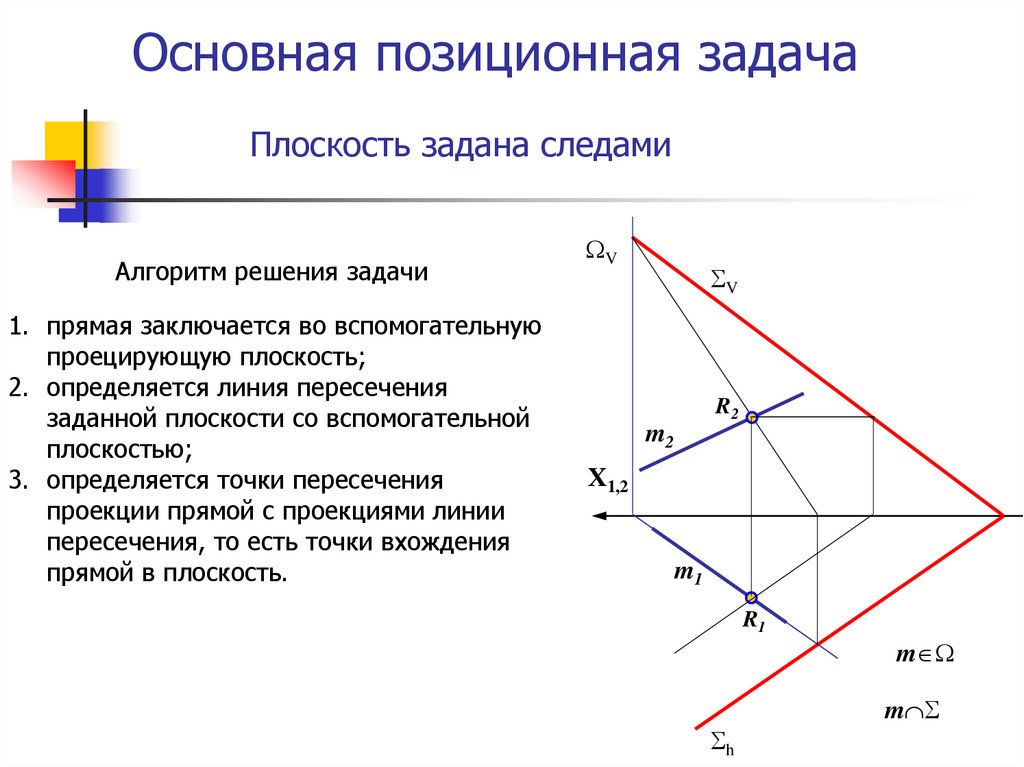
12. Основная позиционная задача
Плоскость задана следамиАлгоритм решения задачи
1. прямая заключается во вспомогательную
проецирующую плоскость;
2. определяется линия пересечения
заданной плоскости со вспомогательной
плоскостью;
3. определяется точки пересечения
проекции прямой с проекциями линии
пересечения, то есть точки вхождения
прямой в плоскость.
V
V
R2
m2
Х1,2
m1
R1
m
h
m
13. Основная позиционная задача
12
B2
l2
k2
n2
Х1,2
B1
A2
k1
l1
n1
A1
1
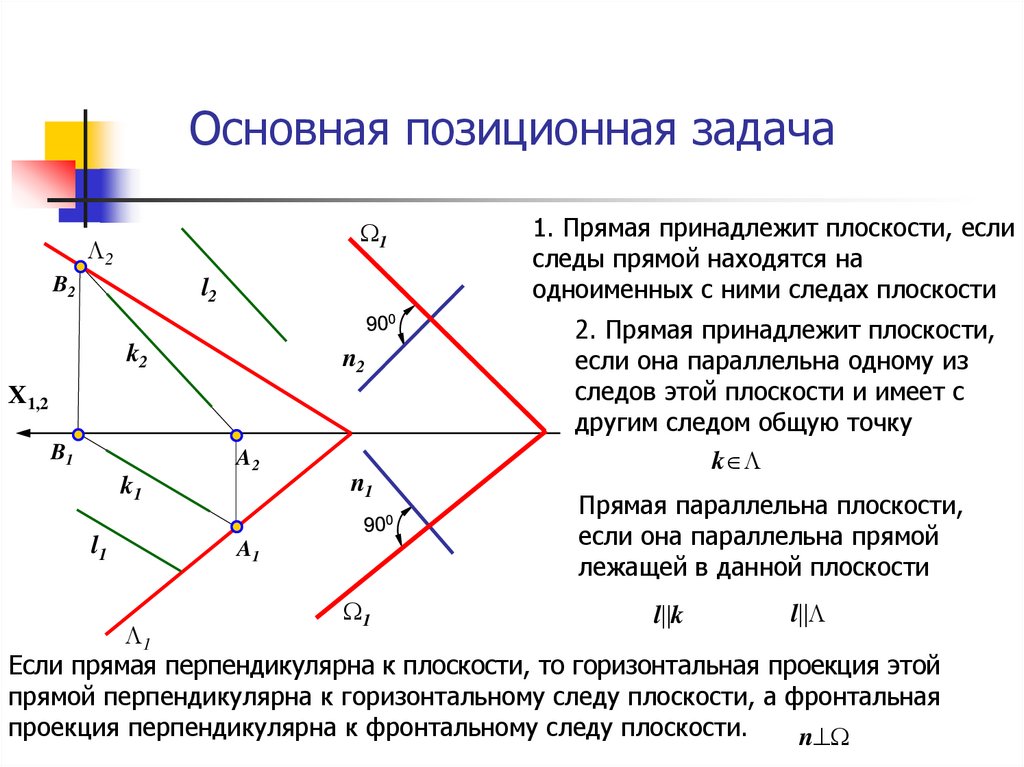
1. Прямая принадлежит плоскости, если
следы прямой находятся на
одноименных с ними следах плоскости
2. Прямая принадлежит плоскости,
если она параллельна одному из
следов этой плоскости и имеет с
другим следом общую точку
k
Прямая параллельна плоскости,
если она параллельна прямой
лежащей в данной плоскости
l k
l
1
Если прямая перпендикулярна к плоскости, то горизонтальная проекция этой
прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная
проекция перпендикулярна к фронтальному следу плоскости.
n
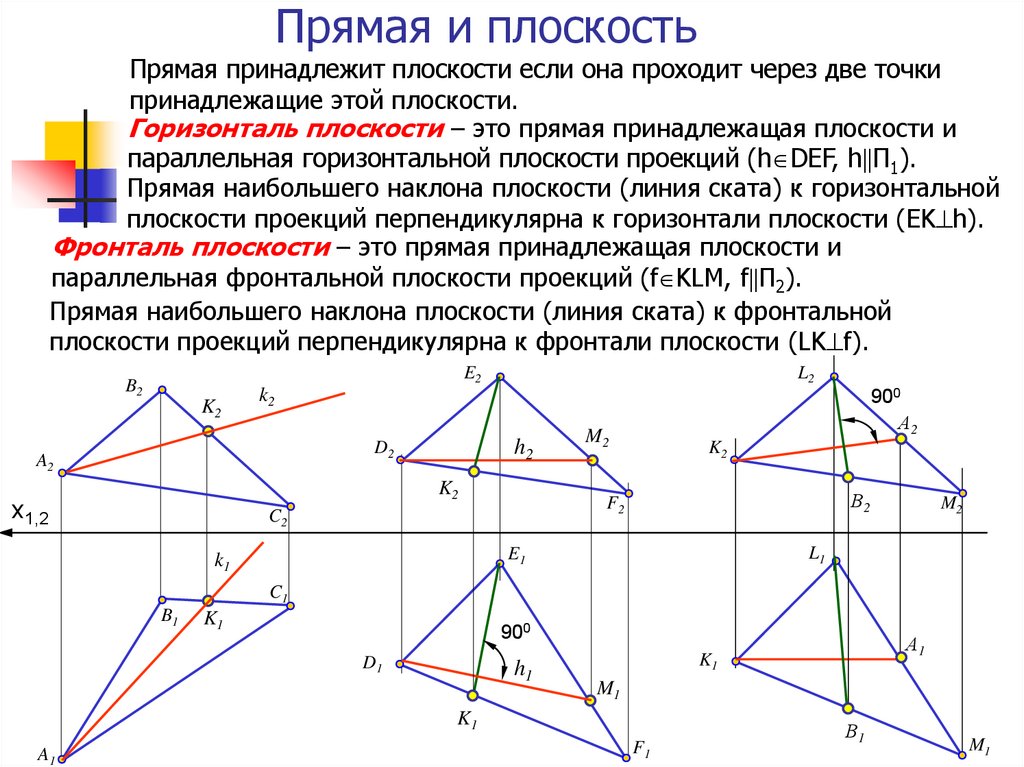
14. Прямая и плоскость
Прямая принадлежит плоскости если она проходит через две точкипринадлежащие этой плоскости.
Горизонталь плоскости – это прямая принадлежащая плоскости и
параллельная горизонтальной плоскости проекций (h DEF, h П1).
Прямая наибольшего наклона плоскости (линия ската) к горизонтальной
плоскости проекций перпендикулярна к горизонтали плоскости (ЕK h).
Фронталь плоскости – это прямая принадлежащая плоскости и
параллельная фронтальной плоскости проекций (f KLM, f П2).
Прямая наибольшего наклона плоскости (линия ската) к фронтальной
плоскости проекций перпендикулярна к фронтали плоскости (LK f).
L2
E2
B2
K2
k2
h2
D2
A2
K2
x1,2
900
А2
M2
K2
В2
F2
C2
L1
E1
k1
M2
C1
B1
K1
900
D1
h1
M1
K1
A1
А1
K1
F1
В1
M1
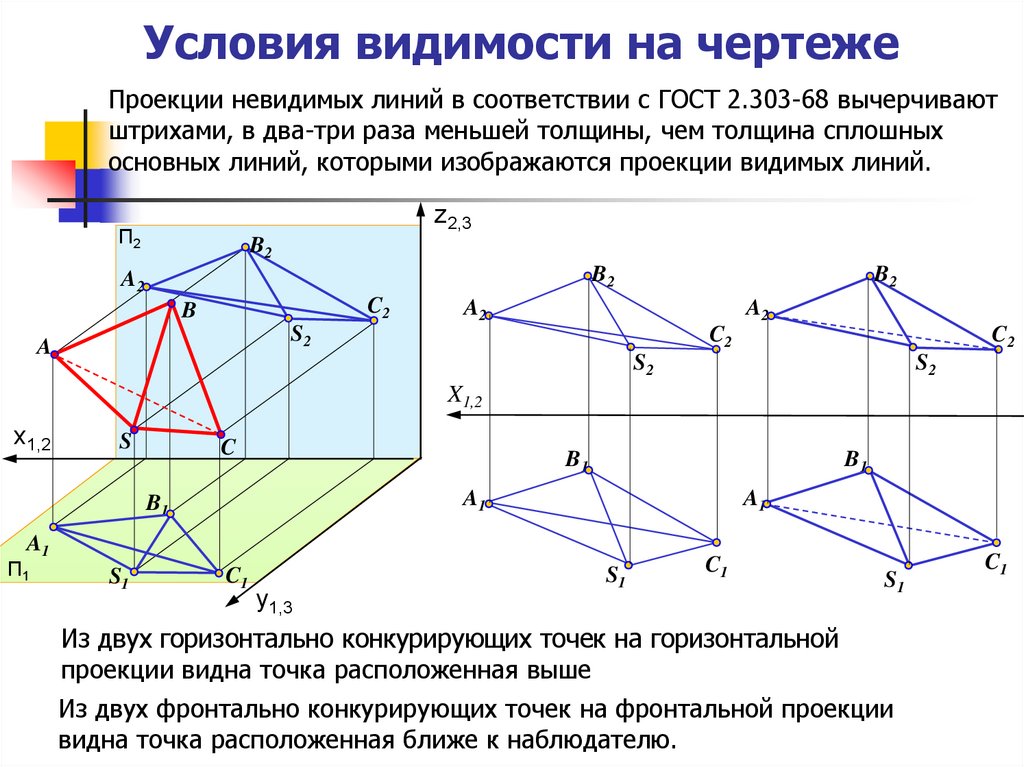
15. Условия видимости на чертеже
Проекции невидимых линий в соответствии с ГОСТ 2.303-68 вычерчиваютштрихами, в два-три раза меньшей толщины, чем толщина сплошных
основных линий, которыми изображаются проекции видимых линий.
z2,3
П2
B2
B2
A2
C2
B
B2
A2
A2
S2
A
C2
C2
S2
S2
X1,2
x1,2
S
C
B1
B1
A1
B1
A1
A1
П1
S1
C1
y1,3
S1
C1
S1
Из двух горизонтально конкурирующих точек на горизонтальной
проекции видна точка расположенная выше
Из двух фронтально конкурирующих точек на фронтальной проекции
видна точка расположенная ближе к наблюдателю.
C1
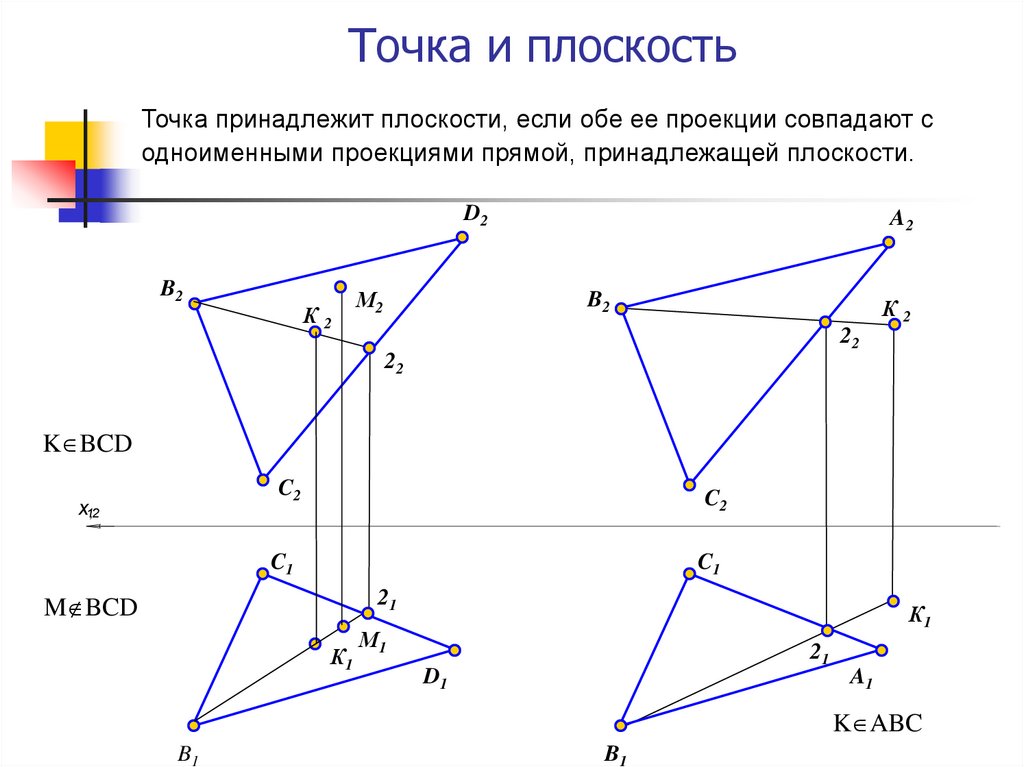
16. Точка и плоскость
Точка принадлежит плоскости, если обе ее проекции совпадают содноименными проекциями прямой, принадлежащей плоскости.
D2
B2
К2
М2
A2
B2
К2
22
22
K BCD
x1,2
C2
C2
C1
C1
21
M BCD
К1
К1
М1
21
D1
A1
K ABC
B1
B1
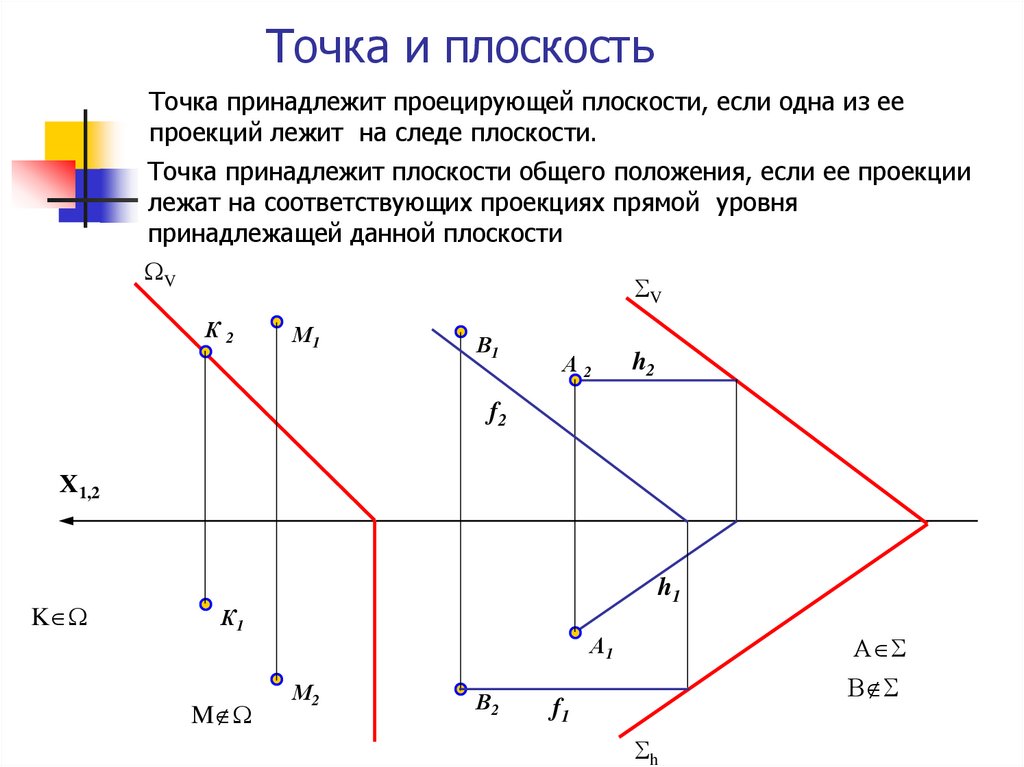
17. Точка и плоскость
Точка принадлежит проецирующей плоскости, если одна из еепроекций лежит на следе плоскости.
Точка принадлежит плоскости общего положения, если ее проекции
лежат на соответствующих проекциях прямой уровня
принадлежащей данной плоскости
V
V
К2
М1
В1
А2
h2
f2
Х1,2
K
h1
К1
M
А1
М2
В2
А
В
f1
h
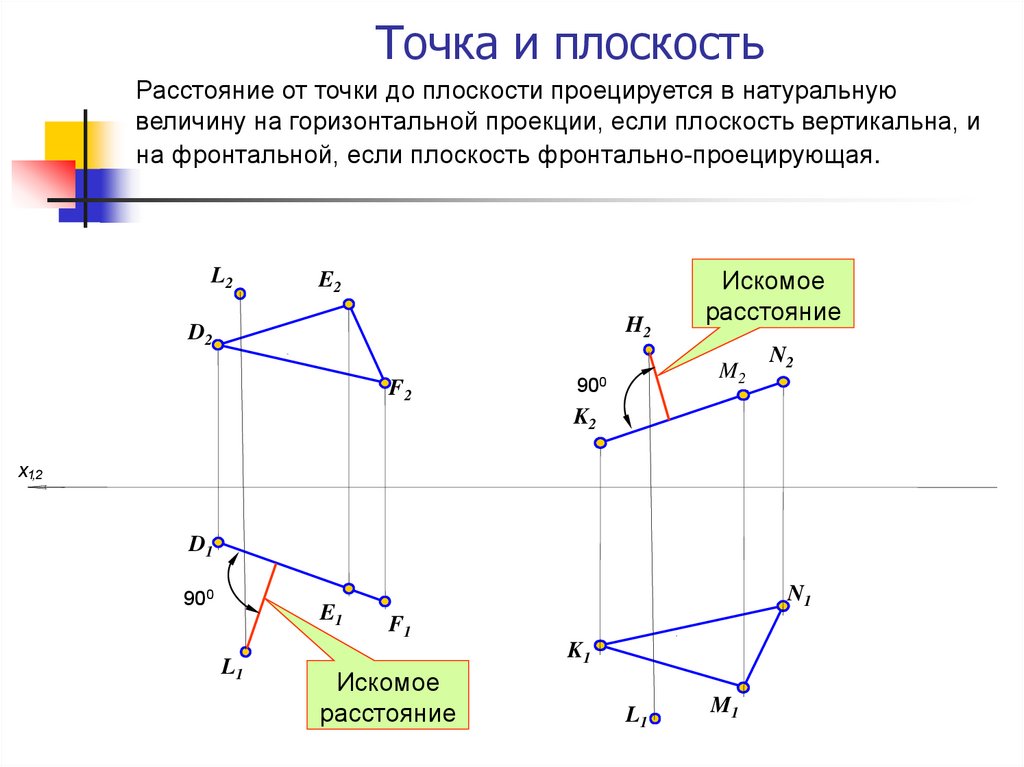
18. Точка и плоскость
Расстояние от точки до плоскости проецируется в натуральнуювеличину на горизонтальной проекции, если плоскость вертикальна, и
на фронтальной, если плоскость фронтально-проецирующая.
L2
E2
H2
D2
F2
Искомое
расстояние
M2
900
N2
K2
x1,2
D1
900
E1
L1
N1
F1
K1
Искомое
расстояние
L1
M1
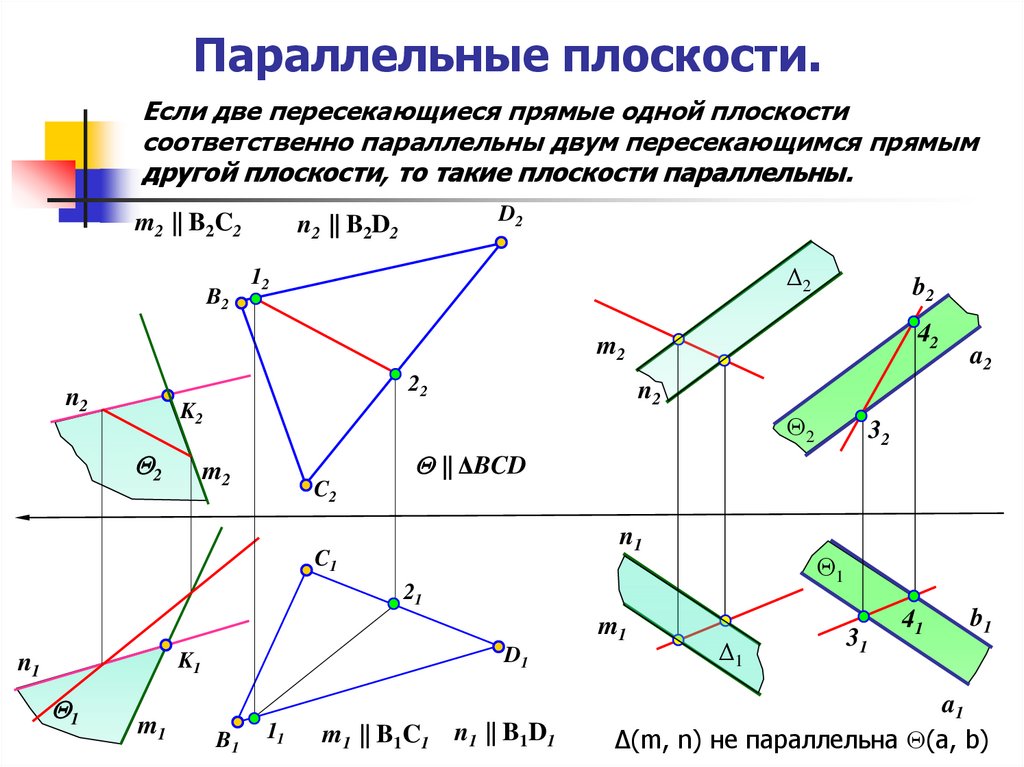
19. Параллельные плоскости.
Если две пересекающиеся прямые одной плоскостисоответственно параллельны двум пересекающимся прямым
другой плоскости, то такие плоскости параллельны.
m2 B2C2
B2
D2
n2 B2D2
Δ2
12
b2
42
m2
22
n2
n2
K2
2
2
C2
n1
C1
1
21
m1
D1
K1
n1
1
m1
B1
32
ΔBCD
m2
a2
11
m1 B1C1 n1 B1D1
Δ1
31
41
b1
a1
Δ(m, n) не параллельна (a, b)
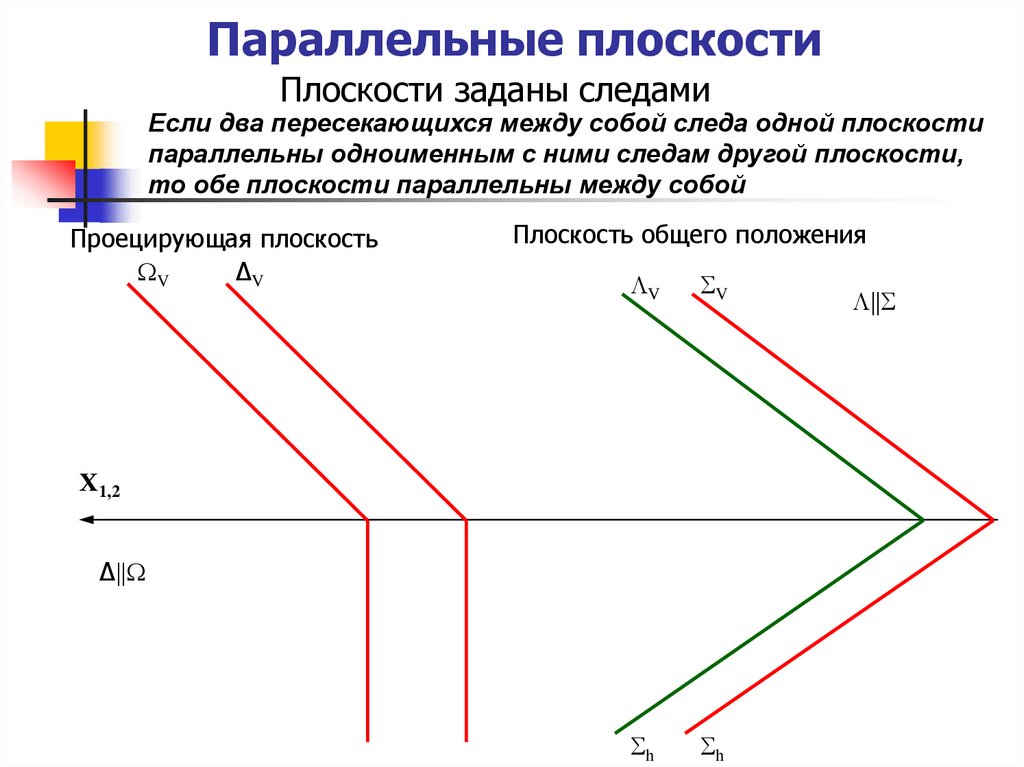
20. Параллельные плоскости
Плоскости заданы следамиЕсли два пересекающихся между собой следа одной плоскости
параллельны одноименным с ними следам другой плоскости,
то обе плоскости параллельны между собой
Проецирующая плоскость
V
ΔV
Плоскость общего положения
V
V
h
h
Х1,2
Δ
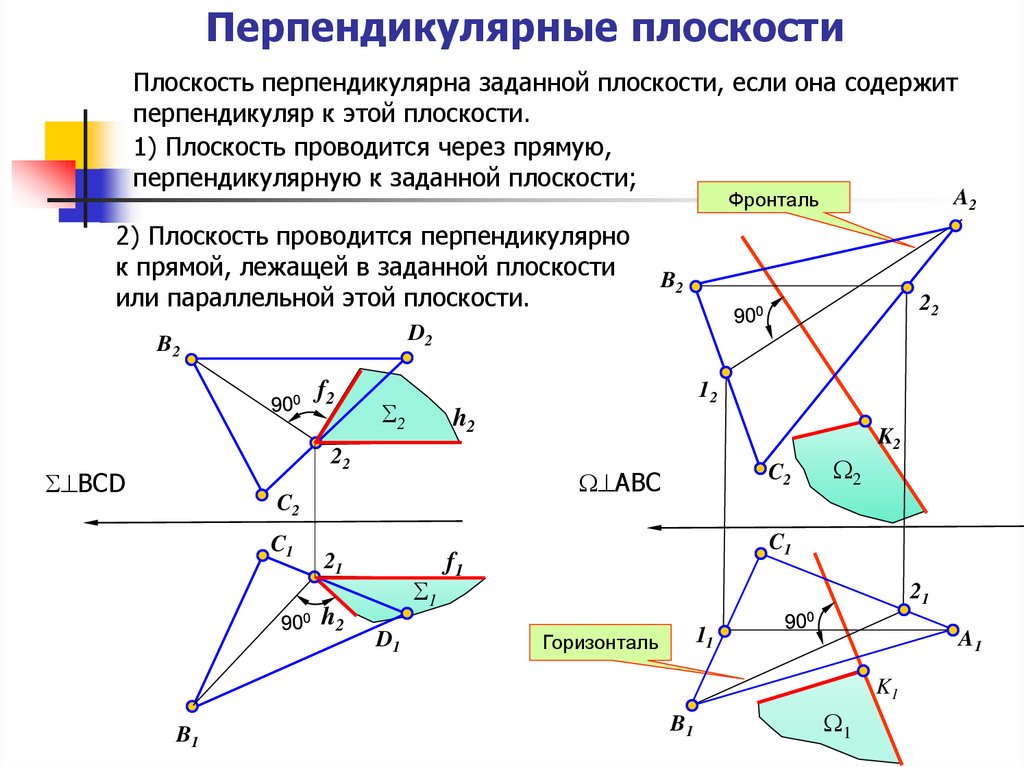
21. Перпендикулярные плоскости
Плоскость перпендикулярна заданной плоскости, если она содержитперпендикуляр к этой плоскости.
1) Плоскость проводится через прямую,
перпендикулярную к заданной плоскости;
Фронталь
2) Плоскость проводится перпендикулярно
к прямой, лежащей в заданной плоскости
или параллельной этой плоскости.
B2
22
D2
B2
f2
12
2
h2
22
BCD
A2
21
h2
C2
ABC
C2
C1
K2
1
D1
2
C1
f1
21
11
Горизонталь
A1
K1
B1
B1
1
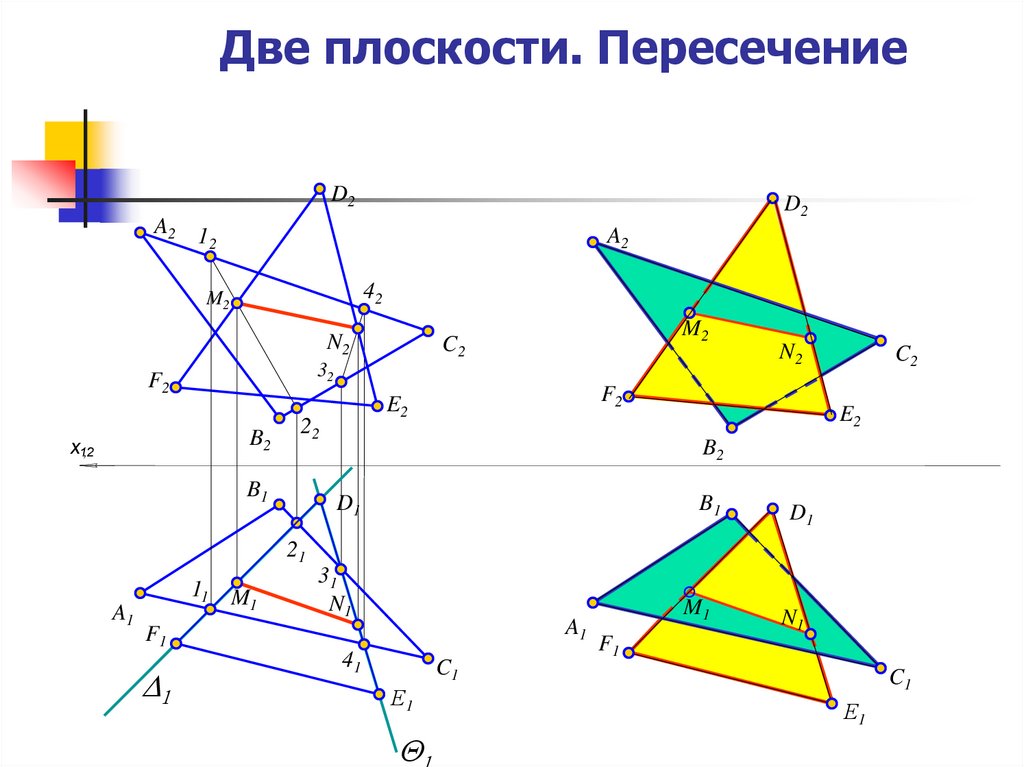
22. Две плоскости. Пересечение
D2D2
A2 1
2
A2
42
M2
N2
32
F2
B2
x1,2
M2
C2
B1
F2
E2
22
N2
C2
E2
B2
D1
B1
D1
31
N1
M1
N1
21
A1
11 M
1
A1
F1
D1
41
C1
Е1
F1
C1
Е1
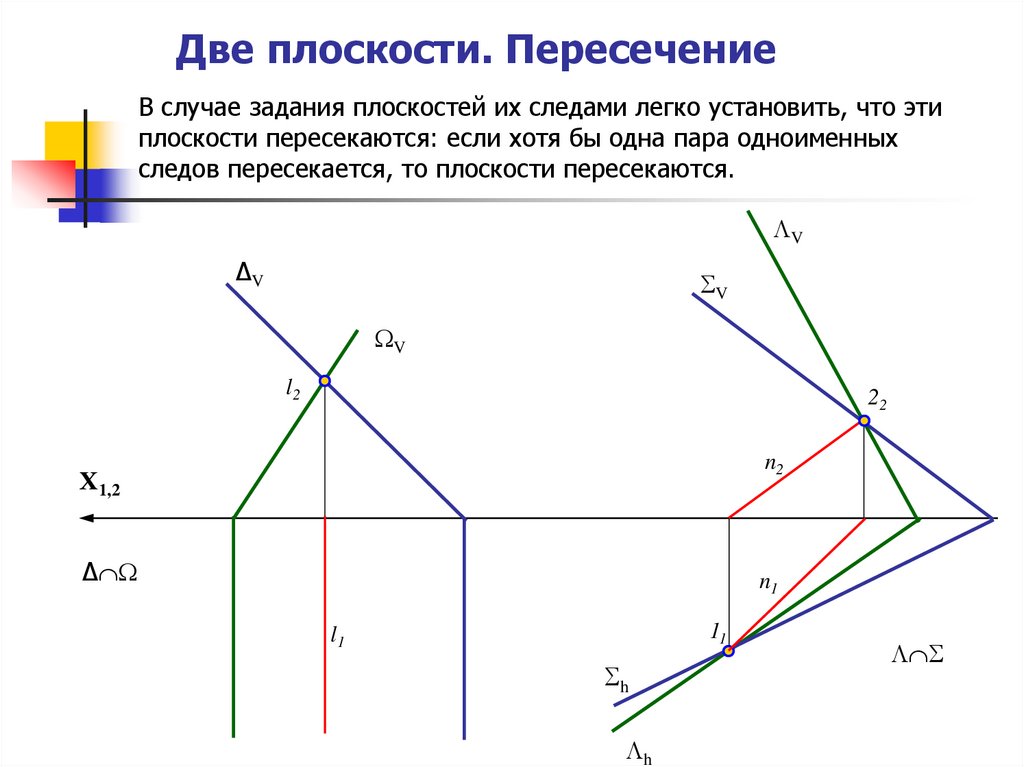
23. Две плоскости. Пересечение
В случае задания плоскостей их следами легко установить, что этиплоскости пересекаются: если хотя бы одна пара одноименных
следов пересекается, то плоскости пересекаются.
V
ΔV
V
V
l2
22
n2
Х1,2
Δ
n1
11
l1
h
h



 Инженерная графика
Инженерная графика








