Похожие презентации:
Интерполирование и смежные вопросы. Приближение функций
1.
1Глава I. Интерполирование и смежные
вопросы. Приближение функций
§1 Постановка задачи приближения функций
Под интерполированием понимается задача приближения функции,заданой аналитически или таблично, другой функцией, быть может, более
простой природы, но близкой в каком-либо смысле к заданой функции.
Так, если исходная функция задана аналитически, то замена её функцией
более простой природы, например, многочленом,возникает, когда:
1)Следует составить таблицу приближенных значений этой функции.
Оперировать с исходной функцийе, имеющей сложное аналитическое
представление,затруднительно, а большая точность не ребуется;
2)многие численные методы построены на замене функции сложной
природы функцией близкой, но более простой природы. Так,например,
решая уравнение f (x) = 0 методом Ньютона, мы заменяем f (x) окрестности рассматриваемой точки x0 линейной функцией f0 (x) = f (x0 ) +
f (x0 )(x − x0 );
3)исходная функция задана таблично - являеся результатом дискретных наблюдений. Для того что бы оперировать стаблично заданой функцией (производить арифметические действия,дифференцироватьб интегрировать и т.д.), последнюю приближают некоторой близкой ей функцией, которая имеет формульне представление.
Часто в качестве прилижающей функции для непрерывной функции
берут полином, применяют так называемое алгебраическое интерполирование. Основания к этому:
а)многочлены являются функциями простой природы;с ними легко
оперировать, действия над многочленами легко поддаются программированию;
б)справедливо свойство полноты многочленов в классе непрерывных
функций(теорема Вейерштрасса).
Существуют различные способы приближения функций при помощи
многочленов. Наиболее распространенным являеся следующий.
На промежутке [a, b],где задана исходная непрерывная функция f (x),
выбирается n + 1 точка - узлы интерполирования:x0 , x1 , . . . , xn ; троится
многочлен Pn (x), степени не выше n,начение которого Pn (xi ) в заданных
точках xi совпадают со значениями f (xi ):
+ . . . + an−1 xi + an = f (xi ) (i = 0, 1, . . . , N ). (1)
Pn (xi ) = a0 xni + a1 xn−1
i
В результате получаем систему N + 1 уравнений с n + 1 неизвестными
a0 , a1 , . . . , an .
Дадим геометрическую интерпритацию рассмотренной задачи (рис.I).
Обозначим Mk точку на плоскости (x, y) с координатами
(xk , f (xk )) k = 0, 1, 2, 3.
2.
2Рис.1
Условия f (xk ) = P3 (xk ) означают, что график многочлена y = P3 (x)
должен проходить через точки M0 , M1 , M2 , M3 . Более общая постановка
задачи интерполирования заключается в следующем.
Пусть для функции f (x) известны её значения в k0 различных точ(0)
(0)
(0)
ках x1 , x2 , . . . , xk0 ; известны значения её производной в k1 различных
(1)
(1)
(1)
точках: x1 , x2 , . . . , xk1 ; и т.д.; известны значения производной порядка
(m)
(m)
(m)
m для f (x) в km различных точках x1 , x2 , . . . , xkm : k0 + k1 + . . . km =
N.
Требуется построить функцию Sn (x) (обобщенный интерполиционный
полином), удовлетворяющую условиям
(k)
(k)
Sn(k) (xi ) = f (k) (xi ),
i = 1, 2, . . . , mk ,
k = 0, 1, . . . , m.
(2)
Для построения Sn (x) выбирают систему линейно-независимых функций ϕ1 (x), ϕ2 (x), . . . , ϕn (x) - простой структуры и Sn (x) ищут в виде
Sn (x) = c1 ϕ1 (x) + . . . + cn ϕn (x).
Для определения c1 , . . . , cn получают линейную систему (2).
Интерполирование вида (1) называется интерполированием по значениям функции. Интерполирование вида (2) назвается интерполированием
с кратными узлами. Погрешность Rn (x) = f (x)−Sn (x) называется остатком интерполирования.
Функции ϕ1 (x), . . . , ϕn (x) выбираются в зависимости от свойств интерполируемой функции f (x). Если в качестве ϕk (x) берут xk−1 , то имеют
дело с алгебраическим интерполированием (функцию f (x) приближают
полиномом). Если же f (x) - периодическая функция (например, имеет
период 2π ), то в качестве функций ϕk (x) целесообразно взять, функции
sin kx, cos kx k = 0, 1, . . . , n. Такой выбор приводит к тригонометрическому интерполированию (функцию f (x) приближают тригонометрическим полиномом).
Если число n функций ϕ1 (x), . . . , ϕn (x) меньше числа узлов x1 , x2 , . . . , xN ,
в которых задана функция f (x), то система (1) и (2) будут переопределен-
3.
3ными (число уравнений больше числа неизвестных). В этом случае неизвестные коэффициенты интерполяционного полинома находятся по принципу
метода наименьших квадратов.
В дальнейшем будут рассмотрены различные виды построения интерполяционного полиномаю Но предварительно остановимся на свойствах
конечных и разделенных разностей,которые для дискретно заданных
функций играют роль, аналогичную производной для функций с непрерывно
изменяющимся аргументом.
§2 Конечные и разделенные разности и их свойства
Конечные разности применяются, когда функция f (x) задана в равноотстоящих узлах xk = x0 + kh
(k = 0, 1, . . . , N ; h > 0):
y0 =
f (x0 ), . . . , yk = f (xk ), . . . , yn = f (xN ), т.е. задана таблица значений
f (x) с шагом n от x0 до xN : x = x0 (h)xN
Конечными разностями I-го порядка f (x) называются числа
y0 = y1 − y0 ,
y1 = y2 − y1 , . . . ,
yN −1 = yN − yN −1 .
Аналогично определяются разности 2-го порядка:
2
2
y0 = y1 − y0 ,
y1 = y2 − y1 , . . . , 2 yN −2 = yN −1 − yN −2 .
Если известны разности порядка k: k y0 , k y1 , . . . , то разности k + 1
порядка определяются соотношениями k+1 y0 = k y1 − k y0 ; k+1 y1 =
k
y2 − k y1 , . . . .
Конечные разности принято записывать в таблицу:
x
x0
y
y0
y
y0
x1
y1
y1
x2
y2
y2
x3
y3
x4
y4
2
2
2
2
y
y0
y1
3
3
3
y
y0
4
4
y
y0
y1
y2
y3
Рассмотрим некоторые свойства.
1)Конечные разность суммы дух функций F (x) = f (x) + g(x) равна
сумме онечных разностей слагаемых
F (xi ) = f (xi ) + g(xi )
Если F (x) = cf (x) c − const, то F (xi ) = c f (xi )
3)Конечная разность от многочлена степени n является многочленом
степени n − 1. Это следует из пп.1 и 2, если учесть, что
xk = (x + h)k − xk = k h xk−1 +
k(k − 1) 2 k−2
hx
+ ....
2!
4)Конечная разность порядк n от многочлена степени n равна постоянной
величине, так что все разности более высокого порядка равны 0.
4.
4РАЗДЕЛЕНИЕ РАЗНОСТЕЙ (разностные отношения)применяются,
когда таблица функции f (x) задана для некоторых значений аргумента
x0 , . . . , xN (не обязательно равностоящих).
Разделенными разностями 1-го порядка называются числа
f (x1 , x0 ) =
f (x1 ) − f (x0 )
f (x2 ) − f (x1 )
, f (x2 , x1 ) =
, ... .
x1 − x0
x2 − x1
Геометрически число f (xi , xi−1 ) есть угловой коэффициент хорды графика
функции f (x). Аналогично, разделенными разностями 2-го порядка называются
числа
f (x2 , x1 , x0 ) =
f (x2 , x1 ) − f (x1 , x0 )
f (x3 , x2 ) − f (x2 , x1 )
, f (x3 , x2 , x1 ) =
, ...
x2 − x0
x3 − x1
Аналогично определяются разностные отношения 3-го порядка
f (x3 , x2 , x1 , x0 ) =
f (x3 , x2 , x1 ) − f (x2 , x1 , x0 )
, ...
x3 − x0
и т.д.
Таблица разделенных разностей:
x
x0
0
f (x0 )
1
Разностные отношения порядка
2
3
4
f (x1 , x0 )
x1
f (x1 )
f (x2 , x1 , x0 )
f (x2 , x1 )
x2
f (x2 )
x3
f (x3 )
x4
f (x4 )
f (x3 , x2 , x1 , x0 )
f (x3 , x2 , x1 )
f (x3 , x2 )
f (x4 , x3 , x2 , x1 , x0 )
f (x4 , x3 , x2 , x1 )
f (x4 , x3 , x2 )
f (x4 , x3 )
СВОЙСТВА
1. Разностное отношение суммы функций F (x) = f (x)+ϕ(x) равно сумме
разностных отношений слагаемых
2. Если F (x) = cf (x), c − const, то F (xi+1 , xi ) = cf (xi+1 , xi ).
3. Разностное отношение порядка n от многочлена степени n есть
постоянная величина, та что разностные отношения более высокого порядка
равны нулю.
В силу пп.1 и 2 это достаточно доказать для f (x) = xn . Имеем f (x1 , x0 ) =
n
xn
1 −x0
= xn−1
+ xn−2
x0 + . . . + xn−1
-полином степени n − 1.
1
1
0
x1 −x0
n
f (xk )
4. f (xn , . . . , x0 ) = k=0 ω (xk ) , где ω(x) = (x−x0 ) . . . (x−xn ) - многочлен,
корнями которого являются точки x0 , x1 , . . . , xn ;
d
ω(x)] xk = (xk − xk−1 )(xk − xk+1 ) . . . (xk − xn ).
dx
Справедливость формулы п.4 устанавливается непосредственной проверкой:
ω (xk ) = [
f (x1 , x0 ) =
f (x1 )
f (x0 )
f (x0 )
f (x1 )
f (x1 ) − f (x0 )
=
+
≡
+
,
x1 − x0
x1 − x0 x0 − x1
ω (x0 ) ω (x1 )
5.
5где ω(x) = (x − x0 )(x − x1 );
f (x2 ,x1 )
f (x1 )
1
1 ,x0 )
2)
1)
− fx(x2 −x
= x2 −x
+ xf2(x
− xf1(x
x2 −x0
x1 −2
−x1
−x0
0
0
f (x0 )
1
1
2)
1)
+ (x2 −xf0(x
+ xf2(x
− x1 −x
(x0 −x1 )(x0 −x2 )
)(x2 −x1 )
−x0
x1 −x2
0
f (x0 )
f (x1 )
f (x2 )
= (x0 −x1 )(x0 −x2 ) + (x1 −x0 )(x1 −x2 ) + (x2 −x0 )(x2 −x1 )
f (x2 , x1 , x0 ) =
=
+
f (x0 )
x0 −x1
=
=
5. Из п.4 следует, что разностное отношение является симметрической
функцией своих аргументов: не изменяется при любой перестановке неизвестных.
6. Справедлива формула f (xk ) = f (x0 ) + (xk − x0 )f (x0 , x1 ) + (xk −
x0 )(xk −x1 )f (x0 , x1 , x2 )+. . .+(xk −x0 )(xk −x1 ) . . . (xk −xk−1 )f (x0 , x1 , . . . , xk ).
Доказательство по индукции. При числе точек k+1 = 2 справедливость
вытекает из определения разностного отношения
f (x1 ) = f (x0 ) + (x1 − x0 )f (x0 , x1 ).
Пусть формула верна для числа точе = k + 1
n. Докажем её для
k = n. По индуктивному предположению имеем
f (xn ) = f (x1 )+(xn −x1 )f (x1 , x2 )+. . .+(xn −x1 ) . . . (xn −xn−1 )f (x1 , x2 , . . . , xn ).
Далее по определению разностных отношений для любого k справедливо
f (x1 , . . . , xk ) = f (x0 , x1 , . . . , xk−1 )+(xk −x0 )f (x0 , x1 , . . . , xk ). Заменив каждое
из разностных отношений (x1 , . . . , xk ), входящее в f (xn ) по этой формуле,
получим
f (xn ) = [f (x0 ) + f (x0 , x1 )(x1 − x0 )] + (xn − x1 )[f (x1 , x0 ) + (x2 − x0 )f (x0 , x1 , x2 )]+
+(xn − x1 )(xn − x2 )[f (x0 , x1 , x2 ) + (x3 − x0 )f (x0 , x1 , x2 , x3 )] + . . . +
+(xn − x1 )(xn − x2 ) . . . (xn − xn−1 )[f (x0 , x1 , . . . , xn−1 ) + (xn − x0 )f (x0 , x1 , . . . , xn )] =
= f (x0 ) + f (x0 , x1 )[(x1 − x0 ) + (xn − x1 )] + f (x0 , x1 , x2 )(xn − x1 )[(x2 − x0 ) + (xn − x2 )]+
+ . . . + (xn − x1 )(xn − x2 ) . . . (xn − xn−1 )[xn−1 − x0 + xn − xn−1 ]f (x0 , . . . , xn ) =
= f (x0 ) + (xn − x0 )f (x0 , x1 ) + . . . + (xn − x0 ) . . . (xn − xn−1 )f (x0 , . . . , xn ).
7. Связь разностных отношений с производными. Если ункция f (x)
- дифференцируемая n раз на [a, b] и точки x0 , x1 , . . . , xn ∈ [a, b], то
существует точка ξ ∈ (a, b) такая, что
f (x0 , x1 , . . . , xn ) =
f (n) (ξ)
.
n!
Для доказательства введем многочлен, определяемый формулой P (x) =
f (x0 ) + (x − x0 )f (x0 , x1 ) + (x − x0 )(x − x1 )f (x0 , x1 , x2 ) + . . . + (x − x0 ) . . . (x −
xn−1 )f (x0 , . . . ,n ). Этот многочлен имеет степень меньшую или равную
n и в силу п.6 обладает свойством:
f (xk ) = P (xk ) , k = 0, 1, . . . , n. Образуем функцию ϕ(x) = f (x) − P (x),
она n раз дифференцируема и ϕ(xk ) = 0, k = 0, 1, . . . , n, т.е. обращается
на [a, b] в нуль в n+1 различных точках. По теореме Ролля, ϕ (x) имеет по
меньшей мере n различных нулей внутри [a, b] ; ϕ (x) − n − 1 различных
6.
6нулей внутри [a, b] ; . . . ; ϕ(n) (x) - один нуль внутри [a, b]. Обозначим этот
нуль через ξ(a < ξ < b). Имеем ϕ(n) (ξ) = f (n) (ξ) − P (n) (ξ) ≡ f (n) (ξ) −
n!f (x0 , x1 , . . . , xn ) = 0. Отсюда f (x0 , . . . , xn ) = n!1 f (n) (ξ), что и требовалось
доказать.
8. Связь разделенных разностей с конечным разностями. Пусть точки
xk - равноотстоящие: xk = x0 + kh, k = 0, 1, . . . , n, h > 0. Тогда
f (x0 , x1 ) =
=
1
x2 −x0
f (x1 )−f (x0 )
x1 −x0
f (x1 )
h
−
=
f (x0 )
h
f (x0 )
,
h
=
f (x0 , x1 , x2 ) =
1
2!h2
2
1
x2 −x0
[ f (x1 , x2 ) − f (x0 , x1 )] =
f (x0 ).
Нетрудно видеть,что при любом n
f (x0 , x1 , . . . , xn ) =
1
n!hn
n
f (x0 )
Теперь можно установить связь конечных разностей с производными.
9. Если f (x) - дифференцируемая n раз функция на [x0 , x0 + nh], то
внутри этого промежутка имеется точка ξ такая что
n
f (x0 ) = hn f (n) (ξ).
Перейдем к задаче построения интерполяционного полинома.
§3 Интерполирование по значениям функции
Вернемся к задаче (1) §1 ,к частному случаю алгебраического интерполирования,
когда в различных узлах интерполирования
x0 , x 1 , . . . , x n
(1)
f (x0 ), f (x1 ), . . . , f (xk )
(2)
заданы значения функции
и требуется построить многочлен
Pn (x) = a0 xn + a1 xn−1 + . . . + an
(3)
совпадающий с f (x) в узлах (1)
Pn (xk ) = f (xk ) ,
k = 0, 1, . . . , n
(4)
Докажем существование и единственность полинома (3),подчиненного
условию (4), если узлы x0 , . . . , xn интерполирования различны, для чего
систему (4) запишем в развернутом виде:
+ . . . + an−1 x0 + an = f (x0 ),
a0 xn0 + a1 xn−1
0
...
(5)
n−1
n
a0 xn + a1 xn + . . . + an−1 xn + an = f (xn )
7.
7Определитель системы (5)
xn0 xn−1
. . . x0 1
0
n−1
n
x x1
. . . x1 1
W = 1
.......................
xnn xn−1
. . . x1 1
n
есть определитель Вандермонда. Он н равен нулю, так как среди чисел
(1) нет совпадающих. Следовательно, система (5) имеет единственное
решение, т.е. полином (3) существует и единствен.
Построенный полином (3) является одной из форм записи интерполяционного
полинома. Рассмотрим другие формы записи, не требующие решения
системы (5).
§4 Интерполяционная формула Лагранжа
Построим многочлен ωk (x), равный единице при x = xk и нулю в остальных
узлах x0 , x1 , . . . , xk−1 , xk+1 , . . . , xn . Очевидно, ωk (x) = c(x − x0 ) . . . (x −
xk−1 )(x−xk+1 . . . (x−xn )). Постоянную c определим из условия ωk (xk ) = 1.
Имеем
c =
1
1
=
(xk − x0 ) . . . (xk − xk−1 )(xk − xk+1 ) . . . (xk − xn )
ω (xk )
, так что
ωk (x) =
ω(x)
(x − xk )ω (xk )
(6)
Тогда очевидно, что
n
n
ωk (x)f (xk ) =
Pn (x) =
k=0
k=0
ω(x)
f (xk )
(x − xk ) ω (xk )
(7)
Действительно, степень Pn (x) не превосходит n и
Pn (xk ) = ωk (xk )f (xk ) = f (xk ),
k = 0, 1, . . . , n
Интерполяционный полином в форме (7) называется интерполяционной
формулой Лагранжа. Он обычно применяется, когда узлы (1) не являются
равноотстоящими.
§5 Интерполяционная формула Ньютона
Существует другая форма записи интерполяционного полинома, именно
интерполяционный многочлен в форме Ньютона:
Pn (x) = f (x0 )+(x−x0 )f (x0 , x1 )+ . . . +(x−x0 )(x−x1 ) . . . (x−xn−1 )f (x0 , . . . , xn )
(8)
Из (8) следует, что чтепень Pn (x) не превосходит n. Кроме того, Pn (xk ) =
f (xk ) , k = 0, 1, . . . , n, что следует из свойства п.6 для разделенных
разностей.
8.
8Формула (8) имеет преимущество перед формулой (7). Так, пусть
полином Pn (x) уже построен и дает недостаточно хорошее приближение,
поэтому возникает надобность в добавлении нового узла. При добавлении
нового узла в формулах (7) и (8) добавляется лишь одно сагаемое. При
этом в формуле (8) прежние слагаемые остаются без изменения, тогда
как в формуле (7) изменяются все слагаемые, в том числе и ранее построенные.
§6 Об остаточном члене интерполирования
Рассмотрим разность
f (x) − Pn (x) = Rn (f, x)
(1)
остаток интерполирования. Если f (x) есть многочлен степени
n, то
Pn (x) ≡ f (x), что следует из единственности интерполяционного полинома.
Если же f (x) на промежуте [a, b], содержащем узлы интерполирования,
не является многочленом степени n, то формула (1) обращается в нуль
только в узлах x0 , x1 , . . . , xn и будет заведомо отлична от тождественного
нуля.
ТЕОРЕМА О ПРЕДСТАВЛЕНИИ Rn (F, X) ДЛЯ ИНТЕРПОЛИРОВАНИЯ
В ФОРМЕ ЛАГРАНЖА. Если f (x) - функция, дифференцируемая n+1
раз на [a, b], содержащем узлы интерполирования x0 , . . . , xn то для любой
точки x ∈ [a, b] существует точка ξ ∈ (a, b) такая ,что
Rn (f, x) =
ω(x) (n+1)
f
(ξ)
(n + 1)!
(2)
где ω(x) = (x − x0 ) . . . (x − xn ).
ДОКАЗАТЕЛЬСТВО. Возьмем точку x ∈ [a, b], отличную от узлов
x0 , . . . , xn , и рассмотрим значения f (x0 ), . . . , f (xn ) , f (x). Согласно свойству
п.6 при k = n + 1 , xk = x , имеем f (x) = f (x0 ) + (x − x0 )f (x0 , x1 ) +
. . . + (x − x0 ) . . . (x − xn−1 )f (x0 . . . , xn ) + ω(x)f (x0 , . . . xn , x) = Pn (x) +
ω(x)f (x0 , . . . , xn , x), так как сумма первых n + 1 слагаемых совпадает
с Pn (x) в форме Ньютона. Таким образом, Rn (f, x) = f (x) − Pn (x) =
ω(x)f (x0 , x1 , . . . , xn , x). По свойству п.7 имеем,
(n+1)
f (x0 , . . . , xn , x) = f (n+1)!(ξ) , отсюда справедливость (2) очевидна для x =
xk , k = 0, 1, 2, . . . , n. Но при x = xk имеем Rn = 0
ω(xk ) (n+1)
и (n+1)!
f
(ξ) = 0, так что формула (2) справедлива при любом x ∈
[a, b]
Рассмотрим задачу минимизации остатка интерполирования на классе
Wn+1 (M ) функций f (x), заданных на [a, b], имеющих производную n + 1
порядка, удовлетворяющую на [a, b] неравенству
|f (n+1) (x)|
M
(3)
Пусть узлы x0 , x1 , . . . ,n ∈ [a, b]. Выясним, от чего зависит точная верхняя
граница r(x, x0 , . . . , xn ) остатка интерполирования функций всего класса
Wn+1 (M ).
9.
9Пусть f (x) - любая функция из Wn+1 (M ). Тогда в силу (2) и (3)
M
M
получим |Rn (f, x)| (n+1)!
|ω(x)|. С другой стороны, для f0 (x) = (n+1)!
ω(x),
принадлежащей Wn+1 (M ), интерполяционный полином Pn совпадает с
тождественным нулем, так как f0 (xk ) = Pn (xk ) = 0 для k = 0, 1, . . . , n;
Pn - полином порядка n обращается в нуль в n + 1 точке.
В силу сказанного
|Rn (f0 , x)| =
так что
M
|ω(x)|
(n + 1)!
r(x, x0 , . . . , xn ) = sup Rn (f, x) =
f ∈ Wn+1 (M )
M
ω(x)
(n+1)!
(4)
(5)
Таким бразом, точная верхняя граница остатка интерполировния на
классе функций Wn+1 (M ) зависит от точки x и узлов интерполирования.
Минимизация остатка интерполирования на промежутке для всего
класса Wn+1 (M ) достигает за счет подбора узлов интерполирования:
надо узлы x0 , . . . , xn ∈ [a, b] подобрать так, чтобы величина maxa x b |ω(x)|
была наименьшей. Доказано, что такой выбор всегда возможен. И если
[a, b] ≡ [−1, 1], то искомыми узлами являются корни полинома Чебышева
Tn+1 = cos[(n + 1) arccos t]
(6)
(2k+1)
Эти корни суть tk = cos 2(n+1)
π
k = 0, 1, . . . , n. Они вещественные,
различные и принадлежат (−1, 1). Для промежутка [a, b] искомые узлы
xk будут
b−a
a+b
xk =
tk +
, k = 0, 1, . . . , n
(7)
2
2
Рассмотрим задачу о минимизации остатка интерполирования в точке.
Эта задача возникает при подборе интерполяционного полинома для
таблично заданной функции.
Пусть f (x) ∈ Wn+1 (M ) и задана таблица
f (x1 ), f (x2 ), . . . , f (xN ),
N
n+1
Какие из точек xi i = 1, . . . , N выбрать в качестве узлов интерполирования
x0 , x1 , . . . , xn , чтобы в заданной точке x точная верхняя граница r(x, x0 , . . . , xn )
была наименьшей? Эта задача решается перебором: в качестве x0 берем
ту из точе xi , для которой разность
|x − xk | (k = 1, 2, . . . , N ) будет наименьшей. В качестве x1 берем ту
из оставшихся из N − 1 точек, для которых |x − xk | есть наименьшая, и
т.д. Очевидно, при таком выборе узлов ω(x) имеет наименьшее значение.
Следовательно, и r(x, x0 , . . . , xn ) будет наименьшим.
§7 Интерполирование по равноотстоящим узлам
С учетом проведенных рассуждений о минимизации остатка интерполирования
рассмотрим принципы построения некоторых интерполяционных формул.
ФОРМУЛА НЬЮТОНА ДЛЯ ИНТЕРПОЛИРОВАНИЯ В НАЧАЛЕ
ТАБЛИЦ.
10.
10Пусть f (x) задана таблично в точках a, a + h, a + 2h, . . . , a + N h,
N n, т.е. известно f (a) = y0 , f (a + h) = y1 , . . . , f (a + N h) = yN .
Выведем формулу для вычисления значения f (x) при x, расположенном
вблизи точки a , a
x
a + h2 . Предполагается, что левее точки a
таблица не задана. Чтобы остаток Rn (f, x) в точке x был наименьшим,
выберем n+1 узлов, ближайших к точке x : x0 = a , x1 = x0 +h, . . . , xn =
x0 + nh. По выбранным узлам напишем интерполяционную формулу (8)
§5
Pn (x) = f (x0 )+(x−x0 )f (x0 , x1 )+ . . . +(x−x0 ) . . . (x−xn−1 )f (x0 , x1 , . . . , xn ).
Заменим разделенные разности в этой формуле через конечные по формуле
k
f (x0 , . . . , xk ) = k!fh(xk 0 ) , k = 1, 2, . . . , n. Получим
Pn (x) = f (x0 ) +
(x−x0 )
1!h
f (x0 ) +
(x−x0 )(x−x1 )
2!h2
1 )...(x−xn−1 )
+ (x−x0 )(x−x
n!hn
Введем новую переменную t =
Pn (a + th) = y0 +
t
1!
y0 +
x−x0
.
h
t(t − 1)
2!
2
n
2
f (x0 ) + . . .
(1)
f (x0 )
Тогда формула (1) запишется
y0 + . . . +
t(t − 1) . . . (t − n + 1)
n!
n
y0
(2)
Формула (2) есть интерполяционный многочлен Ньютона для интерполирования
в начале таблицы. Заметим, что в (2) входят разности, расположенные
в верхней косой строке таблицы разностей.
Пусть интерполируемая функция f (x) имеет (n + 1) производные
на [a, a + nh]. Тогда остаточный член интерполирования при помощи
многочлена (2) в силу формулы (2) §6 запишем
Rn (f, x) = hn+1
t(t − 1) . . . (t − n) (n+1)
f
(ξ), ξ ∈ (a, a + nh),
(n + 1)!
(3)
0
так как ω(x) = (x − x0 ) . . . (x − xn ) при замене x−x
= t, x = a + th,
h
n+1
a ≡ x0 будут ω(a + th) = h t(t − 1) . . . (t − n).
ФОРМУЛА НЬЮТОНА ДЛЯ ИНТЕРПОЛИРОАНИЯ В КОНЦЕ
ТАБЛИЦЫ.
Пусть f (x) задана в точках a, a − h, a − 2h, . . . , a − N h, N
n,т.е.
известны значения y−k = f (a − kh), k = 0, 1, . . . , N .
Требуется построить интерполяционный многочлен по n+1 значениям
функции f (x), предназначенный для вычисления f (x) в точке x: a − h2
x
a. Считаем, что при x = a + kh
, k = 1, 2, . . . значения f (x)
неизвестны. Привлекая для интерполирования узлы x0 = a, x1 = a −
h, . . . , xn = a − nh,запишем интерполяционный полином в форме (8) §5:
Pn (x) = y0 + (x − x0 )f (x0 , x1 ) + . . . + (x − x0 ) . . . (x − xn−1 )f (x0 , . . . , xn ) (4)
Разностные отношения заменяем конечными разностями по формуле
k
f (x0 , . . . , xk ) ≡ f (a, a − h, . . . , a − kh) =
k
y−k
f (a − kh)
≡
k
k!h
k!hk
(5)
11.
11В результате получим
(x − x0 ) . . . (x − xn−1 )
n!hn
(6)
x−a
Вводим новую переменую t = h . Тогда получим интерполяционный
многочлен Ньютона для интерполирования в конце таблицы в виде
Pn (x) = y0 +
(x − x0 )
(x − x0 )(x − x1 )
y−1 +
1!h
2!h2
Pn (a+ht) = y0 +
t
1!
y−1 +
t(t + 1)
2!
2
2
y−2 +. . .+
y−2 +. . .+
t(t + 1 . . . (t + n − 1))
n!
n
n
y−n
(7)
В формулу входят конечные разности, расположенные в нижней косой
строке таблицы разностей.
Остаточный член формулы (7) будет
Rn (f ; x) = hn+1
t(t + 1) . . . (t + n) (n+1)
f
(ξ), ξ ∈ (a − hn, a).
(n + 1)!
Существуют другие виды интерполяционных формул для интерполирования
по равноотстоящим узлам. Вывод их аналогичен выводу формул (2),(7).
Приводим формулы без вывода.
Пусть известна f (x) в узлах . . . , a − 2h, a − h, a, a + h, a + 2h, . . .,
расположенных слева и справа от точки a.
ФОРМУЛА ГАУССА применяется, когда точка интерполирования x
находится в середине таблицы, например a < x < a+h. Интерполяционный
полином Гаусса для интерполирования по n + 1 узлам x0 = a, x1 =
a + h, x2 = a − h, x3 = a + 2h, x4 = a − 2h, . . . , xn = a + (−1)n+1 [ n+1
]h
2
будет
Pn (a + ht) = y0 +
+ t(t−1)(t+1)(t−2)
4!
4
t
1!
y0 +
t(t−1)
2!
y−2 + . . . +
t(t−1)(t+1)
3!
3
t(t−1)(t+1)...[t+(−1)n−1 [ n
]]
2
n!
n
2
y−1 +
y−1 +
(8)
y−[ n2 ] .
ФОРМУЛА БЕССЕЛЯ применяется, когда точка интерполировния
x удовлетворяет неравенству a < x < a + h и расположена ближе к
середина промежутка a + h2 или совпадает с ней. Выбирется n + 1 четное
число узлов: x0 = a, x1 = a + h, x2 = a − h, . . . , xn−1 = a − n−1
h, xn =
2
n+1
a + 2 h. Интерполяционный полином будет
Pn (a + ht) =
+
(t− 12 )t(t−1)
3!
3
y0 +y1
2
y−1 + . . . +
+
+
t− 12
1!
y0 +
t(t−1)(t+1)...(t− n−1
)
2
(n−1)!
(t− 21 )t(t−1)(t+1)...(t− n+1
)
2
n!
2y
−1 +
t(t−1)
2!
n−1 y
2y
0
2
−(n−1)/2 +
2
n
n−1 y
−(n−3)/2
+
y− n−1 .
2
(9)
В формулу (9) входят полусуммы конечных разностей, расположенных
в горизонтальных строках аргументов a и a + h, и нечетные разности
промежуточной горизонтальной строки таблицы
y−n
12.
12x
a−h
y
y−1
y
y−1
a
y0
y0
a+h
y1
2
y
2
y−2
2
y−1
2
y0
y1
a + 2h
3
3
3
y
y−2
y−1
3
y0
y2
4
y
4
y−3
4
4
y−2
y−1
4
5
y
5
y−3
5
y−2
5
y−1
y0
§8 Интерполирование с кратными узлами
(интерполирование Эрмита)
Пусть в m различных вещественных узлах
x1 , x 2 , . . . , x m
(1)
заданы значения функции f (x1 ), . . . , f (xm ) и значения ее производных
до порядка p1 − 1, . . . , pm − 1 соответственно. Так что в каждом узле xj
заданы
f (xj ), f (xj ), . . . , f (pj −1) (xj ) j = 1, 2, . . . , m,
(2)
причем p1 + p2 + . . . + pm = n + 1. Требуется построить полином
Pn (x) = a0 xn + . . . + an−1 x + an ,
(3)
удовлетворяющий условиям
Pn(s) (xj ) = f (s) (xj ), j = 1, 2, . . . , m , s = 0, 1, . . . , pj − 1
(4)
Система (4) есть линеная относительно неизвестных a0 , a1 , . . . , an . Докажем
единственность полинома (3) , удовлетворяющего соотношениям (4). Если
бы таких полиномов оказалось два: Pn (x) и Qn (x) , то полином P −n−Qn
имел бы степень
n и имел бы xj корнем кратности pj , т.е. имел бы
p1 + . . . + pm = n + 1 корней, считая их кратность. Это возможно только,
если Pn − QN ≡ 0. Из единственности интерполяционного многочлена
Эрмита следует и его существование. Действительно, многочлен Эрмита
(3), построенный для функции f (x) ≡ 0, является также единственным, а
это равносильно тому, что однородная система (4) имеет только тривиальное
решение, т.е. определитель системы (4) отличен от нуля, что и доказывает
существование полинома (3).
Установим теорему о представлении остаточного члена интерполирования
Эрмита для вещественной n + 1 раз дифференцируемой функции.
Теорема. Если f (x) - дифференцируемая n + 1 раз на промежутке
[a, b], содержащем узлы интерполирования x1 , . . . , xm , то для любой точки
x ∈ [a, b ] найдется точка ξ ∈ (a, b) такая, что
Rn (f ; x) =
Ω(x) n+1
f (ξ),
(n + 1)!
где Ω(x) = (x − x1 )p1 . . . (x − xm )pm ;
p1 + . . . + pm = n + 1.
(5)
13.
13Доказательство. Возьмем из [a, b] точку x, отличную от узлов x1 , . . . , xm ,
и рассмотрим вспомогательную функцию
F (z) = f (z) − Pn (z) −
Ω(z)
[ f (x) − Pn (x)]
Ω(x)
(6)
Функция F (z) дифференцируема n+1 раз на [a, b]. Её корни - точка x
и узлы x1 , . . . , xm , причем каждый узел xj является корнем кратности pj
для F (z), так что общее число корней F (z), считая кратность, не меньше
n + 2 = p1 + . . . + pm + 1. На основаании обощенной теоремы Ролля,
F (z) = 0 имеет по меньшей мере n + 1 корней внутри [a, b]; F ”(z) = 0
- n корней внутри [a, b], . . . ; F (n+1) (z) = 0 - один корень ξ внутри [a, b].
Имеем
(n + 1)!
F (n+1) (z) = f (n+1) (z) −
[ f (x) − Pn (x)]
Ω(x)
Полагая z = ξ, получим формулу (5)
Построение интерполяционного полинома (3) можно осуществить, решая
систему (4). Здесь мы приводим выражение полинома (3) в форме Эрмита
без вывода
m
Pn (x) =
j=1
Ω(x)
(x − xj )pj
pj −1
S=0
f (S) (xj )
S!
pj −1−S
Crj (x − xj )S+r ,
(7)
r=0
где Crj - число сочетаний из r по j.
Формула Эрмита (7) сложна. Рассмотрим частные её случаи.
a) Узлы x1 , x2 , . . . , xn+1 простые, p1 = . . . = pn+1 = 1,
p1 + p2 + . . . + pn+1 = n + 1 = m , Ω(x) = ω(x) = (x − x1 ) . . . (x − xn+1 ).
Формула (7) переходит в формулу Лагранжа.
б) Пусть m = 1 , т.е. имеется один узел x1 и в нем задны f (x1 ), f (x1 ), . . . , f (n) (x1 ), p1 =
n + 1. Тогда (7) обращается в частную сумму ряда Тейлора для f (x):
n
Pn (x) =
S=0
f (S) (x1 )
(x − xj )S
S!
(8)
в) Рассмотрим интерполирование Эрмита с двуратными узлами. В
узле xj заданы f (xj ) и f (xj ), j + 1, 2, . . . , m, p1 = p2 = . . . = pm =
2, 2 = n + 1. Формула Эрмита будет
m
Pn (x) =
j=1
ω 2 (x)
ω (xj )2 (x − xj )2
f (xj ) 1 −
ω”(xj )
(x − xj ) + f (xj )(x − xj )
ω (xj )
(9)
§9 Обратное интерполирование
Дана таблица функции y = f (x) : y0 , y1 , . . . , yN . Зная значение функции
y ∗ , найти аргумент x∗ , при котором
f (x∗ ) = y ∗
(1)
14.
14Предположим, что на рассматриваемом участке таблицы функция
f (x) монотонна и, следовательно, имеет однозначную обратную функцию
x = f −1 (y) ≡ ϕ(y). В этом случае обратное интерполирование сводится
к обычному для функции x = ϕ(y). Для нахждения приближенного
значения x∗ надо воспользоваться формулой Лагранжа (7) или Ньютона
(8)для неравноотстоящих узлов.
Пусть y = f (x) не имеет однозначной обратной. Построим для f (x)
интерполяционный многочлен P n(x). Задача об определении x∗ сводится
к решению уравнения
P n(x) = y ∗
(2)
Пусть таблица f (x) задана в равноотстоящих узлах x0 , x1 = x0 +
h, . . . , xN = x0 + N h, f (x0 + kh) = yk , k = 0, 1, . . ..
Для определенности считаем, что y0 = 0, а y ∗ удолетворяет неравенствам
y0 < y ∗ < y1 ,поэтому искомое x∗ находится между x0 и x0 + h. Для
f (x) строим интерполяционный многочлен Ньютона в виде (2) §7. Тогда
уравнение (2) запишется
y0 +
t
1!
y0 +
t(t − 1)
2!
2
y0 + . . . +
t(t − 1) . . . (t − n + 1)
n!
n
y0 = y ∗ (3)
Отсюда
t=
t(t − 1)
1
[yx − y0 −
y0
2!
2
y0 − . . . −
t(t − 1) . . . (t − n + 1)
n!
n
y0 ] ≡ g(t)
(4)
Для определения корня уравнения (4) примем метод итерации
tk+1 = g(tk ),
(5)
взяв t0 = 0. Метод итерации (5) будет сходится, например, если | 2 y0
| y0 |, а разности 3 y0 , 4 y0 , . . . малы по сравнению с y0 и 2 y0 . Пусть
t∗ = lim tk . Тогда x∗ = x0 + ht∗ . Этот способ, основанный на решении
k→∞
(5), пригоден и в том сучае, когда f (x) имеет однозначную обратную
функцию.
§10 Интерполирование таблично заданной
функции методом наименьших квадратов
Рассмотрим другой принцип построения аналитического выражения для
таблично заданной функции.
Пусть в точках x1 , . . . , xn ,принадлежащих промежутку [a, b], заданы
значения f (x1 ), . . . , f (xn ).
Для построения интерполирующей функции выбирается система линейнонезависимых функций ϕ0 (x), ϕ1 (x), . . . , ϕm (x) m
n и строится обобщенный
полином
m
Φ(x) =
ck ϕk (x)
k=0
(1)
15.
15Неизвестные коэффициенты c0 , c1 , . . . , cm выбираются из условия
n
[f (xk ) − Φ(xk )]2
min
ck
(2)
k=0
Иначе составляется система n уравнений с m + 1 неизвестными:
m
ck ϕk (xi ) = f (xi ),
i = 1, . . . , n.
(3)
k=0
В качестве решения системы (3) берется обобщенное решение, т.е. решение,
минимализирующее сумму квадратов невязок (2).
Решение поставленной задачи можно осуществить двумя способами.
П е р в ы й способ состоит минимизации функционала
n
2
m
I(c0 , c1 , . . . , cm ) =
f (xi ) −
i=0
ck ϕk (x)
k=0
С этой целью приравниваем нулю частные производные
dI
= −2
dck
n
[ f (xi )−Φ(xi ) ]
i=1
dΦ
= −2
dck
n
[ f (xi )−Φ(xi ) ] ϕk (xi ) = 0,
k = 0, 1, . . . , m,
i=1
что дает систему линейных уравнений
m
aik ci = gk
,
k = 0, 1, . . . , m.
(4)
i=0
где
n
aik =
n
ϕi (xj )ϕk (xj );
gi =
j=1
f (xj )ϕi (xj )
(5)
j=1
Если ввести обозначения ϕi = (ϕi (x1 ), . . . , ϕi (xn ))T , f0 = (f (x1 ), . . . , f (xn ))T ,
то формулы (5) можно записать aik = (ϕi , ϕk ), gi = (f0 , ϕi ). Тогда
система (4) в матричном виде будет
ΓX = ,
где X = (c0 , c1 , . . . , cm )T - вектор неизвестных; = ( 0 , . . . ,
свободных членов;
(ϕ0 , ϕ0 ) (ϕ0 , ϕ1 ) . . . (ϕ0 , ϕm )
...
...
...
Γ = ...
(ϕm , 0 ) (ϕm , ϕ1 ) . . . (ϕm , ϕm )
(6)
T
m)
- вектор
Матрица Γ называется матрицей Грамма, она симметричная. Определитель
матрицы Γ называется определителем Грамма, он отличен от нуля в
силу линейной независимости функций. Составление матрицы Грамма и
последующее решение равносильно применению трансформаций Гаусса
к системе (3).
16.
16Действительно, в матричном виде (3) можно записать
AX = f
(7)
где
ϕ0 (x0 ) ϕ1 (x0 ) . . . ϕm (x0 )
...
...
...
A = ...
ϕ0 (xn ) ϕ1 (xn ) . . . ϕm (xn )
Отсюда AT A = Γ, AT f = g, что и требовалось доказать.
Мы знаем, что переход от системы (3) к системе (5) при численных
расчетах ухудшает обусловленность системы; кроме того, образование
матричного произведения AT A вносит дополнительные ошибки из-за ошибок
округления. Более стабильным методом решения системы (3) является
метод, основанный на применении плоских вращений или отражений.
Этот метод был рассмотрен в [I].
В т о р о й способ построения коеффициентов интерполирующего
полинома методом наименьших квадратов состоит в применении ортогональных
преобразований к решению системы (3) для отыскания её обощенного
решения.
Выбор системы линейно-независимых функций ϕ0 , . . . , ϕm может быть
осуществлен по-разному и диктуется свойствами интерполируемой функции.
Если в качестве системы {ϕk (x)} взять 1, x, x2 , . . . , xm , то мы получим
приближение по методу наименьших квадратов алгебраическими многочленами.
Если узлы интерполирования x1 , . . . , xn равноотстоящие и решение
задачи осуществляется составлением системы с матрицей Грамма, то в
качестве функций ϕ0 (x), . . . , ϕm (x) берут систему ортогональных на
множестве равноотстоящих точек полиномов. В этом случае матрица
Грамма будет диагональной и определение решения системы (5) не предсталяет
труда. Вся трудность переносится на построение ортогональной системы.
Из практики вычислений известно, что процесс ортогонализации протекает
с пропаданием верных знаков. Для увеличения точности приходится
увеличивать число значащих цифр.
§11 Интерполирование функций двух переменных
Пусть функция z = f (x, y) задана на системе равноотстоящих точек
xi = x0 +i h , yj = y0 +j l, где h и l - шаги соответстенно по переменным
x и y. Для краткости обозначим zij = f (xi , yj )
Значения функций z = f (x, y) можно оформить в виде таблицы с
двумя входам
17.
17x
y
x0
x1
x2
...
y0
z00
z10
z20
...
y1
z01
z11
z21
...
y2
z02
z12
z22
...
...
...
...
...
...
Интерполирование функции двух переменных, т.е. определение её
нетабличных значений, можно последовательно проводить по каждому
переменному x и y в отдельности.
Пусть требуется найти z = f (x, y). Фиксируя y = yk ≈ y, интерполируем функцию одной переменной fk (x) = f (x, yk ) и по ней найдем
fk (x) = f (x, yk ). Далее рассматриваем fk (x) как значение f (x, y) при
y = yk . Строим интерполяционный полином для функции f (x, y) по
значениям fk (x) при различных k и находим f (x, y) как значение этого
интерполяционного полинома в точке y = y.
Проиллюстрируем сказанное на примере. Пусть значение
∞
f (x, y) =
e−y
2 t2 −t−x
e−t
dt дается таблицей
−∞
y x
0.00
0.05
0.10
0.4
2.500
2.487
2.456
0.7
1.429
1.419
1.400
1.0
1.000
0.995
0.981
Требуется найти f (0.5; 0.03).
Составляем таблицы
для y = 0:
x
f
0.4 2.500
f
2
f
- 1.071
0.7
1.429
0.642
- 0.429
1.0
1.000
для y = 1, 0:
x
f
0.4
1.000
для y = 0, 05:
x
f
f
0.4 2.487
- 1.068
0.7 1.419
- 0.424
1.0 0.995
f
2
f
- 1.065
0.7
0.995
0.637
- 0.419
1.0
0.981
2
f
0.644
18.
18Находим t =
вычисляем
x − x0
0, 5 − 0, 4
1
=
=
h
0, 3
3
и по формуле Ньютона
f0 = f (0, 5; 0) = 2, 072;
f1 = f (0, 5; 0, 05) = 2, 069;
f2 = f (0, 5; 0, 10) = 2, 033.
Составляем таблицу найденных значений
y
0
f
2.072
0.05
2.069
2
-0.003
-0.033
-0.036
0.10
2.033
Находим l = 0, 05 − 0 = 0, 05; y0 = 0; t =
0, 03 − 0
3
=
и по
0, 05
5
формуле Ньютона вычисляем f (0, 5; 0, 03) = 2, 047.
Рассмотрим интерпоирование функций двух переменных методом Ньютона,
для чего введем в рассмотрение двойные разности.
Пусть функция z = f (x, y) задана двойной таблицей значений zij =
f (xi , yj ), причем шаг по переменной y равен l, по переменной x шаг равен
h, так что yj = y0 + j l , xi = x0 + i h.
Подобно частным производным для непрерывной функции вводим
понятие частной конечной разности:
x zij
= zi+1,j − zij
;
y
zij = zi,j+1 − zij
Повторно применяя эту операцию, получим двойные разности высших
порядков:
m+n
zij =
m+n
xm ,y n
=
m
xm (
n
yn
zij ) =
n
yn (
m
x zij )
,
1+2
2
где положено 0+0 zij = zij ,
zij =
x ( y 2 zij ) =
x (zij+2 −
2 zij+1 + zij ) = (zi+1,j+2 − 2zi+1,j+1 + zi+1,j ) − (zi,j+2 − 2zi,j+1 + zij ) и т.д.
Пользуясь понятием разности от функции двух переменных, можно
строить для нее интерполяционный полином, например, в форме Ньютона.
Обозначим через P (x, y) полином такой, что
m+n
xm , y n P (x0 , y0 )
=
m+n
z00 ,
m, n = 0, 1, 2, . . .
.
(1)
Будем искать P (x, y) в виде
P (x, y) = c00 + c10 (x − x0 ) + c01 (y − y0 ) + c20 (x − x0 )(x − x1 ) +
+ c11 (x − x0 )(y − y0 ) + c02 (y − y0 )(y − y1 ) + . . .
Задача состоит в определении коэффициентов cij . Положив
x = x0 y = y0 ,в силу (1) найдем
c00 = z00 = p(x0 , y0 ).
(2)
19.
19Составим для P (x, y) конечные разности I-го порядка
x
P (x, y) = P (x + h, y) − P (x, y) = c10 h + c20 [(x + h − x0 )(x + h − x1 ) − (x − x0 )(x−
−x1 )] + c11 h (y − y0 ) + . . . = c10 h + c20 h (x − x1 ) + h (x − x0 ) + h2 + c11 h(y − y0 ) + . . . =
= c10 h + c20 h [x − (x0 + h) + x − x0 + h] + c11 h (y − y0 ) + . . . =
= c10 h + 2c20 h(x − x0 ) + c11 h (y − y0 ) + . . . .
(3)
Отсюда, положив x = x0 , y = y0 , находим
c10 h =
1+0
c01 l =
0+1
1+0
z00 =
x P (x0 , y0 ) , т . е.
c10 =
z00 =
y
P (x0 , y0 ) , т . е.
c01 =
z00
h
0+1
z00
l
;
.
Далее подсчитаем для полинома P (x, y) конечные разности 2-го порядка
2
x x P (x, y)
2
x y P (x, y)
2
y x P (x, y)
= 2! c20 h2 + . . . ,
= c11 h l + . . . ,
= 2! c02 l2 + . . . .
Полагая x = x0 , y = y0 и используя равенства (1), находим
c20 =
1
2!
2+0
z00
h2
1+1
, c11 =
lh
z00
, c02 =
1
2!
0+2
z00
l2
Аналогично находятся далнейшие коэффициенты для полинома P (x, y).
В результате получим интерполяционный полином для функций двух
переменных
1+0
P (x, y) = z00 +
1
+
2!
2+0
z00
h2
z00
h
1+1
2
(x − x0 ) + 2
0+1
(x − x0 ) +
z00
lh
l
z00
(y − y0 ) +
0+2
(x − x0 ) (y − x0 ) +
Иногда для удобства вычислений f (x, y)
переменных, полагая
l2
z00
(y − y0 )2 + . . . .
(4)
P (x, y) вводят замену
y − y0
x − x1
y − y1
x − x0
= p ,
= q ,
= p−1 ,
= q − 1 ,... .
h
l
h
l
Формула примет вид
z = f (x, y)
z00 + (p
+ 2pq
1+1
1+0
z00 + q
0+1
z00 + q (q − 1)
1
[p (p − 1)
2!
0+2
z00 ] + . . . .
z00 ) +
2+0
z00 +
(5)
В интерполяционной формуле для P (x, y) удерживают столько членов,
сколько нужно для достижения заданной точности.
20.
20§12 Интерполяционные сплайны
В течении ряда лет чертежники использовали длинные тонкие рейки
из дерева в качечтве лекал, проводя с их помощью плавные кривые
через заданные точки. Эти рейки (или сплайны) зкрепляют на месте,
подвешивая к ним в некоторых точках грузила. Изменяя положение
точек, в которых находятся грузила, а также положение рейки (сплайна)
и грузил, при достаточном числе грузил добиваются, чтобы сплайн проходил
через заданные точки.
Математическим сплайном называют приближенное представление
деформированной оси рейки кусками кубической параболы (различными
между каждой парой грузил) с определенными разрывами производных
в точках прикрепления грузил, где стыкуются 2 параболы.
Математический сплайн простейшего вида имеет непрерывными первую
и вторую производные, а третья производная может в точках стыка
иметь скачки конечные. Это соответствует рейке, имеющей непрерывную
кривизну, скорость изменения которой разрывна в точках прикрепления
грузил.
На практике чертежник не помещает грузила в заданых точках, через
которые должен идти сплайн, да и взаимного соответствия между заданными
точками и грузилами нет. В математическом же аналоге сплайна в качестве
заданных точек будут точки соединения и число заданных точек совпадет
с числом точек соединения, включая концы.
Почему ось деформированной рейки аппроксимируется кубическими
параболами, объясняется следующими рассуждениями.
Если представлять рейку как тонкую балку, то имеет место закон
Бернулли-Эйлера
1
M(x) = E I
R(x)
где M(x) - изгибающий момент; E - модуль Юнга; I - геометричеcкий
момент инерции; R(x) - радиус кривизны кривой, совпадающей с деформированной
1
осью балки. При незначительных изгибах R(x) можно заменить на
,
y (x)
где y(x) - деформированная ось балки, так что
y (x) =
1
M(x).
EI
Так как грузила действуют как простые опры, то M(x) между точками
закрепления грузил есть линейная функция. Отсюда видно, что y(x)
между грузилами есть полином третьей степени.
Во многих задачах сплайны являются более естественным аппаратом
приближения, чем многочлен. К таким задачам относятся практически
важные задачи интерполирования и сглаживания функций, численного
дифференцирования, интегрирования функций и дифференциальных уравнений.
Рассмотрим более подробно кубические сплайны.
Пусть на [a, b] определена сетка
: a = x0 < x 1 < . . . < x N =
b и заданы значения функции Y : y0 , y1 , . . . , yN . Ищется функция
S (Y ; x) (или коротко S (x), S (Y ) ), непрерывная на [a, b] вместе с
первой и второй производными, совпадающая с кубическим полиномом
21.
21на каждом отрезке xj−1
x
xj j = 1, . . . , N и удовлетворяющая
условиям
S (Y ; xj ) = yj , j = 0, 1, . . . , N .
Функция S (Y ; x) называется сплайном относительно сетки , интерполирующим
значения yj в узлах сетки. Сплайн назыается периодическим с периодом
(b − a), если
(p)
(p)
S (a + 0) = S (b − 0) p = 0, 1, 2.
Обозначим S (xj ) = Mj - "моменты" j = 0, 1, . . . , N .
В силу линейности второй производной на [xj−1 , xj ] имеем
S (x) = Mj−1
x − xj − 1
xj − x
+ Mj
, hj = xj − xj−1 .
hj
hj
(1)
Обе части равенства (1) проинтегрируем дважды, получим
S
= Mj−1
(xj − x)3
(x − xj−1 )3
+ Mj
+ c1 x + c2 .
6 hj
6 hj
Постоянные c1 и c2 находим, используя свойства S (xj ) = yj , S (xj−1 ) =
yj−1 . Для c1 и c2 имеем уравнения
Mj h2j
,
6
Mj−1 h2j
+ c2 = yj−1 −
.
6
c 1 xj + c 2 = y j −
c1 xj−1
Отсюда
Mj h2j
Mj−1 h2j
1
1
c1 = yj −
− yj−1 −
,
6
hj
6
hj
Mj h2j xj−1
Mj−1 h2j xj
c2 = − yj −
+ yj−1 −
.
2
hj
6
hj
Окончательно имеем
S
= Mj−1
(xj − x)3
(x − xj−1 )3
+ Mj
+
6 hj
6 hj
Mj−1 h2j
+ yj−1 −
6
Mj h2j
6
xj − x
.
hj
yj −
(x − xj−1 )
+
hj
(2)
Отсюда
Mj h2j
(xj − x)2
(x − xj−1 )2
1
+ Mj
+
yj −
2 hj
2 hj
hj
6
Mj−1 h2j
1
(xj − x)2
−
yj−1 −
+
= − Mj−1
hj
6
2 hj
(x − xj−1 )2
yj − yj−1
Mj − Mj−1
+ Mj
+
−
hj .
2 hj
hj
6
S (x) = − Mj−1
−
(3)
22.
22Это есть выражение для S (x) на [xj−1 , xj ] . Аналогично на [xj , xj+1 ]
(x − xj )2
(xj+1 − x)2
yj+1 − yj
Mj+1 − Mj
+ Mj+1
+
−
hj+1 .
2 hj+1
2 hj+1
h+j+1
6
(4)
Используя непрерывность S (x) при x = xj , из (3) и (4) находим
S (xj + 0) = S (xj − 0) или
S (x) = −Mj
Mj hj+1
yj+1 − yj
Mj+1 − Mj
−
+
hj+1 =
2
hj+1
6
Mj − Mj−1
Mj hj
yj − yj−1
−
+
hj .
= S (xj − 0) =
2
hj
6
(5)
hj
hj + hj+1
hj+1
yj+1 − yj
yj − yj−1
−
+ Mj
+ Mj+1
=
6
3
6
hj+1
hj
(6)
S (xj + 0) = −
Отсюда
Mj−1
Это есть уравнение для опредеения моментов, записанное для точки xj
так, что при j = 1, 2, . . . , N − 1 имеем систему N − 1 уравнения для
определения M1 , M2 , . . . , MN−1 . Запишем (6) в матричной форме
MX = F ,
(7)
y2 − y1
y1 − y0
h1 y 2 − y 1
−
− M0
;
−
h2
h1
6
h2
y1 − y0
yN−1 − yN−2
yN−2 − yN−3 yN − yN−1
yN−1 − yN−2
hN
,... ;
−
;
−
− MN
h1
hN−1
hN−2
hN
hN−1
6
h2
h1 + h2
0
3
6
h
h2 + h3
h3
2
6
3
6
M =
hN−1
6
hN−1 hN−1 + hN
0
6
3
где X = (M1 , . . . MN−1 )T ; F =
T
;
В правую часть F входят неизвестные M0 , MN . Как их найти?
Числа M0 , MN часто определяются из физического смысла задачи.
Рассмотрим различные ситуации, позволяющие определить M0 , MN .
1. Если сплайн - периодический, то должны выполняться соотношения
yN = y0 , yN+1 = y1 , M0 = MN , M1 = MN+1 , h1 = hN+1
(8)
В этом случае первое и последнее уравнения системы (5) будут
h1 + h2
h2
y2 + y1
y1 − y0
h1
M0 + M1
+ M2
=
−
при j = 1,
6
3
6
h2
h1
hN−1
hN−1 + hN
hN
yN − yN−1
yN−1 − yN−2
MN−2
+ MN−1
+ M0
=
−
при j = N − 1
6
3
6
hN
hN −1
(9)
23.
23Появилась новая неизвестная M0 . Следует добавить ещё одно уравнение
для определения ее. Полагая в (6) j = N и используя (8), будем иметь
MN−1
hN
hN−1 + hN
h1
y1 − y0
yN − yN−1
+ M0
+ M1
=
−
6
3
6
h1
hN
(10)
Так, что (6), (9) и (10) дадут возможность найти все моменты.
2. В точках x0 = a и xN = b задаются S (a + 0) = y 0 и
S (b − 0) = y N , т.е. краевые условия. Задание S
в точках a и b
соответствуют случаю двойной консольной балки.
Краевые условия дадут два дополнительных к системе (5) уравнения:
M1 − M0
M 0 h1
y1 − y0
−
+
h1 = y 0 получено из (3) при x = x1
2
h1
6
hN
yN − yN−1
MN − MN−1
S (xN ) = MN
+
−
hN = y N получено из (3) при x = xN−1
2
hN
6
S (x0 ) = −
Перепишем эти уравнения в другом виде:
6 y1 − y0
Mh
M
y − y0
− y0
0 1 + 1 h1 = 1
2 M 0 + M1 =
− y0
h1
h1
3
6
h1
M h
M h
y − yN−1 или
6
yN − yN−1
N−1 N + N N = y N − N
yN −
MN−1 + 2 MN =
6
3
hN
hN
hrmN
3. MN = M0 = 0 - это условие соответствует расположению простых
опор на концах.
4. M0 −λ M1 = 0 0 < λ < 1 - это условие эквивалентно расположению
x0 − λ x 1
простой опоры в точке x1 =
и требованию, что на [x−1 , x0 ]
1−λ
кривая совпадала также с кубической параболой. Как правило, в качестве
λ берут λ = 1/2.
5. Более общие краевые условия
2 M0 + λ0 M1 = d0 ,
µN MN−1 + 2 MN = dN
(12)
здесь λ0 , µN - заданные числа.
Введем обозначения
µj = 1 − λ j , λ j =
hj+1
,
hj + hj+1
j = 1, 2, . . . , N − 1
Преобразуем систему (6) для этого случая, для чего (6) умножим на
6
hj
. Учитывая, что µj = 1 − λj =
, будем иметь из (9)
hj + hj+1
hj + hj+1
µj Mj−1 + 2 Mj + λj Mj+1 =
Системы
2 λ0
µ1 2
. . . µ 2
. . . . . .
0 ...
0 ...
6
hj + hj+1
(6) и (12) в матричном виде
M
0
... ...
0
M
1
... ...
0
.
.
2 λ2 . . . .
. =
... ... ...
.
.
. . . 2 λN−1 M
W−1
. . . µN
2
M
N
yj+1 − yj
yj − yj−1
−
hj+1
hj
d0
d1
..
.
..
.
.
(13)
,
dN−1
dN
(14)
.
24.
24yj+1 − yj
yj − yj−1
6
−
.
hj + hj+1
hj+1
hj
Периодические сплайны
в этом случае порождают систему
M d
1
1
2 λ1 . . . . . . . . .
M
d
µ2 2 λ 2 . . . . . . 2 2
.. ..
. . . . . . . . . . . . . . .
= . ,
.
.
. . . . . . . . . . . . λN−1 ..
. ..
. . . . . . . . . µN
2
M
d
где
dj =
N
(15)
N
h1
hN+1
=
.
hN + hN+1
hN + h1
6. В точках a и b могут быть заданы значения S (a + 0) и
S (b − 0) . Учитывая, что
где M0 = MN ; µN = 1 − λN ; λN =
S (x) = Mj−1
x − xj
xj−1 − x
+ Mj
,
hj
hj
имеем S (a + 0) ≡ −M0 = y 0 и S (b − 0) ≡ −MN = y N - заданные
числа.
Для решения систем (6) и (12) можно применять метод прогонки, так
как матрица систем есть трехдиагональная с доминирующей главной
диагональю. Известно, что в этом случае метод прогонки устойчив к
ошибкам округления.
Укажем еще на два свойства сплайнов, в силу которых сплайн-интерполирование
во многих практически важных случаях является лучшим аппаратом
для аппроксимации, чем интеполирование с помощью полиномов.
1. Свойство наилучшего приближения интерполяционного сплайна.
Пусть дана сетка
: a = x0 < x1 < . . . < xN = b и действительные
числа y0 , . . . , yN . Среди всех функций f (x) , имеющих на [a, b] непрерывную
вторую производную и таких, что f (xi ) = yi (i = 0, 1, . . . , N), сплайн
S (f ; x) с точками соединения xi , для которого S (f ; a) = S (f ; b) =
0, минимизирует интеграл
b
|f (x)|2 dx.
a
Данное свойство еще называют свойством минимальной кривизны.
2. Свойство сходимости. Если функция f (q) (x) (q = 0, 1, 2, 3, 4)
непрерывна на [a, b] , то сплайны S (f ; x) сходятся к функции f (x)
на последовательности сеток
по крайней мере со скоростью || ||q ,
где || || = max hj .
j
(p)
Аналогично производные S (f ; x) сходятся к f (p) (x) 0 p q
по крайней мере со скоростью || ||q−p . Эти скорости оптимальны.
Мы подробно рассмотрели кубические сплайны. Но в практических
задачах могут быть использованы сплайны порядка m
3 . Назовем
m
сплайном S [f ; x] порядка m функцию, являющуюся многочленом степени
m на каждом [xn−1 , xn ] :
S m [f ; x] = Pn,m (x) = an0 + an1 x + . . . + anm xm , x ∈ [xn−1 , xn ] ,
25.
25который удовлетворяет условиям непрерывности производных до m − 1
порядка в точках x1 , . . . , xn :
(k)
(k)
Pn,m
(xn ) = Pn+1,m (xn ) , n = 1, 2, . . . , N − 1 , k = 0, 1, . . . , m − 1.
Производная порядка m может иметь разрывы первого рода в точках
x1 , . . . xn−1 ,но суммируема с квадратом
1
(m)
(x)
Pn,m
2
dx < ∞
0
§13 Численное дифференцирование
Пусть функция f (x) задана таблично, т.е. в узлах x0 , x1 , . . . , xN (не обязательно
равноотстоящих) заданы f (x0 ), f (x1 ), . . . , f (xN ). Ставится задача о вычислении
производной от f (x). Для определения производных таблично заданной
функции строится интерполяционный многочлен для f (x) по значениям
ее в n + 1 узлах, и значение m - й производной интерполяционного
многочлена Pn (x) принимается за приближенное значение m - й производной
функции
f (m) (x) P (m) (x) , m n
(1)
Найдем выражение производной от Pn (x) для случая , когда f (x)
задана в равноотстоящих узлах. В качестве Pn (x) возьмем интерполяционный
полином Ньютона, например, для интерполирования в начале таблицы
t
1!
Pn (x0 + h t) = y0 +
y0 + . . . +
t(t − 1 . . . (t − n + 1))
n!
n
y0 .
Запишем этот полином в виде
n
(k)
Pn (x0 + h t) =
ct
k
f (x0 ) , где ckt =
k=0
t(t − 1) . . . (t − k + 1)
.
k!
Продифференцируем по t обе части равенства m раз
dPn (x)
dP [x0 + ht]
=h
=
dt
dx
n
k=1
2
d2 P [x0 + ht]
2 d Pn (x)
=
h
=
dt2
dx2
d k
c
dt t
n
k
d2 k
c
dt2 t
k=2
f (x0 ) ,
k
f (x0 ) ,
...
n
m
dm P [x0 + ht]
dm k
m d Pn (x)
=
h
=
c
dtm
dxm
dtm t
k=m
Отсюда
Pn(m) (x)
1
= m
h
k
f (x0 ) ,
n
dm ckt
dtm
k=m
k
f (x0 )
(2)
26.
26dm k
c .С
dtm t
Можно упростить эту формулу, выписав явное выражение
этой целью запишем многочлен k! ckt в виде
(k)
(k−1) k−1
t(t − 1) . . . (t − k + 1) = Sk tk + Sk
t
(1)
+ . . . + Sk t .
(3)
(j)
Числа Sk для j k = 1, 2, . . . - целые. Они называются числами Стирлинга
(j)
I-го рода. Числа Sk можно определить из равенства
∞
(j)
ln(1 + x)j
Sk
=
xk , j = 1, 2, . . . .
j!
k!
j=m
Из (3) находим
dm ck
k! mt =
dt
k
(j)
Sk j(j − 1) . . . (j − m + 1)tj−m
(4)
j=m
Подставляя (4) в (2), получим
Pn(m) (x) =
1
nm
k
n
k=m j=m
(j)
Sk
j(j − 1) . . . (j − m + 1)tj−m
k!
k
f (x0 ).
(5)
Обычно в справочниках приводится таблица чисел
(j)
cj k =
Sk
k!
Если в (5) положить t = 0 , т.е. x = x0 , то получим
Pn(m) (x0 )
1
= m
h
n
(m)
Sk
k!
k=m
k
f (x0 ) .
Аналогично можно получить выражение m - й производной для интерполяционного
полинома Ньютона для интерполирования в конце таблицы, т.е. для
полинома
Pn (a + h t) = y0 +
+
t(t + 1) . . . (t + n − 1)
n!
n
t
1!
y−1 +
t(t + 1)
2!
2
y−2 + . . . +
y−1 + c2−t
y−n = y0 + (−1) c −t
2
y−2 + . . . +
n
+(−1)n cn−t
n
(−1)ck−t
y−n ≡
k
f (xn−k ) ,
k=0
−t(−t − 1) . . . (−t − k + 1)
t(t + 1) . . . (t + k − 1)
= (−1)k
где ck−t =
k!
k!
Как и выше, находим
Pn(m) (x)
1
= m
h
n
k
,
(j)
k−j
(−1)
k=m j=m
Sk
j (j − 1) . . . (j − m + 1), tj−m
k!
k
f (xn−k ) .
(6)
27.
27При t = 0, x = xn имеем
Pn(m) (xn )
1
=
hm
n
(m)
(−1)k−m
k=m
Sk
m!
k!
k
f (xn−k ) .
(7)
Можно таким же образом получать производные от интерполяционных
полиномов, представленных в другой форме, например, от интерполяционного
полинома Гаусса, Бесселя и др.
(m)
Так как Pn (k) ≈ f (m) (x) , то естественно поставить вопрос об
оценке остатка при численном дифференцировании. Пусть
Rn(m) (f ; x) = f (m) (x) − Pn(m) (x).
(m)
Докажем теорему о представлении остатка Rn (f ; x) для n + 1 раз
дифференцируемой функции f (x).
Теорема. Пусть x ∈ [α, β], где [α, β] есть наименьший промежуток,
содержащи узлы интерполирования x0 , x1 , . . . xn . И пусть f (x) дифференцируема
n + 1 раз на [a, b] ⊃ [α, β]. Тогда для любой точки x ∈ [a, b] , x∈[α, β]
существует точка ξ ∈ (a, b) такая, что
Rn(m) [f ; x] =
ω (m) (x) (n+1)
f
(ξ) ,
(n + 1)!
(8)
где ω (m) (x) - m - я производная от многочлена
ω(x) = (x − x0 )(x − x1 ) . . . (x − xn ) .
Доказательство. Введем вспомогательную функцию
F (z) = f (z) − Pn (z) − Kω(z),
где K − const, которую определим ниже. Функция F (z) дифференцируема n+1 раз на [a, b] и имеет x0 , . . . , xn корнями на [α, β]. По теореме
Ролля имеем: F (z) обращается в нуль внутр (α, β) по крайней мере в n
различных точках; F (z) - в n − 1 различных точках; F (m) - в n + 1 − m
различных точках. Выберем K так, чтобы F (m) (z) = 0 при z = x, т.е.
F (m) (x) = f (m) (x) − Pn(m) (x) − Kω (m) (x) = 0
Такой выбор возможен, так как ω (m) (z) имеет ровно n + 1 − m корней,
расположенных внутри (α, β), а x∈(α, β) и, следовательно, ω (m) (x) = 0.
Находим
(m)
f (m) (x) − Pn (x)
K =
.
ω (m) (x)
При таком выборе K производная F (m) (z) имеет по меньшей мере
n + 2 − m различных корней на [a, b]. По теореме Ролля F (m+1) (z) имеет
n − m + 1 корней в (a, b) и т.д., F (n+1) (z) - один корень ξ ∈ (a, b), так что
F (n+1) (ξ) = 0 или подробно
F (n+1) (ξ) = f (n+1) (ξ) − (n + 1)! K = 0 , значит : K =
f (n+1) (ξ)
.
(n + 1)!
28.
28Подставляя найденное значение K, получим
f (m) (x) − Pn(m) (x) −
f (n+1) (ξ) (m)
ω (x) = 0 .
(n + 1)!
Отсюда следует справедливость сделанного утверждения.
Замечание. Выражение (8) остаточного члена при численном дифференцировании
имеет место только при x∈[α, β]; x0 , x1 , . . . , xn ∈ [a, b]. Формально оно
может быть получено из остаточного члена для интерполирования Rn (f, x) =
ω(x) (n+1)
f
(ξ) , если считать, что f (n+1) (ξ) постоянная и от x не зависит.
(n + 1)
В действительности же ξ зависит от x.
Глава II. Приближенное вычисление интергралов
§1. Постановка задачи приближенного вычисления
определенных интегралов
Вычисление интеграла
b
f (x) d x = F (b) − F (a)
a
через первообразную функцию далеко не всегда возможно. Приходится
прибегать к приближенному вычислению интегралов. Большинство формул приближенного вычисления интегралов имеет вид
b
n
(n)
(n)
(1)
k=1
a
(n)
(n)
Ak f (xk ) ,
ρ (x) f (x) d x
(n)
(n)
где xk ∈ [a, b], x1 < x2 < . . . < xn - узлы квадратурной формулы,
(n)
числа Ak - коэффициенты квадратурной формулы.
Подынтегральная функция записана в виде ρ(x) f (x). Функция ρ (x)
является фиксированной для рассматриваемой квадратурной формулы и
называется в е с о в о й. Функция f (x) - не фиксированная, принадлежит
широкому классу функций (например, непрерывных), для которых
b
ρ (x) f, (x) d x существует;
a
b
Rn [f ] =
n
(n)
ρ(x) f (x) d x −
a
(n)
Ak f (xk )
k=1
остаточный член интерполяционной формулы.
(2)
29.
29§2. Интерполяционные квадратурные формулы
Часто для построения квадратичных формул применяется способ, построенный
на алгебраическом интерполировании.
Для f (x) строится интерполяционный полином
n
ω(x)
f (x) =
k=1
b
b
n
ρ(x)f (x)d x =
(n)
(n)
(xk )
f (xk ) + R[ f ; x] ,
(n)
f (xk )+
(n)
(xk )
a
(n)
xk )ω
b
(n)
Ak
=
ρ(x)
a
(n)
xk )ω
(n)
n
(n)
ρ(x)Rn [f ; x]dx =
(4)
(xk )
dx ;
(5)
b
ρ(x)Rn [f ; x]dx
Rn [f ] =
(6)
a
Если Rn [f ; x] достаточно мал на [a, b], т.е. f (x) достаточно хорошо
приближается к Pn (x), то Rn [f ] мал, его можно отбросить, тогда
b
n
(n)
(n)
Ak f (xk )
ρ(x)f (x)dx
(7)
k=1
a
(n)
Квадратурная формула (7), где Ak определены по (5), называется
интерполяционной.
Теорема. Для того чтобы квадратурная формула с n узлами была
интерполяционной, необходимо и достаточно, чтобы она была точна,
когда f (x) является полиномом степени n − 1
Необходимость. Пусть (1) - интерполяционная формула. Если
f (x) есть многочлен степени
n − 1, то для f (x) интерполяционный
полином, построенный по n узлам, точный, т.е. Rn [f ; x] = 0 ; докажем,
что
R[f ] = 0.
Пусть f (x) - полином степени n − 1, тогда
f (x) = Pn (x) =
(n)
(n)
(n)
ω(x)(x − xk )ω (xk )f (xk ) .
Умножим на ρ(x) и проинтерполируем
b
(n)
(n)
Ak f (xk )
ρ(x)f (x)dx =
a
b
n
, где
(n)
Ak
k=1
т.е. квадратурная формула является точной.
=
ω(x)dx
(n)
a
(n)
(n)
Ak f (xk )+Rn [f ] ,
k=1
ω(x)
(x −
(3)
b
ρ(x)ω(x)dx
(x −
k=1 a
a
(x −
(n)
xk )ω
(x − xk )ω (xk )
,
30.
30b
n
Достаточность. Пусть (1) точна, т.е. ρ(x)f (x)dx =
k=1
a
(n)
(n)
Ak f (xk )
для любого полинома f (x) степени n − 1, следовательно она точна и
для полинома
ω(x)
ω0 (x) =
, т.е.
(n)
(n)
(x − xk )ω (xk )
b
ρ(x)
a
ω(x)
dx =
(x − xk )ω (xk )
n
(n)
(n)
Ak ω0 (xk ) = Ak
,
k=1
что и означает, что формула интерполяционная.
Определение. Говорят, что квадратурная формула имеет алгебраическую степень точности m, если она точна для
f (x) = xk ,
k = 0, 1, . . . , m и не дает точного результата для xm+1 .
§3. Простейшие интерполяционные квадратурные
формулы
Предполагается, что промежуток [a, b] - конечный, ρ(x) = 1.
(1)
Если взять один узел x1 = c ∈ [a, b], то интерполяционный многочлен
будет f (c) и квадратурная формула примет вид
b
f (c) d x
A1 f (c) , A1 = b − a .
(8)
a
Это формула прямоугольника (рис. 2).
Рис.2
Если c = a, то имеем формулу левых прямоугольников, если
a+b
- средних прямоугольников.
c = b - правых прямоугольников; c =
2
Остаточный член формулы (8)
b
R [f ; c] =
f (x)d x − (b − a)f (c)
a
(9)
31.
31a+b
2
В случае формулы левых и правых прямоугольников считаем f (x)
имеющей непрерывную производную I-го порядка.
По формуле Тейлора f (x)−f (a) = (x−a)f (ξ) , a < ξ < b. Интегрируем
обе части от a до b:
при
c=a ,
c=b ,
c=
b
b
f (x)dx − f (a)(b − a) =
a
(x − a)f (ξ)dx ,
a
b
f (ξ)(x − a)dx. Пусть m = min f (x) , M = max f (x). Так
т.е. R[f ] =
[a,b]
a
[a,b]
как x − a сохраняет знак в [a, b], можем применить теорему о среднем
b
b
(x − a)f (ξ)dx = L
a
(x − a)dx = L
(b − a)2
2
a
где m L M . В силу непрерывности f (x) найдется точка η из [a, b]
такая, что L = f (η).
(b − a)2
Имеем Ra [f ] =
f (η) , a
η
b; для остаточного члена
2
(b − a)2
формулы правых треугольников - Rb [f ] = −
f (η).
2
Для формулы средних прямоугольников предполагаем, что f (x) имеет
непрерывную производную 2-го порядка.
По формуле Тейлора
f (x) − f
a+b
2
1
2
a+b
2
+
x−
=
x−
a+b
2
f
2
f (ξ) , x < ξ <
a+b
2
+
a+b
.
2
Интегрируем по x от a до b:
1
R a + b [f ] =
2
2
b
b
x−
a+b
2
2
f (ξ) d x .
a
a+b
Учитывая, что
x−
2
применяем теорему о среднем
1
2
a+b
x−
2
2
сохраняет знак на [a, b], к интегралу
2
f (ξ) d x =
(b − a)3
f (η) , a
24
η
b
a
Если промежуток (b − a) велик, то формула прямоугольников дает
малую точность. Поэтому [a, b] делят на n частичных промежутков длины
32.
32b−a
, xk = a + k h , k = 0, 1, . . . , n точки деления. На каждом
n
[xk , xk+1 ] применяют формулу прямоугольников
h =
xk+1
f (x) d x = h f (α + k h) , k = 0, 1, . . . , n − 1 ,
xk
где α - некоторая точка из [x0 , x1 ] = [a, a + h] ; при α = a - формула
левых прямоугольников, при α = a+h - формула правых прямоугольников;
h
при α = a +
- формула средних прямоугольников.
2
Большая формула прямоугольников:
b
n−1
xk+1
f (x) d x =
f (x) d x
k=0 x
k
a
b−a
n
n−1
f (α + k h) .
k=0
h
В частных случаях α = a , α = a + h , α = a +
формула
2
называется левых, правых и средних прямоугольников.
Остаточный член равен сумме остаточных членов частичных интегралов
xk+1
R [f ; α; k] =
f (x) d x − h f (α + k h) ,
xk
т.е. R [f ; α] =
n−1
b
R[f ; α; k] =
k=0
при α = a
f (x) d x − h
(b − a)2
f (ξk ) ,
2 n2
(b − a)2
R [f ; a] =
2 n2
Но m
[a, b] , то
f (ξ0 ) + . . . + f (ξn−1 )
n
f (α + k h) ,
k=0
a
R [f ; a; k] =
n−1
xk < ξk < xk+1 ,
n−1
f (ξk ) .
k=0
M и, так как f (x) - непрерывна на
n−1
f (ξk )/n = f (η) , R [f ; a] =
k=0
(b − a)2
f (η) , a
2n
Аналогично
R [f ; a − h] = −
(b − a)2
f (η) ,
2n
h
(b − a)3
R [f ; + a] =
f (η) , a
2
24 n2
η
b .
η
b.
33.
33§4. Формула прямоугольников для вычисления
интегралов от периодических функций
Пусть требуется вычислить
2π
f (x)d x
,
где
f (0) = f (2 π)
0
Строим квадратурную формулу с n узлами
2π
n
(n)
f (x) d x
(n)
Ak f (xk ) .
(1)
k=1
0
Естественно f (x) приближать тригонометрическим полиномом
m
Tn (x) = a0 +
[ak cos k x + bk sin k x] .
(2)
k=1
Говорят, что (1) имеет тригонометрическую степень точности, равную
m, если (1) точна для всех тригонометрических полиномов порядка m и
не точна для полиномов m + 1 порядка.
Докажем, что квадратурная формула (1) с n узлами не может быть
точной для всех тригонометрических полиномов порядка n, как бы ни
были выбраны узлы и коэффициенты; для чего рассмотрим функцию
n
(n)
sin2
f (x) =
k=1
x − xk
2
(3)
(n)
где xk - узлы формулы (1).
Прежде всего установим, что (3) - тригонометрический полином порядка n.
Имеем
(n)
sin2
x − xk
2
=
1
1
(n)
(n)
(n)
1 − cos(x − xk ) =
1 − cos x cos xk − sin x sin xk
2
2
x − xk
- произведе2
k=1
ние тригонометрических полиномов с вещественными коэффициентами
есть тригонометрический полином, порядок которого равен сумме порядков сомножителей, так что (3) - тригонометрический полином порядка
n; для него формула (1) не точна, так как
- тригонометрический полином I-го порядка;
2π
2π n
0
n
(n)
(n)
Ak f (xk ) ≡ 0 .
k=1
sin2
x − xk
d x > 0 , тогда как
sin
2
k=1
2
f (x) d x =
0
(n)
n
34.
34Таким образом, тригонометрическая степень точности формулы (1)
не выше n.
Докажем, что если в качестве (1) взять большую формулу прямоугольников
2π
2π
n
f (x) d x
0
n−1
f
α+k
k=0
2π
n
,
(4)
], то она точна для всех тригонометрических полиномов
где α ∈ [ 0 , 2π
n
порядка n−1. Для этого достаточно показать, что (4) точна, когда f (x) =
cos mx, f (x) = sin mx, m = 0, 1, . . . , n − 1 или для f (x) = e imx , при
m = 0, 1, . . . , n − 1. Для m = 0 f (x) = e0 = 1 формула, очевидно, точна.
Пусть 0 < m n − 1. Имеем
2π
e imx =
1 imx
e
im
2π
0
n−1
= 0,
k=0
0
n−1
n−1
2π
2π
e im(α+k n ) = e imα
=
2π
)=
n
f (α + k
k=0
= e imα
e im n k =
k=0
e
im 2π
k
n
−1
при m = n
e
−1
Аналогично можно доказать, что формула
im 2π
k
n
T
T
n
f (x)dx
0
n
T
f (x)[α + (k − 1) ] ,
n
k=1
где f (x) − T периодическая функция, а α ∈ [ 0 , Tn ] точна, когда f (x)
любой тригонометрический полином порядка n − 1 :
n−1
[ak cos
Tn−1 (x) = a0 +
k=1
2π
2π
kx + bk sin kx]
T
T
Итак установлено, что формула прямоугольника с n узлами является
формулой наивысшей тригонометрической степени точности.
§ 5 Квадратурная формула Ньютона-Котеса
На [a, b] выбирается n − 1 равноотстоящих узлов
(k)
xk = a + kh ,
k = 1, 2, . . . , n , h =
b−a
n
Интерполяционные квадратурные формулы, использующие в качастве
узлов числа a + kh, называются формулами Ньютона-Котеса:
b
n
(n)
f (x)dx
a
Ak f (x)[a + kh]
k=0
35.
35Требуется определить:
b
(n)
Ak
=
ω(x)
(x −
a
(n)
xk )ω
(n)
(xk )
dx,
В интеграле делаем замену t =
Имеем
ω(x) = (x − a)(x − a − h) . . . (x − b)
(x−a)
,
h
x = a + th.
ω(x) = hn+1 t(t − 1)(t − 2) . . . (t − n),
(n)
(n)
(n)
(n)
x − xk = h(t − k)
(n)
(n)
(n)
ω (xk ) = (xk − x0 )(xk − x1 ) . . . (xk − xk−1 )(xk − xk+1 ) . . . (xk − xn ) =
= (−1)n−k hn k!(n − k)! = (k(k − 1) . . . 1)hk (−1)n−k 1 · 2 . . . (n − k)hn−k ,
так что:
(n)
Ak
n
(−1)n−k
=h
k!(n − k)!
t(t − 1) . . . (t − n)dt ,
0
(n)
Ak
= (b −
(n)
a)Bk
,
(n)
Bk
n
(−1)n−k
=
n k!(n − k)!
t(t − 1) . . . (t − n)dt
0
Коэффициенты не зависят от промежутка интегрирования [a, b]. При
(n)
больших n среди Ak есть отрицательные. Рассмотрим частные случаи.
Формула трапеций (рис.3):
b
n=1
f (x)dx
b−a
[f (a)+f (b)]
2
a
Рис.3
3
Если f (x) непрерывна на [a, b], то R1 [f ] = − (b−a)
f (ξ), так как
12
остаточный член интерполяционного полинома по узлам a, b есть
ω(x) (n+1)
1
f
(ξ) ≡ f (x) − P1 (x)
R1 [f ] = f (η)(x − a)(x − b) ≡
2
(n + 1)!
36.
36b
Отсюда
b
f (x)dx −
P1 (x)dx =
a
a
Так как (x − a)(x − b)
теоремой о среднем:
1
2
b
(x − a)(x − b)f (ξ)dx.
a
0 на [a, b], то можно воспользоваться обощенной
b
1
R1 [f ] = f (η)
2
(x − a)(x − b)dx = −
(b − a)3
f (η),
12
a
η
b
a
Формула Симпсона (n = 2) :
b
b−a
a+b
[f (a) + 4f (
) + f (b)]
3· 2
2
f (x)dx
a
Выведем представление остаточного члена R[f ]. Здесь
ω(x) = (x − a)(x −
a+b
)(x − b).
2
Эта функция не сохраняет знак на [a, b], так что поступить, как выше,
нельзя. Если построить интерполяционный полином Эрмита по условиям
P (a) = f (a),
P (
a+b
a+b
) = f(
),
2
2
a+b
a+b
)=f (
), при P (b) = f (b),
2
2
b
то
P(
P (x)dx =
a+b
b−a
[f (a) + 4f (
) + f (b)].
2·3
2
a
Далее надо воспользоваться представлением остаточного члена при
интерполировании полиномом Эрмита
f (x) − P (x) =
Имеем
Ω(x) (4)
a+b 2
f (ξ), Ω(x) = (x − a)(x −
) (x − b) .
4!
2
b
1
R[f ] =
4!
Ω(x) f (4) (ξ)dx.
a
Функция Ω(x) сохраняет знак на [a, b], так что
b
1
R[f ] = f (4) (η)
4!
Ω(x)dx = −
(b − a)5 (4)
f (η), a
2880
η
b
a
Квадратурные формулы Ньютона-Котеса при больших η применять
целесообразно, так кат могут появиться отрецательные коэффициенты.
Выгоднее промежуток [a, b] разбивать на частичные и к ним применять
квадратурные формулы для небольших η.
37.
37Большая формула трапеций:
b
b−a
(n)
(n)
(n)
[f (x0 ) + 2(f (x1 ) + . . . + f (xn−1 )) + f (x(n)
n )].
2n
f (x)dx
a
Остаточный член в предположении что существует непрерывная f (x)
на [a, b], будет
Rn(1) [f ] = −
(b − a)3
f (η),
12 n2
a
η
b,
так как
Rn(1) [f ] =
R(1) [f ; k] = −
k
(b − a)3
12 n2
f (ξk ),
k
f (ξk ) = n f (η).
k
Большая формула Симпсона:
xk+1
b
f (x)dx =
k x
k−1
a
h
[f (xk+1 ) + 4f (xk ) + f (xk−1 )] + R[f ],
3
f (x)dx =
k
где h = (b − a)/n (n - четное число);
b
f (x)dx =
b−a
f (a) + 4 [f (x1 ) + f (x3 ) + . . . + f (xn−1 )]+
3n
a
+2 [f (x2 ) + f (x4 ) + . . . + f (xn−2 )] + f (b) + R[f ].
Остаточный член R[f ] в предположении, что f (4) (x) непрерывна на
[a, b], будет
˜5
h
(b − a)5
−
f (4) (ηk ) = −
2880
90 n5
R[f ] =
k
˜ = 2 h,
h
f
(4)
(ηk ) = f
(4)
k
f (4) (ηk ),
k
h
(b − a)5 (4)
(ξ) , R[f ] = −
f (ξ)
2
180 n4
§ 6 Квадратурные формулы типа Гаусса
Ранее установлено, что интерполяционная квадратурная формула
b
n
(n)
f (x)ρ(x)
a
(n)
Ak f (xk )
(1)
k=1
точна, если f (x) - полином не выше n − 1 степени. Это верно для любого
выбора узлов на [a, b].
38.
38Гаусс поставил задачу повысить степень точности (1) за счет выбора
узлов. Так как можно распорядится выбором n узлов, то естественно
ожидать повышения степени точности формулы на на n единиц. Гаусс
доказал, выбирая надлежащим образом узлы, что можно добиться, чтобы
(1) имела наивысшую степень точности 2n − 1.
Пусть ρ(x) 0 на [a, b],
b
ρ(x)xk dx, k = 0, 1, 2, . . . - существуют.
µk =
(2)
a
Говорят, что функции ϕ(x) и ψ(x) оргтогональны на [a, b] с весом ρ(x),
если
b
ρ(x)ϕ(x)ψ(x)dx = 0
a
Теорема. Для того чтобы квадратурная формула (1) с n узлами была
точна для любого полинома степени 2n − 1, необходимо и достаточно,
чтобы она была интерполяционной и ее узлы x1 , . . . , xn были корнями
многочлена степени n
ω(x) = (x − x1 )(x − x2 ) . . . (x − xn ),
(3)
ортогонального с весом ρ(x) к любому многочлену Q(x) степени < n
b
ρ(x)ω(x)Q(x)dx = 0
(4)
a
Необходимость. пусть (1) точна для всех многочленов степени
2n−1. Докажем, что (1)-интерполяционная и имеет место (4). Интерполяционность
следует из теоремы об интерполяционных формулах. Пусть степень Q(x) <
n, тогда степень ω(x)Q(x) 2n − 1. Полагаем f (x) = ω(x)Q(x).
По условию
b
b
n
Ak Qk (x)ω(xk ) = 0,
k=1
a
a
(n)
ρ(x)ω(x)Q(x)dx =
ρ(x)f (x)dx =
так как ω(xk ) = 0. Необходимость установлена.
Достаточность. Пусть (1) интерполяционная и имеет место (4).
Докажем что она точна для любого полинома f (x) степени 2n−1. Разделим
f (x) на ω(x). Имеем f (x) = ω(x)Q(x) + r(x), r(x) - остаток, степень r(x)
и Q(x) меньше n.
Умножим обе части на ρ(x) и проинтегрируем
b
b
ρ(x)f (x)dx =
a
b
ρ(x)ω(x)Q(x)dx +
a
b
=
a
n
(n)
r(x)ρ(x)dx =
a
ρ(x)r(x)dx =
(n)
Ak r(xk ,
k=1
39.
39так как степень r(x) меньше n, а (1)-интерполяционная.
(n)
(n)
Но r(xk ) = f (xk ), поэтому имеем
b
n
(n)
f (x)ρ(x)dx =
(n)
Ak f (xk )
k=1
a
Т.е. (1) точна для любого полинома f (x) степени 2n − 1.
Квадратурные формулы с n узлами, точные для полиномов степени
2n − 1, называют формулами типа Гаусса.
Вопрос о существовании формулы типа Гаусса сводится к построению
полинома ω(x) степени n, имеющего на [a, b] вещественные корни и ортогонального
на [a, b] с весом ρ(x) ко всем полиномам степени < n.
Докажем существование ω(x), указав способ построения ω(x).
Пусть
µ0 µ1 . . . µ j
b
µ1 µ2 . . . µj+1
∆j =
µk = xk ρ(x)dx
..............
a
µj µj+1 . . . µ2j
Докажем, что ∆j = 0, j = 0, 1, . . . , для чего рассмотрим систему
µ0 a 0
µ1 a 0
....
µj a0
+
+
...
+
µ1 a1
µ2 a1
......
µj+1 a1
+
+
...
+
...
...
...
...
+ µj aj
+ µj+1 aj
........
+ µ2j aj
=0
=0
....
=0
Докажем, что она имеет только нулевое решение. Умножим уравнения
системы на a0 , a1 , . . . , aj и сложим
b
a0
j
ρ(x)
a
. . . + aj
k=0
b
j
j
x ρ(x)
a
b
ak xk dx + a1
j
ak xk dx + . . .
xρ(x)
a
ak xk dx =
k=0
b
k=0
ρ(x) [a0 + a1 x1 + . . . + aj xj ]2 dx = 0
a
Отсюда a0 + a1 x1 + . . . + aj xj = 0, так как ρ(x) 0, т.е. a0 = a1 = . . . =
aj = 0, это доказывает, что ∆j = 0.
Полином
µ0 µ1 . . . µn−1 1
1
µ1 µ2 . . . µ n
x
(5)
ω(x) =
∆n−1 . . . . . . . . . . . . . . . . . .
µn µn+1 . . . µ2n−1 xn
имеет степень n и старший коэффициент, равный 1, так как ∆n−1 = 0.
Образуем
b
ρ(x)ω(x)xk dx =
a
1
∆n−1
µ0
µ1
...
µn
µ1
µ2
....
µn+1
...
...
....
...
µn−1
µn
.....
µ2n−1
µk
µk+1
....
µn+k
=0
40.
40для k = 0, 1, . . . , n−1. Следовательно, ω(x) ортогонален к любому полиному
Q(x) степени n − 1 с весом ρ(x).
Докажем, что корни ω(x) вещественны, разделены и лежат внутри
[a, b].
b
Так как
ρ(x)ω(x) = 0, то внутри [a, b] ω(x) имеет корни нечетной
a
кратности. Пусть m - число корней ω(x) нечетной кратности. Обозначим
их x1 , . . . , xm и составим Q(x) = (x − x1 ) . . . (x − xm ). Тогда ω(x)Q(x)
есть многочлен, у которого в [a, b] все корни четной кратности и, значит,
b
ρ(x)ω(x)Q(x) = 0, потому
ω(x)Q(x) сохраняет знак на [a, b]. Но тогда
a
b
что ρ(x)
0и
ρ(x)dx > 0.
a
Так как ω(x) ортогонален ко всем многочленам степени
n − 1, то
отсюда Q(x) имеет степень n, т.е. m = n. Утверждение доказано: все
корни 1-ой кратности разделены и лежат внутри [a, b].
Существование формулы типа Гаусса - доказано. Установим единственность.
Пусть имеются два многочлена ω(x) и ω∗ (x). Тогда Q(x) = ω(x) − ω∗ (x)
не больше (n − 1)-й степени. Имеем
b
0=
b
ρ(x)Q2 (x)dx = 0 ,
ρ(x)[ω(x) − ω∗ (x)]Q(x)dx =
a
a
что может быть только, если Q(x) ≡ 0 .
Выше мы указали способ построения полинома ω(x) в форме (5) и
доказали его единственность. Укажем другие способы, не требующие
раскрытия определителя (5).Так, коэффициенты ω(x) = xn + an−1 xn−1 +
. . . + a0 могут быть найдены из свойств ортогональности ω(x) с весом
ρ(x) на [a, b] к xk : k = 0, 1, . . . , n − 1.
В результате получим систему линейных алгебраических уравнений
относительно неизвестных коэффициентов an−1 , an−2 , . . . , a0 :
b
ρ(x)ω(x)xk dx = 0
k = 0, 1, . . . , n − 1
a
или в развернутом виде
an−1 µn+k−1 + an−2 µn+k−2 + . . . + a0 µk
(k = 0, 1, . . . , n − 1)
Третий способ построения ω(x) состоит в последовательном построении
полиномов
ω0 (x) = 1, ω1 (x) = x − α1 0 , ω2 (x) = x2 − α21 x − α2 0 , . . . ,
ωn (x) = xn − αn,n−1 xn−1 − . . . − αn 0 ≡ ω(x)
ортогональных с весом ρ(x) на [a, b]. Так для вычисления неизвестных
коэффициентов αkk−1 , . . . , αk0 полинома ωk (x), выписываем условия ортогональности
ωk (x) ко всем полиномам ωi (x) i < k:
b
ρ(x)ωk (x)ωi (x)dx = 0,
a
(i = 0, 1, . . . , k),
41.
41что приводит к решению системы линейно-алгебраических уравнений с
треугольной матрицей коэффициентов.
§ 7 Свойства квадратурных формул типа Гаусса
1. Алгебраическая степень точности формулы типа Гаусса равна
2n − 1. Для установления этого покажем, что квадратурная формула
b
n
(n)
ρ(x)f (x)dx
(n)
Ak f (xk )
(1)
k=1
a
при сделанных предположениях о весовой функции ρ(x) не может быть
точной для полиномов степени 2n ни при каком выборе узлов и коэффициентов.
Обозначим узлы x1 , . . . , xn и рассмотрим многочлен степени 2n
f (x) = ω 2 (x) = (x − x1 )2 . . . (x − xn )2 .
Очевидно, что для него (1) неточна, так как
b
b
ρ(x)ω 2 (x)dx > 0 ,
ρ(x)f (x) =
a
a
n
а квадратурная сумма
Ak f (xk ) =
k=1
n
Ak ω 2 (xk ) = 0.
k=1
Отсюда: формулы типа Гаусса являются формулами наивысшей степени
точности.
2. Коэффициенты Ak квадратурных формул типа Гаусса положительны.
Действительно, возьмем f (x) = [ω(x)/(x − xk )]2 - многочлен степени
2n − 2. Имеем
0, если i = k
f (xi ) =
[ω(xk )]2 , если i = k
Для этого многочлена формула типа Гаусса точна:
b
b
2
ρ(x)[ω(x)/(x − xk )]2 dx = Ak [ω (xk )] .
ρ(x)f (x)dx =
a
a
b
Отсюда Ak > 0, так как
ρ(x)[ω(x)/(x − xk )]2 dx > 0
a
3. Если f (x) на [a, b] имеет непрерывную производную порядка 2n,
то существует такая точка ξ ∈ [a, b], что остаточный член квадратурной
формулы типа Гаусса с n узлами x1 , . . . , xn имеет вид
b
R[f ] = [f
(2n)
ρ(x)ω 2 (x)dx,
(ξ)/(2n!)]
a
42.
42где
ω(x) = (x − x1 ) . . . (x − xn )
Доказательство. Построим интерполяционный многочлен P (x) по
условию
P (xi ) = f (xi ), P (xi ) = f (xi ).
Тогда по формулам, дающим представление остаточного члена Эрмитова
интерполирования, имеем
f (x) = P (x) + [ω 2 (x)/(2n!)]f (2n) (ξ),
где ξ зависит от x и ξ ∈ [a, b]. Поэтому
b
b
ρ(x)f (x)dx =
a
b
ρ(x)ω 2 (x)f (2n) (ξ)dx.
ρ(x)P (x)dx + [1/(2n)!]
a
a
Так как P (x) имеет степень не выше 2n − 1, то первый интеграл заменим
квадратурной суммой
b
n
Ak P (xk ) + R[f ].
ρ(x)f (x)dx =
k=1
a
Отсюда
b
2
R[f ] = (1/(2n)!)
ρ(x)ω (x)f
(2n)
b
f (2n) (η)
(ξ)dx =
(2n)!
a
ρ(x)ω 2 (x)dx.
a
4. Если [a, b] конечен и f (x) непрерывна на [a, b], то имеет место
b
n
(n)
(n)
Ak f (xk )
lim
n→∞
=
k=1
ρ(x)f (x)dx.
a
Надо показать, что
b
Rn [f ] =
n
(n)
ρ(x)f (x)dx −
a
(n)
Ak f (xk ) → 0
при n → ∞.
k=1
Пусть ε > 0.Так как [a, b] конечен и f (x) непрерывна, то по теореме
Вейерштрасса найдется P (x) такой, что
| f (x) − P (x)| < ε ∀ x ∈ [a, b]
Имеем
b
Rn [f ] =
b
ρ(x)[f (x) − P (x)]dx +
a
n
(n)
ρ(x)P (x)dx −
a
(n)
Ak P (xk ) +
k=1
43.
43n
(n)
+
(n)
(n)
Ak [P (xk ) − f (xk )]
k=1
Если N - степень P (x), то при 2n − 1 < N : Rn [P ] = 0.
Тогда при 2n − 1 < N имеем
b
Rn [f ] =
a
|Rn [f ]|
n
ρ(x)[f (x) − P (x)]dx +
k=1
b
ε
(n)
n
ρ(x)dx + ε
(n)
k=1
a
Ak
(n)
(n)
Ak [P (xk ) − f (xk )],
b
2ε ρ(x)dx,
a
что и требоваолсь доказать.
Рассмотрим последовательность квадратичных формул общего вида
(не обязательно Гаусса):
b
n
(n)
ρ(x)f (x)dx
(n)
Ak f (xk )
k=1
a
где [a, b] - конечный; ρ(x) - любая интегрируемая функция на [a, b]. Приведем
теорему о сходимости квадратичных формул без доказательства.
Теорема: Для того чтобы
b
n
(n)
(n)
Ak f (xk )
lim
n→∞
=
k=1
ρ(x)f (x)dx.
(∗ )
a
для любой непрерывной на [a, b] функции f (x), необходимо и достаточно
выполнение условий:
1. Предельное соотношение имеет место если, если f (x) любой многочлен;
2. Имеется такое K, что
n
k=1
(n)
|Ak |
K,
n = 1, 2, . . .
В частности, если (∗) есть интерполяционная квадратурная формула
и имеет положительные коэффициенты, то условия теоремы выполнены.
§ 8 Частные случаи квадратурных формул типа
Гаусса
1. ρ(x) = 1, [a, b] = [1, −1] - квадратурная формула Гаусса
1
n
(n)
f (x)dx
(n)
Ak f (xk )
(1)
k=1
−1
Узлы x1 , . . . , xn есть корни многочлена ω(x) степени n , ортогонального
ко всем многочленам степени n−1. Многочлены, обладающие указанным
свойством, называются полиномами Лежандра
ω(x) =
2n (n!)2
Pn (x),
(2n)!
44.
44где
1
1 dn 2
n
(x − 1) = n ϕ(n) (x)
(2)
n
n
2 n! dx
2 n!
Покажем, что Pn (x) ортогонален к любому полиному Q(x) степени
< n. Имеем
Pn (x) =
1
Pn (x)Q(x)dx =
−1
=
1
2n n!
1
2n n!
[Q(x)ϕ(n−1) (x)
= . . . = (−1)n 2n1n!
1
1
−1
1
−1
Q(x)ϕ(n) (x)dx =
1
−
Q (x)ϕ(n−1) (x)dx] =
(3)
−1
Q(n) (x)ϕ(x)dx.
−1
Если Q(x) - любой многочлен степени < n, то Q(n) (x) ≡ 0 , так что
1
Pn (x)Q(x)dx = 0, если степень Q(x) не превосходит n − 1.
−1
Таким образом, в качестве узлов квадратурной формулы Гаусса надо
взять корни полинома Лежандра (2). Далее установим справедливость
формулы
2
(n)
Ak =
(4)
2
(1 − xk )[Pn (xk )]2
для вычисления коэффициентов формулы Гаусса. С этой целью рассмотри
вычисление интеграла
b
Sk =
a
Pn (x)
Pk (x)dx
(x − xk )
(5)
двумя способами: 1) квадратурная формула Гаусса с n узлами для вычисления
Sk точна, так как подинтегральная функция есть полином степени 2n−2.
Имеем
2
Sk = Ak [Pk (xk )]
(6)
2) интегрируем (5) по частям, положив U = Pn (x)/(x − xk ) :
2
dV = Pn (x)dx : Sk = Pn (x)/(x − xk )
1
−1
1
Pn (x)U (x)dx .
−
−1
Второе слагаемое равно нулю, так как Pn (x) ортогонален ко всем многочленам
степени не выше n − 1. Имеем
Sk = [Pn 2 (1)/(1 − xk )] + Pn 2 (−1)/(1 + xk ).
Докажем, что
Pn (1) = 1 ,
Pn (−1) = (−1)n
(7)
(8)
откуда с учетом (7) и (6) будет следовать справедливость (4).
По формуле Лейбница имеем
1 dn
1
Pn (x) = n
(x − 1)n (x + 1)n = n
n
2 n! dx
2 n!
n
Cnk
k=0
n
dn−k
n d
(1
+
x)
(x − 1)n =
dxn−k
dxn
45.
45=
1
n
2 n!
n
Cnk
k=0
n!
n!
1
(x + 1)k
(x − 1)n−k = n
k!
(n − k)!
2
n
2
[Cnk ] (x + 1)k (x − 1)n−k .
k=0
n
Отсюда Pn (1) = 1, Pn (−1) = (−1) .
Установим справедливость формулы
(n!)4 22n+1
Rn [f ] =
f (2n) (ξ)
2
[(2n)!] (2n + 1)
(9)
для остаточного члена формулы Гаусса в случае, когда f (2n) (x) является
непрерывной на [a, b] функцией. Для этого сначала докажем, что
1
Pn2 (x)dx = 2/(2n + 1)
(10)
−1
Действительно, из (3) при Q(x) = Pn (x) имеет
1
Pn2 (x)dx
(2n)!(−1)n
=
22n (n!)2
−1
1
1
(2n)!
(x − 1) dx = 2 2n
2 (n!)2
n
2
−1
n
(1 − x2 ) dx,
0
Но
π
2
1
n
(1 − x2 ) dx =
0
cos2n+1 ϕdϕ =
(2n)!!
22n (n!)2
=
.
(2n + 1)!!
(2n + 1)!
0
Отсюда следует справедливость (10).
Запишем выражение для Rn [f ], учитывая свойство 3 § 7:
1
f (2n) (ξ)
Rn [f ] =
(2n)!
1
2
Pn2 (x)
ω (x)dx =
−1
=
f (2n) (ξ) (2n)!
(2n)! 2n (n!)2
2
dx =
−1
(n!)4 22n
2
f (2n) (ξ)
3
2n
+
1
[(2n)!]
Здесь мы учли справедливость (10) и связь между ω(x) и Pn (x):
2n (n!)2
ω(x) =
Pn (x).
(2n)!
Справедливость (9) установлена.
√
2. ρ(x) = 1/ 1 − x2 , [a, b] = [−1, 1] - квадратурная формула МелераЧебышева
1
n
√
π
f (x)/ 1 − x2
f (xk ).
(11)
n k=1
−1
Узлами x1 , . . . , xn квадратурной формы Мелера-Чебышева являются
π (k = 1, 2, 3, . . . , n) полинома Чебышева
корни xk = cos 2k−1
2n
Tn (x) = cos n arccos x = 2n−1 xn + . . .
46.
46Для установления этого факта достаточно доказать, что
1
I=
−1
xm cos n arccos x
√
dx = 0
1 − x2
для m = 0, 1, . . . , n − 1.
Имеем при x = cosϕ
π
I=
cosm ϕ cos nϕdϕ = 0,
0
m
так как cosm ϕ =
k = 0, 1, . . . , n − 1 ,
αk cos kϕ
k=0
Коэффициенты формулы (11) все равны: Ak =
Действительно:
Ak =
1
Tn (xk )
1
π
n
для k = 1, . . . , n.
π
Tn (x)
1
1
cos nϕ
dx =
dϕ =
2
Tn (xk ) 0 cos ϕ − xk
1 − x x − xk
π
1
cos nϕ
=
dϕ.
2Tn (xk ) −π cos ϕ − xk
√
−1
(12)
Для вычисления (12) применим квадратурную формулу прямоугольников
с 2n узлами на [−π, π]:
2j − 1
π, j = −n + 1, −n + 2, . . . , 0, 1, . . . , n
2n
ϕj =
Значение подинтегральной функции cos nϕ/ cos ϕ − xk = f (ϕ) при
ϕ = ϕj или, что тоже самое, значение Tn (x)/(xj − xk ) равно 0 при xj = xk
и равно Tn (xk ) при xj = xk . Так как подинтегральная функция четная и
ϕ−j+1 = −ϕj , то f (ϕ−j+1 ) = f (ϕj ) при j = 1, 2, . . . , n. Получим
Ak =
2π
1
π
[Tn (xk ) + Tn (xk )] = .
Tn (xk ) 2n
n
Покажем, что остаточный член формулы (11) можно представить в
виде
πf (2n) (ξ)
R[f ] =
,
(13)
(2n)!22n−1
если f (2n) (x) есть непрерывная на [−1, 1] функция. Имеем
f (2n) (ξ) 1 ω 2 (x)
f (2n) (ξ) 1 Tn2 (x)
√
√
dx =
dx =
(2n)! −1 1 − x2
(2n)! 22n−2 −1 1 − x2
f (2n) (ξ) π
πf (2n) (ξ)
f (2n) (ξ) π
2
cos
nϕ
dϕ
=
(1
−
cos
2nϕ)
dϕ
=
=
(2n)! 22n−2 0
(2n)! 22n−1 0
(2n)! 22n−1
R[f ] =
3. ρ(x) = (1 − x)α (1 + x)β
α > −1, β > −1. Квадратурная формула
1
n
α
(n)
β
(1 − x) (1 + x) f (x)dx =
−1
Ak f (xk )
k=1
(14)
47.
47имеет в качестве узлов корни полинома Якоби
n
(−1)n
−α
β d
(1
−
x)
(1
+
x)
[(1 − x)α+n (1 + x)β+n ].
2n n!
dxn
Pn(α,β) =
(n)
Ее коэффициенты Ak представимы в виде
Ak = 2α+β+1
Γ(α + n + 1)Γ(β + n + 1)
(α,β)
n! Γ(α + β + n + 1)(1 − x2k )[Pn
2
(xk )]
Здесь Γ(x) - интеграл Эйлера.
2
4. ρ(x) = e−x , [a, b] = (−∞, ∞). Квадратурная формула Эрмита
∞
n
−x2
e
(n)
f (x)dx =
Ak f (xk ) + Rn [f ]
k=1
−∞
имеет своими узлами корни полинома Эрмита
Hn = (−1)n e x
(n)
Ak
2
dn −x2
e ,
dxn
√
√
2n+1 n! π
=
π/2n (2n)!]f (2n) (ξ)
,
R
[f
]
=
[n!
n
2
[Hn (xk )]
5. ρ(x) = e−x , [a, b] = (0, ∞) Квадратурная формула Лагера
∞
n
(n)
α −x
Ak f (xk ) + Rn [f ],
x e f (x)dx =
α > −1
k=1
0
имеет узлами корни полинома Лагера
Ln (x) = x− α e x (−1)n
(n)
Ak =
dn α+n −x
[x e ],
dxn
Γ(n + 1)Γ(α + n + 1)
.
xk [Ln (xk )]2
§ 9 Квадратурные формулы Чебышева
Чебышев рассмотрел вопрос о построении квадратурной формулы с равными
коэффициентами
b
n
ρ(x)f (x)dx
a
c
f (xk )
(1)
k=1
√
Частный случай, когда [a, b] = [−1, 1] и ρ = 1/ 1 − x2 , дает формула
Мелера.
b
Считаем, что существуют моменты µk =
a
xk ρ(x)dx и µ0 = 0. В
квадратурную формулу входит n + 1 параметр: n узлов и c. Можно
48.
48надеятся подобрать узлы так, чтобы формула была точна, когда f (x)
- любой полином степени n.
Узлы xk и c будем находить из того условия, что формула должна
быть точной, когда f (x) = xk , k = 0, 1, . . . , n. При f (x) = 1 получим
b
nc =
ρ(x)dx = µ0 ; c = µ0 /n , c = 0, так как µ0 = 0.
a
Для определения узлов получим нелинейную систему
n
xk = nµ1 /µ0 ,
k=1
n
2
xk = nµ2 /µ0 ,
k=1
. . . . . . . . . . . . ,
n
n
xk = nµn /µ0 .
(2)
k=1
Для отыскания x1 , . . . , xn будем разыскивать многочлен
ω(x) = (x − x1 )(x − x2 ) . . . (x − xn ) = xn + a1 xn−1 + . . . + an .
Имеем
ω (x)/ω(x) =
n
1/x − xk . При
, k = 1, . . . , n
k=1
1
1
1
1 xk x2
=
= + 2 + k3 + . . . , так что
x − xk
x 1 − xk /x
x x
x
n
2
3
ω (x)/ω(x) = n/x + s1 /x + s2 /x + . . . ,
xik
si =
(3)
k=1
Умножим (3) на ω(x), получим
n s1
nxn−1 + (n − 1)a1 xn−2 + . . . + an−1 = (xn + a1 xn−1 + . . . + an )[ + 2 + . . .].
x x
Приравниваем коэффициенты при одинаковых степенях x:
s1 + a1 = 0 ,
s2 + a1 s1 + 2a2 = 0 ,
s3 + a1 s2 + a2 s1 + 3a3 = 0 ,
(4)
...........................
sn + a1 sn−1 + a2 sn−2 + . . . + nan = 0 .
Система (2) дает значение s1 , s2 , . . . , sn . Из (2) и (4) последовательно
находим a1 , a2 , . . . , an . Таким образом, вопрос о построении квадратурной
формулы Чебышева свелся к исследованию корней так построенного
многочлена ω(x). Чебышев вычислил узлы для [−1, 1], ρ(x) = 1 для n = 1
до n = 7 и показал, что формула имеет вид
1
f (x)dx
−1
2
n
k=1
f (xk ).
n
Потом было обнаружено, что при n = 8 среди корней ω(x) есть
комплексные, при n = 9 - все корни ω(x) вещественные. ернштейн доказал,
что при n
10 среди корней ω(x) всегда имеются комплексные, т.е.
квадратурная формула Чебышева при n 10 и n = 8 не существует.
49.
49§ 10 Квадратурные формулы Маркова
Пусть требуется построить квадратурную формулу
b
m
ρ(x)f (x)dx
n
Bj f (aj ) +
j=1
a
Ak f (xk ),
(1)
k=1
где узлы aj и xk ∈ [a, b] , при этом aj заданы заранее, а xk выбирается
так, чтобы (1) была точна для всех многочленов возможно более высокой
b
степени. Вес ρ(x) удовлетворяет условиям ρ(x)
0 , µ0 = 0 , µk =
xk ρ(x)dx <
a
∞ , k = 1, 2 . . . .
Пусть
ω(x) = (x − x1 )(x − x2 ) . . . (x − xn ), σ(x) = (x − a1 )(x − a2 ) . . . (x − am ).
За счет выбора коэффициентов можно добиться, чтобы формула была
толчна для полиномов степени n+m−1. Распорядимся еще выбором n
узлов. Следовательно, можно надеяться, что за счет выбора коэффициентов
и узлов формула будет точна для полиномов степени 2n + m − 1.
Теорема Для того чтобы квадратурная формула (1) обращалась в
точное равенство, когда f (x) - любой многочлен степени 2n + m − 1,
необходимо и достаточно, чтобы она была интерполяционной и многочлен
ω(x) был ортогонален с весом ρ(x)σ(x) на [a, b] к любому многочлену
степени меньше n:
b
ρ(x)σ(x)ω(x)Q(x)dx = 0 .
a
Необходимость Пусть формула (1) точна для всех полиномов
2n + m − 1. Тогда она является интерполяционной. Для доказательства
b
ρ(x)σ(x)ω(x)Q(x)dx = 0 для любого полинома Q(x) степени
n−1
a
возьмем в качестве f (x) = ρ(x)σ(x)Q(x) полином степени
b
2n + m − 1.
ρ(x)f (x)dx =
a
m
k=1
Bk f (xk ) +
n
Ak f (xk ) = 0 , что и
k=1
доказывает наше утверждение.
Достаточность Пусть (1) интерполяционная и
b
ρ(x)σ(x)ω(x)xk dx = 0, k = 0, 1, . . . , n − 1. Докажем, что (1) точна
a
для любого полинома степени 2n + m − 1. Пусть f (x) любой полином
степени 2n + m − 1. Разделим f (x) на ω(x)σ(x)
f (x) = ω(x)σ(x)Q(x) + r(x)
(2)
степень Q(x)
(2n + m − 1) − (n + m) = n − 1. Степень r(x) меньше
степени делителя, т.е. степень r(x) n + m − 1. Умножим (2) на ρ(x) и
50.
50проинтегрируем
b
b
ρ(x)f (x)dx =
a
=
m
Bk r(ak ) +
k=1
b
ρ(x)ω(x)σ(x)Q(x)dx +
a
n
ρ(x)r(x)dx =
a
Ak r(xk ), r(xk ) = f (xk ), r(ak ) = f (ak ).
k=1
Коэффициенты квадратурной формулы (1) есть
b
Bs =
a
ρ(x)σ(x)ω(x)dx
, Ak =
(x − as )σ (as )ω(as )
b
ρ(x)σ(x)ω(x)dx
(x − xk )σ(xk )ω (xk )
a
(3)
Для обоснования формул (3) представим подинтегральную функцию
f (x) через интерполяционный полином f (x) = Pm−1+n (x) + R[f ; x],
где
m
Ω(x)
Ω(x)
f (xk ) +
f (ak );
k=1 Ω (xk )(x − xk )
k=1 Ω (ak )(x − ak )
Ω(x) = ω(x)σ(x) = (x − x1 ) . . . (x − xn )(x − a1 ) . . . (x − am );
Ω (xk ) = ω (xk )σ(xk ) + ω(xk )σ (xk ) = ω (xk )σ(xk );
Ω (ak ) = ω (ak )σ(ak ) + ω(ak )σ (ak ) = ω(ak )σ (ak ).
Pm−1+n (x) =
n
b
b
ρ(x)σ(x)ω(x)dx
ρ(x)σ(x)ω(x)dx
, Bk =
a (x − xk )σ(xk )ω (xk )
a (x − ak )σ (ak )ω(ak )
Выведем формулу для остаточного члена квадратурной формулы (1).
Для этого построим интерполяционный полином Эрмита по условиям
P (xk ) = f (xk ) P (xk ) = f (xk ) k = 1, . . . , n P (ak ) = f (ak ) k = 1, . . . , m.
Всего 2n + m условий, так что степень P (x) есть 2n + m − 1.
Отсюда Ak =
b
Пусть f (x) = P (x)+R[f ; x]. Тогда R[f ] =
n
k=1
Bk P (xk )+
n
b
ρR[f, x]dx, так как
a
Ak P (xk ). Если f (x) ∈ C 2n+m , то R[f ; x] =
k=1
b
[a, b]. Тогда R[f ] =
ρ(x)R[f ; x]dx =
a
1
(2n+m)!
b
Из этой формулы следует , что если
ρP (x)dx =
a
b
ω 2 (x)σ(x)
(2n+m)!
f 2n+m (ξ) ξ ∈
ρ(x)ω 2 (x)σ(x)f 2n+m (ξ)dξ.
a
ρ(x)ω 2 (x)σ(x)dx = 0 и f (x) -
a
полином степени 2n + m, то R[f ] = 0, т.е. 2n + m − 1 есть, вообще говоря,
наивысшая степень точности квадратурной формулы Маркова.
Доказанная выше теорема сводит вопрос о существовании квадратурной
формы (1), точной для всех полиномов степени 2n + m − 1, к вопросу о
существовании многочлена ω(x) с вещественными различными корнями,
ортогонального на [a, b] с весом ρ(x)σ(x) к любому полиному Q(x) степени
n−1. Марков указал три случая, когда можно построить формулу (1):
1) a1 = a , σ(x) = (x − a) 0 при x ∈ [a, b]; 2) a1 = b , σ(x) = (x − b) 0
при x ∈ [a, b]; 3) a1 = a, a2 = b , σ(x) = (x − a)(x − b) 0 при x ∈ [a, b].
Рассмотрим эти случаи для ρ = 1 , [a, b] = [1, −1]
1. При m = 1, a1 = −1 имеем
1
n
f (x)dx
−1
Bf (−1) +
Ak f (xk ).
k=1
51.
51Алгебраическая степень точности формулы равна 2n; ω(x) с весом
(1 + x) ортогонален к любому многочлену степени n − 1, так что ω(x)
есть с точностью дог множителя полином Якоби P (0,1) (x). Существует
прямая связь между P (0,1) (x) и полиномами Лежандра. Можно показать:
(1 + x)ω(x) = cn [Pn+1 (x) + Pn (x)],
где Pn (x) и Pn+1 (x) - полиномы Лежандра; cn = const. Таким образом,
x1 , . . . , xn есть корни уравнения
Pn+1 (x) + Pn (x) = 0, B = 2/(n + 1)2 , Ak =
4
(0,1)
(1 + xk )(1 − x2k )[Pn
2
(xk )]
2. Случай m = 1, a1 = b = 1 можно свести к случаю 1., если в
интеграле сделать замену x = a + b − t
3. При a1 = −1 и a2 = 1 имеем
1
n
f (x)dx
B1 f (−1) + B2 f (1) +
Ak f (xk ).
k=1
−1
Алгебраическая степень точности равна 2n + 1. Узлы квадратурной
формулы суть корни многочлена
(x2 − 1)ω(x) = cn [Pn+2 (x) − Pn (x)], cn = const,
B1 = B2 =
2
n+1
1
, Ak = 8
(n + 1)(n + 2)
n + 2 (1 − x2k )[Pn(1,1) (xk )]2
§ 11 Интегрирование сильно осциллирующих
функций
При разложении функции в ряд Фурье и в некоторых других задачах
(например, при построении диаграмм направленности антенн) возникает
необходимость вычисления интегралов вида
1
1
f (x)exp(i2πN x)dx =
−1
1
f (x) cos 2πN xdx + i
−1
f (x)sin2πN xdx,
(1)
−1
где 2πN 1, f (x) - гладкая функция.
Число нулей каждой из пожинтегральных функций на [a, b] приблизительно
равно N . Такие подинтегральные функции могут быть хорошо приближены
полиномами степени n, если n N . Поэтому для вычисления интегралов
от таких функций потребуется применение квадратурных формул, точных
для многочленов высокой степени.
Более целесообразно применять другие способы вычисления интегралов
(1). Рассмотрим два из них.
В первом способе осциллирующий множитель принимается в качестве
весовой функции, а гладкая функция f (x) заменяется интерполяционным
полиномом.
52.
52n
Пусть f (x) ≈ Pn (x) =
k=1
1
ω(x)
f (xk ).
(x − xk )ω (xk )
1
ω(x) cos 2πN x
dx
k=1
−1
−1 (x − xk )ω (xk )
вычисляется точно. Коэффициенты Ak могут быть заданы в виде
Тогда I =
Pn (x) cos 2πN xdx =
n
Ak f (xk ), где Ak =
1
Ak =
cos 2πN x
−1
(x − xp )
dx
(xk − xp )
p=k
так как
ω(x)
(x − x1 )..(x − xk−1 )(x − xk+1 )..(x − xn )
(x − xp )
=
=
(x − xk )ω (xk )
(xk − x1 )..(xk − xk−1 )(xk − xk+1 )..(xk − xn ) p=k (xk − xp )
Легко видеть что
1
R[f ] =
1
n
Ak f (xk ) =
f (x) cos 2πN xdx −
k=1
−1
f n (ξ)
R[f, x]dx =
n!
−1
1
ω(x)dx.
−1
Часто берут n = 3, x1 = −1, x2 = 0, x3 = 1. Полученную формулу
называют формулой Филона. При n = 5 берут узлы x1 = −1, x2 =
−0.5, x3 = 0, x4 = 0.5, x5 = 1.
Второй способ вычисления интеграла от осциллирующей функции
- применение многократного интегрирования по частям. Например, при
τ
вычислении интеграла
1
ϕ(N x)f (x)dx или
0
k раз интегрирование по частям
1
f (x) sin 2πN xdx = −
0
0
sin
f (x) (cos)
2πN xdx применяют
1
f (x)
1
cos 2πN x +
2πN
2πN
0
1
f (1) (x) cos 2πN xdx =
0
1
1
1
=−
[f (1) − f (0)] − f (1) (x) cos 2πN xdx = −
[f (1) − f (0)]+
2πN
2πN
0
k−1 (−1)j+1
1 1 (2)
(2j)
+
f (x) sin 2πN xdx = . . . =
(1) − f (2j) (0)]+
2j+1 [f
2πN 0
j=0 (2πN )
(−1)k 1 (2k)
f (x) sin 2πN xdx.
+
(2πN )2k 0
Внеинтегральный член может быть вычислен с большой точностью, а
второе слагаемое хотя и содержит интеграл от осциллирующей функции,
но оказывает незначительное влияние на значение вычисляемого интеграла
при больших k так как делится на величину (2πN )2k
§ 12 Вычисление несобственных интегралов
Если несобственный интеграл с бесконечными пределами, то его можно
преобразовать в несобственный интеграл с конечными пределами с помощью
замены переменных.
53.
53Иногда несобственный интеграл с бесконечными пределами заменяют
интегралами с конечными пределами, беря эти пределы достаточно большими,
чтобы отброшенной частью пренебречь. Для оценки отбрасываемой части
надо применить асимптотическое разложение подинтегральной функции
и делать оценки отбрасываемой части. Здесь многое зависит от искусства
вычислителя.
Рассмотрим случай несобственных интегралов с конечными пределами.
При их вычислении пользуются методомвыделения особенностей. Существуют
два способа выделения особенностей: мультипликативный и аддитивный.
b
f (x)dx, f (c) = ∞,
Мультипликативный способ. Пусть I =
a
a c b. Представим f (x) в виде f (x) = ρ(x)ϕ(x), где ϕ(x) ограниченная
на [a, b], обладающяя достаточным числом производных ρ(x) > 0, и
существуют моменты.
Функцию ρ(x) рассматриваю как весовую и строят квадратурные
формулы с весом ρ(x) :
b
n
Ak ϕ(xk ),
ρ(x)ϕ(x)dx
например:
k=1
a
1
I=
−1
dx
√
=
1 − x4
1
√
−1
dx
√
.
1 − x2 1 + x2
Подинтегральная функция разрывна в точках ± i
√
√
ρ(x) = 1/ 1 + x2 , ϕ(x) = 1/ 1 + x2
Аддитивный способ. Подинтегральную функцию f (x) редставляют
в виде суммы f (x) = ϕ(x) + ψ(x), где ϕ(x) не имеет особенностей и
достаточно гладкая, а интеграл от ψ(x) может быть найден точными
методами, например:
I=
=
π
2
0
π
2
0
π
2
ln sin xdx = [ln x + ln sinx x ]dx =
ln xdx +
π
2
0
0
ln
sin x
x
dx =
π
2
[ln
π
2
− 1] +
π
2
0
ln sinx x dx.
Второй интеграл берется численно.
Л.В.Канторович, предложивший этот способ, указал некоторые приемы
представления подинтегральной функции в виде f (x) = ϕ(x) + ψ(x).
а) Пусть f (x) = (x − c)α ϕ(x), c ∈ [a, b], α > −1, а ϕ(x) может быть
представлена по формуле Тейлора с остаточным членом , содержащим
производные k - того порядка. Тогда
f (x) = (x − c)α [ϕ(c) +
ϕ(k) (c)
ϕ (c)
(x − c) + . . . +
(x − c)k ]+
1!
k!
+(x − c)α [ϕ(x) − ϕ(c) −
ϕ (x)
ϕ(k) (x)
(x − c) − . . . −
(x − c)k ].
1!
k!
54.
54Здесь ψ(x) = (x − c)α [ϕ(c) + ϕ 1!(c) (x − c) + . . . + ϕ
функция и интеграл от нее берется точно, а
(k) (c)
k!
(x − c)k ] - степенная
ϕ (x)
ϕ(k) (x)
ϕ(x) = (x − c) [ϕ(x) − ϕ(c) −
(x − c) − . . . −
(x − c)k ]
1!
k!
α
непрерывная в точке c и имеет обращающиеся в нуль производные в
точке c до порядка k, так что формулы численного интегрирования к
ней применимы.
б) f (x) = (x − c)α lnp |x − c| ϕ(x), где p - натуральное число;
α > −1, c ∈ [a, b], ϕ(x) - такая же, как в а). Тогда
f (x) = lnp |x − c| [ϕ(c)(x − c)α +
ϕ (c)
ϕ(k) (c)
(x − c)α+1 + . . . +
(x − c)k+α ]+
1!
k!
+ lnp |x−c| [(x − c)α ϕ(x)−(x − c)α ϕ(c)−. . .−
ϕ(k) (x)
(x − c)k+α ] ≡ ϕ(x)+ψ(x).
k!
b
Интеграл
b
ψ(x)dx берется по частям в конечном виде,
a
ϕ(x)dx достаточно
a
точно можно вычислить по формулам квадратур.
в) f (x) = ψ(φ(x)) - аддитивная функция, φ(x) - епрерывная, но
ψ(φ(c)) равна ∞. Имеем
f (x) = ψ[φ(c) + (x − c)φ (c)] + {ψ[φ(x)] − ψ[φ(c) + (x − c)φ (c)]}
Если интеграл от ψ[φ(c) + (x − c)φ (c)] вычисляется точно, то эту
функцию принимаем за ψ :
ϕ(x) = ψ[φ(x)] − ψ[φ(c) + (x − c)φ (c)]
§ 13 Способы повышения точности квадратурных
формулы
Все интерполяционные квадратурные формулы
b
n
ρ(x)f (x)dx
a
Ak f (xk ) + Rn [f ]
(1)
k=1
основаны на замене подинтегральной функции алгебраическим многочленом
на отрезке [a, b] или на его частях.
Естественно ожидать, что точность квадратурной формулы будет
зависеть от гладкости подинтегральной функции. Так, погрешность квадратурных
формул Гаусса с n узлами зависит от того, насколько точно f может
быть на все отрезке [a, b] приближена многочленами степени 2n − 1.
Погрешность формулы трапеции зависит от того, как сильно на каждом
частичном отрезке [xk , xk+1 ] график f (x) отличается от прямой линии,
соединяющей концы соответствующего участка графика. За меру гладкости
функции принимают порядок ее непрерывной дифференцируемости. Поэтому
одним из способов повышения точности квадратурной формулы является
55.
55улучшение гладкости подинтегральной функции. Способы такого повышения
точности квадратурной формулы были рассмотрены в связи с численным
интегрированием несобственных интегралов. отметим только, что повышение
порядка дифференцируемости подинтегральной функции хотя и полезно
для улучшения точности квадратурной суммы, но эффективность повышения
гладкости подинтегральной функции имеет ограниченное значение. Порядок
гладкости для подинтегральной функции, наиболее целесообразный для
данной формулы. будет зависеть от степенп точности квадратурной формулы.
Например, большая формула Симпсона дает точный результат, если f (x)
есть полином третьей степени, так как
(b − a)5 (4)
R[f ] = −
f (ξ) a
180 n4
ξ
b.
Поэтому при увеличении порядка дифференцируемости f (x) стественно
4
3
.
или f (x) ∈ C[a,b]
стремится к тому, чтобы f (x) ∈ C[a,b]
Пусть мы достигли указанной гладкости подинтегральной функции.
Поставим вопрос, можно ли, увеличивая гладкость f (x) ожидать значительного
повышения точности квадратурной формулы Симпсона. Ответ следует
из представления остаточного члена в форме
b
f (4) K(x)dx,
R[f ] =
(2)
a
где ядро K(x) непрерывно и не меняет знака. В форме (2) остаток представим
для любой функции f (x) ∈ C k , если k
4. Так что при одном только
повышении порядка дифференцируемости без целесообразного изменения
свойств f (4) уменьшение R[f ] может наступить только случайно. Уменьшение
R[f ] достигается только при помощью глубоко лежащих средств.
Обычно для подготовки функции к интегрированию руководствуются
следующим правилом.
Если выбранная квадратурная формула имеет алгебраическую степень
точности m − 1, то следует стремиться к тому, чтобы интегрируемая
m
функция f (x) ∈ C[a,b]
.
Второй способ повышения точности квадратурной формулы состоит
в выделении главной части остатка.
Пусть квадратурная формула (1) имеет алгебраическую степень точности
m − 1. Покажем, что
b
f (m) (t)K(t)dt,
R[f ] =
(3)
a
Действительно, всякая функция f (x) ∈ C m на [a, b] может быть представлена
по формуле Тейлора
m−1
f (x) =
i=0
x
(x − a)i (i)
f (a) +
i!
f (m) (t)
a
(x − t)m−1
dt,
(m − 1)!
(4)
56.
56Введем в рассмотрение "гасящую"функцию
при x > t
1
1/2 при x = t
E(x − t) =
0
при x < t
Тогда интеграл с переменной верхней границей в (4) можно заменить
интегралом на промежутке [a, b] :
m−1
f (x) =
i=0
b
(x − a)i (i)
f (a) +
i!
f (m) (t)E(x − t)
(x − t)m−1
dt,
(m − 1)!
(5)
a
Подставим (4) в выражение
b
Rn [f ] =
n
m−1
ρ(x)f (x)dx −
Ak f (xk ) =
i=0
k=1
a
Ak (xk − a)i ] +
−
k=1
ρ(x)(x − a)i dx−
a
b
n
b
f (i) (a)
[
i!
b
f (m) (t)Kn (t)dt =
a
f (m) (t)Kn (t)dt.
a
Здесь
b
Kn (t) =
a
b
=
ρ(x)
t
n
(xk − t)m−1
(x − t)m−1
Ak E(xk − t)
dx −
dx =
ρ(x)E(x − t)
(m − 1)!
(m − 1)!
k=1
(x − t)m−1
dx−
(m − 1)!
x
Ak
k >t
(xk − t)m−1
(x − t)m−1
t = xk
dx = R E(x − t)
,
t=a
(m − 1)!
(m − 1)!
Внеинтегральный член для Rn [f ] равен нулю, так как, по предположению,
квадратурная формула (1) точна для всех полиномов степени m − 1.
Способы выделения главной части из R[f ] тесно связаны со свойствами
ядра K(t). Если значения ядра в какой-то мере равномерно распределены
на отрезке [a, b] и ядро не сильно изменяется ,то на R[f ] наибольшее
значение будет оказывать среднее значение ядра K(t). Поясним это на
примере большой формулы трапеций. Она получается, если [a, b] разделить
на частичные отрезки длиной h и к каждому отрезку применить формулу
трапеций. Квадратурная формула верна для кусочно-линейной функции,
и ее остаток выражается через f (x). Интегральное представление остатка
b
R[f ] =
f (t)K(t)dt.
a
Ядро K(t) будет на [a, b] периодической функцией с малым периодом h.
Так что на R[f ] наибольшее влияние станет оказывать среднее значение
K(t). Этот вывод справедлив для большой формулы Симпсона и большой
формулы прямоугольников, а также для любой квадратурной формулы
57.
57(1). Для выделения из R[f ] главной части полагаем K(t) = C0 + [K(t) −
C0 ], беря за C0 среднее значение
b
1
C0 =
b−a
K(t)dt.
a
b
Имеем R[f ] = C0
b
f (m) (t)dt +
a
f (m) (t)[K(t) − C0 ]dt =
a
b
t
(K(t)−C0 )dt]ba +
= C0 [f (m−1) (b)−f (m−1) (a)]+[f (m) (t)−
a
f (m + 1)(t)L1 (t)dt =
a
b
= C0 [f (m−1) (b)−f (m−1) (a)]+
f (m + 1)(t)L1 (t)dt,
a
t
где L1 (t) = [K(t) − C0 ]dt.
a
b
Из интеграла
f (m + 1)(t)L1 (t)dt в свою очередь может быть выделена
a
главная часть и т.д., пока не будет достигнута нужная степень точности
квадратурной формулы.
После s-кратного выделения из R[f ] главных частей получим
b
n
ρ(x)f (x)dx =
k=1
a
где Ck =
Ak f (xk ) + C0 [f (m−1) (b) − f (m−1) (a)] + . . .
. . . + Cs−1 [f
1
b−a
(m+s−2)
b
(b) − f
(m+s−2)
(6)
(a)] + Rs [f ],
t
Lk (t)dt;
Lk+1 (t) = [Lk − Ck ]dx;
a
L0 (t) = K(t);
a
b
f (m+s) (t)Ls (t)dt.
Rs [f ] =
a
Исходная квадратурная формула была точна для полиномов степени
m − 1. Если к
Ak f (xk ) прибавить одно слагаемое C0 [f (m−1) (b) −
f (m−1) (a)], то получится точность квадратурной суммы, равная m, и т.д.
Добавление очередного слагаемого увеличивает точность квадратурной
суммы на единицу. Формулы (6) позволяют последовательно находить
Ck и Lk (t).
§ 14 Квадратурные формулы Эйлера
Построение квадратурной формулы Эйлера тесно связано с выделение
главной части остатка в интерполяционных квадратурных формулах.
Квадратурные формулы вида (6) § 13:
b
n
ρ(x)f (x)dx =
a
s
Ck−1 [f (m+k−2) (b) − f (m+k−2) (a)]
Ak f (xk ) +
k=1
k=1
58.
58называются формулами Эйлера.
Рассмотрим частный случай - квадратурную формулу Эйлера-Маклорена.
В основе этой формулы лежит формула трапеций
b
f (x)dx =
b−a
[f (a) + f (b)] + R[f ].
2
a
Алгебраическая степень точности равна единице: m − 1 = 1, так что
m = 2.
Если из R[f ] выделить последовательно 2ν раз главную часть остатка,
то получим квадратурную формулу Эйлера-Маклорена вида:
b
ν−1
f (t)dt =
a
b−a
(b − a)2k (2k−1)
[f (a) + f (b)] −
[f
(b) −
2
(2k)!
k=1
−f (2k−1) (a)] + R2ν [f ],
Где
(b − a)2ν b (2ν)
b−t
f Y2ν ( b−a
)dt.
(2ν)! a
- числа Бернулли с четными индексами, вычисляемые по
R2ν [f ] =
Здесь B2k
формуле:
B2k
(−1)k−1 (2k)!
1
1
1
=
(1
+
+
+
+ . . .) ≈ 2(−1)k−1 (2k)!(2π)2k
2k−1
2k
2k
2k
2k
2
π
2
3
4
Y2ν (t) - некоторые полиномы, простымсоотношением связанные с полиномом
Бернулли.
Большая формула Эйлера-Маклорена получается, если [a, b] разбить
на частичные промежутки и к вычислению интегралов применить формулу
Эйлера-Маклорена
b
ν−1
f (x)dx = Tn −
a
k=1
h2k
B2k [f (2k−1) (b) − −f (2k−1) (a)] + R2ν [f ] =
(2k)!
h2
h4
= Tn (x) − [f (b) − f (a)] +
[f (b) − f (a)]−
12
720
h6
[f (5) (b) − f (5) (x)] + . . . + R2ν [f ],
−
30240
где Tn (x) = h [ 12 f (a) + f (a + h) + f (a + 2h) + . . . + 21 f (b)].
Формула Эйлера-Маклорена - частный случай квадратурной формулы
типа Эйлера, построенной на базе формулы трапеций. Очевидно, подобног
рода формулы можно строить, взыыв в качестве базовой любую квадратурную
формулу. В формулу Эйлера-Маклорена входят производные от подинтегральной
функции на концах отрезка интегрирования, что не всегда просто и даже
не всегда возможно вычислить. Часто требуемые производные заменяют
значениями функции, вычисленными в точках a + kh k = 0, 1, . . . , n.
Так, для вычисления f (a) интерополируем f (x) по значениям функции в
59.
59точках a, a+h, a+2h, . . ., используя формулу Ньютона для интерополирования
в начале таблицы
f (x) ≈ f (a + th)
f0 +
t
t(t − 1) 2
∆f0 +
∆ f0 + . . . .
1!
2!
Вычисляем производные от f (a + th) и пологая x = a (t = 0), получим
hf (a) ∆f0 − 21 ∆2 f0 + 1, 3∆3 f0 − 14 ∆4 f0 + 15 ∆5 f0 − . . . ,
11 4
h2 f (a) ∆2 f0 − ∆3 f0 + 12
∆ f0 − 56 ∆5 f0 + . . . ,
7
3
h3 f (a) ∆3 f0 − 2 ∆4 f0 + 4 ∆5 f0 − . . . ,
h4 f (4) (a) ∆4 f0 − 2∆5 f0 + . . . ,
h5 f (5) (a) ∆5 f0 − . . . .
Аналогично, применяя интерополирование по Ньютону в конце таблицы
b = a + nh, a + (n − 1)h, . . . , a, имеем
f (x) = f (b + th)
fn +
t
t(t − 1) 2
∆fn−1 +
∆ fn−2 + . . . .
1!
2!
Отсюда при x = b, t = 0 имеем
hf (b) ∆fn−1 + 12 ∆2 fn−2 + 13 ∆3 fn−3 + 14 ∆4 fn−4 + 15 ∆5 fn−5 + . . . ,
h2 f (b) ∆2 fn−2 + ∆3 fn−3 + 11
∆4 fn−4 + 56 ∆5 fn−5 + . . . ,
12
h3 f (b) ∆3 fn−3 + 32 ∆4 fn−4 + 74 ∆5 fn−5 + . . . ,
h4 f (4) (b) ∆4 fn−4 + 2∆5 fn−5 + . . . ,
h5 f (5) (b) ∆5 fn−5 + . . . .
Отбросив остаточные члены в написанных выражениях для производных
и подставив их в формулу Эйлера-Маклорена, получим после простых
преобразований формулу Грегори.
a+nh
f (x)dx ≈ Tn −
a
h
12
(∆fn−1 − ∆f0 ) −
− 19h
(∆3 fn−3 − ∆3 f0 ) −
720
3h
160
h
24
(∆2 fn−2 + ∆2 f0 )−
(∆4 fn−4 + ∆4 f0 ) −
863h
60480
(∆5 fn−5 − ∆5 f0 ),
Tn (x) = h2 [f (a) + 2f (a + h) + 2f (a + 2h) + . . . + f (b)].
§ 15 Приближенное вычисление кратных интегралов
Рассмотрим различные подходы к построению кубатурных формул вида
n
I=
···
G
ci f (pi ) + R[f ].
f (x1 , . . . , xs )dx1 . . . dxs =
i=1
Совокупность точек p1 , . . . , pN ∈ G называется сеткой узлов кубатурной
формулы; R[f ] - остаточный член.
Будем рассматривать только интегралы от ограниченной функции по
конечным областям. Рассмотрим некоторые способы вычисления интегралов.
Метод повторного применения квадратурных формул. Этот
прием основан на факте, что вычисление кратных интегралов может
60.
60быть осуществлено путем повторного вычисления однократных интегралов.
Рассмотрим для простоты вычисление двойного интеграла s = 2 : I =
f (x, y)dxdy. Пусть G - прямоугольник a x b, c y d. Имеем
G
b
I=
d
dx
a
b
d
f (x, y)dy =
F (x)dx, где F (x) =
c
f (x, y)dy. Для вычисления
a
c
b
F (x)dx применим, например, формулу Симпсона
a
I=
b−a
a+b
[F (a) + 4F (
) + F (b)] + R1 [F (x)],
6
2
где
R1 [F (x)] = −
d
(b − a)5
=− 5
2 × 90
(b − a) (
F 4)(ξ) =
25 × 90
∂ 4 f (ξ, y)
(b − a)5 (d − c) ∂ 4 f (ξ, η)
dy
=
−
,
∂x4
25 × 90
∂x4
c
a < ξ < b, c < η < d
Каждый из интегралов F (a), F (a+b/2), F (b) вычислим также по формуле
Симпсона
d
F (x) =
f (x, y)dy =
d−c
c+d
[f (x, c) + 4f (x,
) + f (x, d)] + Ry [f (x, y)],
6
2
c
d
1
Ry [f (x, y)] =
4!
(y − c)(y −
c+d 2
) (y − d)f (4) (x, η)dy, c < η < d
2
c
Учитывая это, получим
I=
(b−a)(d−c)
36
{[f (a, b) + 4f (a, c+d
) + f (a, d)]
2
+4[f ( a+b
, c) + 4f ( a+b
, c+d
) + f ( a+b
, d)]+
2
2
2
2
+[f (b, c) + 4f (b, c+d
) + f (b, d)]} + R[f ] =
2
=
(b−a)(d−c)
36
(1)
{f (a, c) + f (a, d) + f (b, c) + f (b, d)+
+4[f (a, c+d
) + f (b, c+d
) + f ( a+b
, d) + f ( a+b
, d) + f ( a+b
, c)]+
2
2
2
2
2
+16[f ( a+b
, c+d
)]} + R[f ],
2
2
5
(d−c)
R[f ] = − (b−a)
25 ×90
∂ 4 f (ξ,y)
∂x4
+
(b−a)
6×4!
d
(y − c)(y−
c
(2)
)2 (y − d)[f (4) (a, η) + 4f (4) ( a+b
, η) + f (4) (b, η)] dy
− c+d
2
2
Полученная квадратурная формула (1) содержит f (x, y) в 9 точках.
Из вида остаточного члена (2) следует, что формула точна, если f (x, y)
61.
61- полином степени
3. так же можно получить и другие кубатурные
d
формулы, если для вычисления
F (x)dx и F (x) =
другие квадратурные формулы. Например, если
b
n
F (x)dx =
Ai F (xi ) + R0 [F ],
a
i=1
d
m
F (xi ) =
f (x, y)dy применять
c
f (xi , y)dy =
Bj f (xi , yj ) + R1 [f (xi , yj )],
j=1
c
то получим кубатурную формулу вида
b
d
I=
n
m
f (x, y)dxdy =
a
cij f (xi , yj ) + R[f (x, y)],
i=1 j=1
c
где
n
cij = Ai Bj ;
R[f (x, y)] =
Ai R1 [f (xi , y)] + R0 [F ] =
i=1
d
n
= R1 [
Ai f (xi , y)] + R0 [
i=1
f (x, y)dy].
c
Если область G определена неравенствами a
x
b; ϕ(x)
y
ψ(x), то то построение кубатурных формул можно осуществить аналогично
ψ(x)
b
I=
dx
a
ψ(x)
b
f (x, y)dy =
F (x)dx, F (x) =
a
ϕ(x)
f (x, y)dy.
ϕ(x)
Пусть
ψ(xi )
F (xi ) =
m
f (xi , y)dy =
j=1
ϕ(xi )
I=
n
Ai F (xi ) + R0 =
i=1
(i)
n
m
i=1 j=1
d
R[f ] = R0 [ f (x, y)dy] +
c
n
(i)
Bj f (xi , yj ) + Ri [f (xi , y)],
(i)
(i)
cij f (xi , yj ) + R[f ], cij = Ai Bj ,
Ai Ri [f (xi , y)]
i=1
Если обозначить область G болееобщей структуры, ее можно разбить на
подобласти указанного вида и к каждой из них применить ту или иную
кубатурную формулу.
Метод замены подинтегральной функции интерполяционным
многочленом. Для простоты рассуждения здесь тоже рассмотрим
62.
62вычисление двойного интеграла I =
f (x, y)dxdy. Интерполяционный
G
полином для f (x, y) запишем, например, в виде
N
L(x, y) =
f (xi , yi )Li (x, y), Li (x, y) =
i=1
b d
Тогда I =
f (x, y)dxdy
L(x, y)dxdy =
Ci f (xi , yi ),
i=1
a c
G
N
1, i = j ;
0, i = j .
Ci =
Li (x, y)dxdy.
G
Если область G простая, то Ci вычисляютсчя просто. Так если G прямоугольник и сетка узлов образована пересечением прямых xi = a +
ih, yj = c+jl, h = (b−a)/n, l = (d−c)/2, (i = 0, 1, . . . , n j = 0, 1, . . . , m),
то можно применить интерполяционную формулу Лагранжа
n
m
f (x, y) =
f (xi , yj )
i=0 j=0
ωn (x)ωm (y)
+ R[x, y],
(x − xi )(y − yj )ωn (xi )ωm (yj )
где ωn (x) = (x − x0 )(x − x1 ) . . . (x − xn ), ωm (y) = (y − y0 )(y − y1 ) . . . (y −
yn ), R[x, y] - остаточный член интерполирования f (x, y) по Лагранжу.
Интегрируя эту формулу, получим
b
d
n
m
f (x, y)dxdy =
a
b
Cij =
a
Cij f (xi , yj ) + R[f ],
i=0 j=0
c
ωn (x)
dx
(x − xi )ωn (xi )
d
c
ωm (y)
dy, R[f ] =
c(y − yj )ωm (yj )
b
d
R(x, y)dxdy.
a
c
При вычислении интегралов большой кратности важна задача построения
квадратурных фопмул высокой точности,позволяющих при малом числе
узлов достичь требумой точности. Для достижения этой цели надо использовать
все возможности, какими владеет вычислитель, как-то: выбор системы
координат, выбор квадратурных формул, которые будут применяться
к простым интегралам, свойства области интегрирования (если она не
прямоугольник). Приведем некоторые частные вопросы такого рода.
а) Пусть рассмотривается интеграл в полярной системе координат
I=
F (r, ϕ) r drdϕ
(3)
G
и пусть область интегрирования определяется неравенствами
α ϕ β, 0 r R = R(ϕ). Введем вспомогательную переменную ρ,
положив r = ρR, 0 ρ 1. Тогда интеграл запишется
β
1
F (ρR, ϕ)ρdρR2 dϕ
I=
α
0
(4)
63.
63Отсюда для вычисления двойного интеграла в полярных координатах
при помощи приведения его к интегрированию по координатам r и ϕ
существенный интерес представляет рассмотрение интеграла
1
f (x)x dx
(5)
0
Если хотим построить квадратурную формулу наивысшей степени
точности, то должны узлы взять в корнях многочлена, ортогонального
на [0, 1] с весом ρ(x) = x по всем многочленам степени n−1. Коэффициенты
будут вычисляться по общему правилу.
Для вычисления xk и Ak воспользуемся результатами полученными
для функции ρ(x) = (1 − z)α (1 + z)β . С этой целью в (5) сделаем замену
x = (1 − z)/2, −1 z 1:
1
1
1
f (x)x dx =
4
F (z)(1 − z)dz, F (z) = f ((1 − z)/2).
0
−1
Задача сведется к определению корней многочлена, ортогонального
на [−1, 1] по весу (1 − z) ко всякому многочлену степени n − 1. Этот
многочлен с точностью до множителя совпадает с полиномом Якоби
(0,1)
Pn (z), так что узлы формулы
1
n
Ak f (xk )
f (x)x dx ≈
k=1
0
(0,1)
должны быть связаны с корнями zk многочлена Pn
xk = (1 − zk )/2,
(z) соотношением
k = 1, . . . , n
Для коэффициентов Ak справедливо соотношение
Ak =
1
(1 −
(0,1)
zk2 )[Pn
(zk )]2
б) При вычислении тройного интеграла в сферических координатах
f (ρ, θ, ϕ)r2 drdθdϕ
I=
(V )
путем приведения его к интегрированию по координатам r, θ, ϕ во многих
случаях при интегрировании по радиусу r важную роль играют интегралы
1
x2 f (x) dx
(6)
0
Аналогично как и в случае интеграла (5), здесь можно установить,
что в формуле наивысшей алгебраической точности с весом ρ(x) = x2
64.
64следует в качестве xk брать xk = (1 − zk )/2, где zk - нули полинома
(2,0)
Якоби Pn (x); коэффициенты
Ak =
1
(2,0)
(1 − zk2 )[Pn
(zk )]2
в) Рассмотрим двойной интеграл в декартовых координатах
f (x, y)dxdy
(7)
G
где f (x, y) - непрерывная и достаточно гладкая вобласти G.
При некоторых предположениях об области G интеграл (7) можно
привести к повторному интегралу
y2 (x)
b
I=
F (x)dx,
F (x) =
a
f (x, y)dy,
y1 (x)
где y1 (x), y2 (x),a и b известны. Считаем, что интеграл F (x) можно вычислить
при всех нужных на значениях x.
b
Займемся вычислением интеграла I =
F (x)dx.
a
Функция F (x) зависит как от интегрируемой функции f (x, y), так и
от области G. при выборе квадратурной формулы наивысшей алгебраической
формулы надо учитывать зависимость F (x) от области. Здесь квадратурные
формулы Гаусса, расчитанные на постоянный вес, не всегда дадут наилучший
результат. Естественным весом для интеграла I будут ρ(x) = y2 (x) −
y1 (x), так как площадь полоски, взятой около прямой, параллельной оси
y и проходящей через точку x ∈ [a, b], будет существенно зависеть от
величины разности (y2 (x) − y1 (x)), а следовательно, чем больше y2 −
y1 , тем больше влияние на величину двойного интеграла будет иметь
рассатриваемая полоска. Имеем
b
I=
b
F (x)dx =
a
a
F (x)
ρ(x)
dx ≈
y2 (x) − y1 (x)
n
Ak Φk ;
k=1
(xk )
где Φk = y2 (xFk )−y
; xk - нули полинома, ортогонального с весом ρ(x) =
1 (xk )
y2 (x)−y1 (x) на промежутке [a, b], к полиномам степень которых не первосходит
n − 1.
Неудобство выведенной формулы - ее зависимость от формы области.
Иногда этого неудобства можно избежать. Так, если [a, b] - конечный
промежутоки можно выбрать показатель α, β так, чтобы отношение q(x) =
y2 (x)−y1 (x)
было ограничено снизу и сверху
(x−a)α (x−b)β
0<m
q(x)
M <∞
то можно представить
ρ(x) = ρ1 (x)q(x), ρ(x) = (x − a)α (x − b)β
65.
65и ρ(x) взять за вес, так что
n
F (x)dx =
ρ1 (x)[q(x)F (x)]dx =
ρ(x)Φ(x)dx =
Ak Φ(xk ),
k=1
где Φ(x) = (x − a)−α (x − b)−β F (x)
Примеры. 1. Пусть область интегрирования имеет форму рис.4 ,
причем контур области в точке А имеет соприкосновение 1-го порядка
(т.е. если принять y за независимую переменную, то уравнение контура
вблизи x = a может быть записано в виде x = a + c2 (y − y0 )2 + c3 (y −
y0 )3 + . . ., где c2 = 0. Тогда за вес можно взять (x − a)1/2 ,
b
I=
√
√
x − a ψ(x)dx, ψ(x) = F (x)/ x − a.
a
Рис.4
2. Пусть область интегрирования задана в форме рис.5
Рис.5
66.
66причем контур с прямыми x = a, x = b имеет соприкосновение
первого порядка. За весовую функцию надо взять
ρ(x) =
(x − a)(b − x),
тогда
b
I=
b
(x − a)(b − x)
F (x)dx =
a
a
F (x)
(x − a)(b − x)
dx.
§ 16 Метод Монте-Карло для вычисления интегралов
большой кратности
При построении квадратурных формул мы наряду с формулой получали
оценку ее погрешности на некотором классе функций. Так, в формуле
трапеций была получена оценка constA2 N −2 на классе функций со второй
производной, ограниченной константой A2 ; N - число узлов интегрирования.
Эта оценка является гарантированной на всем классе функций, т.е. она
гарантирует, что погрешность приближенного вычисления интеграла не
превосходит определенной величины, если подинтегральная функция принадлежит
рассматриваемому классу. При таком подходе мы ориентируемся на величину
погрешности, которую дает "наихудшая"функция из рассматриваемого
класса, так что для конкретного интеграла эта оценка может быть слишком
завышенной. Для ряда классов функций, как, например, для класса ∗)
Cr (A1 , . . . , As ),эта оценка настолько плоха, что не дает никакой надежды
на получение приближенного вычисления интеграла с требуемой точностью.
Так, если f ∈ C1 (A, . . . , A) r = 1, Ak = A , то для того, чтобы
гарантировать погрешность меньшую, чем 0.01 , надо взять число узлов,
удовлетворяющее неравенству N −s 0.01, т.е. N 100s . Уже при s = 6
такое требование на число узлов является практически невыполнимым:
нет методов вычисления интеграла с гарантированной оценкой погрешности
меньшей, чем 0.01. Как выйти из этого затруднения ? Надо отказаться
от получения строгой гарантированной оценкипогрешности, а получить
погрешность лишь с определенной степенью достоверности. Одним из
методов, в котором погрешность оценивается с некоторой достоверностью,
является метод Монте-Карло. Опишем его.
Пусть требуется вычислить приближенное значение интеграла
I[f ] =
f (p)dp,
G
в качестве p1 , . . . , pN берем случайные независимые точки из области
G, одинаково распределенные в G с плотностью распределения ρ(p) :
f (p )
ρ(p)dp = 1. Пусть sj [f ] = ρ(pjj ) , j = 1, . . . , N - случайные независимые
G
величины, одинаково распределенные в G:
M.0. sj [f ] =
ρ(p)
G
f (p)
dp ≡ I[f ]
ρ(p)
67.
67D(sj [f ]) = M.0.s2j [f ] − (M.0.s[f ])2 =
=
G
(p) 2
ρ(p)[ fρ(p)
] dp −
Положим
G
(p)
ρ(p)[ fρ(p)
]dp = I[f 2 ] − (I[f ])2 ≡ D[f ].
N
1
sN [f ] =
N
j = 1sj [f ],
Тогда
1
M.0.sN [f ] =
N
N
j = 1M.0.sj [f ] = I[f ],
N
1
1
j
=
1D[s
(f
)]
=
D[f ].
j
N2
N
Рассмотрим случайную величину
D[sN (f )] =
sN [f ] − I[f ]
D[f ]/N
.
В силу центральной предельной теоремы эта случайная величина
распределена ассимптотически нормально с функцией распределения
∞
1
φ(y) = √
2 π
exp (
−t2
)dt.
2
y
Вероятность, что случайные с такой функцией распределения не превосходит
по модулю числа y > 0, ассимптотически равна
1
ρ0 (y) = 1 − √
π
∞
exp (
−t2
)dt.
2
y
Таким образом, при N больших с вероятностью, близкой к ρ0 , выполняется
неравенство
|sN [f ] − I[f ]| y D[f ]/N
(∗ )
Так при y = 3 и y = 5, получаем, что неравенства
|sN − I|
3
D[f ]/N ,
|sN − I|
5
D[f ]/N
выполняется соответственно с вероятностью 0.997 и 0.99999.
————————
∗)
через Cr (A1 , . . . , As ) обозначен класс функций, имеющих по xk непрерывные
производные до rk − 1 порядка, и производная порядка rk ограничена по
модулю числом Ak (k = 1, 2, . . . , s).
В правой части (*) стоит неизвестная величина D[f ] = I[f 2 ] − (I[f ])2 ,
которую можно оценить, имея информацию о вычисленных значениях
f [pj ]:
1
D[f ] ≈ DN [f ] =
[sj (f ) − sN (f )]2 .
N −1
Опишем одну из схем метода Монте-Карло.
68.
68Пусть 1−ν - уровень надежности, с которой следует получить приближенное
значение интеграла, ε - заданная точность.
Алгоритм вычисления сводится к следующим этапам.
1. Определим y из равенства
1
ν=
2π
∞
exp (
−t2
)dt.
2
y
2. Последовательно вычисляем случайные точки Pn n = 1, . . . и величины
t1 (f ) = s1 (f ) = f [p1 ],
d1 (f ) = D1 (f ) = 0,
tn (f ) = tn−1 (f ) + f (Pn ),
dn (f ) = dn−1 (f ) +
n
n−1
Dn (f ) = dn (f )/n − 1,
sn (f ) = tn (f )/n,
[f (Pn ) − sn (f )]2 ,
λn [f ] = y
Dn (f )/n.
Если λn < ε, то вычисление прекращают и полагают sn (f ) ≈ I[f ],
при этом считают, что с вероятностью 1 − ν выполняется
|sN [f ] − I[f ]| < ε.
Метод Монте-Карло относится к недетерминированным методам. Рассмотрим
отрицательные и положительные характеристики этого метода. Отрицательные
факторы:
1. Необходимо иметь в распоряжении последовательность независимых
точек pi с заданым законом распределения. Обычно для этой цели используют
датчики случайных (псевдослучайных) чисел с равномерным законом
распределения на [0,1]. При помощи преобразований получают случайные
числа с заданным законом распределения.
2. Малость погрешности метода обеспечивается с некоторой вероятностью.
Положительные факторы:
1) порядок оценки погрешности не зависит от размерности вычисляемого
интеграла;
2) метод не требует гладкости подинтегральной функции, применим
к разрывным функциям.
§ 17 Некоторые подходы к решению многомерных
задач
Трудоемкость решения задачи резко возрастет с ростом размерности
задачи. Это является причиной отсутсвия стандартных методов решения
широких классов многомерных задач со столь же высокой точностью,
как и в одномерном случае. Но многомерные задачи и не требуют высокой
точности в решении , так как многомерные матеметические задачи возникают
обычно из описания сложных процессов и , как правило, эти описания
являются сами довольно грубыми.
69.
69Но не следует думать, что решение многомерных задач - безнадежное
дело. Решение ряда многомерных задач сводится к решению следующих
трех типов задач.
Пусть в некоторой области s мерного пространства G заданы точки
p1 , . . . , pn и значение функции f в этих точках. Требуется: а) получить
приближение к значению функции f в точке p ; б) получить приближение
к значению некоторой производной от функции f в точке p ; в) вычислить
интеграл I(f ) = f (p)ρ(p)dp. Здесь ρ(p) - весовая функция.
G
Простейшими способами решения этих задач являются: 1) способ
неопределенных коэффициентов; 2) метод наименьших квадратов; 3) метод
регуляризации.
Пусть из каких-то соображений известно, что функция f (p) хорошо
приближается линейными комбинациями
N
Bi ωi (p).
(1)
i=1
В методе неопределенных коэффициентов неизвестные коэффициенты
Bi находятся из системы
N
Bi ωi (pq ) = f (pq ), q = 1, . . . , N.
(2)
i=1
Если определитель системы (2) отличен от нуля, то матрица системы (2)
имеет обратную матрицу (обозначим ее через A).
Тогда
N
Bi =
aiq f (pq ),
(3)
q=1
так что
N
f (p)
g(p) ≡
zq (p)f (pq ),
q=1
где
N
zq (p) =
aiq ωi (p).
q=1
Получив f (p) в форме (3), можно решить любую из трех типов многомерных
задач f (p∗ ) ≈ g(p∗ ); Df (p∗ ) ≈ Dg(p∗ ), где D - некоторый оператор
дифференцирования; I(f ) ≈ I(g) =
N
q=1
cq f (pq ), cq = I(zq ).
В методе наименьших квадратов определение коэффициентов Bi для
g(p) =
n
n
Bi ωi (p), n
N находится из решения переопределенной системы
i=1
Bi ωi (pq ) = f (pq ), q = 1, 2, . . . , N с матрицей размеров N × n (N
i=1
или (что то же ) из условия min φ(g),
B1 ,...,Bn
где
N
φ(g) =
n
Bi ωj (pk )]2 ρ(pk ); ρ(pk ) - весовая функция.
[f (pk ) −
k=1
j=1
n)
70.
70В основе метода лежат следующие соображения: малость величины
φ(g) обеспечивает близость g к f (p) в точках pk ; при n
N функция
g(p) содержит относительно мало параметров и потому у нее меньше
возможностей отличатся от f (p) вне узлов по сравнению со случаем n =
N.
В методе регуляризации приближение отыскивается в виде g(p) =
N
Bi ωi (p). Коэффициенты Bi выбираются из условия минимума выражения
i=1
φ(λ, g) = φ(g) + λψ(g),
λ>0
Функционал ψ(g) подбирается из следующего условия: если значение
этого функционала невелико, то функция g обладает определенной гладкостью.
Например, в качестве ψ(g) берут приближение к интегралу |grad g(p)|2 dp
G
λ
Пусть минимум φ(λ, g) достигается при некоторых B1λ , . . . , BN
N
g
(λ)
Biλ ωi (p).
(p) =
i=1
Рассмотрим крайние случаи λ = 0 и λ очень большое. Имеем
N
N
ψ(0, g) =
Bi ωi (pq ) − f (pq )]2 .
pq [
q=1
Если det |ωi (pq ) = 0, то система
(4)
i=1
N
Bi ωi (pq ) = f (pq ), q = 1, . . . , N имеет
i=1
решение и на ее решении правая часть (4) обращается в нуль. В то же
время всегда φ(λ, g) 0, так что нижняя грань достигается на упомянутом
решении. Тогда g 0 (p) совпадает с интерполяционным полиномом с узлами
интерполяции pi .
При больших λ в функционале φ(λ, g) определяющим является второе
слагаемое, нижняя грань которого достигается на гладкой функции. Поэтому
есть основания ожидать, что при промежуточных λ функция g (λ) (p)
будет гладкой и в то же время не сильно отличающейся от приближаемой
функции в узлах.
Приведенное рассуждение является неопределнным (не указаны ωi (p),
ничего не сказано о распределнии точек p и класса рассматриваемых
функций), но тем не менее такой подход часто приводит к конструированию
нового метода решения задачи, если учесть конкретные физические условия.
Литература
1. Кублановская В.Н. Численные методы алгебры. Учебное пособие.
Изд.ЛКИ,1978.
2. Мысовских И.П. Лекции по методам вычислений. - М.: Физматгиз,
1962.
3. Бахвалов Н.С. Численные методы. - М.: Наука, 1973.

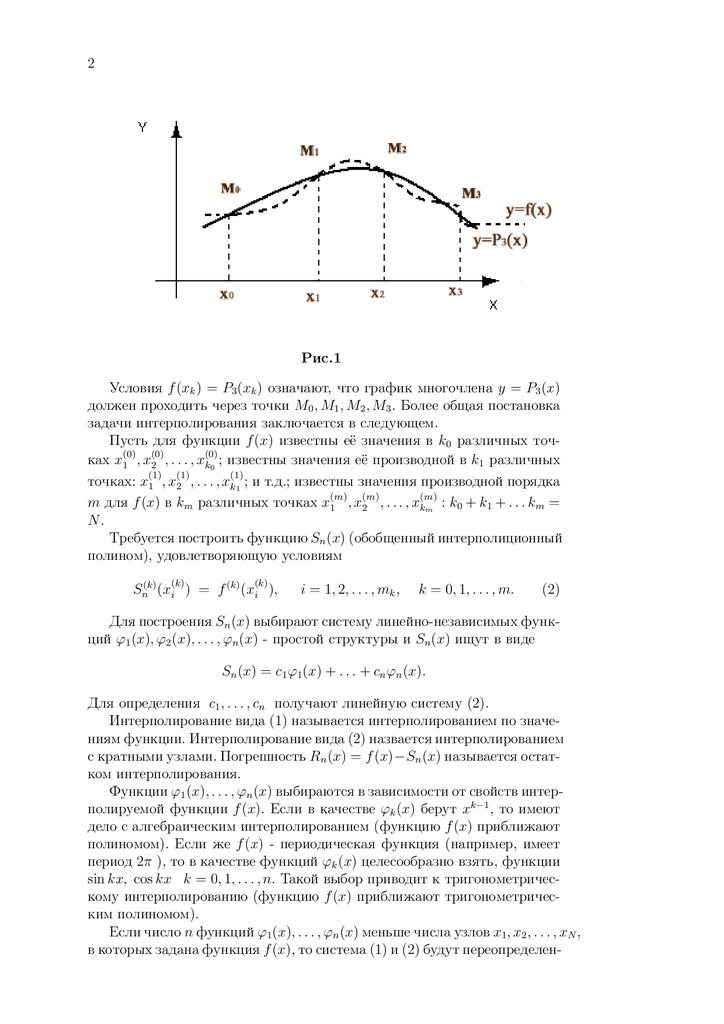




































































 Математика
Математика








