Похожие презентации:
Интерполяция функций
1. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
Лекция №31
2.
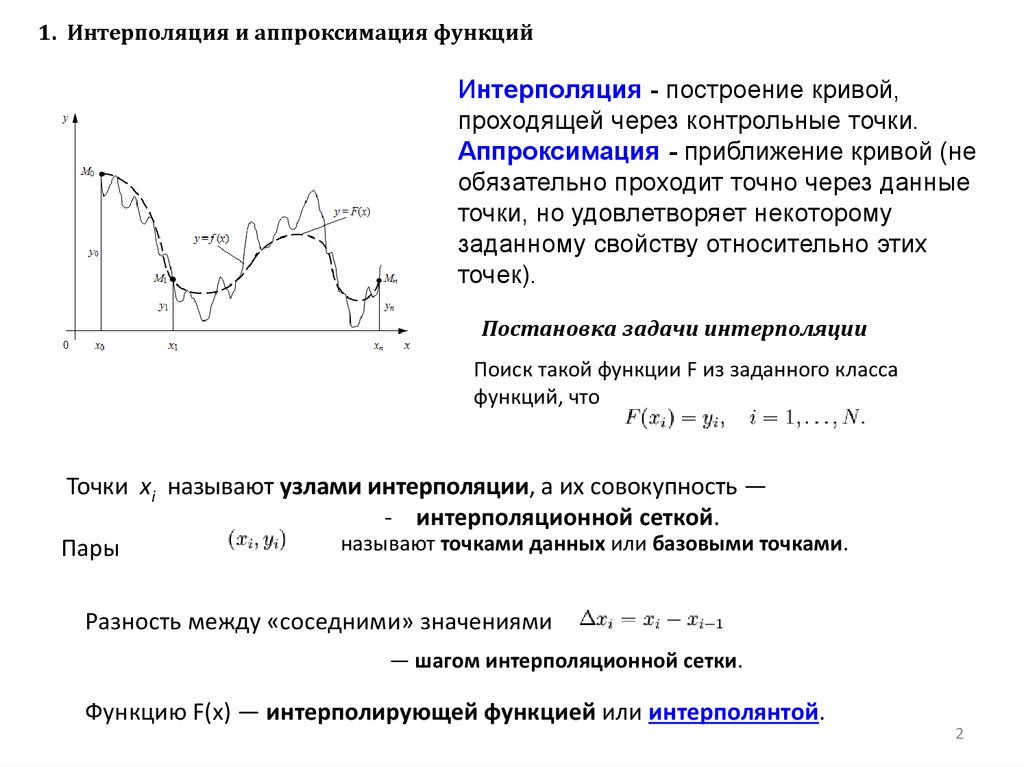
1. Интерполяция и аппроксимация функцийИнтерполяция - построение кривой,
проходящей через контрольные точки.
Аппроксимация - приближение кривой (не
обязательно проходит точно через данные
точки, но удовлетворяет некоторому
заданному свойству относительно этих
точек).
Постановка задачи интерполяции
Поиск такой функции F из заданного класса
функций, что
Точки xi называют узлами интерполяции, а их совокупность —
- интерполяционной сеткой.
называют точками данных или базовыми точками.
Пары
Разность между «соседними» значениями
— шагом интерполяционной сетки.
Функцию F(x) — интерполирующей функцией или интерполянтой.
2
3.
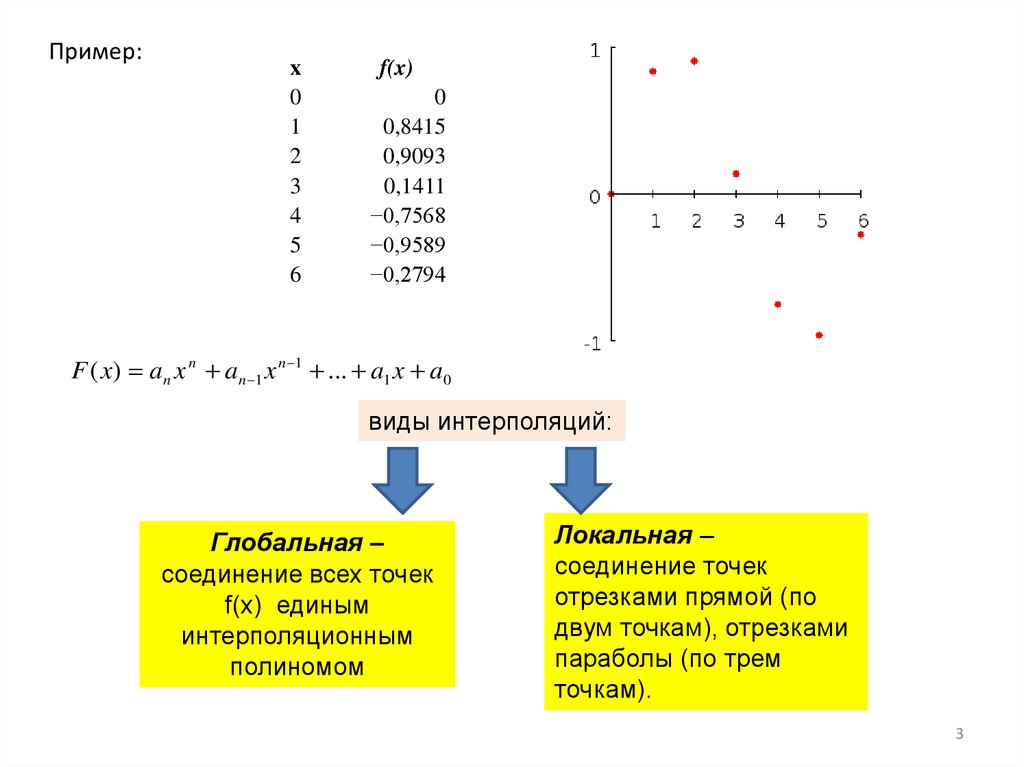
Пример:x
0
1
2
3
4
5
6
f(x)
0
0,8415
0,9093
0,1411
−0,7568
−0,9589
−0,2794
F ( x) a n x n a n 1 x n 1 ... a1 x a 0
виды интерполяций:
Глобальная –
соединение всех точек
f(x) единым
интерполяционным
полиномом
Локальная –
соединение точек
отрезками прямой (по
двум точкам), отрезками
параболы (по трем
точкам).
3
4.
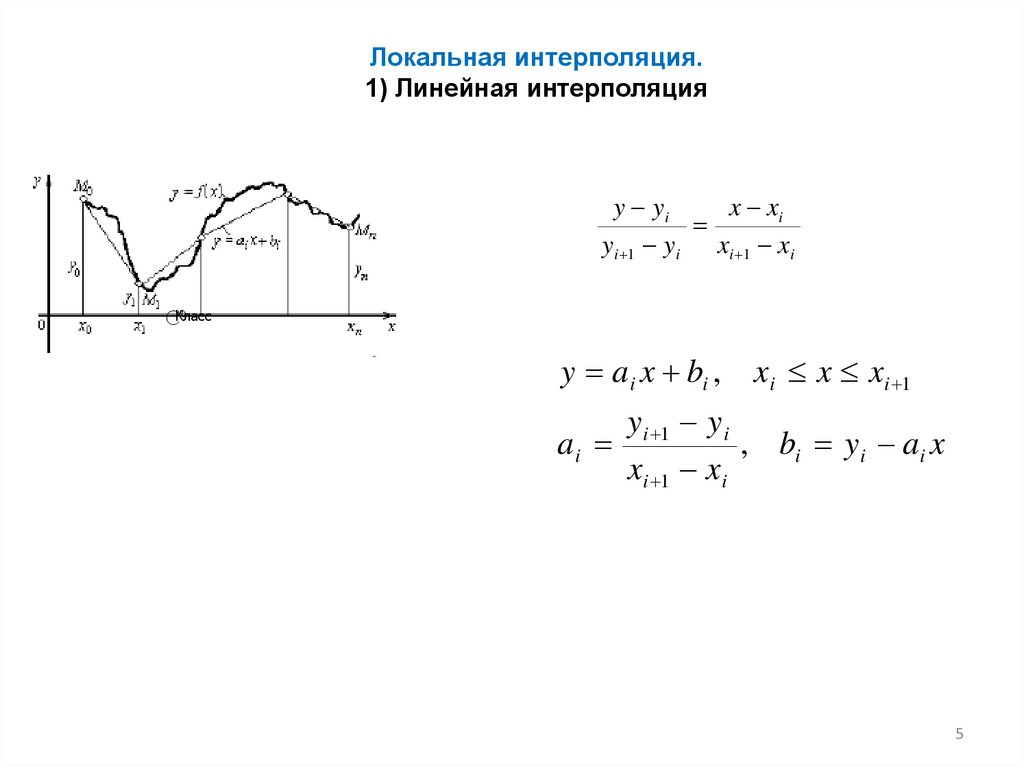
Локальная интерполяция.1) Линейная интерполяция
y yi
x xi
yi 1 yi xi 1 xi
CКласс
0
y ai x bi , xi x xi 1
y i 1 y i
ai
, bi y i ai x
xi 1 xi
5
5.
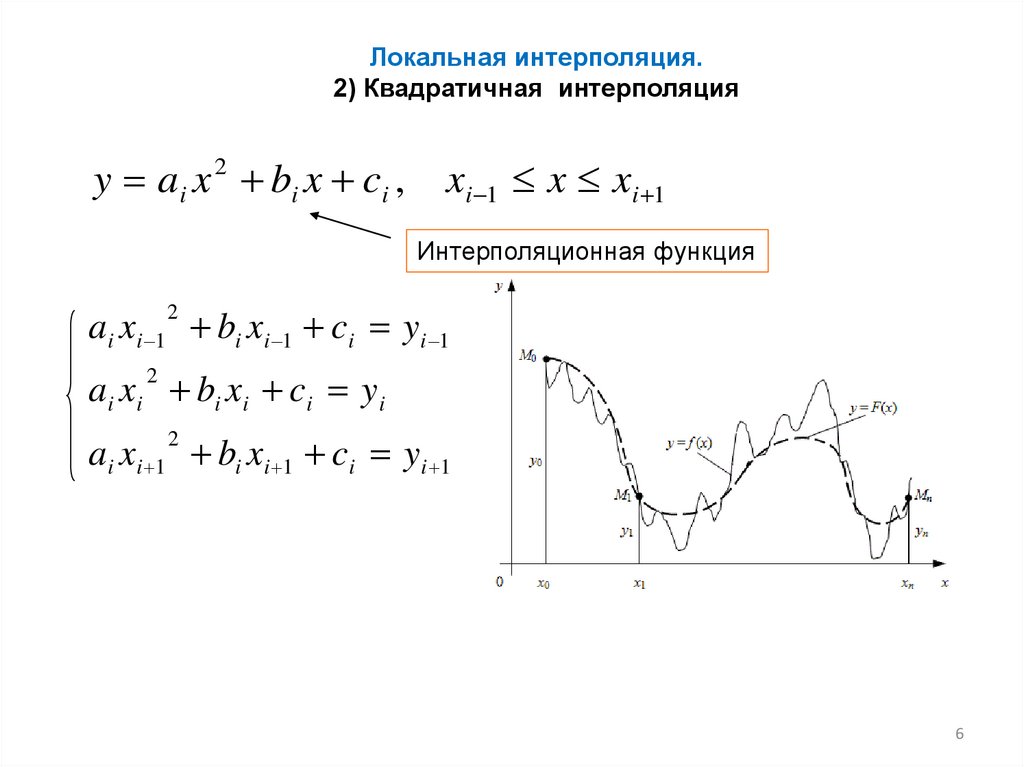
Локальная интерполяция.2) Квадратичная интерполяция
y ai x bi x ci ,
2
xi 1 x xi 1
Интерполяционная функция
ai xi 1 bi xi 1 ci y i 1
2
ai xi bi xi ci y i
2
ai xi 1 bi xi 1 ci y i 1
2
6
6.
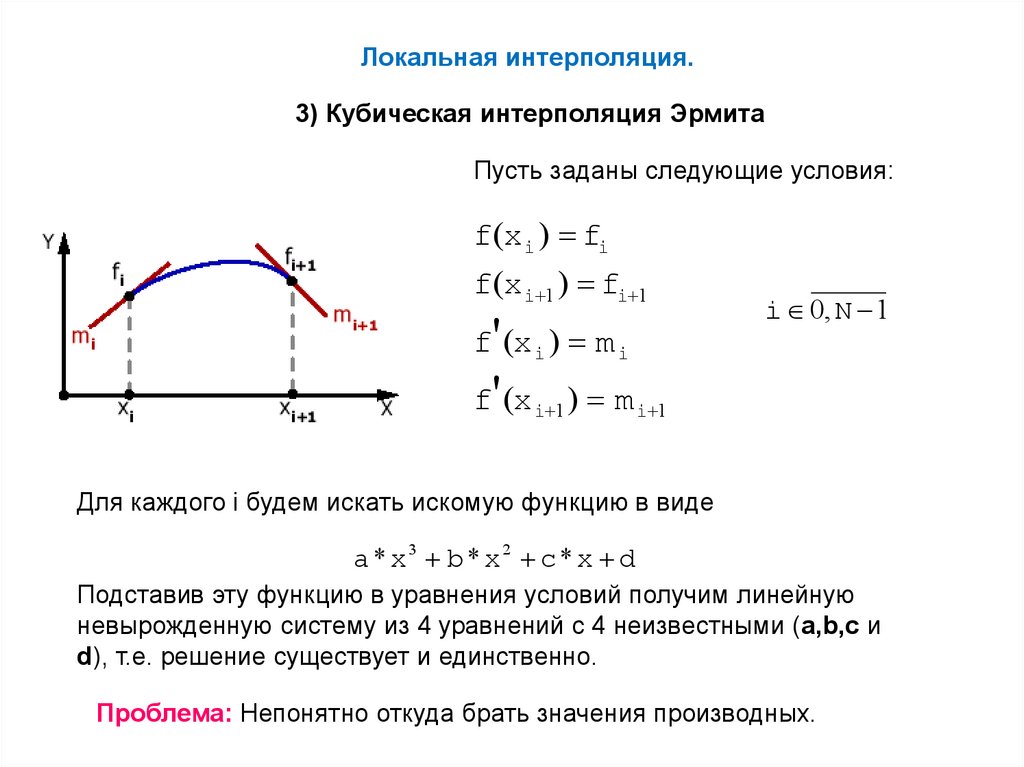
Локальная интерполяция.3) Кубическая интерполяция Эрмита
Пусть заданы следующие условия:
f(xi ) fi
f(xi 1 ) fi 1
f' (xi ) m i
i 0, N 1
f' (xi 1 ) m i 1
Для каждого i будем искать искомую функцию в виде
a * x3 b * x 2 c * x d
Подставив эту функцию в уравнения условий получим линейную
невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и
d), т.е. решение существует и единственно.
Проблема: Непонятно откуда брать значения производных.
7.
СплайныСплайн - кусочный полином степени K с непрерывной производной
степени K-1 в точках соединения сегментов.
Далее нас будут интересовать кубические сплайны.
Понятие сплайна пришло из машиностроения, где сплайном называли
гибкую линейку, закрепив которую в нужных местах, добивались плавной
кривой, которую затем чертили по этой линейке. Форма такой линейки,
если ее рассматривать как функцию y(x), будет удовлетворять
уравнению Эйлера-Бернулли:
M(x)
y' ' (x)
E *I
где M(x) - момент изгиба вдоль рейки, E - модуль Юнга. зависящий от
свойств материала рейки, I - момент инерции, определяемый формой
кривой. Если зафиксировать некоторые точки подпорками, то момент
изгиба на каждом отрезке
[xi , xi 1 ], i 0, N 1
меняется по линейному закону: M(x) = A*x + B , подставляя в исходное
уравнение получаем:
A*x B
y' ' (x)
E *I
дважды интегрируя получаем уравнение кривой на данном отрезке
y(x) a * x3 b * x 2 c * x d
8.
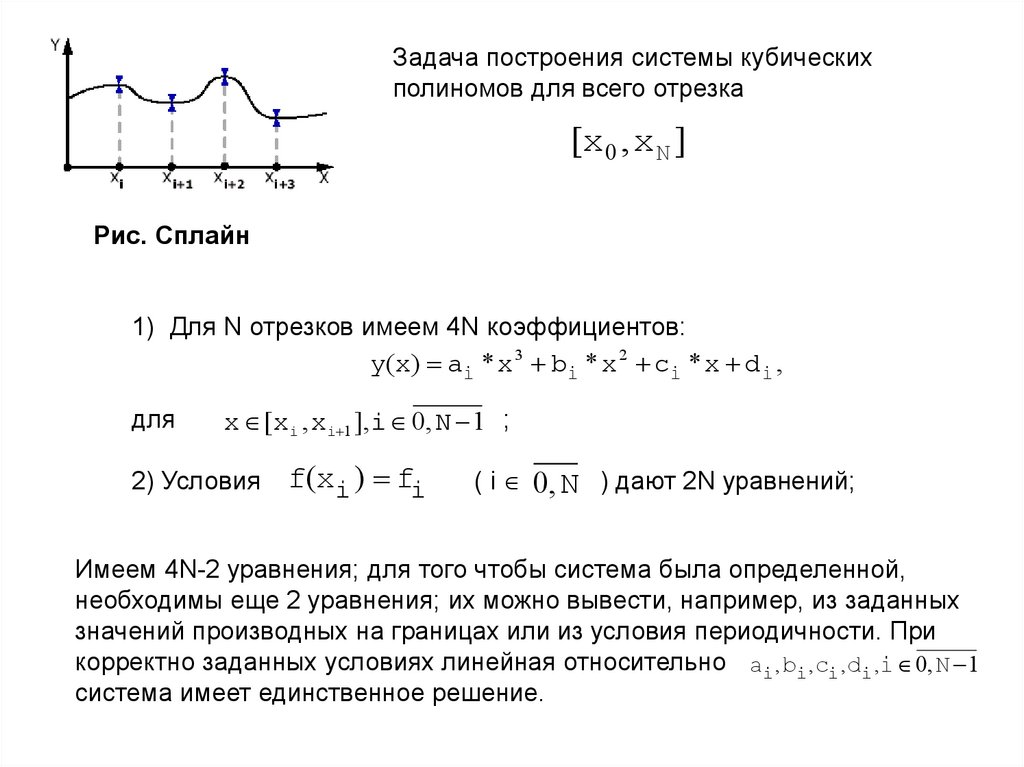
Задача построения системы кубическихполиномов для всего отрезка
[x 0 , x N ]
Рис. Сплайн
1) Для N отрезков имеем 4N коэффициентов:
y(x) ai * x 3 bi * x 2 ci * x di ,
для
x [xi , xi 1 ], i 0, N 1 ;
2) Условия
f(xi ) fi
( i 0, N ) дают 2N уравнений;
Имеем 4N-2 уравнения; для того чтобы система была определенной,
необходимы еще 2 уравнения; их можно вывести, например, из заданных
значений производных на границах или из условия периодичности. При
корректно заданных условиях линейная относительно ai , bi , ci , di , i 0, N 1
система имеет единственное решение.
9.
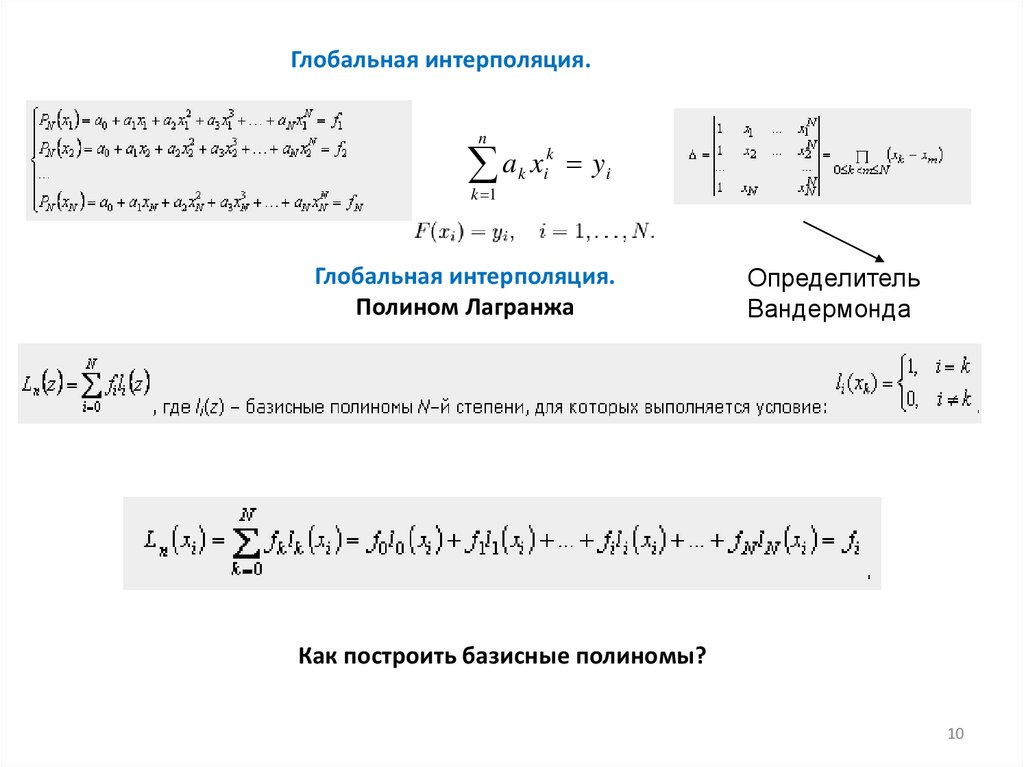
Глобальная интерполяция.n
a x y
k 1
k
k
i
i
Глобальная интерполяция.
Полином Лагранжа
Определитель
Вандермонда
Как построить базисные полиномы?
10
10.
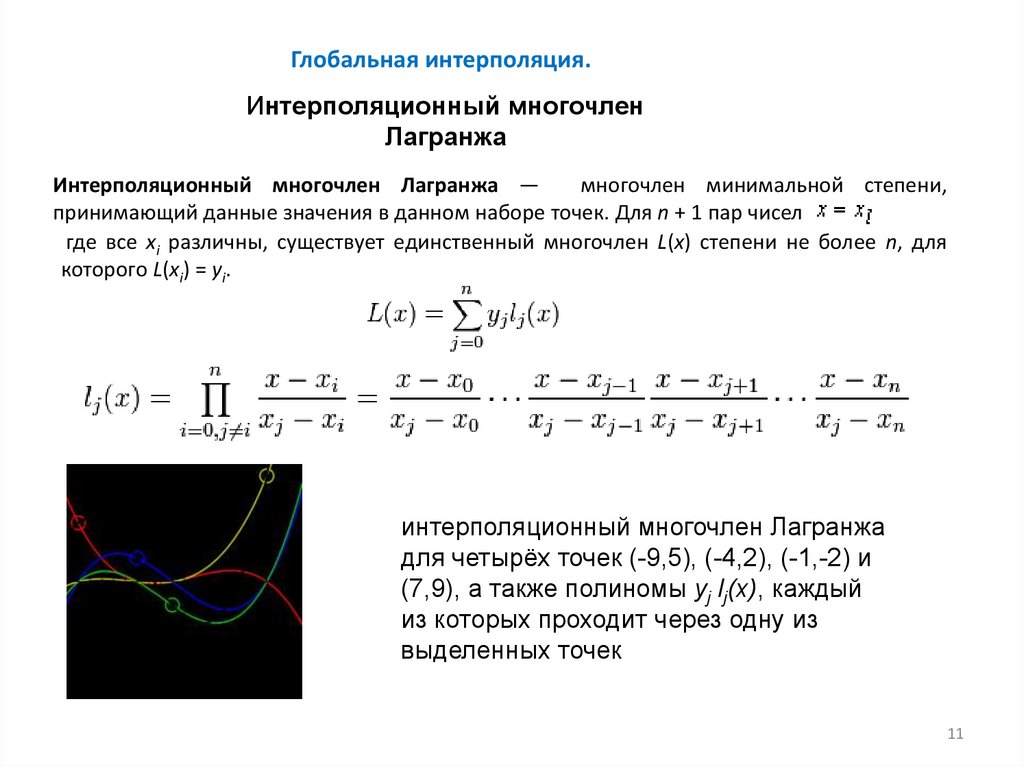
Глобальная интерполяция.Интерполяционный многочлен
Лагранжа
Интерполяционный многочлен Лагранжа —
многочлен минимальной степени,
принимающий данные значения в данном наборе точек. Для n + 1 пар чисел
где все xi различны, существует единственный многочлен L(x) степени не более n, для
которого L(xi) = yi.
интерполяционный многочлен Лагранжа
для четырёх точек (-9,5), (-4,2), (-1,-2) и
(7,9), а также полиномы yj lj(x), каждый
из которых проходит через одну из
выделенных точек
11
11.
Интерполяционный многочлен ЛагранжаN
N
N
i 0
i 0
LN (x) fi LiN (x) fi
(x xj)
j 0 ,j i
N
(xi xk )
k 0 ,k i
N
N
(x)
i
L
(x xj)
j 0 ,j i
N
(xi xk )
N
(x )
i j
L
j
i
δ
k 0 ,k i
Получаем непрерывную функцию, проходящую через все точки.
Минусы:
1)Требует значительного объема вычислений для нахождения значения
функции в произвольной точке.
2)Неопределенное поведение построенной функции между узлами.
Будем рассматривать интерполирующие функции, которые задаются
отдельно на каждом отрезке, что позволяет лучше учитывать локальное
поведение требуемой функции и избежать громоздких вычислений (так как
на каждом из отрезков интерполирующая функция имеет по возможности
простой вид).
12.
Определение: Разделенная разность функции f(x) для x xl иx xk
f ( xl ) f ( xk ) fl f k
[ xl ; xk ].
xl xk
xl xk
Определение: Повторная разность от разделенной разности есть
разделенная разность второго порядка
[ x0 ; x1; x2 ]
[ x0 ; x1 ] [ x1; x2 ] f0 f1 f1 f 2 1
x x x x x x x x x x
1
0
1
2
2
1 0
2
0 1
x0 x2
f0
f1
f2
.
( x0 x1 ) ( x0 x2 ) ( x1 x0 ) ( x1 x2 ) ( x2 x0 ) ( x2 x1 )
Определение: Разделенная разность N-ого порядка
n
fi
.
(
x
x
)
...
(
x
x
)
(
x
x
)
...
(
x
x
)
i 0
i
1
i
i 1
i
i 1
i
n
[ x0 ; x1;...; xn ]
13
13.
ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ НЬЮТОНАшаг таблицы h = хi+1 - xi (i = 0, 1, 2, ..., n) = const
конечные разностями первого порядка:
D yi = yi+1 - yi (i = 0, 1, 2, ...).
D 2yi = D yi + 1 - D yi = (yi+2 - yi+1) - ( yi+1 - yi) = yi+2 - 2yi+1 + yi.
конечные разности второго порядка:
D 2yi = D yi+1 - D yi (i = 0, 1, 2, ...)
D 3yi = D 2yi + 1 - D 2yi = (D yi + 2 - D yi + 1) - (D yi + 1 - D yi)
= ( yi + 3 - 2yi + 2 + yi + 1) - (yi + 2 - 2yi + 1 + yi ) =yi + 3 - 3yi + 2+ 3yi + 1 - yi
таблица конечных разностей
x
y
Dy
D 2y
D 3y
x0
y0
D y0
D 2y0
D 3y0
x1
y1
D y1
D 2y1
D 3y1
x2
y2
D y2
D 2y2
...
x3
y3
D y3
...
x4
y4
...
...
...
...
14
14.
Первая интерполяционная формула НьютонаPn(x) = a0 + a1 (x - x0) + a2 (x - x0) (x - x1) +
+ a3 (x - x0) (x - x1) (x - x2) + ... + an (x - x0) (x - x1) ∙ ... ∙ (x - xn-1).
y0 = Pn (x0) = a0 a0= y0.
y1 = Pn(x1) = a0 + a1 (x1 - x0) = a0 + a1 h
y2 = Pn (x2) = a0 + a1 (x2 - x0) + a2 (x2 - x0) (x2 - x1) = a0+ 2 a1h + 2 a2h2.
a0 y0
y1 a0 y1 y0 Dy0
h
h
h
y2 a0 2a1h y1 y0 2Dy0 D2 y0
a2
2
2
2h
2h
2h 2
a1
Dk y 0
, k = 0, 1, 2,... n
ak
k
k! h
Dy 0
Dn y 0
Pn ( x) y 0
( x x0 ) ....
( x x0 )( x x1 )( x x2 )....( x xn 1 )
h
n!h n
15
15.
Dy 0Dn y 0
Pn ( x) y 0
( x x0 ) ....
( x x0 )( x x1 )( x x2 )....( x xn 1 )
n
h
n!h
х = х0 + ht
x x1 x x0 h
t 1
h
h
Первая интерполяционная формула Ньютона для
интерполирования вперед:
Pn ( x) y 0 t Dy 0
t (t 1) 2
t (t 1).....(t n 1) n
D y 0 ....
D y0
2!
n!
При n=1 – линейная интерполяция
P1 (x) = у0 t D у0.
При n=2 – квадратичная интерполяция
P2 ( x) y 0 t Dy 0
t (t 1) 2
D y0
2!
16
16.
Вторая интерполяционная формула Ньютонаt
x x0
h
Вторая интерполяционная формула Ньютона
для интерполирования назад:
Pn 2 ( x) yn t Dyn 1
t (t 1) 2
t (t 1).....(t n 1) n
D yn 2 ....
D y0
2!
n!
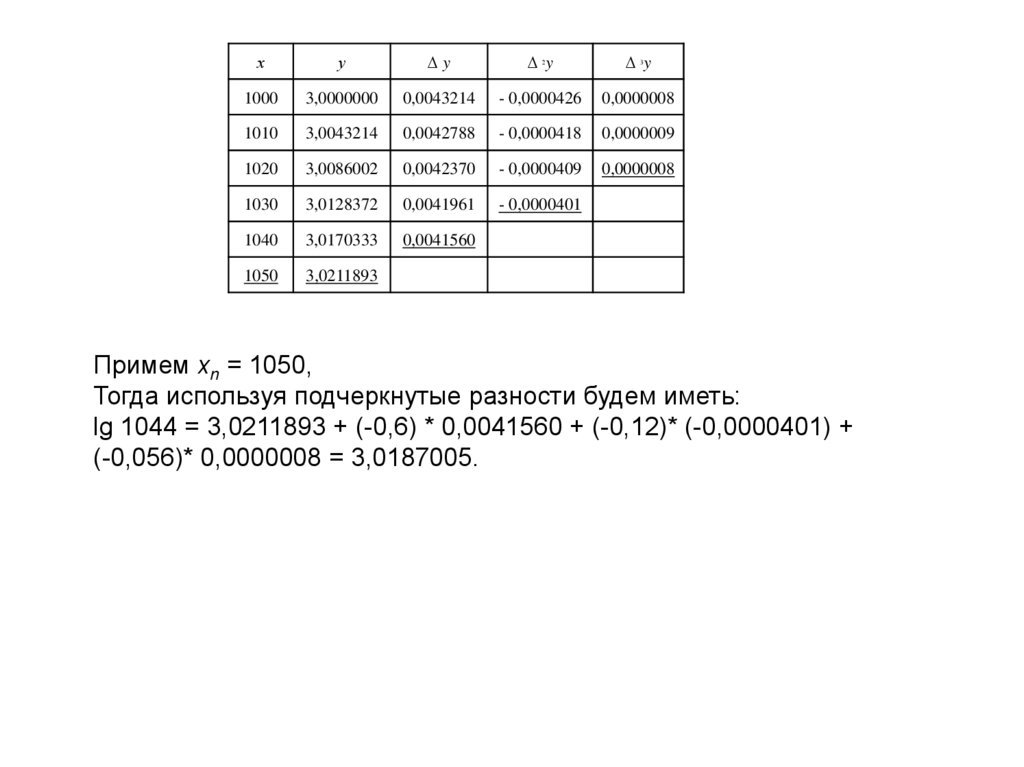
Пример. Дана таблица значений y = lg x семизначных логарифмов Найти lg 1044.
Таблица разностей функции у = lg x.
Примем xn = 1050
у
Dy
D y
2
D y
lg 1044 =
1000
3,0000000
0,0043214
- 0,0000426
0,0000008
3,0086002
1010
3,0043214
0,0042788
- 0,0000418
0,0000009
1030
3,0128372
1020
3,0086002
0,0042370
- 0,0000409
0,0000008
1040
3,0170333
1030
3,0128372
0,0041961
- 0,0000401
1050
3,0211893
1040
3,0170333
0,0041560
1050
3,0211893
х
у
1000
3,0000000
х
1010
3,0043214
1020
3
17
17.
ху
Dy
D y
2
D y
1000
3,0000000
0,0043214
- 0,0000426
0,0000008
1010
3,0043214
0,0042788
- 0,0000418
0,0000009
1020
3,0086002
0,0042370
- 0,0000409
0,0000008
1030
3,0128372
0,0041961
- 0,0000401
1040
3,0170333
0,0041560
1050
3,0211893
3
Примем xn = 1050,
Тогда используя подчеркнутые разности будем иметь:
lg 1044 = 3,0211893 + (-0,6) * 0,0041560 + (-0,12)* (-0,0000401) +
(-0,056)* 0,0000008 = 3,0187005.
18.
Метод наименьших квадратовПусть для исходных данных xi, fi, i=1,…,N, выбран вид эмпирической
зависимости:
с неизвестными
коэффициентами
. Запишем сумму квадратов отклонений
между вычисленными по эмпирической формуле и заданными опытными
данными:
.
Параметры
функции
будем находить из условия минимума
.
19.
Известно, что в точке минимума все частные производныеот по
равны нулю:
(1)
В качестве эмпирической функции рассмотрим полином
.
Формула (1) для определения суммы квадратов отклонений примет вид:
(2)
Вычислим производные:
20.
Приравнивая эти выражения нулю и собирая коэффициенты принеизвестных
, получим следующую систему линейных уравнений:
Нормальная система уравнений
Получаем коэффициенты
.
21.
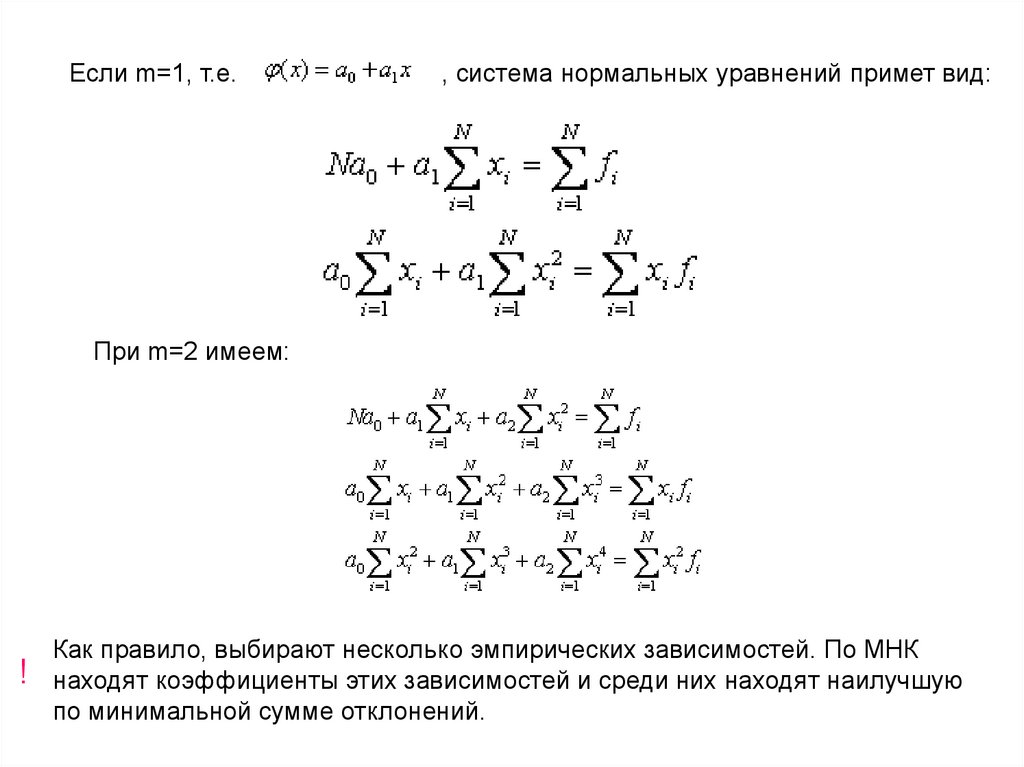
Если m=1, т.е., система нормальных уравнений примет вид:
При m=2 имеем:
!
Как правило, выбирают несколько эмпирических зависимостей. По МНК
находят коэффициенты этих зависимостей и среди них находят наилучшую
по минимальной сумме отклонений.
22.
Точность интерполяцииГрафик интерполяционного полинома у = j (х) проходит через заданные
точки, т. е., значения полинома j (х) и данной функции у = f (х) совпадают
в узлах х = хi (i = 0, 1, .., . n). Если функция f (х) сама является полиномом
степени n, то имеет место тождественное равенство f (х) = j (х). В общем
случае в точках, отличных от узлов интерполяции
R(x) = f (х) - j (х).
Эта разность и есть погрешность интерполяции, и называется
остаточным членом интерполяционной формулы.
• Остаточный член интерполяционного полинома Лагранжа
( x x0 )( x x1 )....( x x n ) ( n 1)
f
( )
(n 1)!
- производная n+1-го порядка, если
RL ( x)
f ( n 1) ( )
M n 1 max f ( n 1) ( x)
x0 x x n
то
RL ( x)
( x x0 )( x x1 )....( x x n )
M n 1
(n 1)!
23
23.
• Остаточный член первой интерполяционной формулы Ньютонаx x0
t (t 1)(t 2)....(t n) ( n 1)
n 1
RP ( x)
f
( )h , t
(n 1)!
h
• Остаточный член второй интерполяционной формулы Ньютона
RP ( x)
Если
f
( n 1)
x x0
t (t 1)(t 2)....(t n) ( n 1)
f
( )h n 1 , t
(n 1)!
h
Dn 1 y 0
( ) n 1
h
• Остаточный член первой интерполяционной формулы Ньютона
RP ( x)
t (t 1)(t 2)....(t n) n 1
D y0 ,
(n 1)!
• Остаточный член второй интерполяционной формулы Ньютона
RP ( x)
t (t 1)(t 2)....(t n) n 1
D yn
(n 1)!
24













 Математика
Математика








