Похожие презентации:
Логарифмы и их свойства
1. 1) 2)
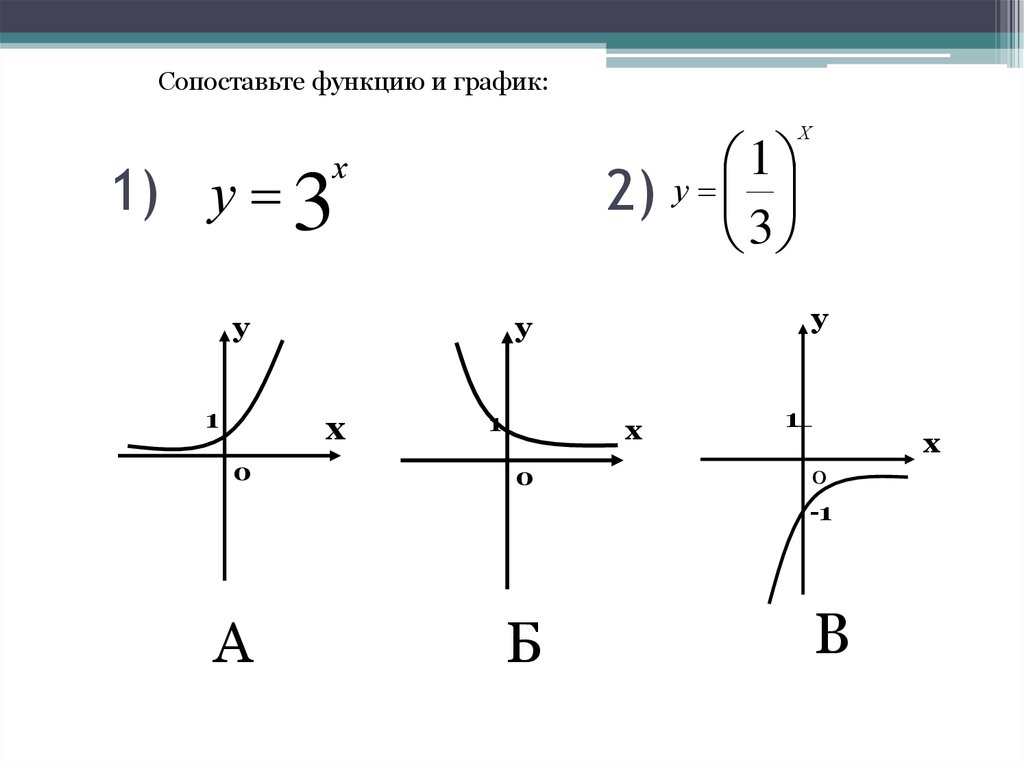
Сопоставьте функцию и график:1
2) у
3
х
1) у 3
у
1
0
А
у
у
х
1
х
0
Б
Х
1
х
0
-1
В
2. Найдите ошибку:
12
х
3
4
х
1 1
6 6
х 1
3
0
х 0
х 2
2
х
1
4
х
3 81
х 4
3. Логарифмы и их свойства
4. Цели урока:
Определение логарифма
Основное логарифмическое тождество
Основные свойства логарифмов
Формула перехода от одного основания к
другому
5.
Определение.Логарифмом числа b по основанию а
называется показатель степени, в
которую нужно возвести в основание а,
чтобы получить b.
loga b
а
=b
6. Понятие логарифма
log a b xa b
x
a >0 a ≠1 b>0
7.
Основное логарифмическое тождествоloga b
а
=b
8.
Уравнение ах=b, где а>0 и а≠1При b≤0 не имеет корней;
При b>0 имеет единственный корень.
loga b
а
=b
9.
Пример 1.Пример 2.
Пример 3.
log2 32 = 5
log5 0 ,04 = -2
1
log 3 = - 4
9
10.
00
2 .loga a = 1
1 . loga 1 = 0
0
3 . loga xy = loga x + loga y
x
4 . loga = loga x - loga y
y
0
0
p
5 . loga x = p loga x
11.
12.
13.
logb xloga x =
logb a
14.
log10 a lg aДесятичный логарифм
lg 7
0 ,8451
log0 , 3 7 =
=
= -1,6162
lg 0 ,3 - 0 ,5229
15.
log2 5 = alog2 3 = b
Выразить log2 300 через а и b.
log2 300 =
2
2
= log2 ( 3 • 5 • 2 ) = log2 3 + 2 log2 5 + 2 log2 2 =
= b + 2a + 2.
16.
Прологарифмируем выражение37
8а
4
b
по основанию 2
(Выразим его через log2 a и log2 b )
Решение:
4
7
log2 ( 8 a3 7 b 4 ) = log2 ( 2 3 • a3 • b ) =
4
= 3 log2 2 + 3 log2 a + log2 b =
7
4
= 3 + 3 log2 a + log2 b
7
17.
Найдём х, еслиlog5 x = log5 7 + 2 log5 3 - 3 log5 2.
2
7 •3
63
log5 x = log5 ( 3 ) = log5
2
8
63
x=
= 7 ,875
8
18.
Найти значение выраженияlg 72 - lg 9
lg 28 - lg 7
72
lg
3
lg 72 lg 9
lg
8
lg
2
3 lg 2 3
9
2
lg 28 lg 7 lg 28 lg 4 lg 2
2 lg 2 2
7
19.
20.
Шаблон «Классная доска»:http://fppt.ru/338-shkolnaya-doska.html
Шаблон "Линейка и циркуль":
http://templated.ru/ingeneriya/400-lineyka-i-cirkul.html
Изображения учебников:
http://cs306311.vk.me/v306311395/1689/toaRIVLHluo.jpg
http://www.picszone.ru/img.php?url=http://izhevsk.ru/forums/icons/forum_pi
ctures/008799/8799346.jpg















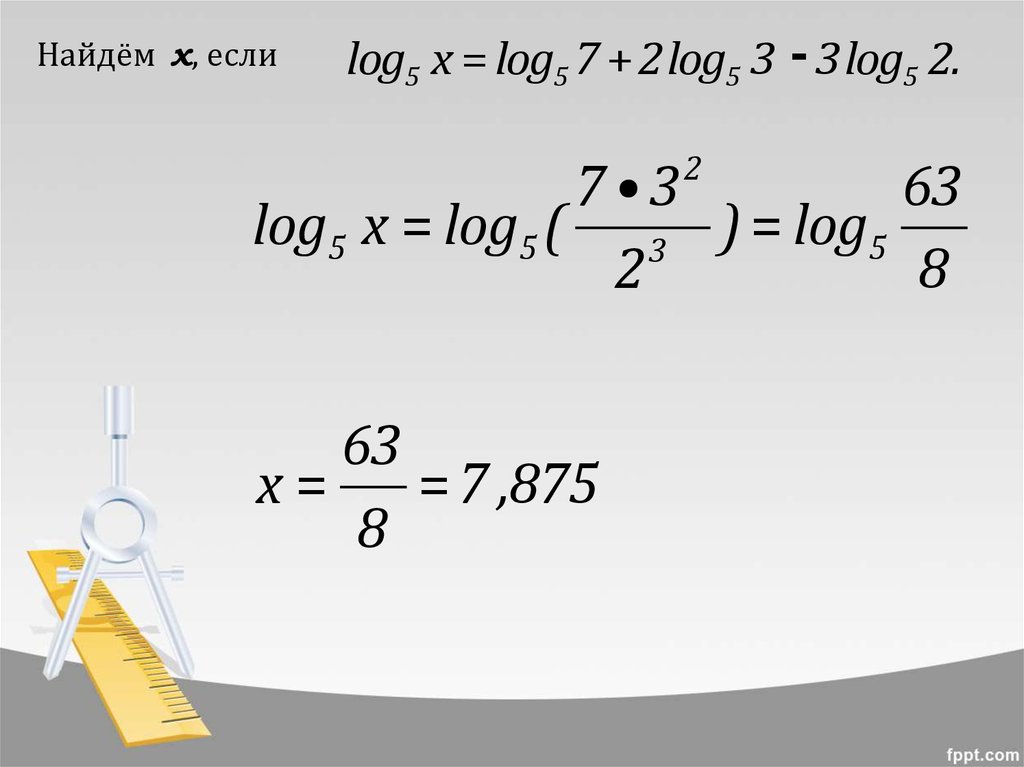



 Математика
Математика








