Похожие презентации:
Понятие логарифма, основные свойства логарифмов
1.
Лекция по алгебре.Тема:
понятие логарифма,
основные свойства
логарифмов.
Преподаватели математики Хохлова С.Н., Мещенко Н.В.
2. Решите уравнение.
1)Мы искали
х показатель степени,
Решить
а надо
в, где
а 0основание
и а 1, b0,5 ,0
0,5х =32,уравнение
в который
возвести
х = - 5.
чтобы получить 32.
значит, найти показательстепени,
2)
х
в который
надоМы
возвести
основание
a,
искали показатель
степени,
1
27, в который надо возвести основание
чтобы
число b
3 получить
чтобы получить 27.
х 3.
1
,
3
3)
Показатель
– это
и есть логарифм
4х+1+4х = 320степени
, Мы искали
показатель степени,
(при
определенных
условиях).
4х(4+1)
= 320
, в который надо возвести
основание 4,
4х = 64 ,
чтобы получить 64.
х = 3.
3.
Определение.Логарифмом числа b
(b > 0) по
основанию a ( a > 0, a 1) называется
показатель степени c, в которую нужно
возвести основание a, чтобы получить
число b , т.е. если ac = b , то можно
записать logab = c .
4.
Примеры.1) log232, здесь b = 32, a = 2, c = 5.
log232 = 5 , т. к. 25 = 32 .
2) log50,04 ,
здесь b = 0,04, a = 5, c = - 2.
log50,04 = - 2, т. к. 5-2 = 1/25 = 0,04 .
3) Найти х, такое, что log8х = 1/3.
По определению логарифма
х = 81/3 = 2.
5.
Основное логарифмическое тождество.c
a
= b logab = c
Откуда получаем основное
логарифмическое тождество
(b > 0, a > 0, a 1)
a
loga b
b
6.
Примеры.log0,5 6
1) 0,5
2)
5
5
2log5 3
log5 3
6 .
(( 5 ) )
3.
2 log5 3
7. Свойства логарифмов.
1) loga 1 0.5.1) log a x
p
p log a x.
1
5.2) log p b log a b.
2) loga a 1.
p
a
3) loga xy loga x loga y
logc b
6) loga b
x
4) loga loga x loga y
logc a
y
a
logc b
b
logc a
1
Следствие: 1) loga b
logb a
n
Следствие: 2) log m b log a b.
m
a
Следствие : 3) log a b log b
n
a
8.
Свойства логарифмов, примеры.2
1) log 2 27 2log 2 3 log 2 log 2 33 2log 2 3 log 2 2 log 2 3
3
3log 2 3 2log 2 3 log 2 2 log 2 3 log 2 2 1
Использовались свойства 4 , 5.1 и 2.
1
1
2) log 1 2 log 1 8 log 1 (4 18 ) log 1 2 log 1 8 2 log 1 (4 18 )
2
3
3
3
3
3
3
1
2
log 1 (2 8 ) log 1 (4 18 ) log 1
3
1
log 1 1
3
3
3
3
2 8
1
2
4 18
log 1
3
2
3
2
2 3 2
Использовались свойства
5.1, 3, 4 и 2.
1
2
9.
Свойства логарифмов, примеры.1
3) log 9 (log 4 4 ) log 9 log 4 4 log 32 (3 1 )
3
1
1
log 3 3
2
2
Свойства 5.1, 2 , следствие 2 .
3
Действия спо
десятичными
логарифмами.
Логарифмы
основанию 10
называют
2
3
2
3
log
a
lg
4) lg0,001 lg 1000логарифмами:
lg 10 3 10
lg10 alg10
десятичными
3
5
3
5
3
3
5
Примеры: 1)
2
3 lg100=
5
2 1 lg10 -24 1 1 2
2)5 lg0,0001=
3
3) lg100000000= 8
5
3
10.
Формула перехода от одного основаниялогарифма к другому, примеры.
log 5 0,5
log 5 0,5
log 5 0,5
1)
log 8 0,5
24
log 5 24 log 5 3
log 5 8
log 5
3
1
1
1
log 23 2
3
3
lg10
1
3
2) log 310 lg 27 log 27 1
lg 3 0
3 lg 3 3
lg3
lg3
11.
Домашнее задание.1) Разобрать и выучить лекцию.
2) Никольский, 10 кл., п.5.1, 5.2
№ 5.4, 5.8( а, б, в, е, и), 5.9(1,2 стр.)
12. Свойства логарифмов.
1) loga 1 0.2) loga a 1.
a
loga b
3) loga xy loga x loga y
x
4) loga loga x loga y
y
p
5.1) log a x p log a x.
1
5.2) log p b log a b.
p
a
6) loga b
logc b
logc a
b
a
logc b
b
logc a
Следствия :
1
1) log b
a
log a
b
n
2) log
log a b.
m
a
m
3) log b log b
a
bn
a





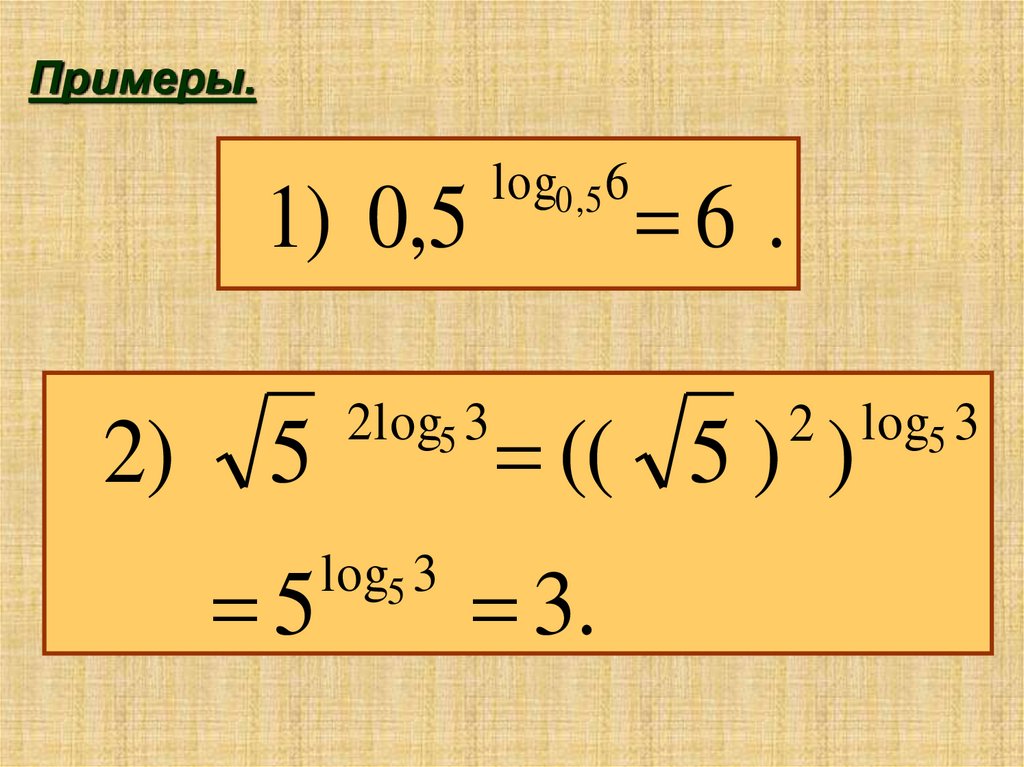






 Математика
Математика








