Линейчатые поверхности. Образование поверхностей

1.

Линейчатые поверхности
Образование поверхностей

2.

Линейчатой поверхностью называется
поверхность, образованная перемещением
прямолинейной образующей по одной или
более направляющим

3.

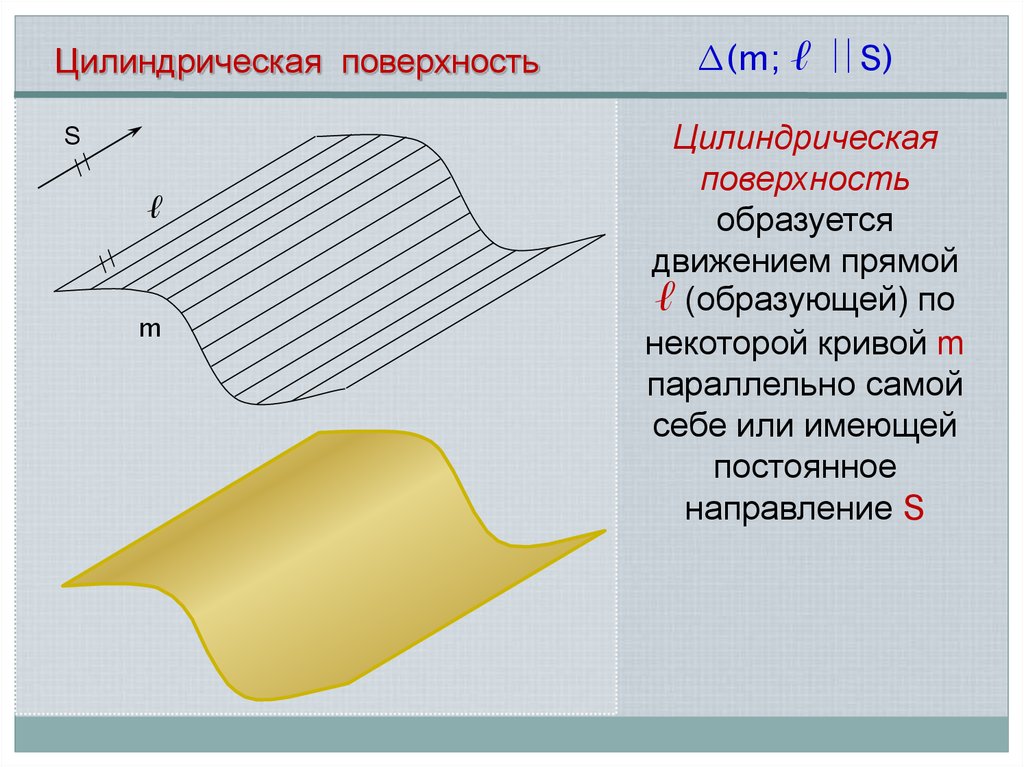
Цилиндрическая поверхность
S
ℓ
m
∆(m; ℓ S)
Цилиндрическая
поверхность
образуется
движением прямой
ℓ (образующей) по
некоторой кривой m
параллельно самой
себе или имеющей
постоянное
направление S

4.

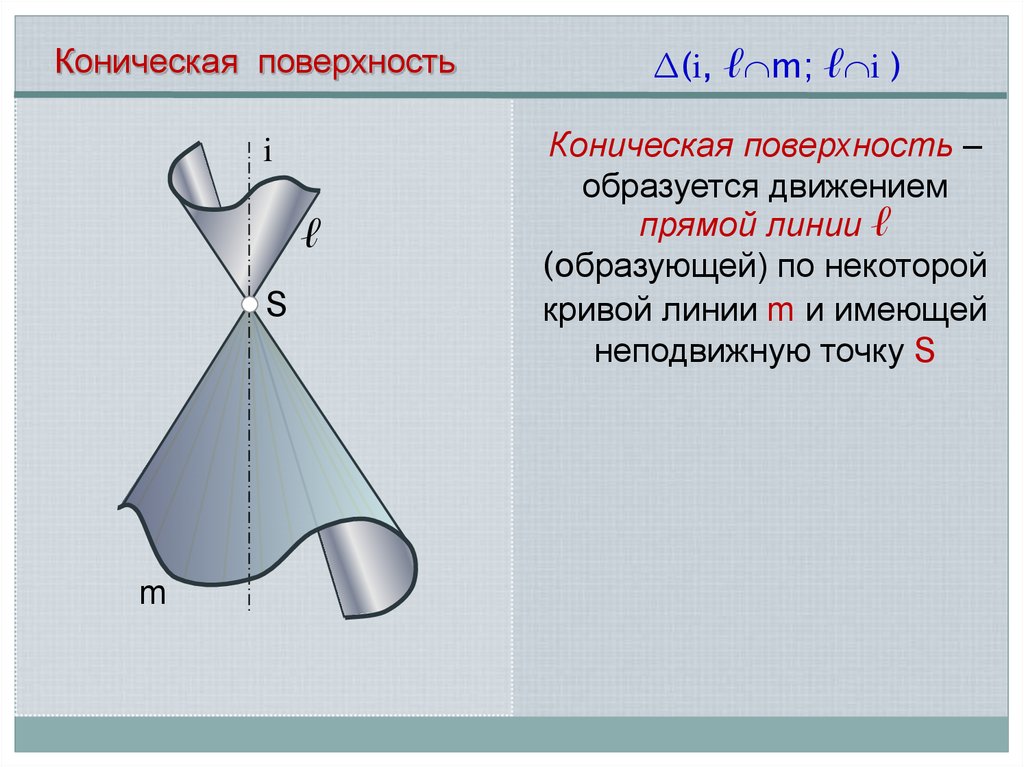
Коническая поверхность
i
ℓ
S
m
∆(i, ℓ m; ℓ i )
Коническая поверхность –
образуется движением
прямой линии ℓ
(образующей) по некоторой
кривой линии m и имеющей
неподвижную точку S

5.

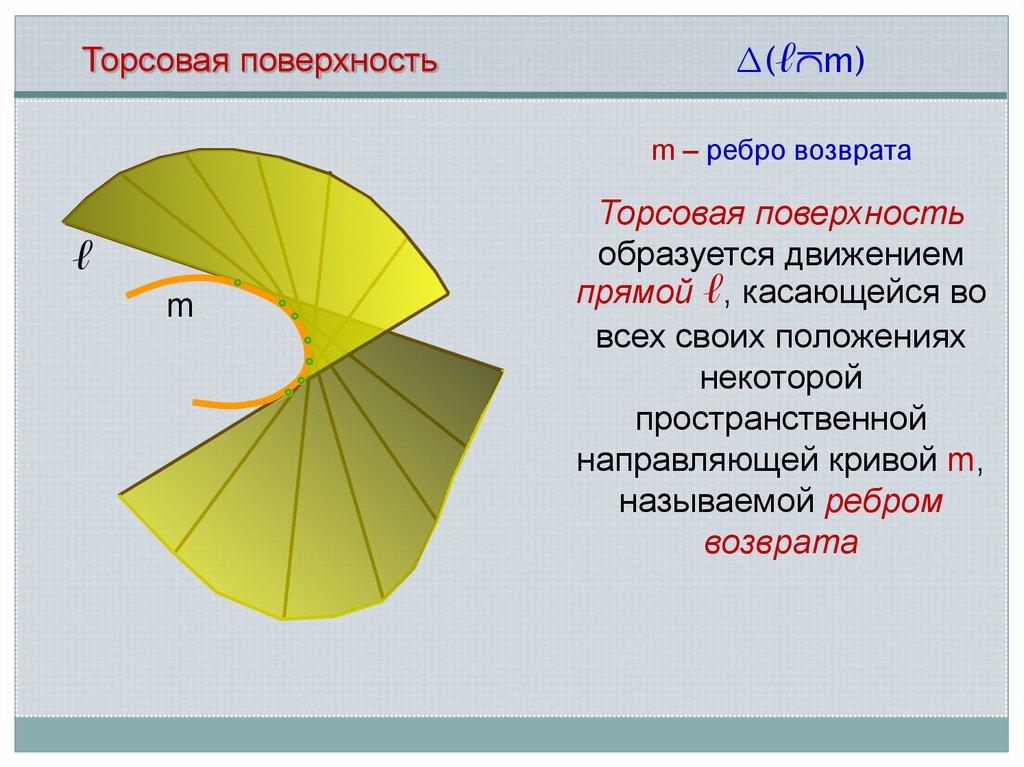
Торсовая поверхность
∆(ℓ m)
m – ребро возврата
ℓ
m
Торсовая поверхность
образуется движением
прямой ℓ, касающейся во
всех своих положениях
некоторой
пространственной
направляющей кривой m,
называемой ребром
возврата

6.

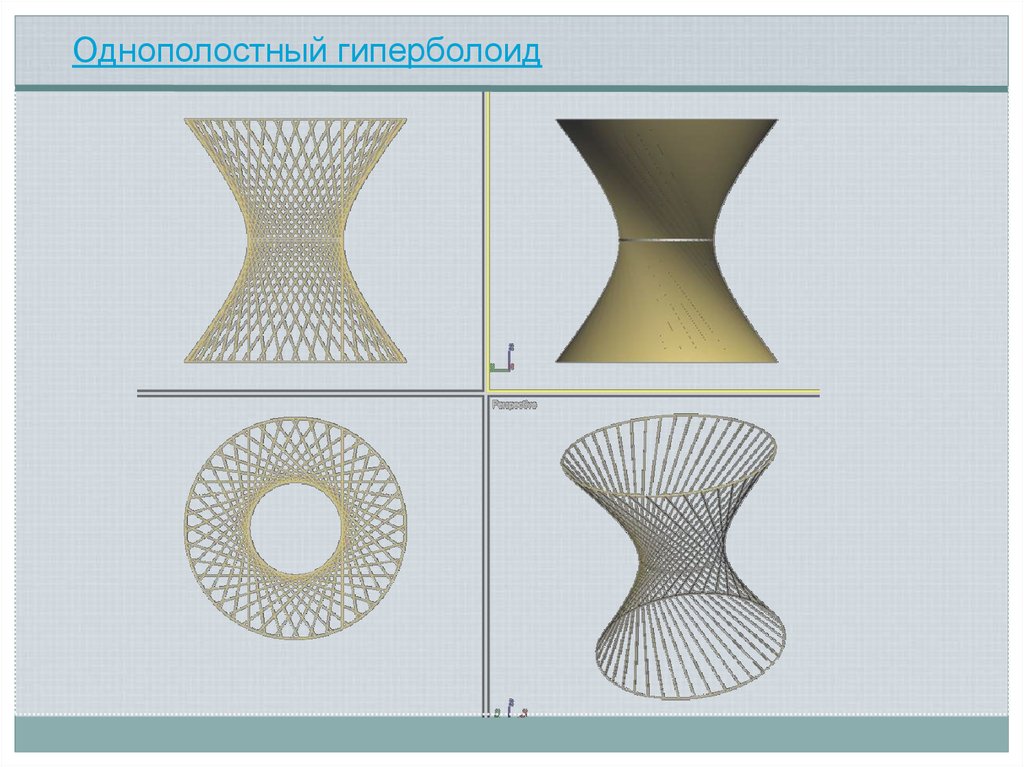
Однополостный гиперболоид

7.

Многогранные поверхности – это
поверхности, образованные частями
(отсеками) пересекающихся плоскостей
Многогранником называется тело,
ограниченное многогранной поверхностью,
состоящей из плоских многоугольников
Отсеки плоскостей называются гранями,
а линии их пересечения – ребрами
Точки пересечения ребер называются
вершинами

8.

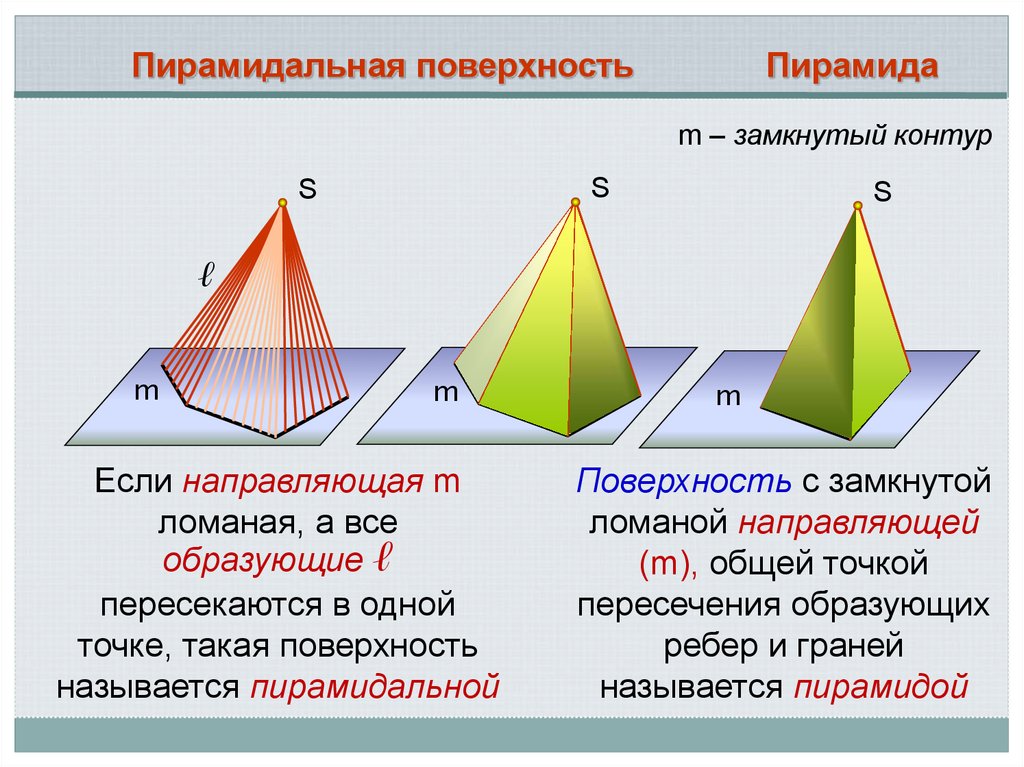
Пирамидальная поверхность
Пирамида
m – замкнутый контур
S
S
S
ℓ
m
m
Если направляющая m
ломаная, а все
образующие ℓ
пересекаются в одной
точке, такая поверхность
называется пирамидальной
m
Поверхность с замкнутой
ломаной направляющей
(m), общей точкой
пересечения образующих
ребер и граней
называется пирамидой

9.

Принадлежность точки поверхности

10.

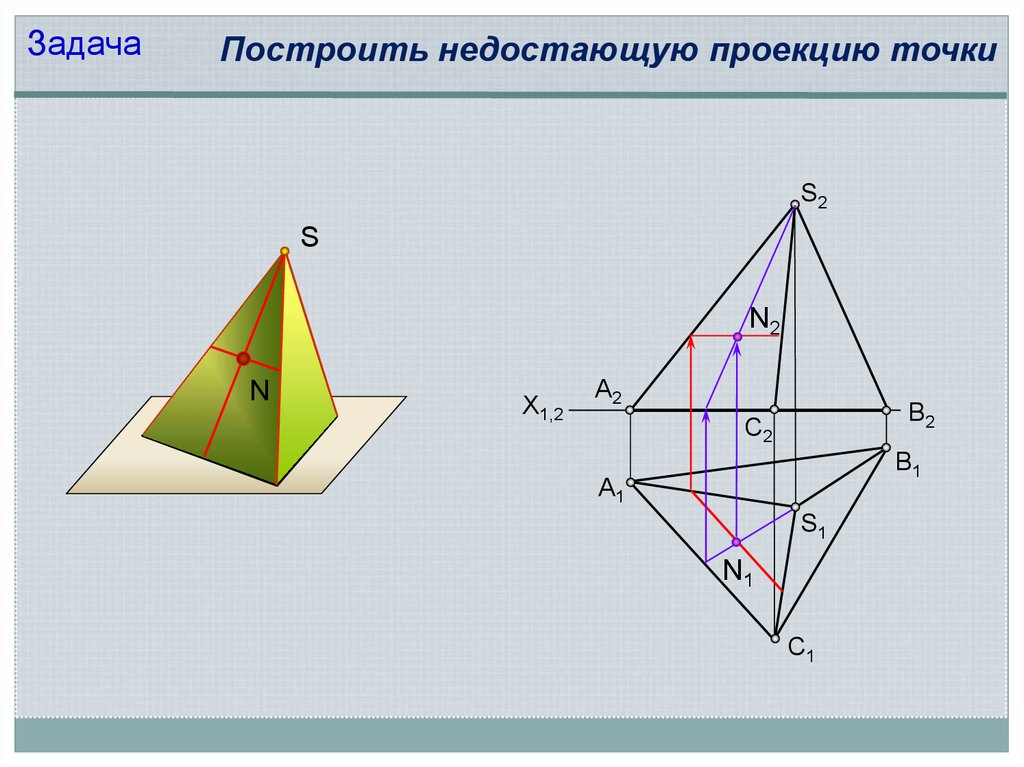
Задача
Построить недостающую проекцию точки
S2
S
N2
N
X1,2
А2
В2
С2
В1
А1
S1
N1
С1

11.

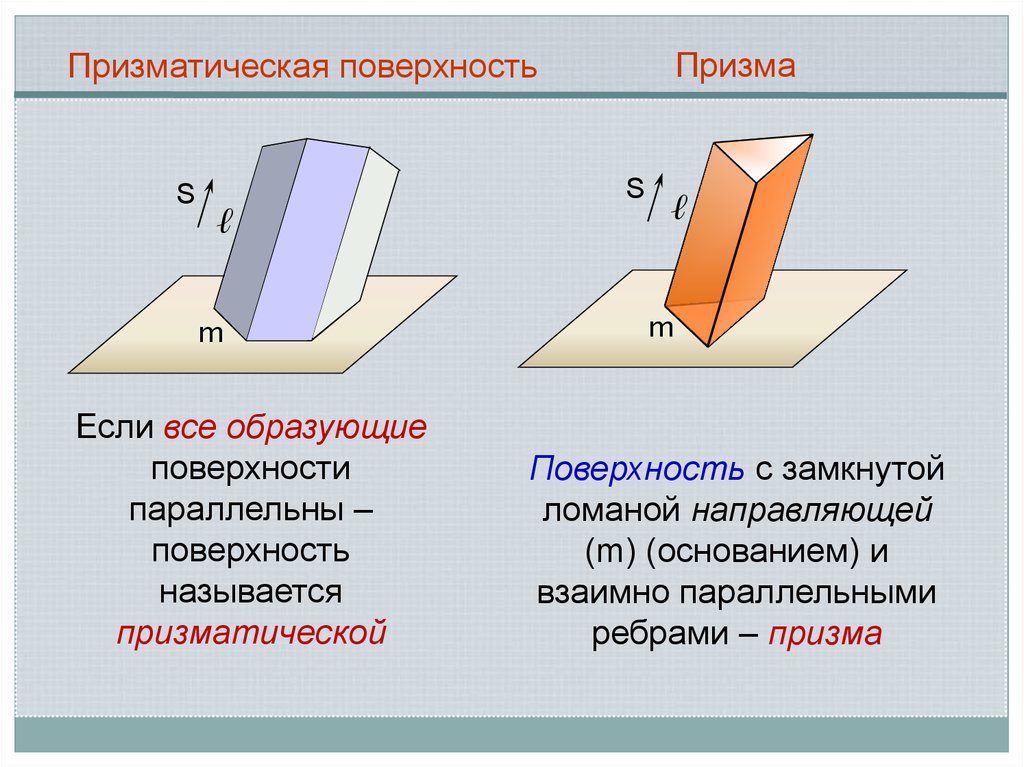
Призма
Призматическая поверхность
S
ℓ
m
Если все образующие
поверхности
параллельны –
поверхность
называется
призматической
S
ℓ
m
Поверхность с замкнутой
ломаной направляющей
(m) (основанием) и
взаимно параллельными
ребрами – призма

12.

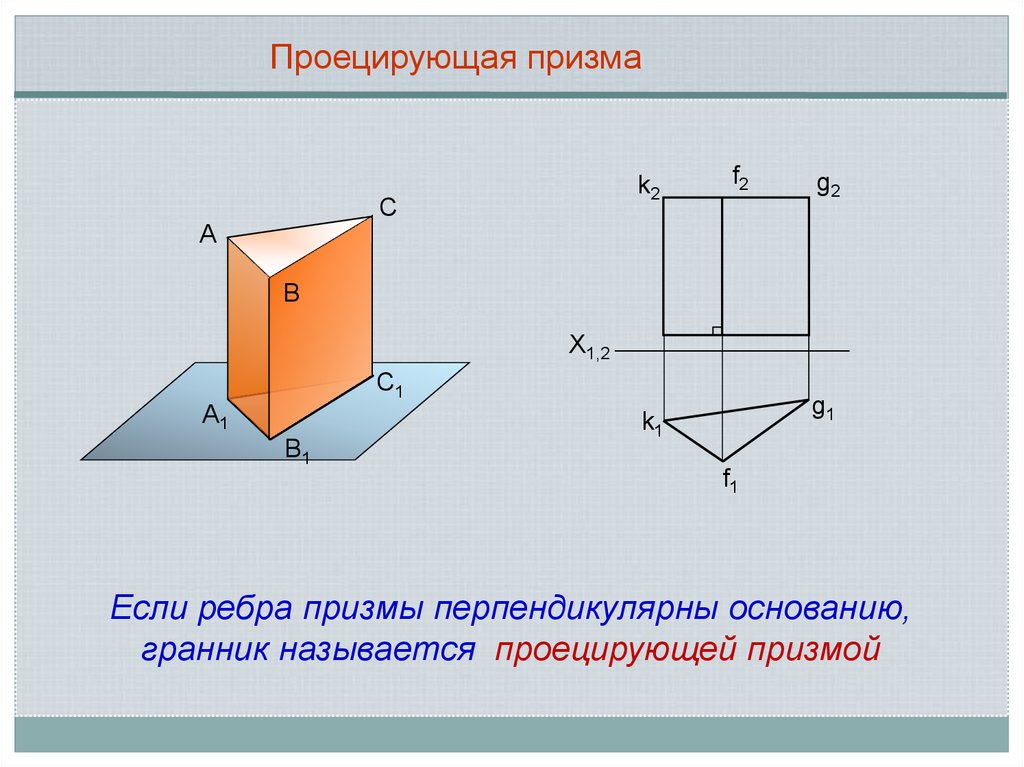
Проецирующая призма
k2
С
А
f2
g2
В
X1,2
С1
А1
В1
g1
k1
f1
Если ребра призмы перпендикулярны основанию,
гранник называется проецирующей призмой

13.

Поверхности Каталана

14.

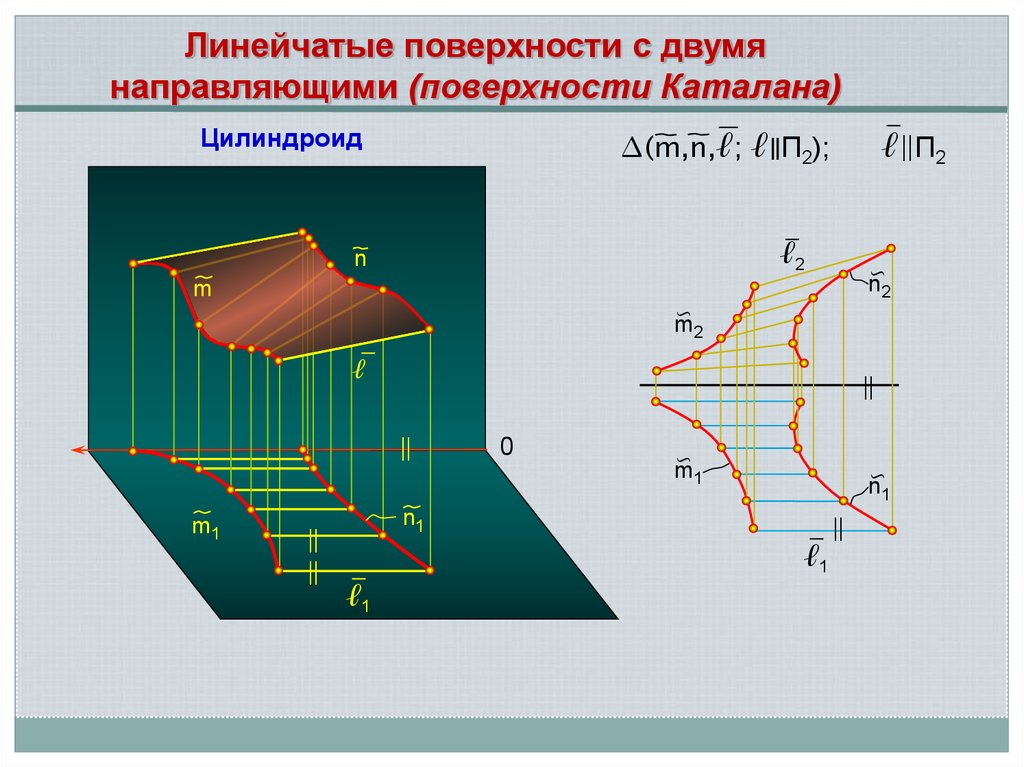
Линейчатые поверхности с двумя
направляющими (поверхности Каталана)
Цилиндроид
∆(m,n,ℓ; ℓ∥П2);
ℓ∥П2
ℓ2
n
m
∽
n2
∽
m2
ℓ
∥
∥
m1
∥
∥
0
∽
m1
∽
n1
n1
ℓ1
ℓ1
∥

15.

Гипар
Поверхность с плоскостью параллелизма и двумя
скрещивающимися направляющими называется
гиперболическим параболоидом, или косой
плоскостью

16.

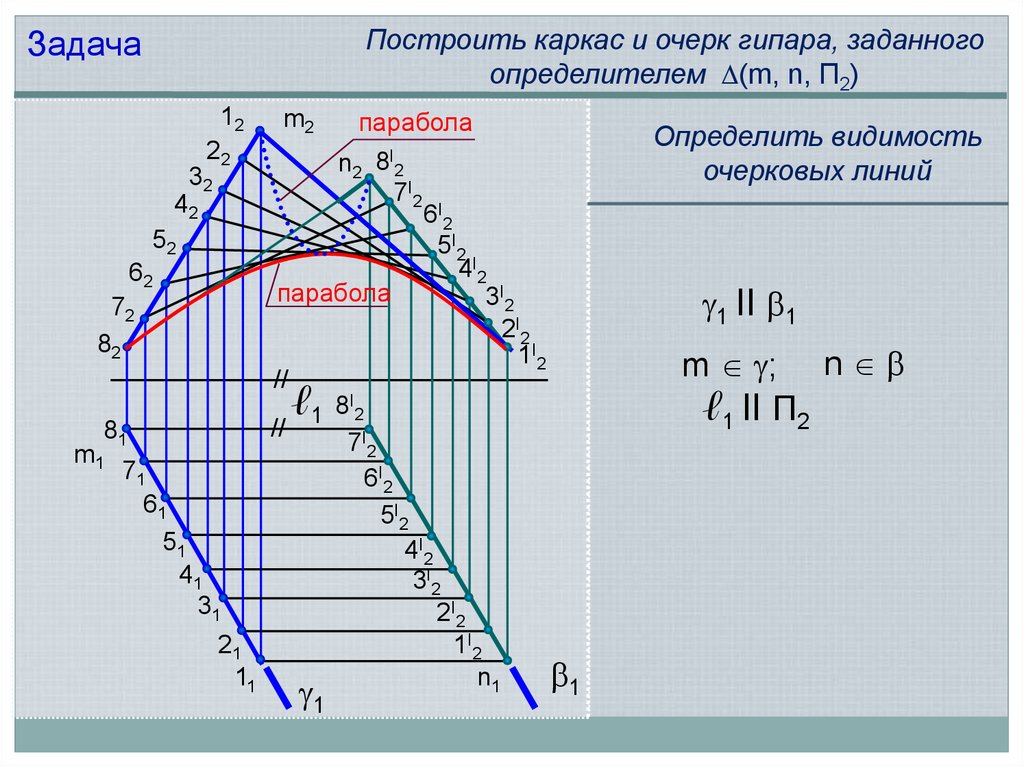
Построить каркас и очерк гипара, заданного
определителем (m, n, П2)
Задача
12
22
парабола
n2 8I2
32
7I2
42
6I2
52
5I2
4I2
62
парабола
3I2
72
2I2
82
1I2
//
ℓ1 8I2
//
81
I
7
2
m1
71
6I2
61
5I2
51
4I2
41
3I2
31
2I2
21
1I2
11
n1
1
m2
1
Определить видимость
очерковых линий
1 ll 1
m ; n
ℓ1 ll П2

17.

Винтовая поверхность
Винтовой поверхностью называют поверхность,
образованную винтовым движением образующей
Винтовым движением называют движение, при
котором каждая точка А образующей вращается
вокруг неподвижной оси i и одновременно
перемещается поступательно вдоль этой оси

18.

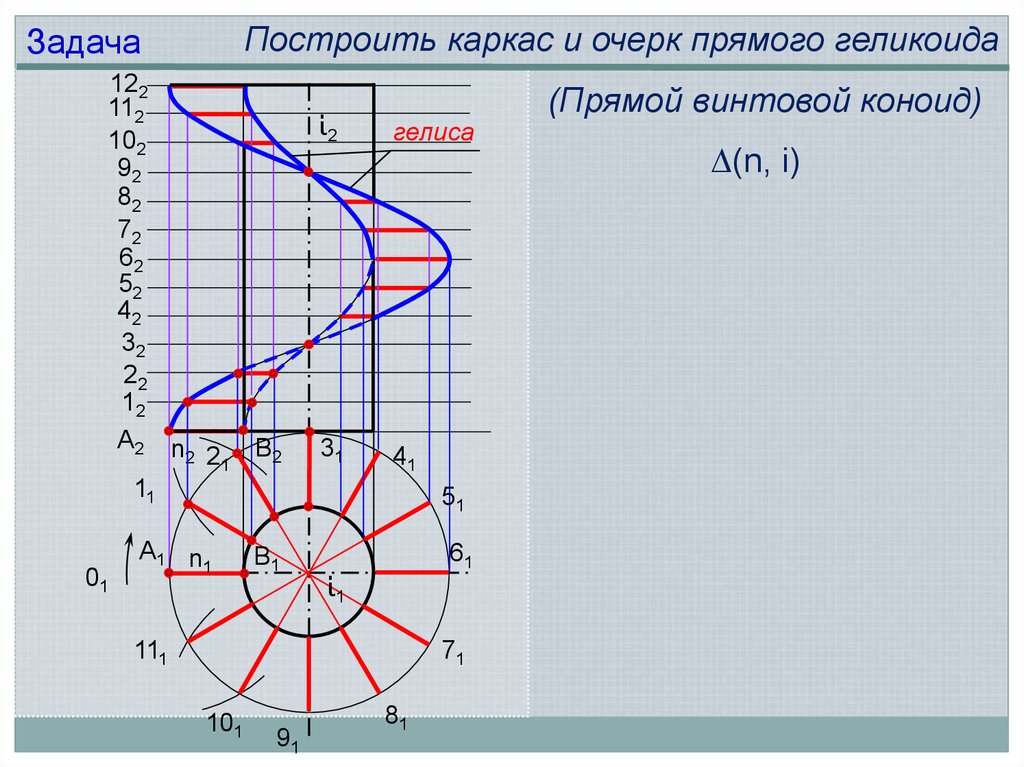
Построить каркас и очерк прямого геликоида
Задача
122
112
102
92
82
72
62
52
42
32
22
12
А2 n
2 21 В2
11
01
А1 n
1
В1
ί2
гелиса
31
41
51
61
ί1
111
71
101
91
81
(Прямой винтовой коноид)
(n, i)

19.

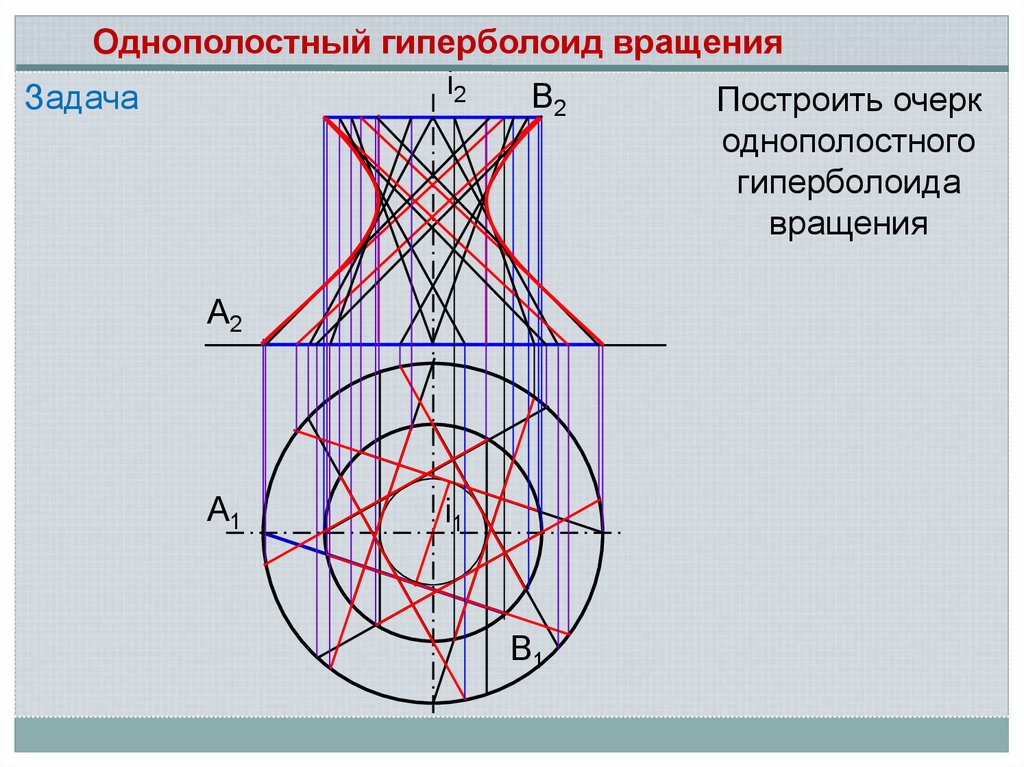
Однополостный гиперболоид вращения
i2
В2
Задача
Построить очерк
однополостного
гиперболоида
вращения
А2
А1
i1
В1