Кривые линии

1.

Кривые линии

2.

гипербола
С
А
В
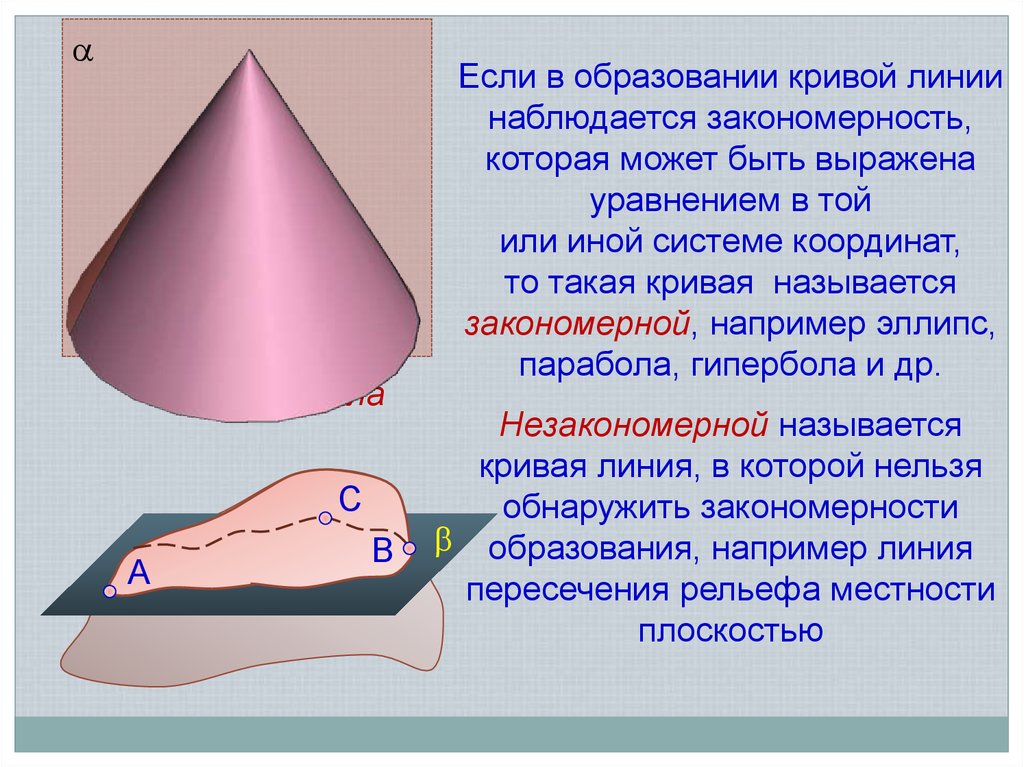
Если в образовании кривой линии
наблюдается закономерность,
которая может быть выражена
уравнением в той
или иной системе координат,
то такая кривая называется
закономерной, например эллипс,
парабола, гипербола и др.
Незакономерной называется
кривая линия, в которой нельзя
обнаружить закономерности
образования, например линия
пересечения рельефа местности
плоскостью

3.

Если уравнение кривой линии представляет собой
алгебраический многочлен, то она называется
алгебраической
Если кривую нельзя задать
алгебраическим многочленом, то она называется
трансцендентной

4.

Линии, все точки которых не принадлежат одной
плоскости, называются пространственными
Порядок алгебраической пространственной
кривой определяется числом ее точек
пересечения с плоскостью
ℓ
2
1
Пi
4
3

5.

Линии, все точки которых принадлежат одной
плоскости, называются плоскими
Порядок плоской алгебраической кривой
определяется числом ее точек пересечения с
прямой линией
m
ℓ
1
2

6.

B
g
m
A
F
t
gi
Bi
Fi
Пi
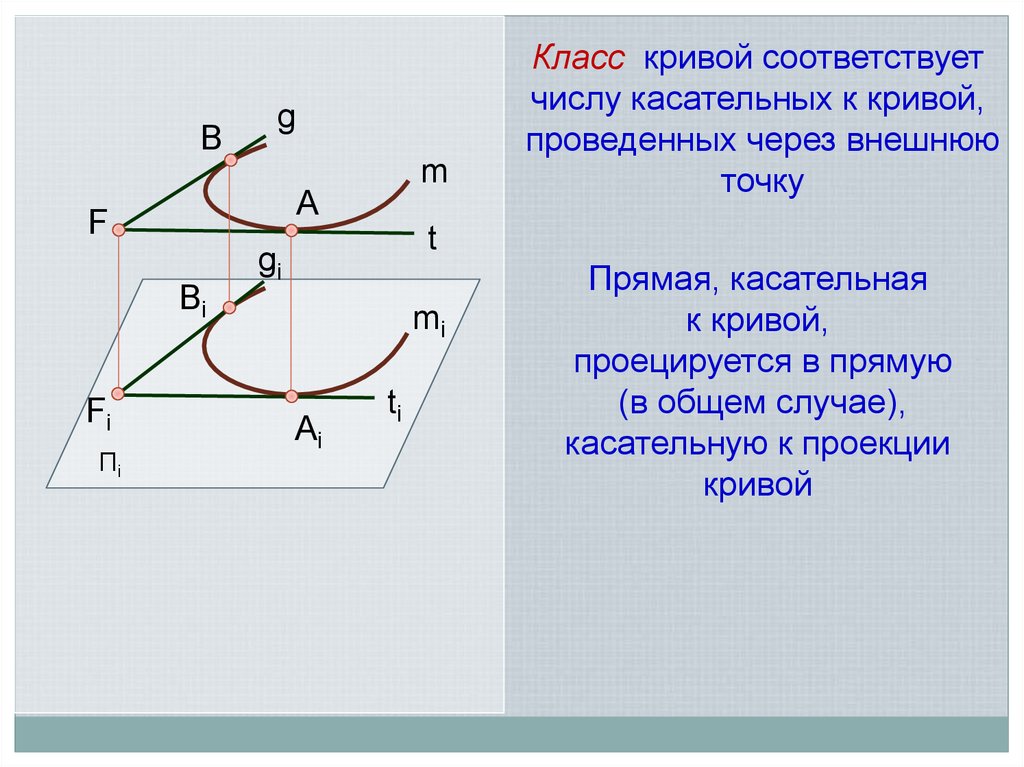
Класс кривой соответствует
числу касательных к кривой,
проведенных через внешнюю
точку
mi
Ai
ti
Прямая, касательная
к кривой,
проецируется в прямую
(в общем случае),
касательную к проекции
кривой

7.

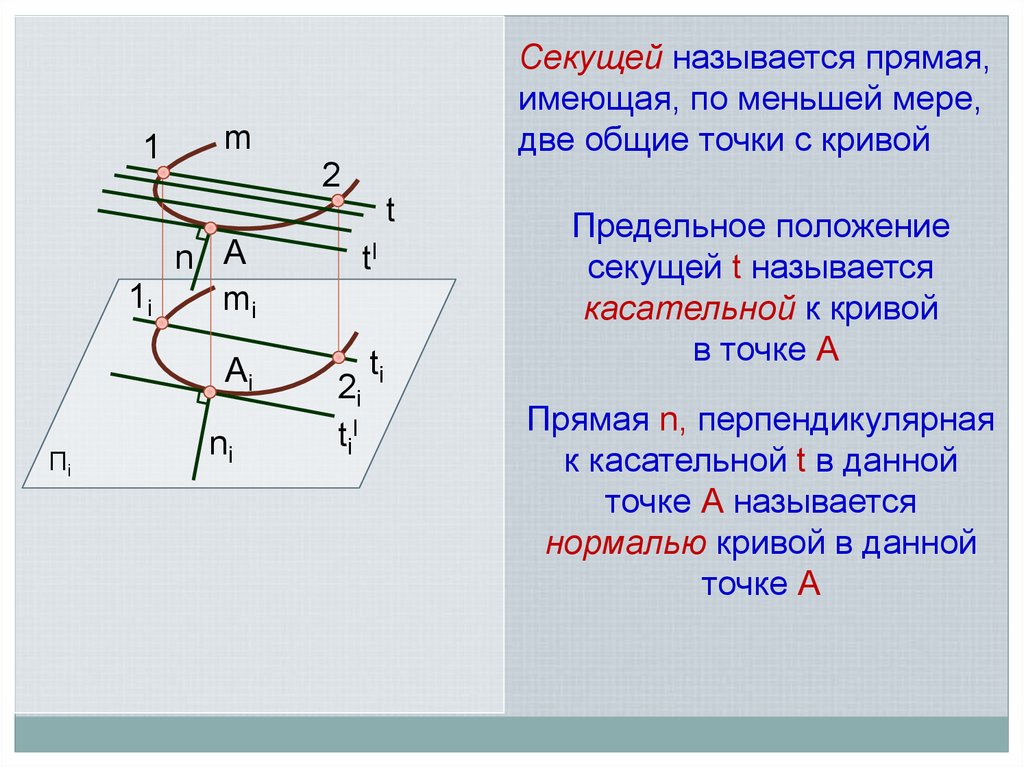
1
Секущей называется прямая,
имеющая, по меньшей мере,
две общие точки с кривой
m
2
t
Пi
n A
1i
mi
tI
Ai
ti
ni
2i
tiI
Предельное положение
секущей t называется
касательной к кривой
в точке А
Прямая n, перпендикулярная
к касательной t в данной
точке А называется
нормалью кривой в данной
точке А

8.

Особые точки кривой

9.

Точки перегиба (Н) – точки, в которых кривая
проходит на другую сторону касательной прямой,
сохраняя касание
Двойная или узловая точка (А) – это точка,
в которой кривая пересекает сама себя
Точки возврата первого ряда (В), в которой кривая
подходит к точке двумя ветвями,
имеющими в точке В общую касательную
и расположенными по разные стороны
от касательной
Точки возврата второго ряда С, в которой
кривая подходит к точке двумя ветвями,
имеющими в точке С общую касательную,
расположенную (вблизи точки С) по одну
сторону от обеих ветвей кривой