График и свойства степенной функции

1.

График и свойства
степенной функции

2.

Частные случаи степенной функции
у 12
у=х3
10
Определение
8
6
у=х2
4
2
0
-5
-4
-3
-2
-1
-2
0
1
2
3
4
х
5
у=х
У=ХР
-4
-6
ГДЕ Р- ЗАДАННОЕ
-8
ДЕЙСТВИТЕЛЬНОЕ
-10
-12
у=1/х
ЧИСЛО
–НАЗЫВАЕТСЯ
СТЕПЕННОЙ ФУНКЦИЕЙ
содержание

3.

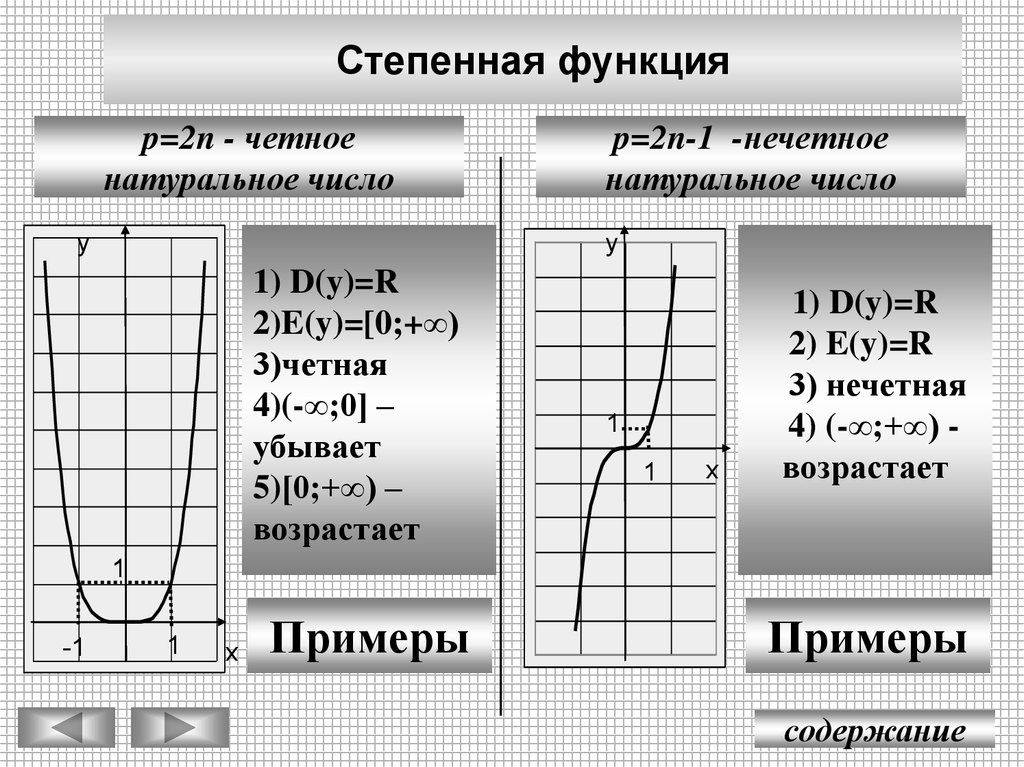
Степенная функция
p=2n - четное
натуральное число
у
p=2n-1 -нечетное
натуральное число
у
1) D(y)=R
2)E(y)=[0;+∞)
3)четная
4)(-∞;0] –
убывает
5)[0;+∞) –
возрастает
1
1
х
1) D(y)=R
2) E(y)=R
3) нечетная
4) (-∞;+∞) возрастает
1
-1
1
х
Примеры
Примеры
содержание

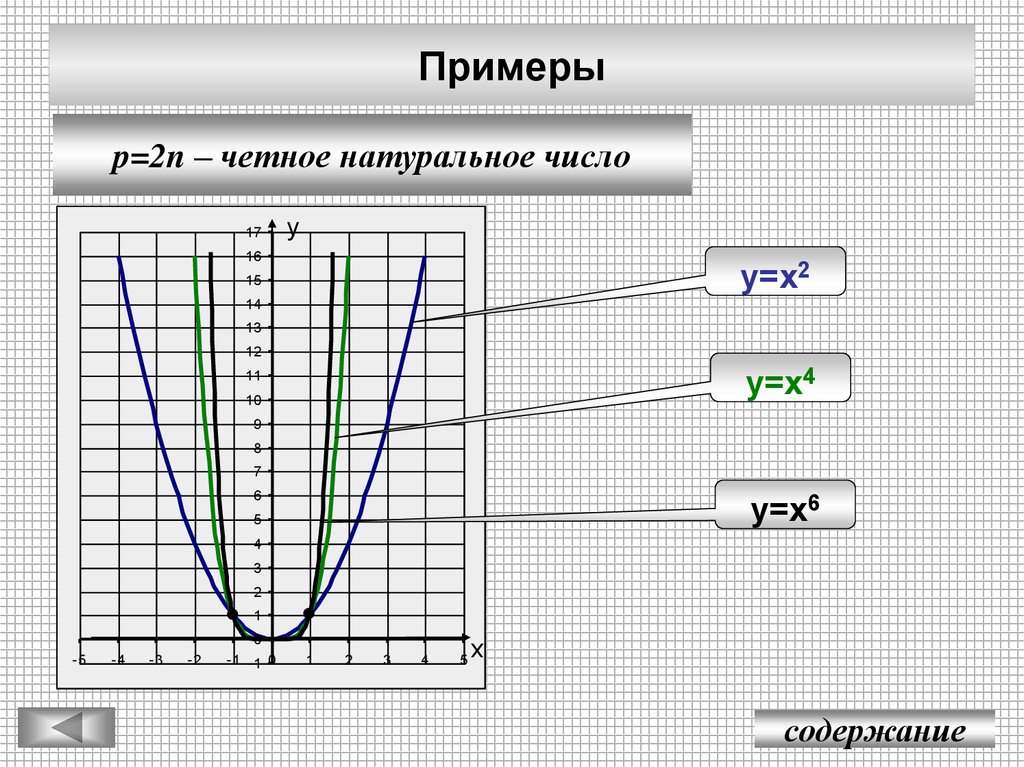
4. Примеры

p=2n – четное натуральное число
17
у
16
у=х2
15
14
13
12
у=х4
11
10
9
8
7
6
у=х6
5
4
3
2
1
-5
-4
-3
-2
0
-1 -1 0
1
2
3
4
5
х
содержание

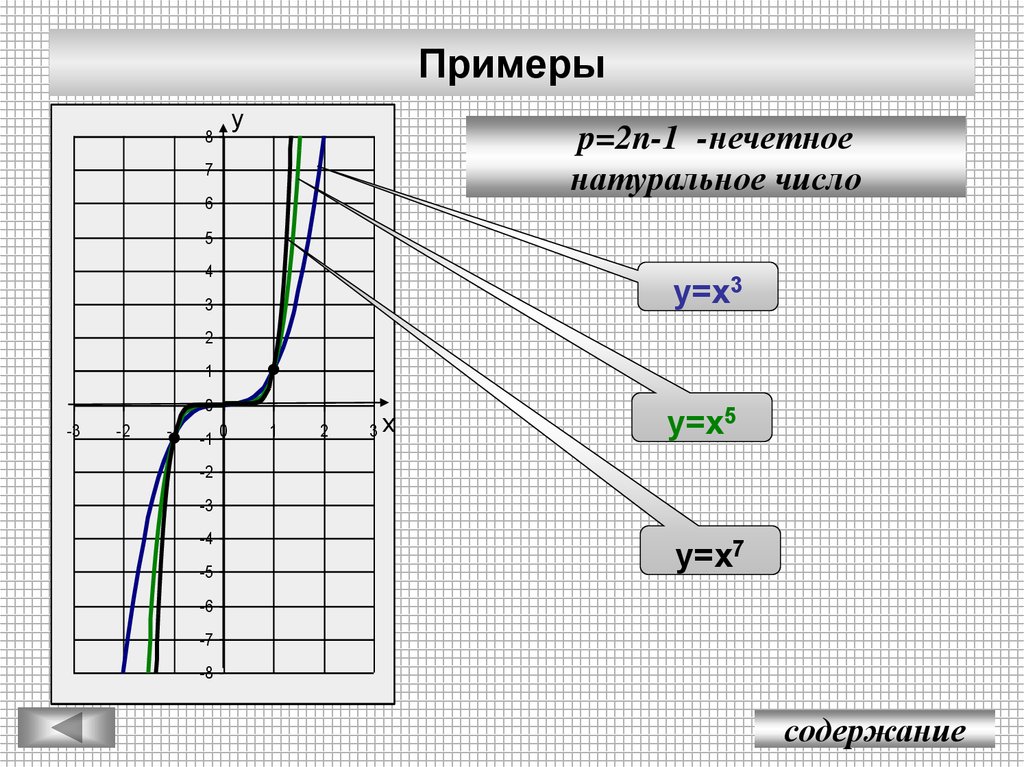
5. Примеры

8
у
p=2n-1 -нечетное
натуральное число
7
6
5
4
у=х3
3
2
1
0
-3
-2
-1
-1 0
1
2
3х
у=х5
-2
-3
-4
-5
у=х7
-6
-7
-8
содержание

6.

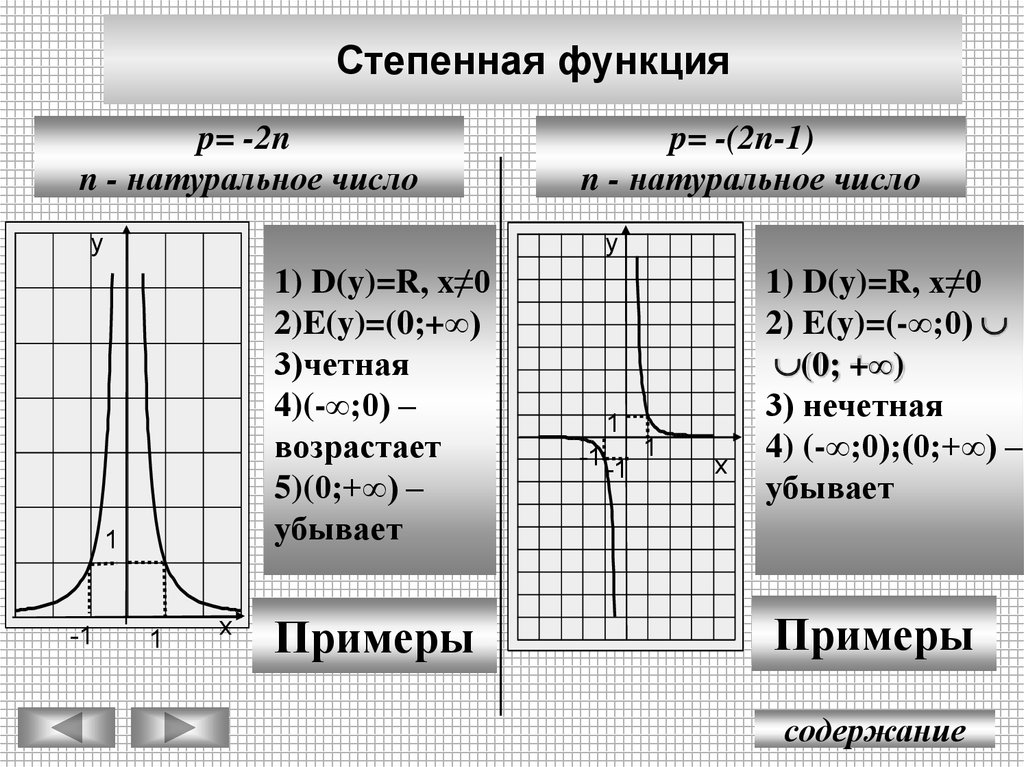
Степенная функция
p= -2n
n - натуральное число
у
у
1) D(y)=R, x≠0
2)E(y)=(0;+∞)
3)четная
4)(-∞;0) –
возрастает
5)(0;+∞) –
убывает
1
-1
p= -(2n-1)
n - натуральное число
1
х
Примеры
1
-1 -1 1
х
1) D(y)=R, х≠0
2) E(y)=(-∞;0)
(0; +∞)
3) нечетная
4) (-∞;0);(0;+∞) –
убывает
Примеры
содержание

7.

Примеры
p= -2n, n - натуральное число
у
7
у=х-2
6
5
4
у=х-4
3
2
у=х-6
1
0
-4
-3
-2
-1
0
1
2
3
4
х
содержание

8.

Примеры
p= -(2n-1) , n - натуральное число
9
у
8
7
6
у=х-1
5
4
3
у=х-3
2
1
0
-5
-4
-3
-2
-1 -1 0
-2
-3
1
2
3
4
5
х
у=х-5
-4
-5
-6
-7
-8
-9
содержание

9.

Степенная функция
p= m, m>1,
m-нецелое число
p= m , 0<m<1
m - нецелое число
у
у
1) D(y)=[0;+∞)
2)E(y)=[0;+∞)
3) [0;+∞) –
возрастает
1
1
х
1)D(y)=[0;+∞)
2) E(y)=[0;+∞)
3) [0;+∞) - возрастает
1
0 1
х
Примеры
Примеры
содержание

10.

Примеры
p= m, m>1, m-нецелое число
9
у
8
у=х2,7
7
6
5
у=х1,5
4
3
у=х1,3
2
1
0
0
1
2
3
4
5
х
содержание

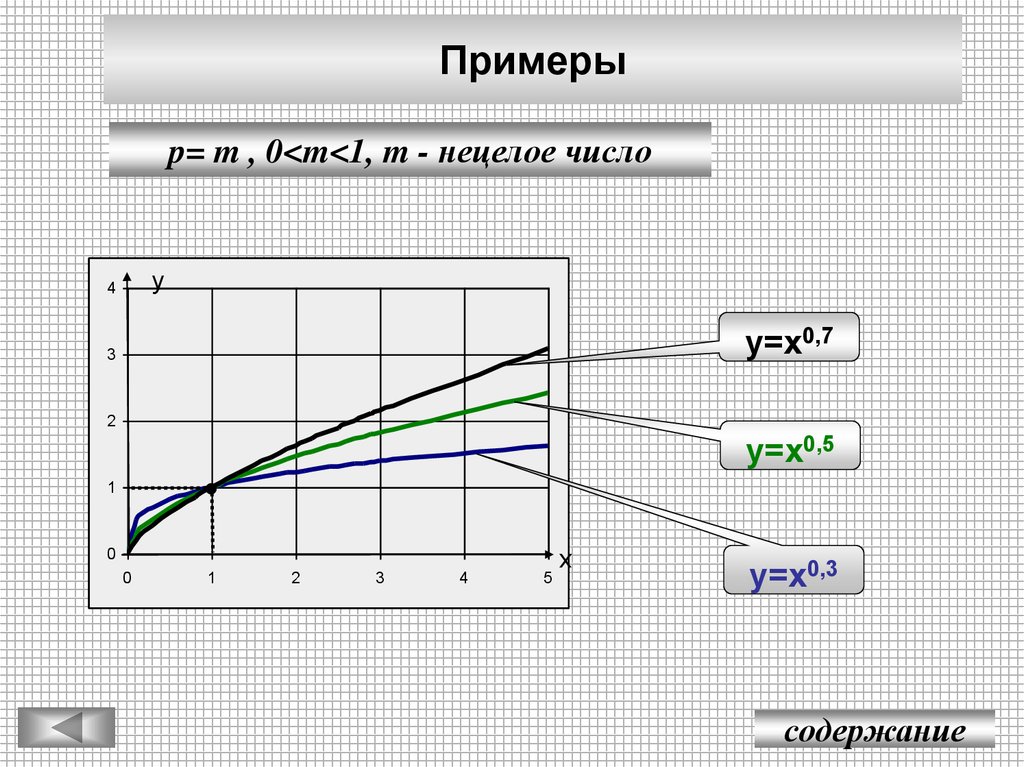
11.

Примеры
p= m , 0<m<1, m - нецелое число
у
4
у=х0,7
3
2
у=х0,5
1
0
0
1
2
3
4
5
х
у=х0,3
содержание

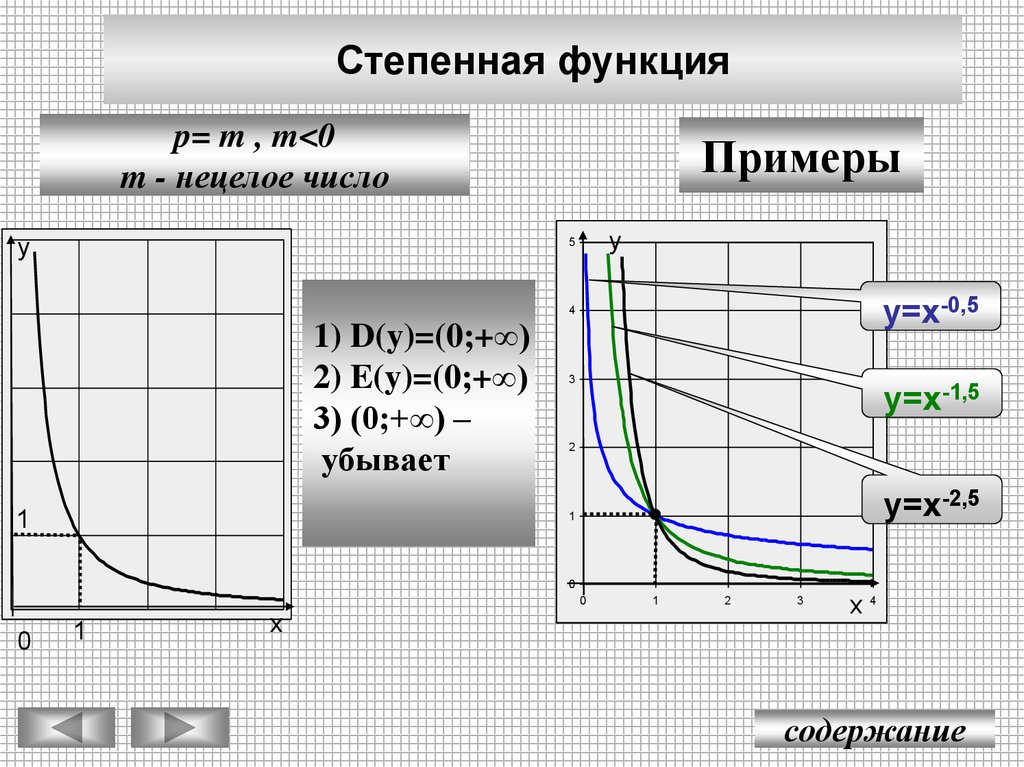
12.

Степенная функция
p= m , m<0
m - нецелое число
у
Примеры
у
5
у=х-0,5
4
1) D(y)=(0;+∞)
2) E(y)=(0;+∞)
3) (0;+∞) –
убывает
3
у=х-1,5
2
у=х-2,5
1
1
0
0
0
1
х
1
2
3
х4
содержание