Компьютерные модели

1.

2.

«Если
человеку каждый раз,
столкнувшись с очередной
жизненной задачей, приходилось
бы с нуля решать ее, то едва ли
прогресс человечества достиг бы
сегодняшних высот.
Разумеется, каждый человек и
общество в целом опирается на
опыт предшествующих поколений»

3.

Эта
цитата из учебника
«Информатика 10 - 11» авторов
А. Г. Гейн, А. И. Сенокосов,
Н. А. Юнерман является главной
отправной точкой представляемой
здесь работы
Цель этой работы — рассказать как,
используя материалы учебника,
мы выстраиваем единую линию в
изучении темы
«Компьютерные модели» в 6 классе
МБОУ — лицей №4 г. Краснодар

4.

Заметим,
что в первой четверти
учащиеся знакомились с
электронными таблицами
Во второй четверти изучался
теоретический материал по теме
« Моделирование»
На тему «Компьютерные модели»
отводится 8 часов в течение
третьей учебной четверти.

5.

Учащиеся
понимают значения терминов
модель и моделирование
Могут рассказать о видах моделей
и
привести примеры
Знают этапы решения задач
с
применением компьютера
Знакомы с понятием
«адекватность
модели»

6.

В
процессе изучения темы
«Компьютерные модели»
ученики
выполняют практические работы,
логическим завершением которых
являются задача о разумном подходе к
потреблению природных ресурсов
Решая задачу «Прирост массы
растений»,дети постепенно
уточняют и совершенствуют модели,
последовательно переходя от одной
модели к другой

7. «Прирост массы растений»

Модель
неограниченного
роста
Модель
ограниченного
роста
Модель
потребления
возобновляемых
ресурсов

8.

Вспомогательная задача:
«Рост числа фазанов»

9. Сформулируем задачу

–В 1937 г. на остров Протекшн завезли 8
фазанов.
–Никто на этих фазанов не охотился (ни
люди, ни звери), корма и воды было
вдоволь, и через год фазанов стало 26, а
ещё через год их было 83
–Сколько будет фазанов через заданное
число лет?

10. I Постановка задачи

Выделим существенные факторы
Окружающая среда выступает как регулятор
прироста количества фазанов. Факторов,
влияющих на жизнь фазанов много и все их
учесть в принципе невозможно.
Поэтому условимся рассматривать
воздействие окружающей среды на
численность популяции фазанов как
черный ящик

11.

Вход
Численность
фазанов
на начало года
Выход
Число
фазанов по
прошествии
года

12.

Естественно также предположить,
что прирост числа фазанов через год
пропорционален уже имеющемуся
количеству особей.
Таким образом, мы выделяем два
существенных фактора:
Начальное количество особей — М0
Коэффициент прироста за 1 год — К

13. I I Создание математической модели

Число фазанов по истечению n лет
обозначим Mn , тогда прирост за
один год составит
Mn+1 — Mn или К* Mn
Установим связь между параметрами
модели:
Mn +1 = Mn *(К+1)
Построенную модель называют
моделью неограниченного роста

14.

Проверим, является ли эта модель адекватной?
Напомним, что модель адекватна
рассматриваемому объекту (про цессу или
явлению), если при решении задачи она дает
удовлетворительные результаты.
Используя исходные данные задачи, вычислим
значение коэффициента прироста К=(268)/8=2,25
Найдем число фазанов по истечении первого и
второго года
При n=0 М1=8*(2,25+1)=26
При n=1 М2=26*(2,25+1)=84,5
Полученный результат можно признать
удовлетворительным.

15. I I I Компьютерная модель

За д а ча : Рост числ а ф а за нов
М од е л ь не ог ра ниче нног о роста
Год
0
1
2
3
4
5
К оэф ф иц ие нт прироста
Н а ча л ьное числ о ф а за нов
Числ о ф а за нов че ре з г од
Числ о ф а за нов че ре з д ва г од а
2 ,2 5
8
26
84
273
887
2 882

16. Сделаем выводы

Мы построили
модель неограниченного роста.
Легко заметить, что численность особей
растет в геометрической прогрессии, с
учетом исходного предположения о том, что
действие окружающей среды сказывается
только на скорости прироста фазанов.
Нетрудно предположить, что применить эту
модель можно для любых живых организмов.

17.

Прирост массы растений
Модель неограниченного
роста

18. Cформулируем задачу

Используя
модель неограниченного роста,
проследить за изменением массы
растений в двух климатических
зонах: тундре и тайге

19. I Постановка задачи

Очевидно, что масса растений на
различных территориях будет
увеличиваться с разной скоростью.
Будем использовать значения
коэффициента размножения,
экспериментально полученные
учеными — биологами для растений в
различных природных зонах.

20.

Пусть начальная масса растений на
некотором участке в каждой из
климатических зон равнялась 1 тонне,
а значение коэффициента прироста для
тундры и тайги составляет
0,6 и 1,8 соответственно.
Напомним два существенных фактора для
решения задачи:
Начальная масса растений — М0
Коэффициент прироста за 1 год — К

21. I I Математическая модель

Будем использовать уже знакомую нам
модель неограниченного роста
Mn+1 = Mn *(К+1)

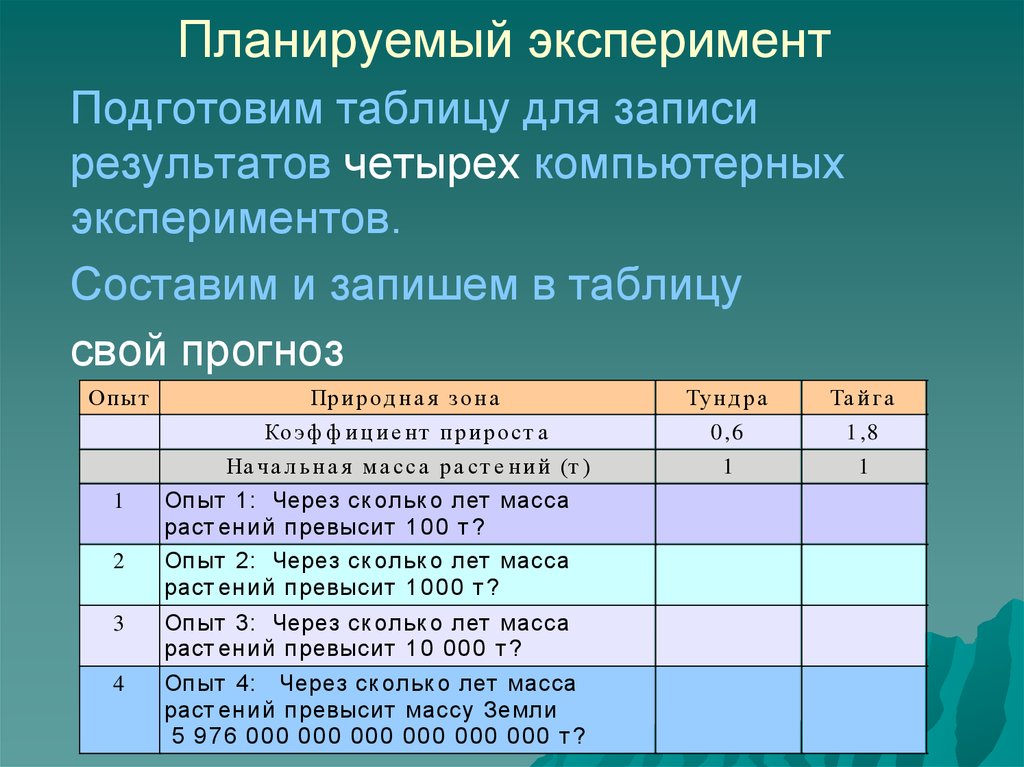
22. Планируемый эксперимент

Подготовим таблицу для записи
результатов четырех компьютерных
экспериментов.
Составим и запишем в таблицу
свой прогноз
Оп ыт
Пр и р о д н а я з о н а
Ту н д р а
Та й г а
Ко э ф ф и ц и е нт п р и р о ст а
0 ,6
1 ,8
На ч а л ь н а я м а с с а р а ст е н и й (т )
1
1
1
Оп ыт 1: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 т ?
2
Оп ыт 2: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 0 т ?
3
Оп ыт 3: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 0 0 т ?
4
Оп ыт 4: Через ск ольк о лет масса
раст ен и й п ревысит массу Земли
5 976 000 000 000 000 000 000 т ?

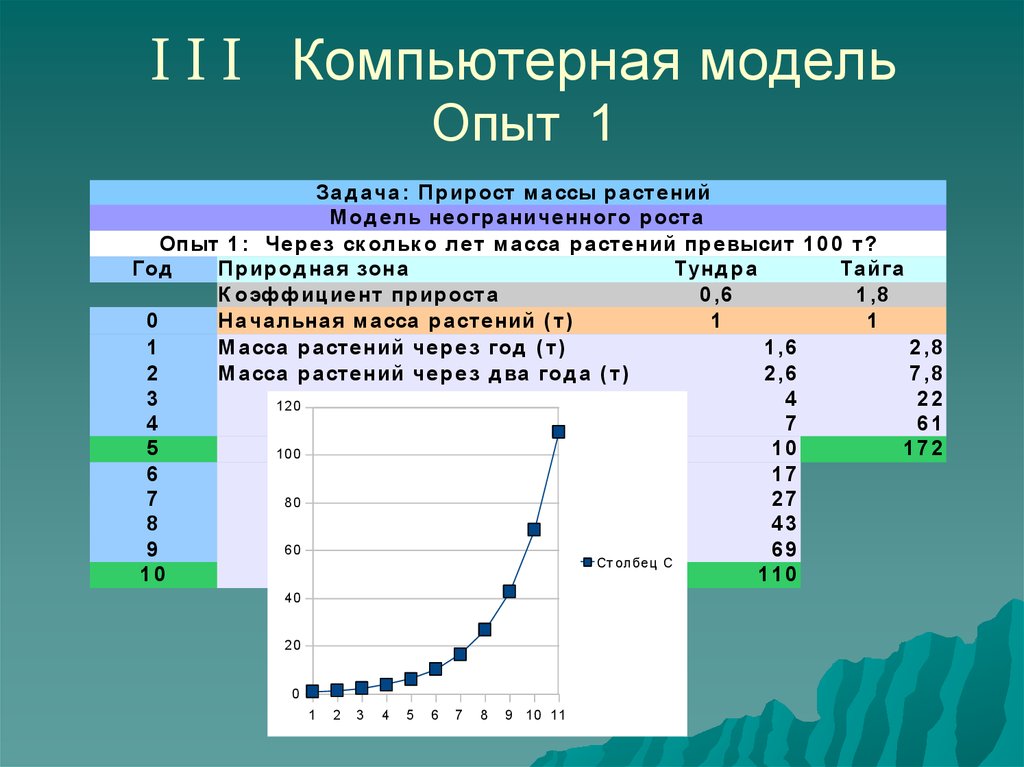
23. I I I Компьютерная модель Опыт 1

З а д а ча : П р ир ост ма ссы р а сте ний
М од е ль не ог р а ниче нног о р оста
Опыт 1 : Че р е з ск ольк о ле т ма сса р а сте ний пр е высит 1 0 0 т?
Год
П р ир од на я зона
Тунд р а
Та йг а
К оэф ф иц ие нт пр ир оста
0 ,6
1 ,8
0
Н а ча льна я ма сса р а сте ний ( т)
1
1
1
М а сса р а сте ний че р е з г од ( т)
1 ,6
2 ,8
2
М а сса р а сте ний че р е з д ва г од а ( т)
2 ,6
7 ,8
3
4
22
120
4
7
61
5
10
172
100
6
17
7
27
80
8
43
60
9
69
Ст о лбе ц C
10
110
40
20
0
1
2
3
4
5
6
7
8
9 10 11

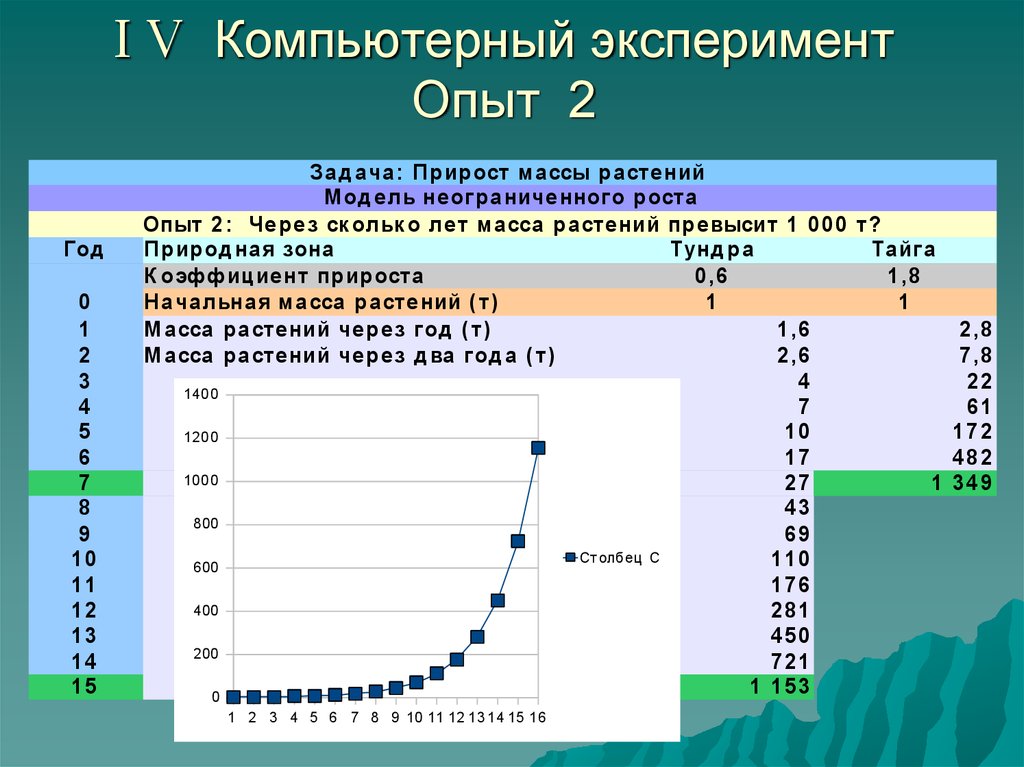
24. I V Компьютерный эксперимент Опыт 2

Год
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
З а д а ча : П р ир ост ма ссы р а сте ний
М од е ль не ог р а ниче нног о р оста
Опыт 2 : Че р е з ск ольк о ле т ма сса р а сте ний пр е высит 1 0 0 0 т?
П р ир од на я зона
Тунд р а
Та йг а
К оэф ф иц ие нт пр ир оста
0 ,6
1 ,8
Н а ча льна я ма сса р а сте ний ( т)
1
1
М а сса р а сте ний че р е з г од ( т)
1 ,6
М а сса р а сте ний че р е з д ва г од а ( т)
2 ,6
4
140 0
7
10
120 0
17
100 0
27
1
43
800
69
Ст олб ец C
110
600
176
400
281
450
200
721
1 153
0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2 ,8
7 ,8
22
61
172
482
349

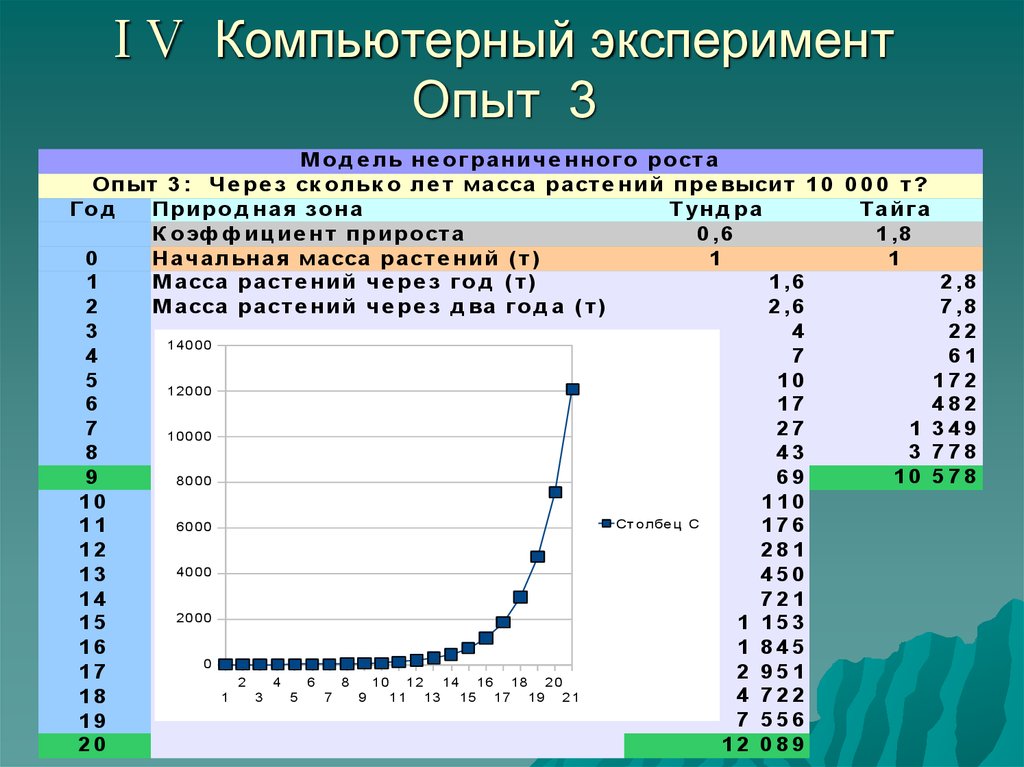
25. I V Компьютерный эксперимент Опыт 3

М о д е ль н е о г р а н и ч е н н о г о р о ст а
Оп ыт 3 : Ч е р е з ск о льк о ле т ма сса р а ст е н и й п р е выси т 1 0 0 0 0 т ?
Го д
Природ ная зона
Тунд ра
Тайга
К о эф ф и ц и е н т п р и р о ст а
0 ,6
1 ,8
0
Н а ч а льн а я ма сса р а ст е н и й ( т )
1
1
1
М а сса р а ст е н и й ч е р е з г о д ( т )
1 ,6
2 ,8
2
М а сса р а ст е н и й ч е р е з д ва г о д а ( т )
2 ,6
7 ,8
3
4
22
14000
4
7
61
5
10
172
12000
6
17
482
7
27
1 349
10000
3 778
8
43
10 578
9
69
8000
10
110
Ст
олбец
C
6000
11
176
12
281
4000
13
450
14
721
2000
15
1 153
16
1 845
0
17
2 951
2
4
6
8
10 12 14 16 18 20
1
3
5
7
9
11 13 15 17 19 21
4 722
18
7 556
19
20
12 089

26. I V Компьютерный эксперимент Опыт 4

22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
1
2
3
6
10
16
1
2
3
5
8
13
22
35
57
91
146
233
374
598
957
532
451
923
277
043
069
30
49
79
126
202
324
519
830
329
126
402
444
711
937
300
681
089
343
150
840
144
631
809
495
992
188
101
362
380
949
518
228
765
824
519
230
767
228
765
824
518
229
966
745
192
908
852
164
262
419
071
713
541
865
585
735
777
443
2
6
16
47
132
370
1 038
2 907
8 142
1
4
12
35
98
274
769
155
034
896
310
468
910
550
940
233
1
3
9
25
72
203
570
597
472
522
062
175
892
699
158
444
445
046
131
768
150
421
181
6
19
53
150
422
183
314
280
986
761
730
446
250
301
444
845
967
709
587
844
764
340
952
465
104
693
940
433
878
259
925
990
774
768
552
746
090
052
946
650
620
738
868
630
765
744
283
393
301
045
127
956
675
090
650
830
229
043
322
903
529
682
311
471
120
338
546
331
928
599
079
621
740
074
407
540
910
300
000
000
000
000
000
000
929
800
641
395
506
616
325
711
791
214
998
595
470
710
200
700
700
000
000
000
000
000
000
000
000
000
000
000

27.

Занесем результаты компьютерного
эксперимента в таблицу, сравним с
прогнозом
Проанализируем и сделаем выводы
Оп ыт
Пр и р о д н а я з о н а
Ту н д р а
Та й г а
Ко э ф ф и ц и е нт п р и р о ст а
0 ,6
1 ,8
На ч а л ь н а я м а с с а р а ст е н и й (т )
1
1
1
Оп ыт 1: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 т ?
1 0 л ет
5 л ет
2
Оп ыт 2: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 0 т ?
1 5 л ет
7 л ет
3
Оп ыт 3: Через ск ольк о лет масса
раст ен и й п ревысит 1 0 0 0 0 т ?
2 0 л ет
9 л ет
4
Оп ыт 4: Через ск ольк о лет масса
раст ен и й п ревысит массу Земли
5 976 000 000 000 000 000 000 т ?
1 0 7 л ет
4 9 л ет

28.

В течение жизни одного поколения вся
планета превратится в «зеленое море»
растений! Есть над чем призадуматься...
Налицо нарушение фундаментального
закона природы — закона сохранения
массы. Видно не все удачно в построенной
нами модели.
Принцип адекватности говорит еще и о том,
что никакая модель не эквивалентна
реальному объекту (процессу или явлению).

29.

Модель неограниченного роста хорошо
согласуется с практикой, пока масса
живых организмов остается достаточно
малой.
В некоторых случаях это условие может
выполняться годами и экспериментально
опровергнуть такую модель бывает
довольно трудно.

30.

Продолжим работу над
совершенствованием
модели

31.

Прирост массы растений
Модель ограниченного роста

32.

Почему же, однажды родившись,
модели не живут вечно?
Некоторые из них исчезают, едва
появившись на свет.
Другие живут столетиями.
Но даже модели, построенные
лучшими умами человечества,
все равно сменяются другими.
Что управляет этой сложной жизнью
моделей?

33.

Прежде всего: растут знания человека
человека об окружающем мире, вот и
меняются модели.
И второе: смена модели может
происходить и в силу того, что она не
согласуется с более общими законами,
открытыми человеком при исследовании
природы и общества.

34.

Конечно, ни при каких, даже самых благоприятных,
условиях масса растений не может превысить
массу планеты.
Выдвинем предположение, что имеется екоторое
предельное значение массы растений,
«проживающих» на той или иной территории.
Так, ученые показали, что запас массы растений
не может превосходить 20 т на гектар в полярной
зоне и 350 т на гектар в лесной зоне.
Это означает, что рост растений ограничен.

35.

И еще одно предположение: чем ближе масса
растений к предельно допустимой, тем меньшим
становится коэффициент прироста К, так как
сначала растения быстро набирают массу, а затем
их рост замедляется.
Совершенствуя модель, ученые — биологи
предложили использовать новую величину —
коэффициент пропорциональности А

36. Cформулируем задачу

Используя модель
ограниченного роста, проследить за
изменением массы растений в двух
климатических зонах:
тундре и тайге.

37. I Постановка задачи

Существенных факторы:
Начальная масса растений — М0
Коэффициент прироста за 1 год — Кn
Предельное значение массы живых
организмов — L
Коэффициент пропорциональности — А

38. I I Математическая модель

Зададим связи между параметрами модели:
Коэффициент прироста будет меняться по
формуле
Кn=А*( L - Mn),
где коэффициент пропорциональности
находится из соотношения
А= К/( L - M0).
Поэтому формула примет вид
Mn+1 = Mn + Mn *А*( L - Mn ).
Эту модель принято называть
моделью ограниченного роста.

39. Планируемый эксперимент

Подготовим таблицу для записи
результатов трех компьютерных
экспериментов
Оп ы т
Пр и р о д н а я з о н а
Не о гр а н и ч е н н ы й р о с т
Ту н д р а
Та й га
1
Опыт 1 :
Че р е з ск ольк о ле т ма сса
ра сте ний пр е высит 1 0 0 т?
10 ле т
5 ле т
2
Опыт 2 :
Че р е з ск ольк о ле т ма сса
ра сте ний пр е высит 1 0 0 0 т?
15 ле т
7 ле т
3
Опыт 3 :
Че р е з ск ольк о ле т ма сса
ра сте ний пр е высит 1 0 0 0 0
т?
20 ле т
9 ле т
Огр а н и ч е н н ы й
р о ст
Ту н д р а
Та й га

40.

Сравним новые результаты,
полученные при испытании
модели ограниченного роста
с результатами аналогичных опытов,
полученных при работе
с моделью неограниченного роста

41. I I I Компьютерная модель Опыт 3

Год
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Зад ача: Прирост массы расте ний
М од е л ь ограниче нного роста
Опыт 3 : Ч е ре з ск ол ьк о л е т масса расте ний пре высит 1 0 0 0 0 т?
Еж е год ное уме ньш е ние
Природ ная зона
Тунд ра
Тайга
к оэф ф иц ие нта прироста К К оэф ф иц ие нт прироста
К
0 ,6
1 ,8
Тунд ра
Тайга
К оэф ф иц ие нт пропорц ионал ьности А 0 ,0 0 0 0 5 5 0 ,0 0 0 1 6 4
Пре д е л ьное значе ние массы L (т)
11 000
11 000
0 ,6 0 0 0 0
1 ,8 0 0 0 0
Начал ьная масса расте ний (т)
1
1
0 ,5 9 9 9 7
1 ,7 9 9 7 1
М асса расте ний че ре з год (т)
1 ,6
2 ,8
0 ,5 9 9 9 1
1 ,7 9 8 8 8
М асса расте ний че ре з д ва год а (т)
2 ,6
7 ,8
0 ,5 9 9 8 3
1 ,7 9 6 5 7
4
22
0 ,5 9 9 7 0
1 ,7 9 0 1 2
7
61
0 ,5 9 9 4 8
1 ,7 7 2 1 5
10
171
0 ,5 9 9 1 4
1 ,7 2 2 5 0
17
475
0 ,5 9 8 5 9
1 ,5 8 8 7 1
27
1 2 9 2 ,1
0 ,5 9 7 7 2
1 ,2 5 2 7 8
43
3 3 4 4 ,8
120 00
0 ,5 9 6 3 2
0 ,5 6 7 0 3
68
7 5 3 5 ,1
0 ,5 9 4 0 9
109
11 808
100 00
0 ,5 9 0 5 5
174
0 ,5 8 4 9 4
277
800 0
0 ,5 7 6 0 9
439
0 ,5 6 2 2 9
692
600 0
0 ,5 4 1 0 5
1
0
82
Ст олб ец E
0 ,5 0 9 1 3
1 667
400 0
0 ,4 6 2 8 3
2 515
0 ,3 9 9 3 2
3 680
200 0
0 ,3 1 9 1 7
5 149
0 ,2 2 9 5 2
6 793
0
0 ,1 4 4 4 7
2
4
6
8 10 12 14 16 18 20 22 24
8 352
1
3
5
7
9 11 13 15 17 19 21 23
0 ,0 7 8 6 5
9 558
0 ,0 3 7 6 4
10 310

42. Неограниченный рост (для сравнения)‏

Неограниченный рост
(для сравнения)
М о д е ль н е о г р а н и ч е н н о г о р о ст а
Оп ыт 3 : Ч е р е з ск о льк о ле т ма сса р а ст е н и й п р е выси т 1 0 0 0 0 т ?
Го д
Природ ная зона
Тунд ра
Тайга
К о эф ф и ц и е н т п р и р о ст а
0 ,6
1 ,8
0
Н а ч а льн а я ма сса р а ст е н и й ( т )
1
1
1
М а сса р а ст е н и й ч е р е з г о д ( т )
1 ,6
2 ,8
2
М а сса р а ст е н и й ч е р е з д ва г о д а ( т )
2 ,6
7 ,8
3
4
22
14000
4
7
61
5
10
172
12000
6
17
482
7
27
1 349
10000
3 778
8
43
10 578
9
69
8000
10
110
Ст олбец C
6000
11
176
12
281
4000
13
450
14
721
2000
15
1 153
16
1 845
0
17
2 951
2
4
6
8
10 12 14 16 18 20
1
3
5
7
9
11 13 15 17 19 21
4 722
18
7 556
19
20
12 089

43. I V Компьютерный эксперимент

Проанализируем результаты и сделаем
выводы
Оп ы т
Пр и р о д н а я з о н а
Не о гр а н и ч е н н ы й
р о ст
Огр а н и ч е н н ы й
р о ст
Ту н д р а
Та й га
Ту н д р а
Та й га
1
Оп ыт 1 :
Ч е р е з ск ол ьк о л е т
ма сса ра ст е н ий
п р е высит 1 0 0 т ?
10 ле т
5 ле т
10 ле т
5 ле т
2
Оп ыт 2 :
Ч е р е з ск ол ьк о л е т
ма сса ра ст е н ий
п р е высит 1 0 0 0 т ?
15 ле т
7 ле т
15 ле т
7 ле т
3
Оп ыт 3 :
Ч е р е з ск ол ьк о л е т
ма сса ра ст е н ий
п р е высит 1 0 0 0 0 т ?
20 ле т
9 ле т
2 3 го д а
10 ле т

44.

Так как для решения задачи применяется модель
ограниченного роста,
то наблюдается ежегодное
уменьшение коэффициента прироста,
что не может не сказаться на величине массы
растений.
Результаты первых двух опытов при относительно
малых массах растений совпадают.
Результаты третьего эксперимента говорят о том,
что наряду с увеличением массы растений стало
наблюдаться
замедление их роста.

45.

Задачи управления

46. Модель потребления возобновляемых ресурсов

Сколько
можно
брать у
природы?
Модель потребления
возобновляемых ресурсов

47.

Человек, познавая природу и общество, все
активнее и шире вмешивается в действие
факторов, влияющих на функционирование этих
систем. Влияние это, чаще сознательное,
преследует цель — заставить систему
функционировать нужным человеку образом, то
есть управлять системой
Рассмотрим проблему добычи леса.
Лес относится к так называемым возобновляемым
ресурсам. Возникает задача управления: сколько
леса можно рубить ежегодно, чтобы обеспечить
его нормальное воспроизводство?

48.

За основу для решения задачи возьмем уже
знакомую нам модель ограниченного роста.
Отметим, что появился еще один существенный
фактор — воздействие человека.
Будем считать, что объем вырубаемого леса в
течение года не меняется, поэтому формула
изменится незначительно:
Mn+1 = Mn + Mn *А*( L - Mn ) - R,
где R — это объем вырубки.
Такую модель называют моделью потребления
возобновляемых ресурсов

49. Cформулируем задачу

Используя модель потребления
возобновляемых ресурсов,
найти оптимальный объем вырубки,
при котором будет обеспечено его
нормальное воспроизводство.

50. I Постановка задачи

Решать задачу будем только для одной
климатической зоны — тайга
Существенных факторы:
Начальная масса растений — М0
Коэффициент прироста за 1 год — Кn
Предельное значение массы живых
организмов — L
Коэффициент пропорциональности — А
Объем вырубки — R

51. I I Математическая модель

Удобно рассмотреть еще одну величину:
ежегодный прирост — Р
Зададим связи между параметрами модели:
Mn+1 = Mn + Mn *А*( L - Mn ) - R,
Коэффициент прироста будет меняться
по формуле
Кn=А*( L - Mn ),
где коэффициент пропорциональности
находится из соотношения
А= К/( L - M0)
Ежегодный прирост рассчитывается
по формуле Р= Mn *А*( L - Mn )

52. Планируемый эксперимент

Подготовим таблицу для записи результатов
четырех компьютерных экспериментов.
Построим графики изменения массы
древесины.
Оп ы т
Пр и р о д н а я з о н а
1
Оп ыт 1:
Объем еж ег одн ой вырубк и древеси н ы 1 000 т
2
Оп ыт 2:
Объем еж ег одн ой вырубк и древеси н ы 3 000 т
3
Оп ыт 3:
Объем еж ег одн ой вырубк и древеси н ы 5 000 т
4
Оп ыт 4: Найт и опт имальн ый объем еж ег одн ой вырубк и
леса, п ри к от ором будет сох ран ят ься ег о н ормальн ое
восп рои звод ст во
Та й га

53. I I I Компьютерная модель Опыт 1

З а д а ч а : Ск ол ьк о м ож но бр а ть у пр ир од ы?
М од е л ь потр е бл е ния возобновл яе м ых р е сур сов
Год
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Опыт 1 :
Объе м е ж е г од ной выр убк и д р е ве сины 1 0 0 0 т
У м е ньш е ние Еж е г од ный П р ир од на я зона
Та йг а
к оэф ф иц ие нта
пр ир ост К оэф ф иц ие нт пр ир оста
К
1 ,8
пр ир оста К
м а ссы Р К оэф ф иц ие нт пр опор ц иона л ьности А
0 ,0 0 0 1 6 4
Та йг а
Та йг а
Объе м е ж е г од ной выр убк и д р е ве сины R ( т) 1 0 0 0
П р е д е л ьное зна ч е ние м а ссы L ( т)
11 000
0 ,1 6 3 6 5
Н а ч а л ьна я м а сса р а сте ний ( т)
10 000
0 ,0 5 9 4 9
1 637
М а сса р а сте ний ч е р е з г од ( т)
10 637
0 ,1 1 9 5 9
633
М а сса р а сте ний ч е р е з д ва г од а ( т)
10 269
0 ,0 8 2 2 6
1 228
10 497
0 ,1 0 4 6 0
864
10 361
10 800
0 ,0 9 0 9 0
1 084
10 445
0 ,0 9 9 1 8
949
10 394
10 600
0 ,0 9 4 1 3
1 031
10 425
0 ,0 9 7 1 9
981
10 406
0 ,0 9 5 3 3
1 011
10 418
10 400
0 ,0 9 6 4 6
993
10 411
0 ,0 9 5 7 7
1 004
10 415
Ст
о
лбе
ц
E
10 200
0 ,0 9 6 1 9
997
10 412
0 ,0 9 5 9 4
1 002
10 414
0 ,0 9 6 0 9
999
10 413
10 000
0 ,0 9 6 0 0
1 001
10 413
0 ,0 9 6 0 5
1 000
10 413
0 ,0 9 6 0 2
1 000
9 800
10 413

54. I V Компьютерный эксперимент Опыт 2

Год
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
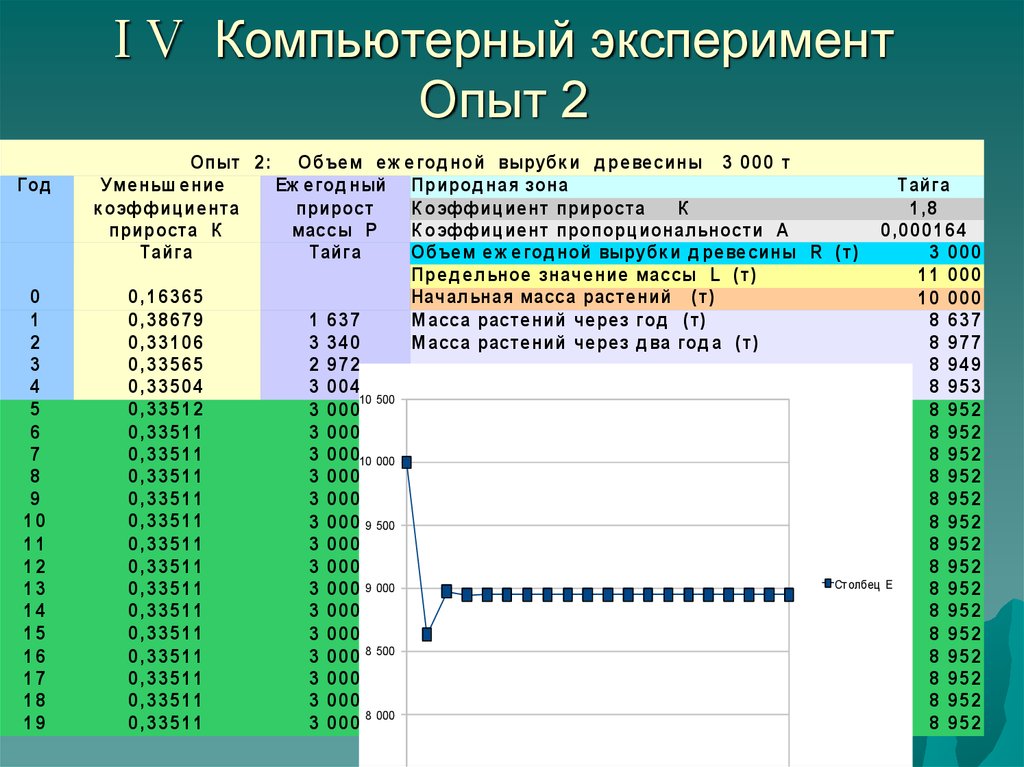
Опыт 2 : Объе м е ж е год ной вырубк и д ре ве сины 3 0 0 0 т
У ме ньш е ние
Еж е год ный Природ ная зона
Тайга
к оэф ф иц ие нта
прирост
К оэф ф иц ие нт прироста
К
1 ,8
прироста К
массы Р
К оэф ф иц ие нт пропорц ионал ьности А
0 ,0 0 0 1 6 4
Тайга
Тайга
Объе м е ж е год ной вырубк и д ре ве сины R (т)
3 000
Пре д е л ьное значе ние массы L (т)
11 000
0 ,1 6 3 6 5
Начал ьная масса расте ний (т)
10 000
0 ,3 8 6 7 9
1 637
М асса расте ний че ре з год (т)
8 637
0 ,3 3 1 0 6
3 340
М асса расте ний че ре з д ва год а (т)
8 977
0 ,3 3 5 6 5
2 972
8 949
0 ,3 3 5 0 4
3 004
8 953
10 500
0 ,3 3 5 1 2
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 0 0 010 000
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 0 0 0 9 500
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
Ст
олбец
E
0 ,3 3 5 1 1
3 0 0 0 9 000
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
8 500
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
0 ,3 3 5 1 1
3 000
8 952
8 000
0 ,3 3 5 1 1
3 000
8 952

55. Опыт 3

Зад ач а: Ск ол ьк о мож но брать у природ ы?
М од е л ь потре бл е ния возобновл яе мых ре сурсов
Год
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Опыт 3 :
Объе м е ж е год ной вырубк и д ре ве сины 5 0 0 0 т
У ме ньш е ние Еж е год ный Природ ная зона
к оэф ф иц ие нта
прирост
К оэф ф иц ие нт прироста
К
прироста К
массы Р К оэф ф иц ие нт пропорц ионал ьности А
Тайга
Тайга
Объе м е ж е год ной вырубк и д ре ве сины R ( т)
Пре д е л ьное знач е ние массы L ( т)
0 ,1 6 3 6 5
Нач ал ьная масса расте ний ( т)
0 ,7 1 4 0 9
1 637
М асса расте ний ч е ре з год ( т)
0 ,7 5 6 7 9
4 739
М асса расте ний ч е ре з д ва год а ( т)
0 ,7 8 5 4 3
4 825
0 ,8 0 6 6 9
4 870
0 ,8 2 3 5 2
4 897
12 000
0 ,8 3 7 4 9
4 915
0 ,8 4 9 5 2
4 927
0 ,8 6 0 1 8
4 935
10 000
0 ,8 6 9 8 8
4 941
0 ,8 7 8 9 0
4 945
8 000
0 ,8 8 7 4 6
4 948
0 ,8 9 5 7 3
4 949
0 ,9 0 3 8 6
4 950
6 000
0 ,9 1 1 9 8
4 950
0 ,9 2 0 2 3
4 950
0 ,9 2 8 7 5
4 948
4 000
0 ,9 3 7 6 8
4 945
0 ,9 4 7 2 0
4 942
2 000
0 ,9 5 7 5 3
4 937
0 ,9 6 8 9 4
4 930
0 ,9 8 1 7 9
4 921
0
0 ,9 9 6 5 7
4 910
1 ,0 1 3 9 9
4 894
-2 000
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
Тайга
1 ,8
0 ,0 0 0 1 6 4
5 000
11 000
10 000
6 637
6 376
6 201
6 071
5 968
5 882
5 809
5 744
5 685
5 629
5 577
5 527
5 477
5 427
5 377
Ст олбец E
5 325
5 270
5 212
5 149
5 079
5 001
4 910
4 804

56. Опыт 4

Зад ача: Ск ольк о мож но брать у природ ы?
М од е ль потре бле ния возобновляе мых ре сурсов
О пыт 4: На йти о птима льный о бъе м е ж е го д но й выр убк и ле са , пр и к о то р о м буд е т со хр а няться е го но р ма льно е во спр о изво д ство
Год
У ме ньш е ние
к оэф ф иц ие нта
прироста К
Тайга
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0 ,1 6 3 6 5
0 ,1 6 3 7 3
0 ,1 6 3 6 9
0 ,1 6 3 7 1
0 ,1 6 3 7 0
0 ,1 6 3 7 1
0 ,1 6 3 7 0
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
0 ,1 6 3 7 1
Еж е год ный
прирост
массы Р
Тайга
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
637
637
637
637
637
637
637
637
637
637
637
637
637
637
637
637
Природ ная зона
К оэф ф иц ие нт прироста
К
К оэф ф иц ие нт пропорц иональности А
Объе м е ж е год ной вырубк и д ре ве сины R (т)
Пре д е льное значе ние массы L (т)
Начальная масса расте ний (т)
М асса расте ний че ре з год (т)
М асса расте ний че ре з д ва год а (т)
Тайга
1 ,8
0 ,0 0 0 1 6 4
1 637
11 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
Ст о лб е ц E
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
10 000
9 999
9 999
9 999
1
2
3
4
5
6
7 8
9 10 11 12 13 14 15 16 17

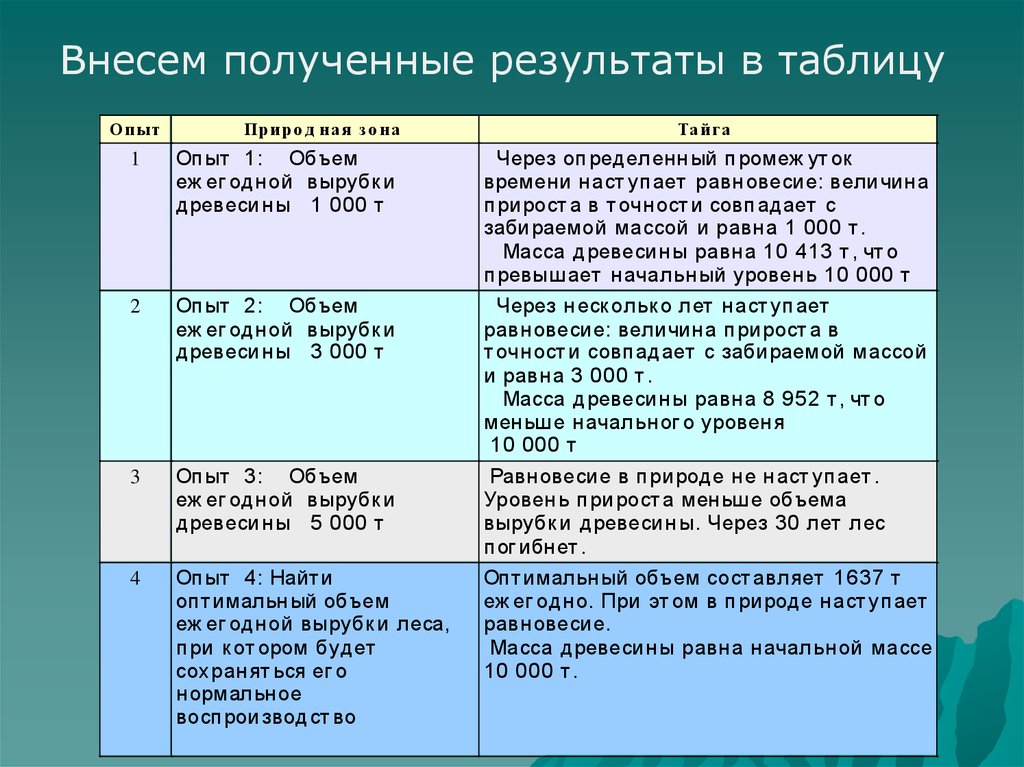
57.

Внесем полученные результаты в таблицу
Оп ыт
Пр и р о д н а я з о н а
Та й г а
1
Оп ыт 1: Объем
еж ег од н ой вырубк и
д ревеси н ы 1 000 т
Через оп ред ел енн ый п ром еж ут ок
врем ени н аст уп ает равн овеси е: вели чин а
п ри рост а в т очн ост и совп ад ает с
заби раем ой м ассой и равн а 1 000 т .
Масса д ревеси н ы равн а 10 413 т , чт о
п ревыш ает н ачал ьн ый уровен ь 10 000 т
2
Оп ыт 2: Объем
еж ег од н ой вырубк и
д ревеси н ы 3 000 т
Через н еск ол ьк о л ет н аст уп ает
равн овеси е: вели чин а п ри рост а в
т очн ост и совп ад ает с заби раем ой м ассой
и равн а 3 000 т .
Масса д ревеси н ы равн а 8 952 т , чт о
м ен ьш е н ачал ьн ог о уровен я
10 000 т
3
Оп ыт 3: Объем
еж ег од н ой вырубк и
д ревеси н ы 5 000 т
Равн овеси е в п ри род е н е н аст уп ает .
Уровен ь п ри рост а м ен ьш е объем а
вырубк и д ревеси н ы. Через 30 л ет л ес
п ог ибн ет .
4
Оп ыт 4: Найт и
опт им ал ьн ый объем
еж ег од н ой вырубк и л еса,
п ри к от ором буд ет
сох ран ят ься ег о
н орм ал ьн ое
восп рои звод ст во
Опт им ал ьн ый объем сост авл яет 1637 т
еж ег од н о. При эт ом в п ри род е н аст уп ает
равн овеси е.
Масса д ревеси н ы равн а н ачал ьн ой м ассе
10 000 т .

58. Проанализируем полученные результаты и сделаем выводы

Для того чтобы, ресурсы возобновлялись
уровень запасов древесины оставался
равным начальному, можно производить
ежегодную вырубку леса в объемах,
не превышающих 1 640 тонн

59. Успехов !

60. Примечание

Список
литературы:
«Информатика 10 - 11» авторы:
А. Г. Гейн, А. И. Сенокосов,
Н. А. Юнерман
Все
фотографии, использованные в
презентации, являются авторскими