Похожие презентации:
Неединичные обратные связи и инвариантность системы к задающему воздействию
1.
Министерство образования и науки Российской Федерациифедеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ВОЕНМЕХ» им. Д.Ф. УСТИНОВА
Кафедра Н1
Мехатроника и робототехника
К.т.н., доцент Савельев Б.Н.
Иллюстративный материал
(конспекта лекций)
Часть третья
Санкт – Петербург
2013 г.
2.
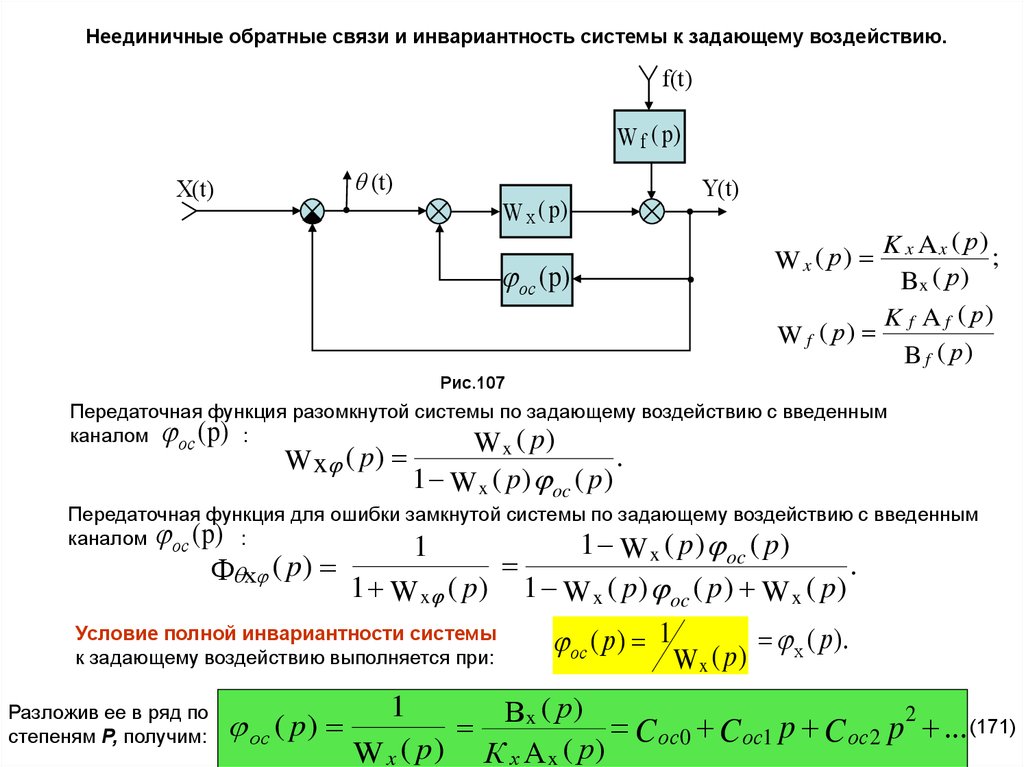
Неединичные обратные связи и инвариантность системы к задающему воздействию.f(t)
W f ( p)
Х(t)
(t)
Y(t)
W x ( p)
K x A x ( р) ;
(
р
)
Wx
Bx ( р )
K f A f ( р)
(
р
)
Wf
B f ( р)
ос (p)
Рис.107
Передаточная функция разомкнутой системы по задающему воздействию с введенным
каналом ос ( p) :
W x ( p)
W x ( p )
1 W x ( p ) oc ( p )
.
Передаточная функция для ошибки замкнутой системы по задающему воздействию с введенным
каналом ос ( p) :
1 W x ( p ) oc ( p )
1
.
Ф х ( p)
1 W x ( p ) 1 W x ( p ) oc ( p ) W x ( p )
Условие полной инвариантности системы
к задающему воздействию выполняется при:
Разложив ее в ряд по
степеням Р, получим:
ос ( р) 1
W x ( p)
х ( р).
1
( р)
ос ( p )
Вx
C ос0 C ос1 p C ос 2 p 2 ... (171)
W x ( p) К х А x ( р)
3.
Коэффициенты ошибок САРЭтот метод оценки точности САР применим как для задающего, так и для возмущающего воздействий.
Если воздействие (управляющее х(t ) или возмущающее f (t ) ) изменяется в установившемся
процессе достаточно плавно и имеет конечное число производных, то ошибку системы можно
представить в виде ряда. Изображение по Лапласу ошибки САР по воздействию можно представить:
( s ) Ф ( s ) ( s ),
передаточная функция для ошибки САР по
Ф ( s) -воздействию
(t ) ;
(s ) - изображение по Лапласу воздействия (t )
(управляющего х(t ) или возмущающего f (t ) ).
Разложив передаточную функцию Ф ( s ) в ряд по степеням s , получим:
i
- ряд, сходящийся при малых s , т. е. в установившемся
( s ) ( 0 si ) ( s ), процессе
изменения y (t ) при заданном (t ) .
i 1 i!
где:
2
d (t )
(t )
d
d 2
....
уст (t ) ( 0 p ) (t ) d o d 1
2
dt
dt
i 1 i!
Переходя к оригиналу, получим:
Величины
i
i
i и называют коэффициентами ошибок системы по соответствующему воздействию.
Они могут быть найдены как коэффициенты разложения передаточной функции для ошибки САР
m
в ряд Тейлора при
0:
s
о [Ф ( s)]s o ,
d Ф ( s )
] s o .
m [
m
ds
Часто удобнее находить коэффициенты d i , которые можно получить в результате деления
полинома числителя на полином знаменателя передаточной функции для ошибки САР.
m
А ( s ) a o a 1 s .... a m s
2
s
Ф ( s )
d o d 1 d 2 s ....
n
b o b 1 s .... b n s
B ( s )
Для САР с астатизмом порядка к
Коэффициенты ошибок: о d o ; i d i i!
0
dФ ( s )
] s o , .....,
1 [
ds
о 1 .... (к 1)
4.
Связь коэффициентов ошибок с коэффициентами инвариантных входовКоэффициенты i инвариантных входов могут быть получены из коэффициентов ошибок САР
i или d i
сi
.
i!
Они и вводятся для исключения соответствующих составляющих ошибки,
представленной в форме ряда производных от воздействия.
Для управляющего воздействия
До введения комбинированного управления передаточная функция замкнутой САР по задающему
1
воздействию:
W
x (s)
1 Ф x ( s ) 1
1 d хi si
Ф x (s)
1 W x (s)
1 W x (s)
i o
При введении комбинированного управления передаточная функция замкнутой САР по
задающему воздействию: Ф x ( s ) [1
x ( s )]Ф x ( s ) [1 x ( s )](1 Ф x ( s )),
а передаточная функция для ошибки от задающего воздействия:
Ф x ( s) 1 Ф x ( s) 1 [1 x ( s)](1 Ф x ( s)) 1 [1 x ( s )](1 d xi si )
Условие инвариантности САР к воздействию
:
i 0
i
Ф
i
x (s ) 1 [1 x ( s )](1 d xi s ) 0
d xi s
i 0
1
2
i
0
, из которого:
x (s )
xo
x1
x2
(
s
)
i
W
x
1 d xi s
i 0
Для возмущающего воздействия
W f (s)
Передаточная функция САР для ошибки по f (t ) :
d fi si
Ф f ( s )
1 W x ( s ) i o
При введении комбинированного управления по возмущению:
f (s) W x (s) W f ( s )
i
f ( s )(1 d xi s ) d fi si
Ф f ( s )
1 W x ( s)
d fi si
i 0
i o
W f (s)
C fo C f 1 s C f 2 s2 C f 3 s3... i 0
Приравнивая ее 0, получим: f ( s )
W x (s)
1 d xi si
i 0
х(t )
C C s C s ...
5.
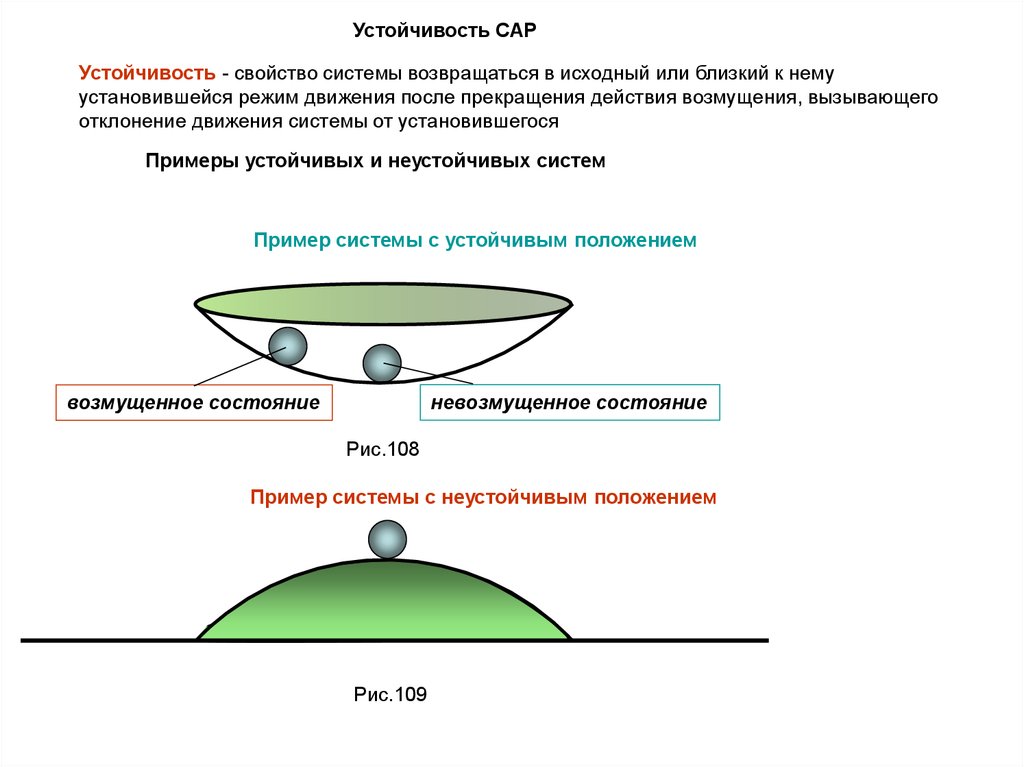
Устойчивость САРУстойчивость - свойство системы возвращаться в исходный или близкий к нему
установившейся режим движения после прекращения действия возмущения, вызывающего
отклонение движения системы от установившегося
Примеры устойчивых и неустойчивых систем
Пример системы с устойчивым положением
невозмущенное состояние
возмущенное состояние
Рис.108
Пример системы с неустойчивым положением
Рис.109
6.
Система с устойчивым движениемСистема с неустойчивым движением
Рис.110
Рис.111
7.
Определение устойчивости на случаи движения систем было введено А.М.Ляпуновым, поэтомутакое понятие называют устойчивостью по Ляпунову.
Систему уравнений, описывающих процессы в оригинале (его математическую модель) можно
представить в форме Каши:
i
(172)
i
d y (t )
F ( y1,....... y n, t ); (i 1,2,.....n) ,
dt
где: yi (t ) - переменные состояния; n- порядок системы;{ y (t ),.., y (t )} Y (t ) - вектор состояния.
1
n
Заданное движение системы характеризуется законом изменения координат y1o (t ),...., y no (t )
и называется невозмущенным движением системы.
Уравнение (172) можно переписать для отклонений
yi (t ) yi (t ) yio (t )
d yi (t )
f i ( y1,......, y n, t ); (i 1,2,.....n) ,
dt
(173)
Уравнения (173) называют уравнениями возмущенного движения, а начальные значения
отклонений yi 0 - возмущениями. При y 0 - невозмущенное движение системы.
i0
Невозмущенное движение системы называется устойчивым, если при всех возмущениях меньших
некоторого значения , отклонения переменных состояния | yi (t ) |будут меньше значений
при t . Обычно это условие записывается так: | y (t ) | при | y | и t .
i
i0
i
i
(
весовые
коэффициенты
для
выравнивания
размерностей
переменных).
i
(i 1,...., n), система называется асимптотически устойчивой.
Если lim yi (t ) 0
t
Графическая иллюстрация для системы второго порядка:
y2
y 20
y10 y
1
Рис.112 устойчивая
y2
y 20
y10 y
1
Рис.113 асимптотически устойчивая
y2
y 20
y10 y
1
Рис.114 неустойчивая
8.
Рассмотрим от чего зависит устойчивость линейной САРy x (t ) Ф x ( p) x(t ) y f (t ) Ф f ( p) f (t )
A f ( р)
A
x ( р)
(
р
)
.
; Фf
Ф x ( р)
B( р )
В( р )
- передаточные функции системы по
управляющему и возмущающему воздействиям
Раскрывая полиномы, получим уравнения движения САР в операторной форме
где:
n
n 1
m
(bn p bn 1 p ... b1 p 1) y x t (amх p ... a1х p a0 х) х t
n
n 1
r
(bn p bn 1 p ... b1 p 1) y f t (arf p ... а1 f p a0 f ) f t
Решение каждого из этих уравнений можно представить в виде двух составляющих: частного
решения неоднородного уравнения с правой частью, описывающего вынужденный установившийся
процесс в системе, и общего решения однородного уравнения, описывающего переходный процесс в
системе:
y(t) yч (t ) yоб (t ) y уст (t ) yп (t )
Система будет устойчива, когда при
t yп (t ) 0
Найдем эту составляющую, решая уравнение:
n
Его решением является:
n 1
(bn p bn 1 p ... b1 p 1) y x t 0
y п (t ) C i esit
n
, где:
i 1
начальных условий;
Ci - постоянные интегрирования, определяемые из
n
si - корни характеристического уравнения bn s bn 1 sn 1 ... b1 s 1 0 ;
s - комплексная переменная.
Чтобы определить устойчивость САР нет необходимости строить переходный процесс,
9.
Корневой критерий устойчивостиВыясним, какими свойствами должны обладать корни характеристического уравнения (ХУ)
системы, чтобы она была устойчивой.
Корни могут быть вещественными, комплексно-сопряженными или комплексными.
1. Пусть один из корней ХУ системы является:
1.1. Вещественный отрицательный
1 1 , он даст в решении дифф. уравнения
1 , которая при t будет стремиться к 0, т.е. затухать.
составляющую
С1 е
t
С1 е
t
s
1.2. Вещественный положительный 1
1 , которая при
составляющую
С1 еs1t
s
1
t
, даст в решении дифф. уравнения
будет неограниченно возрастать.
С1
t
Рис.115
2. Пусть два корня ХУ системы является комплексно-сопряженными:
2.1. Корни с отрицательной вещественной частью, т.е. 1, 2 1 j .
( j )t
( j )
Они дадут в решении дифф. уравнения две составляющие С1 е 1
С 2 е 1 t , которые,
используя формулы Эйлера и преобразования тригонометрических функций, можно привести к виду:
s
( 1 j )t
С1 е
( 1 j )t
С 2 е
e 1t (C12 sin cos t C12 j cos sin t )]1(t )
e 1t C12 sin( t ),
где введены обозначения:
C1 C 2 C12sin , C1 C 2 C12cos , C12
2 ( C12 C 22 ) ,
arctg C1 C2 ,
C1 C2
10.
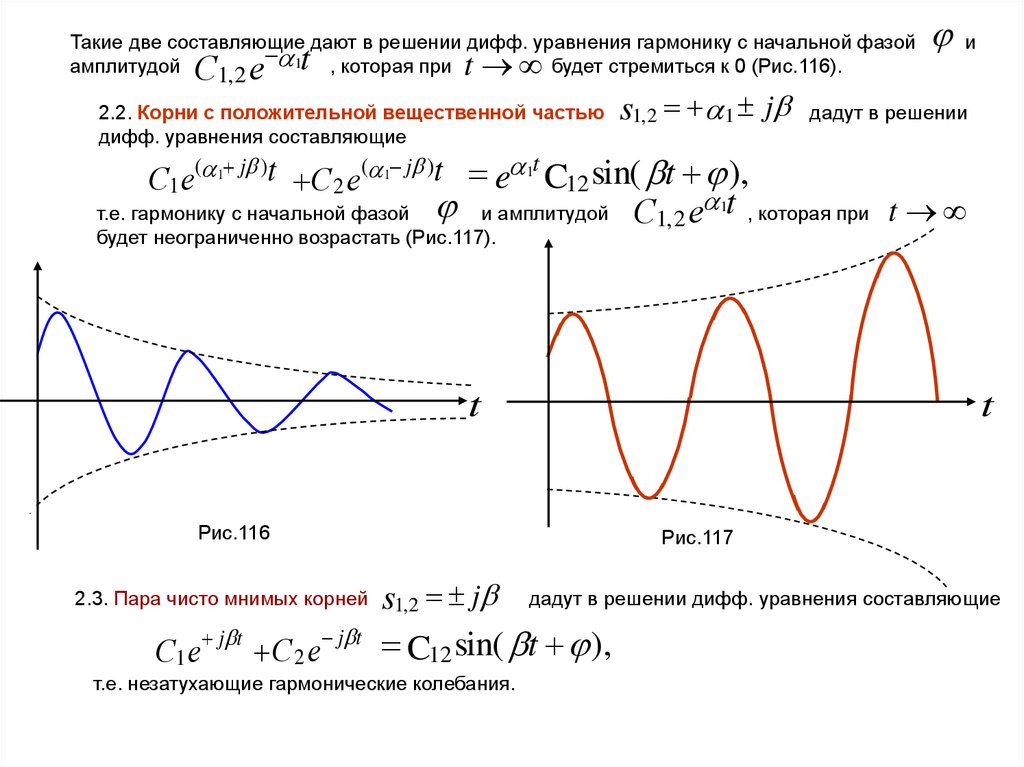
Такие две составляющие дают в решении дифф. уравнения гармонику с начальной фазой1 , которая при
амплитудой
t будет стремиться к 0 (Рис.116).
С1, 2 е
t
2.2. Корни с положительной вещественной частью
дифф. уравнения составляющие
( j )t
С1 е 1
s1,2 1 j
и
дадут в решении
e 1t C12 sin( t ),
и амплитудой С1, 2 е 1t , которая при t
( j )t
С 2 е 1
т.е. гармонику с начальной фазой
будет неограниченно возрастать (Рис.117).
t
Рис.116
Рис.117
2.3. Пара чисто мнимых корней
С1 е
j t
С 2 е
t
j t
s1,2 j дадут в решении дифф. уравнения составляющие
C12 sin( t ),
т.е. незатухающие гармонические колебания.
11.
Система устойчива, если при t переходная составляющая y п (t ) (общеерешение дифференциального
уравнения движения системы) стремиться к 0, т.е. все
n
составляющие
C i esit затухают.
i 1
Проведенный анализ показывает, что необходимым и достаточным условием этого является
отрицательность вещественных частей всех корней характеристического уравнения системы.
Отображая корни ХУ на комплексной плоскости, легко убедиться, что корни с отрицательной
вещественной частью будут находиться слева от оси мнимых.
Корневой критерий устойчивости
Im
можно сформулировать так:
Система устойчива, если все корни ее характеристического
уравнения лежат на комплексной плоскости слева от оси
мнимых, т.е. имеют отрицательные вещественные части.
0
Рис.118
Re
Если хотя бы один вещественный корень или пара
комплексных корней лежат в правой полуплоскости,
система неустойчива.
Границей устойчивости является ось мнимых
Система будет на границе устойчивости, например, при чисто мнимых корнях.
В этом случае в ней будут протекать незатухающие колебания, поэтому ось мнимых называют
колебательной границей устойчивости.
Если вещественный корень равен 0, система тоже находится на границе устойчивости.
Она будет устойчива не относительно регулируемой переменной, а относительно скорости ее
изменения. Такие системы называют нейтрально устойчивыми.
12.
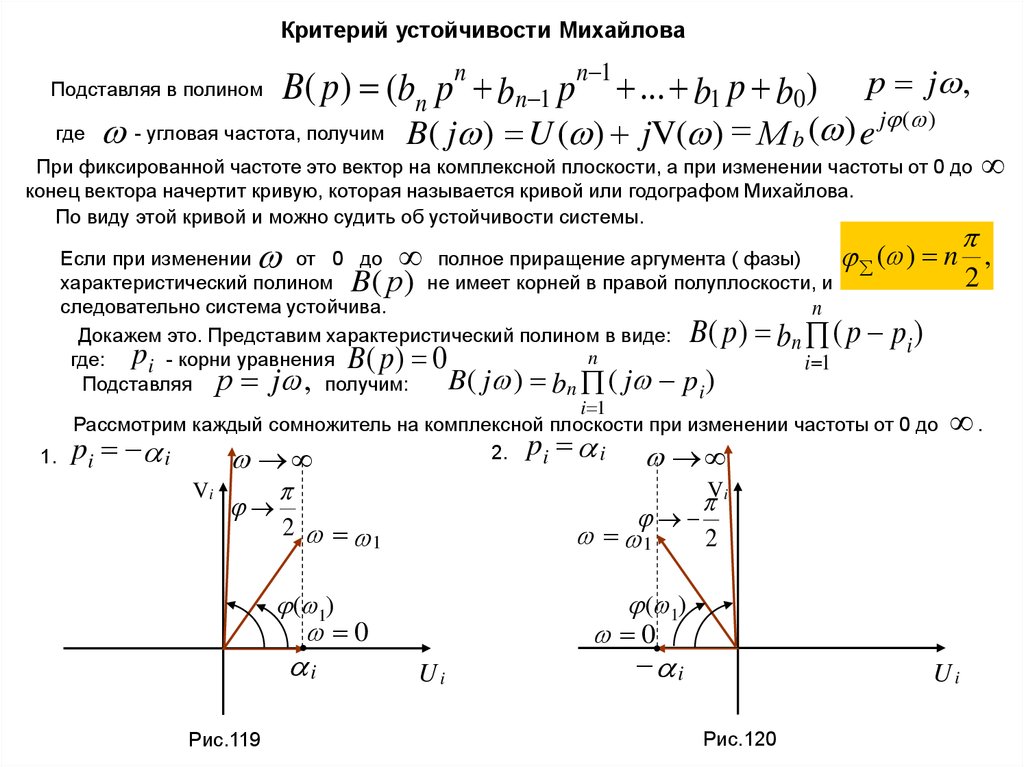
Критерий устойчивости МихайловаB( p) (bn pn bn 1 pn 1 ... b1 p b0)
Подставляя в полином
где
р j ,
- угловая частота, получим B( j ) U ( ) jV( ) М b ( ) e j ( )
При фиксированной частоте это вектор на комплексной плоскости, а при изменении частоты от 0 до
конец вектора начертит кривую, которая называется кривой или годографом Михайлова.
По виду этой кривой и можно судить об устойчивости системы.
Если при изменении
от 0 до
полное приращение аргумента ( фазы)
( ) n ,
2
характеристический полином B( р ) не имеет корней в правой полуплоскости, и
следовательно система устойчива.
n
Докажем это. Представим характеристический полином в виде:
n
i
n
где: pi - корни уравнения
i 1
B ( j ) b n ( j p i )
Подставляя р j , получим:
i 1
Рассмотрим каждый сомножитель на комплексной плоскости при изменении частоты от 0 до
.
2. pi i
1. pi i
B( p) b ( p p )
B( p) 0
Vi
2
1
V
i
1
2
( 1)
0
( 1)
0
i
Рис.119
Ui
i
Ui
Рис.120
13.
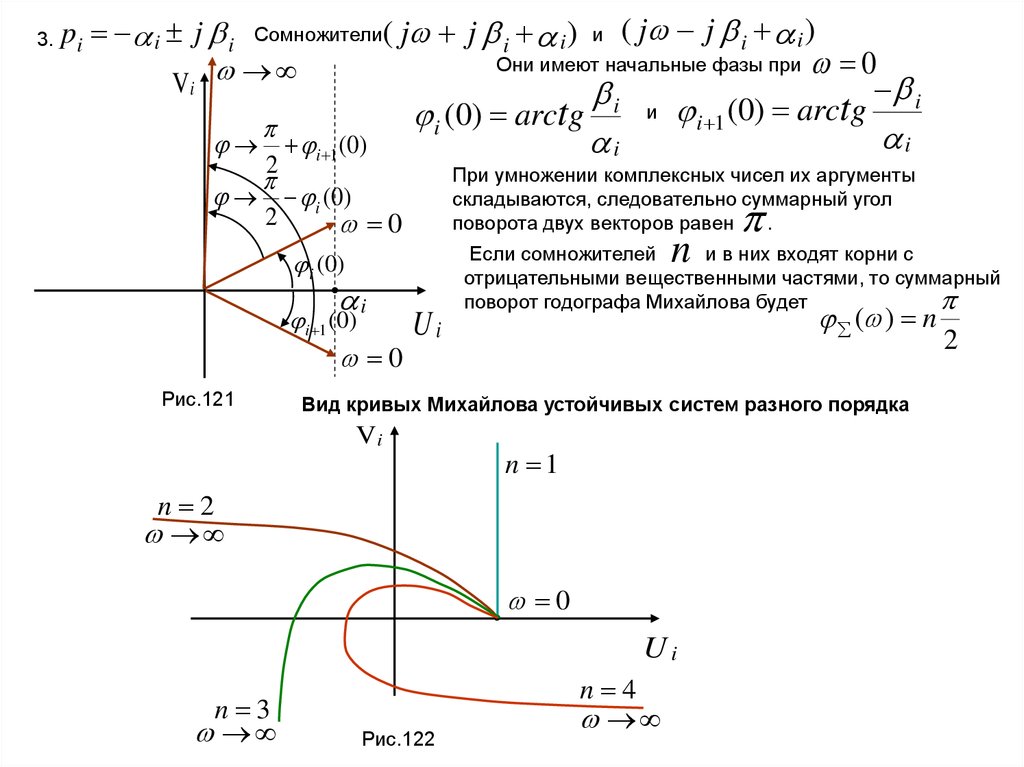
3.pi i j i Сомножители( j j i i ) и ( j j i .i )
Они имеют начальные фазы при 0
Vi
i 1 (0)
2
i (0)
2
0
i
i (0) arctg
i
i
0
Рис.121
i 1 (0) arctg
n
Ui
Если сомножителей
и в них входят корни с
отрицательными вещественными частями, то суммарный
поворот годографа Михайлова будет
( ) n
2
Вид кривых Михайлова устойчивых систем разного порядка
Vi
n 1
n 2
0
Ui
n 3
i
При умножении комплексных чисел их аргументы
складываются, следовательно суммарный угол
поворота двух векторов равен
.
i (0)
i 1 (0)
и
i
Рис.122
n 4
14.
Вид кривых Михайлова неустойчивых систем разного порядка.(при различном числе корней с положительной вещественной частью)
При наличие корней характеристического уравнения с положительной вещественной частью
приращение аргумента при изменении частоты от 0 до
будет ( ) 0.5n
Если корней
и среди них
корней с положительной вещественной частью, то суммарный
поворот годографа Михайлова будет:
(n m) m n m
n
m
2
2
2
При четном количестве корней с положительной вещественной частью кривая будет начинаться (
)
справа
0 от оси мнимых на nвещественной оси, т.к. свободный член характеристического комплекса
будет положительным.
B ( j ) b n ( j p i )
i 1
При нечетном количестве корней с положительной вещественной частью кривая будет начинаться (
)
слева
0от оси мнимых на вещественной оси, т.к. свободный член характеристического комплекса
будет отрицательным.
Рассмотрим различные случаи:
Vi
1. n 2, m 1 2 0.5 1 0
2. n 3, m 1 3 0.5 1 0.5
1
3. n 3, m 2 3 0.5 2 0.5
4. n 4, m 2 4 0.5 2 0
0
0
г
Ui
Для систем на границе устойчивости
5. n 4, pi ,i 1 j г
6. n 4, pi 0
4
2
Рис.123
3
6
5
15.
Можно не строить кривую, а искать частоты, соответствующие точкам пересечения с осями,т.е. корни приравненных нулю вещественной и мнимой частей характеристического комплекса.
B( j ) U ( ) jV( )
Ui - частоты, соответствующие пересечению кривой с осью мнимых;
Vi - частоты, соответствующие пересечению кривой с осью вещественных.
V( ) 0
Для устойчивых систем частоты Ui и Vi должны чередоваться, т.е.
0 V1 U1 V2 U2 V3 U1 ....
U ( ) 0
Например, для систем 3-го порядка характеристический комплекс:
3
2
(
j
(
j
b1 j b0 U ( ) jV( )
)
)
b2
B( j ) b3
U ( ) b0 b2 2 0
Корни:
Отсюда
V1 o;
b0
U1
b2
Для устойчивой САР
b0 b3
V( ) b1 b3 3 0
b0
U1
b2
b1
V2
b3
b1
V2
b3
b1 b2
Это соответствует основному условию устойчивости САР по критерию Гурвица.
16.
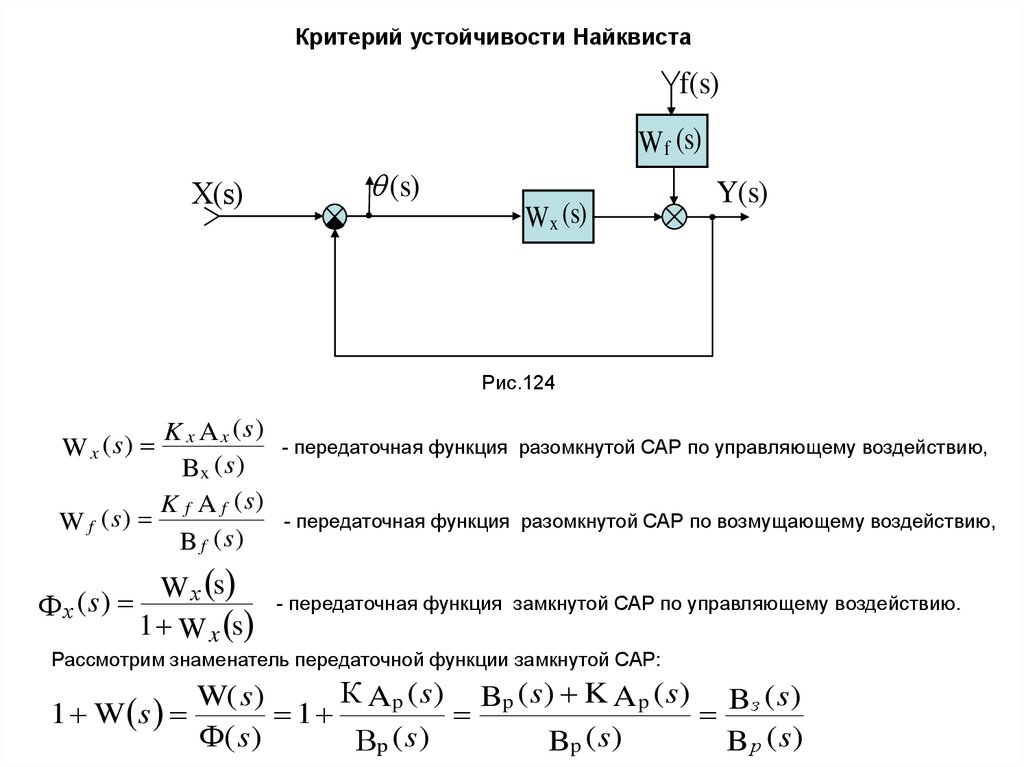
Критерий устойчивости Найквистаf(s)
Wf (s)
Х(s)
(s)
Wx (s)
Y(s)
Рис.124
K x A x (s)
(
s
)
Wx
Bx ( s )
K f A f (s)
(
s
)
Wf
B f (s)
W х s
(
s
)
х
1 W x s
- передаточная функция разомкнутой САР по управляющему воздействию,
- передаточная функция разомкнутой САР по возмущающему воздействию,
- передаточная функция замкнутой САР по управляющему воздействию.
Рассмотрим знаменатель передаточной функции замкнутой САР:
К A p ( s ) Bp ( s ) K A p ( s ) Bз ( s )
W( s )
1 W s
1
Ф( s )
Вр ( s )
Bp ( s )
B р (s)
17.
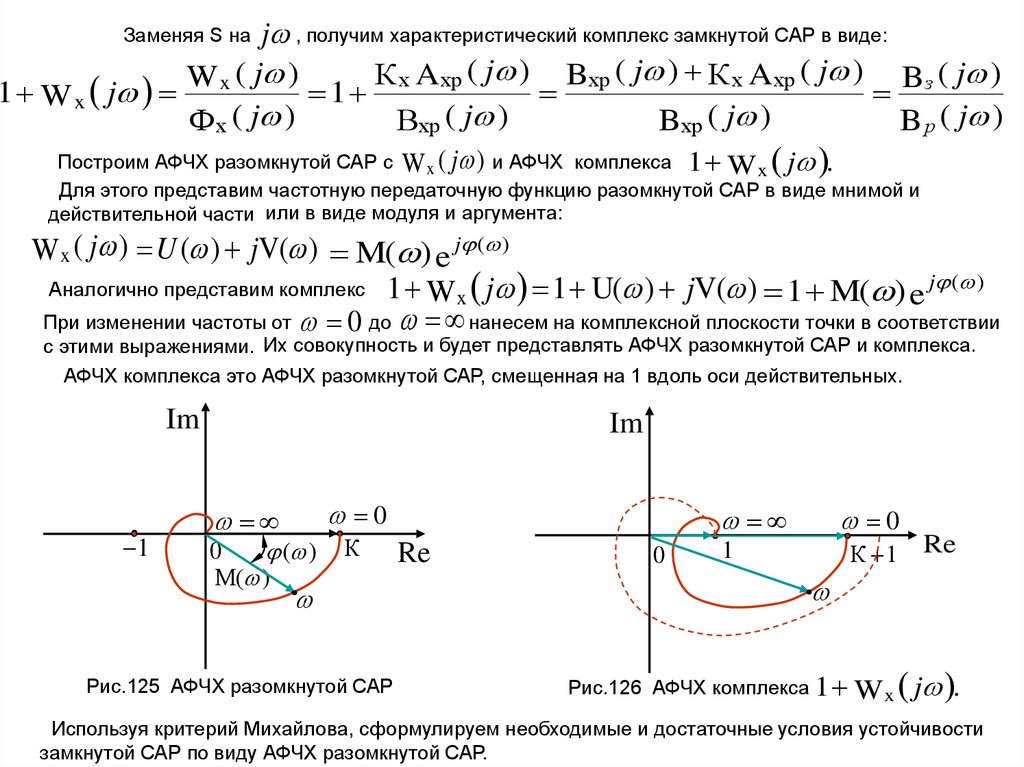
j , получим характеристический комплекс замкнутой САР в виде:К х A хp ( j ) Bхp ( j ) К х A хp ( j ) Bз ( j )
W
x ( j )
1 W x j
1
Ф х ( j )
Вхр ( j )
Bхp ( j )
B р ( j )
Построим АФЧХ разомкнутой САР с W x ( j ) и АФЧХ комплекса 1 W x j .
Заменяя S на
Для этого представим частотную передаточную функцию разомкнутой САР в виде мнимой и
действительной части или в виде модуля и аргумента:
Wx ( j ) U ( ) jV( ) M( ) e j ( )
1 Wx j 1 U( ) jV( ) 1 M( ) e j ( )
При изменении частоты от 0 до нанесем на комплексной плоскости точки в соответствии
Аналогично представим комплекс
с этими выражениями. Их совокупность и будет представлять АФЧХ разомкнутой САР и комплекса.
АФЧХ комплекса это АФЧХ разомкнутой САР, смещенная на 1 вдоль оси действительных.
Im
1
Im
0
0
( )
М( )
К
Рис.125 АФЧХ разомкнутой САР
Re
0
0
К 1
1
Re
Рис.126 АФЧХ комплекса 1 W x
j .
Используя критерий Михайлова, сформулируем необходимые и достаточные условия устойчивости
замкнутой САР по виду АФЧХ разомкнутой САР.
18.
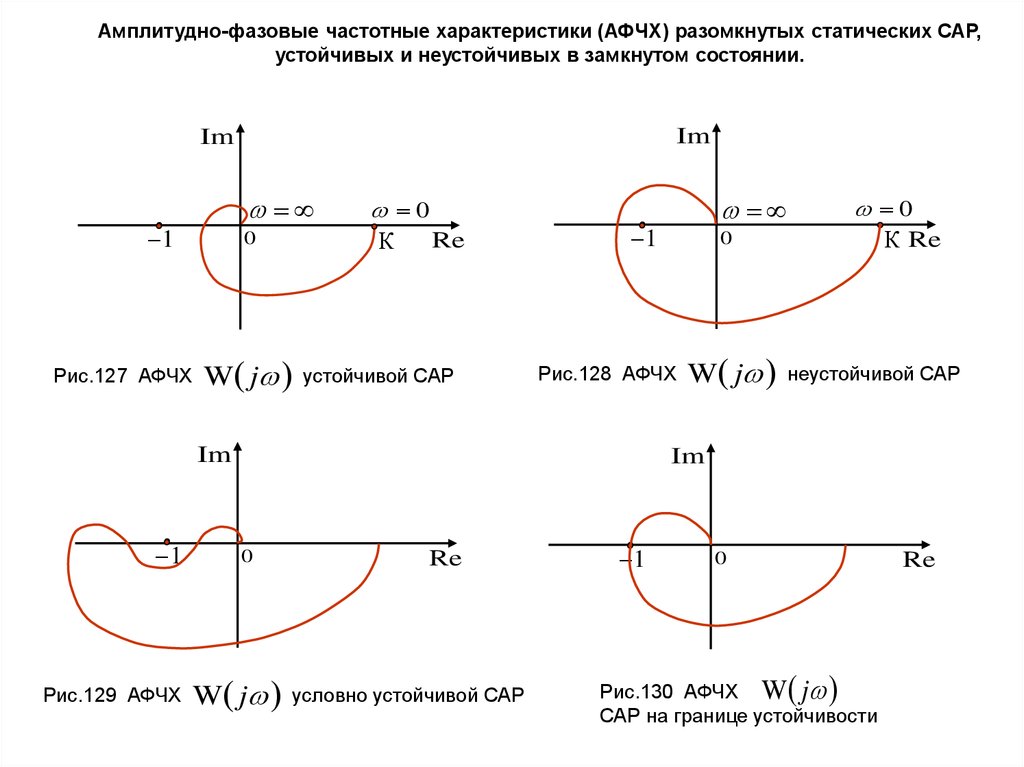
Амплитудно-фазовые частотные характеристики (АФЧХ) разомкнутых статических САР,устойчивых и неустойчивых в замкнутом состоянии.
Im
Im
1
Рис.127 АФЧХ
0
W j
0
Re
К
устойчивой САР
1
Рис.129 АФЧХ
0
К Re
0
Рис.128 АФЧХ
Im
1
W j
неустойчивой САР
Im
0
W j
Re
условно устойчивой САР
1
0
Re
Рис.130 АФЧХ W j
САР на границе устойчивости
19.
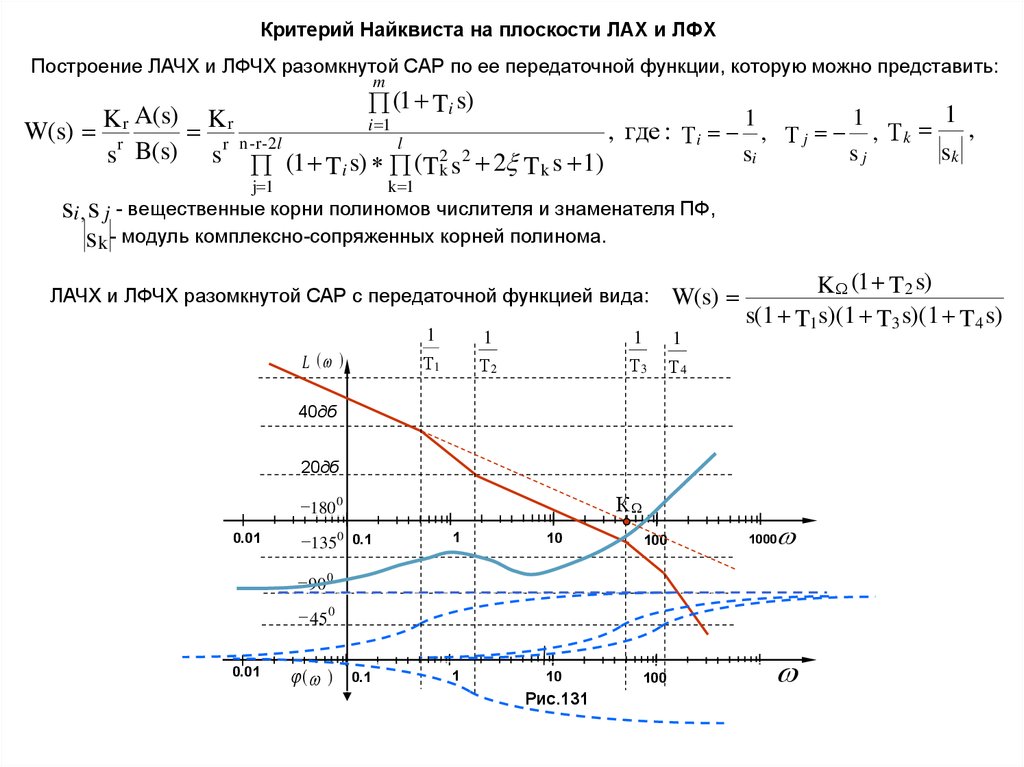
Критерий Найквиста на плоскости ЛАХ и ЛФХПостроение ЛАЧХ и ЛФЧХ разомкнутой САР по ее передаточной функции, которую можно представить:
m
(1 Ti s)
1
1
1
K
K
r A(s)
r
i 1
,
W(s) r
r n -r -2l
,
где
:
,
,
Т
k
Тj
Тi
l
sk
sj
si
s B(s) s (1 T s) (T 2 s2 2 T s 1)
i
k
k
j 1
k 1
si , s j - вещественные корни полиномов числителя и знаменателя ПФ,
sk - модуль комплексно-сопряженных корней полинома.
ЛАЧХ и ЛФЧХ разомкнутой САР с передаточной функцией вида:
L ( )
W(s)
1
1
1
1
Т1
Т2
Т3
Т4
K (1 T 2 s)
s(1 T1 s)(1 T3 s)(1 T 4 s)
40дб
20дб
К
180 0
0.01
1350 0.1
1
10
100
1
10
100
1000
90 0
45 0
0.01
( )
0.1
Рис.131
20.
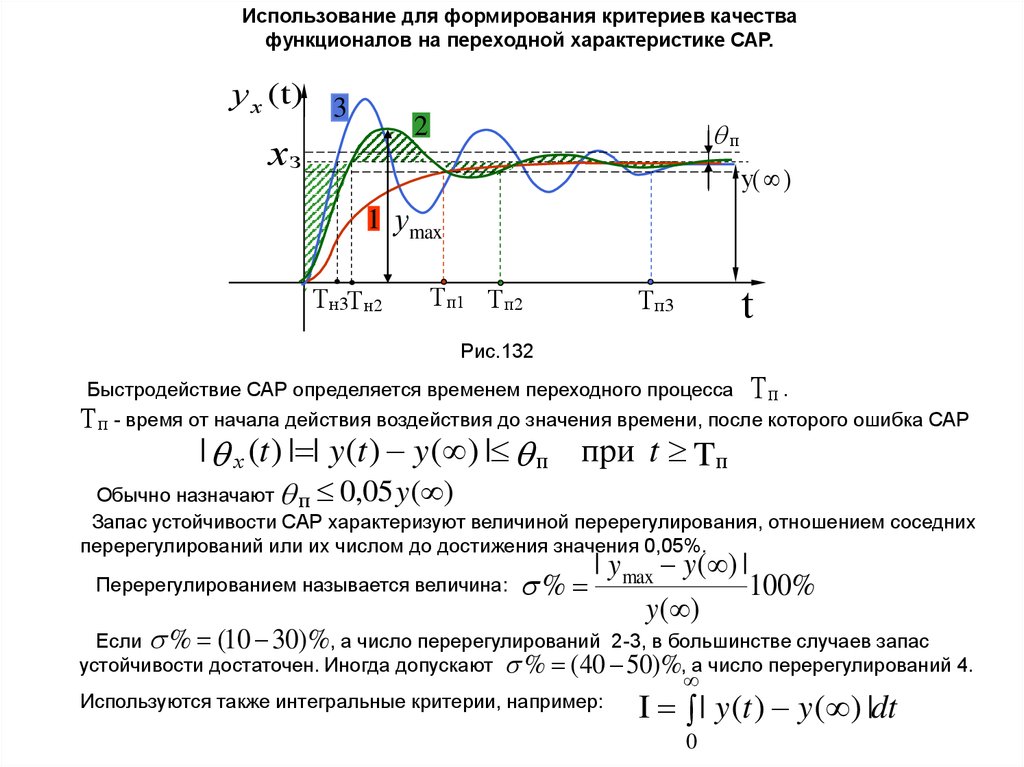
Использование для формирования критериев качествафункционалов на переходной характеристике САР.
у х (t) 3
2
хз
п
y( )
1 у max
Тн3Т н2
Т п1 Т п2
t
Тп3
Рис.132
Быстродействие САР определяется временем переходного процесса Т п .
Т п - время от начала действия воздействия до значения времени, после которого ошибка САР
| х (t ) | | y(t ) y( ) | п при t Tп
Обычно назначают п 0,05 y ( )
Запас устойчивости САР характеризуют величиной перерегулирования, отношением соседних
перерегулирований или их числом до достижения значения 0,05%.
Перерегулированием называется величина:
| y max y ( ) |
%
100%
y ( )
Если % (10 30)%, а число перерегулирований 2-3, в большинстве случаев запас
устойчивости достаточен. Иногда допускают % (40 50)%, а число перерегулирований 4.
Используются также интегральные критерии, например:
I | y (t ) y ( ) |dt
0
21.
Корневые критерии качестваIm
Im
i
i
0
Рис.133
Ближайший к оси мнимых корень
рi i
Составляющая в переходном процессе этого
i t
корня:
yi (t ) C i e
yi (Т п) C i ( 0,05) ,
1 1
Т п lп
i
При 0,05
1
1
3
lп
Тп
i 0,05 i
Назначив
найдем:
0
Re
Re
Рис.134
Ближайший к оси мнимых корень
рi i j
Составляющая в переходном процессе этих корней:
yi (t ) C i e it sin( t )
Положив
yi (Т п) C i ( 0,05)
sin( t ) 1
Тп
При
1
i
0,05
и
, получим:
1
1
1
3
lп
Тп
i 0,05 i
lп
Величина
i называется степенью устойчивости, которая определяет быстроту затухания
переходного процесса в САР.
22.
ii
Отношение
называется колебательностью.
yi (t ) C i e it sin( t )
t t1 амплитуда равна:
Пара комплексно сопряженных корней дают составляющую
Оценим зетухание амплитуды колебаний за период. При
Через период
Величину
Т
t
С1 C e i 2
2
2
i (t1 )
С2 C e
C1 e C1 e
2
C
1 C2
1 C 2
C1
C1
Подставляя выражения для
С1
и
называют затуханием за период.
С 2 , получим:
1 e
В САР затухание за период должно быть не менее 90%. При
2
, откуда:
0,9 2,72
2
1
ln
1
При заданной колебательности на плоскости корней характеристического уравнения возникает
запретная область, границей которой являются два луча с углом наклона:
i
arctg arctg
i
Im
i
0
Re
Рис.135
23.
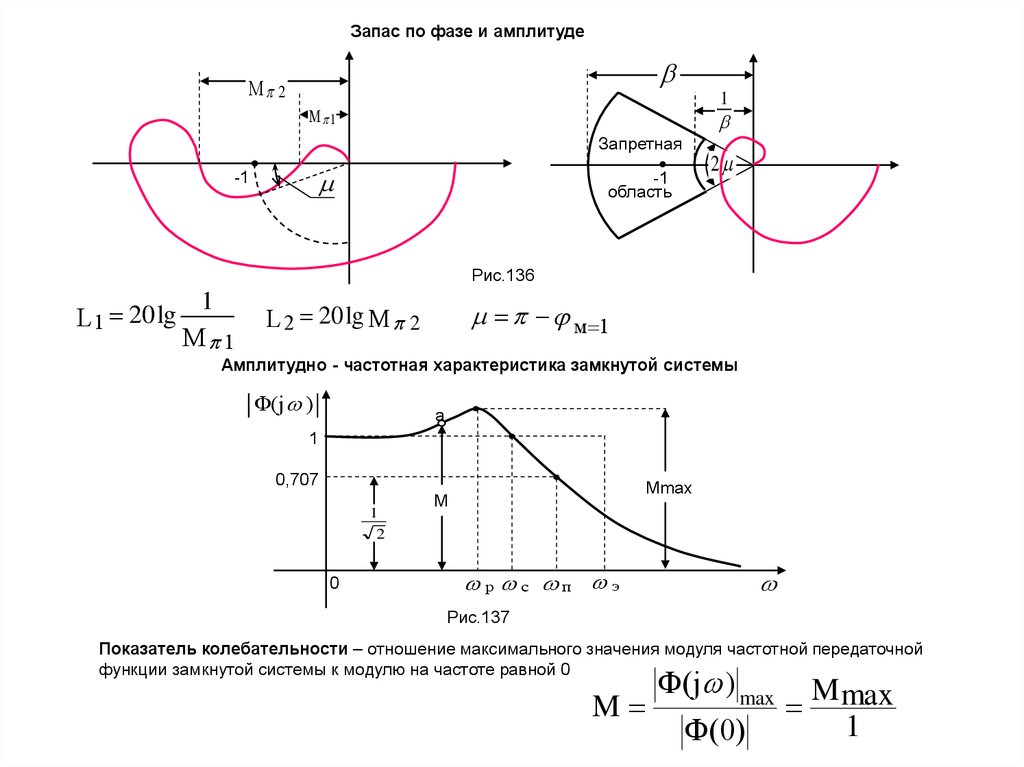
Запас по фазе и амплитудеМ 2
1
М 1
Запретная
-1
2
-1
область
Рис.136
L1 20 lg
1
М 1
м 1
L 2 20 lg М 2
Амплитудно - частотная характеристика замкнутой системы
Ф(j )
а
1
0,707
1
2
0
Мmax
М
р с п э
Рис.137
Показатель колебательности – отношение максимального значения модуля частотной передаточной
функции замкнутой системы к модулю на частоте равной 0
M
Ф(j ) max
Ф(0)
M max
1
24.
Отображение показателя колебательности на плоскости АФЧХ разомкнутой системыW( j )
| const
M | Ф j | |
1 W( j )
W j U( ) jV( ) M( ) e j ( )
2
V2
U
M
1 U( ) 2 V2
2
V2 M 2 U2 V2
1
U
М
2
2
2
2
2
2
M 2U M U (M 1) V (M 1) 0
2
4
4
2
2 U M 2
M
M
M
2
V
2
U
2
2
2
M 1
M2 1
M2 1 M 1
2
U C 2 V2 R 2
R M
2
M 1
2
C M
2
M 1
- уравнение окружности с радиусом R
и смещением по оси вещественных на
C
25.
Отображение показателя колебательности на плоскости АФЧХМ=1
Im
М=0.83
М=1.2
М=0.77
М=1.3
М=0.67
М=1.5
М=0.5
М=0.25
М=2
М=4
0
-1
W(j )
Рис.138
Re
26.
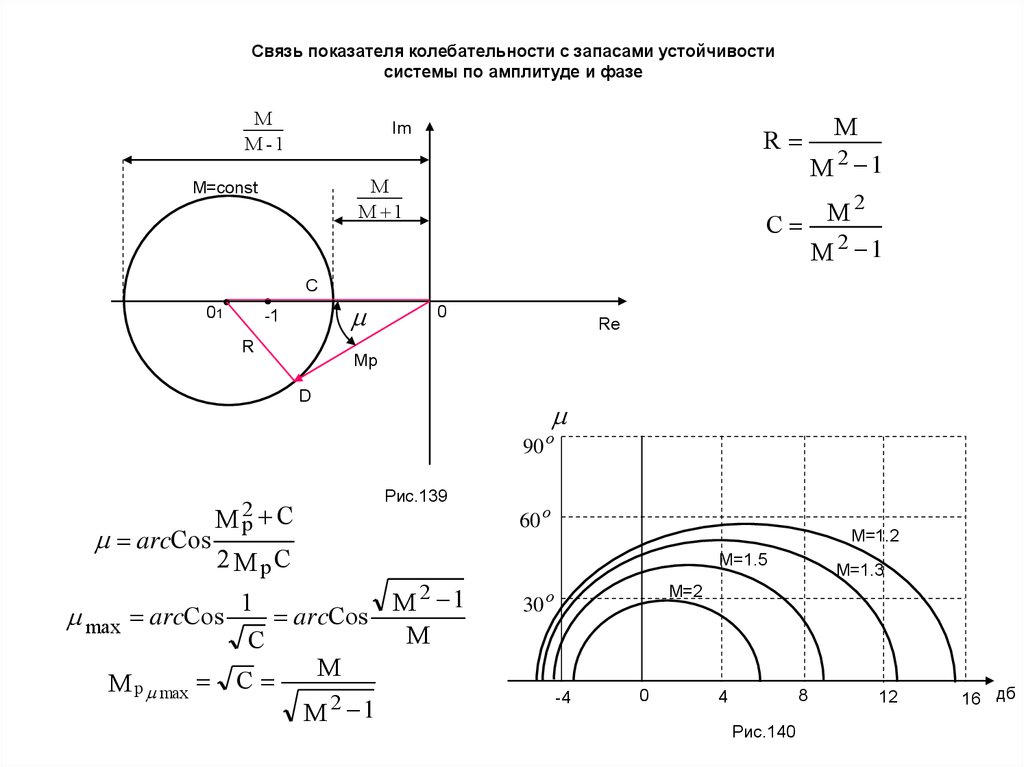
Cвязь показателя колебательности с запасами устойчивостисистемы по амплитуде и фазе
М
М -1
Im
R
М
М 1
М=const
M
M 2 1
2
М
С
M 2 1
C
01
-1
R
0
Re
Мр
D
90
arcCos
M 2p C
Рис.139
о
60 о
М=1.2
2M pC
M 2 1
1
arcCos
max arcCos
M
C
M
M p max C
M 2 1
М=1.5
М=1.3
М=2
30 о
-4
0
8
4
Рис.140
12
16 дб
27.
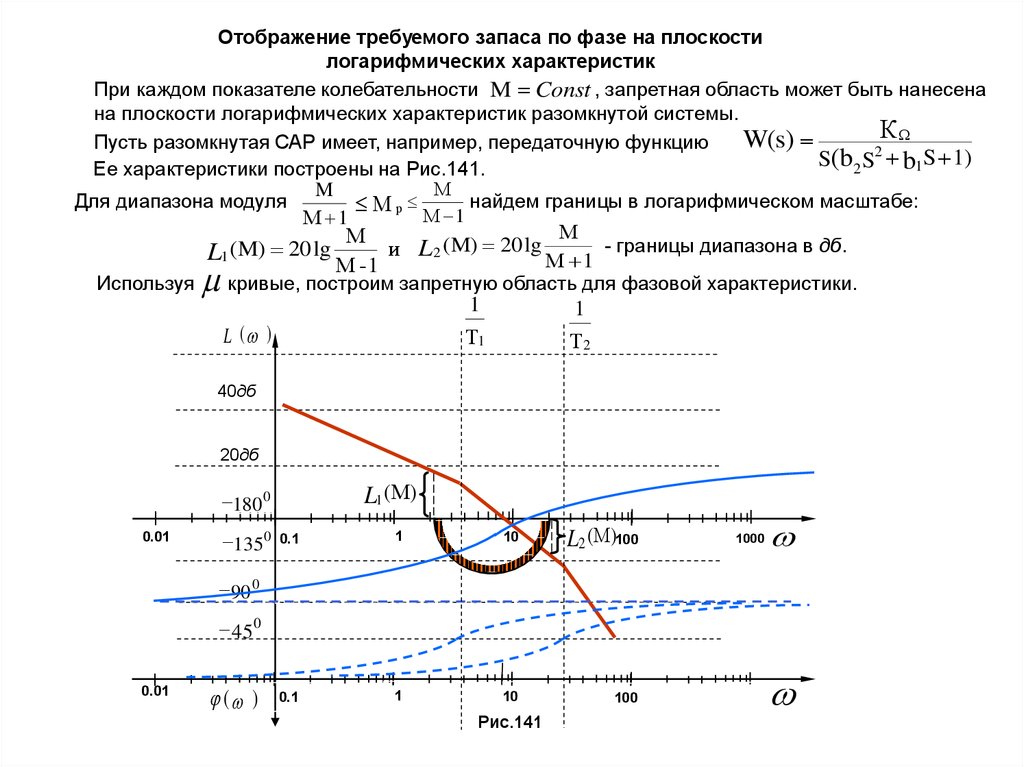
Отображение требуемого запаса по фазе на плоскостилогарифмических характеристик
При каждом показателе колебательности M Const , запретная область может быть нанесена
на плоскости логарифмических характеристик разомкнутой системы.
К
W(s)
Пусть разомкнутая САР имеет, например, передаточную функцию
2
S(b2 S b1S 1)
Ее характеристики построены на Рис.141.
М
M
Для диапазона модуля
М р М 1 найдем границы в логарифмическом масштабе:
М 1
М
М
L1 (M) 20 lg М - 1 и L2 (M) 20 lg М 1 - границы диапазона в дб.
Используя
кривые, построим запретную область для фазовой характеристики.
L ( )
1
1
Т1
Т2
40дб
20дб
L1 (М)
180 0
0.01
1350
0.1
1
10
L2 (М)100
0.1
1
10
100
1000
90 0
45 0
0.01
( )
Рис.141
28.
Отображение показателей качества САР наплоскости логарифмических характеристик
Основные показатели качества САР: точность в установившихся типовых режимах работы, запасы
по амплитуде и фазе, быстродействие, могут быть отображены на плоскости логарифмических
характеристик разомкнутой системы. Это позволяет сформулировать требования к ЛАХ и ЛФХ
разомкнутой системы, обеспечивающих после замыкания требуемые показатели САР.
Рассмотрим точность в типовых установившихся режимах.
Обычно она задается в виде ошибки m САР при воспроизведении ею заданных максимальных
скоростей m и ускорений m или заданного гармонического воздействия с амплитудой Х m и
эквивалентной частотой к. Последний может быть представлен: Х (t ) X m
к
Sin
Xm
Ошибку САР при гармонического воздействии представим: m Ф ( j к ) X m
1 W(j k )
Xm
X
m
Т.к. m X m , то W( j к ) 1 и m
W( j к )
W(j k )
m
х
Это выражение позволяет отобразить требования по
точности на плоскость ЛАХ.
L ( )
L( k ) 20lg W( j к ) 20lg Xm
Ордината контрольной точки Ак, ниже которой не
должна проходить ЛАХ при к
40дб
m
m
m
С другой стороны для гармоники к
,а Хm
m
m
Если m const, а m уменьшать, то к , а Х m ,
2
получим для Ак прямую с наклоном -20дб/дек,
Если m const , а m уменьшать, то к , а Х m
2
пропорционально m, для Ак получим прямую -40дб/дек
К m m - добротность САР по скорости.
К m m - добротность САР по ускорению.
о К - называется базовой частотой.
L ( k )
20дб
180 0
Ак
Запретная
область по
точности
1350 0.1
1
к
10 о
К
100
К
90 0
45 0
( )
0.1
1
10
Рис.142
100
29.
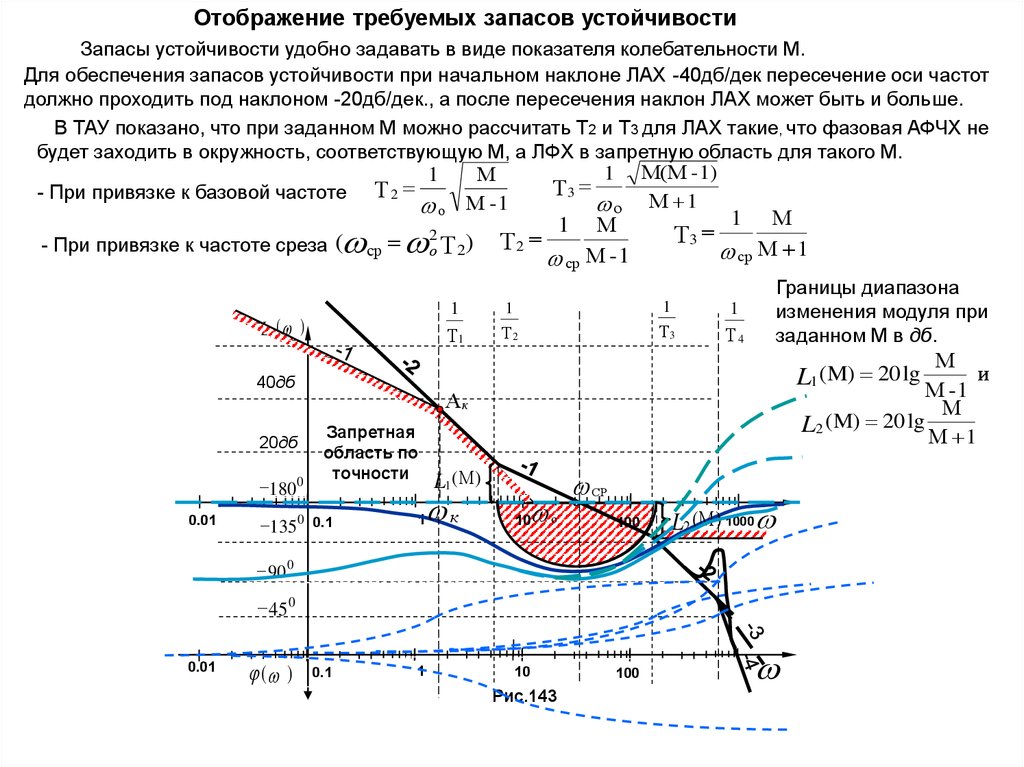
Отображение требуемых запасов устойчивостиЗапасы устойчивости удобно задавать в виде показателя колебательности М.
Для обеспечения запасов устойчивости при начальном наклоне ЛАХ -40дб/дек пересечение оси частот
должно проходить под наклоном -20дб/дек., а после пересечения наклон ЛАХ может быть и больше.
В ТАУ показано, что при заданном М можно рассчитать Т2 и Т3 для ЛАХ такие, что фазовая АФЧХ не
будет заходить в окружность, соответствующую М, а ЛФХ в запретную область для такого М.
1 М(М - 1)
1
М
Т
3
Т
2
- При привязке к базовой частоте
о М 1
о М -1
ср
- При привязке к частоте среза (
L ( )
2
о
Т 2)
М
Т2
ср М - 1
Т3
1
1
1
1
Т1
Т2
Т3
М
ср М 1
1
1
Т4
Границы диапазона
изменения модуля при
заданном М в дб.
М
40дб
20дб
180 0
0.01
1350
L1 (M) 20 lg М - 1 и
Ак
Запретная
область по
точности
0.1
1
0.1
1
М
L2 (M) 20 lg М 1
L1 (М)
к
о
СР
10
100
L2 (М) 1000
10
100
90 0
45 0
0.01
( )
Рис.143
30.
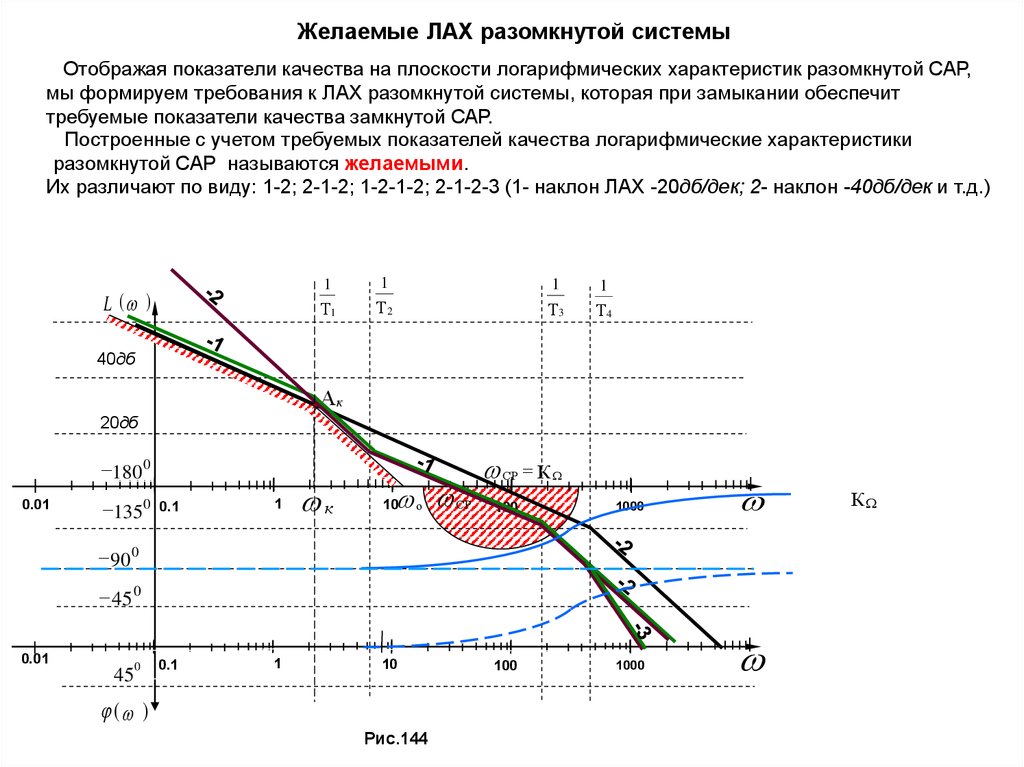
Желаемые ЛАХ разомкнутой системыОтображая показатели качества на плоскости логарифмических характеристик разомкнутой САР,
мы формируем требования к ЛАХ разомкнутой системы, которая при замыкании обеспечит
требуемые показатели качества замкнутой САР.
Построенные с учетом требуемых показателей качества логарифмические характеристики
разомкнутой САР называются желаемыми.
Их различают по виду: 1-2; 2-1-2; 1-2-1-2; 2-1-2-3 (1- наклон ЛАХ -20дб/дек; 2- наклон -40дб/дек и т.д.)
L ( )
1
1
1
1
Т1
Т2
Т3
Т4
40дб
Ак
20дб
180 0
0.01
1350
0.1
1
0.1
1
к
СР К
10
100
1000
10
100
1000
о СР
90 0
45 0
0.01
45
0
( )
Рис.144
К
31.
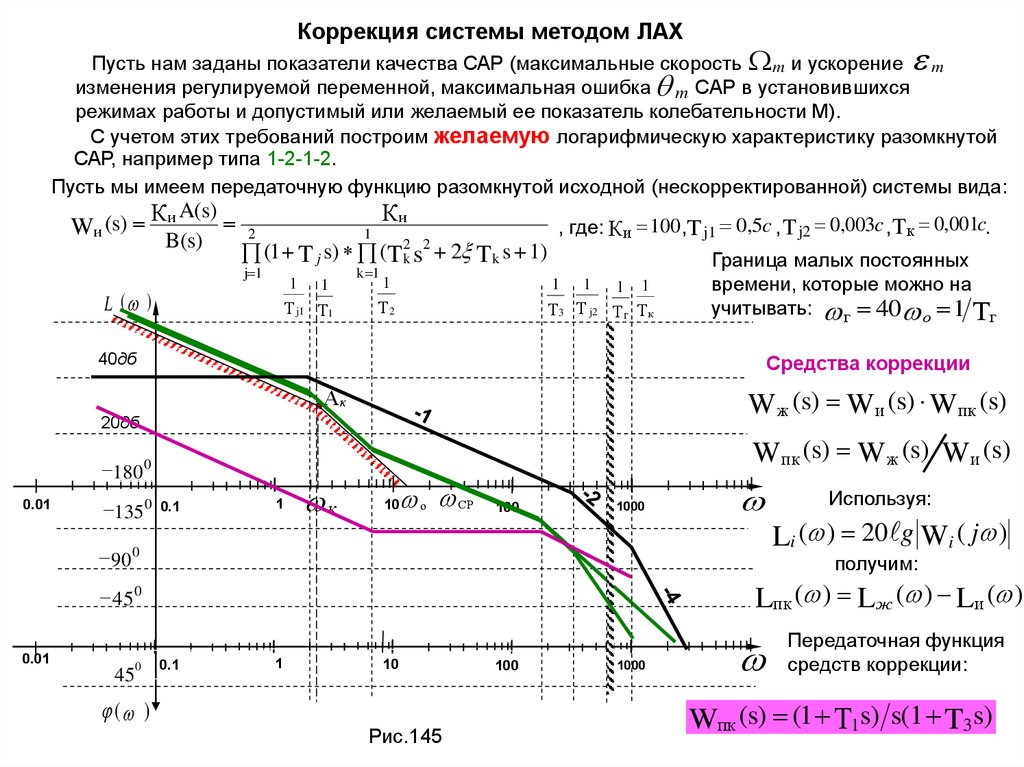
Коррекция системы методом ЛАХПусть нам заданы показатели качества САР (максимальные скорость m и ускорение m
изменения регулируемой переменной, максимальная ошибка m САР в установившихся
режимах работы и допустимый или желаемый ее показатель колебательности М).
С учетом этих требований построим желаемую логарифмическую характеристику разомкнутой
САР, например типа 1-2-1-2.
Пусть мы имеем передаточную функцию разомкнутой исходной (нескорректированной) системы вида:
W и (s)
Ки A(s)
B(s)
Ки
2
1
j 1
k 1
2 2
2
k
(1 T j s) (T s
1
L ( )
1
Т j1 Т1
T k s 1)
, где: К и 100,T j1 0,5c , T j2 0,003c , Tк 0,001c.
1
1
Т2
Т 3 Т j2 Т г Тк
1
1
1
Граница малых постоянных
времени, которые можно на
учитывать: г 40 о 1 Тг
Средства коррекции
40дб
Wж (s) Wи (s) Wпк (s)
Ак
20дб
Wпк (s) W ж (s) Wи (s)
180 0
0.01
1350
0.1
1
к
10
о СР
100
1000
90 0
45
0
( )
Li ( ) 20 g Wi ( j )
получим:
Lпк ( ) Lж ( ) Lи ( )
45 0
0.01
Используя:
0.1
1
10
Рис.145
100
1000
Передаточная функция
средств коррекции:
Wпк (s) (1 Т1s) s(1 T3 s)














 Физика
Физика








