Похожие презентации:
Расчет линейных разветвленных цепей
1. Расчет электрической цепи переменного тока
I1I
Xc1
R1
I2
R2
XL2
2. Дано:
• U=200B (действующие значение)• R1=12 Oм, Xc1=16 Ом(В первой цепи)
• R2=20 Ом, XL=150 Ом(Во второй цепи)
3. Определим:
• I1-? (Ток в первой ветви)• I2-? (Ток во второй ветви)
• I общ.-?(Общий ток или ток в неразветвленной части
цепи)
• Q-? (Реактивная мощность)
• P-?(Активная мощность)
• S-?(Полная мощность)
• Построить векторную диаграмму токов.
4. Задание на семестровую контрольную работу
Дано:U=250-дата рожденияR1- дата рождения+10
Xc1-дата рождения +5
R2- дата рождения +20
XL2- дата рождения +15
Найти:
• I1-? (Ток в первой ветви)
• I2-? (Ток во второй ветви)
• I общ.-?(Общий ток или ток в неразветвленной части цепи)
• Q-? (Реактивная мощность)
• P-?(Активная мощность)
• S-?(Полная мощность)
• Построить векторную диаграмму токов.
5. Определим токи в ветвях
• I=U/R, так как сопротивление ветвиактивное и реактивное, то в ветви
имеется полное сопротивление
2
2
C
L
Z R (X X )
I=U/Z
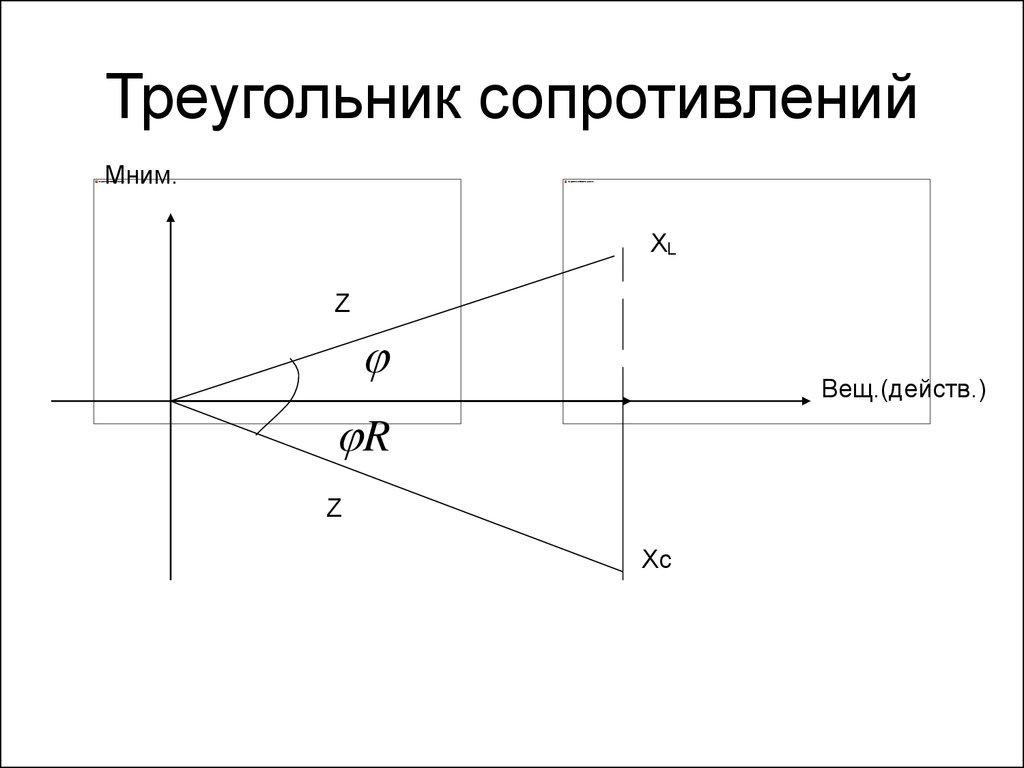
6. Треугольник сопротивлений
Мним.XL
Z
Вещ.(действ.)
R
Z
Xc
7. Ток в первой ветви
UI1
Z1
U
R1 ( X c1 )
2
2
200
200
10 A
144 256
400
Ток во второй ветви
U
I2
Z2
U
R2 ( X L )
2
2
200
200
8A
400 225
625
8. Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла
X c1 16sin 1
0.8
Z1
20
sin 1 53o10'
X L1 15
sin 2
0.6
Z 2 20
sin 2 37 o
9. Находим cos1, cos2, т.к. через косинусы фазовых углов находятся активные составляющие тока
R1 16cos 1
0.6
Z1 20
R2 20
cos 2
0.8
Z 2 25
10. Определим активные и реактивные составляющие токов ветвей
I a1 I1 * cos 1 10 * 0.6 6 AI a 2 I 2 * 0 .8 6 .4 A
I p1 I1 * sin 1 10 * ( 0.8) 8 A
I p 2 I 2 * sin 1 8 * 0.6 4.8 A
11. Ток в неразветвленной цепи
I ( I a1 I a 2 ) 2 ( I p1 I p 2 ) 2 (6 6.4) 2 ( 8 4.8) 2 153,76 10,24 164 12,806 AОпределить коэффициент мощности всей цепи
I a1 I a 2
6 6.4
cos
0.9682
I
12.806
12. Активные и реактивные мощности ветвей\всей цепи
P1 I1 * R1 10 2 *12 1200 Вт2
P2 I 2 * R2 8 * 20 1280 Вт
2
2
Робщ. Р1 Р2 1200 1280 2480 Вт
Q1 I1 * X c 10 *16 1600 Вар
2
2
Q2 I 2 * X L 8 *15 960 Вар
2
2
Qобщ. Q1 Q2 1600 960 640 Вар
Q1 отрицательное, так как угол φ1 <0(Емкостной характер нагрузки)
13. Определим общую мощность
SP2 Q2
2480 2 ( 640) 2
6150400 409600 2561.2 BA
Проверяем результат:
S 2561.2
I
12.806 A
U
200
Результат по току совпадает, следовательно мощность посчитана верно.
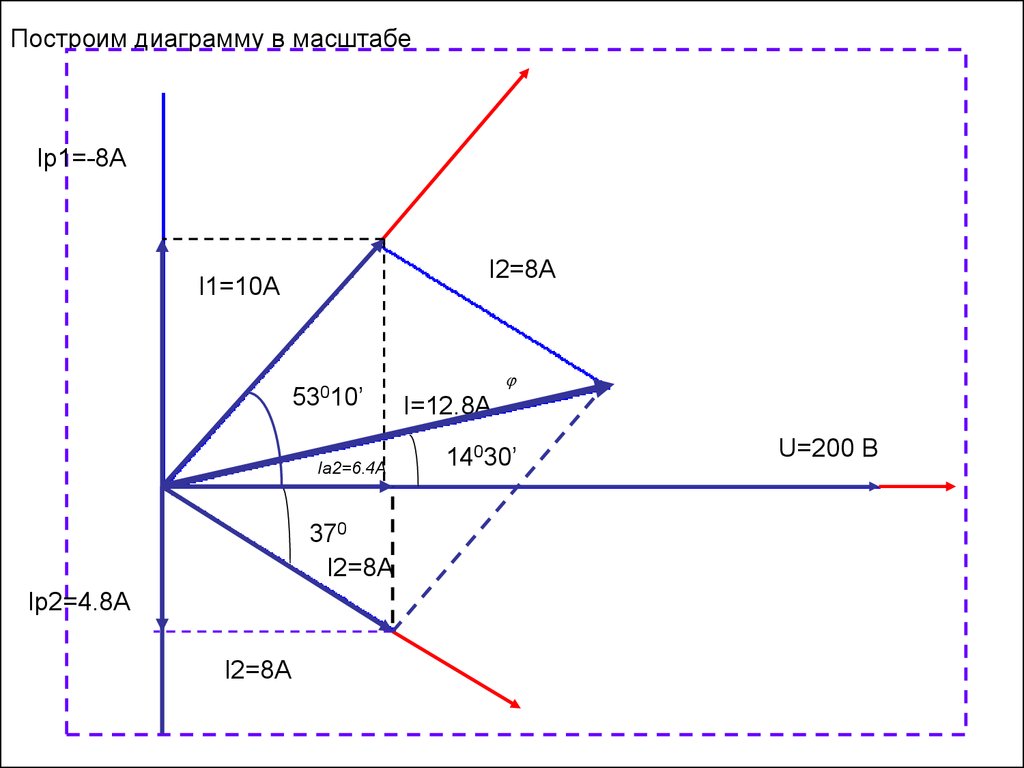
14.
Построим диаграмму в масштабеIр1=-8A
I2=8A
I1=10A
53010’
Ia2=6.4A
370
I2=8A
Ip2=4.8A
I2=8A
I=12.8A
14030’
U=200 B












 Физика
Физика








