Разветвленные цепи однофазного тока. Лекция №4

1.

ЛЕКЦИЯ №4
РАЗВЕТВЛЕННЫЕ ЦЕПИ
ОДНОФАЗНОГО ТОКА

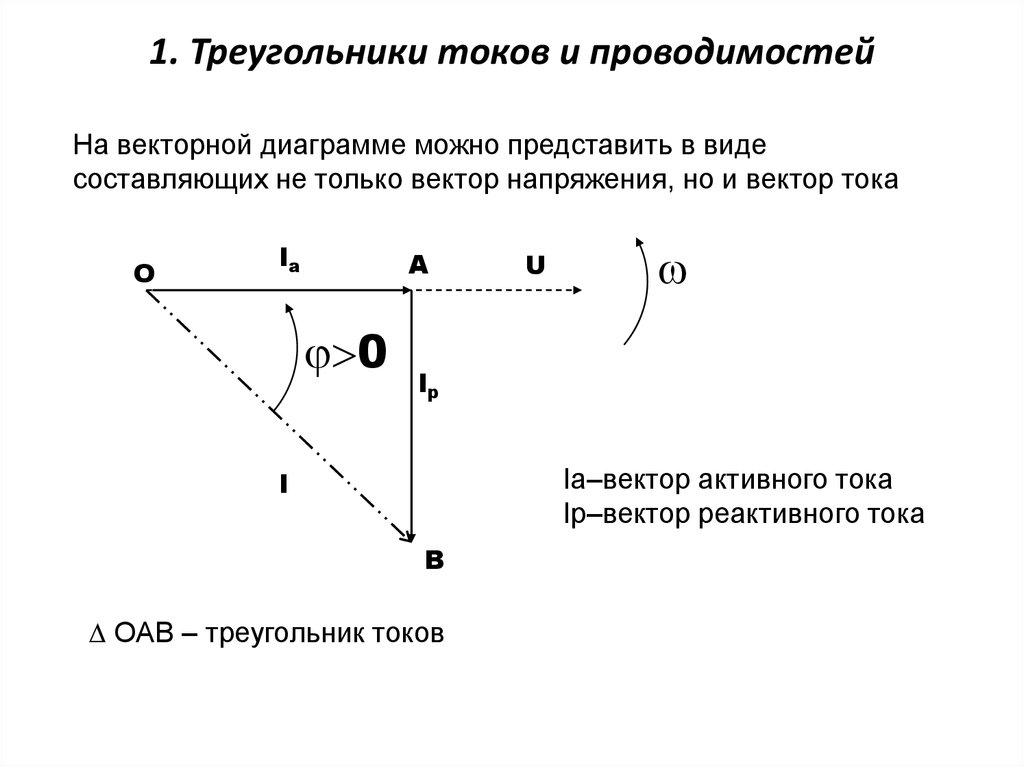
2. 1. Треугольники токов и проводимостей

На векторной диаграмме можно представить в виде
составляющих не только вектор напряжения, но и вектор тока
О
Ia
А
0
U
Ip
Iа–вектор активного тока
Iр–вектор реактивного тока
I
В
ОАВ – треугольник токов

3.

I а I cos ;
I p I sin ;
I Iа2 I p2 ;
Преобразуем эти соотношения к виду, в который войдут проводимости.
Воспользуемся соотношениями (из треугольника сопротивлений);
U
r
X
I ; cos ; sin ;
Z
Z
Z
U r
r
I а I cos U 2 U g ;
Z Z
Z
r
g 2 активная проводимость, 1/Ом
Z

4.

U X
X
I p I sin U 2 U b;
Z Z
Z
X
b 2
Z
реактивная проводимость, 1/Ом
U
I U y;
Z
1
y
Z
полная проводимость, 1/Ом
Размерность всех проводимостей одинаковая
r 0; z 0; g 0;
если
X 0; b 0;
если
X 0; b 0;

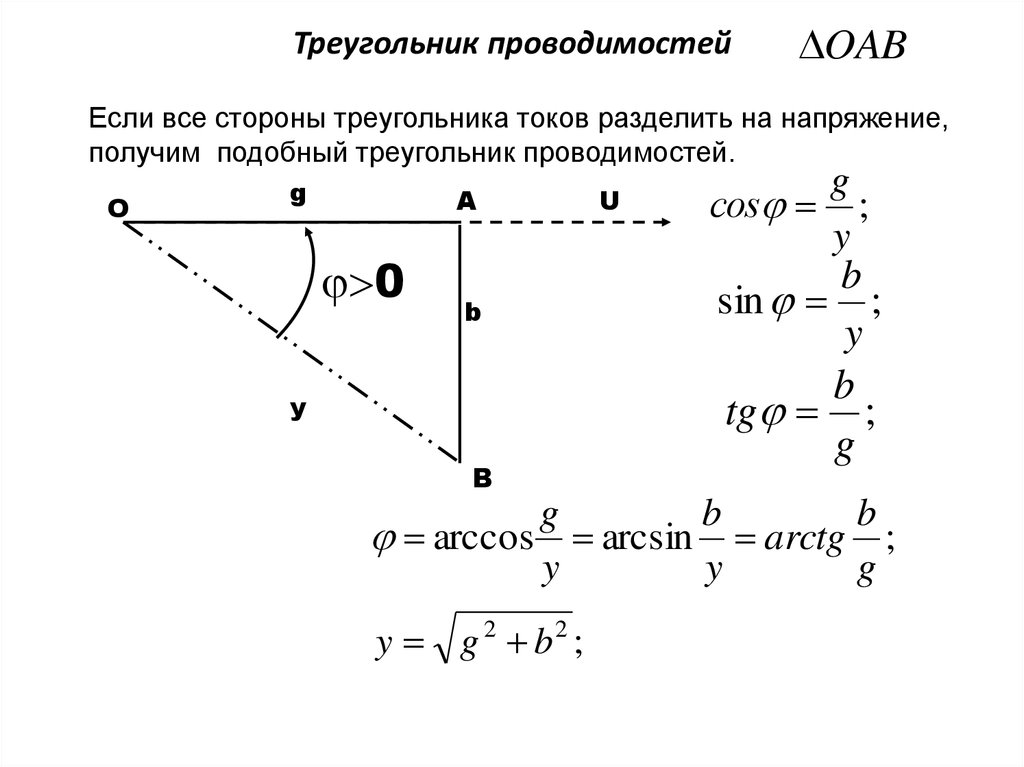
5. Треугольник проводимостей

OAB
Если все стороны треугольника токов разделить на напряжение,
получим подобный треугольник проводимостей.
О
g
А
0
b
y
В
U
g
сos ;
y
b
sin ;
y
b
tg ;
g
g
b
b
arccos arcsin arctg ;
y
y
g
y g 2 b2 ;

6. Полные сопротивление и проводимости взаимообратимы

1
Z ;
y
1
y ;
Z
y Z 1;
Активные и реактивные сопротивления и проводимости
взаимообратимы лишь в частных случаях:
1) r 0;
2)
r 0;
3) r
X L 0;
X L 0;
X C 0;
r
r
1
g 2 2
;
2
r
Z
r (X L XC )
X C 0; b ( X L 2X C )
Z
0; X L 0; X C 0;b ( X L 2X C )
Z
bС
(X L XC )
1
bL ;
2
2
XL
r (X L XC )
(X L XC )
1
bС ;
2
2
XС
r (X L XC )
1
(без минуса).
XС

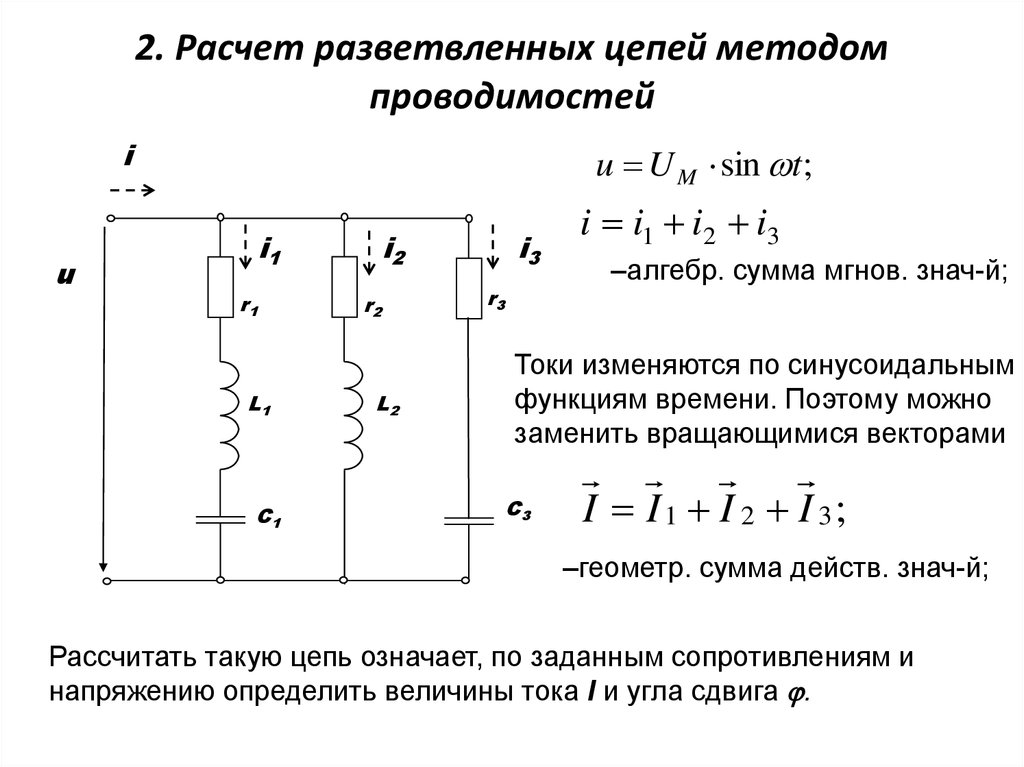
7. 2. Расчет разветвленных цепей методом проводимостей

i
u
u U M sin t ;
i1
r1
L1
C1
i2
r2
L2
i3
r3
i i1 i2 i3
–алгебр. сумма мгнов. знач-й;
Токи изменяются по cинусоидальным
функциям времени. Поэтому можно
заменить вращающимися векторами
C3
I I 1 I 2 I 3;
–геометр. сумма действ. знач-й;
Рассчитать такую цепь означает, по заданным сопротивлениям и
напряжению определить величины тока I и угла сдвига .

8.

Метод проводимостей основан на представлении токов в ветвях
в виде произведения напряжения на соответствующую
проводимость.
Для неразветвленной части цепи запишем:
I U y;
I а U g;
I P U b;
b
arcsin ;
y
Если на одном графике построить треугольники токов для всей
цепи и параллельных ветвей, то можно сделать 3 важных
вывода:
1) Активный ток в неразветвленной части цепи равен
арифметической сумме активных токов в каждой из ветвей
в отдельности:
I а I а1 I а 2 I а 3 U g1 U g 2 U g 3 U ( g1 g 2 g 3 ) U g ;
Активная проводимость всей цепи равна арифметической
сумме активных проводимостей каждой из ветвей в
отдельности:
g g1 g 2 g 3

9.

2) Реактивный ток в неразветвленной части цепи равен
алгебраической сумме реактивных токов в каждой из ветвей в
отдельности:
I Р I Р1 I Р 2 I Р3 U b1 U b2 U b3 U (b1 b2 b3 ) U b;
Реактивная проводимость всей цепи равна алгебраической
сумме реактивных проводимостей каждой из ветвей в
отдельности:
b b1 b2 b3 – алгебраическая сумма
3) Полная проводимость всей схемы равна
y g 2 b2 ;
Располагая полученными формулами, расчет можно вести
аналитически, не прибегая к графическому построению.

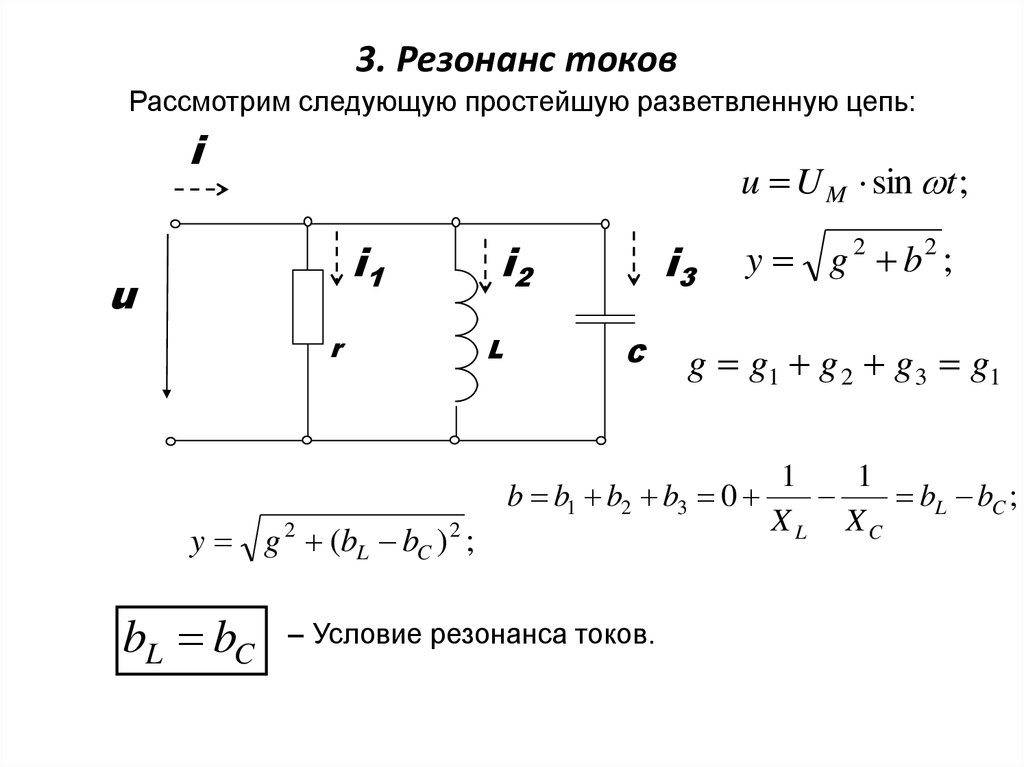
10. 3. Резонанс токов

Рассмотрим следующую простейшую разветвленную цепь:
i
u U M sin t ;
i1
u
r
y g 2 (bL bC ) 2 ;
bL bC
i2
L
i3
С
y g 2 b2 ;
g g1 g 2 g 3 g1
b b1 b2 b3 0
– Условие резонанса токов.
1
1
bL bC ;
X L XC

11.

Векторная диаграмма при резонансе токов
В качестве исходного вектора удобно выбрать вектор напряжение.
I=Ia
=0
U
Ia
IC
IL

12. Особенности резонанса токов

1) Полная проводимость всей цепи равна активной проводимости.
y g 2 (bL bC ) 2 g ;
2) ток в неразветвленной части цепи и приложенное к ней напряжение
g g
совпадают по фазе
сos
y
g
1; 0;
3) Ток в неразветвленной части цепи достигает минимальное значение
I U y U g I МИН ;
4) Ток в неразветвленной части цепи равен активному току
I U y U g Iа ;
5) Токи в ветвях с индуктивностью и емкостью равны руг другу и
противоположны по направлению. Эти токи могут значительно
превышать ток в неразветвленной части цепи:
I L IC ;

13. 4. Мощность однофазного тока. Треугольники мощностей. Коэффициент мощности.

Если все стороны треугольника токов умножить на напряжение,
получим треугольник мощностей:
О
Ia*U=P
0
А
IP*U=Q
U
OAB – треугольник мощностей
I*U=S
В
S U I – полная мощность, ВА
P I a U U I сos
– активная мощность, Вт;
Q I P U U I sin
– реактивная мощность, ВАр
P S сos ; Q S sin ; S P 2 Q 2 ;

14. КОЭФФИЦИЕНТ МОЩНОСТИ

В ЭЛЕКТРОТЕХНИКЕ принято
МОЩНОСТИ.
сos
называть КОЭФФИЦИЕНТОМ
Источник электроэнергии должен выбираться на полную мощность,
а в приемнике в полезную преобразуется только активная
мощность. Поэтому повышение коэффициента мощности
представляет собой важную задачей. Это повышение может быть
осуществлено различными методами:
1) Подключением параллельно входным зажимам электропитания
специальных конденсаторов;
2) Применением электромашинных синхронных компенсаторов;
3) Отключением электрооборудования, работающего в режиме
Холостого Хода.

15. 5. СИМВОЛИЧЕСКИЙ МЕТОД АНАЛИЗА И РАСЧЕТА ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Метод основан на использовании комплексных чисел (КЧ).
Существенное упрощение расчетов достигается путем замены
вращающихся векторов, изображающих синусоидальные функции
времени комплексными числами. В этом случае оказывается
возможным распространить все методы расчета цепей
постоянного тока на цепи переменного тока.
j 1 – мнимая единица
Вводится понятие комплексной плоскости,

16.

+j
а2
А
+1
0
a1
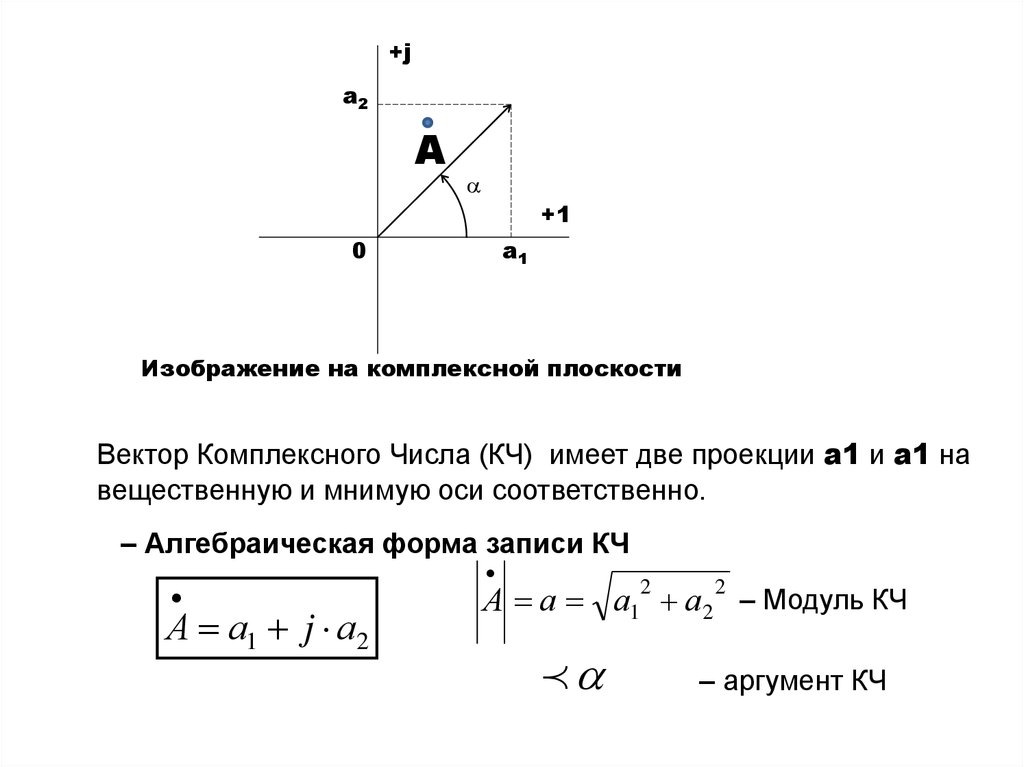
Изображение на комплексной плоскости
Вектор Комплексного Числа (КЧ) имеет две проекции а1 и а1 на
вещественную и мнимую оси соответственно.
– Алгебраическая форма записи КЧ
А а1 j а2
2
2
А а а1 а2 – Модуль КЧ
– аргумент КЧ

17.

- Тригонометрическая форма записи КЧ
а1 а cos ;
а2 а sin ;
А а (cos j sin );
- Показательная форма записи КЧ
Если воспользоваться формулой Эйлера , то получим
показательную форму записи КЧ:
А а е j ;

18.

Комплексно сопряженные числа
Сопряженными называются два таких КЧ, у которых
действительные части одинаковые, а мнимые отличаются только
знаком. Обозначаются со звездочкой наверху
*
А а1 j а2 а(cos j sin ) a е j ;

19. 6. ЗАКОНЫ ОМА И КИРХГОФА В СИМВОЛИЧЕСКОЙ ФОРМЕ

Закон Ома в символической форме
I
U
;
Z
Z r j ( X L X C ) – комплекс полного сопротивления;
1
– комплекс полной проводимости;
Y g jb
Z
Первый закон Кирхгофа в символической форме
n
I
0;
К 1 К
Второй закон Кирхгофа в символической форме
m
E
i 1
i
n
I
К 1 К
ZK;

20.

Комплекс мощности
*
S U I U e j u I e j i U I e j ( u i ) U I e j ;
S U I (cos j sin ) P jQ;
Действительная часть комплекса полной мощности равна
активной мощности, а мнимая часть – реактивной части.