Похожие презентации:
Вынужденные гармонические колебания стержней с распределенной массой при изгибе
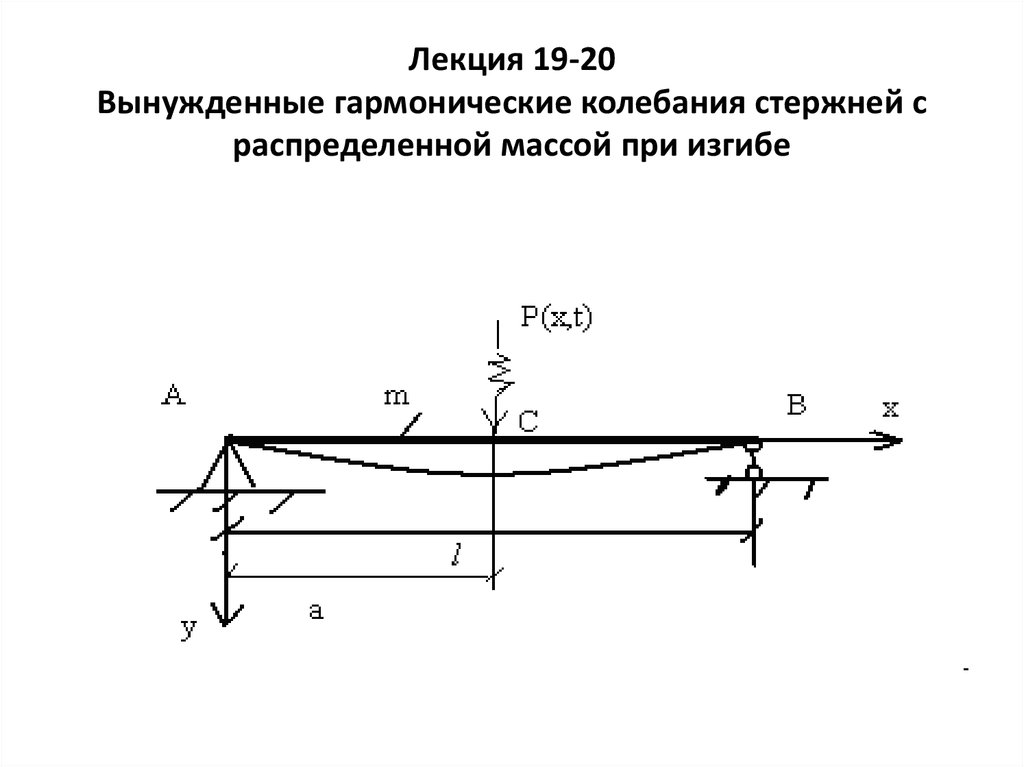
1. Лекция 19-20 Вынужденные гармонические колебания стержней с распределенной массой при изгибе
2. Дифференциальное уравнение вынужденных колебаний
4EI
y
m
2
y
x 4
t 2
y y o y част
PSin t ,
y ( x, t ) y ( x) Sin t
y m y P
,
4
2
EI t
EI
x
y y o yчаст
4
2
2
sk 4
m
u l
kl,
EI
2
4
m k2
EI
m
k
,
EI
2
4
3. Если на балке рассматриваются 2 участка (АС, СВ), то решение уравнения (1) необходимо составлять на каждом участке и
использоватьусловия
сопряжения на границе участков.
Например, на 1 участке нет внешней
нагрузки, поэтому уравнение (1) можно
рассматривать как однородное и
использовать решение однородного
уравнения.
4. Решение дифференциального уравнения на 2-х участках
y1/ (0)M 1 (0)
Q1 (0)
y1 ( x) y1 (0) A(kx)
B(kx) 2 C (kx) 3 D(kx)
k
k EI
k EI
ch(kx) Cos(kx)
A(kx)
,
2
ch(kx) Cos(kx)
C (kx)
,
2
sh(kx) Sin (kx)
B(kx)
,
2
sh(kx) Sin (kx)
D(kx)
2
M 1
Q1
y 2 ( x ) y1 ( x ) 2
C ( kx1 ) 3
D ( kx1 ),
k EI
k EI
M 1 M 1 ,
Q1 Q1 ,
x1 x a
5. Формула для амплитудной функции прогибов на любом участке балки для случая действия системы гармонических сосредоточенных сил,
моментови
равномерно распределенных нагрузок
y / ( 0)
M ( 0)
Q ( 0)
y ( x) y (0) A(kx)
B(kx) 2 C (kx) 3 D(kx)
k
k EI
k EI
Pi
Mi
q i
3 D k ( x ai ) 2 C k ( x ai ) 4 A k ( x ai ) 1
1 k EI
1 k EI
1 k EI
6. Формулы для амплитудных функций прогибов, изгибающих моментов и поперечных сил
M ( 0)Q ( 0)
C ( kx)
2
kEI
k EI
P
Mi
q
2 i C k ( x a i )
B k ( x a i ) 3 i D k ( x a i )
1 k EI
1 k EI
1 k EI
y ( x ) y (0) kD( kx) y (0) A( kx)
/
/
B ( kx)
M ( x ) EIy (0) k 2 C( kx ) EIy / (0)kD (kx ) M (0)A (kx )
Q(0)
B(kx )
k
P
q i
C k ( x a i ) ,
i B k ( x a i ) M i A k ( x a i )
2
1 k
1
1 k
Q( x ) EIy (0)k 3 B( kx ) EIy / (0)k 2 C(kx ) M (0) kD (kx ) Q(0)A(kx )
Pi A k ( x a i ) M i kD k ( x a i )
1
1
1
q i
k
B k ( x a i )
7. Граничные условия для балки шарнирно опертой двумя концами, находящейся под действием сосредоточенной силы Р
∆М1 =0, ∆Q1=P, ∆qi =0x 0
y1 (0) 0, M 1 (0) 0,
x l
y 2 (l ) 0, M 2 (l ) 0
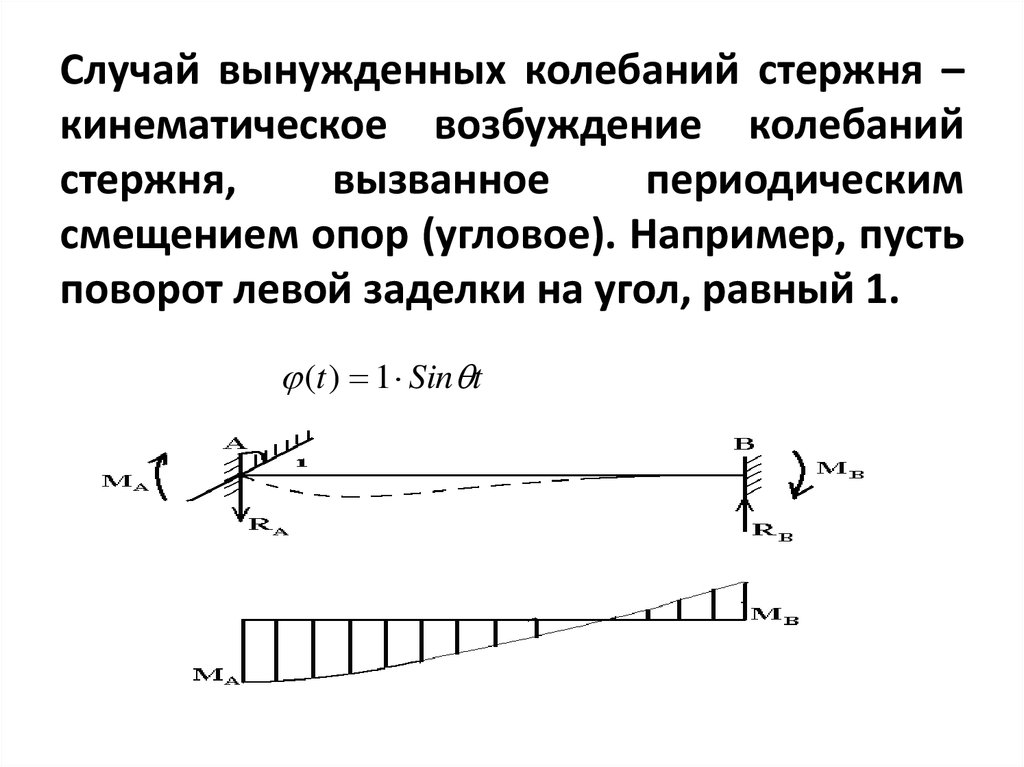
8. Случай вынужденных колебаний стержня – кинематическое возбуждение колебаний стержня, вызванное периодическим смещением опор
(угловое). Например, пустьповорот левой заделки на угол, равный 1.
(t ) 1 Sin t
9. Решение и граничные условия
MAQA
1
y1 ( x) B(kx) 2 C (kx) 3 D(kx)
k
k EI
k EI
y(0) 0,
y (0) 1,
/
2
m
u l4
EI
Mo M A,
Qo Q A
10. Формулы для реактивных моментов и сил
4 EI6 EI
MA
2 (u ), R A 2 5 (u ),
l
l
2 EI
6 EI
MB
3 (u ), RB 2 6 (u ),
l
l
u chuSinu shuCosu
2 (u )
4
1 chuCosu
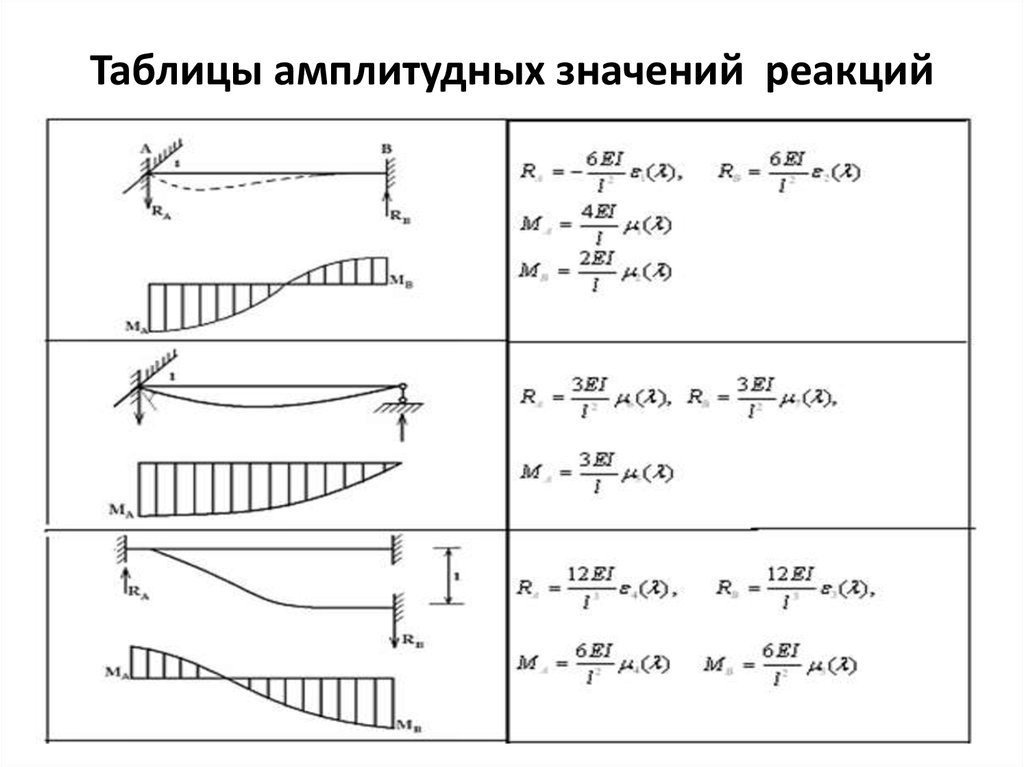
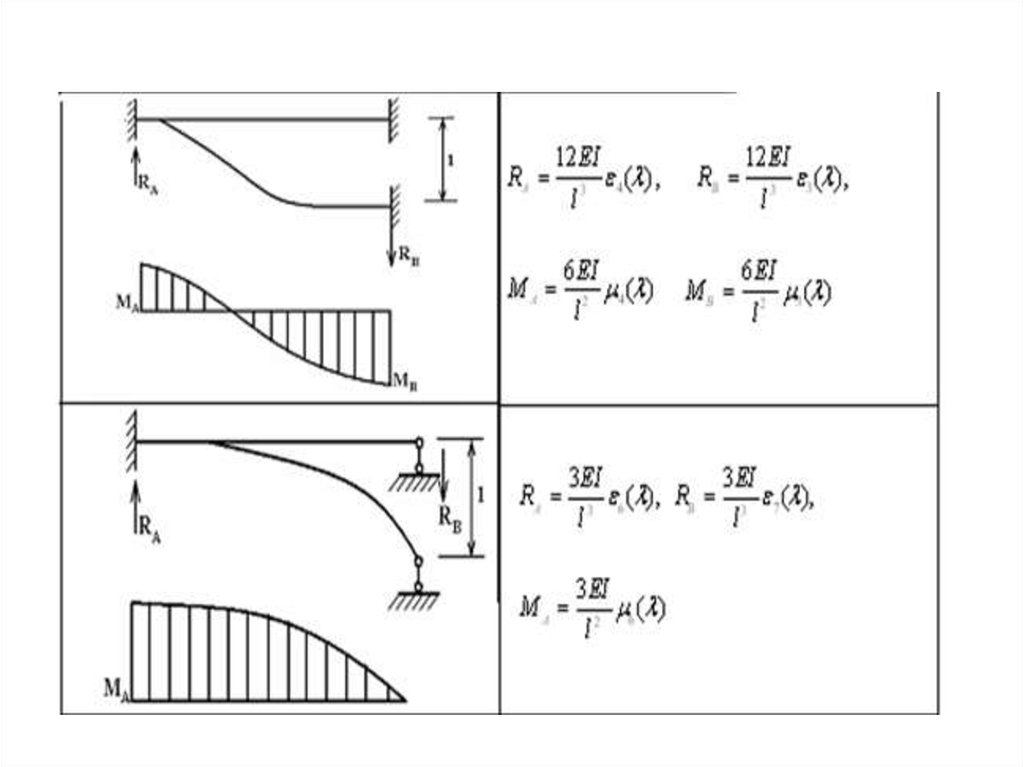
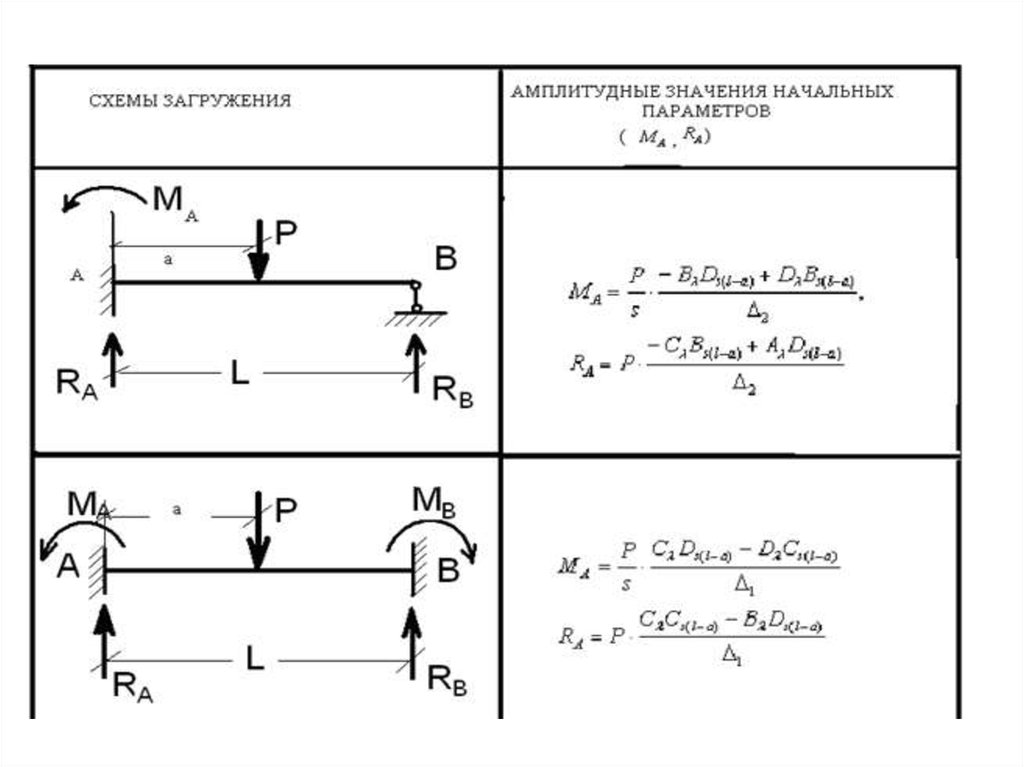
11. Таблицы амплитудных значений реакций
12.
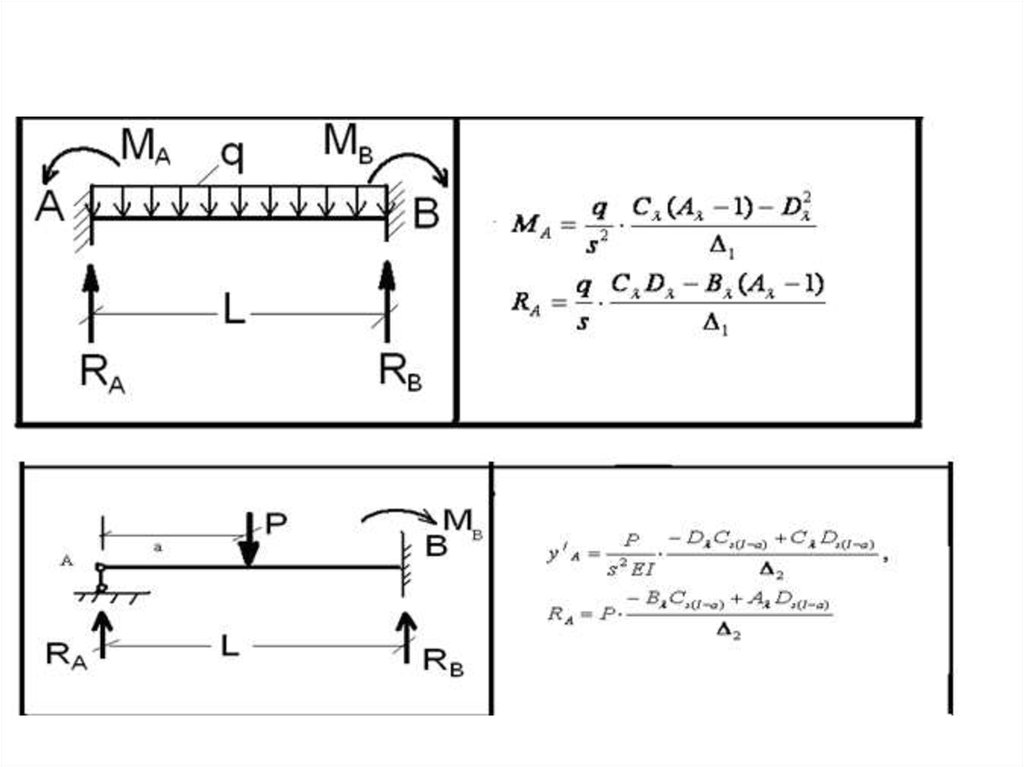
13.
14.
15. Круговые функции
16.
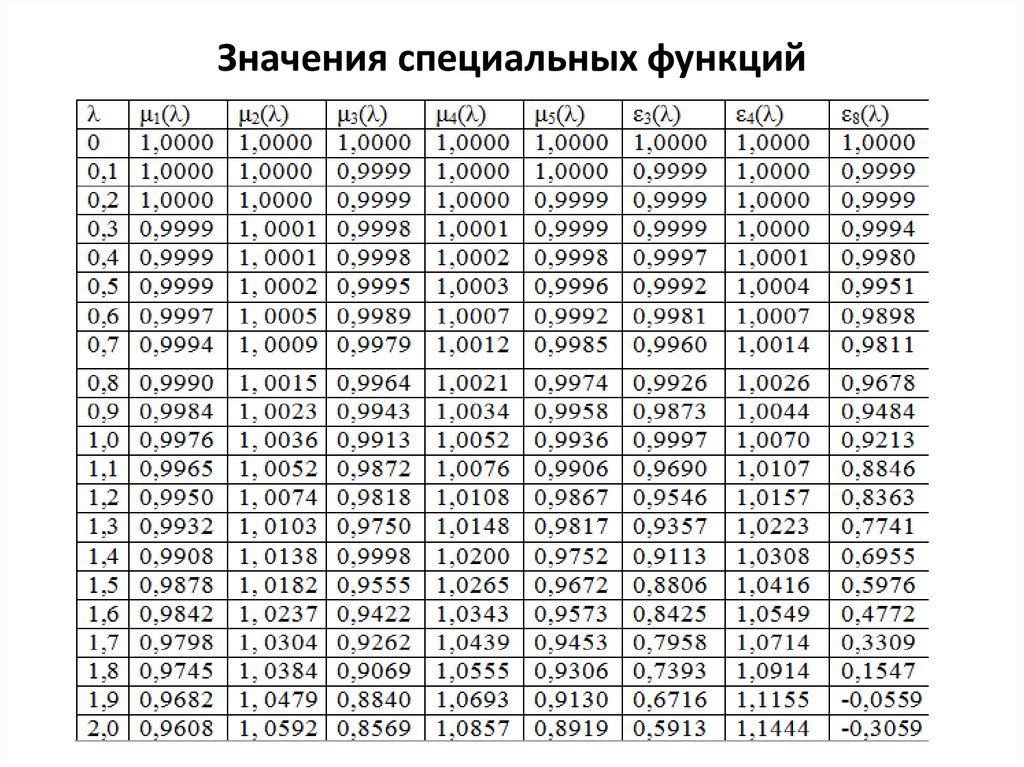
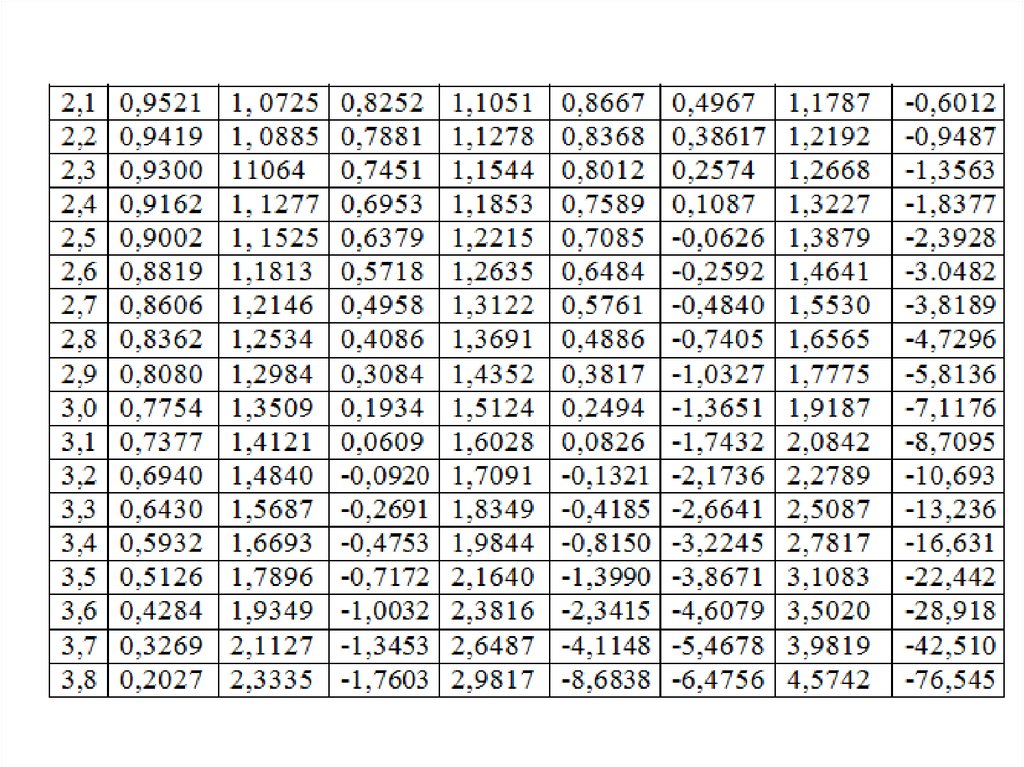
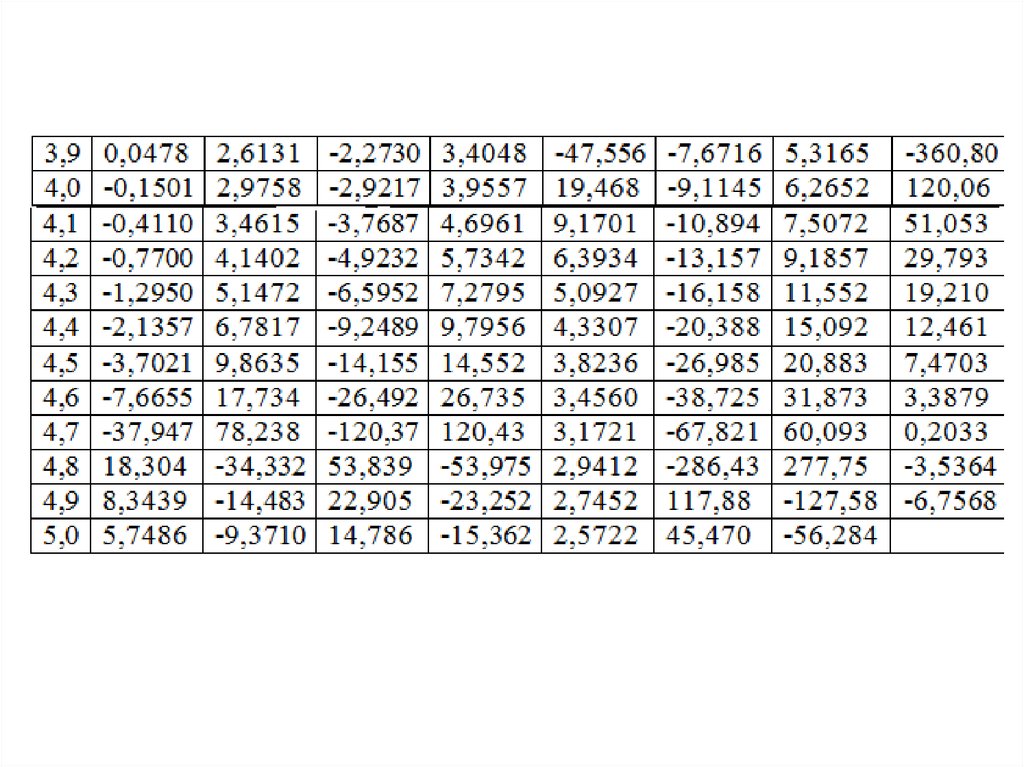
17. Значения специальных функций
18.
19.
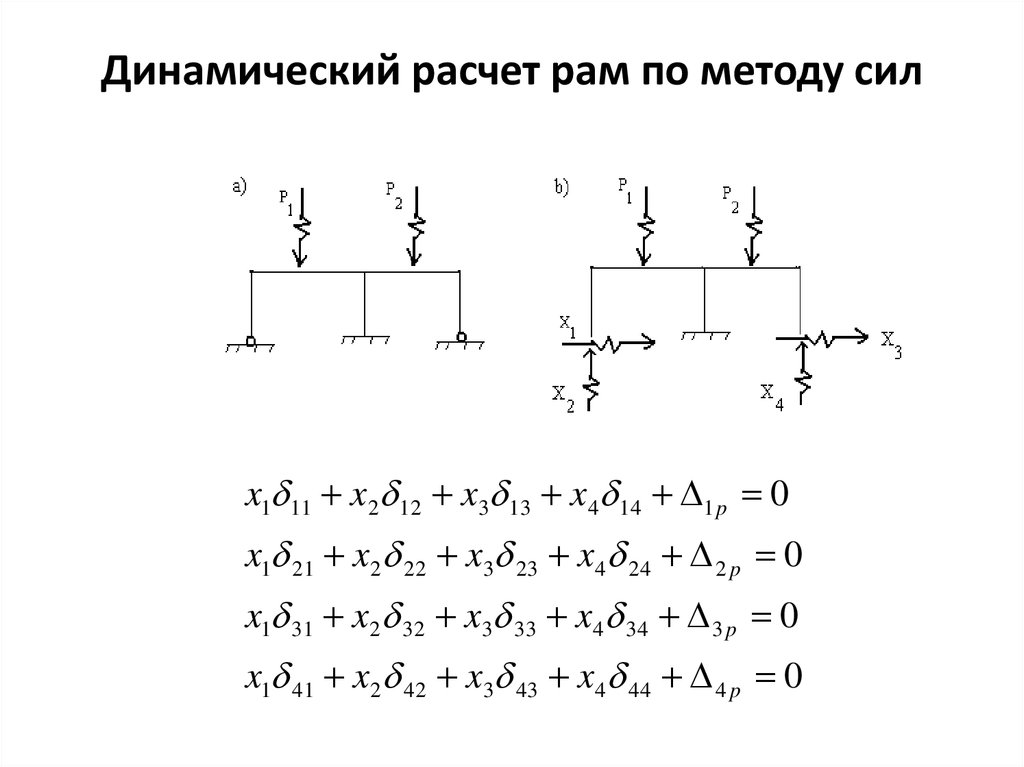
20. Динамический расчет рам по методу сил
x1 11 x2 12 x3 13 x4 14 1 p 0x1 21 x2 22 x3 23 x4 24 2 p 0
x1 31 x2 32 x3 33 x4 34 3 p 0
x1 41 x2 42 x3 43 x4 44 4 p 0
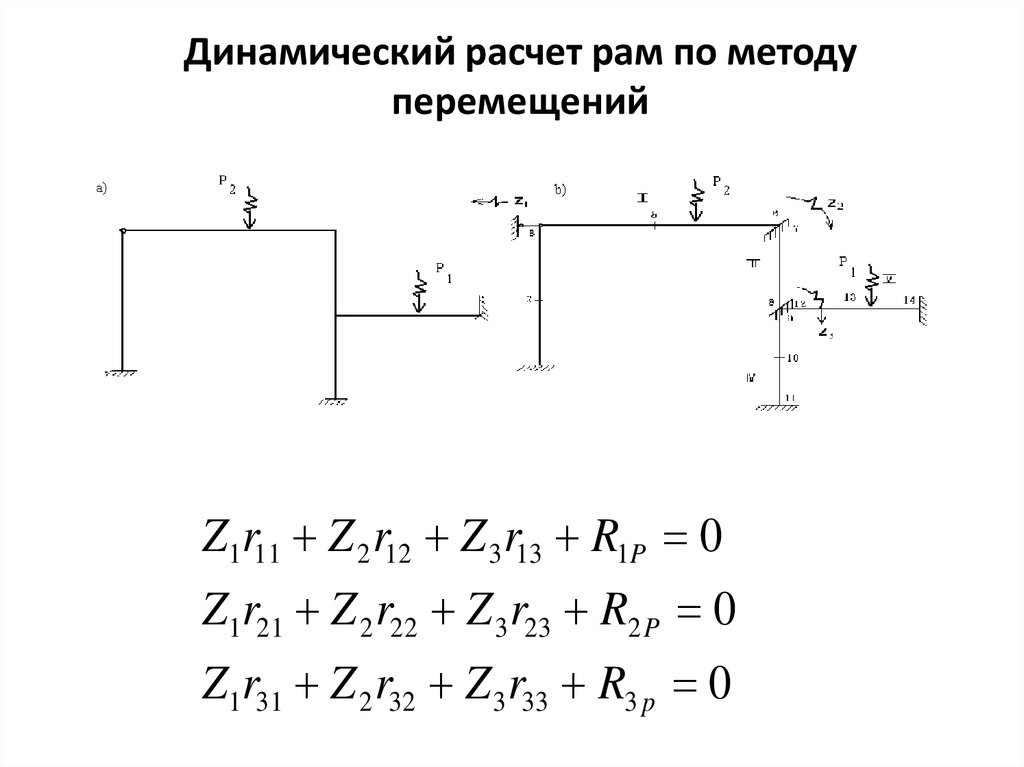
21. Динамический расчет рам по методу перемещений
Z1r11 Z 2 r12 Z 3 r13 R1P 0Z1r21 Z 2 r22 Z 3 r23 R2 P 0
Z1r31 Z 2 r32 Z 3 r33 R3 p 0









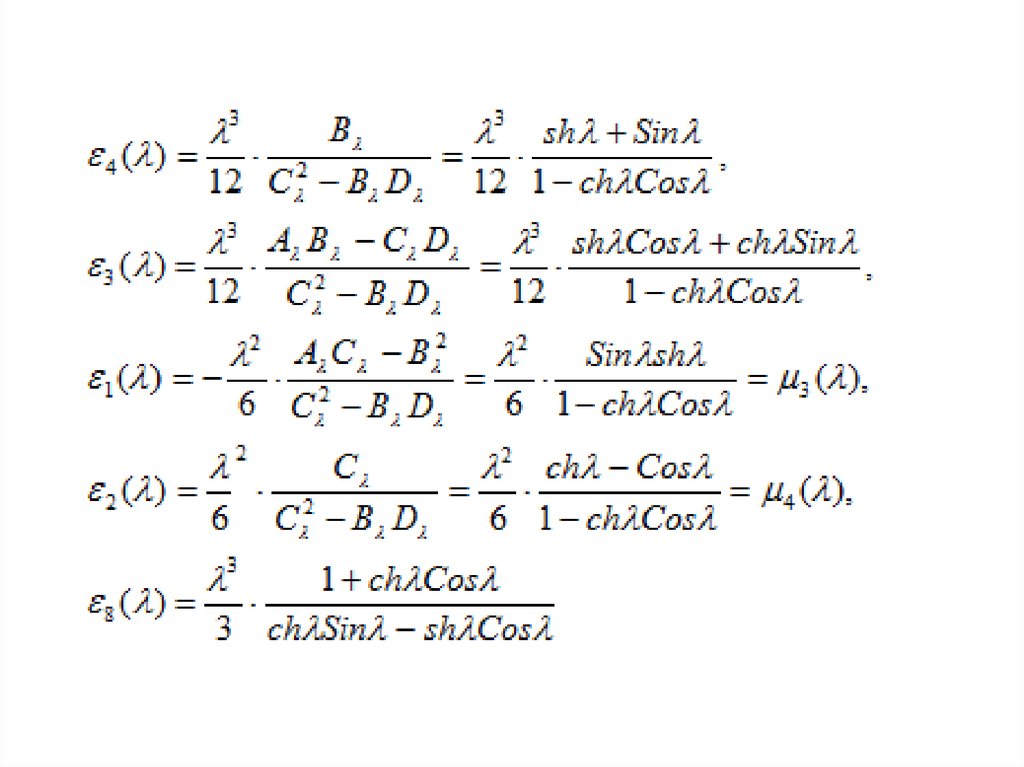

 Математика
Математика








