Математические модели систем распределения информации

1.

ВОЕННАЯ АКАДЕМИЯ СВЯЗИ
22 кафедра (сетей связи и систем коммутации)
Дисциплина
СЕТИ СВЯЗИ И СИСТЕМЫ КОММУТАЦИИ
Раздел 1. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ ИНФОРМАЦИИ
Тема № 1 “Потоки вызовов, нагрузка и качество
обслуживания”
Занятие №2(групповое)
“Математические модели систем распределения
информации”

2.

Цели и вопросы занятия
2
Изучить компоненты математических моделей систем
распределения информации и их условные обозначения,
используемые в технической литературе
Учебные вопросы:
1.Компоненты математических моделей систем
распределения информации.
2.Классификация Кендалла-Башарина.

3.

Л И Т Е Р А Т У Р А:
3
1. Зотов В. М. Основы теории распределения информации.
– СПб.: ВАС, 2013 г.
1. Зотов В. М. Основы теории телетрафика. – СПб.: ВАС,
2004 г.
1.
3. Теория телетрафика / Корнышев Ю.Н., Пшеничников
А.П., Харкевич А.Д. Учебник для вузов. – М.: Радио и
связь, 1996 г.

4.

4
1.Компоненты математических
моделей
1.
систем распределения информации

5.

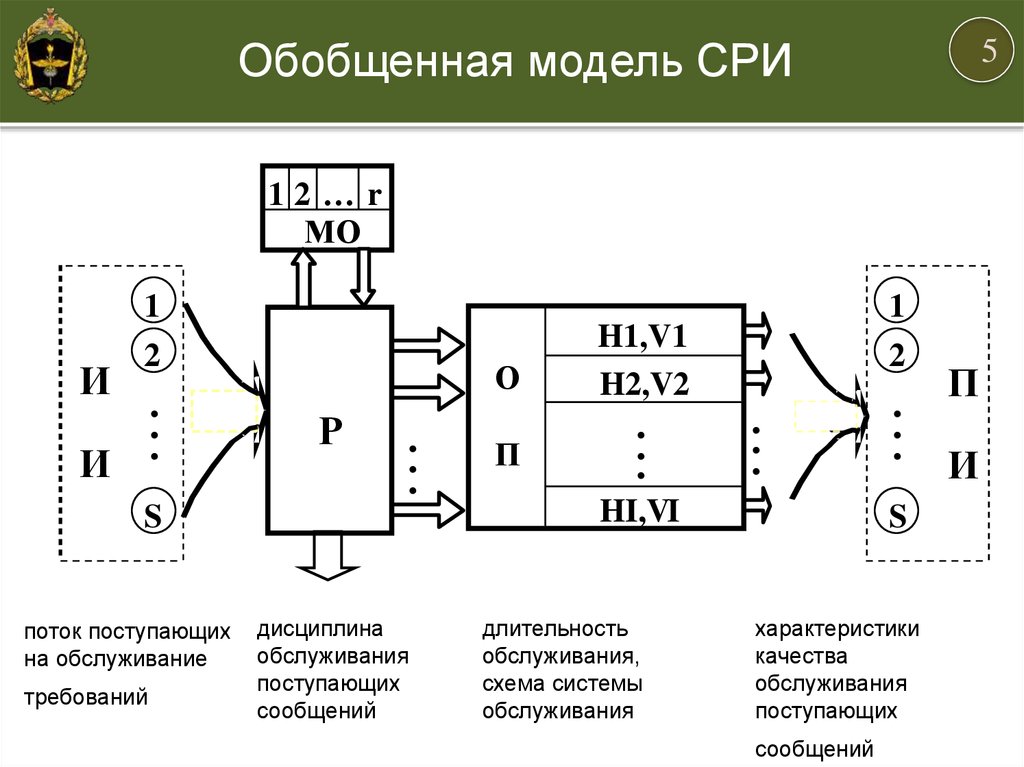
Обобщенная модель СРИ
5
12…r
МО
1
И
1
2
.
.
И .
О
Р
.
.
.
S
поток поступающих
на обслуживание
требований
дисциплина
обслуживания
поступающих
сообщений
П
H1,V1
H2,V2
.
..
2
..
.
HI,VI
длительность
обслуживания,
схема системы
обслуживания
.
.
.
S
характеристики
качества
обслуживания
поступающих
сообщений
П
И

6.

Основные понятия
Вероятность события есть численная мера
степени объективной возможности этого
события.
P(A) = n / m
Вероятность может принимать значения от 0 до 1.
6

7.

Основные понятия
Случайные величины могут быть двух типов:
дискретные (прерывные), принимающие только
отделённые друг от друга значения, которые можно
пронумеровать;
непрерывные (аналоговые), которые могут
принимать любое значение из некоторого промежутка.
7

8.

Основные понятия
Математическое описание случайных величин
предполагает задание закона распределения,
устанавливающего соответствие между
значениями
случайной
величины
и
вероятностью их появления.
8

9.

Способы задания закона распределения
9
а) аналитически в виде математического выражения, отражающего зависимость
вероятности от значения случайной величины:
Pn(X=k) = Сnk pk qn-k, 0<р<1, k = 0, 1, 2, …, n;
i
λ τ λτ
Pi τ
е .
i!
б) таблично в виде ряда распределения случайной величины, в котором
перечислены возможные значения случайной величины и соответствующие им
вероятности:
в) графически в виде многоугольника
распределения, где по оси абсцисс
откладываются возможные значения
случайной величины, а по оси ординат –
вероятности этих значений

10.

Непрерывные случайные величины
10
Функция
распределения
вероятностей F(x)
случайной
величины
X
представляет
собой
вероятность того, что случайная величина X
примет значение меньшее, чем некоторое заданное
значение x:
Вероятность
того,
что
случайная
величина
примет значение из некоторого интервала (a, b),
определяется через функцию распределения как

11.

t
,
0
;
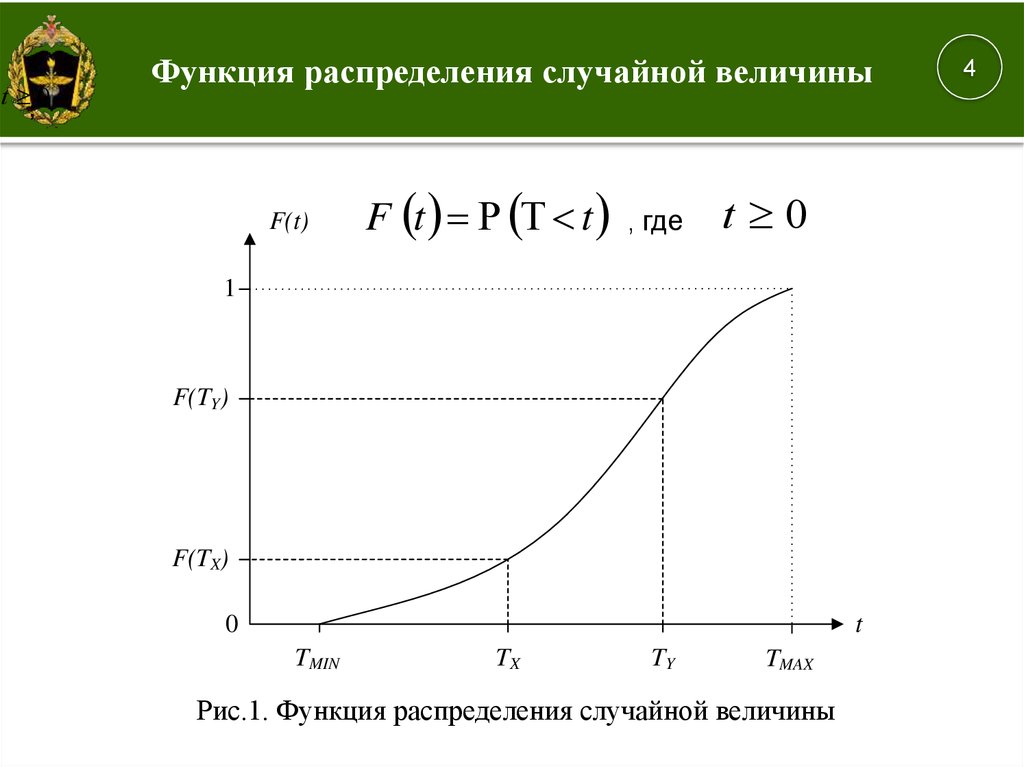
Функция распределения случайной величины
F(t)
F t t
, где
t 0
1
F(TY)
F(TX)
0
t
TMIN
TX
TY
TMAX
Рис.1. Функция распределения случайной величины
4

12.

Числовые характеристики случайной
величины
12
среднее значение, около которого группируются
возможные значения случайной величины;
степень разбросанности этих значений относительно
среднего;
асимметрию (или «скошенность») плотности
распределения и так далее.
Начальные моменты рассматриваются
относительно начала координат.
Центральные моменты рассматриваются
относительно математического ожидания,
то есть центра распределения.

13.

Начальный момент s-го порядка
Первый начальный момент α1[X ] случайной
величины
Х
называется
математическим
ожиданием
или
средним
значением случайной
величины и обозначается М[X] = α1[X ].
1
3

14.

Центральный момент s-го порядка
1
4
Разность между значениями случайной величины
и
ее математическим
ожиданием (X – М[X])
представляет
собой
отклонение случайной
величины Х от ее математического ожидания и
называется центрированной случайной величиной.

15.

Дисперсия
1
5
Второй
центральный
момент
называется
дисперсией
случайной величины и обозначается
D[X]= β2[X].
Среднее квадратическое отклонение (стандартное отклонение)
σ(X) = √D(X).

16.

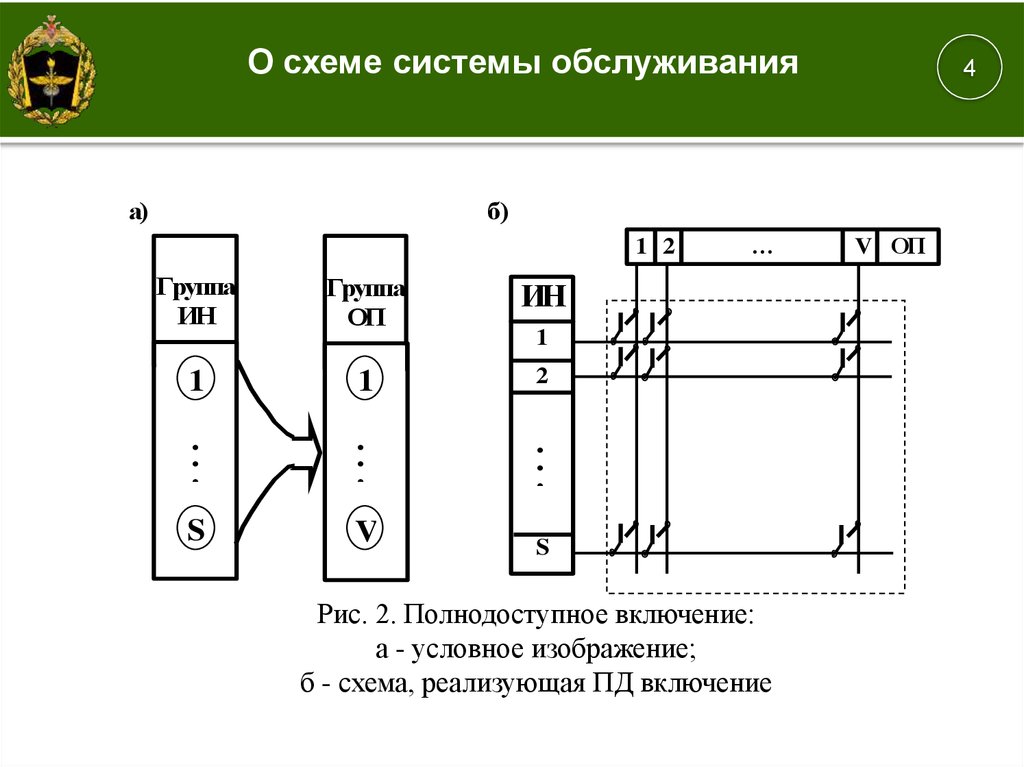
О схеме системы обслуживания
а)
4
б)
1 2
Группа
ИН
Группа
ОП
ИН
1
1
2
.
.
.
.
.
.
.
.
.
S
V
S
…
1
1.
Рис. 2. Полнодоступное включение:
а - условное изображение;
б - схема, реализующая ПД включение
V ОП

17.

,
О дисциплине обслуживания
tс
4
- способы обслуживания вызовов (без потерь, с потерями, с ожиданием)
б)
а)
Z
S=V
p=0
tож=0
r=0
Y
в)
S>V
p>0
tож=0
r=0
Z
Y=Z(1-p)
Z
S>V
p=0
tож>0
r 8
Y=Z
R
- порядок обслуживания вызовов системой РИ (в порядке очередности, в
случайном порядке, с приоритетами);
- режимы искания выходов схемы (свободное, групповое, вынужденное,
серийное и т.д.)

18.

О характеристиках качества обслуживания
1.
p (tож > 0);
4

19.

4
2.Классификация1.Кендалла-Башарина

20.

4
Цель: компактная запись математических моделей
Первый
символ
условной
записи
обозначает
функцию
распределения
промежутков между вызовами, второй - функцию распределения длительности
обслуживания, третий и последующие - схему и дисциплину обслуживания.
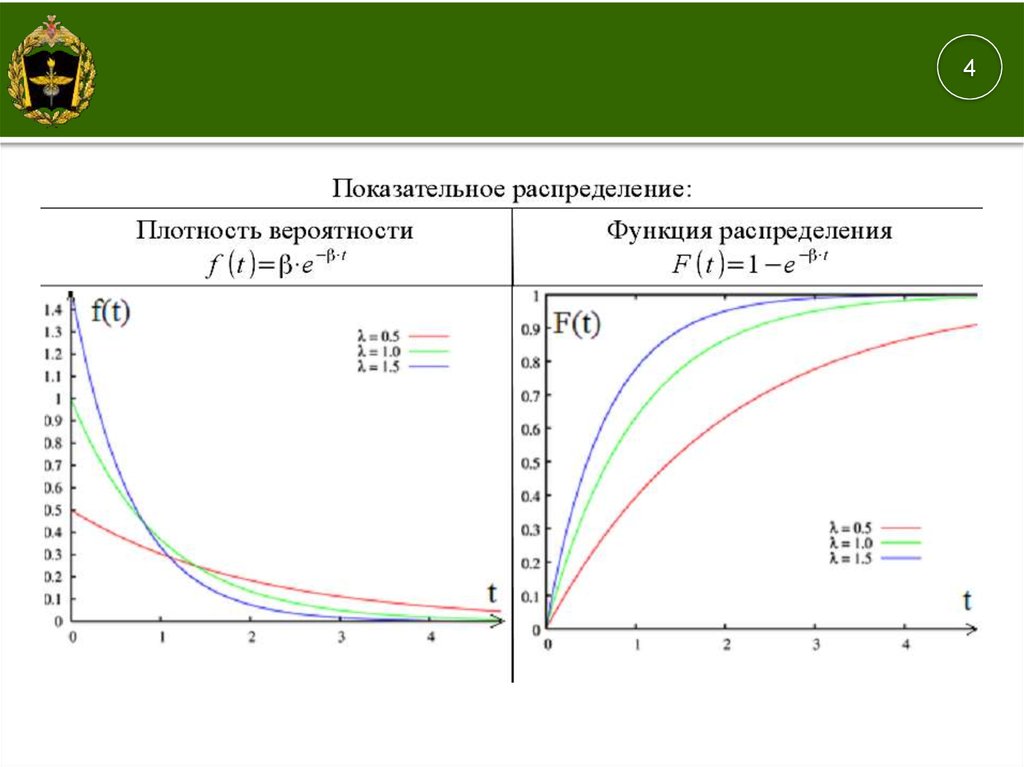
1. следующие обозначения:
Конкретные виды распределений получили
M – показательное (экспоненциальное) распределение;
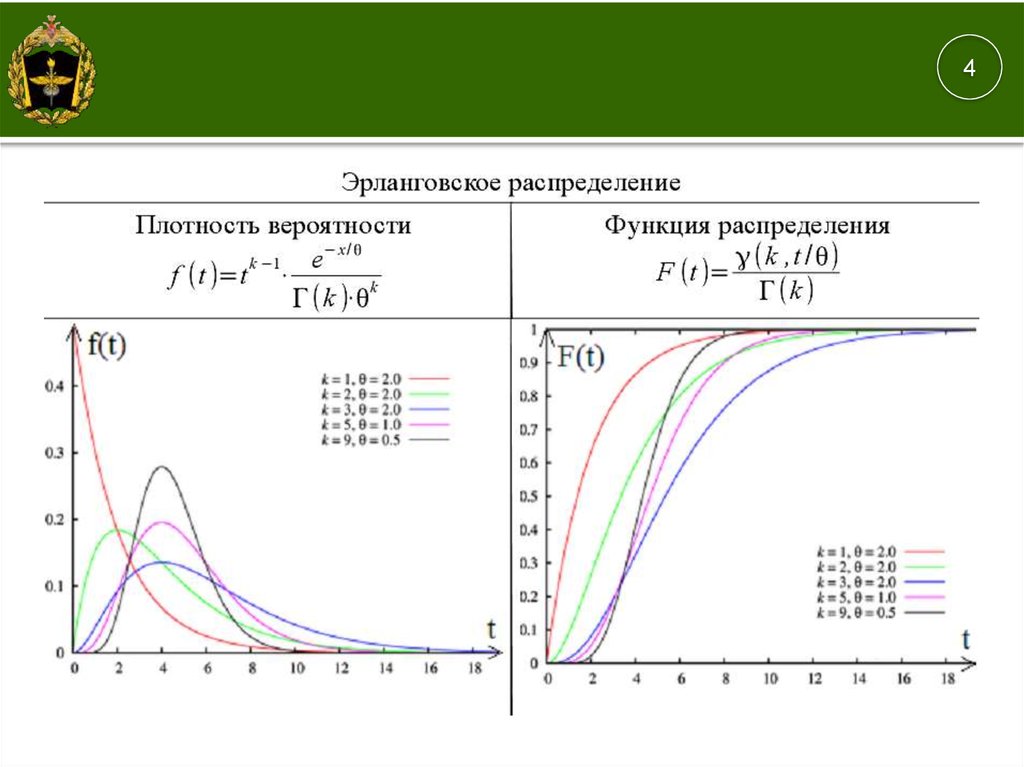
E – эрланговское (гамма) распределение;
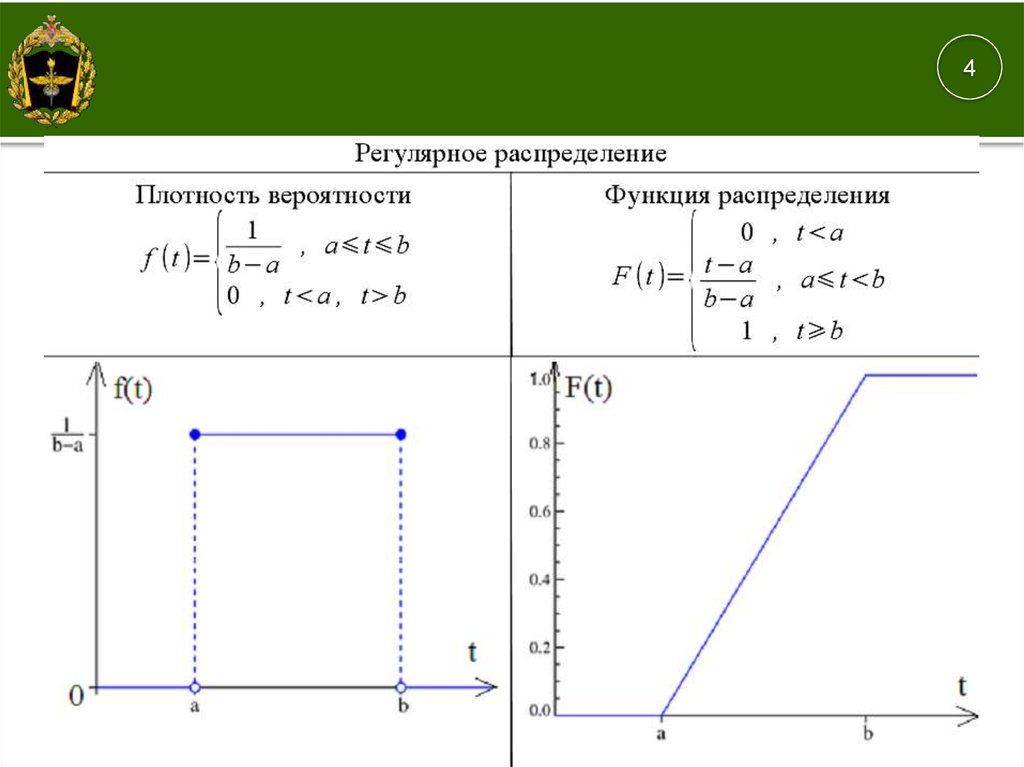
D – детерминированное (регулярное), что соответствует постоянным интервалам
между вызовами или постоянной длительности обслуживания;
G – произвольное распределение.
Примеры записи:
M/M/S
M /M /V

21.

4
1.

22.

4
1.

23.

4
1.