Математические модели потоков телефонных вызовов

1.

ВОЕННАЯ АКАДЕМИЯ СВЯЗИ
22 кафедра (сетей связи и систем коммутации)
Дисциплина
СЕТИ СВЯЗИ И СИСТЕМЫ КОММУТАЦИИ
Раздел 1. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ ИНФОРМАЦИИ
Тема № 1 “Потоки вызовов, нагрузка и качество
обслуживания”
Занятие №4(групповое)
“Математические модели потоков телефонных вызовов”

2.

Цели и вопросы занятия
2
Изучить свойства и характеристики основных математических моделей потоков
телефонных вызовов
Учебные вопросы:
1.Простейший поток. Свойства и характеристики.
2.Примитивный поток. Свойства и характеристики.
3.Поток с повторными вызовами.
4.Потоки Пальма и Эрланга.

3.

Л И Т Е Р А Т У Р А:
3
1.Зотов В. М. Основы теории распределения
информации. – СПб.: ВАС, 2013 г.
2. Теория телетрафика / Корнышев Ю.Н., Пшеничников
А.П., Харкевич А.Д. Учебник для вузов. – М.: Радио и
1.
связь, 1996 г.

4.

Характеристики потоков вызовов
19
Λ 0, t – математическое ожидание
Ведущая функция потока
числа вызовов, поступающих в интервале времени [0, t)
Параметр потока - предел отношения вероятности поступления хотя бы
одного вызова за время [t, t + ) к длине этого отрезка времени при → 0
lim 0
1 t , t
(t )
Интенсивность стационарного потока - математическое ожидание
числа вызовов, поступающих в единицу времени
Λ 0, t t ,
Для нестационарных потоков:
средняя интенсивность нестационарного потока:
t1 , t2
мгновенная интенсивность нестационарного потока: t lim
Λ 0, t2 Λ 0, t1
,
t2 t1
Λ 0, t Λ 0, t
t 0

5.

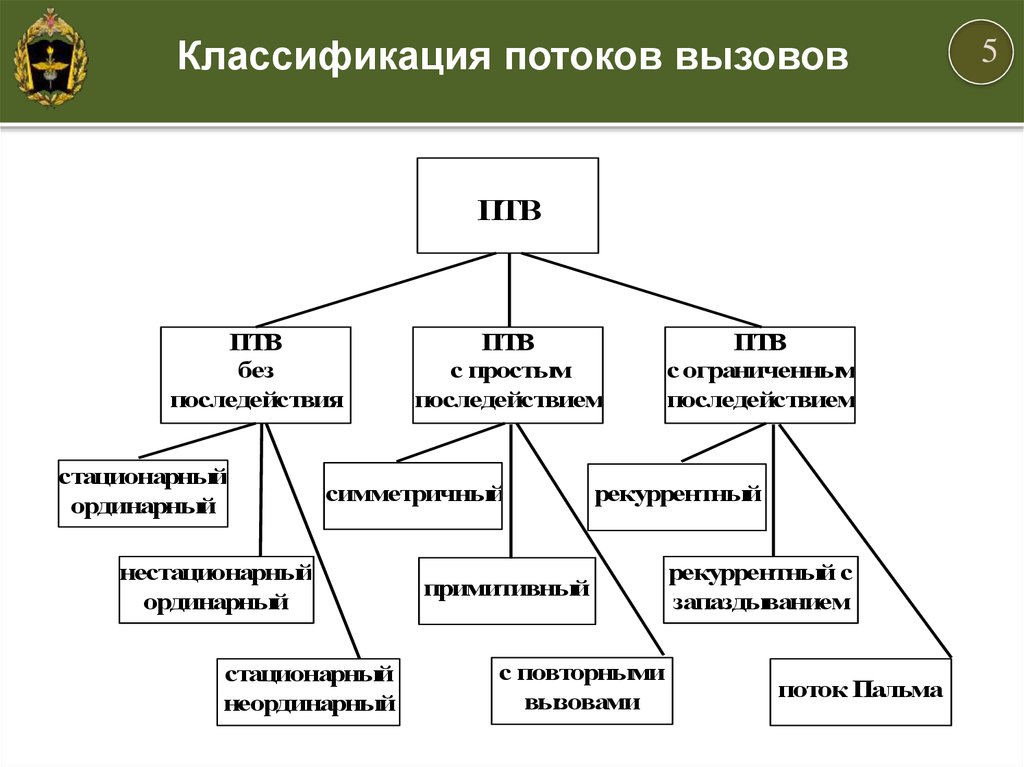
Классификация потоков вызовов
ПТВ
ПТВ
без
последействия
стационарный
ординарный
ПТВ
с простым
последействием
симметричный
нестационарный
ординарный
стационарный
неординарный
ПТВ
с ограниченным
последействием
рекуррентный
примитивный
с повторными
вызовами
рекуррентный с
запаздыванием
поток Пальма
5

6.

5
Вариант 1
1. Дайте понятие ординарности.
2. Вызовы поступают на 3, 5, 6, 9, 13, 18 и 26 единице условного времени.
Отобразить графически все возможные способы задания потоков.
Вариант 2
1. Дайте понятие стационарности. 1.
2. Какими из трех известных свойств может обладать (не обладать) поток
вызовов от 10 абонентов. Ответ обосновать.
Вариант 3
1. Дайте понятие последействия.
2. Чему равна интенсивность стационарного потока вызовов, если
известно, что за 4 часа поступило 64 вызова?

7.

5
1.
1. Простейший поток.
Свойства и
характеристики

8.

1 вопрос
Простейшим
потоком
6
вызовов
ППВ
называется
стационарный ординарный поток без последействия.
Поток может быть задан семейством вероятностей
поступления i вызовов за время , которые определяются
по формуле Пуассона:
λ τ
Pi τ
i
1.
i!
е
λτ
i i 1 λτ/i
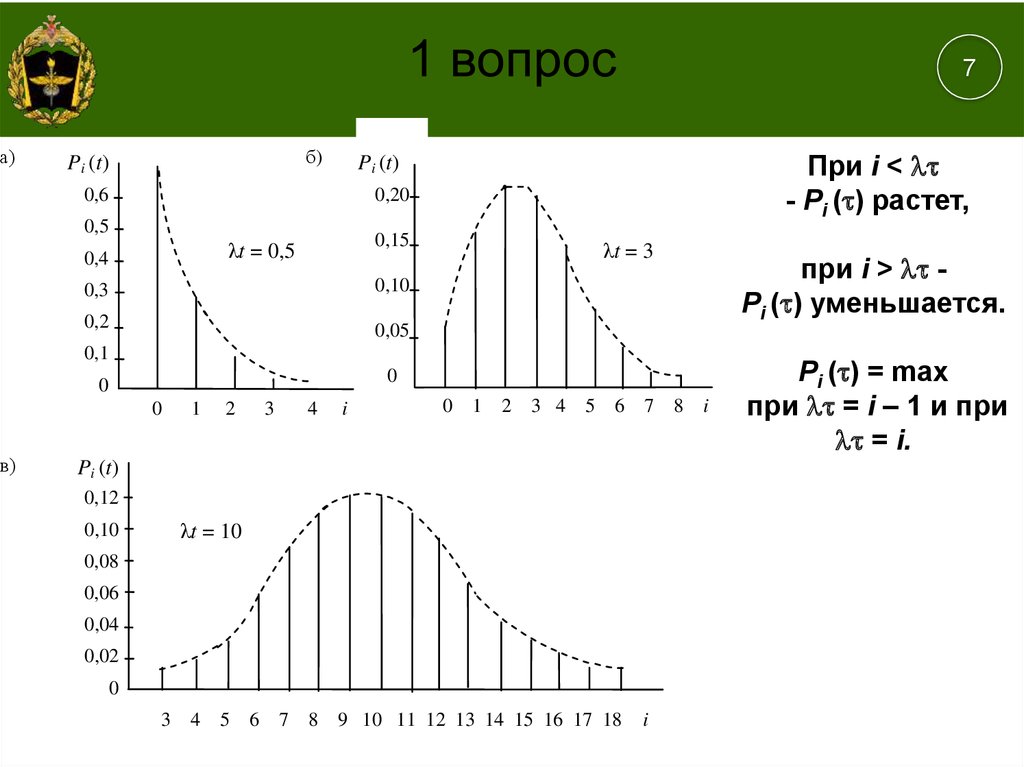
При i < - Pi ( ) растет, при i > - Pi ( ) уменьшается.
Pi ( ) = max при = i – 1 и при = i.

9.

7
а)
б)
Pi (t)
При i <
- Pi ( ) растет,
Pi (t)
0,6
0,20
0,5
0,15
λt = 0,5
0,4
0,3
0,10
0,2
0,05
λt = 3
при i > Pi ( ) уменьшается.
0,1
0
0
0
в)
1
2
3
4
i
0
1
21. 3 4 5
6 7 8
Pi (t)
0,12
λt = 10
0,10
0,08
0,06
0,04
0,02
0
3
4
5
6
7 8
9 10 11 12 13 14 15 16 17 18
i
i
Pi ( ) = max
при = i – 1 и при
= i.

10.

8
1.

11.

9
Другой способ задания случайного потока - определение
закона распределения вероятностей промежутков времени
между вызовами.
Функция распределения F (z) - вероятность того, что
промежуток времени между вызовами будет меньше
заданного z
.
F z Ρ Z z1.
Это равносильно вероятности 1(z) того, что за промежуток z
поступит хотя бы один вызов: Ρ Z z 1 Ρ Z z 1 π 0 z .
λ τ
Pi τ
i
Используя формулу Пуассона
получим:
λ z
F z 1
0
0!
i!
е
λτ
e λz 1 e λz , z 0.
, при i=0

12.

D I λt.
10
M ( Z ) zf ( z ) dz 1 / λ;
0
D Z z 2 f z d z Μ 2 Z 1 λ 2 ;
σ Z
D Z 1 λ .
0
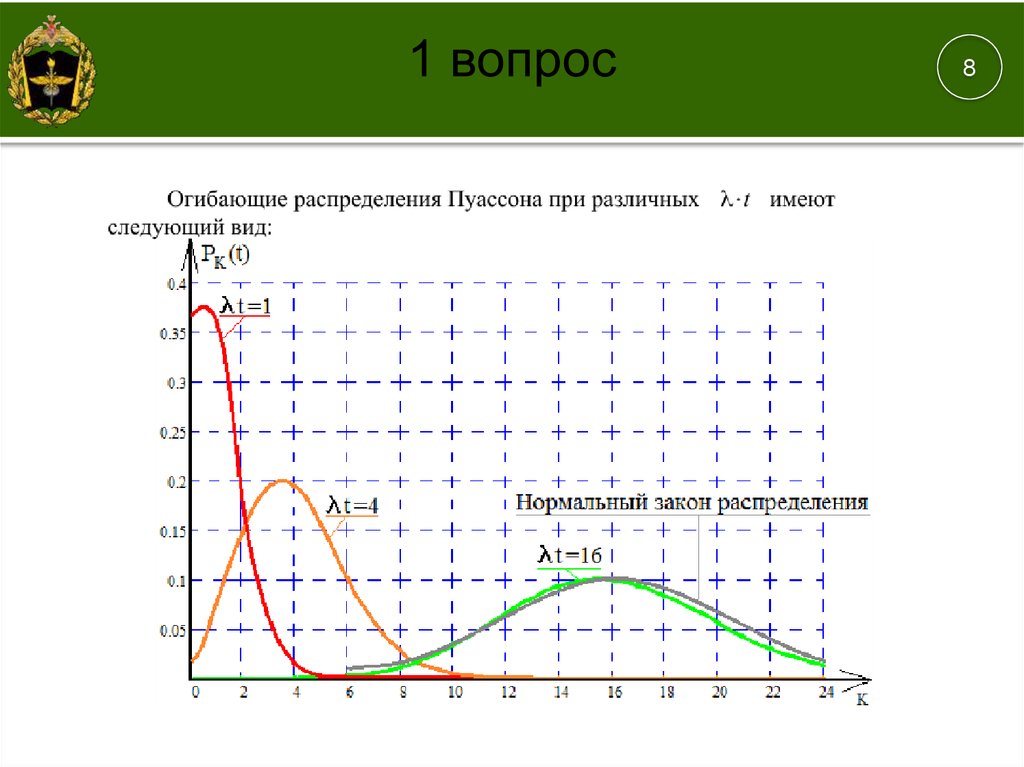
математическое ожидание и дисперсия числа вызовов за промежуток t:
Μ I i Ρi t e
.
i 1
λt
i1. λt i! λt ,
i
D I λt.
i 1
При объединении независимых простейших потоков с параметрами
1 , n образуется общий простейший поток с параметром 1 n
При разъединении поступающего простейшего потока с параметром
n направлений, поток i-го направления также будет простейшим.
на

13.

11
2. Примитивный поток. Свойства и
1.
характеристики.

14.

12
Примитивным называется поток с простым последействием,
параметр которого зависит только от
числа свободных
источников вызовов и прямо пропорционален их числу, т. е.
λ i S i α,
1.
– параметр потока вызовов от одного
свободного источника.
Среднее значение параметра:
i
pi ,
i
где pi – вероятность того, что занято i источников.
Среднее значение параметра от одного
источника:
= / S,

15.

где
13
1 / tсв ,
tсв
–
средняя
= 1 / tсв tзан ,
продолжительность
промежутка
свободности
источника; t зан – средняя продолжительность промежутка занятости
источника.
Распределение промежутка свободности
подчиняется показательному
1.
закону с параметром :
Ρ tсв t 1 e α t .
И, наконец,

16.

14
1.
3. Поток с повторными
вызовами

17.

15
Поток, состоящий из первичных и вторичных (повторных) вызовов,
будем называть потоком с повторными вызовами. Относится он к числу
потоков с простым последействием.
Параметр потока вторичных (повторных) вызовов определяется
произведением числа источников повторных вызовов j на параметр
потока от одного источника v.
1.
Параметр суммарного потока для случаев первичных простейшего и
примитивного соответственно составляет
λ λ jν
j
и
λ S i j λ jν .
S i j j

18.

16
1. и Эрланга
4. Потоки Пальма

19.

4 вопрос
16
Поток с одинаково распределенными промежутками времени между
вызовами
F1 F2 F называется рекуррентным.
Поток с F2 F3 F и
1.
F1 F
называется рекуррентным с запаздыванием.
Ординарный стационарный рекуррентный поток с
запаздыванием называется потоком Пальма.
Важными для практики образцами потоков Пальма являются потоки
Эрланга, которые образуются в результате «просеивания» простейших
потоков.

20.

4 вопрос
16
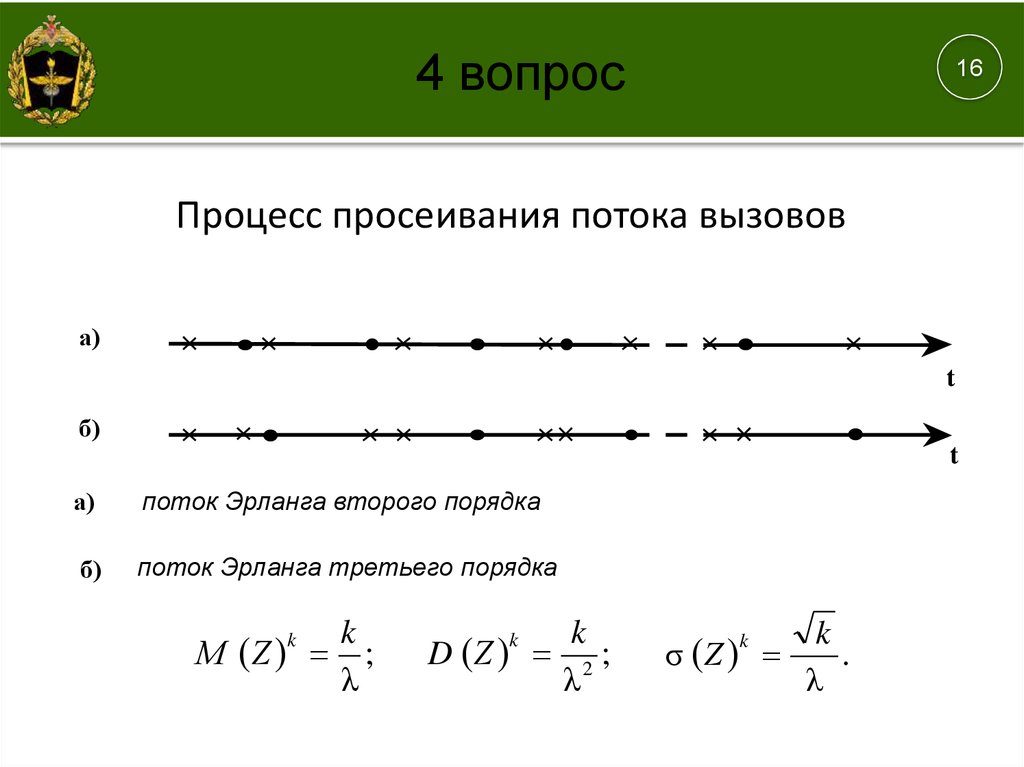
Процесс просеивания потока вызовов
а)
t
1.
б)
t
а)
поток Эрланга второго порядка
б)
поток Эрланга третьего порядка
k
Μ Ζ ;
λ
k
k
D Ζ 2 ;
λ
k
σ Ζ
k
k
.
λ