Структурная механика композитов. Слоистый композит

1.

СТРУКТУРНАЯ МЕХАНИКА КОМПОЗИТОВ
I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
2. Моделирование свойств однонаправленного
композита при различных видах нагружения
i. Продольное растяжение
а. Композит, армированный непрерывными
волокнами
b. Композит, армированный короткими
волокнами
ii. Трансверсальное растяжение
iii. Сдвиг в плоскости волокон
iv. Продольное сжатие
v. Трансверсальное сжатие
3. Моделирование свойств хаотично армированного
композита
4. Моделирование свойств тканевого композита
5. Характеристики упругости композитного монослоя
i. Композит, армированный непрерывными
волокнами
ii. Композит, армированный короткими волокнами
iii. Тканевый композит
iv. Характеристики однонаправленного
композитного монослоя в направлении θᵒ
v. Хаотично армированный композит
6. Связь между напряжениями и деформациями
i. Закон Гука для изотропного материала
ii. Особенности деформирования ортотропных
материалов
iii. Закон Гука для ортотропного материала в
главной системе координат
iv. Закон Гука для ортотропного материала в
произвольной системе координат
II. СЛОИСТЫЙ КОМПОЗИТ
1. Основные положения теории слоистых пластин
2. Деформации слоистого композита
3. Силы и моменты, действующие на слоистый
композит
4. Матрицы жесткости слоистого композита
5. Деформация и кривизна срединной плоскости
6. Напряжения и деформации в слоях композита
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
1. Теории прочности однонаправленного композита
i. Теория максимальных напряжений
ii. Теория максимальных деформаций
iii. Теория Аззи-Цая-Хилла
iv. Теория Цая-Ву
2. Методы прогнозирования прочности слоистого
композита
i. Метод последовательного разрушения слоев
ii. Метод прогнозирования прочности слоистого
композита с учетом накопления микроповреждений
3. Метод оценки прочности хаотично армированных
композитов
i. Подход Хана
ii. Подход Хальпина-Кардоса
1

2.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
КОМПОЗИТНЫЙ МОНОСЛОЙ – это тонкий слой материала, представленный однонаправленным,
хаотично армированным или тканевым композитом
Основные определения:
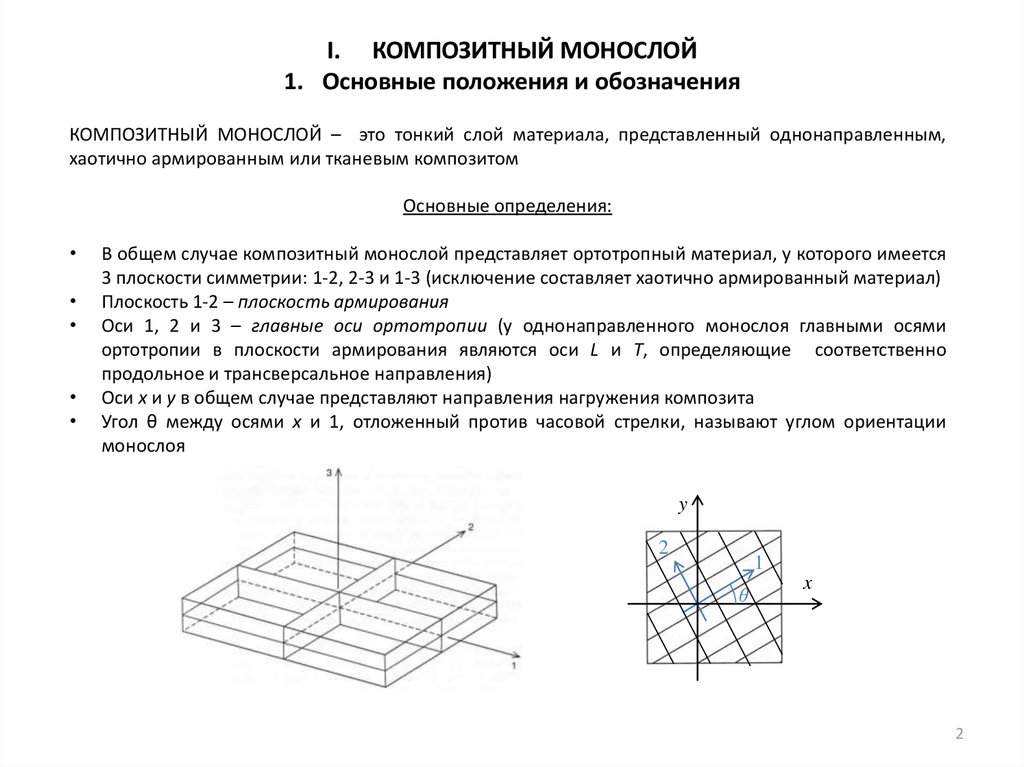
В общем случае композитный монослой представляет ортотропный материал, у которого имеется
3 плоскости симметрии: 1-2, 2-3 и 1-3 (исключение составляет хаотично армированный материал)
Плоскость 1-2 – плоскость армирования
Оси 1, 2 и 3 – главные оси ортотропии (у однонаправленного монослоя главными осями
ортотропии в плоскости армирования являются оси L и T, определяющие соответственно
продольное и трансверсальное направления)
Оси x и y в общем случае представляют направления нагружения композита
Угол θ между осями x и 1, отложенный против часовой стрелки, называют углом ориентации
монослоя
y
2
1
θ
x
2

3.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
Межслойные компоненты тензоров напряжений и деформаций
σ33, τ31, τ32, а также ε33, γ31, и γ32 в рассмотрение композитного
монослоя обычно не включают, сохраняя в тензорах
напряжений
и
деформаций
только
внутрислойные
компоненты:
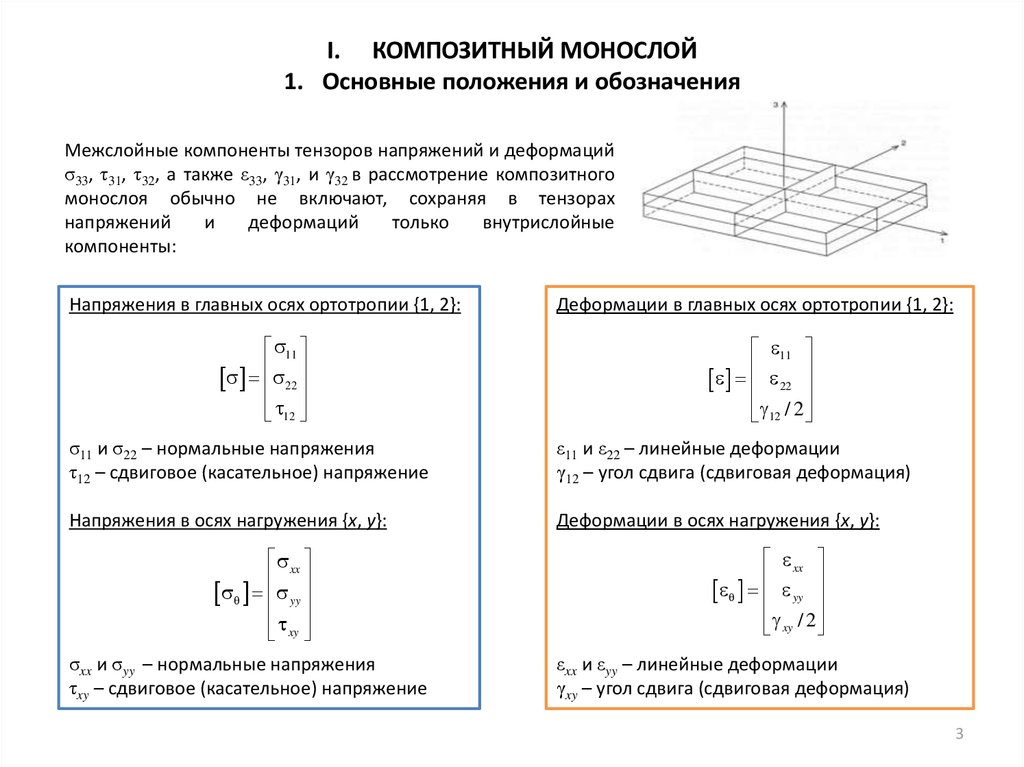
Напряжения в главных осях ортотропии {1, 2}:
Деформации в главных осях ортотропии {1, 2}:
11
22
12
11
22
12 / 2
σ11 и σ22 – нормальные напряжения
τ12 – сдвиговое (касательное) напряжение
ε11 и ε22 – линейные деформации
γ12 – угол сдвига (сдвиговая деформация)
Напряжения в осях нагружения {x, y}:
Деформации в осях нагружения {x, y}:
xx
yy
xy
σxx и σyy – нормальные напряжения
τxy – сдвиговое (касательное) напряжение
xx
yy
xy / 2
εxx и εyy – линейные деформации
γxy – угол сдвига (сдвиговая деформация)
3

4.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
y
2
1
θ
x
Характеристики прочности
композитного монослоя в главных осях ортотропии {1, 2}:
σ1tu, и σ2tu
σ1cu и σ2сu
τ12u
– пределы прочности при растяжении вдоль главных осей ортотропии
– пределы прочности при сжатии вдоль главных осей ортотропии
– предел прочности при сдвиге в плоскости армирования
Характеристики упругости
композитного монослоя в главных осях ортотропии {1, 2}:
E1 и E2
G12
– модули упругости в направлениях главных осей ортотропии
– модуль сдвига в плоскости армирования
4

5.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
ТИПЫ КОМПОЗИТНЫХ МОНОСЛОЕВ
Однонаправленный композит
Композит,
армированный
непрерывными
волокнами
Композит,
армированный
короткими
волокнами
Хаотичноармированный
композит
Тканевый
композит
5

6.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных
видах нагружения
Свойства однонаправленного композитного монослоя определяются взаимодействием его
волокон и матрицы. Рассмотрим эти свойства при различных видах нагружения.
Виды нагружения однонаправленного композита
Трансверсальное
растяжение
Сдвиг в плоскости
волокон
Продольное
сжатие
Трансверсальное
сжатие
короткие волокна
непрерывные волокна
Продольное
растяжение
6

7.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
ДОПУЩЕНИЯ, используемые при моделировании взаимодействия матрицы и волокон
однонаправленного композита, армированного непрерывными волокнами:
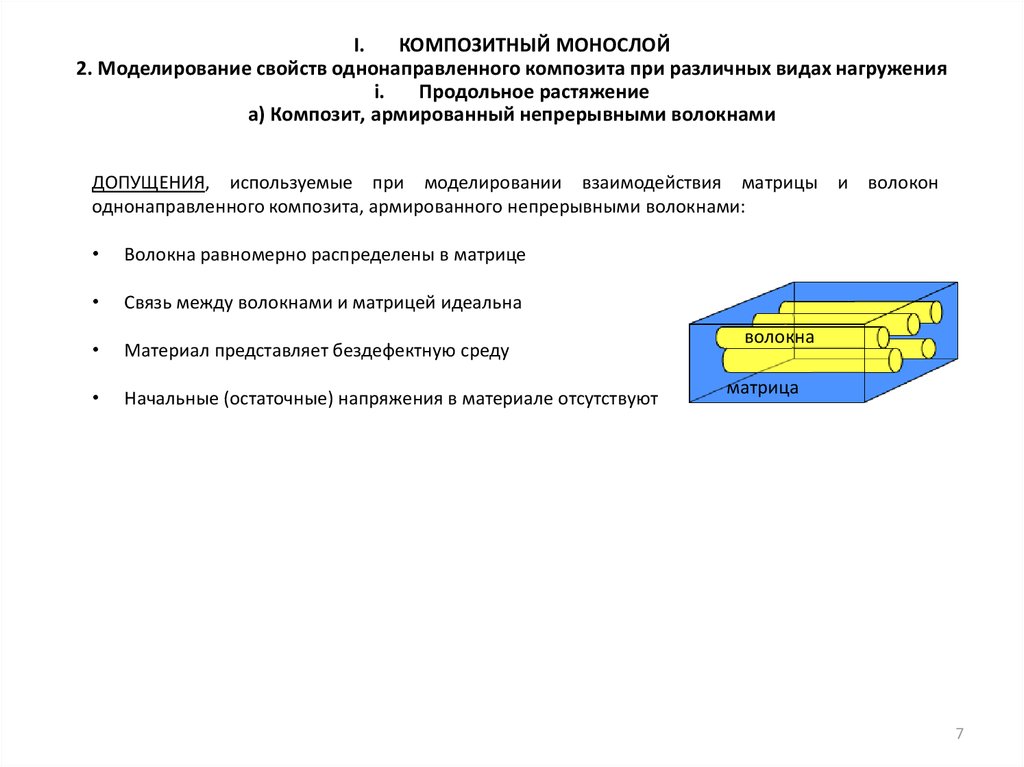
Волокна равномерно распределены в матрице
Связь между волокнами и матрицей идеальна
Материал представляет бездефектную среду
Начальные (остаточные) напряжения в материале отсутствуют
волокна
матрица
7

8.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
Характеристики прочности однонаправленного композитного монослоя:
o
o
o
o
o
предел прочности при растяжении вдоль волокон – σLtu
трансверсальный предел прочности при растяжении – σTtu
предел прочности при сдвиге – τLTu
предел прочности при растяжении вдоль волокон – σLcu
трансверсальный предел прочности при растяжении – σTcu
y
L
T
θ
x
Характеристики жесткости однонаправленного композитного монослоя:
o
o
o
продольный модуль упругости – EL
трансверсальный модуль упругости – ET
внутрислойный модуль сдвига – GLT
Напряжения и деформации в главных осях монослоя {L, T}
Напряжения :
σLL – продольное напряжение
σTT – трансверсальное напряжение
τLT – сдвиговое (касательное)
напряжение
Деформации:
εLL – продольная деформация
εTT – трансверсальная деформация
γLT – угол сдвига (сдвиговая
деформация)
8

9.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
ДОПУЩЕНИЯ, используемые при моделировании взаимодействия матрицы и волокон
однонаправленного композита, армированного длинными волокнами:
Свойства волокон при растяжении и сдвиге описываются линейно-упругим законом
Диаграмма сдвига волокон
Диаграмма растяжения волокон
Ef
fu
fu
Gf
σfu – предел прочности волокон при растяжении
τfu – предел прочности волокон при сдвиге
Ef – продольный модуль упругости волокон
Gf – модуль сдвига волокон
9

10.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
ДОПУЩЕНИЯ, используемые при моделировании взаимодействия матрицы и волокон
однонаправленного композита, армированного длинными волокнами:
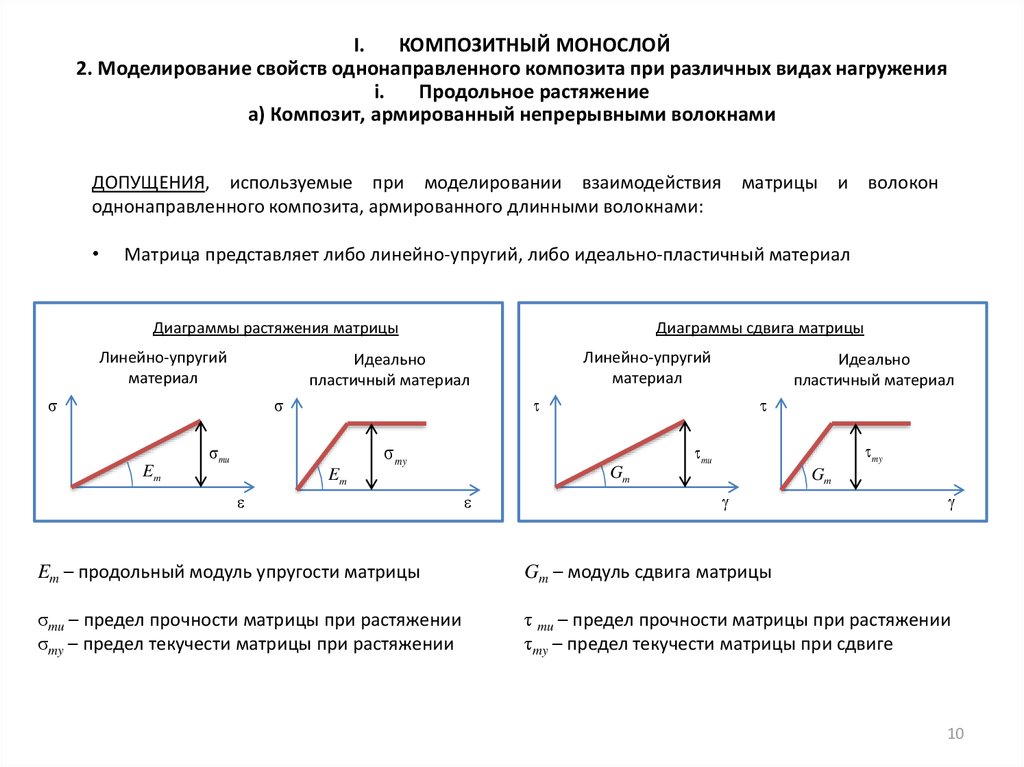
Матрица представляет либо линейно-упругий, либо идеально-пластичный материал
Диаграммы растяжения матрицы
Линейно-упругий
материал
Диаграммы сдвига матрицы
Идеально
пластичный материал
Em
Линейно-упругий
материал
Идеально
пластичный материал
my
mu
my
mu
Gm
Em
Gm
Em – продольный модуль упругости матрицы
Gm – модуль сдвига матрицы
σmu – предел прочности матрицы при растяжении
σmy – предел текучести матрицы при растяжении
τ mu – предел прочности матрицы при растяжении
τmy – предел текучести матрицы при сдвиге
10

11.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
Продольный модуль упругости
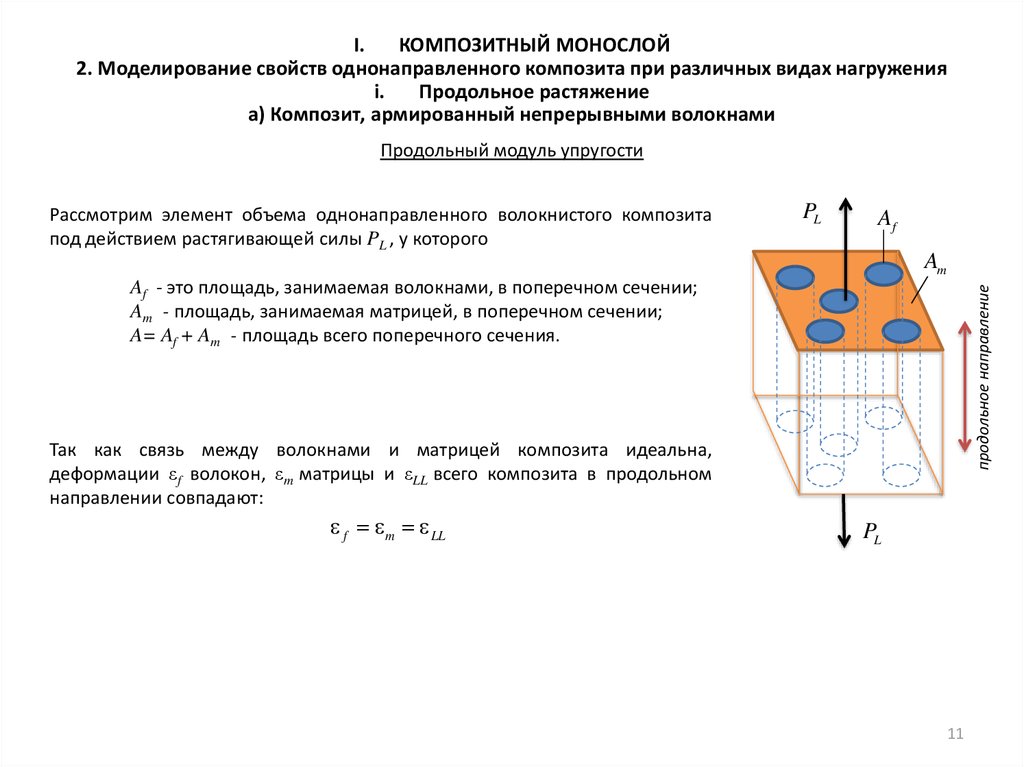
Рассмотрим элемент объема однонаправленного волокнистого композита
под действием растягивающей силы PL , у которого
PL
Af
Am
продольное направление
Af - это площадь, занимаемая волокнами, в поперечном сечении;
Am - площадь, занимаемая матрицей, в поперечном сечении;
A= Af + Am - площадь всего поперечного сечения.
Так как связь между волокнами и матрицей композита идеальна,
деформации εf волокон, εm матрицы и εLL всего композита в продольном
направлении совпадают:
f m LL
PL
11

12.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
Продольный модуль упругости
Продольная сила, действующая на рассматриваемый элемент
объема может быть представлена в виде суммы:
PL
Af
Am
продольное направление
PL Pf Pm
Перепишем это выражение через соответствующие напряжения σ и
площади:
LL A f Af m Am
Разделив это выражение на площадь поперечного сечения и, приняв
во внимание, что
vf
Af
A
и
vm
Am
1 v f
A
PL
это
объемные доли волокон и матрицы в композите
соответственно, в результате получим:
LL f
Af
A
m
Am
f v f m vm
A
12

13.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
Продольный модуль упругости
Разделив
последнее
выражение
на
деформации
f m LL ,
с учетом закона Гука при одноосном растяжении получим
ПРАВИЛО СМЕСЕЙ ДЛЯ ПРОДОЛЬНОГО МОДУЛЯ
УПРУГОСТИ ОДНОНАПРАВЛЕННОГО КОМПОЗИТА :
EL E f v f Em v m E f v f Em (1 v f )
продольное направление
ВЫВОДЫ: модуль упругости однонаправленного композита вдоль волокон:
Em EL E f
находится в пределах:
возрастает по линейному закону с ростом объемной доли волокон;
в наибольшей степени определяется модулем упругости материала волокон.
13

14.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
ПРЕДЕЛ ПРОЧНОСТИ
ВДОЛЬ ВОЛОКОН ПРИ РАСТЯЖЕНИИ
Ltu fu v f m v m
Здесь σ'm – напряжение в матрице, соответствующее
разрушению волокон при растяжении композита.
напряжение
Прочность вдоль волокон при растяжении
волокно
m
композит
ДОЛЯ НАГРУЗКИ, ПРИХОДЯЩАЯСЯ НА ВОЛОКНА
Pf
PL
f vf
f v f m (1 v f )
Ef v f
E f v f Em (1 v f )
матрица
fu
Для эффективного упрочнения композита объемная доля волокон должна
быть выше критического значения (при выводе этого выражения
предполагали, что матрица разрушается сразу же после разрушения
волокон):
деформация
v fcr
mu m
fu m
14

15.

ПРИМЕР.
Однонаправленный композит содержит 60% углеродных
волокон в эпоксидной матрице.
Модуль упругости
Предел прочности
Свойства волокон
Ef = 345 ГПа
σfu = 2480 MPa
Свойства матрицы
Em = 3,45 ГПа
σmU = 138 MPa
напряжение
I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
а) Композит, армированный непрерывными волокнами
волокно
m
композит
матрица
Определить:
• продольный модуль упругости композита;
• продольный предел прочности композита при растяжении.
fu
деформация
РЕШЕНИЕ.
Продольный модуль упругости композита
EL E f v f Em (1 v f ) 345 0,6 3,45 (1 0,6) 208 ГПа
Напряжение в матрице,
соответствующее разрушению волокон
m fu
Продольный предел прочности композита
Ltu fu v f m v m 2480 0,6 24,8 0,4 1500 МПа
Em
3,45
2480
24,8 МПа
Ef
345
15

16.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
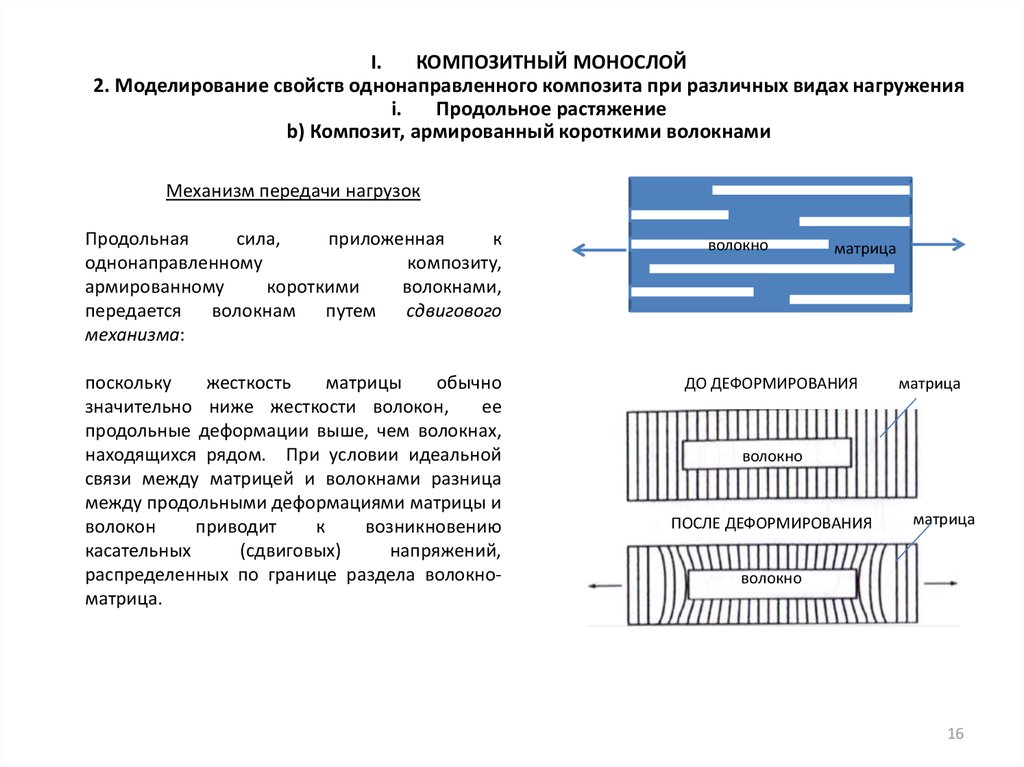
Механизм передачи нагрузок
Продольная
сила,
приложенная
к
однонаправленному
композиту,
армированному
короткими
волокнами,
передается
волокнам
путем
сдвигового
механизма:
поскольку
жесткость
матрицы
обычно
значительно ниже жесткости волокон,
ее
продольные деформации выше, чем волокнах,
находящихся рядом. При условии идеальной
связи между матрицей и волокнами разница
между продольными деформациями матрицы и
волокон
приводит
к
возникновению
касательных
(сдвиговых)
напряжений,
распределенных по границе раздела волокноматрица.
волокно
матрица
ДО ДЕФОРМИРОВАНИЯ
матрица
волокно
ПОСЛЕ ДЕФОРМИРОВАНИЯ
матрица
волокно
16

17.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
ДОПУЩЕНИЯ, используемые при моделировании прочности при растяжении в продольном
направлении однонаправленного композита, армированного короткими волокнами:
напряжения на торцах волокон отсутствуют
взаимодействия соседних волокон не рассматривают
свойства волокон при растяжении описывают линейным законом, а матрица при сдвиге
представляет собой жестко-пластичный материал (модель Келли-Тайсона)
Диаграмма сдвига матрицы
Диаграмма растяжения волокон
fU
my
Ef
σfu – предел прочности
волокон при растяжении
τmy – предел текучести
матрицы при сдвиге
17

18.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
продольное направление
Уравнение равновесия
элементарного отрезка волокна длиной dx
при растяжении вдоль волокон:
d 2f
4
f
d f
d 2f
4
f d f d x my 0
Здесь
my
f – продольное напряжение в волокне на
расстоянии x от его нижнего торца
my – сдвиговое напряжение на границе
раздела волокно-матрица (предел
текучести матрицы)
d f – диаметр волокна
После следующих преобразований последнего выражения:
d f
dx
4 my
df
x
4
f my d x
df 0
получим распределение нормальных напряжений по длине волокна
f ( x)
4 my
df
x
18

19.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
lf
Согласно полученному выражению
lf
f ( x)
2
max f
x
x
my
4 my
df
x
нормальные напряжения распределены по
линейному закону – они равны нулю на
торцах волокна и возрастают с ростом
расстояния x от торцов к центру
Сдвиговые напряжения по половинам длины
волокна распределены по постоянному
закону (допущение Келли-Тайсона).
x
my
x
lf
19

20.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
Рост
растягивающей
силы
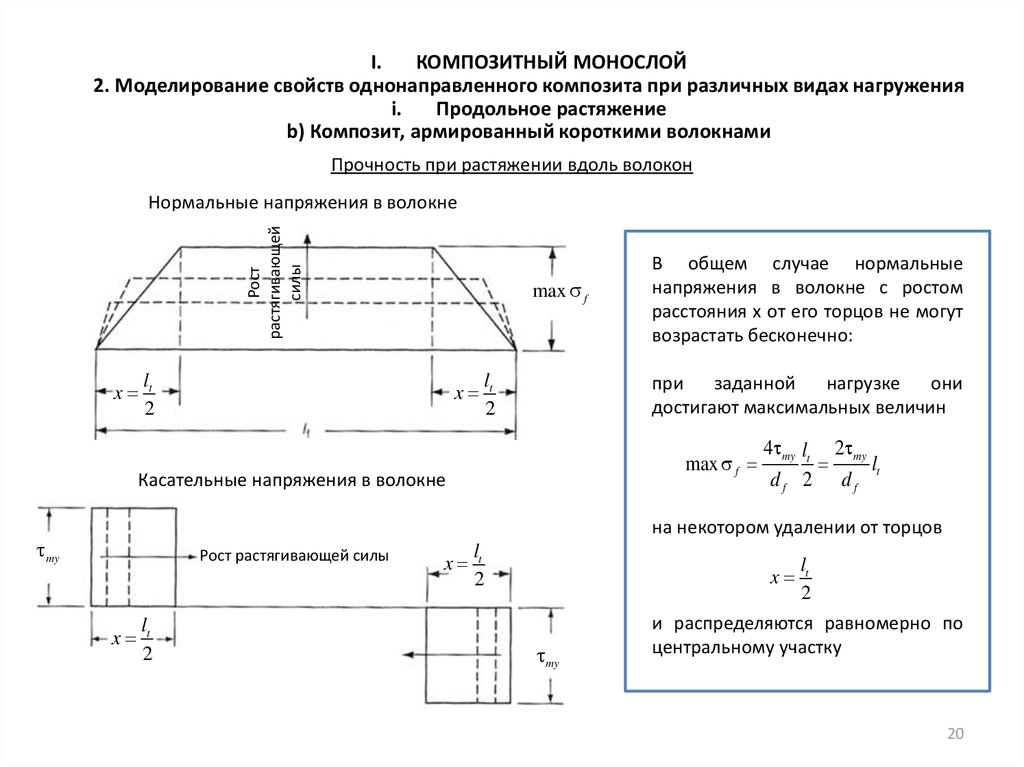
Нормальные напряжения в волокне
x
max f
lt
2
x
lt
2
В общем случае нормальные
напряжения в волокне с ростом
расстояния x от его торцов не могут
возрастать бесконечно:
при
заданной
нагрузке
они
достигают максимальных величин
max f
Касательные напряжения в волокне
4 my lt 2 my
lt
df 2 df
на некотором удалении от торцов
my
Рост растягивающей силы
x
lt
2
x
lt
2
x
my
lt
2
и распределяются равномерно по
центральному участку
20

21.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
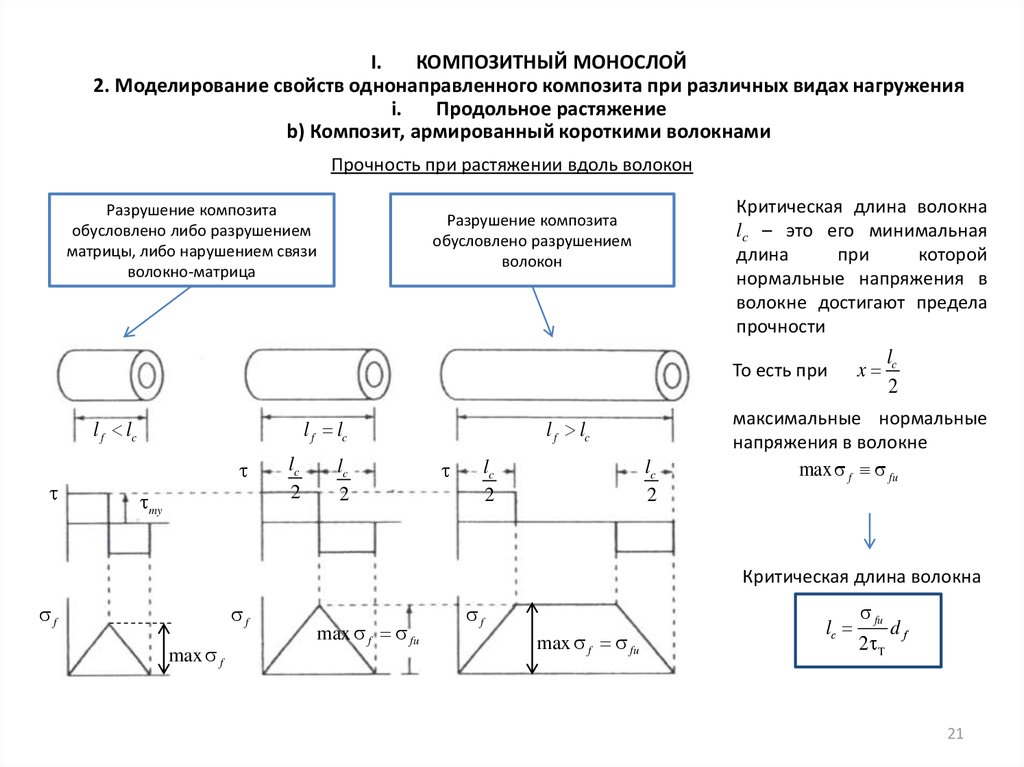
Разрушение композита
обусловлено либо разрушением
матрицы, либо нарушением связи
волокно-матрица
Критическая длина волокна
lc – это его минимальная
длина
при
которой
нормальные напряжения в
волокне достигают предела
прочности
Разрушение композита
обусловлено разрушением
волокон
То есть при
l f lc
l f lc
my
lc
2
lc
2
lc
2
lc
2
максимальные нормальные
напряжения в волокне
l f lc
x
lc
2
max f fu
Критическая длина волокна
f
f
max f
max f fu
f
max f fu
lс
fu
2 T
df
21

22.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
1. Рассмотрим случай, когда l f lc
Среднее напряжение в волокне при этом равно
2
f
l f
lf / 2
0
2
2
f ( x)dx S
lf
lf
1 l
f max f
2 2
1
max f
2
S
С учетом равенств
в итоге получим
max f
f
lf
2lc
lf
lc
fu
fU и
lf
df
f ( x)
lс
fu
2 T
fu
df
x
lf
my
Для определения прочности композита с короткими
волокнами, модифицируем немного выражение для
определения прочности композита с длинными
волокнами:
Ltu fu v f m v m
Ltu f v f mU v m
Продольный предел прочности при lf < lc
l
Ltu f my v f mu v m
df
max f
f
2
lc
2
f
mU
Ltu
22

23.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
Прочность при растяжении вдоль волокон
f ( x)
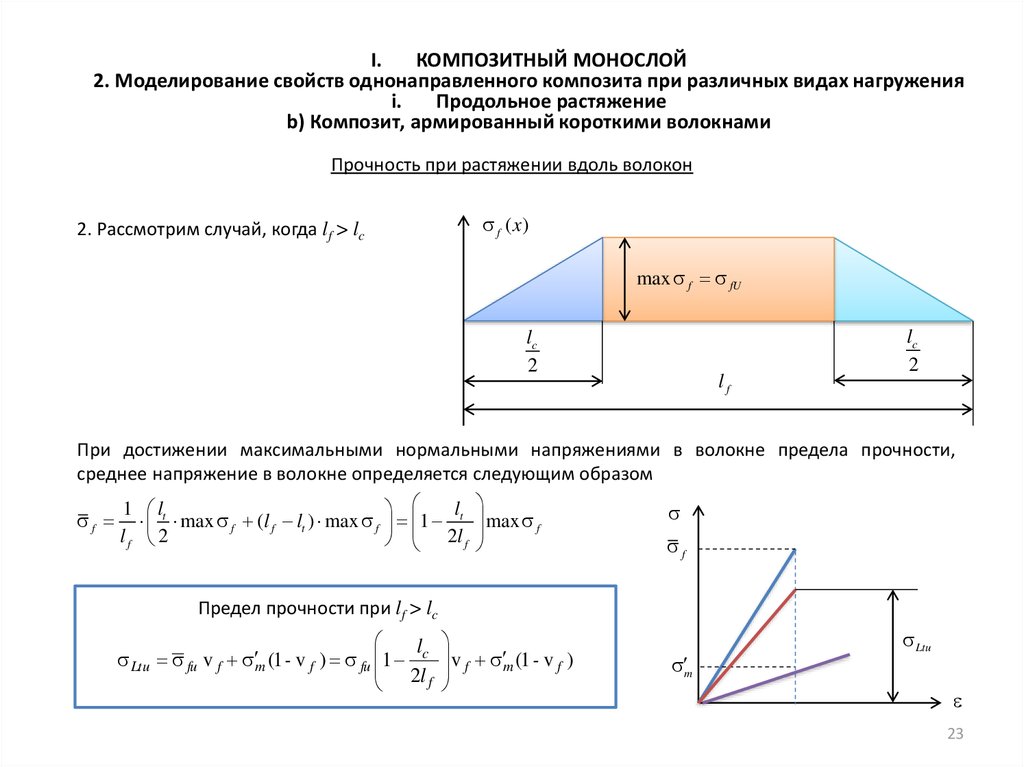
2. Рассмотрим случай, когда lf > lc
max f fU
lc
2
lf
lc
2
При достижении максимальными нормальными напряжениями в волокне предела прочности,
среднее напряжение в волокне определяется следующим образом
f
1
lf
l
t max f (l f lt ) max f
2
lt
1
2l f
max f
f
Предел прочности при lf > lc
l
Ltu fu v f m (1 - v f ) fu 1 c
2l f
v f m (1 - v f )
m
Ltu
23

24.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
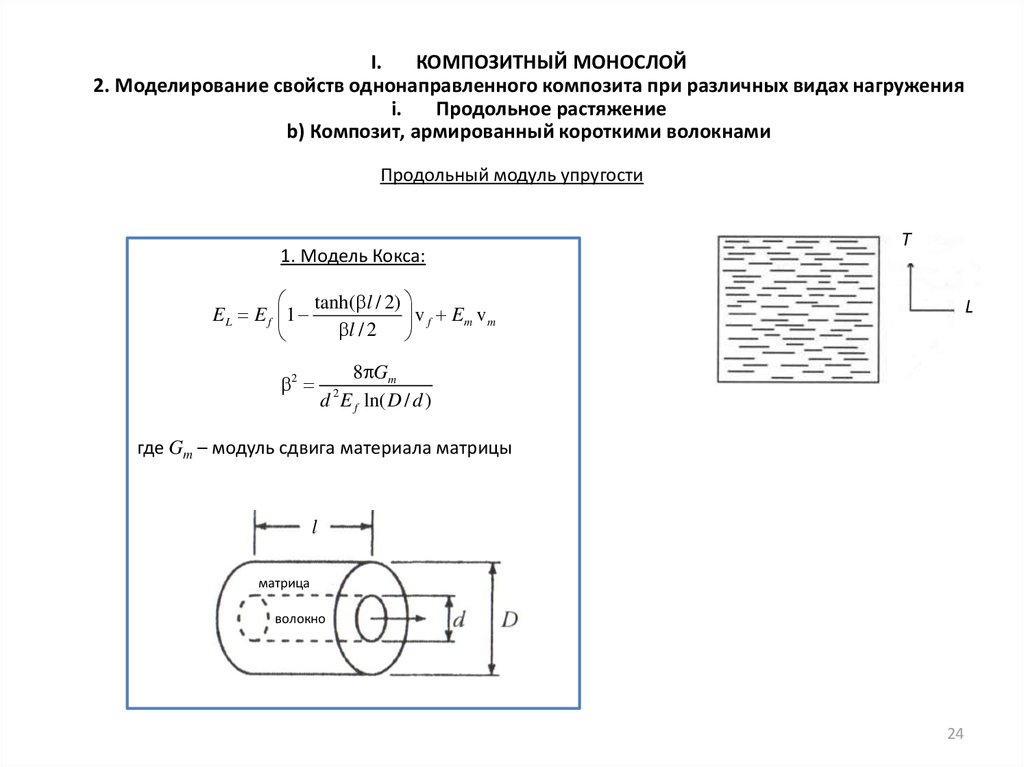
Продольный модуль упругости
1. Модель Кокса:
T
tanh( l / 2)
EL E f 1
v f Em v m
l / 2
2
L
8 Gm
d E f ln( D / d )
2
где Gm – модуль сдвига материала матрицы
l
матрица
волокно
24

25.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
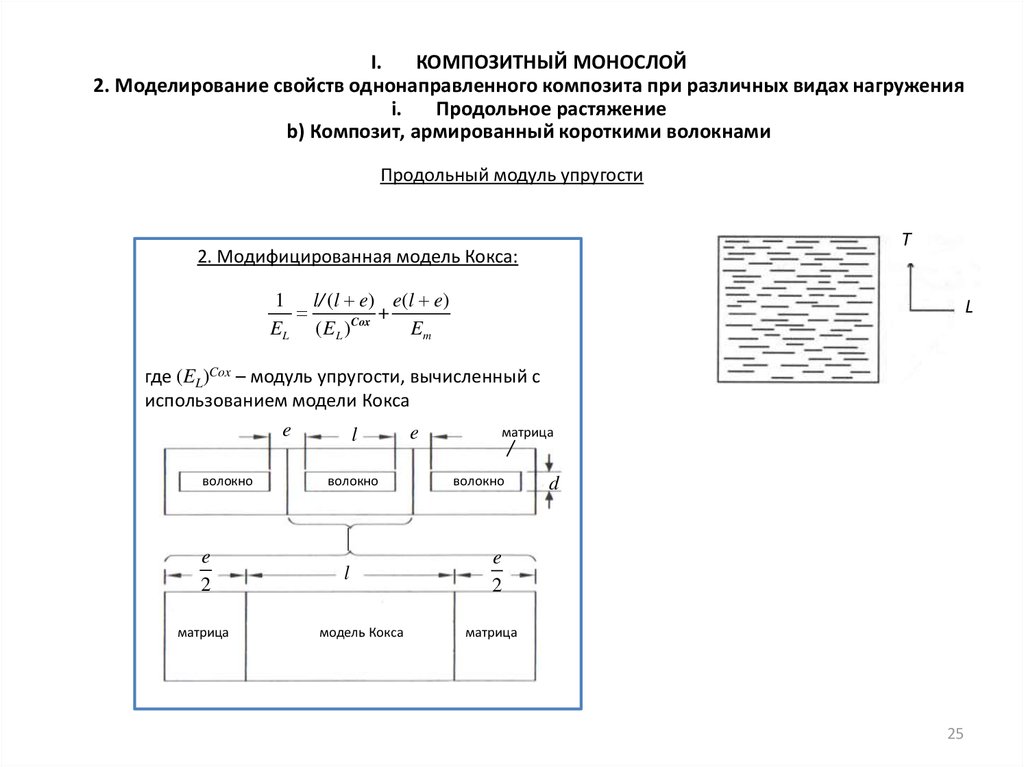
Продольный модуль упругости
T
2. Модифицированная модель Кокса:
1 l/ (l e) e(l e)
+
EL ( EL )Cox
Em
L
где (EL)Cox – модуль упругости, вычисленный с
использованием модели Кокса
e
волокно
e
2
матрица
l
волокно
l
модель Кокса
e
матрица
волокно
d
e
2
матрица
25

26.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах нагружения
i.
Продольное растяжение
b) Композит, армированный короткими волокнами
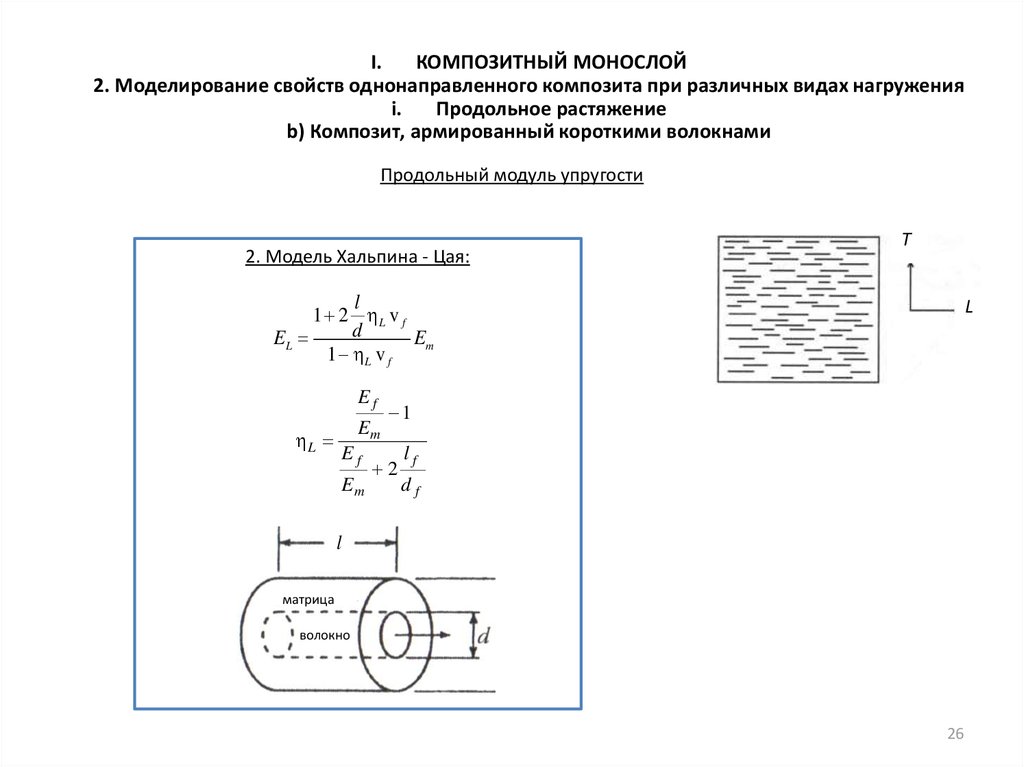
Продольный модуль упругости
2. Модель Хальпина - Цая:
T
l
1 2 L v f
d
EL
Em
1 L v f
Ef
Em
L
Ef
Em
L
1
2
lf
df
l
матрица
волокно
26

27.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
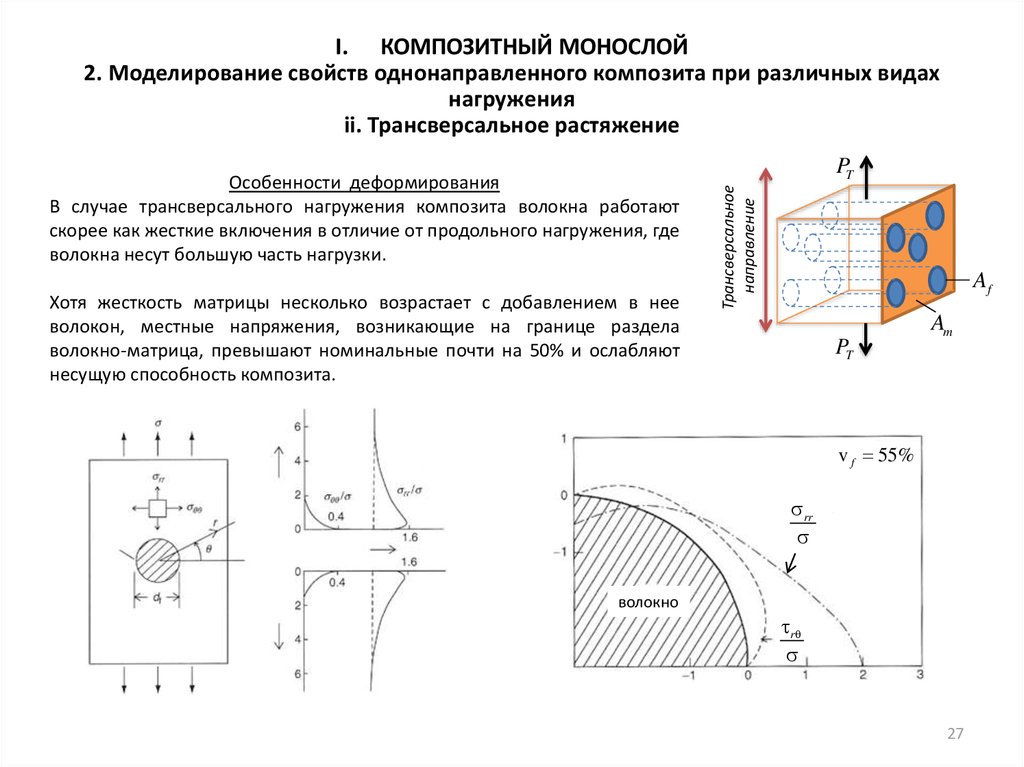
ii. Трансверсальное растяжение
Хотя жесткость матрицы несколько возрастает с добавлением в нее
волокон, местные напряжения, возникающие на границе раздела
волокно-матрица, превышают номинальные почти на 50% и ослабляют
несущую способность композита.
PT
Трансверсальное
направление
Особенности деформирования
В случае трансверсального нагружения композита волокна работают
скорее как жесткие включения в отличие от продольного нагружения, где
волокна несут большую часть нагрузки.
Af
PT
Am
v f 55%
rr
волокно
r
27

28.

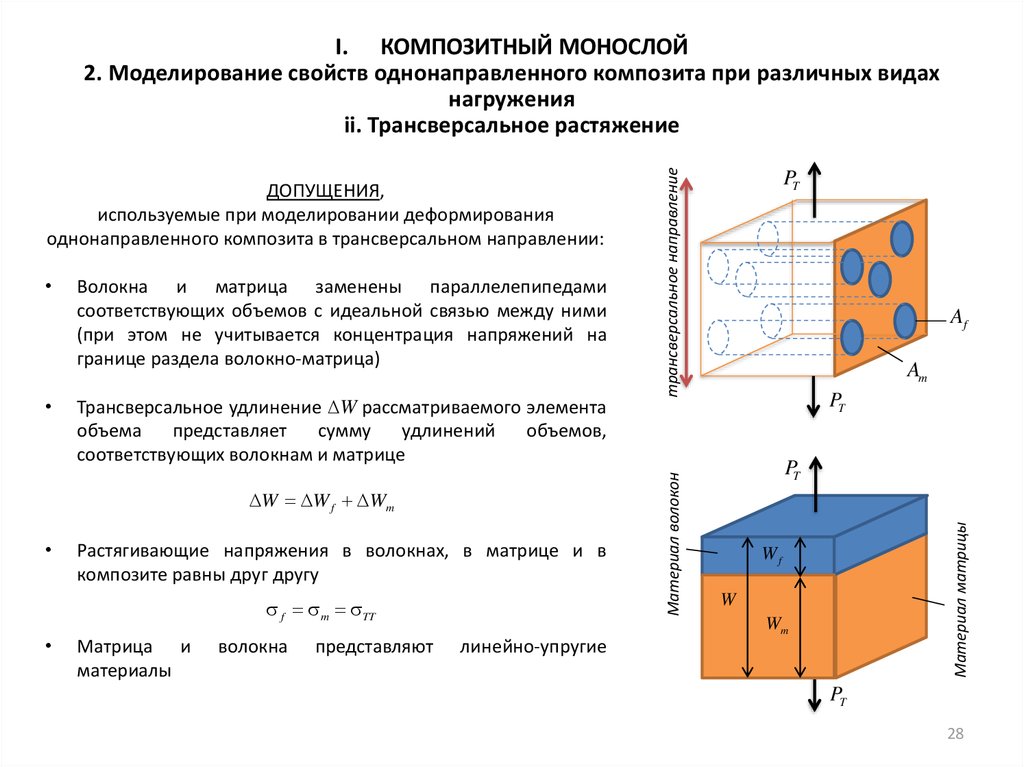
Волокна и матрица заменены параллелепипедами
соответствующих объемов с идеальной связью между ними
(при этом не учитывается концентрация напряжений на
границе раздела волокно-матрица)
Трансверсальное удлинение ΔW рассматриваемого элемента
объема
представляет
сумму
удлинений
объемов,
соответствующих волокнам и матрице
W W f Wm
Растягивающие напряжения в волокнах, в матрице и в
композите равны друг другу
f m TT
Матрица и
материалы
волокна
представляют
PT
Af
Am
PT
PT
Материал матрицы
Материал волокон
ДОПУЩЕНИЯ,
используемые при моделировании деформирования
однонаправленного композита в трансверсальном направлении:
трансверсальное направление
I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
ii. Трансверсальное растяжение
Wf
W
Wm
линейно-упругие
PT
28

29.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
ii. Трансверсальное растяжение
Трансверсальный модуль упругости
W
W
f
W f
m
Wf
Wm
Wm
полное удлинение рассматриваемого элемента объема в
трансверсальном направлении может быть переписано
TTW f W f mWm
Разделив это выражение на W, получим
TT
Wf
W
f v f m v m , где v f
, а vm m
W
W
PT
Wf
W
Приняв во внимание следующее:
TT
TT
ET
f
f
Ef
m m
Em
Материал матрицы
TT
Материал волокон
Поскольку
Wm
PT
f m TT
получим
ПРАВИЛО СМЕСЕЙ ДЛЯ ТРАНСВЕРСАЛЬНОГО МОДУЛЯ
УПРУГОСТИ ОДНОНАПРАВЛЕННОГО КОМПОЗИТА
v
1
v
f m
ET E f Em
29

30.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
ii. Трансверсальное растяжение
ТРАНСВЕРСАЛЬНЫЙ ПРЕДЕЛ ПРОЧНОСТИ
Ttu
mu
, где
K
E
1 v f 1 m
E f
K
4v f
1 E m
1
Ef
Здесь Kσ – это коэффициент концентрации напряжений
трансверсальное направление
Трансверсальный предел прочности
PT
Выражение, определяющее трансверсальную прочность однонаправленного
армированного длинными волокнами, получается на основе ДОПУЩЕНИЯ:
Af
Am
PT
композита,
трансверсальная прочность такого композита при растяжении ограничена соответствующим пределом
прочности матрицы
Вывод: трансверсальная прочность однонаправленного композита, армированного длинными
волокнами, снижается с увеличением модуля упругости волокон, а также с увеличением объемной
доли волокон
30

31.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
ii. Трансверсальное растяжение
Модуль
упругости
Предел
прочности
Свойства
волокон
Ef = 345 ГПа
σfu = 2480 MPa
Свойства
матрицы
Em = 3,45 ГПа
σmu = 138 MPa
ПРИМЕР.
Для однонаправленного эпоксидного углепластика,
армированного длинными волокнами, с объемной
долей волокон 70% сравнить:
А) модули упругости
Б) пределы прочности
в продольном и трансверсальном направлении.
РЕШЕНИЕ.
А) Продольный модуль упругости
EL E f v f Em (1 v f ) 345 0,7 3,45 (1 0,7) 243 ГПа
Трансверсальный модуль упругости
v 1 v f
ET f
E
Em
f
1
1
0,7 1 0,7
11,2 ГПа
345
3,45
Отношение продольного к трансверсальному модулю упругости
EL 243
21,7
ET 11,2
31

32.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
ii. Трансверсальное растяжение
Модуль
упругости
Предел
прочности
Свойства
волокон
Ef = 345 ГПа
σfu = 2480 MPa
Свойства
матрицы
Em = 3,45 ГПа
σmu = 138 MPa
ПРИМЕР.
Для однонаправленного эпоксидного углепластика с
объемной долей волокон 70% сравнить:
А) модули упругости
Б) пределы прочности
в продольном и трансверсальном направлении.
РЕШЕНИЕ.
Б) Продольный предел прочности
E
3,45
Ltu fu v f m v m fu v f fu m v m 2,48 0,7 2,48
0,3 1743 М Па
Ef
345
Трансверсальный предел прочности
E
4 0,7 3,45
1 m
1
1
E
mu
f
345
mu
138 29,4 МПа
3,45
K
E
1 0,7 1
1 v f 1 m
345
E
f
1
Ttu
4vf
Отношение продольного к трансверсальному пределу прочности
Ltu 1743
52,3
Ttu 29,4
32

33.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
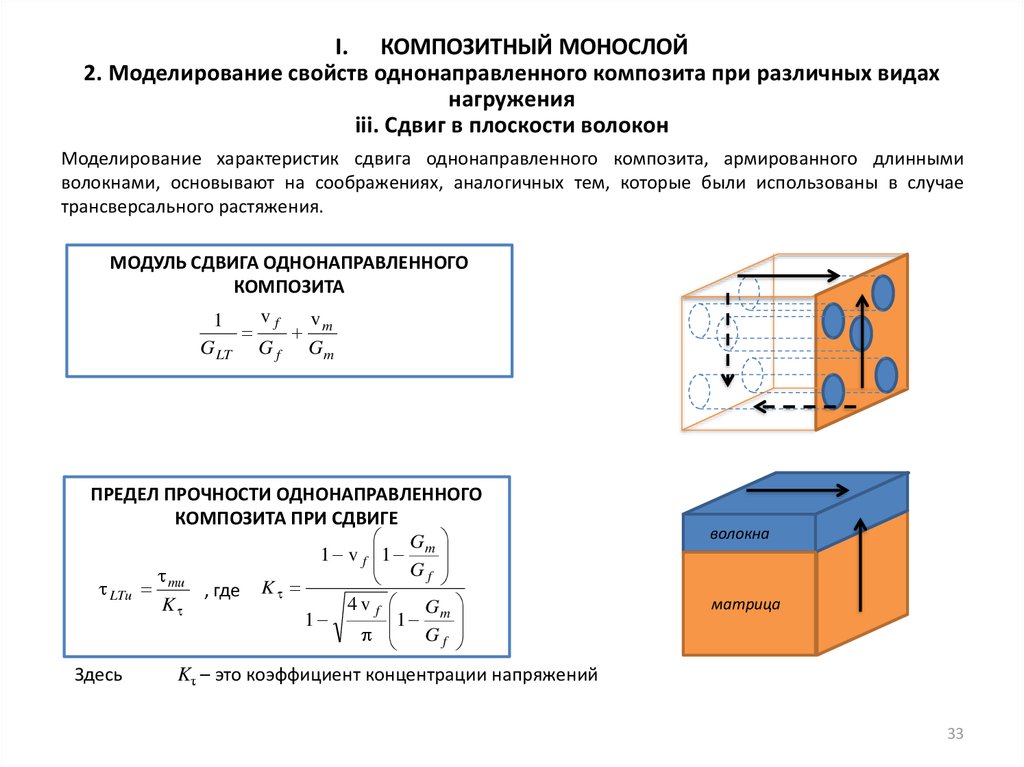
iii. Сдвиг в плоскости волокон
Моделирование характеристик сдвига однонаправленного композита, армированного длинными
волокнами, основывают на соображениях, аналогичных тем, которые были использованы в случае
трансверсального растяжения.
МОДУЛЬ СДВИГА ОДНОНАПРАВЛЕННОГО
КОМПОЗИТА
vf
v
1
m
G LT G f Gm
ПРЕДЕЛ ПРОЧНОСТИ ОДНОНАПРАВЛЕННОГО
КОМПОЗИТА ПРИ СДВИГЕ
G
1 v f 1 m
G f
mu
LTu
, где K
4v f
K
1 G m
1
G f
Здесь
волокна
матрица
Kτ – это коэффициент концентрации напряжений
33

34.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
iV. Продольное сжатие
Формы разрушения и прочность при сжатии:
1) Потеря устойчивости волокон
Одна из важных функций матрицы в композите – это обеспечение боковой поддержки волокон при
продольном сжатии. Композиты на основе полимерных матриц, у которых модуль упругости может быть
на несколько порядков ниже модулей упругости волокон, при продольном сжатии часто разрушаются изза местной потери устойчивости волокон.
А) EXTENSIONAL MODE
(обычно происходит при низкой объемной доле
волокон vf < 20%)
Предел прочности
Lcu 2 v f
v f Em E f
3(1 v f )
Б) SHEAR MODE
(обычно происходит при высокой объемной
доле волокон vf > 20%)
Предел прочности
Gm
Lcu
1 v f
34

35.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
iV. Продольное сжатие
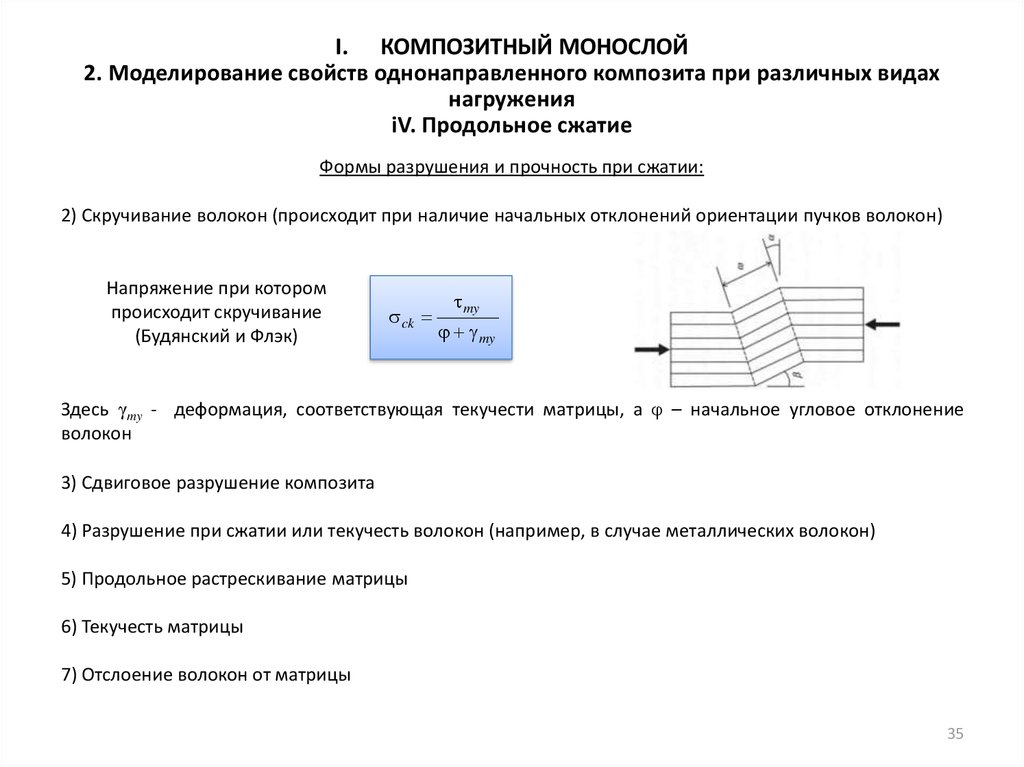
Формы разрушения и прочность при сжатии:
2) Скручивание волокон (происходит при наличие начальных отклонений ориентации пучков волокон)
Напряжение при котором
происходит скручивание
(Будянский и Флэк)
ck
my
my
Здесь γmy - деформация, соответствующая текучести матрицы, а φ – начальное угловое отклонение
волокон
3) Сдвиговое разрушение композита
4) Разрушение при сжатии или текучесть волокон (например, в случае металлических волокон)
5) Продольное растрескивание матрицы
6) Текучесть матрицы
7) Отслоение волокон от матрицы
35

36.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
iV. Продольное сжатие
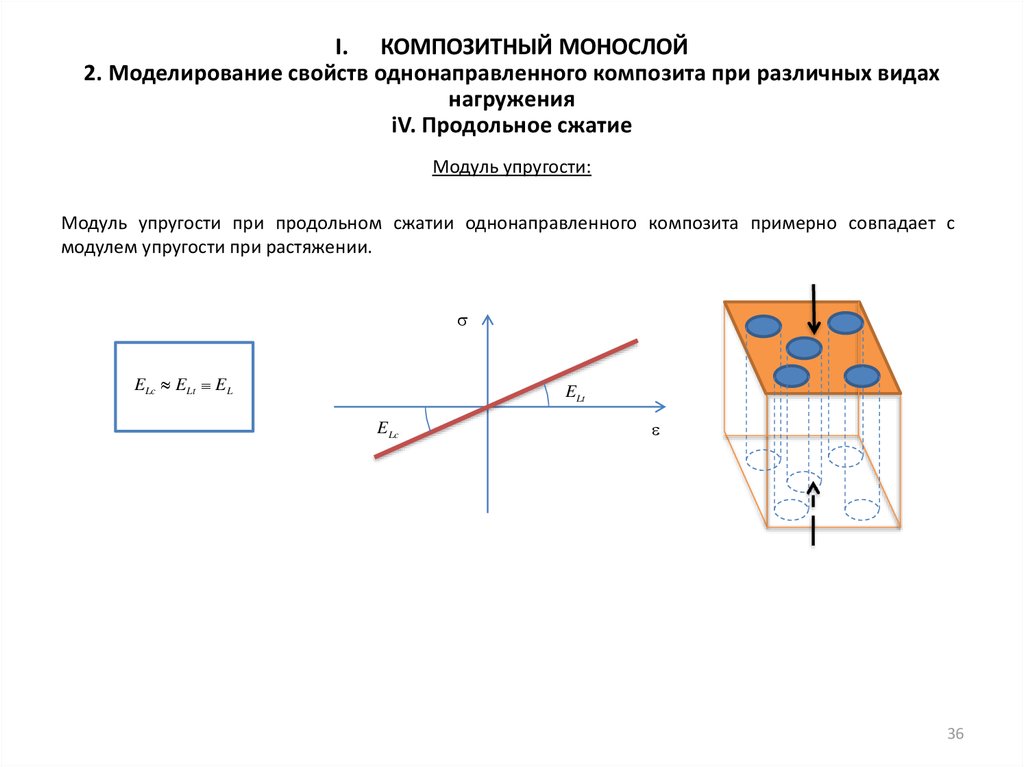
Модуль упругости:
Модуль упругости при продольном сжатии однонаправленного композита примерно совпадает с
модулем упругости при растяжении.
ELc ELt EL
ELt
ELc
36

37.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
2. Моделирование свойств однонаправленного композита при различных видах
нагружения
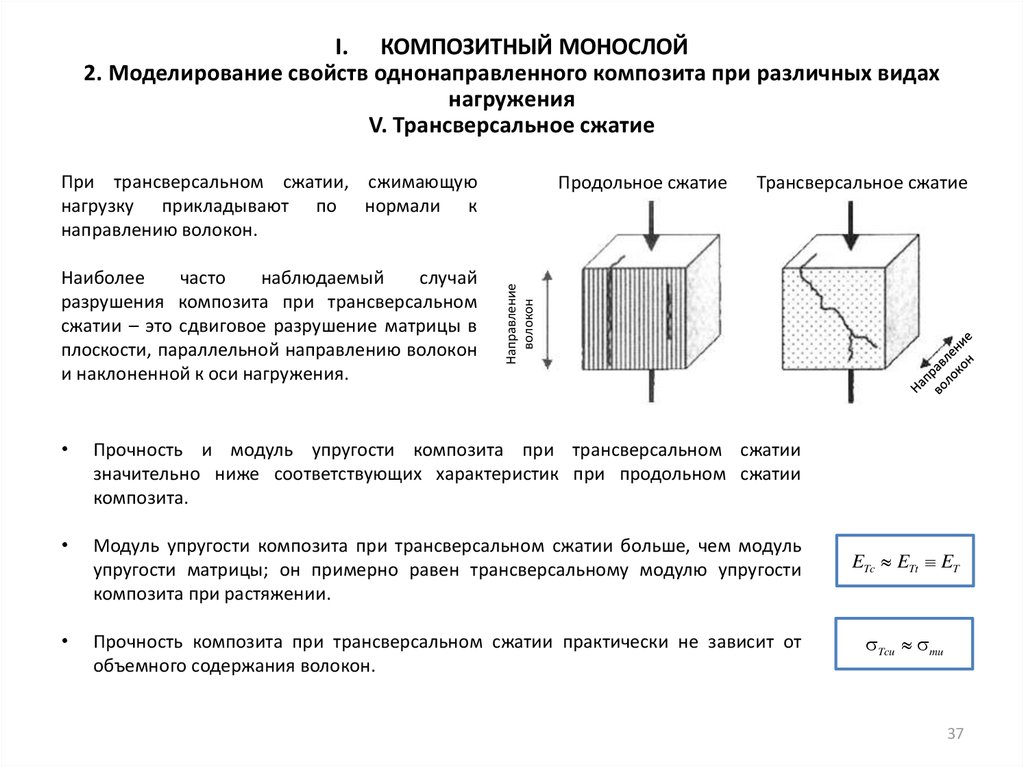
V. Трансверсальное сжатие
При трансверсальном сжатии, сжимающую
нагрузку прикладывают по нормали к
направлению волокон.
Трансверсальное сжатие
Направление
волокон
Наиболее
часто
наблюдаемый
случай
разрушения композита при трансверсальном
сжатии – это сдвиговое разрушение матрицы в
плоскости, параллельной направлению волокон
и наклоненной к оси нагружения.
Продольное сжатие
Прочность и модуль упругости композита при трансверсальном сжатии
значительно ниже соответствующих характеристик при продольном сжатии
композита.
Модуль упругости композита при трансверсальном сжатии больше, чем модуль
упругости матрицы; он примерно равен трансверсальному модулю упругости
композита при растяжении.
Прочность композита при трансверсальном сжатии практически не зависит от
объемного содержания волокон.
ETc ETt ET
Tcu mu
37

38.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
3. Моделирование свойств хаотично армированного композита
Особенности хаотичного армирования
Известно, что хаотично армированные композиты проявляют изотропию свойств. Если длина включений
(усы, микроволокна, нанотрубки) мала по сравнению с толщиной монослоя, то можно считать, что
включения равномерно распределяются в пространстве материала, обеспечивая его одинаковыми
интегральными характеристиками во всех направлениях (3D изотропия).
Однако, если говорить о наиболее распространенных в промышленности волокнистых композитах,
армированных короткими волокнами (например, ХАСП), то следует отметить, что длина волокон таких
материалов значительно превышает толщину монослоя. Волокна при этом распределяются равномерно
только в плоскости армирования монослоя. Поэтому такой материал называют 2D изотропным (или
изотропным в плоскости армирования).
3D изотропия
2D изотропия
ХАСП
38

39.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
3. Моделирование свойств хаотично армированного композита
Характеристики упругости
1. Подход Кокса :
Допущения:
• ориентация волокон в пространстве более важна, чем их длина, поэтому для упрощения выражений
короткие волокна в модели можно заменить бесконечными
• хаотичная структура композита заменяется регулярной, где: а) в случае 2D изотропного композита
волокна равномерно распределяются по всем направлениям плоскости армирования; б) в случае 3D
изотропного композита – по всем направлениям пространства.
• влиянием матрицы можно пренебречь
Подход Кокса для 2D изотропного композита
Подход Кокса для 3D изотропного композита
Модуль упругости:
1
E Ef v f
3
Модуль упругости:
1
E Ef v f
6
Модуль сдвига:
1
G Ef v f
8
Модуль сдвига:
G
Коэффициент Пуассона:
1
3
Коэффициент Пуассона:
1
Ef v f
15
1
4
39

40.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
3. Моделирование свойств хаотично армированного композита
Характеристики упругости
2. Подход Цая – Пагано (2D изотропный материал )
Для оценки интегральных характеристик упругости композитов, хаотично армированных в плоскости
армирования, Цай и Пагано сохранили первые два допущения подхода Кокса:
• ориентация волокон в пространстве более важна, чем их длина, поэтому для упрощения выражений
короткие волокна в модели заменяются бесконечными
• хаотичная структура композита заменяется регулярной, где волокна равномерно распределяются по
всем направлениям плоскости армирования
Однако, в отличие от Кокса, они кроме волокон включили в рассмотрение также и матрицу.
Подход Цая-Пагано для 2D изотропного композита
Модуль упругости:
3
5
E EL ET
8
8
Модуль сдвига:
1
1
G EL ET
8
4
Коэффициент Пуассона:
E
1
2G
40

41.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
3. Моделирование свойств хаотично армированного композита
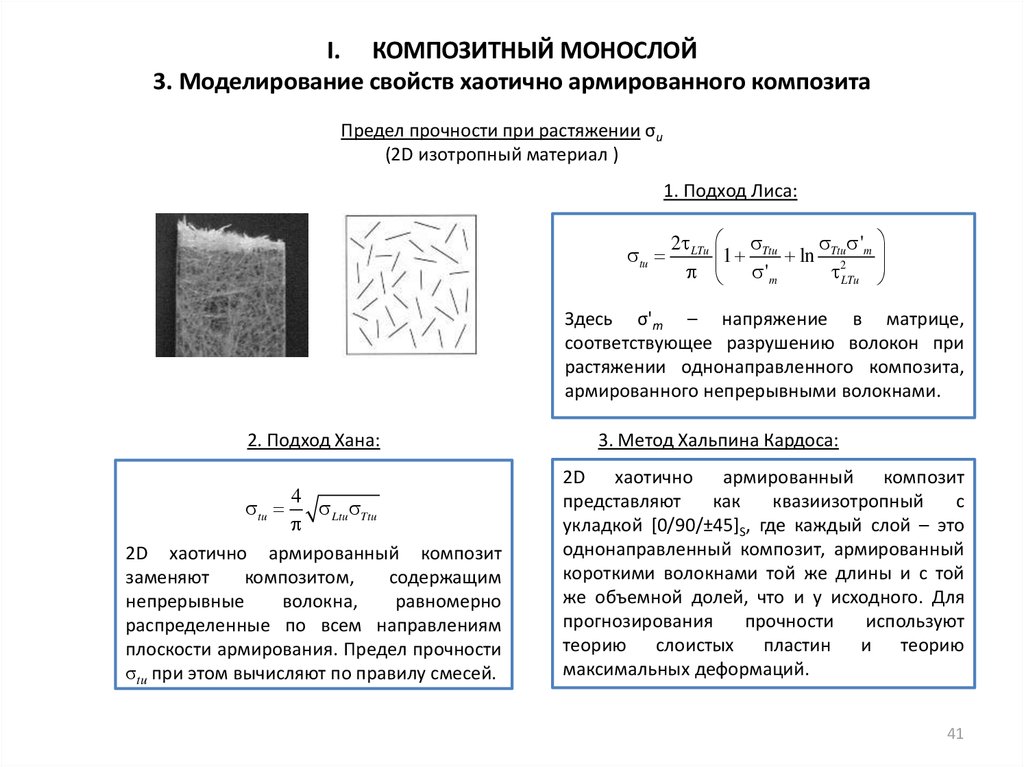
Предел прочности при растяжении σu
(2D изотропный материал )
1. Подход Лиса:
tu
2 LTu Ttu
Ttu 'm
1
ln
'm
2LTu
Здесь σ'm – напряжение в матрице,
соответствующее разрушению волокон при
растяжении однонаправленного композита,
армированного непрерывными волокнами.
2. Подход Хана:
4
Ltu Ttu
2D хаотично армированный композит
заменяют
композитом,
содержащим
непрерывные
волокна,
равномерно
распределенные по всем направлениям
плоскости армирования. Предел прочности
σtu при этом вычисляют по правилу смесей.
tu
3. Метод Хальпина Кардоса:
2D хаотично армированный композит
представляют
как
квазиизотропный
с
укладкой [0/90/±45]S, где каждый слой – это
однонаправленный композит, армированный
короткими волокнами той же длины и с той
же объемной долей, что и у исходного. Для
прогнозирования
прочности
используют
теорию слоистых пластин и теорию
максимальных деформаций.
41

42.

Допущения:
Монослой условно состоит из двух слоев
однонаправленно армированных искривленными
волокнами в направлении основы и утка
Направления нитей основы и утка определяется
соответственно индексами «о» и «у»
Толщины слоев пропорциональны объемному
содержанию волокон:
h1
vf o
vf
h
h2
vf у
vf
h
Уток
I. КОМПОЗИТНЫЙ МОНОСЛОЙ
4. Моделирование свойств тканевого композита
Основа
vf о vf у vf
β
Искривленную форму волокон представляют в
виде ломаной, состоящей из прямолинейных
участков, наклон которых определяется углом β
Распрямление волокон в процессе нагружения не
учитывают
h1
β
h
=
+
h2
42

43.

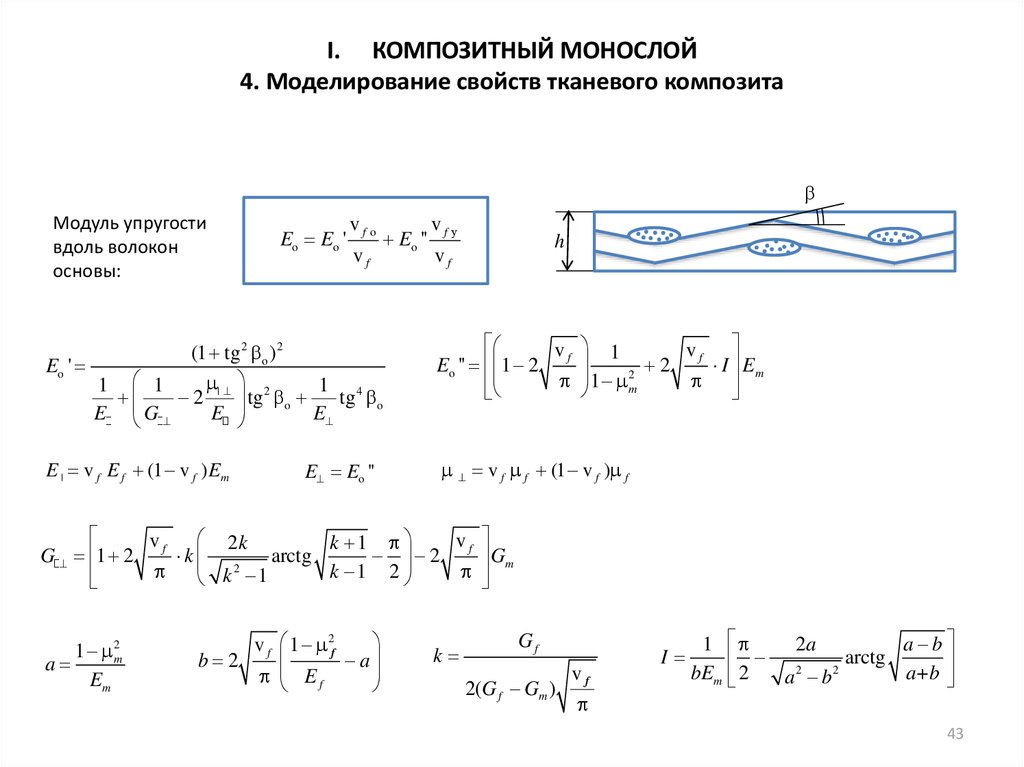
I. КОМПОЗИТНЫЙ МОНОСЛОЙ
4. Моделирование свойств тканевого композита
β
Модуль упругости
вдоль волокон
основы:
Eo Eo '
vf o
vf
Eo ''
vf у
h
vf
(1 tg 2 o ) 2
Eo '
1 1
1 4
2 tg 2 o
tg o
E G
E
E
vf 1
vf
Eo '' 1 2
2
I Em
1 2m
E v f E f (1 v f ) Em
v f f (1 v f ) f
E Eo ''
2k
v
v
k 1
G 1 2 f k
arctg
2 f Gm
2
k 1 2
k 1
1 2m
a
Em
v f 1 2f
b 2
a
Ef
k
Gf
2(G f Gm )
vf
I
1
2a
a b
arctg
bEm 2
a+b
a 2 b2
43

44.

I. КОМПОЗИТНЫЙ МОНОСЛОЙ
4. Моделирование свойств тканевого композита
β
Модуль упругости
вдоль волокон
утка:
Eу Eу '
vf у
vf
Eу ''
vf o
vf
h
Модуль упругости вдоль волокон утка определяется путем перемены мест индексов «о» и «у» в
расчетных выражениях
Модуль сдвига в
плоскости
армирования:
2k
v
v
k 1
Gоу G 1 2 f k
arctg
2 f Gm
2
k 1 2
k 1
Коэффициенты
Пуассона в плоскости
армирования:
оу
v f E
v f о E v f у Eу '
уо
v f E
v f о Eо ' v f у E
44

45.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
КОМПОЗИТНЫЙ МОНОСЛОЙ
Однонаправленный композит
Композит,
армированный
непрерывными
волокнами
Композит,
армированный
короткими
волокнами
Хаотичноармированный
композит
Тканевый
композит
45

46.

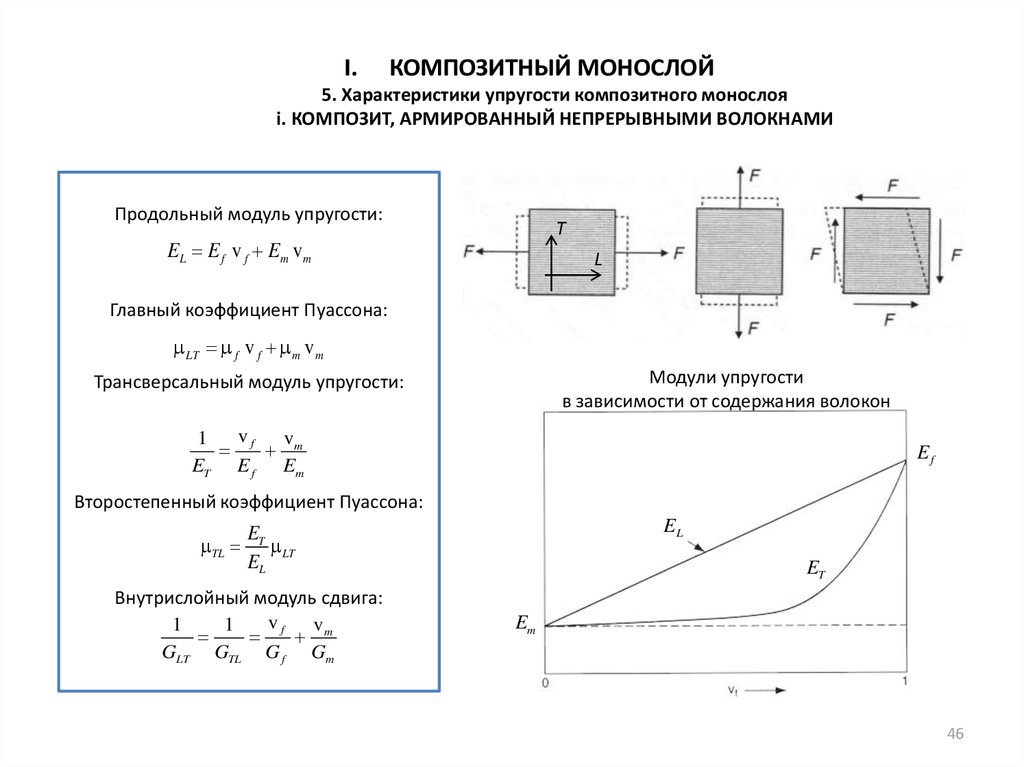
I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. Характеристики упругости композитного монослоя
i. КОМПОЗИТ, АРМИРОВАННЫЙ НЕПРЕРЫВНЫМИ ВОЛОКНАМИ
Продольный модуль упругости:
T
EL E f v f Em v m
L
Главный коэффициент Пуассона:
LT f v f m v m
Модули упругости
в зависимости от содержания волокон
Трансверсальный модуль упругости:
v
1
v
f m
ET E f Em
Ef
Второстепенный коэффициент Пуассона:
EL
E
TL T LT
EL
Внутрислойный модуль сдвига:
v
1
1
v
f m
GLT GTL G f Gm
ET
Em
46

47.

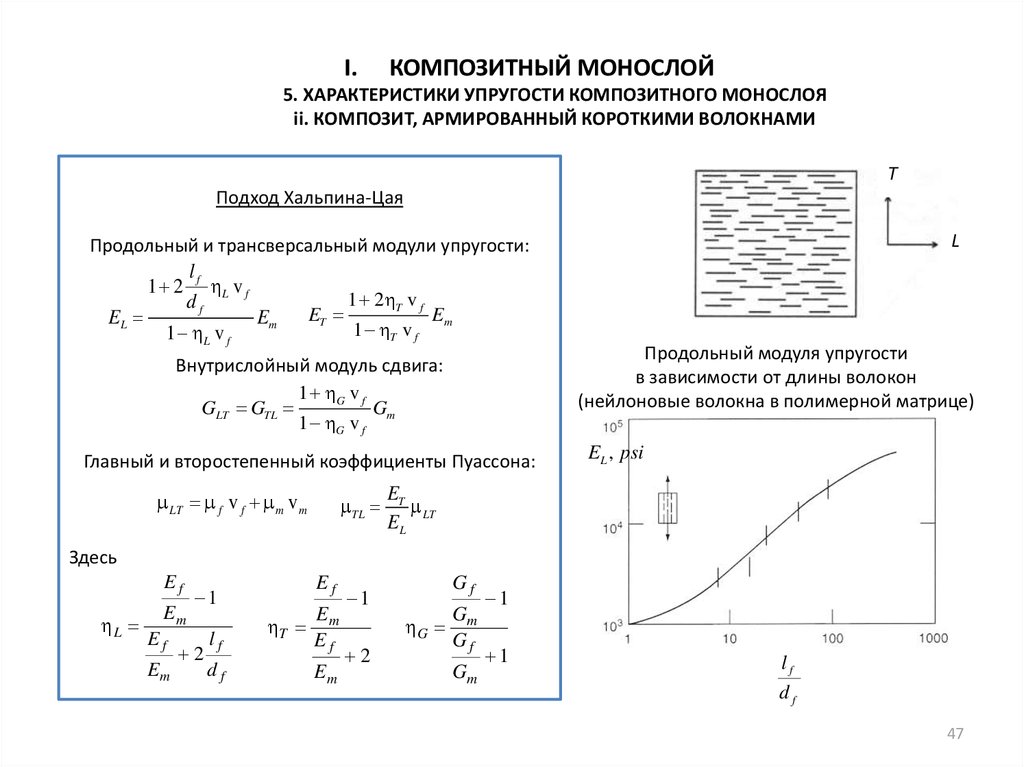
I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
ii. КОМПОЗИТ, АРМИРОВАННЫЙ КОРОТКИМИ ВОЛОКНАМИ
T
Подход Хальпина-Цая
Продольный и трансверсальный модули упругости:
l
1 2 f L v f
1 2 T v f
df
ET
Em
EL
Em
1 T v f
1 L v f
Внутрислойный модуль сдвига:
1 G v f
GLT GTL
Gm
1 G v f
Главный и второстепенный коэффициенты Пуассона:
LT f v f m v m
TL
L
Продольный модуля упругости
в зависимости от длины волокон
(нейлоновые волокна в полимерной матрице)
EL , psi
ET
LT
EL
Здесь
Ef
L
Em
Ef
Em
1
2
Ef
lf
E
T m
Ef
df
Em
1
2
Gf
G
G m
Gf
Gm
1
1
lf
df
47

48.

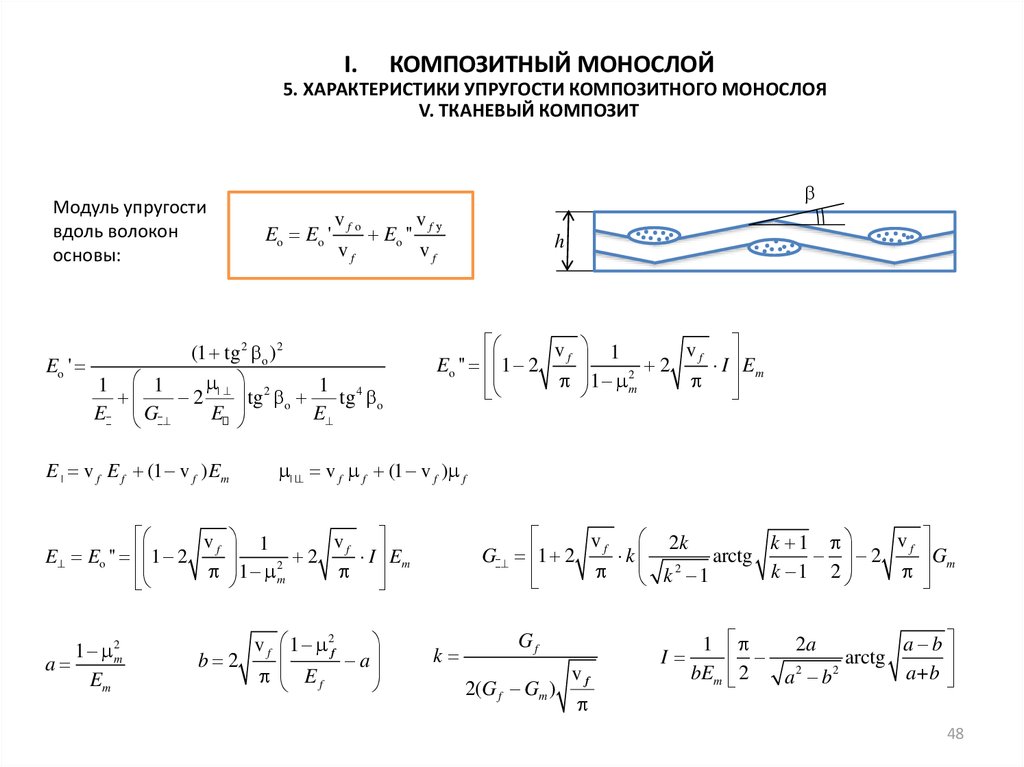
I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
V. ТКАНЕВЫЙ КОМПОЗИТ
Модуль упругости
вдоль волокон
основы:
β
Eo Eo '
vf o
vf
Eo ''
(1 tg 2 o ) 2
Eo '
1 1
1 4
2 tg 2 o
tg o
E G
E
E
E v f E f (1 v f ) Em
vf у
h
vf
vf 1
vf
Eo '' 1 2
2
I Em
1 2m
v f f (1 v f ) f
v 1
vf
E Eo '' 1 2 f
2
I Em
2
1
m
1 2m
a
Em
v f 1 2f
b 2
a
Ef
2k
v
v
k 1
G 1 2 f k
arctg
2 f Gm
2
k 1 2
k 1
k
Gf
2(G f Gm )
vf
I
1
2a
a b
arctg
bEm 2
a+b
a 2 b2
48

49.

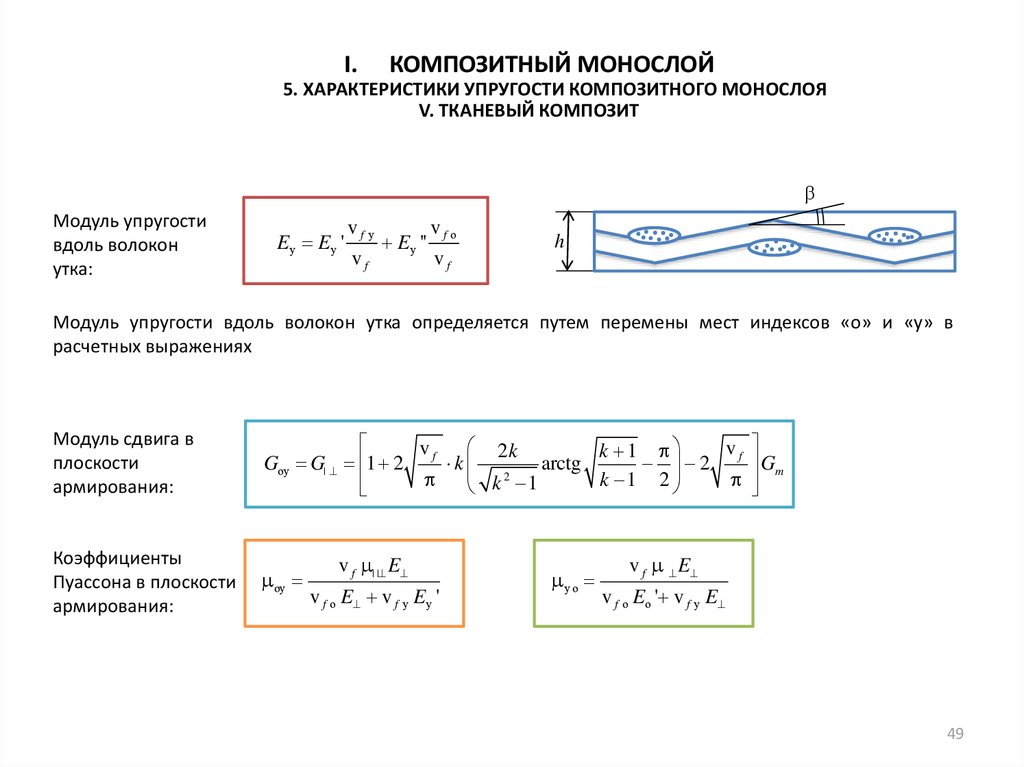
I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
V. ТКАНЕВЫЙ КОМПОЗИТ
β
Модуль упругости
вдоль волокон
утка:
Eу Eу '
vf у
vf
Eу ''
vf o
vf
h
Модуль упругости вдоль волокон утка определяется путем перемены мест индексов «о» и «у» в
расчетных выражениях
Модуль сдвига в
плоскости
армирования:
2k
v
v
k 1
Gоу G 1 2 f k
arctg
2 f Gm
2
k 1 2
k 1
Коэффициенты
Пуассона в плоскости
армирования:
оу
v f E
v f о E v f у Eу '
уо
v f E
v f о Eо ' v f у E
49

50.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
iii. ХАРАКТЕРИСТИКИ ОДНОНАПРАВЛЕННОГО КОМПОЗИТНОГО МОНОСЛОЯ В НАПРАВЛЕНИИ θᵒ
Модуль упругости в направлении оси x:
Θ – это угол между осями L и x
однонаправленного композитного монослоя
1 cos 4 sin 4 1 1
2
12 sin 2 2
Ex
E1
E2
4 G12
E1
Модуль упругости в направлении оси y:
y
1
2
x
θ
1 sin 4 cos 4 1 1
2
12 sin 2 2
Ey
E1
E2
4 G12
E1
Модуль сдвига в осях {x, y}:
Gxy / G12
1 1 2 12 1 1 2 12 1
1 2
sin 2
Gxy
E1
E2 E1
E2 G12
Главный коэффициент Пуассона:
1 1 2 12 1
1 2
xy EL 12
sin 2
E
4
E
E
G
1
2
12
1
xy / 12
Ex / E1
Второстепенный коэффициент Пуассона:
E
21 2 12
E1
50

51.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
5. ХАРАКТЕРИСТИКИ УПРУГОСТИ КОМПОЗИТНОГО МОНОСЛОЯ
iV. ХАОТИЧНО АРМИРОВАННЫЙ КОМПОЗИТ
Подход Кокса
для 2D изотропного композита
Подход Кокса
для 3D изотропного композита
Модуль упругости:
1
E Ef v f
3
Модуль упругости:
1
E Ef v f
6
Модуль сдвига:
1
G Ef v f
8
Модуль сдвига:
G
Коэффициент Пуассона:
1
3
Подход Цая-Пагано
для 2D изотропного композита
Модуль упругости:
3
5
E EL ET
8
8
Модуль сдвига:
1
1
G EL ET
8
4
Коэффициент Пуассона:
Коэффициент Пуассона:
1
Ef v f
15
1
4
3D изотропия
2D изотропия
E
1
2G
51

52.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
i. Закон Гука для изотропного материала
Закон Гука выражает линейную связь между
напряжений и деформаций.
компонентами
Для изотропного материала закон Гука имеет следующий вид:
xx
xx
S
yy
yy
xy / 2
xy
0
1
1
0
, S 1
E
0
0 1
yy
– матрица податливости
xy
xy
y
xx
xx
x
xy
xy
yy
И наоборот:
xx
yy Q
xy
0
1
xx
E
1
1
Q S
0 – матрица жесткости
2
,
1
yy
0 0 1
xy / 2
У изотропного материала при повороте осей x и y на любой угол матрицы жесткости и податливости
не меняются.
52

53.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
ii. Особенности деформирования ортотропных материалов
Одна из основных особенностей ортотропных материалов, отличающая их от традиционных изотропных,
таких как как стали и сплавы, – это связанность продольных и угловых деформаций
Деформирование
в главных осях {L, T}
При нагружении
растяжением (или
сжатием)
возникают только
продольные
деформации
При нагружении
сдвигом
возникают только
сдвиговые
деформации
Деформирование
в произвольных осях {x, y}
При нагружении
растяжением (или
сжатием)
возникают не только
продольные
деформации,
но и угловые
При нагружении
сдвигом возникают
не только угловые
деформации, но и
продольные
53

54.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
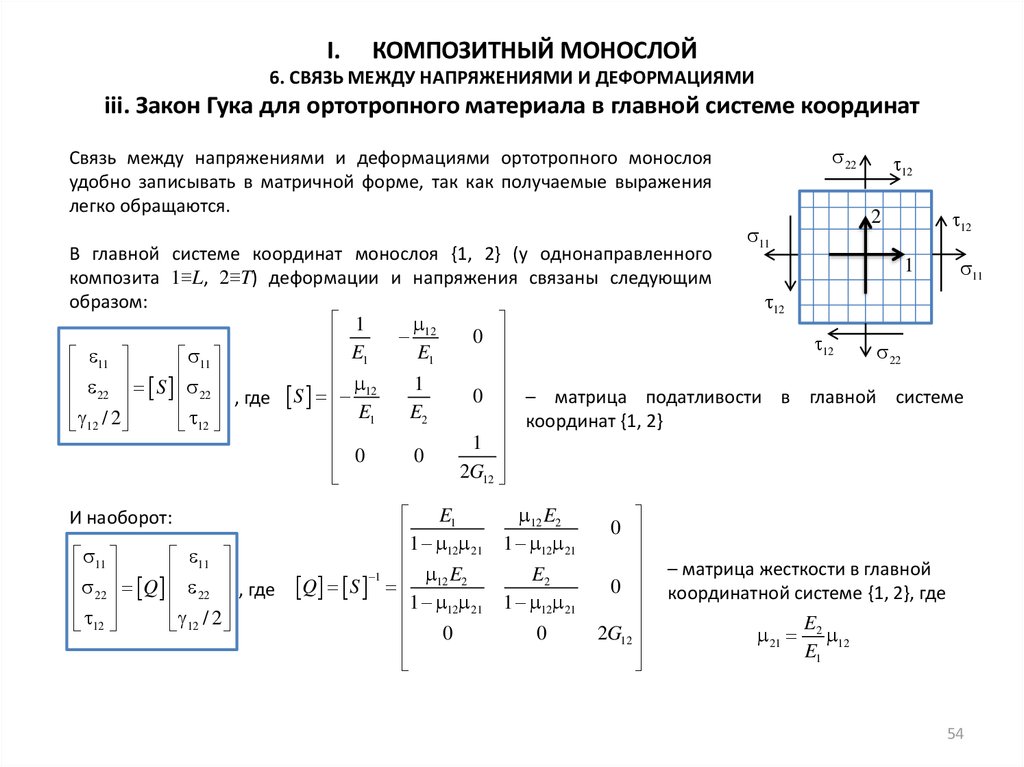
iii. Закон Гука для ортотропного материала в главной системе координат
22
Связь между напряжениями и деформациями ортотропного монослоя
удобно записывать в матричной форме, так как получаемые выражения
легко обращаются.
11
12
2
12
В главной системе координат монослоя {1, 2} (у однонаправленного
1
11
композита 1≡L, 2≡T) деформации и напряжения связаны следующим
образом:
12
1
12
0
12
E
E
22
1
11
11
1
S
1
0 – матрица податливости в главной системе
22 22 , где S 12
E2
12 / 2
12
E1
координат {1, 2}
1
0
0
2G12
И наоборот:
11
11
Q
22 22 , где
12
12 / 2
E1
1
12 21
E
1
Q S 12 2
1 12 21
0
12 E2
1 12 21
E2
1 12 21
0
0
0
2G12
– матрица жесткости в главной
координатной системе {1, 2}, где
E
21 2 12
E1
54

55.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
iv. Закон Гука для ортотропного материала в произвольной системе координат
В произвольной системе координат {x, y}, повернутой на угол θ относительно главных осей 1 и 2
ортотропного монослоя, напряжения и деформации монослоя связаны следующим образом:
y
xx
xx
yy S yy
xy / 2
xy
xx
yy Q
xy
xx
yy
xy / 2
S T S T
– матрица податливости в координатной системе {x, y}
Q T Q T
– матрица жесткости в координатной системе {x, y}
1
1
2
1
θ
x
cos 2
sin 2
2sin cos
1
cos 2
2sin cos – матрица поворота на угол θ, а T ( ) T ( )
T sin 2
sin cos sin cos cos 2 sin 2
Компоненты напряжений и деформаций в главной системе координат монослоя:
xx
11
T
22 yy
xy
12
xx
11
T
22 yy
xy / 2
12 / 2
55

56.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
iv. Закон Гука для ортотропного материала в произвольной системе координат
ПРИМЕР.
Однонаправленный
композит,
армированный
непрерывными волокнами под углом θ = –30ᵒ к оси x,
нагружен нормальными напряжениями σxx = 10 МПа.
θ= – 30ᵒ
Определить напряжения в главных осях монослоя.
РЕШЕНИЕ.
2
sin 2
2sin cos xx
11 cos
sin 2
cos 2
2sin cos 0
22
2
2
12 sin cos sin cos cos sin 0
После подстановки θ = –30ᵒ и σxx=10 МПа получим:
σ11=7,5 МПа, σ22=2,5 МПа, τ12=4,33 МПа
56

57.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
iv. Закон Гука для ортотропного материала в произвольной системе координат
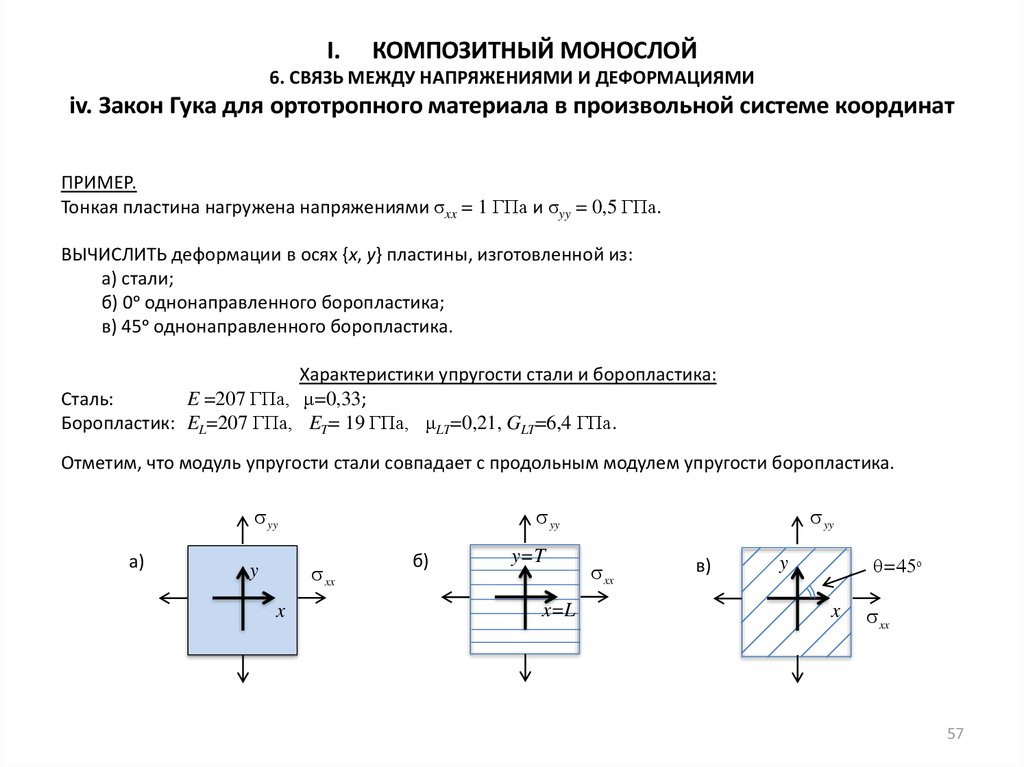
ПРИМЕР.
Тонкая пластина нагружена напряжениями σxx = 1 ГПа и σyy = 0,5 ГПа.
ВЫЧИСЛИТЬ деформации в осях {x, y} пластины, изготовленной из:
а) стали;
б) 0ᵒ однонаправленного боропластика;
в) 45ᵒ однонаправленного боропластика.
Характеристики упругости стали и боропластика:
Сталь:
E =207 ГПа, μ=0,33;
Боропластик: EL=207 ГПа, ET= 19 ГПа, μLT=0,21, GLT=6,4 ГПа.
Отметим, что модуль упругости стали совпадает с продольным модулем упругости боропластика.
yy
а)
yy
xx
y
x
б)
y=T
x=L
yy
xx
в)
θ=45ᵒ
y
x
xx
57

58.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
iv. Закон Гука для ортотропного материала в произвольной системе координат
РЕШЕНИЕ.
yy 0,5 ГПа
а) Сталь – изотропный материал:
xx
0 yy
0,33 0 1 4,03
1
1
1
1
0 yy
0,33
1
0 0,5 0,82 10 3
yy E 1
207
xy / 2
0
0
1
0
0
1,33
0
0
xy
xx 1 ГПа
y
x
εxx=4,03·10-3, εyy=0,82·10-3, γxy=0
Получили очевидный результат: сдвиговых деформаций нет, а εxx > εyy
б) 0ᵒ однонаправленный боропластик – ортотропный материал, у которого оси {L,T} совпадают с осями
нагружения {x,y} :
yy 0,5 ГПа
1
LT
0,21
1
0
0
y=T
E
EL
207
LL 207
LL L
xx 1 ГПа
1 4,32
1
1
LT
0 TT 0,21
0 0,5 25,3 10 3
x=L
TT E
ET
19
L
LT / 2
0
0
LT
1
1
0
0
0
0
12,8
2
G
LT
εxx=4,32·10-3, εyy=25,3·10-3, γxy=0
Результат качественно отличается от предыдущего: εxx < εyy при σxx > σ yy, хотя и частично совпадает с ним
(сдвиговые деформации отсутствуют)
58

59.

I.
КОМПОЗИТНЫЙ МОНОСЛОЙ
6. СВЯЗЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
iv. Закон Гука для ортотропного материала в произвольной системе координат
в) 45ᵒ однонаправленный боропластик – ортотропный материал, у которого главные оси повернуты на
угол θ=45ᵒ по отношению к осями {x,y} нагружения
Матрица податливости в осях {x, y} определяется следующим образом:
1
E
2
2
c
s
2s c) L
1
S T S T s2 c2 2s c LT
EL
s c s c c 2 s 2
1
0
T
xx
xx
Подставив в выражение yy S yy
xy / 2
xy
LT
EL
1
ET
0
0
c2 s2
2s c
2
0 s
c 2 2s c , где c ≡ cos(θ), а s ≡ sin(θ)
s c s c c2 s2
1
T
2GLT
yy 0,5 ГПа
матрицу податливости [Sθ] и напряжения: σxx=1 ГПа, σyy=0,5 ГПа и τxy=0,
получим деформации в осях {x, y}:
θ=45ᵒ
y
x
xx 1 ГПа
εxx=40,326·10-3, εyy=1,270·10-3, γxy= – 35,86·10-3
Результат заметно отличается от предыдущих – при нагружении растяжением появились сдвиговые
деформации
59