Три секрета прочности волокнистых композитов

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Динамика, прочность машин и сопротивление материалов»
Дисциплина «Механика композиционных материалов»
Лекция 1.2. Три секрета
прочности волокнистых
композитов.
Лектор:
д.т.н., профессор
Полилов А.Н.
Москва, 2020

2.

ТРИ СЕКРЕТА ПРОЧНОСТИ
ВОЛОКНИСТЫХ
КОМПОЗИТОВ

3.

План лекции №1.2:
1.2.1.Первый секрет – масштабный эффект прочности
волокон.
1.2.2. Второй секрет – остановка трещины поверхностью
раздела.
1.2.3.Третий
секрет
–
статистический
характер
прочности волокон.
1.2.4. О линейной механике разрушения.
1.2.5. Об асимптотическом решении задачи
про
остановку трещины поверхностью раздела.
1.3.6. О роли касательных напряжений и оптимальных
(равнопрочных) свойствах волокнистых композитов.
1.2.7. О распределении Вейбулла.

4.

Три секрета прочности волокнистых
композитов
Первый секрет - масштабный
эффект прочности волокон
Оценка прочности, полученная Гриффитсом
- удельная работа разрушения,
- длина дефекта
а)
б)
Зависимости прочности – (а) и её
обратной величины – (б) от диаметра
волокна

5.

Масштабный эффект (Scale effect)
«РОЛЬ ВОЛОКОН»
Эксперимент Гриффитса со стеклянными волокнами (1911 г.)

6.

7.

Теория Гриффитса-Ирвина
Алан Арнольд Гриффитс
(1893-1963) – A.A.Griffith
1. Механика разрушения
• Теоретическая
прочность,
концентрация
напряжений
2. Механика композитов
• Прочность тонких бездефектных волокон
• Стекло: пузырьки - давление, волокна –
эластика Эйлера, испытания петлей.

8.

Энергетический критерий
Гриффитса
G – удельная работа разрушения, т.е. энергия
необходимая
для
образования
единицы
поверхности
dU – затраченная работа
dS – площадь трещины
Gс – критическая скорость высвобождения
энергии
Энергетический критерий в
упрощенном виде (без учета
диссипации энергии и
динамических эффектов):
Схемы трещин в растягиваемых:
трехмерном теле – а и в пластине – б

9.

Общая накопленная
упругая энергия:
U 2 (V k0l 3 ) / (2 E )
Качественный результат для
пластины толщиной t (=1) со
сквозной трещиной длиной
2l:
U (V k2tl ) / (2 E );
2
Изменение упругой
энергии:
dS 2 ldl
dU 3 2 k0l 2 dl / (2 E )
dU 2 dS
EGc
3k0
; k1
(1 2 )
k1l
4
2
dU 2tk2l dl / E; dS tdl;
dU / dS Gc EGc / (k2l ).
Для сквозной трещины в
широкой пластинке в
условиях плоского
напряженного состояния:
2 EGc / ( l )
Для плоской деформации:
2EGc / [(1 2 ) l ].

10.

1.2.4. О линейной механике
разрушения
dU 3 kl dl / (2E )
2
2
U 2 (V k1hl 2 ) / (2 E );
dU 2 2 hk1l dl / (2 E ); dS 2hdl;
dU / dS
kE / l.

11.

ТРИ СЕКРЕТА ПРОЧНОСТИ ВОЛОКНИСТЫХ
КОМПОЗИТОВ
2-й секрет
Торможение (остановка,
задержание, стопорение)
трещины поверхностью раздела
Crack arrest by weak interface

12.

Три секрета прочности композитов
limK 1 2
b 0
a
А.Н.Полилов,
f
1,82
12

13.

Торможение трещины поверхностью
раздела
Причина нехрупкости композитов при
растяжении вдоль волокон заключается в
наличии около кончика трещины сложного
напряжённого состояния, которое
вызывает расщепление, тормозящее
развитие трещины.

14.

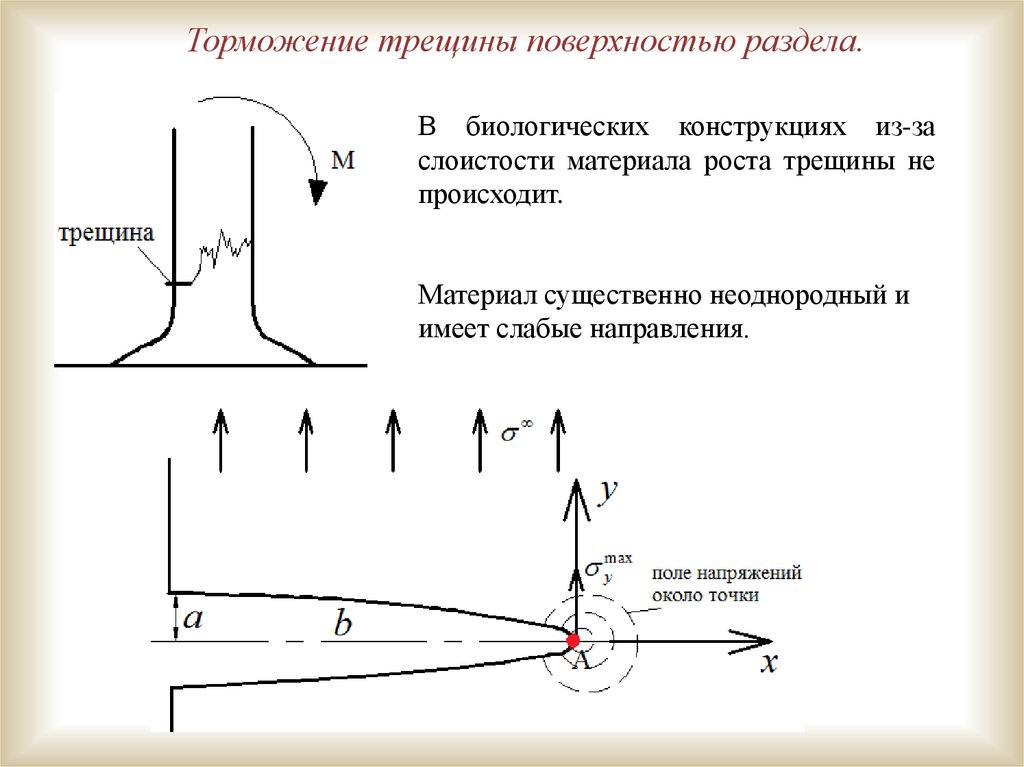
Торможение трещины поверхностью раздела.
В биологических конструкциях из-за
слоистости материала роста трещины не
происходит.
Материал существенно неоднородный и
имеет слабые направления.

15.

Торможение трещины поверхностью раздела
Причина нехрупкости композитов при растяжении вдоль волокон заключается в
наличии около кончика трещины сложного напряженного состояния, которое
вызывает расщепление, тормозящее развитие трещины.
Рис.3 Распределение
x
Рис.4 Распределение
y

16.

Механизм торможения (схематически)
Микроснимки
картин роста трещины
в слюде: когда
трещина
упирается в границу
слоев – слева,
и когда трещина
проходит вдоль слоев
– справа.
Прочность слева в 20
раз выше.

17.

Торможение трещины поверхностью
раздела
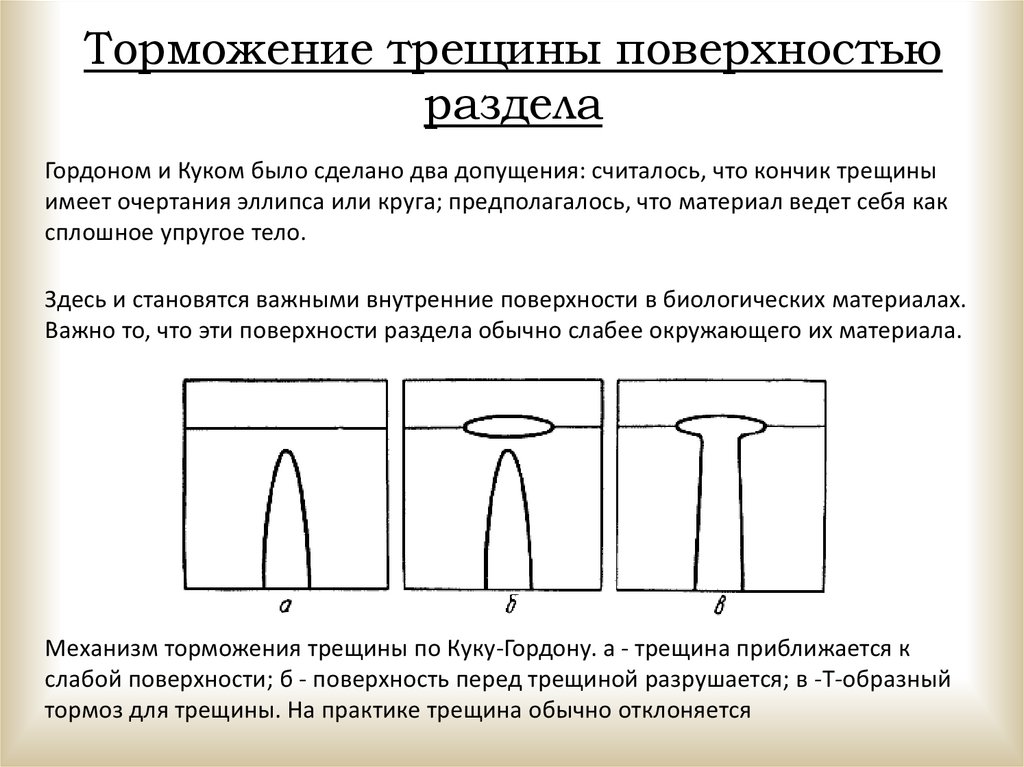
Гордоном и Куком было сделано два допущения: считалось, что кончик трещины
имеет очертания эллипса или круга; предполагалось, что материал ведет себя как
сплошное упругое тело.
Здесь и становятся важными внутренние поверхности в биологических материалах.
Важно то, что эти поверхности раздела обычно слабее окружающего их материала.
Механизм торможения трещины по Куку-Гордону. a - трещина приближается к
слабой поверхности; б - поверхность перед трещиной разрушается; в -Т-образный
тормоз для трещины. На практике трещина обычно отклоняется

18.

а)
б)
Схемы остановки трещины поверхностью раздела:
а) по Гордону – расщепление перед трещиной;
б) уточненная схема – расщепление на контуре

19.

Второй секрет — остановка трещины поверхностью раздела
Схемы остановки трещины поверхностью раздела: а) по Гордону — расщепление перед трещиной; б)
уточненная схема — расщепление на контуре

20.

Второй секрет – нехрупкость. Торможение
трещины границей раздела.
Mechanism of crack arrest by weak interface

21.

Максимальное
значение
напряжений перед кончиком
трещины при у=0,
xx
x a b
2
2
2
2/3 2/3
1
2
(
2/3
1
2 )
2/3
выражается формулой
xx 0 t ( 1 2 )(t 4/3 t 2/3 1)2/3
xx
t 1 2
lim 4/3 2/3 3/2
yy (t t 1)
if 0
/ 1 2t / (1 t ) / ( 1/ 4 при t 1)
xx
yy
2
xx
yy

22.

1.2.6. О роли касательных напряжений и
оптимальных (равнопрочных) свойствах
волокнистых композитов
Условие равнопрочности:
xy
*
y*
в
Для эллиптических
отверстий в изотропном
случае:
xy*
y*
0,32 при a b
0, 29 при a b
0, 25 при a b

23.

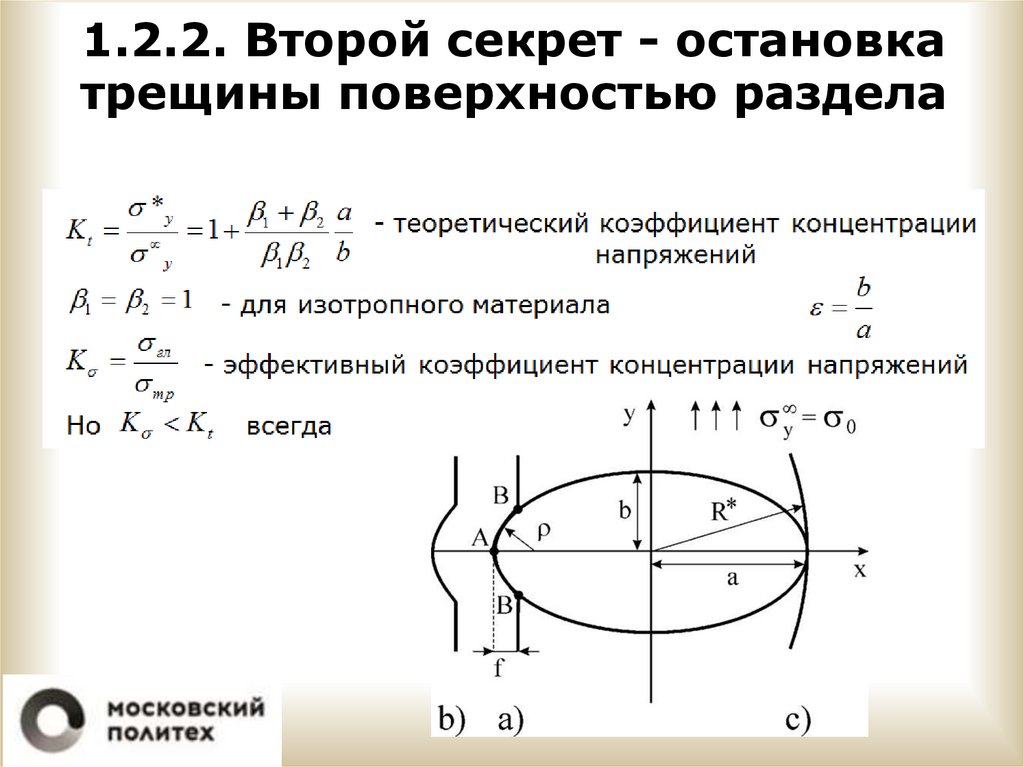
1.2.2. Второй секрет - остановка
трещины поверхностью раздела

24.

yy p
xx 2 Re 12 1 ( z1 ) 22 2 ( z2 )
yy 2 Re 1 ( z1 ) 2 ( z2 )
Где:
xy 2 Im 1 1 ( z1 ) 2 2 ( z2 )
z1,2 x i 1,2 y
z1,2
p 2,1
1
1,2
1
2 1 2 a 1,2b z 2 a 2 2b 2
1,2
1,2
1,2 2
1/ 2
1/ 2
( E / G 2 ( E / G 2 ) 4 E / E
yx
x
xy
yx
x
y
x xy
2

25.

Задержка трещины поверхностью раздела
x 2 Re( 12 1 ( z1 ) 22 2 ( z2 ))
y 2 Re( 1 ( z1 ) 2 ( z2 ))
xy 2 Im( 1 1 ( z1 ) 2 2 ( z2 ))
z1,2 x i 1,2 y
1,2
z1,2
p 2,1
1
1
2 1 2 a 1,2b z 2 a 2 2b 2
1,2
1,2
1,2 2
1/ 2
1/ 2
( E / G 2 ( E / G 2 ) 4 E / E
yx
x
xy
yx
x
y
x xy
2
z=acosα+ibsinα, b/a=ε<<1, cos2α=1-kε2+o(ε2)

26.

1.2.5. Об асимптотическом
решении задачи про остановку
трещины поверхностью раздела
Надо сравнивать наибольшие напряжения на контуре:
x* / y* 12 / (1 t )2 (
1
4
при
1 t 1) x / y* (
1
при
5
t 1).

27.

«Оптимальные прочностные свойства волокон и
матрицы в условиях концентрации напряжений.»

28.

Для ортотропного материала зависимость от
формы отверстия.
В пределе при
P a xy
1
2 0, xy ; * 1/ 2 1 2 ( 1 2 )
2 b y
*
*

29.

Зависимости наибольших напряжений около
эллиптической трещины
от степени анизотропии материала.

30.

Оптимальные прочностные
свойства волокон и матрицы в
условиях концентрации напряжений.
Вывод об основной роли касательных
напряжений в возникновении расщепления
позволяет сформулировать условие
равнопрочности в виде.
xy
yy
в

31.

Критерий “оптимальности” (равнопрочности) в условиях
концентрации напряжений
n1 m1 n1
c1
n 2 m2 n 2
c2
либо отношение max напряжений равно отношению прочностей:
*
xy
[ ]
*
y [ в ]
xy*
y*
0.32
0.29
0.25
0.29
0.32
при a b
при a b 0.5
жёсткая шайба 0
при a b
при a b

32.

xy
*
y
*
0.095, 0.091
в
для дуба ,
для сосны соответствующие
отношения равны 0.14 и
0.093.

33.

Оценим рациональную объемную долю волокон p
E y Eв ; в в ; Ex Eм ,
0
1
p ( в ) Eв Eм A( ),
2
0 2
A( ) =2-3 – слабо зависящая от объёмной доли функция
при p разрушение начнётся с разрыва волокон,
при
p - с расщепления.
У стеклопластика
p 20 30%.

34.

СПАСИБО ЗА ВНИМАНИЕ!

35.

Часть 1. Три секрета прочности
композитов
limK 1 2
b 0
a
А.Н.Полилов,
f
1,82
35

36.

Третий секрет – статистический характер
прочности волокон
Прочность пучка эффективной длины
а
б
Функции распределения – б и плотности
распределения – а прочности волокон

37.

1.2.3. Третий секрет - статистический
характер прочности волокон

38.

Иллюстрация понятия
эффективной длины Le
Сравнение прочности волокон с
разными типами дефектов на базе
испытаний и на эффективной
длине

39.

Третий секрет — статистический характер прочности волокон
Эффективная длина Le
Сравнение прочности волокон с
разными типами дефектов на базе
испытаний и на эффективной длине

40.

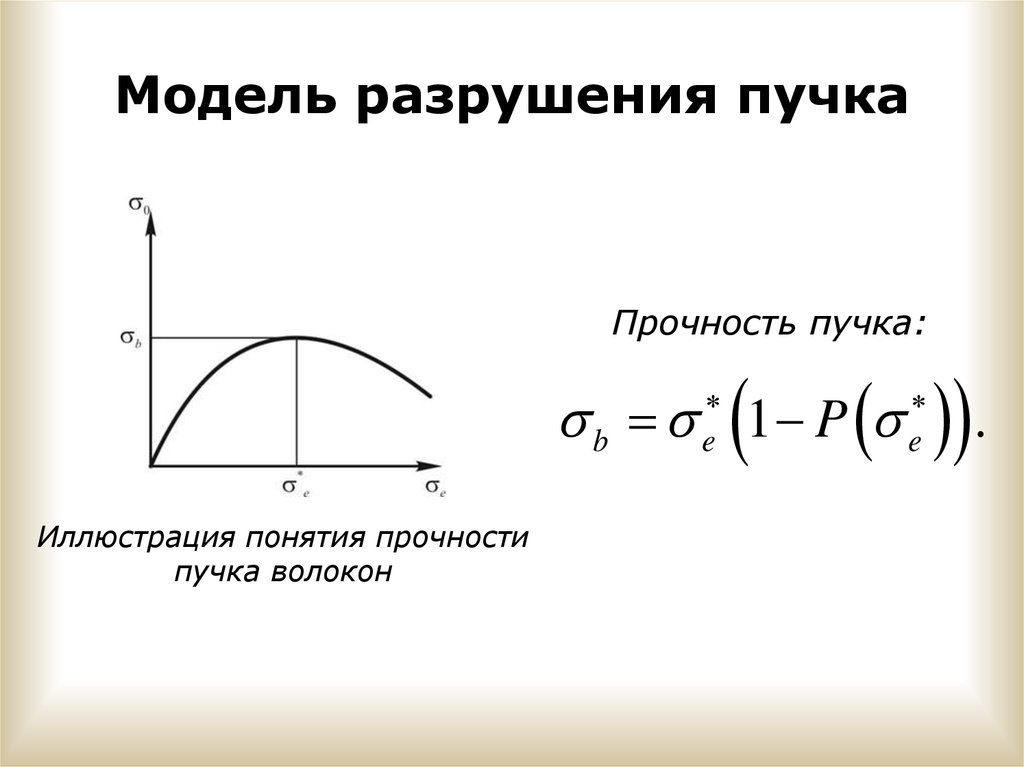
Модель разрушения пучка
Прочность пучка:
b 1 P
e
Иллюстрация понятия прочности
пучка волокон
e
.

41.

Равномерное распределение
прочности
Функция плотности
равномерного распределения
1 ;
p
0;
;
; ,
Функция распределения:
/ ;
P 0;
1;
;
;
.
Средняя прочность волокон:
2 2
1
f
.
2
2
Критическое эффективное
напряжение и прочность пучка
1 2
f .
b
4
2
e
При нулевой минимальной
прочности:
1
1
1
f ; b f .
2
4
2

42.

1.2.7. О распределении Вейбулла
Функция плотности распределения прочности
p ( )
dP( , L)
L 1
L
(
)
exp[
( ) ].
d
L0
L0
Распределение
Вейбулла
более
обосновано
применительно
к
прочности
волокон,
чем
традиционное нормальное распределение Гаусса,
которое,
во-первых,
симметрично,
во-вторых,
допускает бесконечные и отрицательные значения
прочности.

43.

Распределение Вейбулла
Гипотеза Вейбулла состоит в том, что прочность
материала можно рассматривать, как прочность цепи, и
разрушение соответствует разрыву слабейшего звена
этой цепи. Теория «слабого звена» применительно к
волокнам выглядит более логичной, чем для обычных
квазиоднородных сплавов, где разрушение, возникшее
в одной точке (в одном элементе характерного
размера), может ещё не означать разрушение всей
конструкции.
Применительно к прочности волокон функцию
распределения Вейбулла выбирают в следующем виде
n
L
P( , L) 1 exp[ (
) ].
N
L0 '

44.

Функция плотности
распределения прочности:
p( )
dP( , L) L 1
L
( ) exp[ ( ) ].
d
L0 ' '
L0 '
Табулированная гамма-функция:
1
1 x1/ exp x dx.
0
Коэффициент реализации z
прочности
1/
b Lt
z
f Le e
1
.
1 1/
Коэффициент реализации прочности волокон в
однонаправленном композите в зависимости от
эффективной длины и параметра α ширины
гистограммы
α
5
10
20
z(10)
1,04
0,95
0,94
z(20)
1,19
1,01
0,98

45.

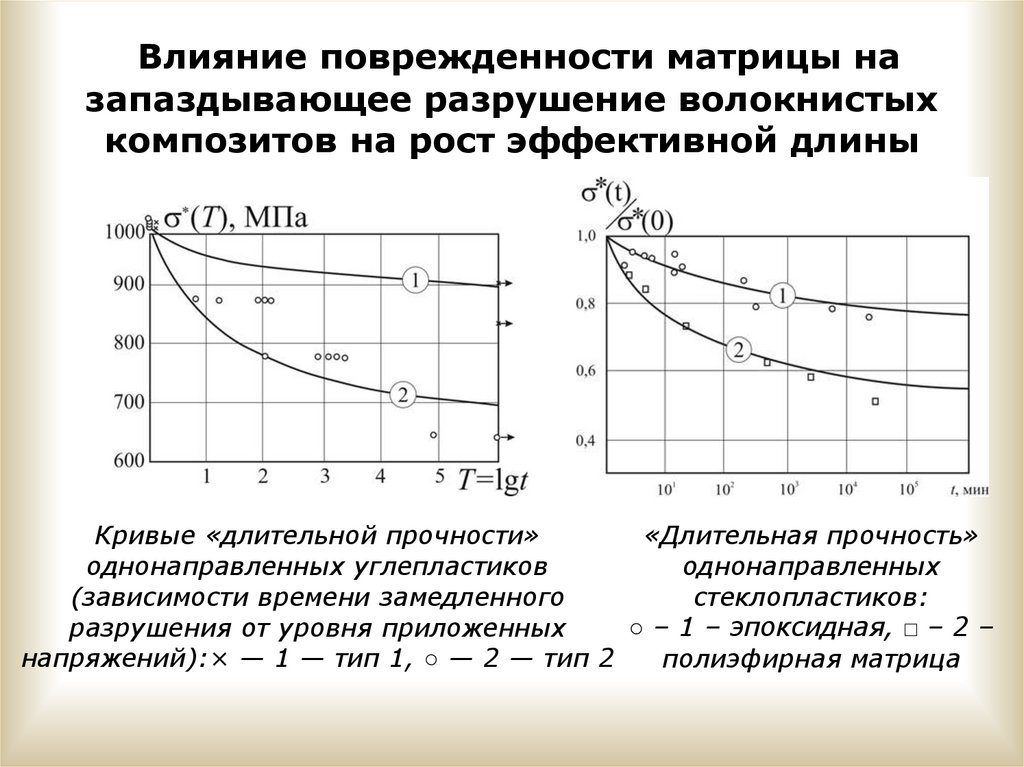
Влияние поврежденности матрицы на
запаздывающее разрушение волокнистых
композитов на рост эффективной длины
Кривые «длительной прочности»
«Длительная прочность»
однонаправленных углепластиков
однонаправленных
(зависимости времени замедленного
стеклопластиков:
○ – 1 – эпоксидная, □ – 2 –
разрушения от уровня приложенных
напряжений):× — 1 — тип 1, ○ — 2 — тип 2
полиэфирная матрица

46.

Влияние матрицы на
поврежденность около отверстия…