Структурная механика композитов. Композитный монослой

1.

СТРУКТУРНАЯ МЕХАНИКА КОМПОЗИТОВ
I. КОМПОЗИТНЫЙ МОНОСЛОЙ
1. Основные положения и обозначения
2. Моделирование свойств однонаправленного композита
при различных видах нагружения
i. Продольное растяжение
а. Композит, армированный непрерывными
волокнами
b. Композит, армированный короткими
волокнами
ii. Трансверсальное растяжение
iii. Сдвиг в плоскости волокон
iv. Продольное сжатие
v. Трансверсальное сжатие
3. Моделирование свойств хаотично армированного
композита
4. Моделирование свойств тканевого композита
5. Характеристики упругости композитного монослоя
i. Композит, армированный непрерывными
волокнами
ii. Композит, армированный короткими волокнами
iii. Тканевый композит
iv. Характеристики однонаправленного композитного
монослоя в направлении θᵒ
v. Хаотично армированный композит
6. Связь между напряжениями и деформациями
i. Особенности деформирования композитного
монослоя
ii. Закон Гука для ортотропного материала в главной
системе координат
iii. Закон Гука для ортотропного материала в
произвольной системе координат
II. СЛОИСТЫЙ КОМПОЗИТ
1. Основные положения теории слоистых пластин
2. Деформации слоистого композита
3. Силы и моменты, действующие на слоистый
композит
4. Матрицы жесткости слоистого композита
5. Деформация и кривизна срединной плоскости
6. Напряжения и деформации в слоях композита
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
1. Теории прочности однонаправленного композита
i. Теория максимальных напряжений
ii. Теория максимальных деформаций
iii. Теория Аззи-Цая-Хилла
iv. Теория Цая-Ву
2. Методы прогнозирования прочности слоистого
композита
i. Метод последовательного разрушения слоев
ii. Метод прогнозирования прочности слоистого
композита с учетом накопления микроповреждений
(метод Сапожникова)
3. Методы оценки прочности хаотично армированных
композитов
i. Подход Хана
ii. Метод Хальпина-Кардоса
1

2.

II. СЛОИСТЫЙ КОМПОЗИТ
1.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СЛОИСТЫХ ПЛАСТИН
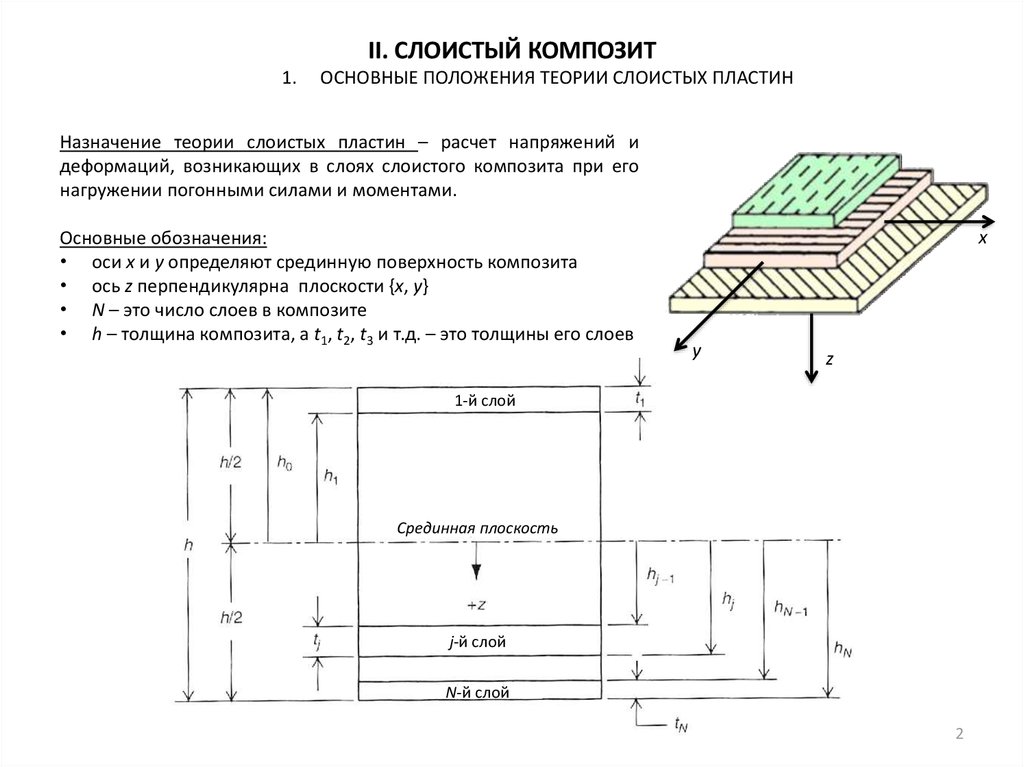
Назначение теории слоистых пластин – расчет напряжений и
деформаций, возникающих в слоях слоистого композита при его
нагружении погонными силами и моментами.
Основные обозначения:
• оси x и y определяют срединную поверхность композита
• ось z перпендикулярна плоскости {x, y}
• N – это число слоев в композите
• h – толщина композита, а t1, t2, t3 и т.д. – это толщины его слоев
x
y
z
1-й слой
Срединная плоскость
j-й слой
N-й слой
2

3.

II. СЛОИСТЫЙ КОМПОЗИТ
1.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СЛОИСТЫХ ПЛАСТИН
Основные допущения:
напряженное состояние в композите плоское (поскольку его
ширина значительно превышает толщину)
связь между слоями идеальна
распределение деформаций по толщине композита линейно
на макроуровне слои однородны
свойства слоев подчиняются закону Гука для ортотропного (в
общем случае) или изотропного (в случае хаотично
армированного композита) материала
x
y
z
Пошаговая процедура расчета напряжений в слоях:
расчет матрицы податливости (или жесткости) слоистого композита
расчет деформаций и кривизн срединной плоскости композита, возникающих под воздействием
приложенных к нему сил и моментов
расчет деформаций в слоях композита
εxx, εyy и γxy
расчет напряжений в слоях композита
σxx, σyy, τxy
3

4.

II. СЛОИСТЫЙ КОМПОЗИТ
2. ДЕФОРМАЦИИ СЛОИСТОГО КОМПОЗИТА
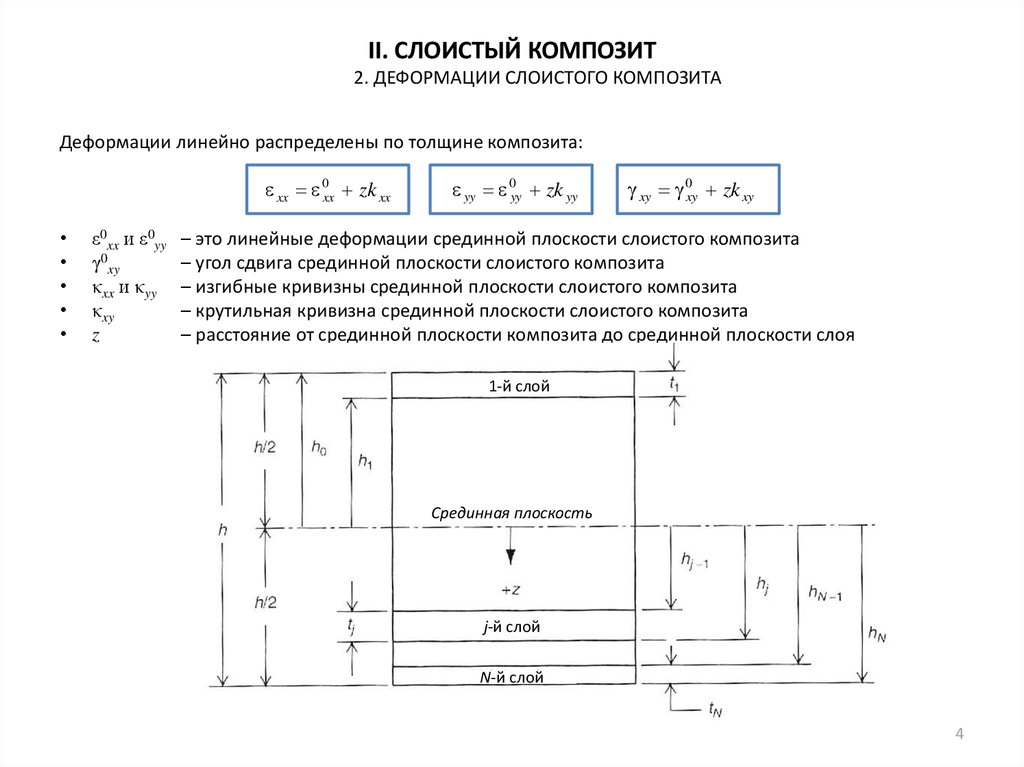
Деформации линейно распределены по толщине композита:
xx 0xx zk xx
ε0xx и ε0yy
γ0xy
κxx и κyy
κxy
z
yy 0yy zk yy
xy 0xy zk xy
– это линейные деформации срединной плоскости слоистого композита
– угол сдвига срединной плоскости слоистого композита
– изгибные кривизны срединной плоскости слоистого композита
– крутильная кривизна срединной плоскости слоистого композита
– расстояние от срединной плоскости композита до срединной плоскости слоя
1-й слой
Срединная плоскость
j-й слой
N-й слой
4

5.

II. СЛОИСТЫЙ КОМПОЗИТ
3. СИЛЫ И МОМЕНТЫ, ДЕЙСТВУЮЩИЕ НА СЛОИСТЫЙ КОМПОЗИТ
Силы и моменты, приложенные к композиту, связаны с деформациями и кривизнами его срединной
поверхности следующим образом:
0xx
N xx
k xx
0
N yy A yy B k yy
0xy / 2
N xy
k xy / 2
0xx
M xx
k xx
0
M
B
D
k
yy
yy
yy
0xy / 2
M xy
k xy / 2
Nxx и Nyy – это погонные (то есть приходящиеся на единицу ширины композита ) нормальные силы
в направлениях осей x и y соответственно
Mxx и Myy – погонные изгибающие моменты в плоскостях xz и yz соответственно
Nxy
– погонная поперечная сила
Mxy
– погонный крутящий момент
5

6.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
Матрица [A]
Матрица [B]
Матрица [D]
A Q j (h j h j 1 )
B 1 Q j (h 2j h 2j 1 )
D 1 Q j (h 3j h 3j 1 )
N
j 1
A11
A A12
A16
A12
A22
A26
2 A16
2 A26
2 A66
N
2
B11
B B12
B16
Элементы A16 и A26
матрицы [A] отвечают за
наличие связи
растяжение - сдвиг
j 1
N
– число слоев в композите
[Qθ]j – матрица жесткости j-того слоя
B12
B22
B26
2 B16
2 B26
2 B66
Матрица [B] отвечает за
наличие связей:
растяжение – изгиб,
растяжение – кручение,
сдвиг – кручение
N
3
j 1
D11
D D12
D16
D12
D22
D26
2 D16
2 D26
2 D66
Элементы D16 и D26
матрицы [D] отвечают за
наличие связи
изгиб - кручение
E1
1
2
12 21
cos 2
sin
2sin cos
E
1
cos 2
2sin cos Q 12 2
Q T Q T T sin 2
1 12 21
sin cos sin cos cos 2 sin 2
0
hj-1 – расстояние от срединной плоскости до верхней части j-того слоя
hj
– расстояние от срединной плоскости до нижней части j-того слоя
12 E2
1 12 21
E2
1 12 21
0
0
0
2G12
6

7.

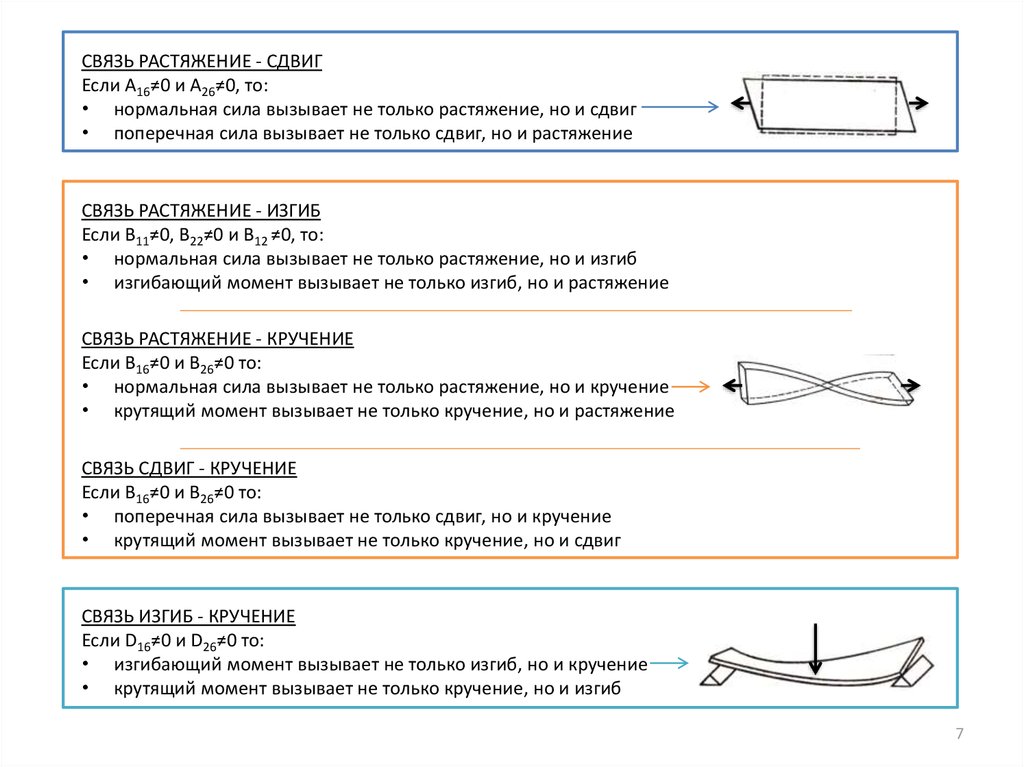
СВЯЗЬ РАСТЯЖЕНИЕ - СДВИГ
Если A16≠0 и A26≠0, то:
• нормальная сила вызывает не только растяжение, но и сдвиг
• поперечная сила вызывает не только сдвиг, но и растяжение
СВЯЗЬ РАСТЯЖЕНИЕ - ИЗГИБ
Если B11≠0, B22≠0 и B12 ≠0, то:
• нормальная сила вызывает не только растяжение, но и изгиб
• изгибающий момент вызывает не только изгиб, но и растяжение
СВЯЗЬ РАСТЯЖЕНИЕ - КРУЧЕНИЕ
Если B16≠0 и B26≠0 то:
• нормальная сила вызывает не только растяжение, но и кручение
• крутящий момент вызывает не только кручение, но и растяжение
СВЯЗЬ СДВИГ - КРУЧЕНИЕ
Если B16≠0 и B26≠0 то:
• поперечная сила вызывает не только сдвиг, но и кручение
• крутящий момент вызывает не только кручение, но и сдвиг
СВЯЗЬ ИЗГИБ - КРУЧЕНИЕ
Если D16≠0 и D26≠0 то:
• изгибающий момент вызывает не только изгиб, но и кручение
• крутящий момент вызывает не только кручение, но и изгиб
7

8.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
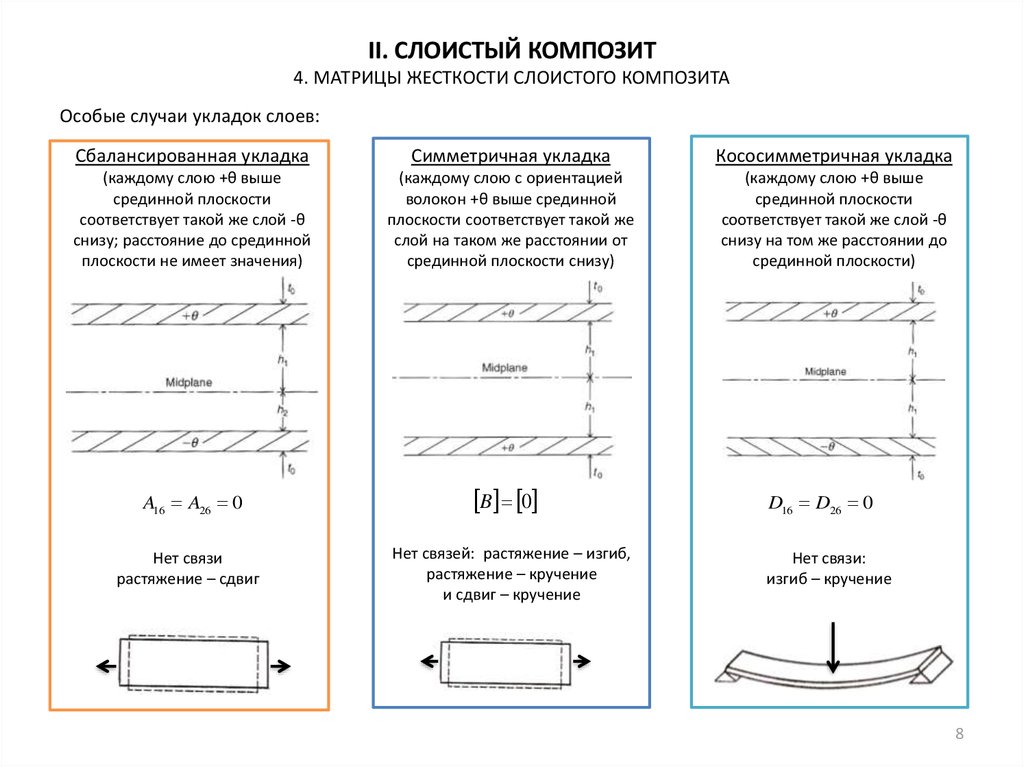
Особые случаи укладок слоев:
Сбалансированная укладка
Симметричная укладка
Кососимметричная укладка
(каждому слою +θ выше
срединной плоскости
соответствует такой же слой -θ
снизу; расстояние до срединной
плоскости не имеет значения)
(каждому слою с ориентацией
волокон +θ выше срединной
плоскости соответствует такой же
слой на таком же расстоянии от
срединной плоскости снизу)
(каждому слою +θ выше
срединной плоскости
соответствует такой же слой -θ
снизу на том же расстоянии до
срединной плоскости)
A16 A26 0
B 0
Нет связи
растяжение – сдвиг
Нет связей: растяжение – изгиб,
растяжение – кручение
и сдвиг – кручение
D16 D26 0
Нет связи:
изгиб – кручение
8

9.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
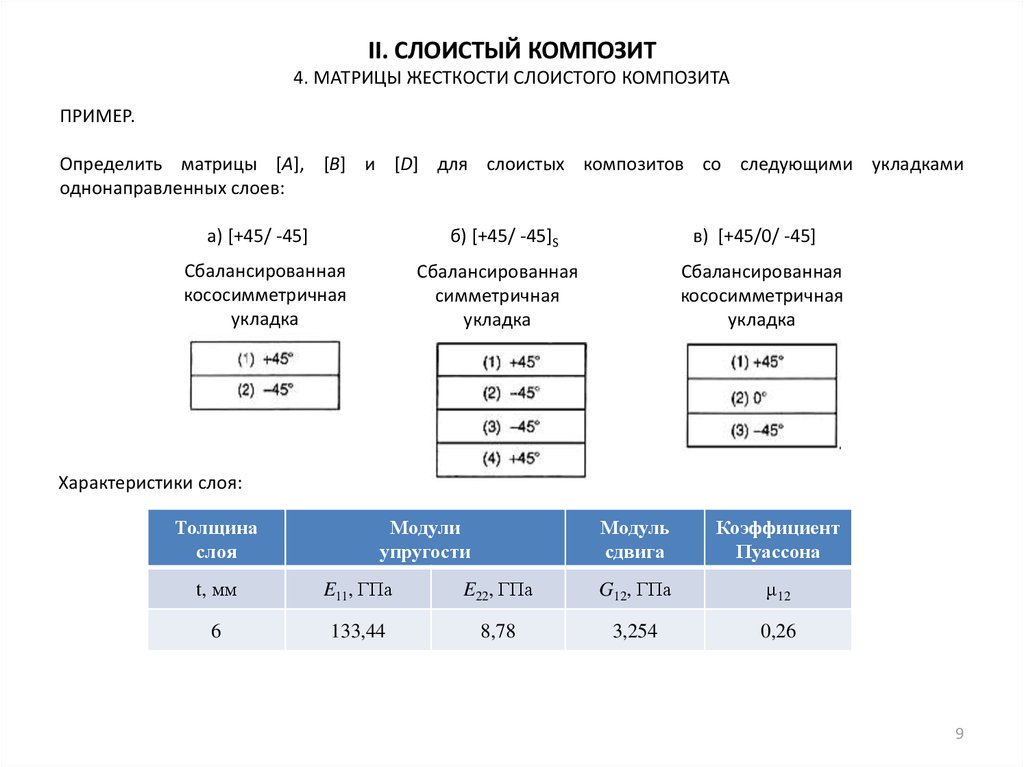
ПРИМЕР.
Определить матрицы [A], [B] и [D] для слоистых композитов со следующими укладками
однонаправленных слоев:
а) [+45/ -45]
б) [+45/ -45]S
Сбалансированная
кососимметричная
укладка
в) [+45/0/ -45]
Сбалансированная
симметричная
укладка
Сбалансированная
кососимметричная
укладка
Характеристики слоя:
Толщина
слоя
Модули
упругости
Модуль
сдвига
Коэффициент
Пуассона
t, мм
E11, ГПа
E22, ГПа
G12, ГПа
μ12
6
133,44
8,78
3,254
0,26
9

10.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
РЕШЕНИЕ.
Второстепенный коэффициент Пуассона:
21
E2
12 0,017
E1
Матрицы жесткости слоев (индексы «0», «45» и «-45» соответствуют направлениям укладки слоев):
12 E2
E1
0
1
1 12 21
12 21
E
E2
0
Q 0 12 2
Q 45 T ( 45) Q 0 T (45)
Q 45 T (45) Q 0 T ( 45)
1 12 21 1 12 21
0
0
2G12
После подстановки исходных данных в эти выражения и с учетом того, что матрица поворота имеет
следующий вид,
cos 2
sin 2
2sin cos
2
2
cos
2sin cos
T sin
sin cos sin cos cos 2 sin 2
в итоге получим:
θ=0
0
134 2,29
Q 0 2,29 8,819 0 ГПа
0
0
6,508
θ = +45
40,1 33,6 62,6
Q 45 33,6 40,1 62,6 ГПа
31,3 31,3 69,1
θ = -45
40,1 33,6 62,6
Q 45 33,6 40,1 62,6 ГПа
31,3 31,3 69,1
10

11.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
а) Подставим в матрицы [A], [B] и [D]:
A Q 45 (h1 h0 ) Q 45 (h2 h1 )
B Q 45 (h12 h02 ) Q 45 (h22 h12 )
2
1
D Q 45 (h13 h03 ) Q 45 (h23 h13 )
3
1
найденные жесткости слоев [Q]+45, [Q]-45 и величины
h0=-0,006 м, h1=0
и
h2=0,006 м.
В итоге получим:
481 403 0
Н
A 403 481 0 106
м
0
0 830
0
1,25
0
0
1,25 106 Н
B 0
1,13 1,13
0
0
5,78 4,84
D 4,84 5,78 0 103 Нм
0
0
9,96
У композита со сбалансированной укладкой слоев A16=A26=0 (отсутствие связи растяжение – сдвиг),
кроме того здесь B11=B22=B12=0 (отсутствие связи растяжение – изгиб) и D16=D26=0 (отсутствие связи
изгиб – кручение) поскольку композит кососимметричен.
11

12.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
б) Подставим в матрицы [A], [B] и [D]:
A Q 45 (h1 h0 h4 h3 ) Q 45 (h2 h1 h3 h2 )
B Q 45 (h12 h02 h42 h32 ) Q 45 (h22 h12 h32 h22 )
2
1
D Q 45 (h13 h03 h43 h33 ) Q 45 (h23 h13 h33 h23 )
1
3
найденные жесткости слоев и величины
h0=-0,012 м, h1=-0,006 м, h2=0,
h3=0,006 м
и
h4=0,012 м.
В итоге получим:
0
963 806
Н
A 806 963 0 106
м
0
0 1660
0 0 0
B 0 0 0 106 Н
0 0 0
46,2 38,7 54,0
D 38,7 46,2 54,0 103 Нм
27,0 27,0 79,6
У симметричного композита со сбалансированной укладкой слоев A16=A26=0 (отсутствие связи
растяжение – сдвиг) и [B]=0 (отсутствие связей растяжение – изгиб, растяжение – кручение и сдвиг –
кручение).
12

13.

II. СЛОИСТЫЙ КОМПОЗИТ
4. МАТРИЦЫ ЖЕСТКОСТИ СЛОИСТОГО КОМПОЗИТА
в) Подставим в матрицы [A], [B] и [D]:
A Q 45 (h1 h0 ) Q 0 (h2 h1 ) Q 45 (h3 h2 )
B Q 45 (h12 h02 ) Q 0 (h22 h12 ) Q 45 (h32 h22 )
2
1
D Q 45 (h13 h03 ) Q 0 (h23 h13 ) Q 45 (h33 h23 )
3
1
найденные жесткости слоев и величины
h0=-0,09 м,
h1=-0,03 м,
h2=0,03 м
и
h3=0,09 м.
В итоге получим:
0
1,29 0,42
Н
A 0,42 0,53 0 109
м
0
0
0,87
0
4,51
0
0
4,51 106 Н
B 0
2,25 2,25
0
0
21,2 15,8
D 15,8 18,9 0 103 Нм
0
0 32,5
У кососимметричного композита D16=D26=0 (отсутствие связи изгиб – кручение), а поскольку укладка
сбалансирована, то A16=A26=0 (отсутствие связи растяжение – сдвиг), кроме того B11=B22=B12=0
(отсутствие связи растяжение – изгиб)
13

14.

II. СЛОИСТЫЙ КОМПОЗИТ
5. ДЕФОРМАЦИЯ И КРИВИЗНА СРЕДИННОЙ ПЛОСКОСТИ
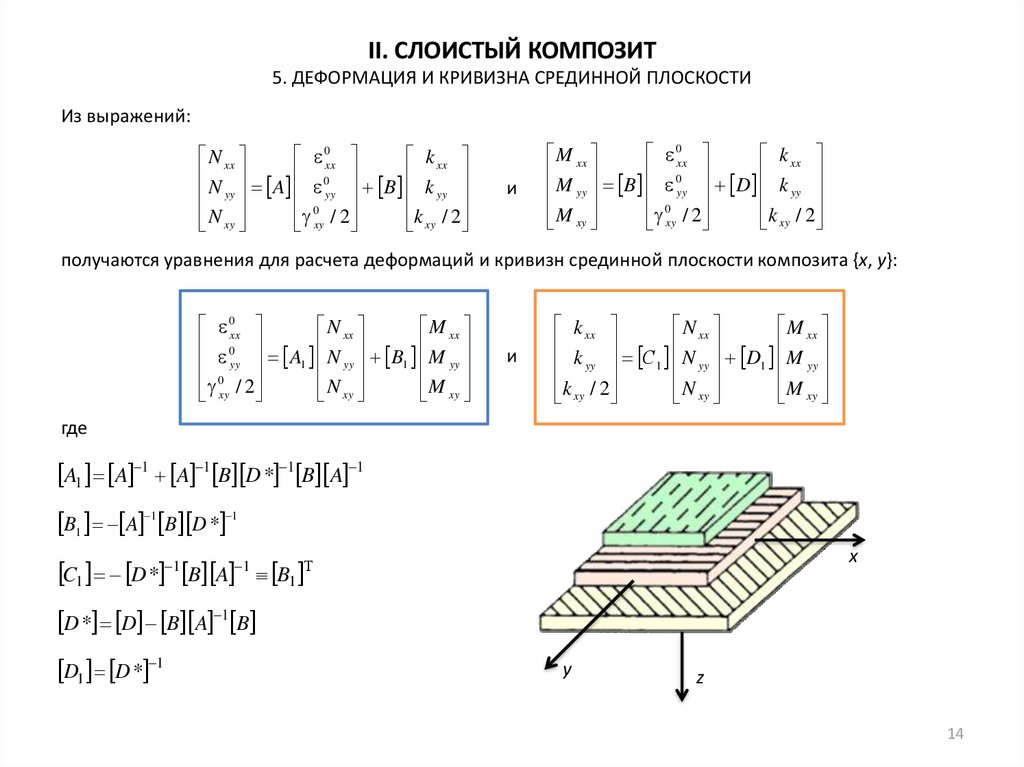
Из выражений:
0xx
N xx
k xx
0
N yy A yy B k yy
0xy / 2
N xy
k xy / 2
и
0xx
M xx
k xx
0
M
B
D
k
yy
yy
yy
0xy / 2
M xy
k xy / 2
получаются уравнения для расчета деформаций и кривизн срединной плоскости композита {x, y}:
0xx
N xx
M xx
0
A
N
B
M
yy
1
yy
1
yy
0xy / 2
N xy
M xy
и
k xx
N xx
M xx
k yy С1 N yy D1 M yy
k xy / 2
N xy
M xy
где
A1 A 1 A 1 B D * 1 B A 1
B1 A 1 B D * 1
C1 D * B A
1
1
x
B1
D * D B A 1 B
D1 D * 1
y
z
14

15.

II. СЛОИСТЫЙ КОМПОЗИТ
6. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В СЛОЯХ КОМПОЗИТА
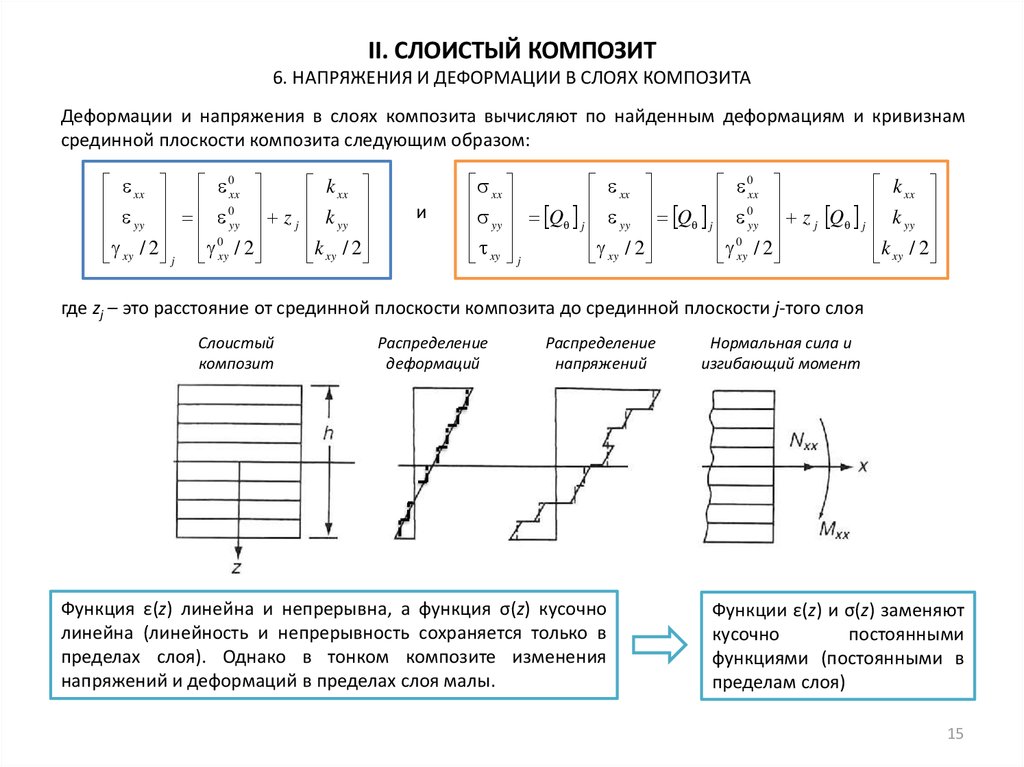
Деформации и напряжения в слоях композита вычисляют по найденным деформациям и кривизнам
срединной плоскости композита следующим образом:
xx
0xx
0
yy yy z j
xy / 2
0
j xy / 2
k xx
k yy
k xy / 2
и
xx
xx
0xx
0
yy Q j yy Q j yy z j Q j
xy
xy / 2
0xy / 2
j
k xx
k yy
k xy / 2
где zj – это расстояние от срединной плоскости композита до срединной плоскости j-того слоя
Слоистый
композит
Распределение
деформаций
Распределение
напряжений
Функция ε(z) линейна и непрерывна, а функция σ(z) кусочно
линейна (линейность и непрерывность сохраняется только в
пределах слоя). Однако в тонком композите изменения
напряжений и деформаций в пределах слоя малы.
Нормальная сила и
изгибающий момент
Функции ε(z) и σ(z) заменяют
кусочно
постоянными
функциями (постоянными в
пределам слоя)
15

16.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
Волокнистые композиты, как правило, представляют не только неоднородные, но и анизотропные
материалы, поэтому теории прочности и критерии пластичности:
• критерий максимальных касательных напряжений Треска-Сен-Венана;
• критерий октаэдрических касательных напряжений Губера-Мизеса;
• теория прочности Мора;
используемые для традиционных материалов (сталей и сплавов) не используются.
Вместо этого используют специально разработанные для композитов теории и методы оценки прочности:
Теории прочности
ортотропного
композита
Методы прогнозирования
прочности слоистого
композита
Теория максимальных
напряжений
• Метод последовательного
разрушения слоев
Теория максимальных
деформаций
Теория Аззи-Цая-Хилла
Теория Цая-Ву
Методы оценки прочности
хаотично армированного
композита
Подход Хана
Метод Хальпина-Кардоса
Метод прогнозирования
прочности слоистого
композита с учетом
накопления
микроповреждений
(метод Сапожникова)
16

17.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
i. Теория максимальных напряжений
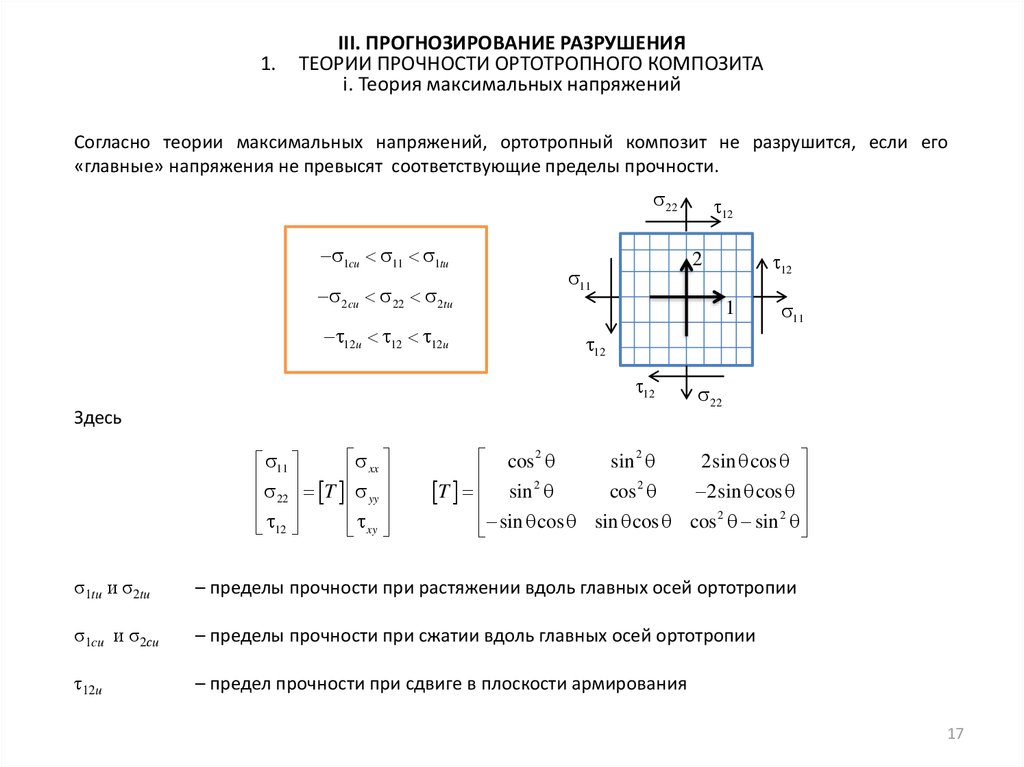
Согласно теории максимальных напряжений, ортотропный композит не разрушится, если его
«главные» напряжения не превысят соответствующие пределы прочности.
22
1cu 11 1tu
2 cu 22 2tu
12u 12 12u
12
2
11
1
11
12
12
Здесь
xx
11
T
22 yy
xy
12
12
22
cos 2
sin 2
2sin cos
cos 2
2sin cos
T sin 2
sin cos sin cos cos 2 sin 2
σ1tu и σ2tu
– пределы прочности при растяжении вдоль главных осей ортотропии
σ1cu и σ2сu
– пределы прочности при сжатии вдоль главных осей ортотропии
τ12u
– предел прочности при сдвиге в плоскости армирования
17

18.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
i. Теория максимальных напряжений
В случае растяжения однонаправленного композита вдоль оси x, возникают
только напряжения σxx, a σyy = τxy=0.
В главных осях:
11 xx cos 2
Условие прочности:
Здесь
σLtu, и σTtu
σLcu и σTсu
τLTu
22 xx sin 2
xx
T
12 xx sin cos
y
L
θ x
xx
Ttu
LTu
xx min Ltu2 ;
;
2
cos sin sin cos
– пределы прочности при растяжении вдоль и поперек волокон
– пределы прочности при сжатии вдоль и поперек волокон
– предел прочности при сдвиге в плоскости армирования
Безопасное напряжение σxx зависит от ориентации волокон:
при малых углах θ форма разрушения
соответствует продольному растяжению
композита
разрушающее
напряжение
Ltu
cos 2
при больших углах θ форма разрушения
соответствует трансверсальному растяжению
композита
разрушающее
напряжение
Ttu
sin 2
при средних углах θ реализуется сдвиговая форма разрушения
LTu
разрушающее
напряжение sin cos
18

19.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
ii. Теория максимальных деформаций
Согласно теории максимальных деформаций, ортотропный композит не разрушится, если его
главные деформации не превысят предельных значений деформаций, соответствующих пределам
прочности.
22
12
1cu 11 1tu
2 cu 22 2tu
12u 12 12u
11
1
xx
11
T
22 yy
xy
12
ε1tu и ε2tu
ε1cu и ε2сu
γ12u
11
12
12
Здесь
12
2
22
cos 2
sin 2
2sin cos
cos 2
2sin cos
T sin 2
sin cos sin cos cos 2 sin 2
– деформации, соответствующие пределам прочности при растяжении вдоль главных
осей ортотропии
– деформации, соответствующие пределам прочности при сжатии вдоль главных осей
ортотропии
– угол сдвига, соответствующий пределу прочности при сдвиге в плоскости
армирования
19

20.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
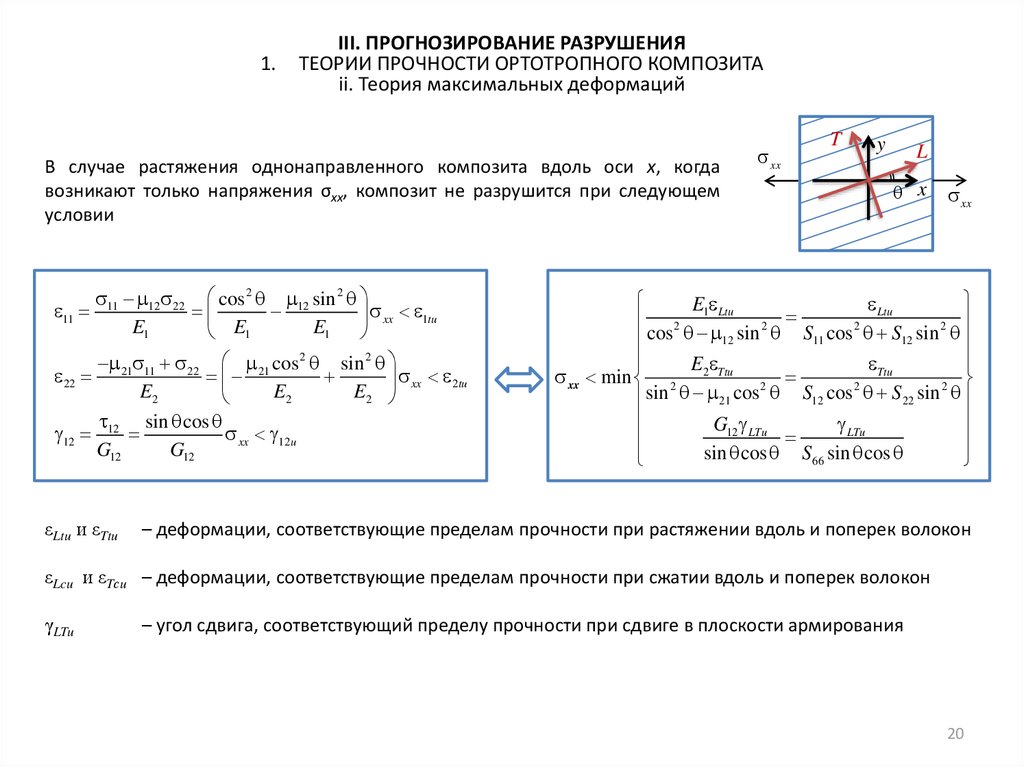
ii. Теория максимальных деформаций
В случае растяжения однонаправленного композита вдоль оси x, когда
возникают только напряжения σxx, композит не разрушится при следующем
условии
11
11 12 22 cos 2 12 sin 2
xx 1tu
E1
E
E
1
1
21 11 22 21 cos 2 sin 2
22
xx 2tu
E2
E2
E2
sin cos
12 12
xx 12u
G12
G12
εLtu и εTtu
xx
T
y
L
θ x
xx
E1 Ltu
Ltu
2
2
2
2
cos
sin
S
cos
S
sin
12
11
12
E
Ttu
xx min 2 2 Ttu 2
2
2
sin 21 cos S12 cos S22 sin
G12 LTu
LTu
sin cos S66 sin cos
– деформации, соответствующие пределам прочности при растяжении вдоль и поперек волокон
εLcu и εTсu – деформации, соответствующие пределам прочности при сжатии вдоль и поперек волокон
γLTu
– угол сдвига, соответствующий пределу прочности при сдвиге в плоскости армирования
20

21.

1.
I.
ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
iii. Теория Аззи-Цая-Хилла
22
Согласно теории Аззи-Цая-Хилла, разрушение ортотропного
композита произойдет при выполнении следующего условия:
112 22
1tu
2
11
2
1tu
2
22
2
2 tu
2
12
2
12 u
1
Здесь
• σ1tu, и σ2tu – пределы прочности при растяжении вдоль главных осей
ортотропии, а τ12u – предел прочности при сдвиге в плоскости
армирования
• σ11 > 0 и σ22 > 0
12
12
2
11
1
11
12
12
22
В случае, если одно из главных напряжений отрицательно, следует заменить соответствующий предел
прочности при растяжении на предел прочности при сжатии:
при σ11 > 0 и σ22 < 0
2
112 11 22 22
122
2 2 2 1
12tu
1tu
2 cu 12u
при σ11 < 0 и σ22 > 0
2
112 11 22 22
122
2 2 2 1
12cu
1cu
2tu 12u
при σ11 < 0 и σ22 < 0
2
112 11 22 22
122
2 2 2 1
12cu
1cu
2 cu 12u
Здесь σ1cu и σ2сu – это пределы прочности при сжатии вдоль главных осей
21

22.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
iii. Теория Аззи-Цая-Хилла
В случае растяжения однонаправленного композита
вдоль оси x, когда возникают только напряжения σxx,
композит не разрушится при условии
xx
T
y
L
θ x
xx
xx
1
cos 4 sin 2 cos 2 sin 4 sin 2 cos 2
2
2Ltu
2Ltu
Ttu
2LTu
Здесь
σLtu и σTtu
– пределы прочности при растяжении вдоль и поперек волокон
σLcu и σTсu
– пределы прочности при сжатии вдоль и поперек волокон
τLTu
– предел прочности при сдвиге в плоскости армирования
22

23.

1.
III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
iv. Теория Цая-Ву
22
Согласно теории Цая-Ву, разрушение ортотропного композита
произойдет при выполнении следующего условия
2
22
2
66 12
1
Здесь величины F1, F2 и т.д. называют коэффициентами прочности и
вычисляют следующим образом:
1
1
F1
1tu 1cu
1
1
F2
2tu 2 cu
1
F11
1tu 1cu
1
F22
2tu 2 cu
F66
12
1
1
1 1
1
1
1
1 2
1
u
u
2
2 u 1tu 1cu 2tu 2 cu
2 tu 2 cu
1tu 1cu
2
где σu – это разрушающее напряжение
Здесь
σ1tu, и σ2tu
σ1cu и σ2сu
τ12u
22
2
12 u
1. Из испытания на равномерное двухосное растяжение
2. Путем выбора из рекомендованного диапазона:
11
12
Величину F12 определяют следующими способами:
F12
12
2
11
F1 11 F2 22 F6 12 F F22 F 2 F12 11 22 1
2
11 11
12
1
1
F11 F22 F12 0
2
– пределы прочности при растяжении вдоль главных осей ортотропии
– пределы прочности при сжатии вдоль главных осей ортотропии
– предел прочности при сдвиге в плоскости армирования
23

24.

1.
12 const
I.
ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
ТЕОРИИ ПРОЧНОСТИ ОРТОТРОПНОГО КОМПОЗИТА
iv. Теория Цая-Ву
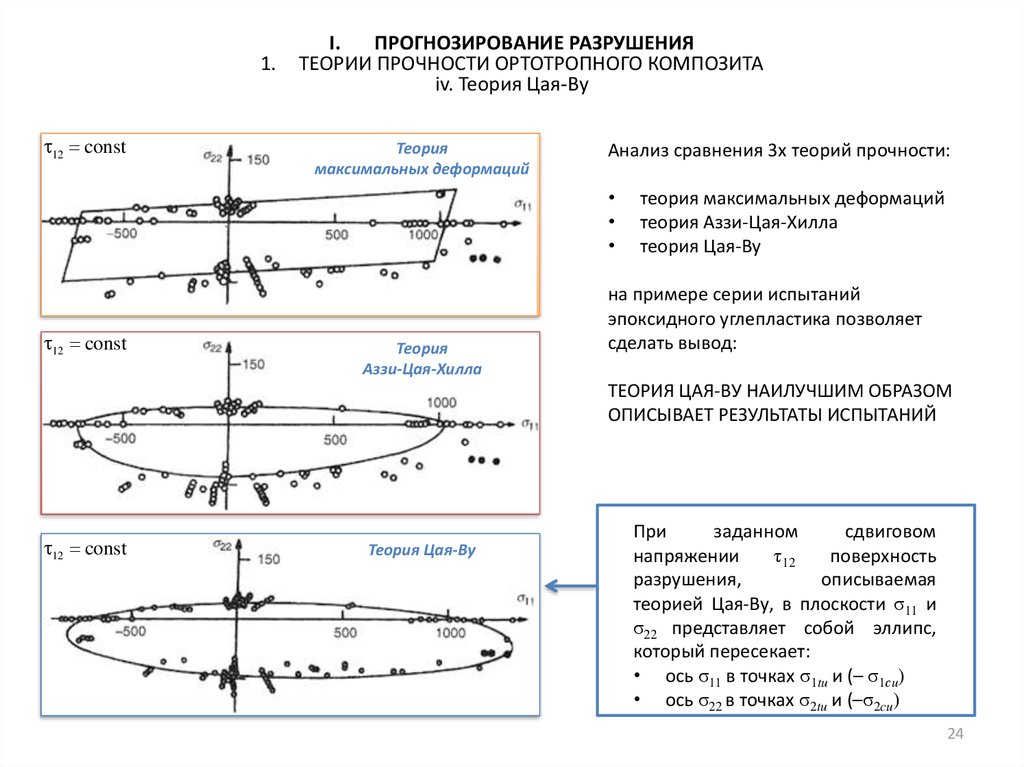
Теория
максимальных деформаций
Анализ сравнения 3x теорий прочности:
12 const
Теория
Аззи-Цая-Хилла
теория максимальных деформаций
теория Аззи-Цая-Хилла
теория Цая-Ву
на примере серии испытаний
эпоксидного углепластика позволяет
сделать вывод:
ТЕОРИЯ ЦАЯ-ВУ НАИЛУЧШИМ ОБРАЗОМ
ОПИСЫВАЕТ РЕЗУЛЬТАТЫ ИСПЫТАНИЙ
12 const
Теория Цая-Ву
При
заданном
сдвиговом
напряжении
τ12
поверхность
разрушения,
описываемая
теорией Цая-Ву, в плоскости σ11 и
σ22 представляет собой эллипс,
который пересекает:
• ось σ11 в точках σ1tu и (– σ1сu)
• ось σ22 в точках σ2tu и (–σ2cu)
24

25.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
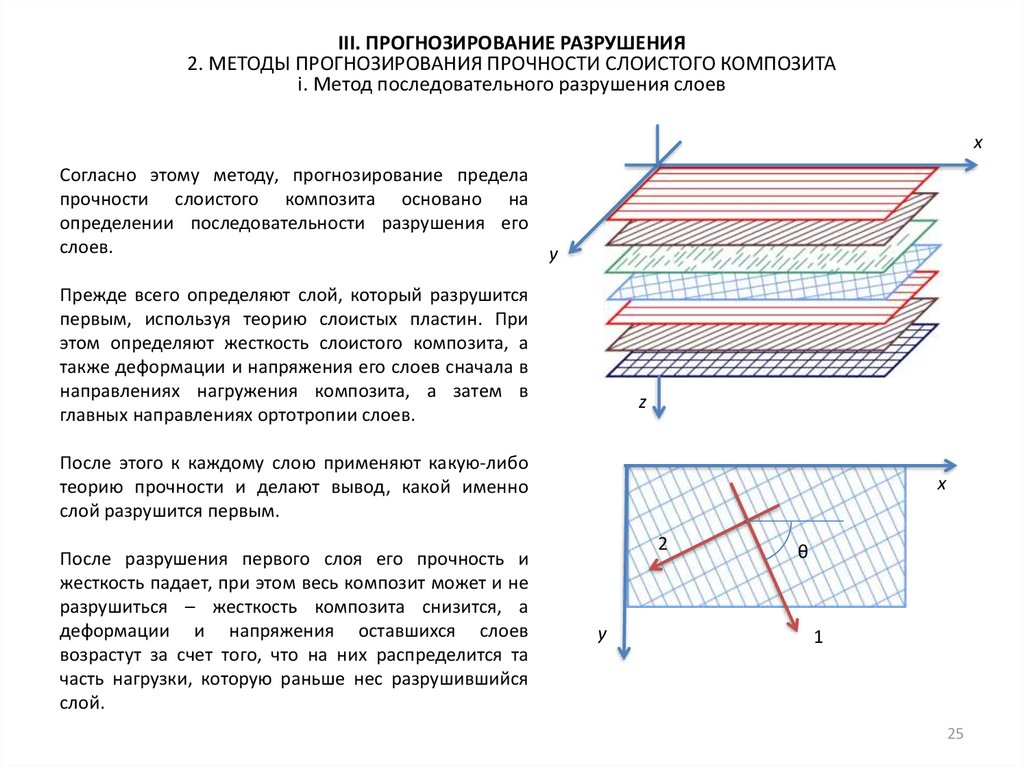
i. Метод последовательного разрушения слоев
x
Согласно этому методу, прогнозирование предела
прочности слоистого композита основано на
определении последовательности разрушения его
слоев.
y
Прежде всего определяют слой, который разрушится
первым, используя теорию слоистых пластин. При
этом определяют жесткость слоистого композита, а
также деформации и напряжения его слоев сначала в
направлениях нагружения композита, а затем в
главных направлениях ортотропии слоев.
z
После этого к каждому слою применяют какую-либо
теорию прочности и делают вывод, какой именно
слой разрушится первым.
После разрушения первого слоя его прочность и
жесткость падает, при этом весь композит может и не
разрушиться – жесткость композита снизится, а
деформации и напряжения оставшихся слоев
возрастут за счет того, что на них распределится та
часть нагрузки, которую раньше нес разрушившийся
слой.
x
2
y
θ
1
25

26.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
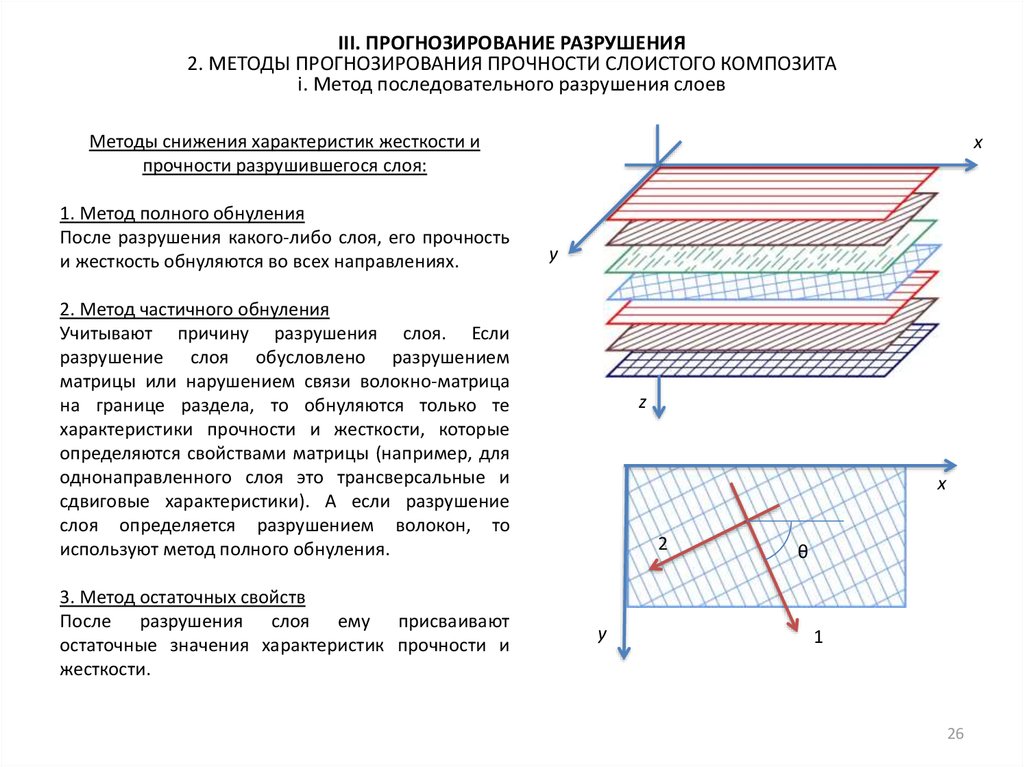
i. Метод последовательного разрушения слоев
Методы снижения характеристик жесткости и
прочности разрушившегося слоя:
1. Метод полного обнуления
После разрушения какого-либо слоя, его прочность
и жесткость обнуляются во всех направлениях.
x
y
2. Метод частичного обнуления
Учитывают причину разрушения слоя. Если
разрушение слоя обусловлено разрушением
матрицы или нарушением связи волокно-матрица
на границе раздела, то обнуляются только те
характеристики прочности и жесткости, которые
определяются свойствами матрицы (например, для
однонаправленного слоя это трансверсальные и
сдвиговые характеристики). А если разрушение
слоя определяется разрушением волокон, то
используют метод полного обнуления.
3. Метод остаточных свойств
После разрушения слоя ему присваивают
остаточные значения характеристик прочности и
жесткости.
z
x
2
y
θ
1
26

27.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
i. Метод последовательного разрушения слоев
Процедура метода последовательного
разрушения слоев:
Расчет напряжений и деформаций в слоях с
использованием теории слоистых пластин
2.
Применение какой-либо теории прочности
для определения слоя, который разрушится
первым
3.
Пересчет жесткости композита
4.
Пересчет напряжений и деформаций в
оставшихся слоях
5.
Повторение п.2-п.4 до полного разрушения
композита.
σxx
Предел прочности
композита
1.
Разрушение
композита
Разрушение
3го слоя
Разрушение
2го слоя
Разрушение
1го слоя
εxx
27

28.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
ii. Метод прогнозирования прочности слоистого композита с учетом накопления микроповреждений
(метод Сапожникова)
Основные положения:
1. Слоистый композит состоит из
идеально склеенных
однонаправленных слоев, каждый из
которых представлен набором
параллельно соединенных ячеек,
обладающих разбросом прочностных
свойств и разрушающихся независимо
друг от друга вдоль волокон, поперек
волокон или при сдвиге (механизмы 1,
2 и 3 соответственно)
2. Материал разрушается хрупко в результате накопления рассеянных
по объему микроповреждений
3. Повреждения по механизмам 1, 2 и 3 считаются независимыми, а
разброс характеристик прочности по каждому механизму описывается
нормальным законом распределения
Nyy
y 2
x 1
Nxy
Nxx
4. Нагружение слоистого композита реализуется с помощью погонных
сил Nxx, Nyy и Nxy пропорционально одному параметру
28

29.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОД ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
ii. Метод прогнозирования прочности слоистого композита с учетом накопления микроповреждений
(метод Сапожникова)
Основные положения :
5. Рост микроповреждений в слоях композита сопровождается снижением жесткости, что учитывается
путем введения в расчет секущих модулей j-того слоя :
E1c E1 (1 W1 )
E2c E2 (1 W2 )
G12c G12 (1 W3 )
c
12
12 (1 W1 ) c21 21 (1 W2 )
которые используются для записи матрицы [A]с секущих модулей, определяющей связь между
напряжениями и деформациями:
A
c
N
A Q j t j
c
c
j 1
Здесь N – число слоев, а tj – это толщина j-того слоя
E1c
12 E2c
0
1 c c 1 c c
12 21
12 21
cos 2
sin 2
2sin cos
c
c
c
1
c
E2
T sin 2
cos 2
2sin cos
Q j T Q j T Q cj 12cE2 c
0
c
c
1 12 21 1 12 21
sin cos sin cos cos 2 sin 2
c
0
0
2G12
Здесь [Q]сj и [Qθ]сj – это редуцированные матрицы жесткости j-того слоя соответственно в главных осях
ортотропии слоя и в осях нагружения композита, а θ – это угол укладки волокон j-того слоя
29

30.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
2. МЕТОДЫ ПРОГНОЗИРОВАНИЯ ПРОЧНОСТИ СЛОИСТОГО КОМПОЗИТА
ii. Метод прогнозирования прочности слоистого композита с учетом накопления микроповреждений
(метод Сапожникова)
Результаты расчетов:
Углепластик, растяжение вдоль [90]
1 – [0/±35]2S , 2 – [0/±15]2S
Углепластик [±30]4S, растяжение вдоль [0]
1 – деформация εхx, 2 – деформация εуy
Углепластик: [±45]4S, растяжение вдоль [0]
1 – деформация εхx, 2 – деформация εуy
Стеклопластик [±30]S, растяжение вдоль [0]
1 – деформация εхx, 2 – деформация εуy
30

31.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
3. МЕТОДЫ ОЦЕНКИ ПРОЧНОСТИ ХАОТИЧНО АРМИРОВАННЫХ КОМПОЗИТОВ
i. Подход Хана
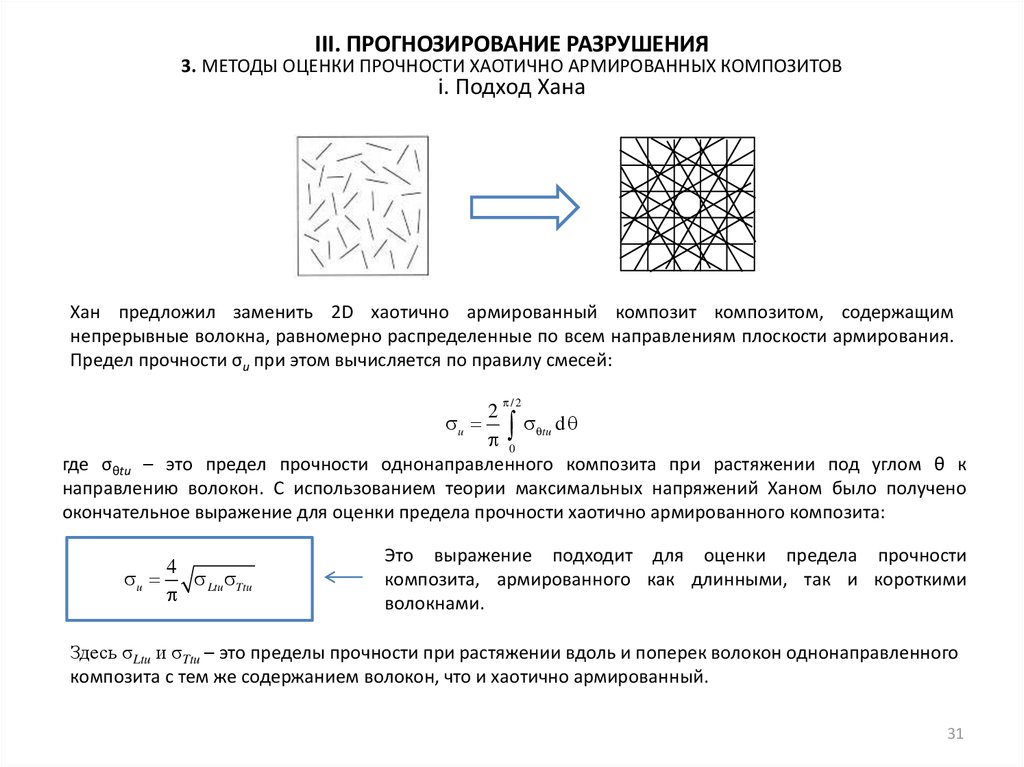
Хан предложил заменить 2D хаотично армированный композит композитом, содержащим
непрерывные волокна, равномерно распределенные по всем направлениям плоскости армирования.
Предел прочности σu при этом вычисляется по правилу смесей:
/2
2
u tu d
0
где σθtu – это предел прочности однонаправленного композита при растяжении под углом θ к
направлению волокон. С использованием теории максимальных напряжений Ханом было получено
окончательное выражение для оценки предела прочности хаотично армированного композита:
4
u
Ltu Ttu
Это выражение подходит для оценки предела прочности
композита, армированного как длинными, так и короткими
волокнами.
Здесь σLtu и σTtu – это пределы прочности при растяжении вдоль и поперек волокон однонаправленного
композита с тем же содержанием волокон, что и хаотично армированный.
31

32.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
3. МЕТОДЫ ОЦЕНКИ ПРОЧНОСТИ ХАОТИЧНО АРМИРОВАННЫХ КОМПОЗИТОВ
ii. Метод Хальпина-Кардоса
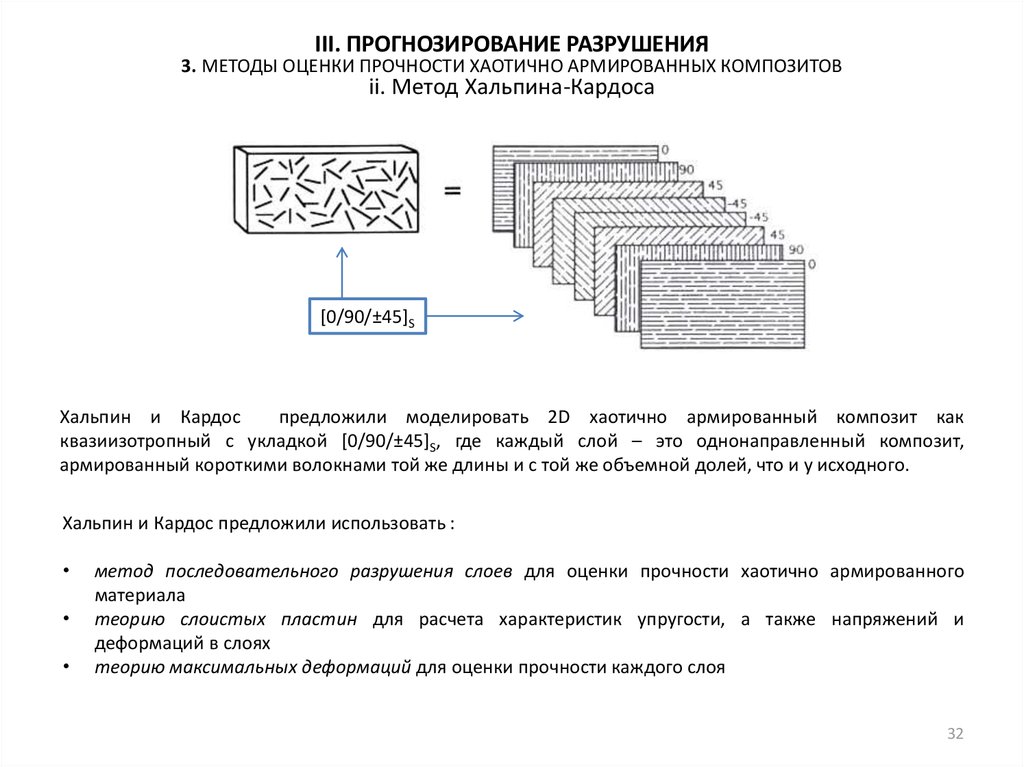
[0/90/±45]S
Хальпин и Кардос
предложили моделировать 2D хаотично армированный композит как
квазиизотропный с укладкой [0/90/±45]S, где каждый слой – это однонаправленный композит,
армированный короткими волокнами той же длины и с той же объемной долей, что и у исходного.
Хальпин и Кардос предложили использовать :
метод последовательного разрушения слоев для оценки прочности хаотично армированного
материала
теорию слоистых пластин для расчета характеристик упругости, а также напряжений и
деформаций в слоях
теорию максимальных деформаций для оценки прочности каждого слоя
32

33.

III. ПРОГНОЗИРОВАНИЕ РАЗРУШЕНИЯ
3. МЕТОДЫ ОЦЕНКИ ПРОЧНОСТИ ХАОТИЧНО АРМИРОВАННЫХ КОМПОЗИТОВ
ii. Метод Хальпина-Кардоса
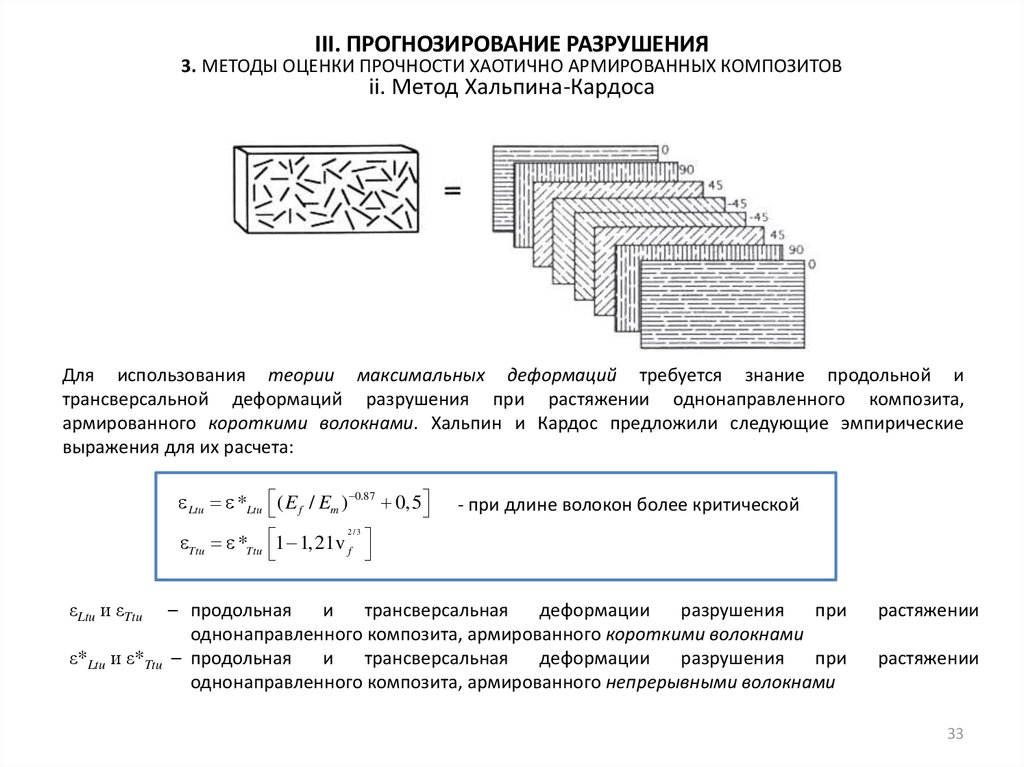
Для использования теории максимальных деформаций требуется знание продольной и
трансверсальной деформаций разрушения при растяжении однонаправленного композита,
армированного короткими волокнами. Хальпин и Кардос предложили следующие эмпирические
выражения для их расчета:
Ltu *Ltu ( E f / Em ) 0.87 0,5
2/3
Ttu *Ttu 1 1,21v f
εLtu и εTtu
- при длине волокон более критической
и
трансверсальная
деформации
разрушения
при
– продольная
однонаправленного композита, армированного короткими волокнами
и
трансверсальная
деформации
разрушения
при
ε*Ltu и ε*Ttu – продольная
однонаправленного композита, армированного непрерывными волокнами
растяжении
растяжении
33