Прямая пропорциональная зависимость

1. Прямая пропорциональная зависимость

График функции y = kx
По учебнику Никольского С.М. «Алгебра-8»
Вишняков А.Ю.

2.

Повторение.
Функцией называется зависимость, при
которой каждому значению независимой
переменной соответствует единственное
значение зависимой переменной.
Х
Y
Способы задания функции:
- описательный;
- табличный;
- аналитический (формула);
- графический.

3. Прямая пропорциональная зависимость

Функцию вида y = kx, где k – заданное не
равное нулю число, называют прямой
пропорциональной зависимостью.
Действительно, если y1 = kx1 и y2 = kx2, то
y1 y2
k
x1 x2
,т.е. величины х и y – прямо
пропорциональны.
k - коэффициент пропорциональности

4. Примеры

y 3x.
Пример 1. Функция задана формулой
Заполните таблицу:
x
y
-2
6
-3
9
3
-4
-9
12
5
-15
Пример 2. Задайте формулой прямую
пропорциональную зависимость, если
при х 24 значение функции y 264.
Решение. Из формулы функции y = kx выразим
коэффициент k = y:x и подставим численные
значения переменных. Получаем: k = 264:(-24) = -11.
Значит, y = -11x .

5. График функции y = kx

6.

Построение графика
функции y=2x по точкам
x
-2 -1 0 1
2
y
-4 -2 0 2
4
у
(2;4)
(1;2)
1
0
(-1;-2)
(-2;-4)
1
х

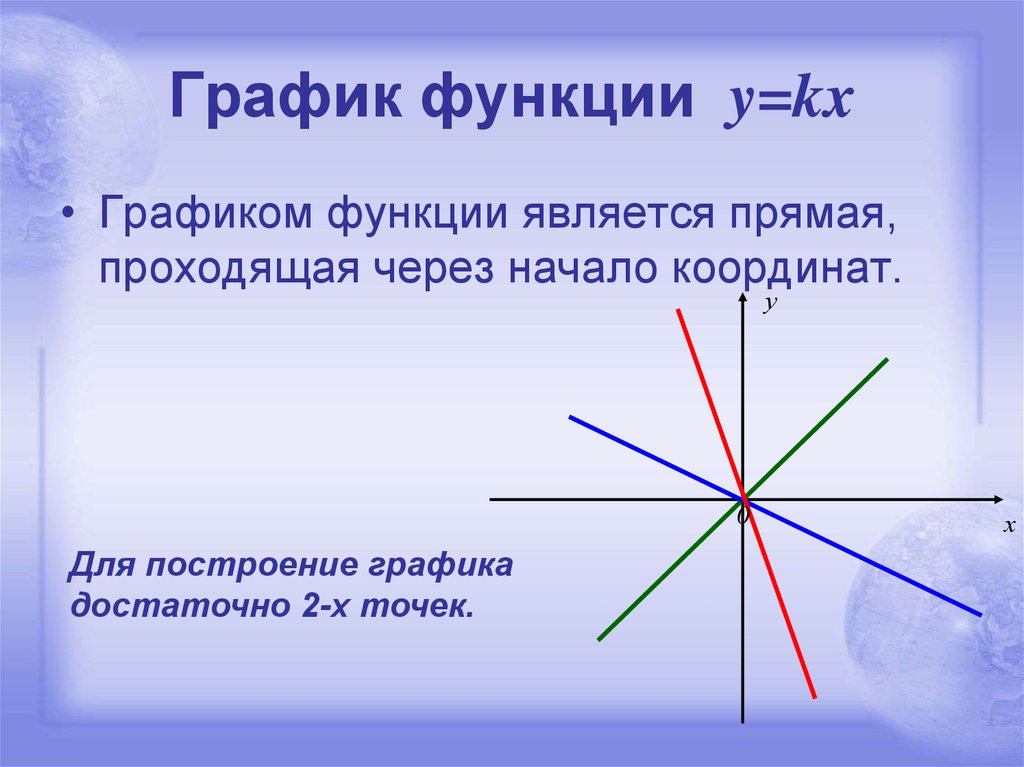
7. График функции y=kx

• Графиком функции является прямая,
проходящая через начало координат.
у
0
Для построение графика
достаточно 2-х точек.
х

8.

1. Если k>0, то х и y имеют одинаковые знаки и прямая
расположена в 1 и 3 координатных четвертях.
2. Если k<0,то х и y имеют противоположные знаки и
прямая расположена во 2 и 4 координатных четвертях.
y
y
α
0
α
x
α – острый угол
k – угловой коэффициент прямой
0
x
α – тупой угол

9.

Быстрый способ
построения
графика y=kx

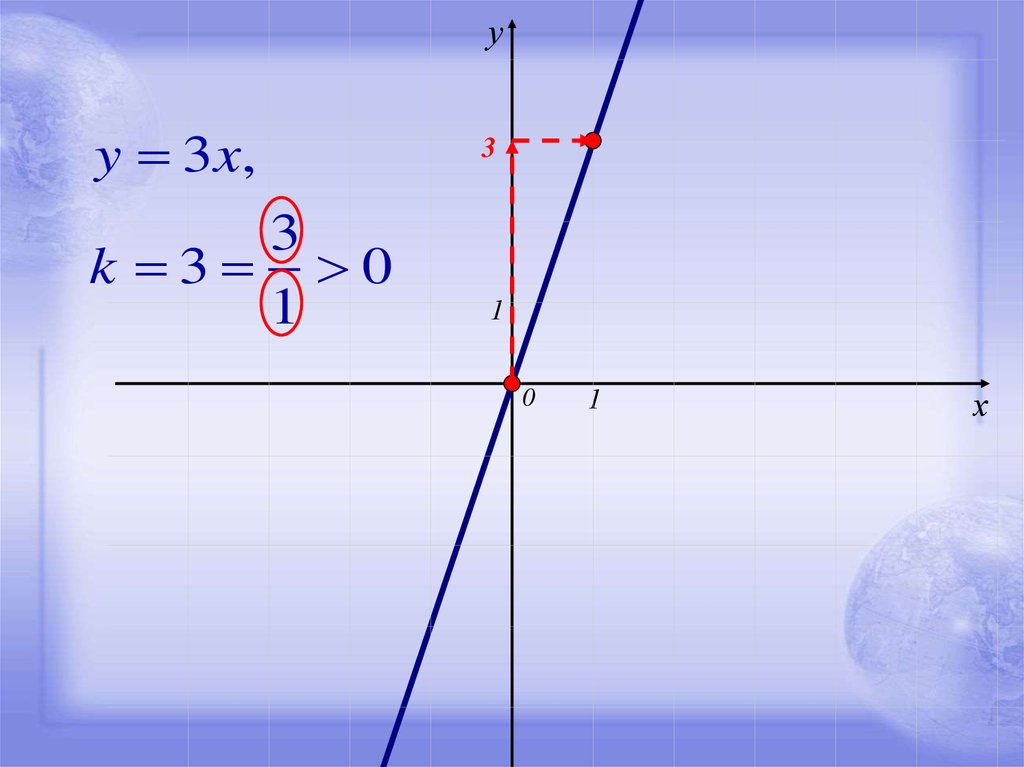
10.

у
y 3 x,
3
k 3 0
1
3
1
0
1
х

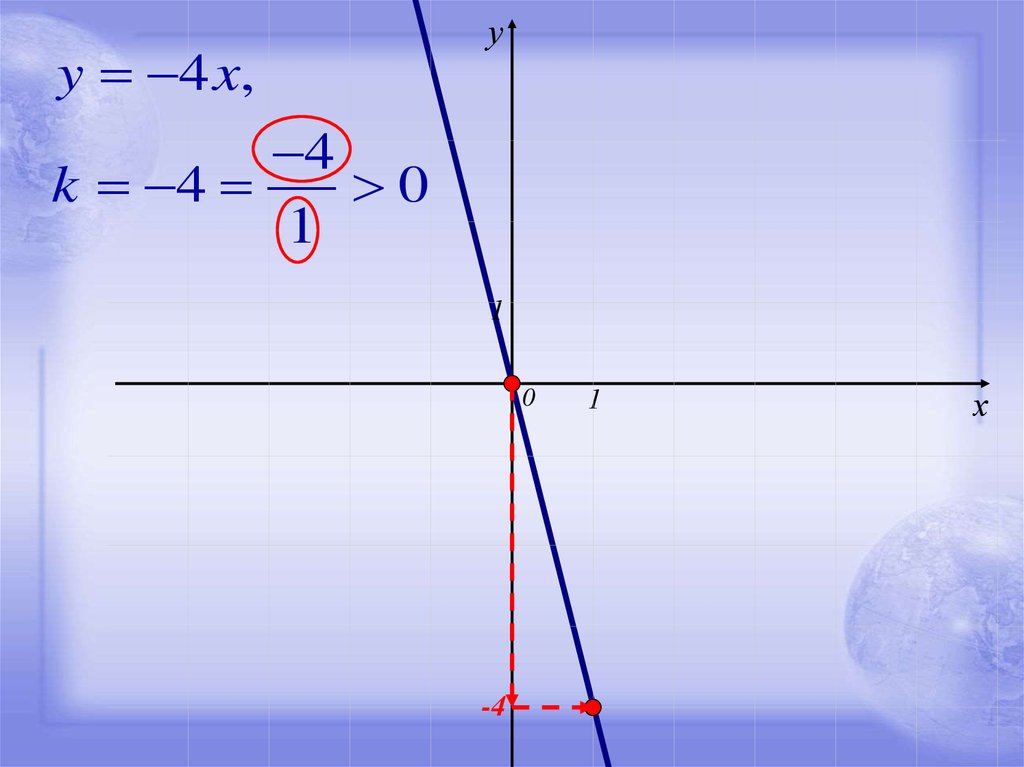
11.

y 4 x,
у
4
k 4
0
1
1
0
-4
1
х

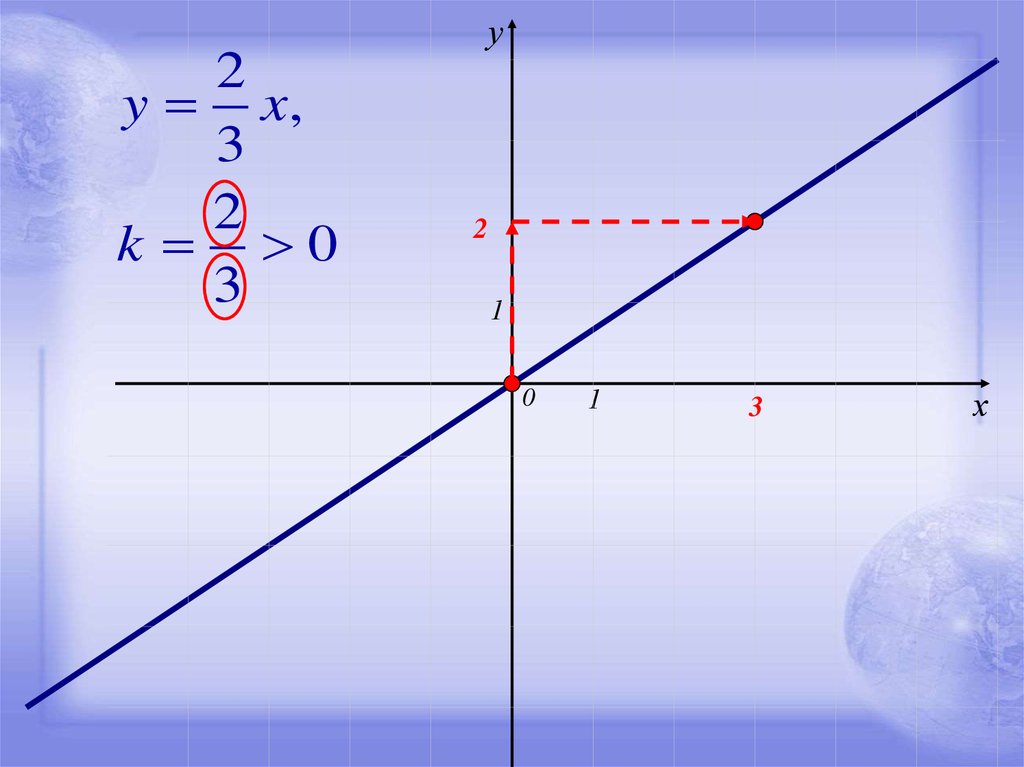
12.

у
2
y x,
3
2
k 0
3
2
1
0
1
3
х

13.

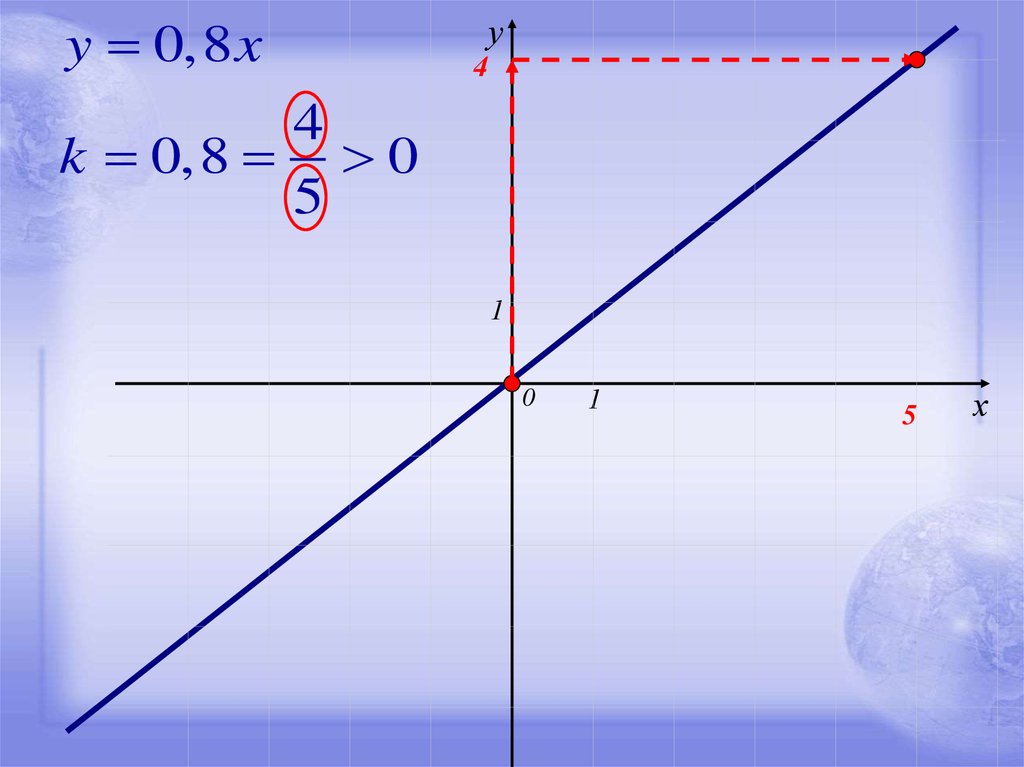
y 0,8 x
у
4
4
k 0,8 0
5
1
0
1
5
х

14.

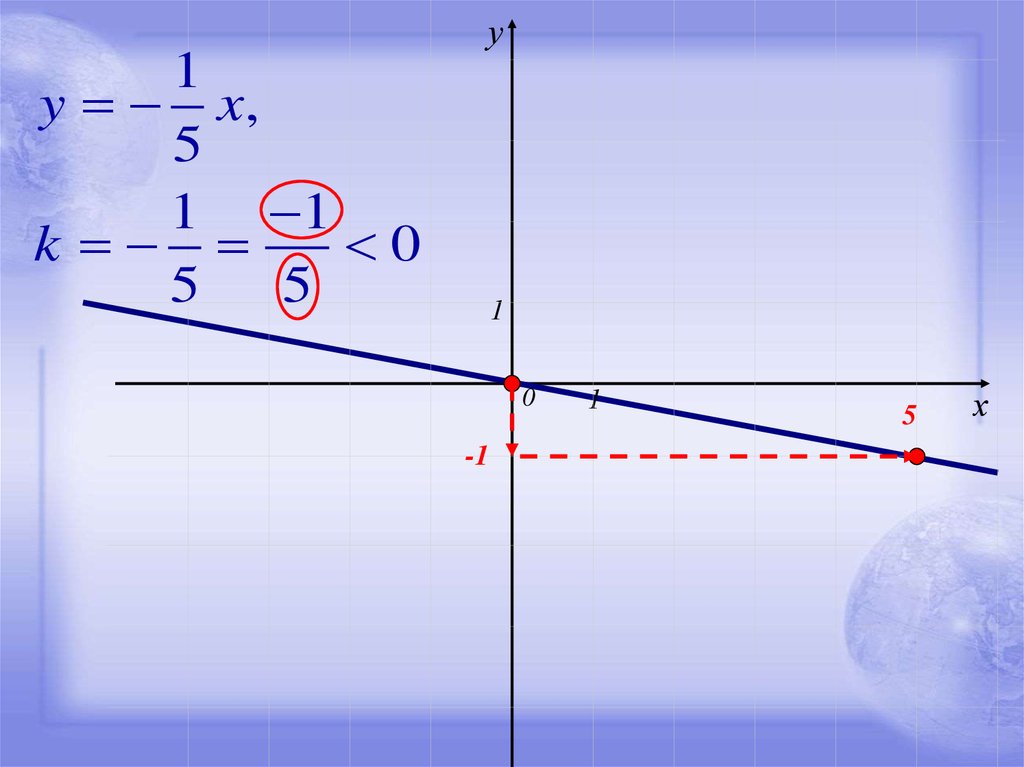
у
1
y x,
5
1 1
k
0
5
5
1
0
-1
1
5
х

15. Постройте самостоятельно графики указанных функций

1) y 5 x;
6) y 3 x;
2) y 2 x;
7) y 1, 2 x;
3
3) y x;
7
1
4) y 1 x;
3
5) y 2,5 x;
2
8) y x;
3
2
9) y 1 x;
3
10) y 1, 25 x.

16.

17. Задание на дом

П.6.1, 6.2
№ 337, 340, 343