Похожие презентации:
Оптимизация нелинейных систем
1. Оптимизация нелинейных систем
2.
3.
Если в математической модели оптимизационной задачиимеются нелинейные зависимости, для решения этой
задачи
используются
методы
нелинейного
программирования.
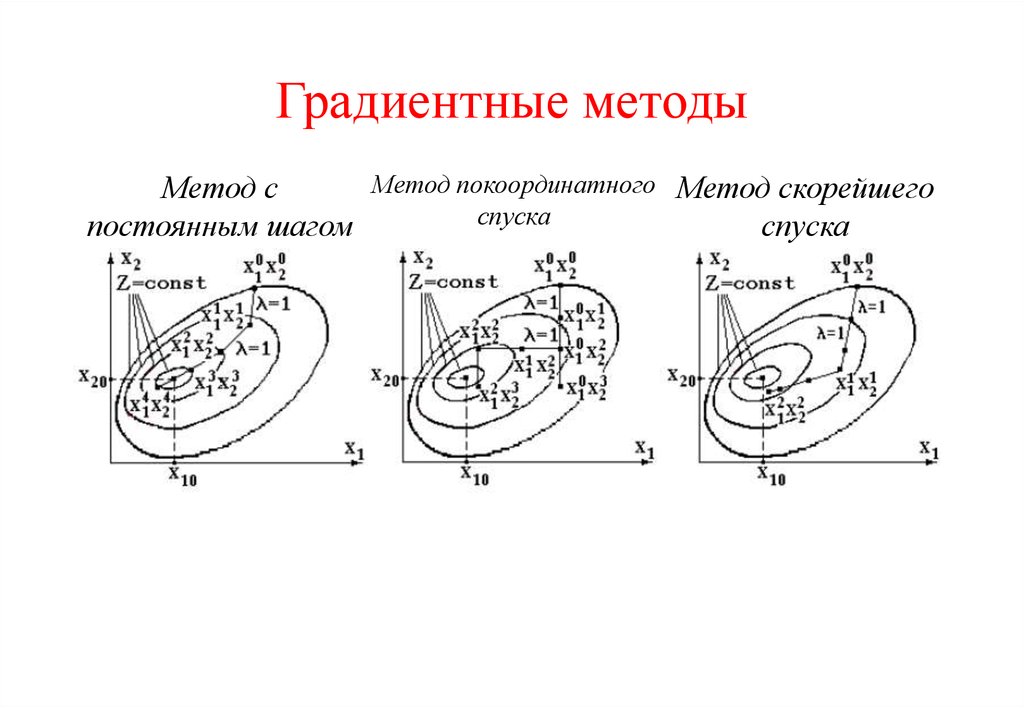
4. Градиентные методы
Метод покоординатного Метод скорейшегоМетод с
спуска
постоянным шагом
спуска
5. Градиентные методы
Метод покоординатного Метод скорейшегоМетод с
спуска
постоянным шагом
спуска
1. Исходное (нулевое) приближение x10, x20.
2. Z0 = Z(x10, x20).
3. grad Z(x10, x20)
4. Определение
4. Шаг длиной λ в 4. Определение большей по
модулю частной
оптимальной длины шага
направлении −grad
производной ∂Z/∂xi →
λопт, например,
0
0
Z(x1 , x2 ) → точка изменение xi на λ до тех пор,
параболической
пока Z не начнет
аппроксимацией → шаг
(x11,x21)
увеличиваться → изменение длиной λопт в направлении
…
другой координаты → точка −grad Z(x10, x20) → точка
(x11,x21)
…
(x11,x21)
…
6.
Врезультате
вычислительного
процесса
последовательно осуществляется «спуск» к минимуму
функции Z. Вычислительная процедура заканчивается,
когда относительное изменение целевой функции на
предыдущем i-м и последующем (i+1)-м шагах оказывается
меньше заданной точности вычислений ε:















 Программирование
Программирование








