Похожие презентации:
Первое начало термодинамики
1.
Лекция 92. §§ Внутренняя энергия газа
В модели идеального газа силамивзаимодействия молекул пренебрегают
Внутренняя энергия газа равна сумме
энергий теплового движения молекул:
i
i
N i
U N k BT
N Ak BT RT
2
2
NA 2
Внутренняя энергия не зависит от
способа перевода системы в данное
состояние (функция состояния)
02
3. §§ Работа и теплота
Вычислим работу газа при расширенииp – давление газа
F = pS – сила, действующая
на поршень со стороны газа
элементарная работа
A F ( y )dy pS dy pdV
A
V2
pdV – работа газа при расширении
V1
от
V1 до V2
03
4.
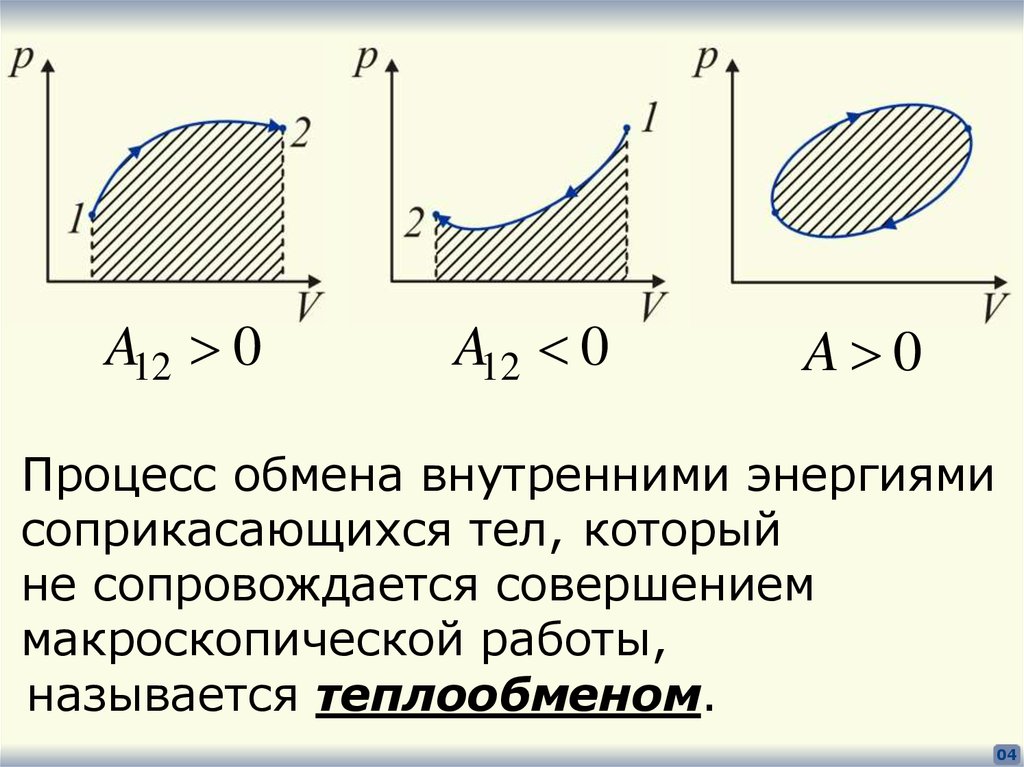
A12 0A12 0
A 0
Процесс обмена внутренними энергиями
соприкасающихся тел, который
не сопровождается совершением
макроскопической работы,
называется теплообменом.
04
5. §§ Первое начало
Термодинамическая система называетсяизолированной, если отсутствует
всякий обмен энергией между ней
и внешней средой
Для изолированной системы выполняется
закон сохранения и превращения
энергии – полная энергия не изменяется
при любых процессах, происходящих
в этой системе.
05
6.
Рассмотрим контакт системв адиабатической оболочке.
Пусть системой α совершена
работа A, тогда
U1 U 2 A
неподвижная
теплопроводящая
перегородка
U1 U1 U 2 U 2 A
или
U1 U 2 U 2 U1 A
Обозначим Q U 2 U1
– убыль энергии системы β (количество
теплоты, полученное системой α)
06
7.
Получаем математическую формулировкуI-го начала термодинамики
Q U 2 U1 A
Теплота Q, полученная системой, идет
на приращение ее внутренней энергии
ΔU = U2 – U1 и совершение работы A
Q dU A
07
8. §§ Теплоемкость
Теплоемкость вещества –физическая величина, равная
количеству теплоты, необходимому
для нагревания вещества на 1 K
C
Q
dT
[C ] Дж К
Различают теплоемкость вещества
при постоянном давлении Cp
и постоянном объеме CV.
08
9.
1 QУдельная теплоемкость: C
m
dT
[C ] Дж (кг К)
1 Q
Молярная теплоемкость: C
dT
[C ] Дж (моль К)
Из первого начала
Q dU A
найдем молярную теплоемкость газа
i
CdT RdT pdV
2
09
10.
1)V = const
i
i
CV dT RdT CV R
2
2
2) p = const
i
C p dT RdT pdV
2
рассмотрим уравнение М–К:
d ( pV ) d ( RT ) pdV Vdp RdT
0
pdV RdT
10
11.
i 2i 2
R
C p dT
RdT C p
2
2
Для идеального газа справедливо
уравнение Майера
C p CV R
Для твердых тел и жидкостей
Cp ≈ CV
11
12. §§ Изотермический процесс
Это бесконечно медленный процесс,т.к. в системе должно установиться
термодинамическое равновесие
Закон Бойля–Мариотта:
pV const
Изменение внутренней энергии
i
U R T 0
2
12
13.
1-е начало термодинамикиQ A
т.е. вся переданная рабочему телу
теплота идет на совершение телом
работы
Работа газа при изотермическом
расширении:
A
V2
V2
pdV
V1
V1
RT
V
dV RT ln(V2 V1 )
13
14. §§ Адиабатический процесс
(S = const, S – энтропия)Это – очень быстрый процесс, чтобы
не происходил обмен энергией
с окружающей средой или он был бы
несущественным
Уравнение Пуассона: pV const
CP CV – показатель адиабаты
pV RT , следовательно
TV
1
const
1
p
T const
14
15.
1-е начало термодинамики0 U A A U
т.е. работа совершается за счет убыли
энергии системы
Работа газа при адиабатическом
процессе:
T2
A U CV (T2 T1 ) CV T1 1
T1
V 1
R
1
CV T1 1 CV
1
V2
15
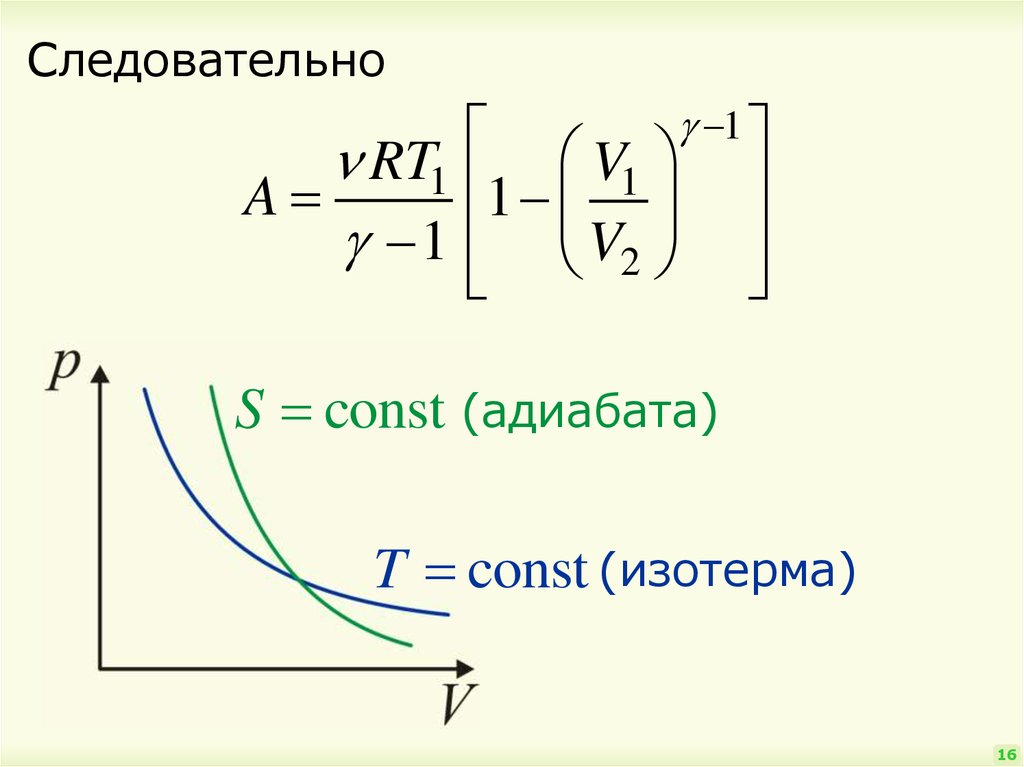
16.
Следовательно1
V1
RT1
1
A
1 V2
S const (адиабата)
T const (изотерма)
16
17. §§ Политропические процессы
Процесс, в котором теплоемкостьостается постоянной величиной,
называется политропическим
(политропным).
Рассмотренные процессы p,V,T,S = const
– частные случаи политропного процесса
Получим его общее уравнение:
Q dU A CdT CV dT pdV
pV RT
pdV Vdp RdT
17
18.
сделаем заменуR = Cp–CV и выразим dT
(C CV )dT pdV
pdV Vdp
dT
(C p CV )
C CV
( pdV Vdp) pdV
C p CV
C p CV
1 C C
V
pdV Vdp
18
19.
C C p dVdp
C CV V
p
n – показатель политропы
Интегрируя, получаем
ln V ln p const
n
или
pV const – уравнение
n
политропы
19
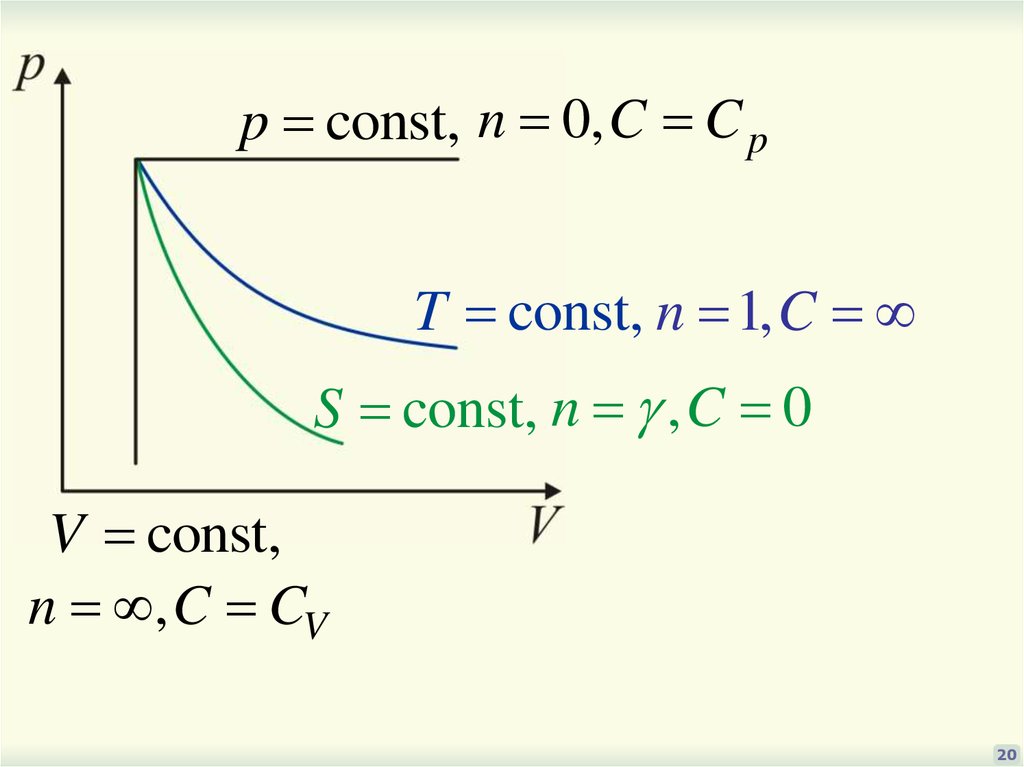
20.
p const, n 0, C C pT const, n 1, C
S const, n , C 0
V const,
n , C CV
20
21.
Работа газаA
V2
V1
pdV pV
n
1 n
p1V1
V2
1 1 n
n 1 V1
n
p1V1
n
p1V1
V2
dV
Vn
V
1
21

















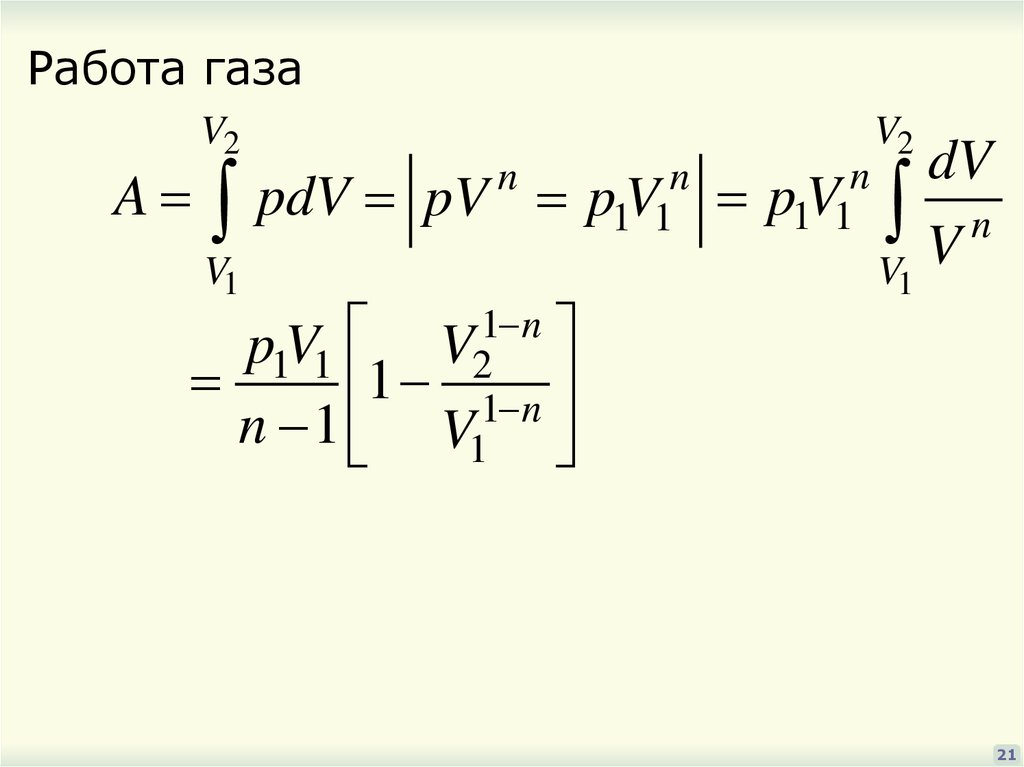
 Физика
Физика