Основы классической термодинамики. Первое начало термодинамики. (Лекция 10)

1. Лекция № 10

Основы классической
термодинамики.
Первое начало
термодинамики

2. Внутренняя энергия

i
i ст .св. k B T
2
i
i
U i ст .св . N k B T N k B T N A
2
2
i
U R T
2

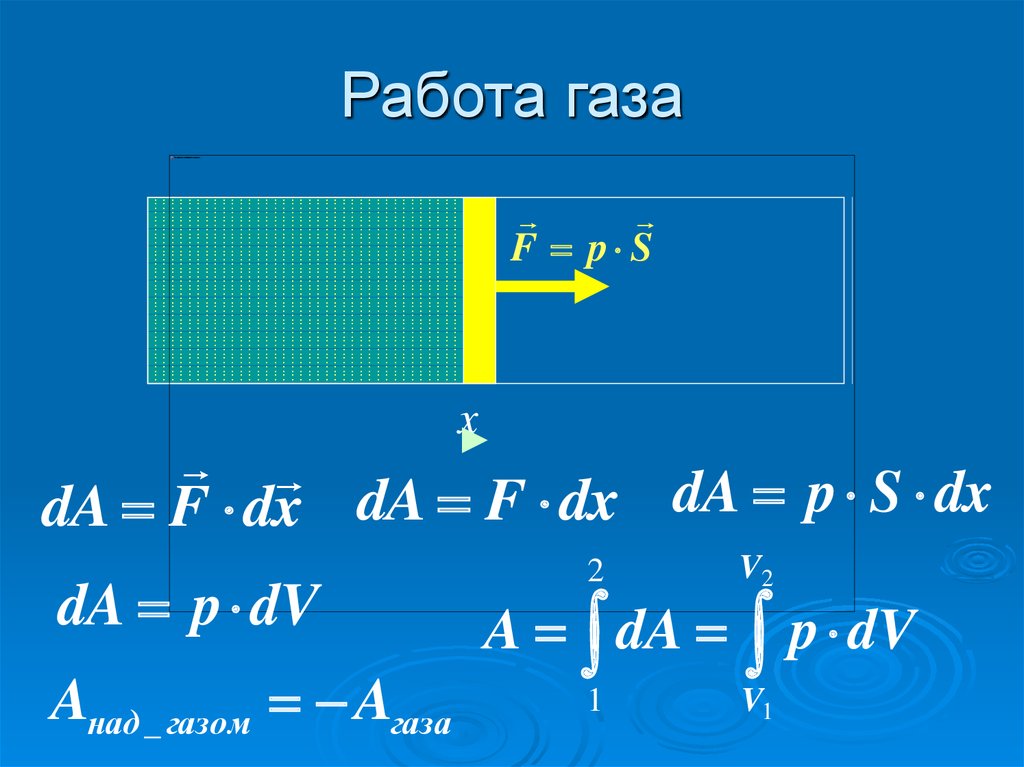
3. Работа газа

F p S
x
dA F dx dA F dx dA p S dx
dA p dV
Aнад _ газом Aгаза
2
A dA
1
V2
V1
p dV

4. Теплота

Теплота – это
количество энергии,
которое тело
получает или теряет
в процессе
теплопередачи.
Измеряется в Дж.

5. Теплоёмкость

Полная :
Удельная :
Молярная :
C уд
C пол
dQ
dT
dQ
C уд
m dT
dQ
Cм
dT
См
Дж
К
Дж
кг К
Дж
моль К

6. Первое начало термодинамики

Q U A
dQ dU dA
Q dU A

7. Изопроцессы

pV RT
pV
R const
T
Изопроцессы – термодинамические
процессы, во время которых масса и
ещё одна из физических величин –
параметров состояния – остаются
неизменными.

8.

Изохорический процесс (закон Шарля)
V =const
T2 > T1
Т1
Р1
Т2 Р2
Р2 > Р1
Jacques
Alexandre
César Charles
1746–1823
Q Q
U
UA
Р
i
U R T
2 i
i
U R T V p
2
2
A 0
T
A
V2
V1
p dV
C мV
Q
i
R
dT 2

9.

Изобарический процесс
(Закон Гей-Люссака )
Р =const
Т1
V1
T2 < T1
Т2 V2
Joseph Louis
Gay-Lussac
1778 – 1850
V2 < V1
i 2
C м p V
R
Q U A
2
i
i
U R T p V
2
2
T
A p V R T
V
i 2
i 2
A p dV Qp
(V2 V1 ) R T
p V
V
2
2
2
1

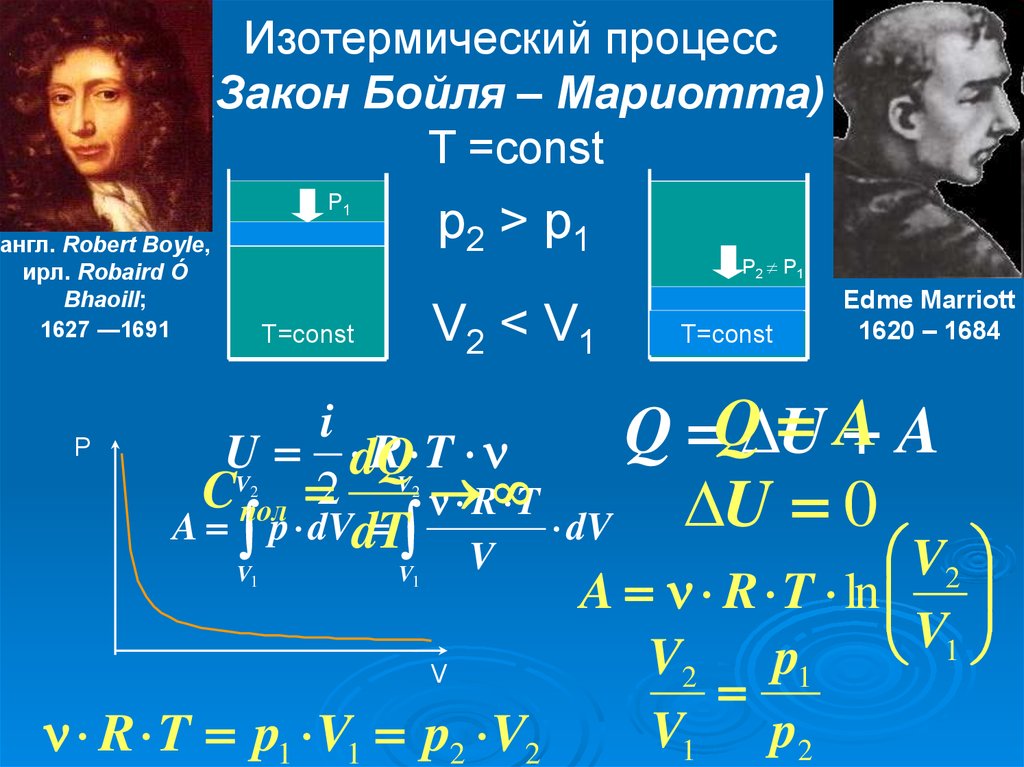
10.

Изотермический процесс
(Закон Бойля – Мариотта)
T =const
Р1
англ. Robert Boyle,
ирл. Robaird Ó
Bhaoill;
1627 —1691
Р
p2 > p 1
V2 < V1
T=const
i
U dQ
R T
CVпол 2 V
R
T
A
2
2
V1
V1
p dVdT
V
V
R T p1 V1 p2 V2
Р2 Р1
T=const
Edme Marriott
1620 – 1684
Q Q
UA
A
U 0
dV
V2
A R T ln
V1
V2
p1
V1 p2

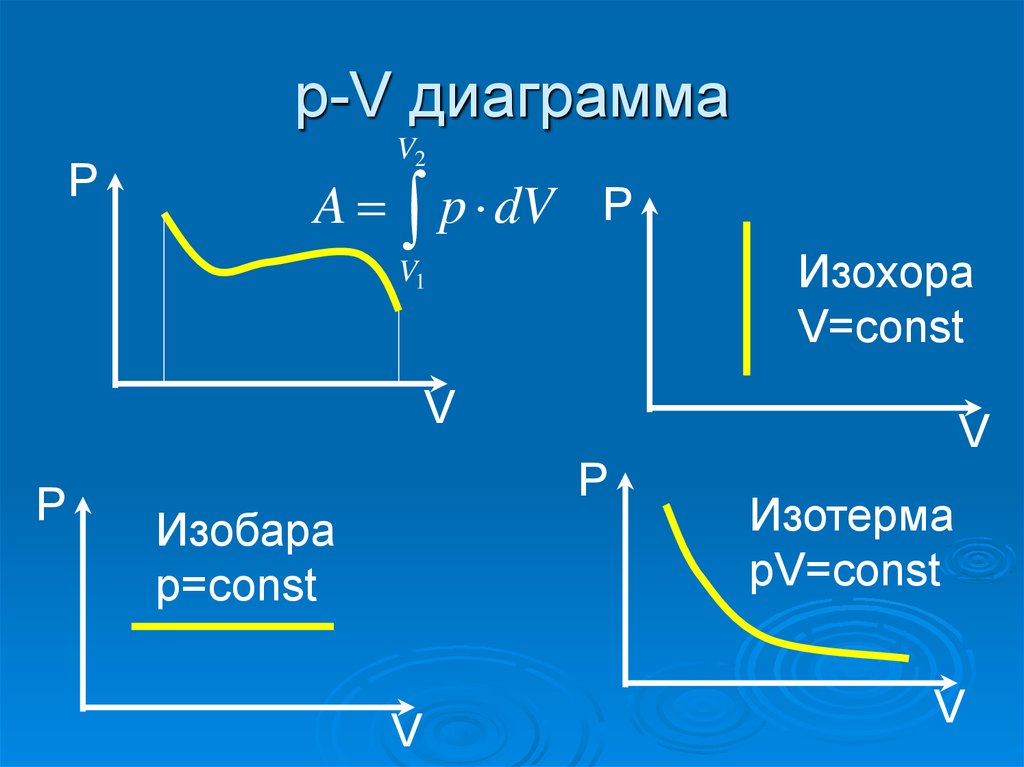
11. p-V диаграмма

Р
A
V2
Р
p
dV
V1
Изохора
V=const
V
Р
Р
Изобара
p=const
V
V
Изотерма
pV=const
V

12. Адиабатический процесс

13. Адиабатический процесс

Q 0
Q 0
Q dU A
i
RdT pdV 0
2
pV RT
pdV Vdp RdT
i
i
pdV Vdp pdV 0
2
2
i 2
i
pdV Vdp
2
2

14. Адиабатический процесс

i 2
i
pdV Vdp
2
2
i 2 dV
dp
i V
p
i 2 dV
dp
i
V
p
ln V ln p const '
ln( pV ) const '
i 2
i

15. Адиабатический процесс

ln( pV ) const '
pV const уравнение адиабаты
i 2 Cp
показатель адиабаты
i
CV
Р
Адиабата
pVγ=const

16. Политропический процесс

Q dU A
C const Q C dT
i
RdT pdV CdT
2
pV RT
pdV Vdp RdT
i
i
pdV Vdp
pdV Vdp pdV C
2
2
R
i 2
i
(
R C ) pdV ( R C )Vdp
2
2

17.

Политропический процесс
i 2
i
(
R C ) pdV ( R C )Vdp
2
2
dV
dp
n
V
p
ln( pV ) const '
C CV
dV
dp
n
V
p
n ln V ln p const '
n
n
C Cp

18.

Политропический процесс
ln( pV ) const '
n
pV const уравнение политропы
n
n
C Cp
C CV
показатель политропы