Задача о рюкзаке. Backpack problem

1. Задача о рюкзаке Backpack problem

2.

Вы грабитель.

3.

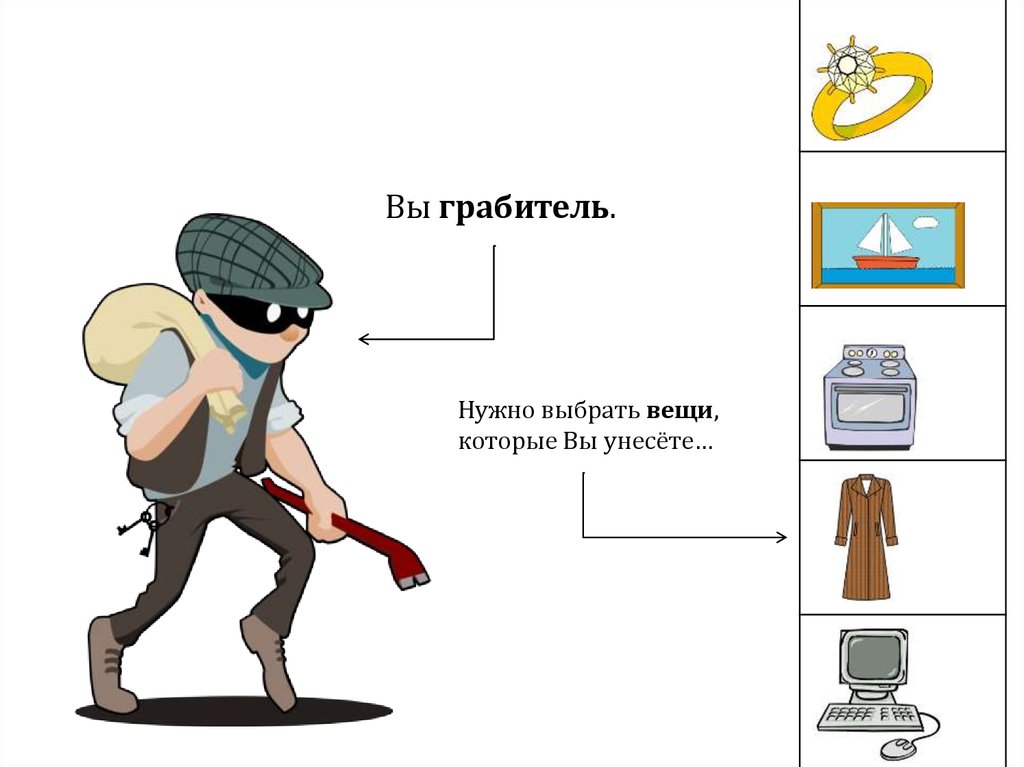
Вы грабитель.
Нужно выбрать вещи,
которые Вы унесёте…

4.

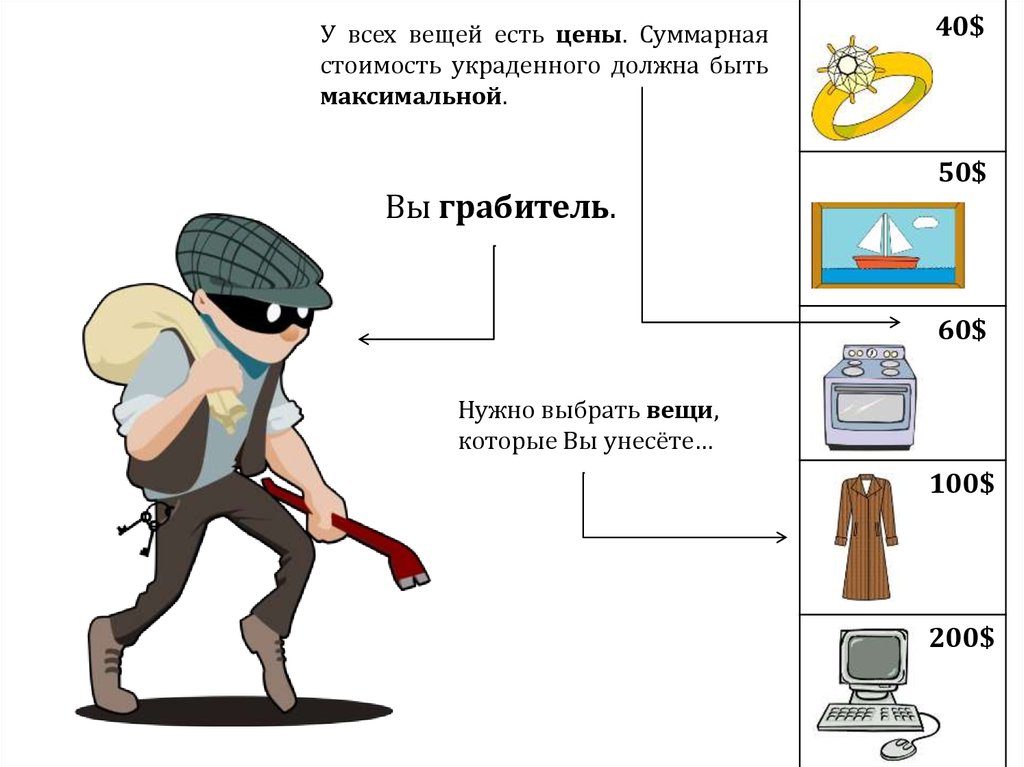
У всех вещей есть цены. Суммарная
стоимость украденного должна быть
максимальной.
Вы грабитель.
40$
50$
60$
Нужно выбрать вещи,
которые Вы унесёте…
100$
200$

5.

40$
У всех вещей есть цены. Суммарная
стоимость украденного должна быть
максимальной.
3 кг
Вы грабитель.
3 кг
50$
60$
Нужно выбрать вещи,
которые Вы унесёте…
5 кг
100$
12 кг
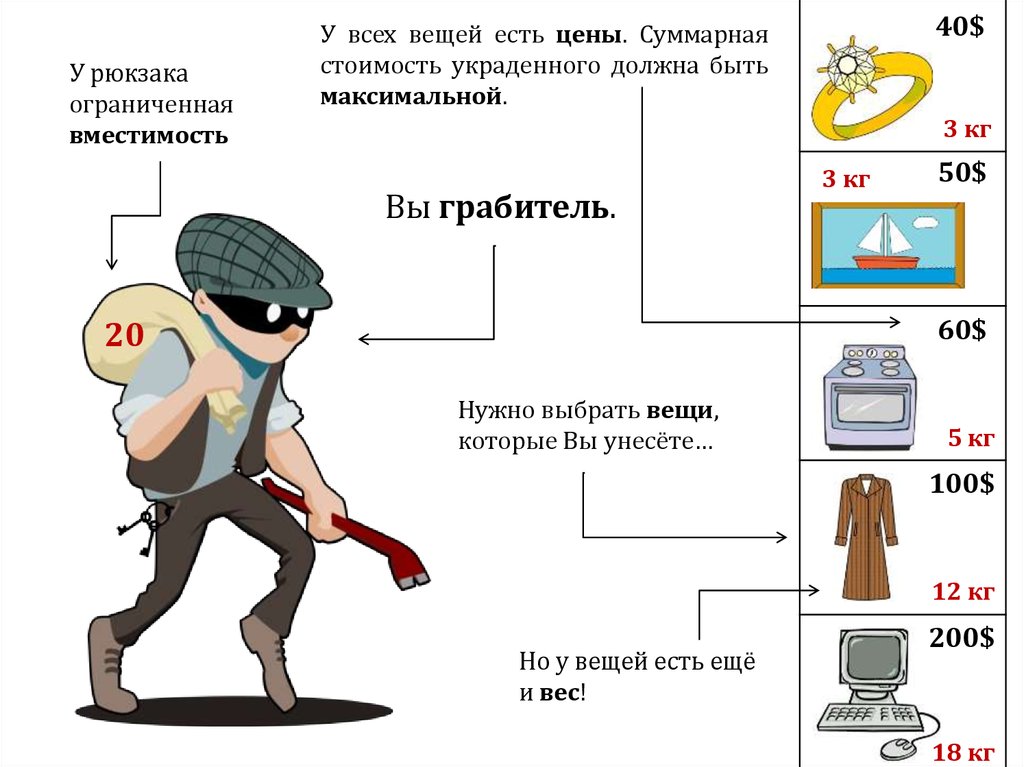
Но у вещей есть ещё
и вес!
200$
18 кг

6.

У рюкзака
ограниченная
вместимость
40$
У всех вещей есть цены. Суммарная
стоимость украденного должна быть
максимальной.
3 кг
Вы грабитель.
3 кг
50$
60$
20
Нужно выбрать вещи,
которые Вы унесёте…
5 кг
100$
12 кг
Но у вещей есть ещё
и вес!
200$
18 кг

7.

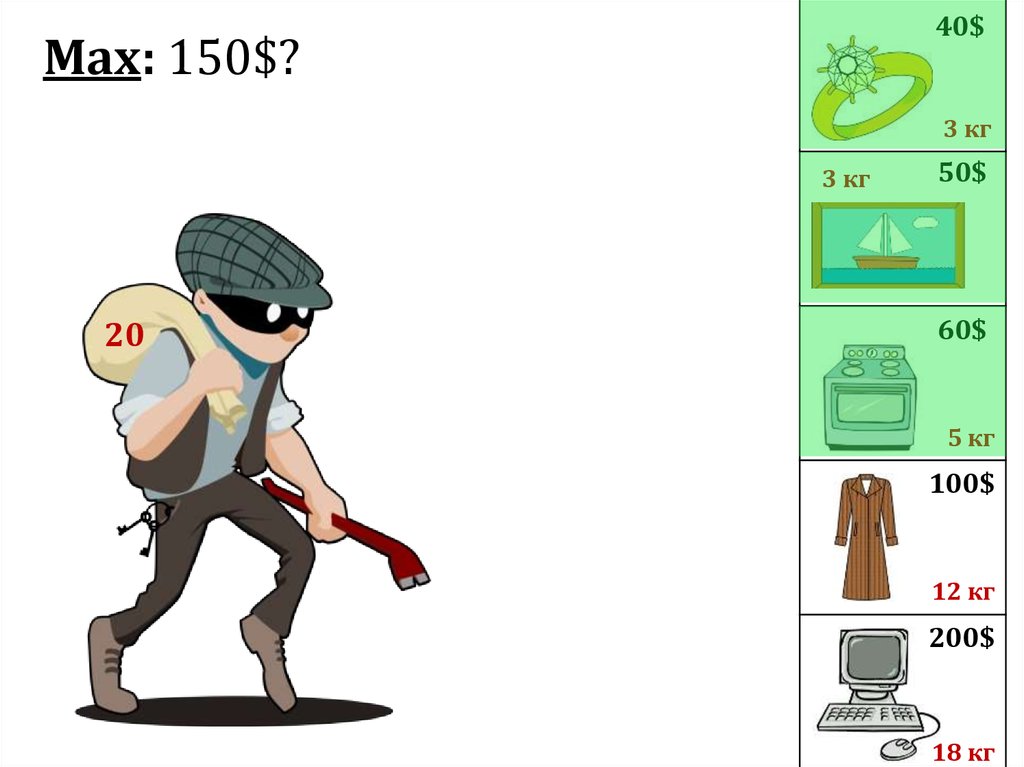
40$
Max: 150$?
3 кг
3 кг
20
50$
60$
5 кг
100$
12 кг
200$
18 кг

8.

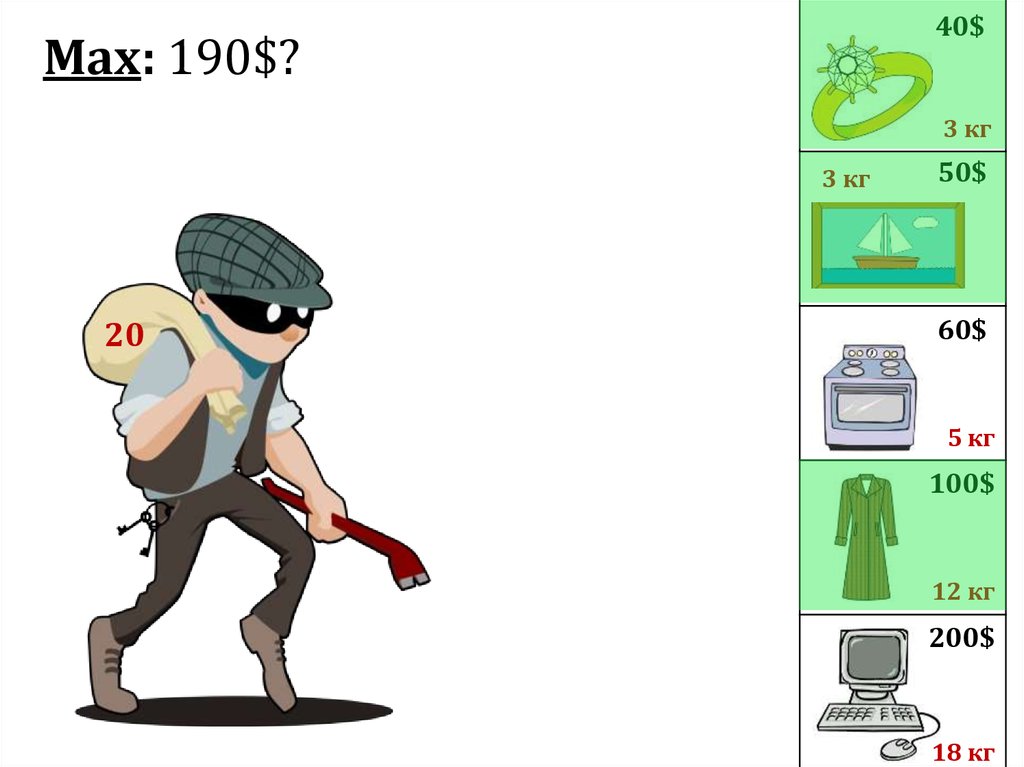
40$
Max: 190$?
3 кг
3 кг
20
50$
60$
5 кг
100$
12 кг
200$
18 кг

9.

40$
Max: 200$?
3 кг
3 кг
20
50$
60$
5 кг
100$
12 кг
200$
18 кг

10.

40$
Max: 210$!
3 кг
3 кг
20
50$
60$
5 кг
100$
12 кг
200$
18 кг

11.

40$
Max: 210$!
3 кг
3 кг
20
50$
60$
5 кг
100$
12 кг
200$
18 кг

12.

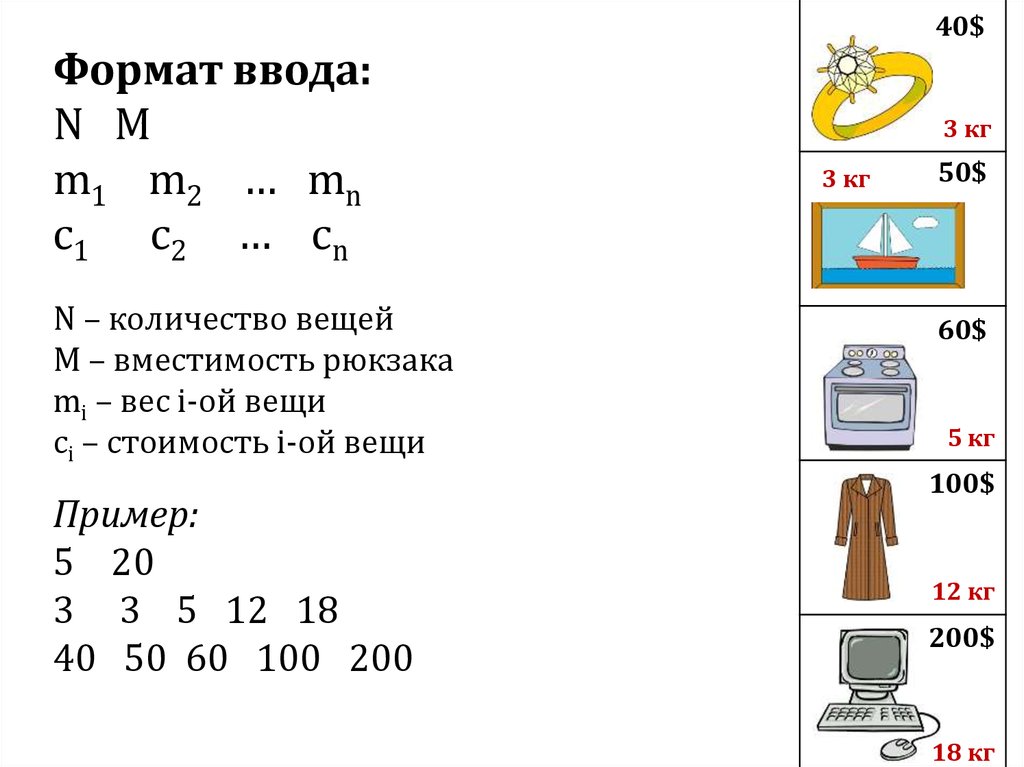
Формат ввода:
N M
m1 m2 … mn
c1 c 2 … cn
N – количество вещей
M – вместимость рюкзака
mi – вес i-ой вещи
ci – стоимость i-ой вещи
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

13.

Формат ввода:
N M
m1 m2 … mn
c1 c 2 … cn
N – количество вещей
M – вместимость рюкзака
mi – вес i-ой вещи
ci – стоимость i-ой вещи
Пример:
5 20
3 3 5 12 18
40 50 60 100 200
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

14.

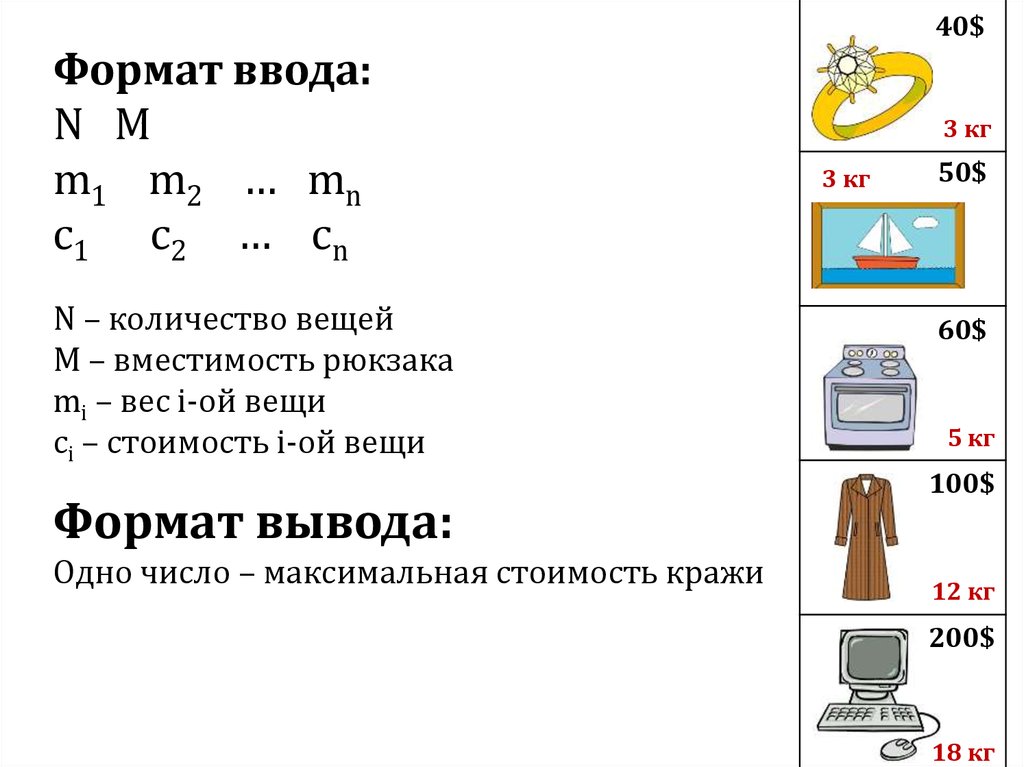
Формат ввода:
N M
m1 m2 … mn
c1 c 2 … cn
N – количество вещей
M – вместимость рюкзака
mi – вес i-ой вещи
ci – стоимость i-ой вещи
Формат вывода:
Одно число – максимальная стоимость кражи
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

15.

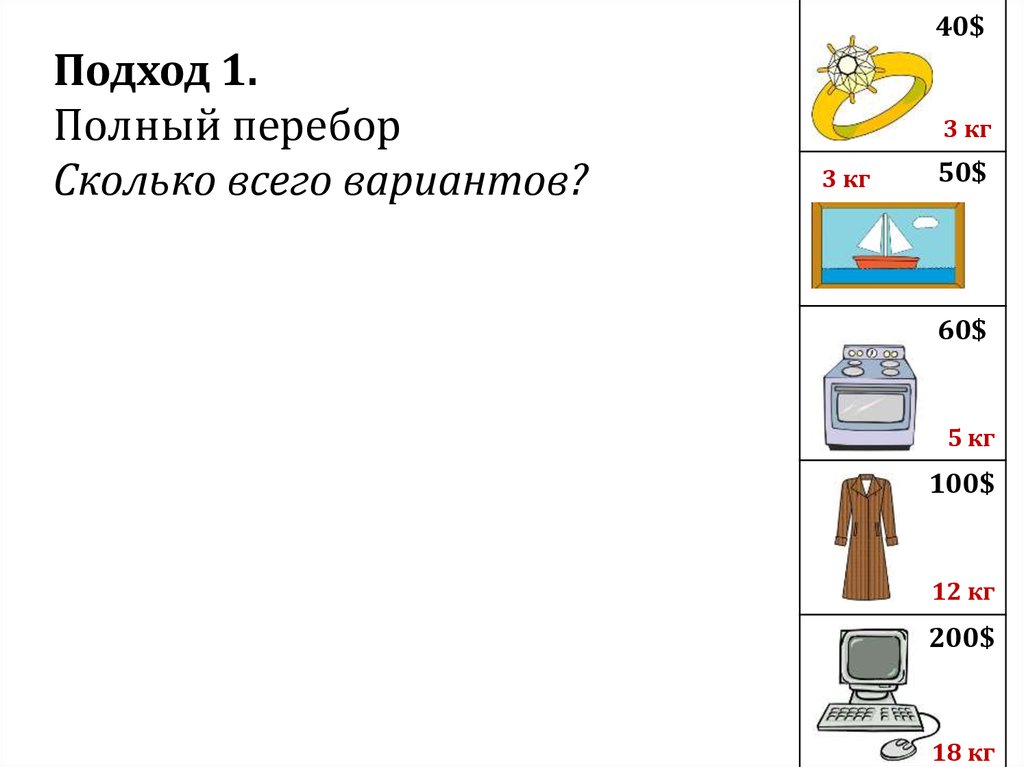
Подход 1.
Полный перебор
Сколько всего вариантов?
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

16.

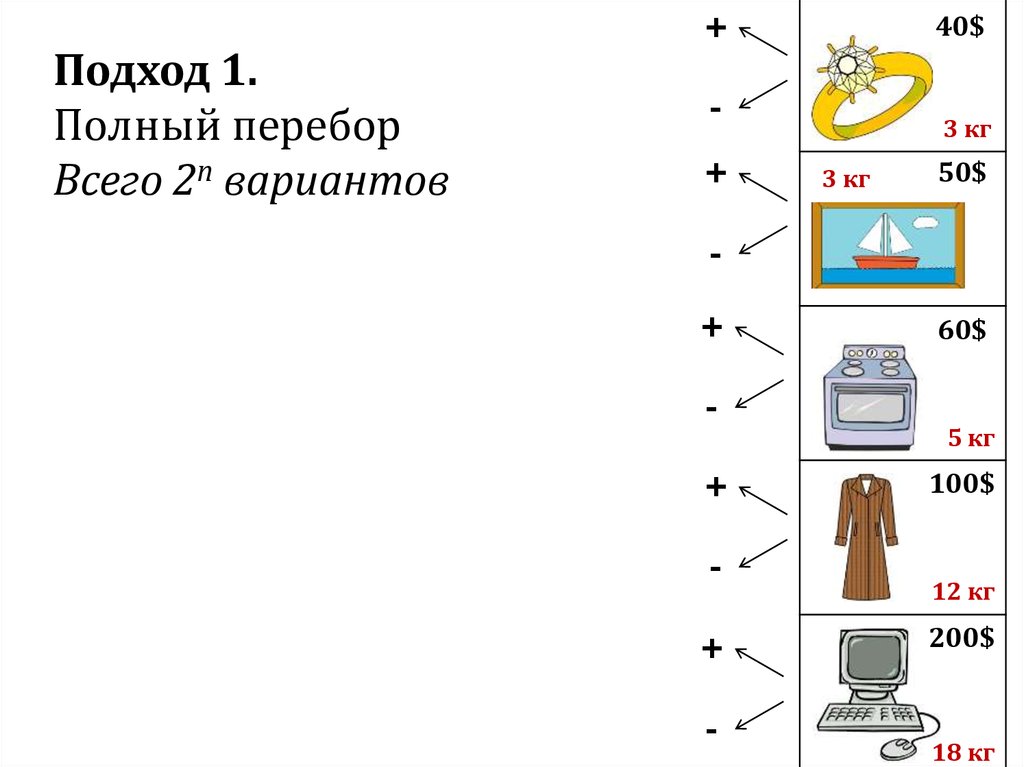
Подход 1.
Полный перебор
Сколько всего вариантов?
Каждый предмет мы можем взять
или не взять…
+
40$
+
3 кг
3 кг
50$
+
+
+
-
60$
5 кг
100$
12 кг
200$
18 кг

17.

Подход 1.
Полный перебор
Всего 2n вариантов
+
40$
+
3 кг
3 кг
50$
+
+
+
-
60$
5 кг
100$
12 кг
200$
18 кг

18.

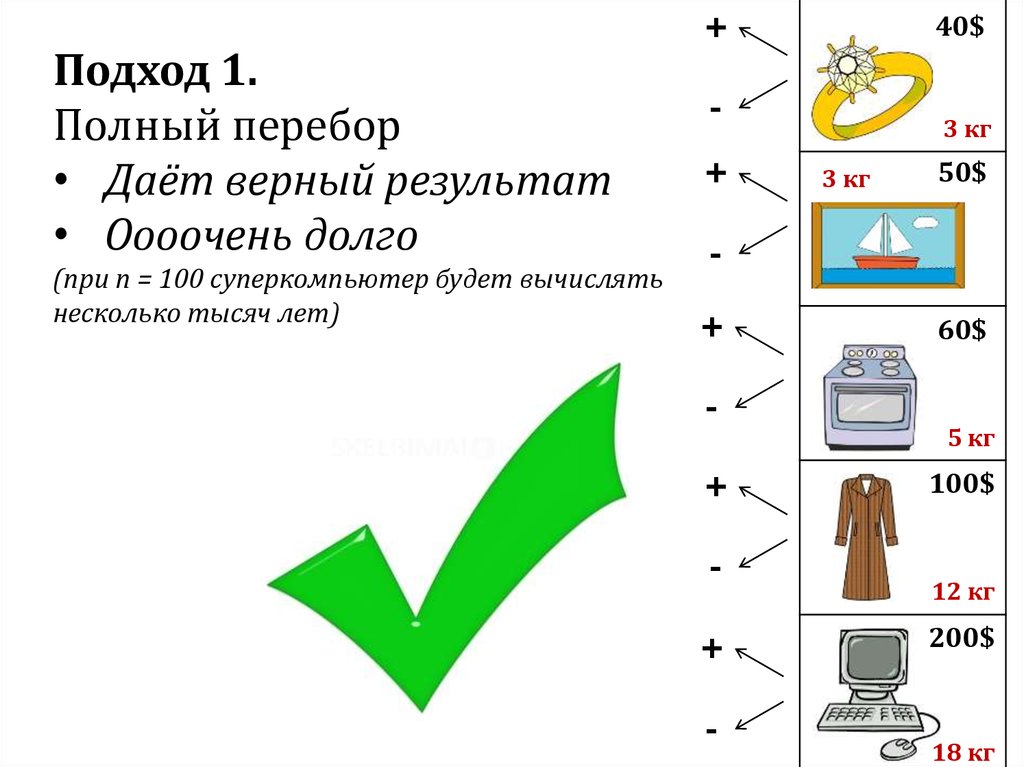
Подход 1.
Полный перебор
• Даёт верный результат
• Оооочень долго
(при n = 100 суперкомпьютер будет вычислять
несколько тысяч лет)
+
40$
+
3 кг
3 кг
50$
+
+
+
-
60$
5 кг
100$
12 кг
200$
18 кг

19.

Подход 2.
Брать самую дорогую вещь
• Не всегда будет давать
максимальный ответ
40$
3 кг
3 кг
50$
(уже в нашем примере не работало)
• Приведите пример из трёх
вещей
60$
5 кг
100$
12 кг
200$
18 кг

20.

Подход 3.
Рассчитать плотность каждой
вещи: сi/mi.
Брать вещи, в порядке
убывания плотности, пока
влезают.
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

21.

Подход 3.
Рассчитать плотность каждой
вещи: сi/mi.
Брать вещи, в порядке
убывания плотности, пока
влезают.
• Тоже не всегда будет
давать правильный ответ.
(приведите пример)
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

22.

Подходы 2-3.
Последние два алгоритма
назывались жадными.
Для данной задачи они не
подходят.
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

23.

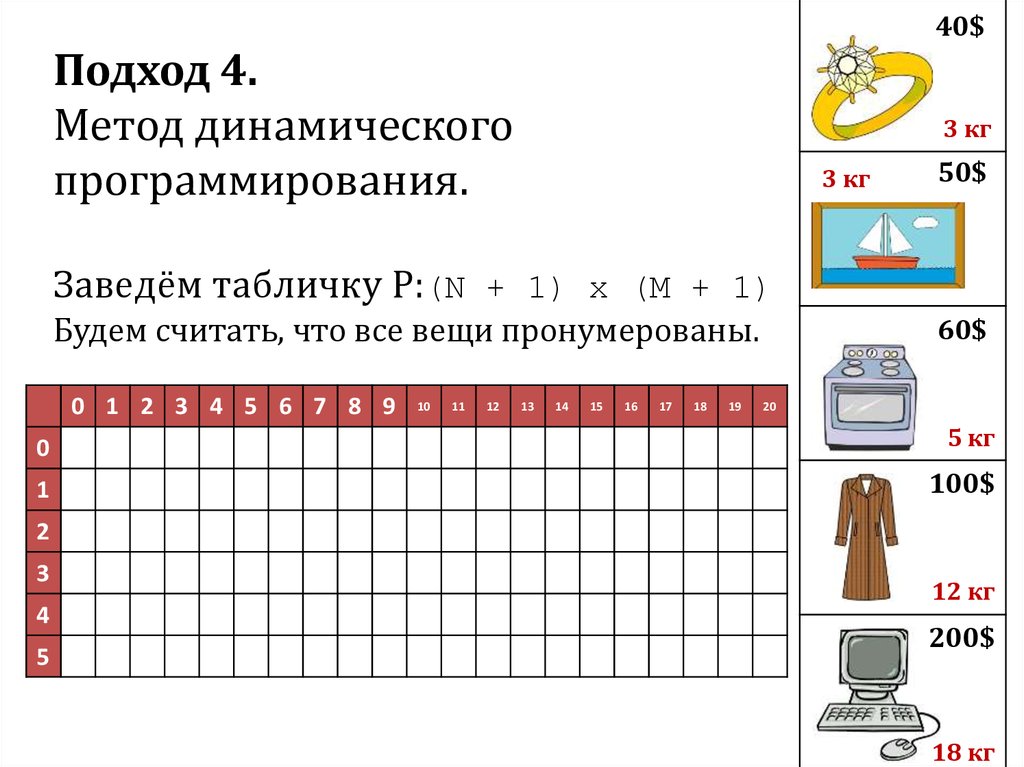
Подход 4.
Метод динамического
программирования.
40$
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$
18 кг

24.

Подход 4.
Метод динамического
программирования.
Заведём табличку (N
40$
3 кг
3 кг
50$
+ 1) x (M + 1)
60$
5 кг
100$
12 кг
200$
18 кг

25.

40$
Подход 4.
Метод динамического
программирования.
3 кг
3 кг
50$
Заведём табличку P:(N + 1) x (M + 1)
Будем считать, что все вещи пронумерованы.
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
60$
20
0
5 кг
1
100$
2
3
4
5
12 кг
200$
18 кг

26.

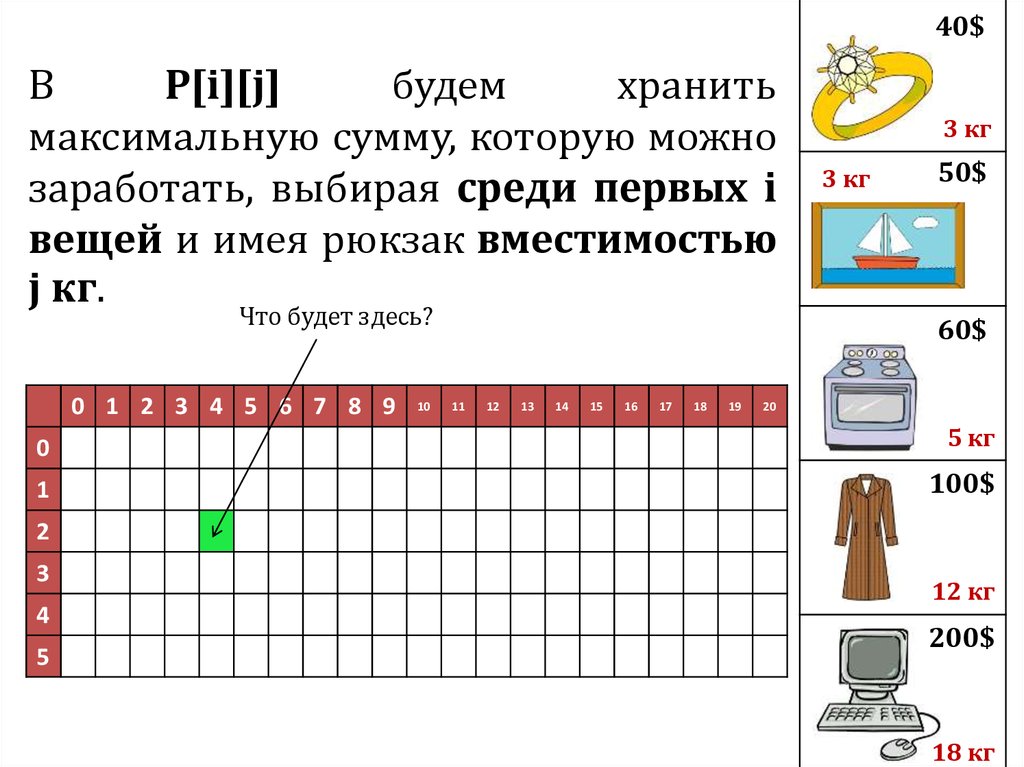
40$
В
P[i][j]
будем
хранить
максимальную сумму, которую можно
заработать, выбирая среди первых i
вещей и имея рюкзак вместимостью
j кг.
3 кг
3 кг
50$
60$
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
0
5 кг
1
100$
2
3
4
5
12 кг
200$
18 кг

27.

40$
В
P[i][j]
будем
хранить
максимальную сумму, которую можно
заработать, выбирая среди первых i
вещей и имея рюкзак вместимостью
j кг.
Что будет здесь?
0 1 2 3 4 5 6 7 8 9
10
3 кг
3 кг
50$
60$
11
12
13
14
15
16
17
18
19
20
0
5 кг
1
100$
2
3
4
5
12 кг
200$
18 кг

28.

40$
В
P[i][j]
будем
хранить
максимальную сумму, которую можно
заработать, выбирая среди первых i
вещей и имея рюкзак вместимостью
j кг.
Выбираем среди первых двух вещей
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
10
11
12
13
14
15
16
17
18
19
20
3 кг
3 кг
50$

29.

40$
В
P[i][j]
будем
хранить
максимальную сумму, которую можно
заработать, выбирая среди первых i
вещей и имея рюкзак вместимостью
j кг.
Выбираем среди первых двух вещей.
Рюкзак вместимостью 4 кг.
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
10
11
12
13
14
15
16
17
18
19
20
3 кг
3 кг
50$

30.

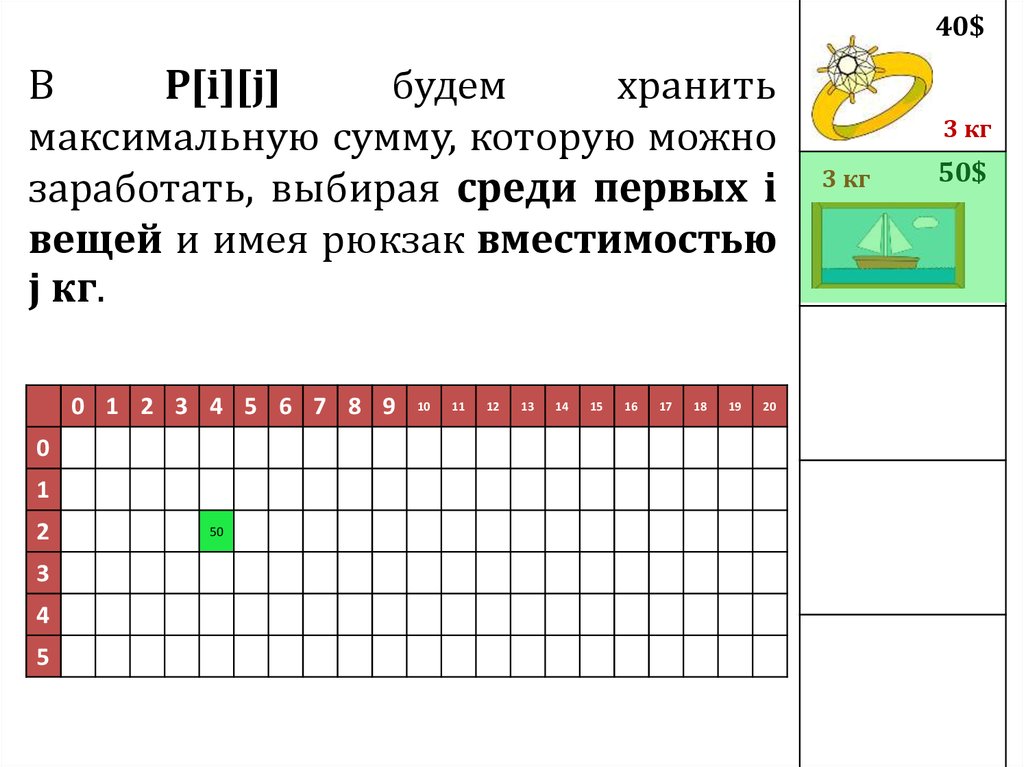
40$
В
P[i][j]
будем
хранить
максимальную сумму, которую можно
заработать, выбирая среди первых i
вещей и имея рюкзак вместимостью
j кг.
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
50
10
11
12
13
14
15
16
17
18
19
20
3 кг
3 кг
50$

31.

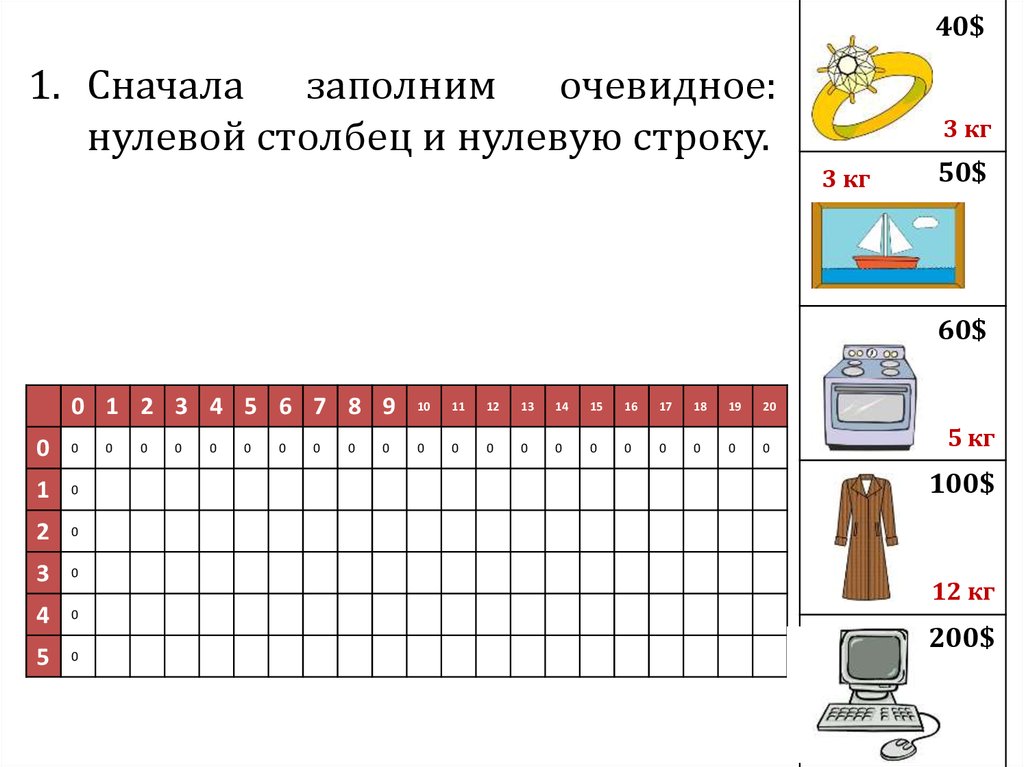
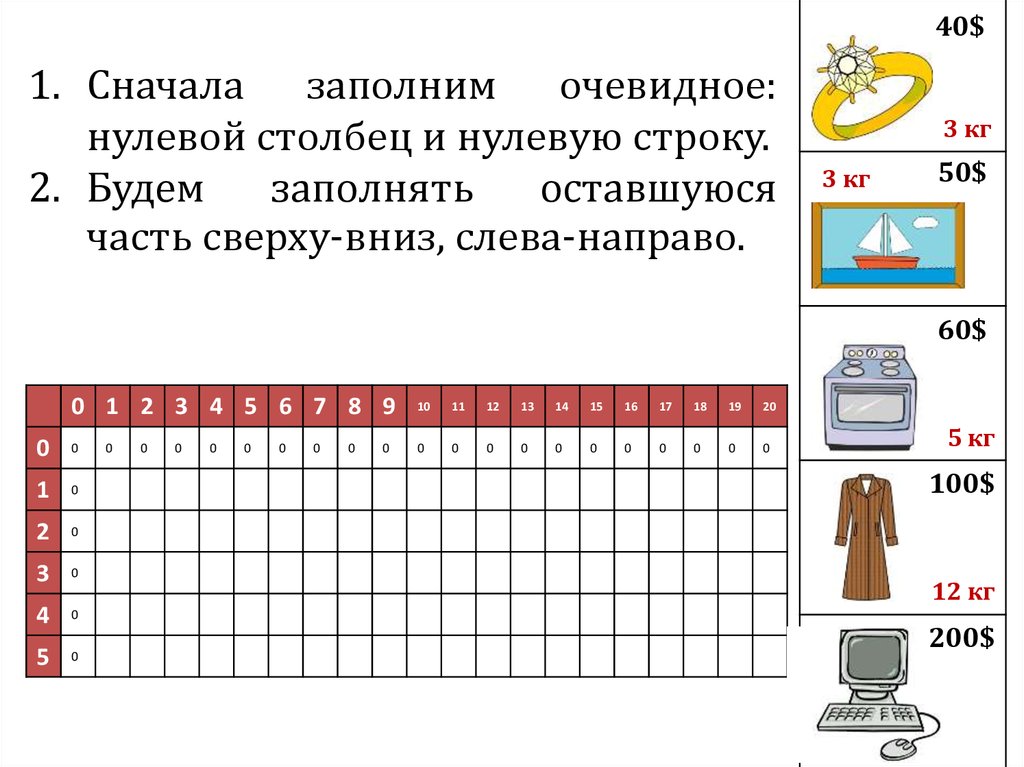
40$
1. Сначала заполним очевидное:
нулевой столбец и нулевую строку.
Как?
3 кг
3 кг
50$
60$
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
0
5 кг
1
100$
2
3
4
5
12 кг
200$

32.

40$
1. Сначала заполним очевидное:
нулевой столбец и нулевую строку.
3 кг
3 кг
50$
60$
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
3
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

33.

40$
1. Сначала заполним очевидное:
нулевой столбец и нулевую строку.
2. Будем
заполнять
оставшуюся
часть сверху-вниз, слева-направо.
3 кг
3 кг
50$
60$
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
3
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

34.

40$
1. Сначала заполним очевидное:
нулевой столбец и нулевую строку.
2. Будем
заполнять
оставшуюся
часть сверху-вниз, слева-направо,
выражая
каждый
следующий
ответ через предыдущие.
0 1 2 3 4 5 6 7 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
3
0
4
0
5
0
0
0
0
0
0
0
0
0
0
3 кг
3 кг
50$
60$
5 кг
100$
12 кг
200$

35.

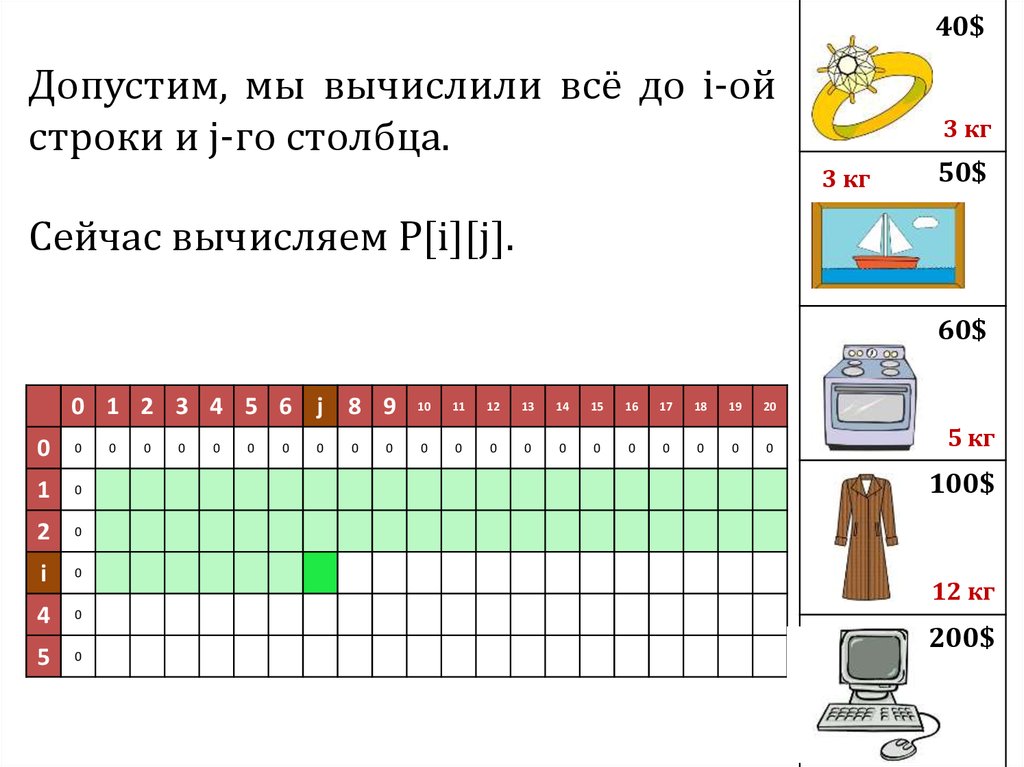
40$
Допустим, мы вычислили всё до i-ой
строки и j-го столбца.
3 кг
3 кг
50$
Сейчас вычисляем P[i][j].
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

36.

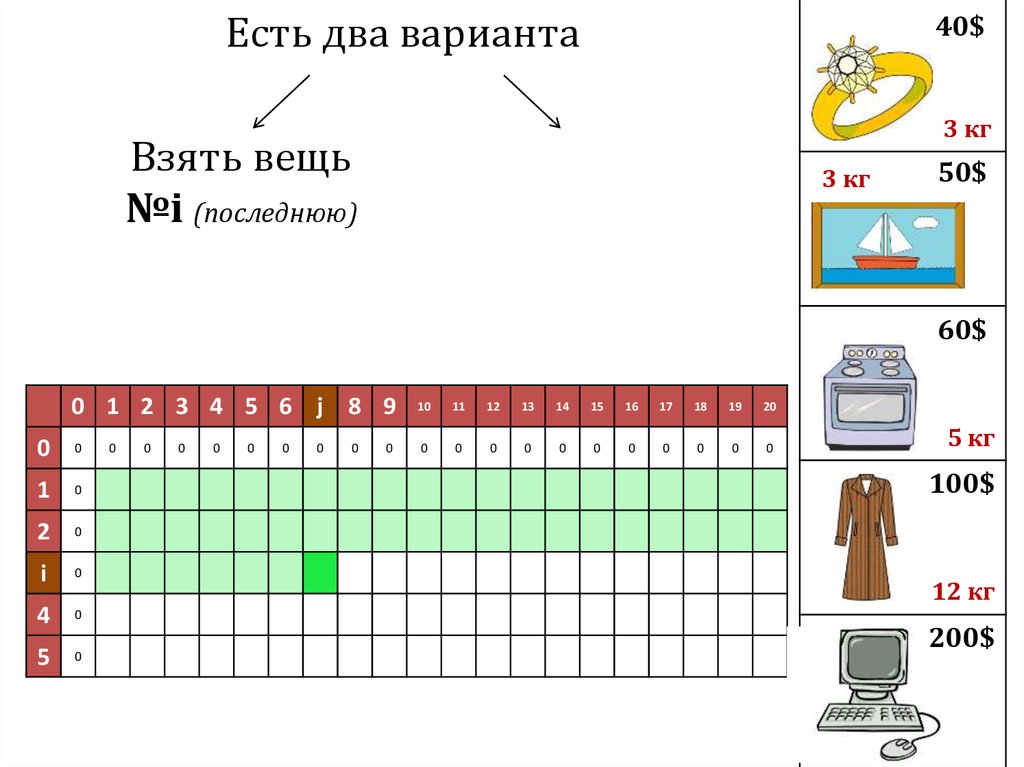
Есть два варианта
40$
3 кг
Взять вещь
№i (последнюю)
3 кг
50$
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

37.

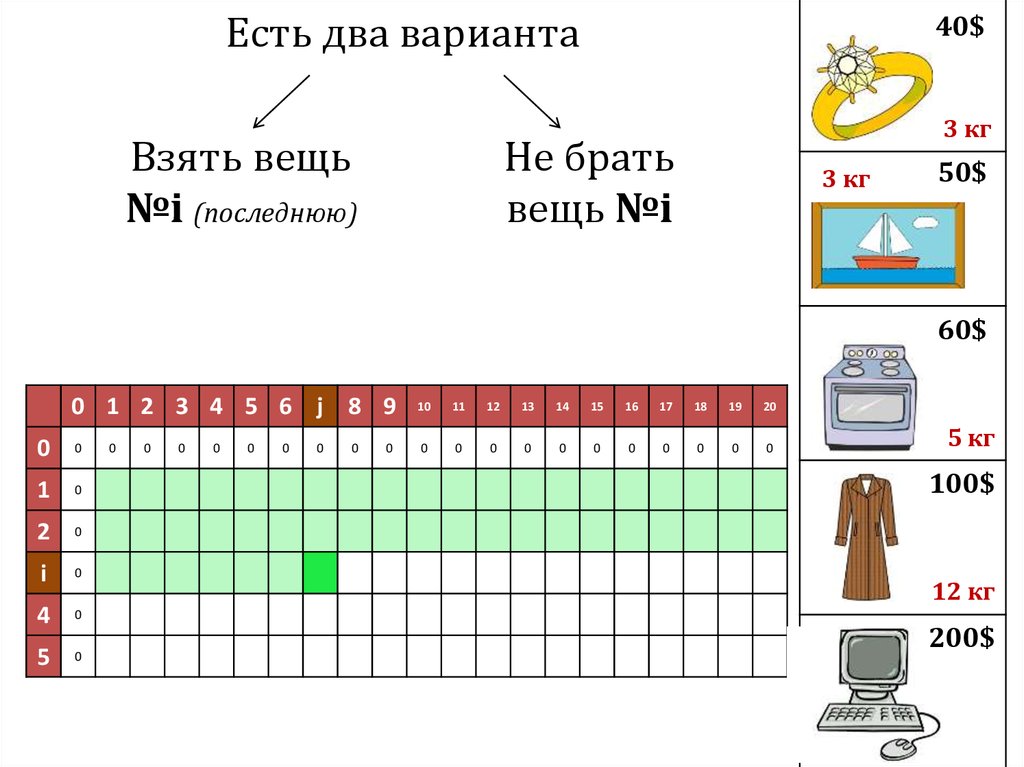
Есть два варианта
Взять вещь
№i (последнюю)
40$
3 кг
Не брать
вещь №i
3 кг
50$
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

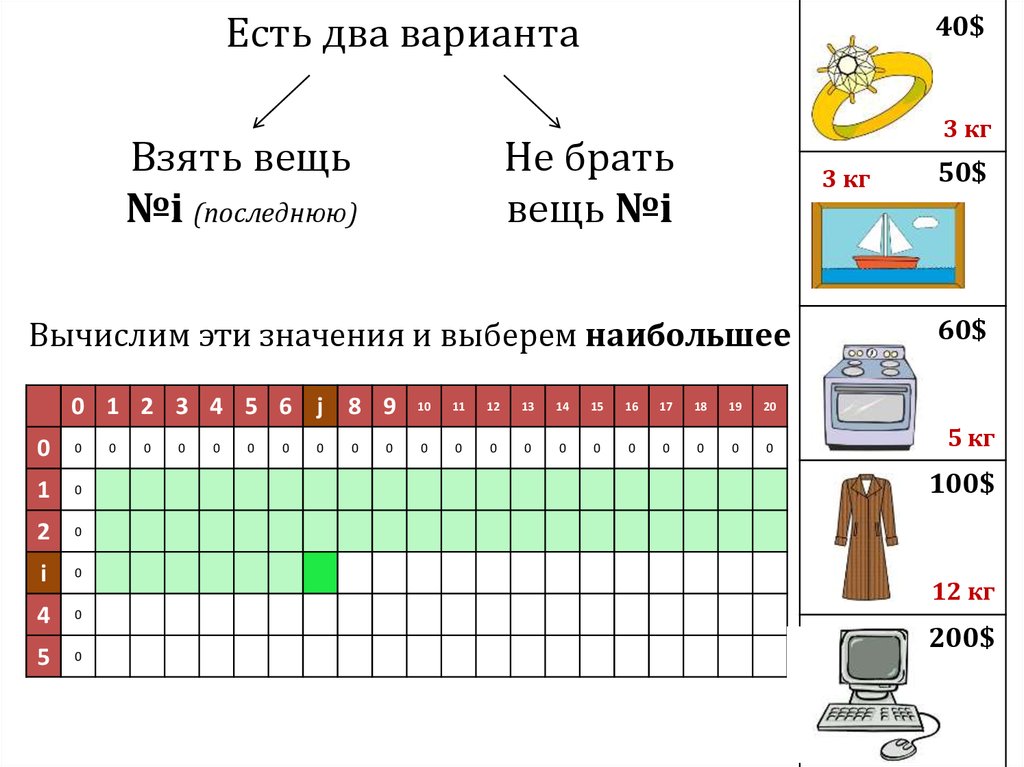
38.

Есть два варианта
Взять вещь
№i (последнюю)
40$
3 кг
Не брать
вещь №i
3 кг
Вычислим эти значения и выберем наибольшее
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
60$
5 кг
100$
12 кг
200$

39.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
3 кг
Только, если влезает.
Что это значит?
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

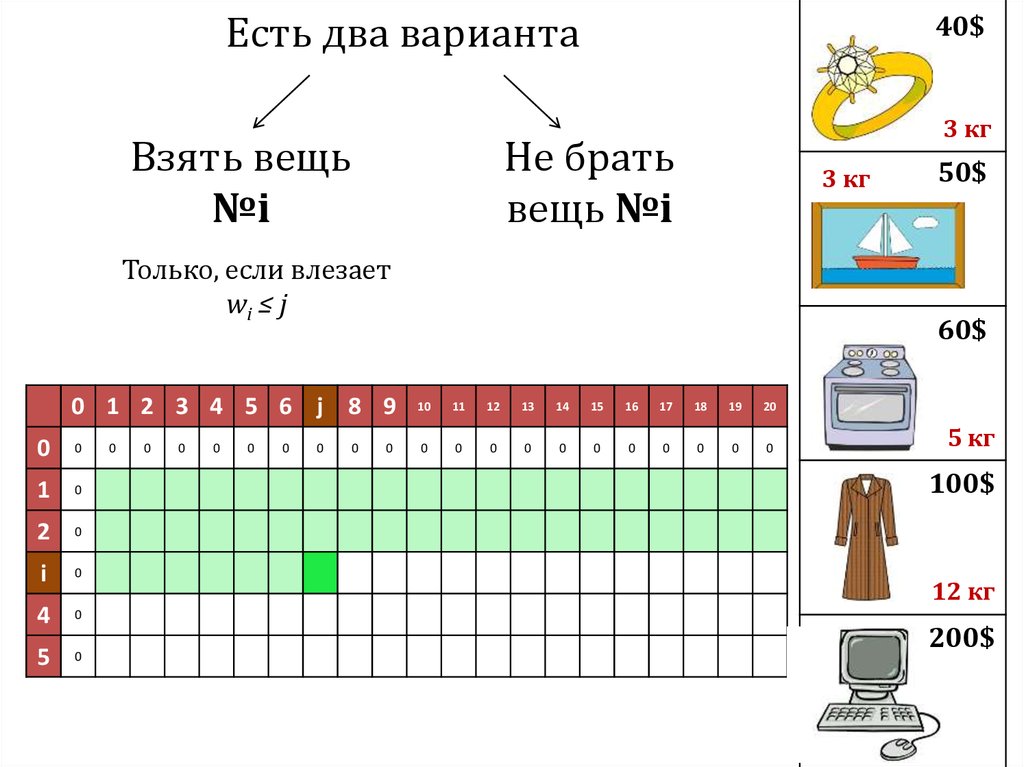
40.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
3 кг
Только, если влезает
wi ≤ j
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

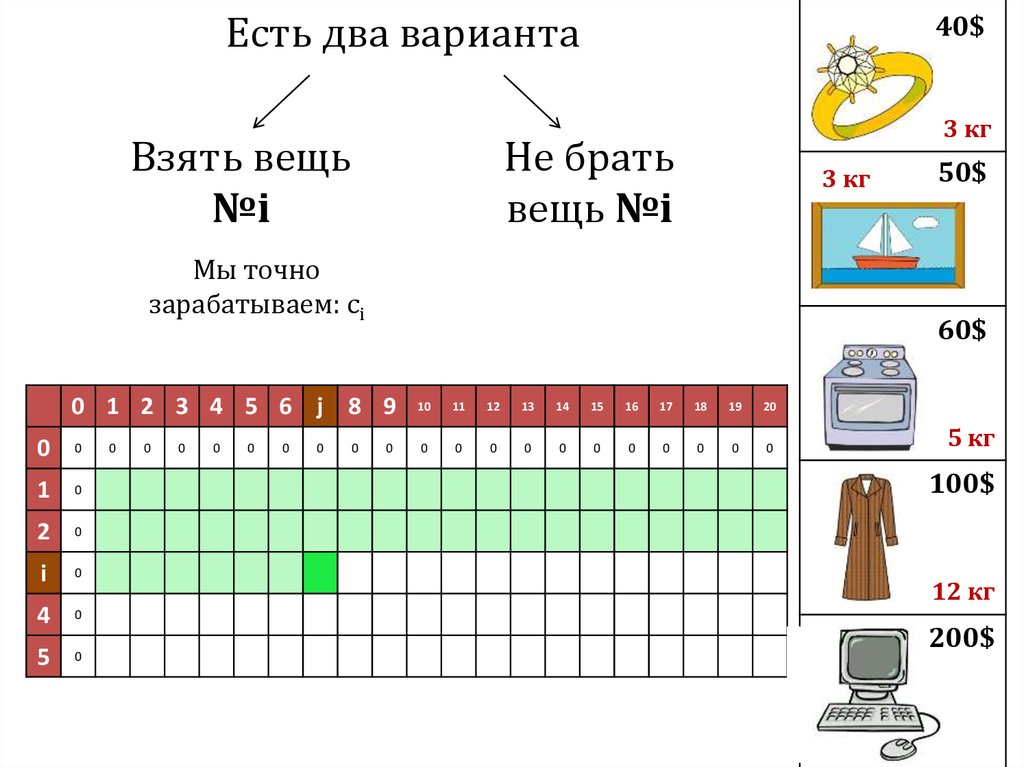
41.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
3 кг
Мы точно
зарабатываем: ci
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
50$
0
5 кг
100$
12 кг
200$

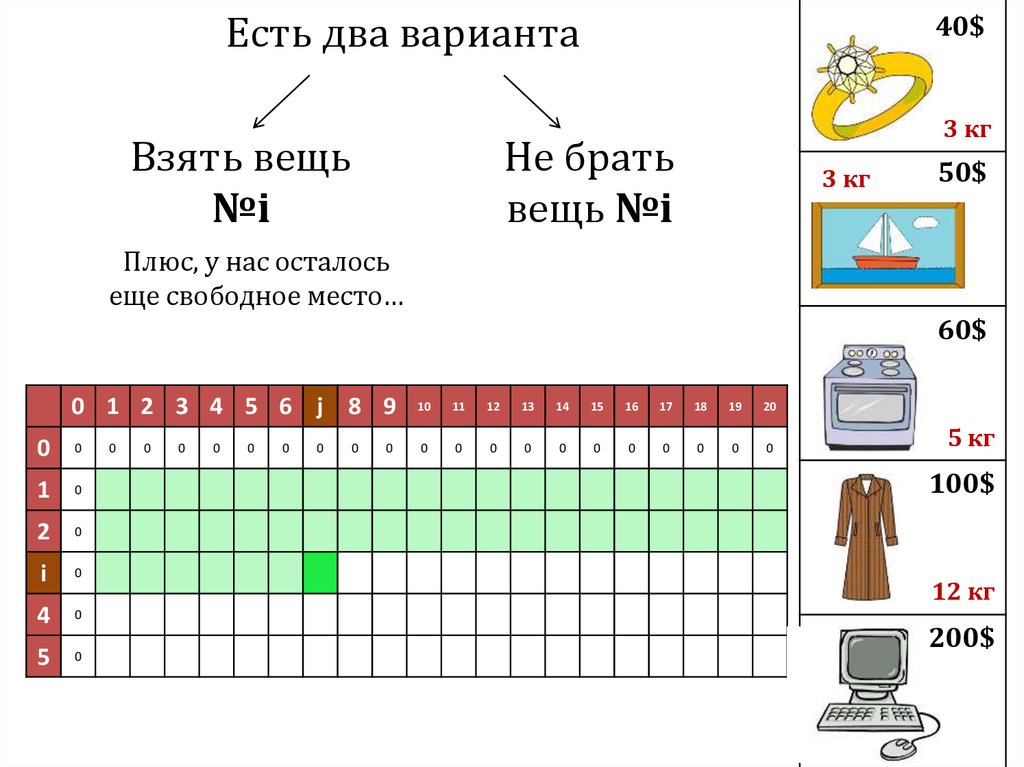
42.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
3 кг
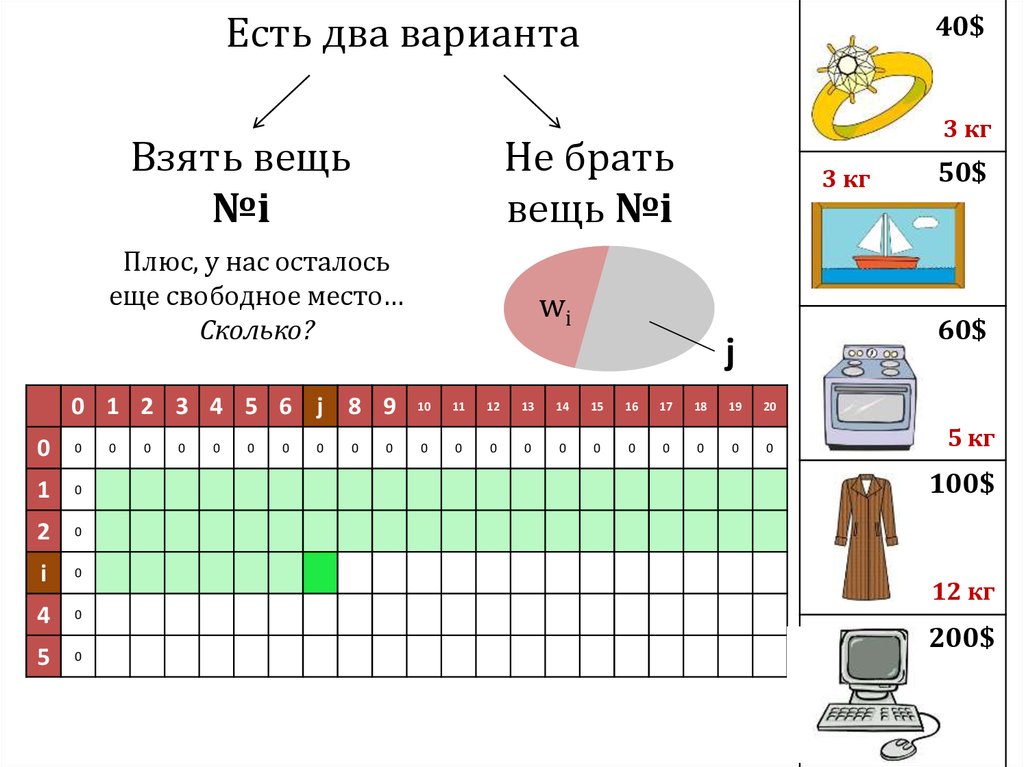
50$
Плюс, у нас осталось
еще свободное место…
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
5 кг
100$
12 кг
200$

43.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
Плюс, у нас осталось
еще свободное место…
Сколько?
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

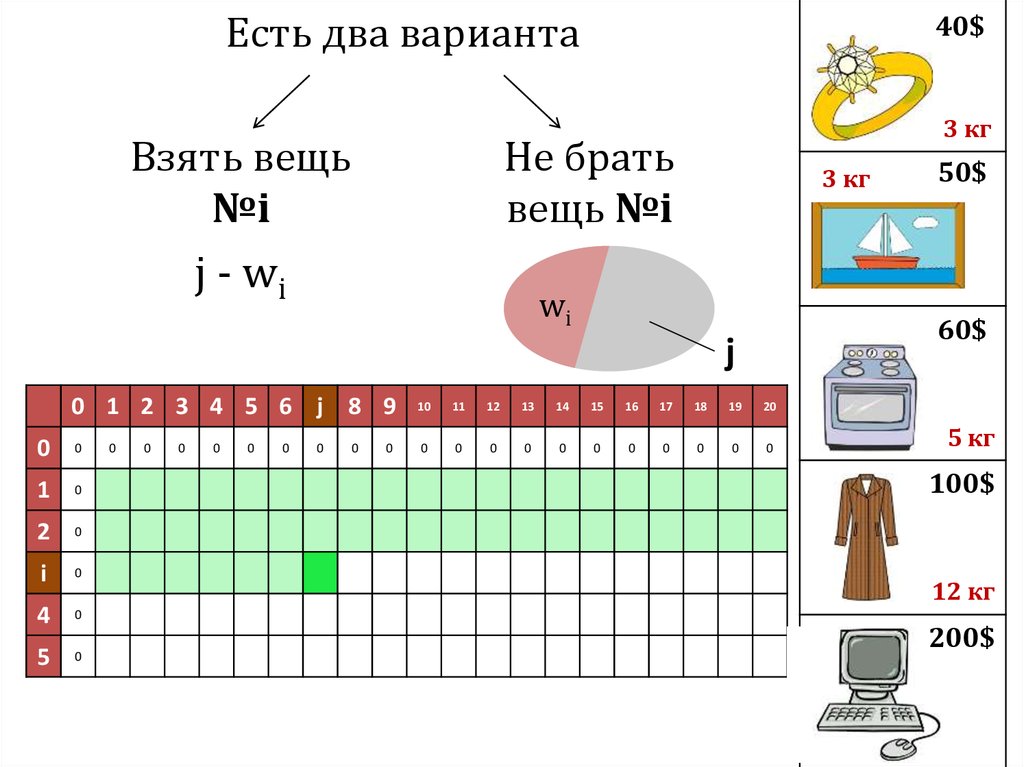
44.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
j - wi
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

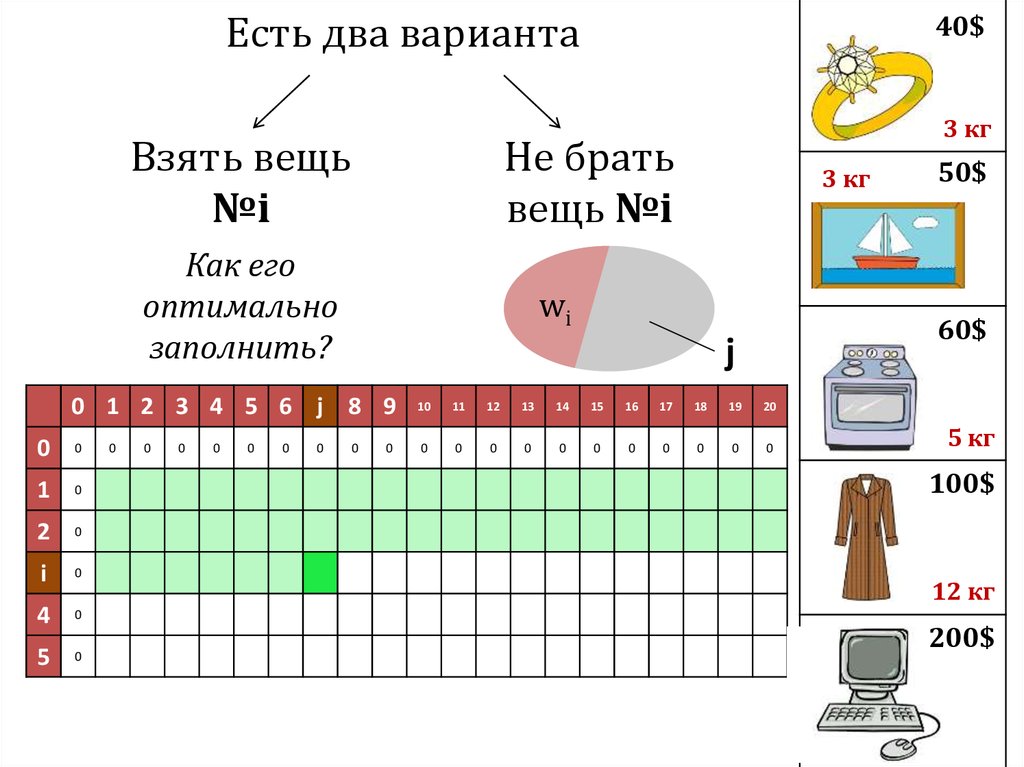
45.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
Как его
оптимально
заполнить?
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

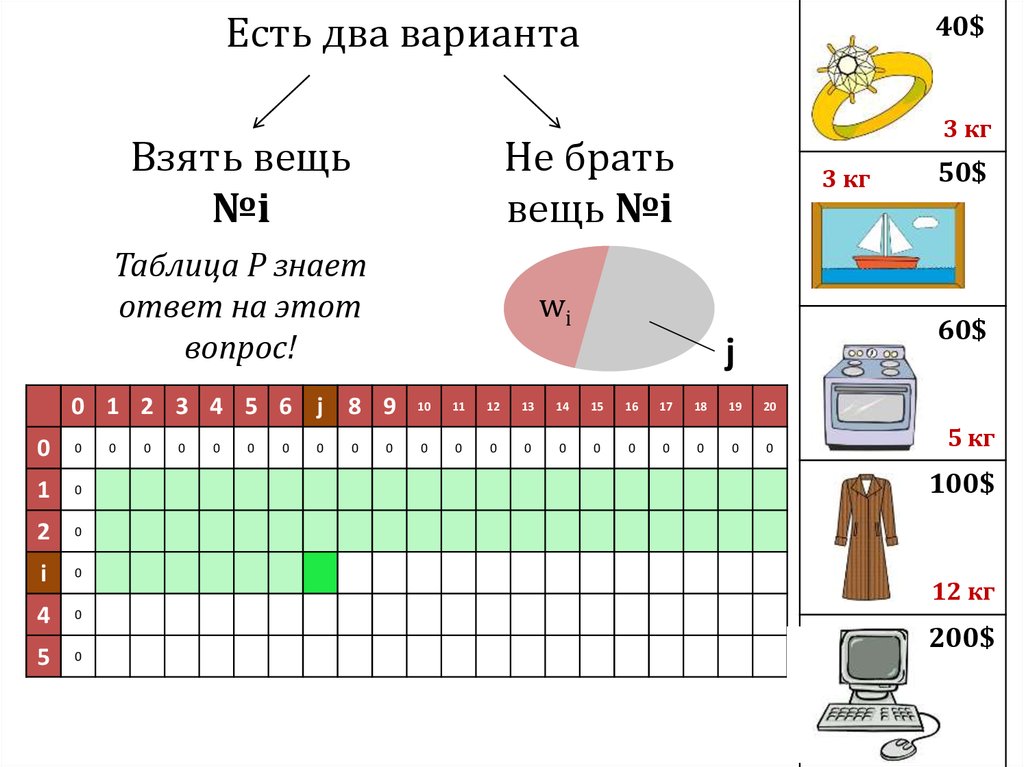
46.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
Таблица P знает
ответ на этот
вопрос!
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

47.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
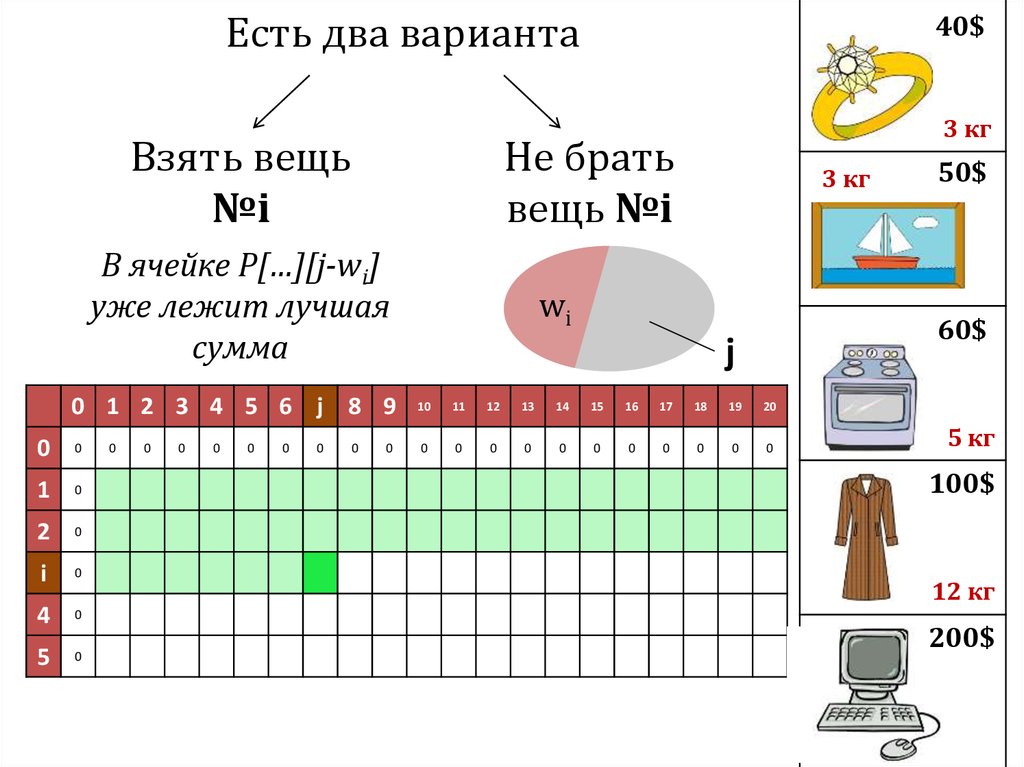
В ячейке P[…][…]
уже лежит лучшая
сумма
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

48.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
В ячейке P[…][j-wi]
уже лежит лучшая
сумма
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

49.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
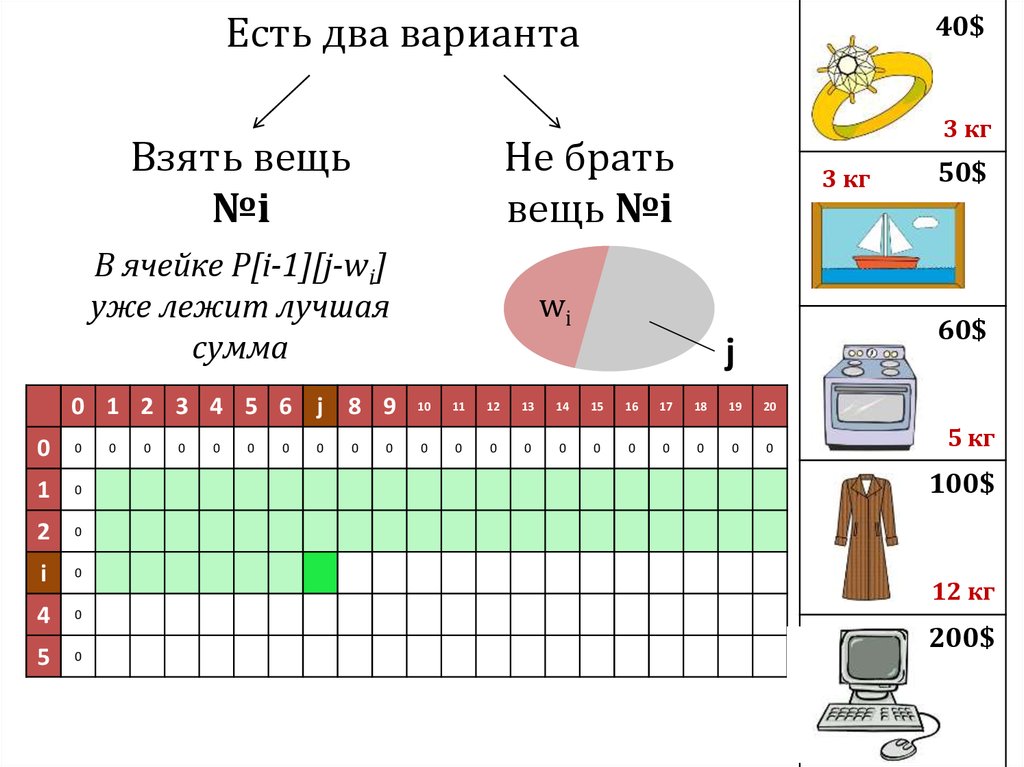
В ячейке P[i-1][j-wi]
уже лежит лучшая
сумма
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

50.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
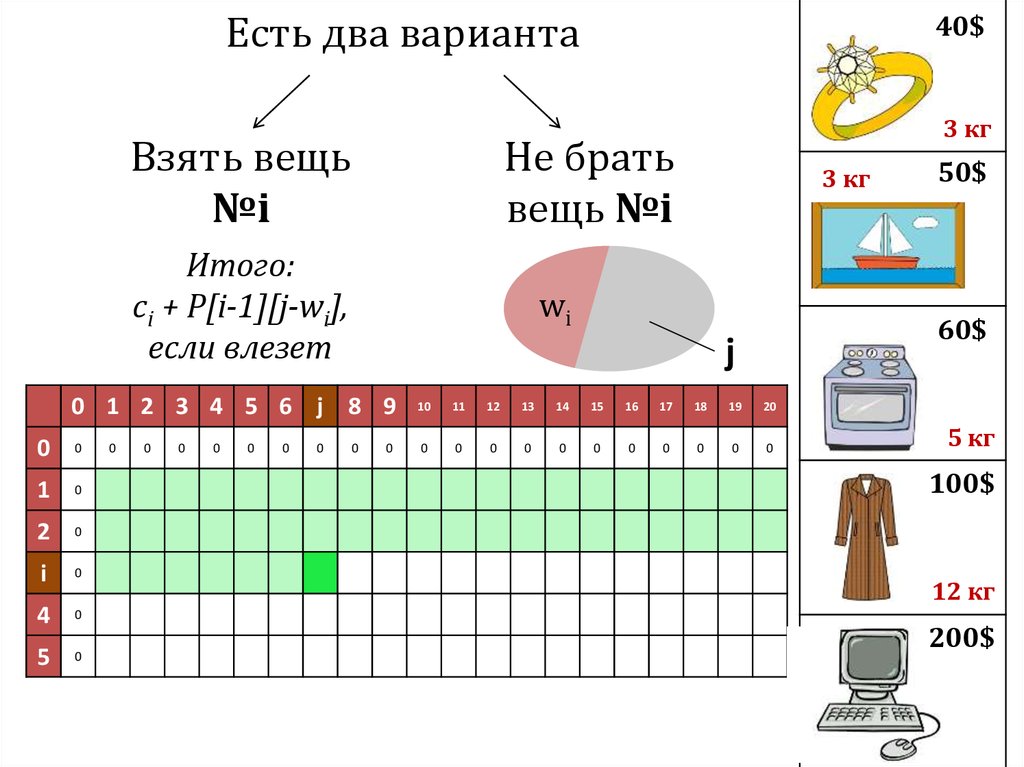
Итого:
ci + P[i-1][j-wi],
если влезет
3 кг
wi
60$
j
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

51.

Есть два варианта
Взять вещь
№i
40$
3 кг
Не брать
вещь №i
3 кг
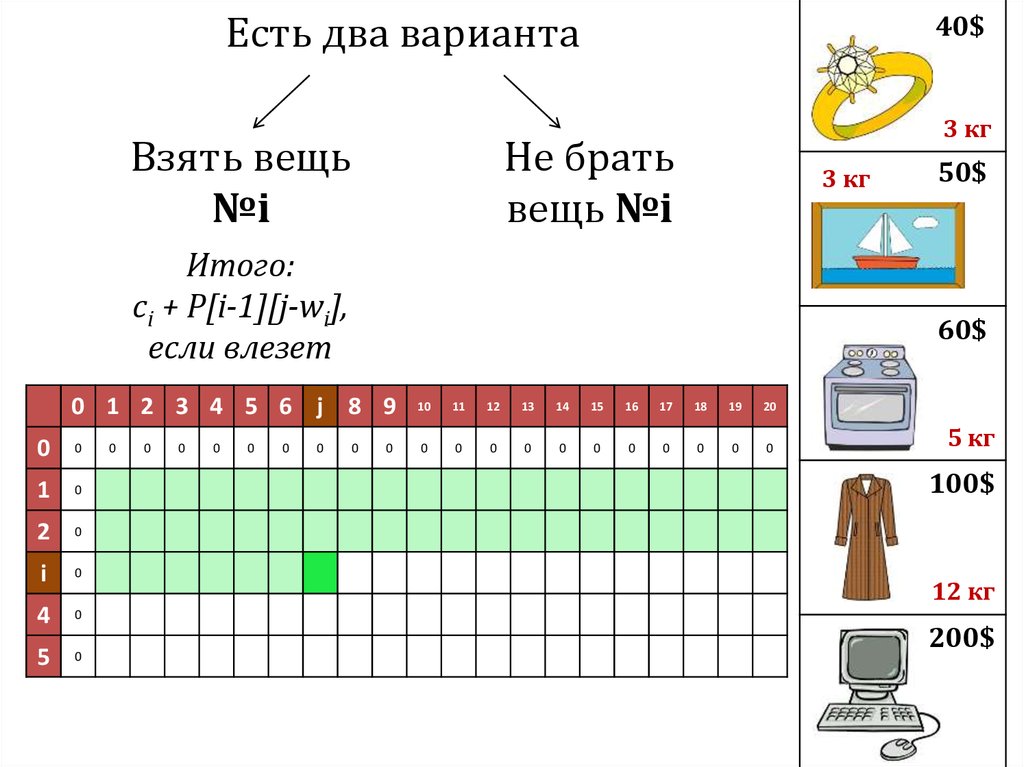
Итого:
ci + P[i-1][j-wi],
если влезет
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
50$
0
0
5 кг
100$
12 кг
200$

52.

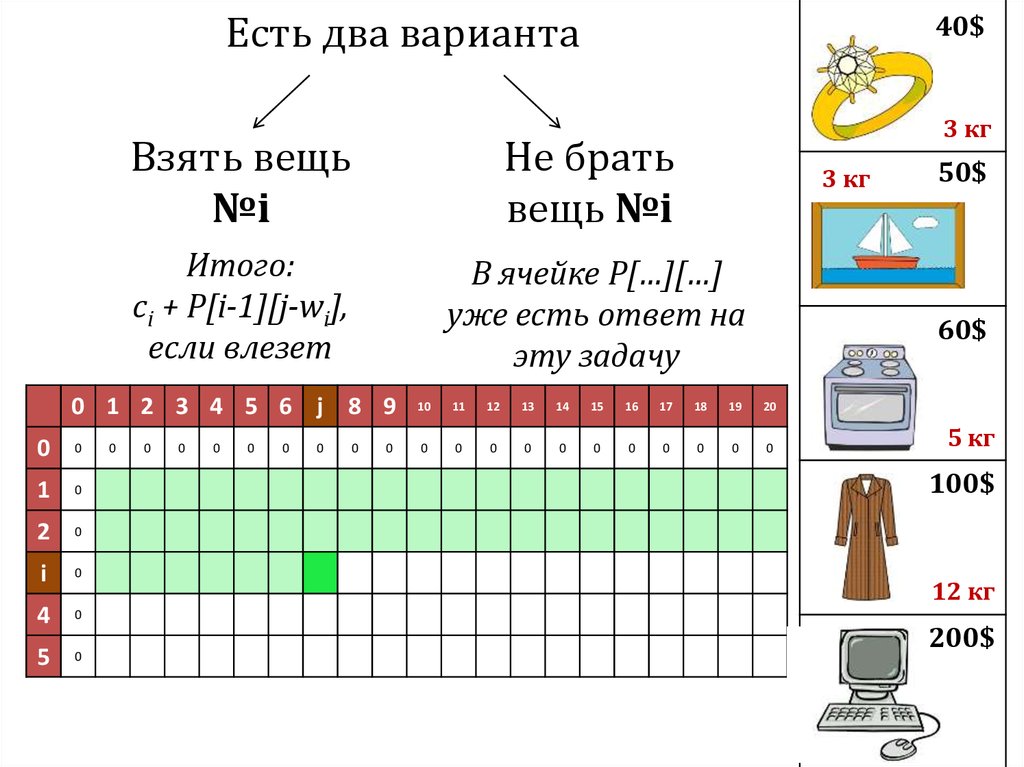
Есть два варианта
40$
3 кг
Взять вещь
№i
Не брать
вещь №i
Итого:
ci + P[i-1][j-wi],
если влезет
В ячейке P[…][…]
уже есть ответ на
эту задачу
3 кг
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

53.

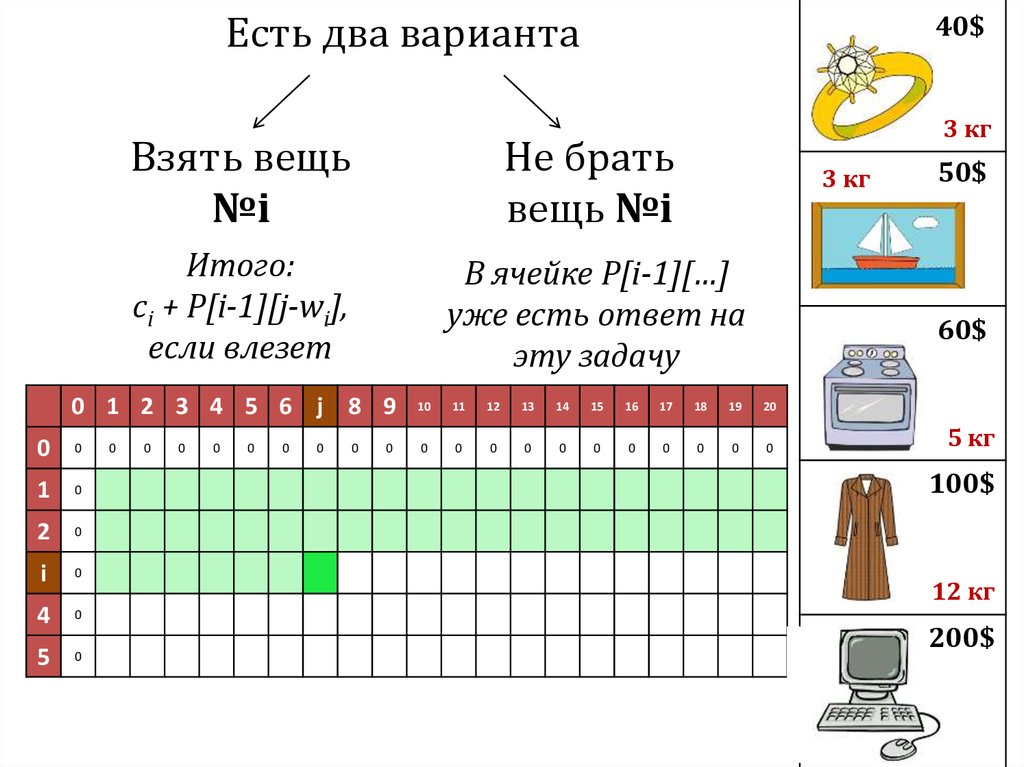
Есть два варианта
40$
3 кг
Взять вещь
№i
Не брать
вещь №i
Итого:
ci + P[i-1][j-wi],
если влезет
В ячейке P[i-1][…]
уже есть ответ на
эту задачу
3 кг
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
12 кг
200$

54.

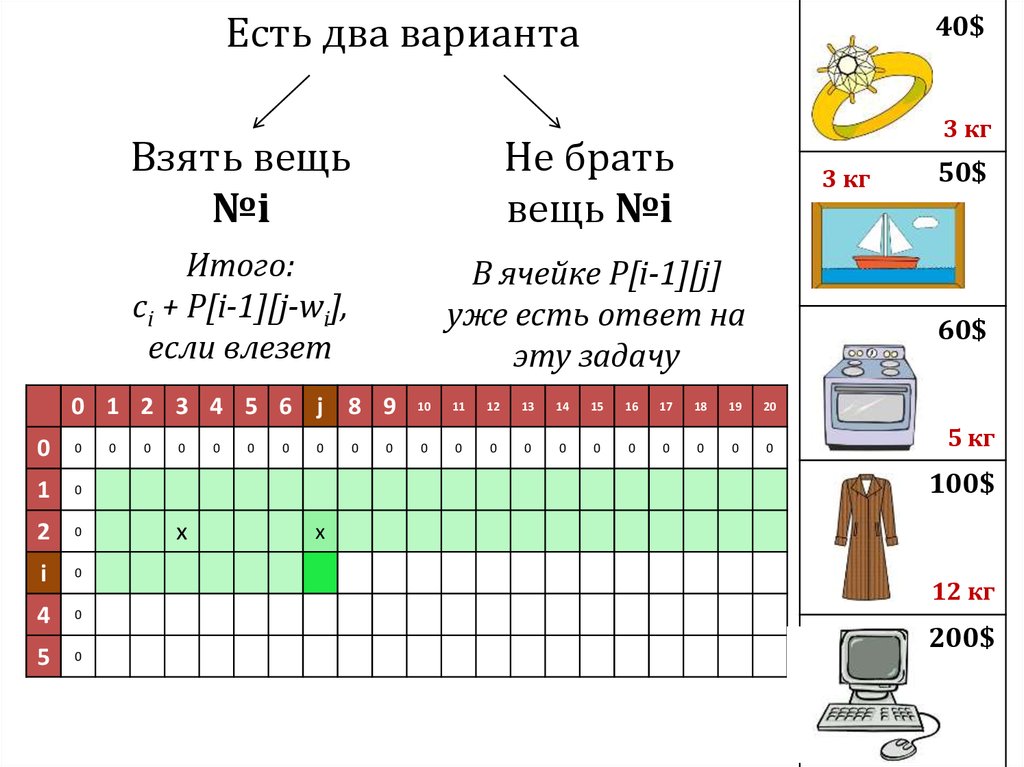
Есть два варианта
40$
3 кг
Взять вещь
№i
Не брать
вещь №i
Итого:
ci + P[i-1][j-wi],
если влезет
В ячейке P[i-1][j]
уже есть ответ на
эту задачу
3 кг
60$
0 1 2 3 4 5 6 j 8 9
10
11
12
13
14
15
16
17
18
19
20
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
0
i
0
4
0
5
0
0
0
0
0
0
0
0
0
0
50$
5 кг
100$
x
x
12 кг
200$