Теорема о равенстве односторонних углов. Теорема о свойстве односторонних углов

1.

Теорема о равенстве
соответственных углов.
Теорема о свойстве
односторонних углов

2.

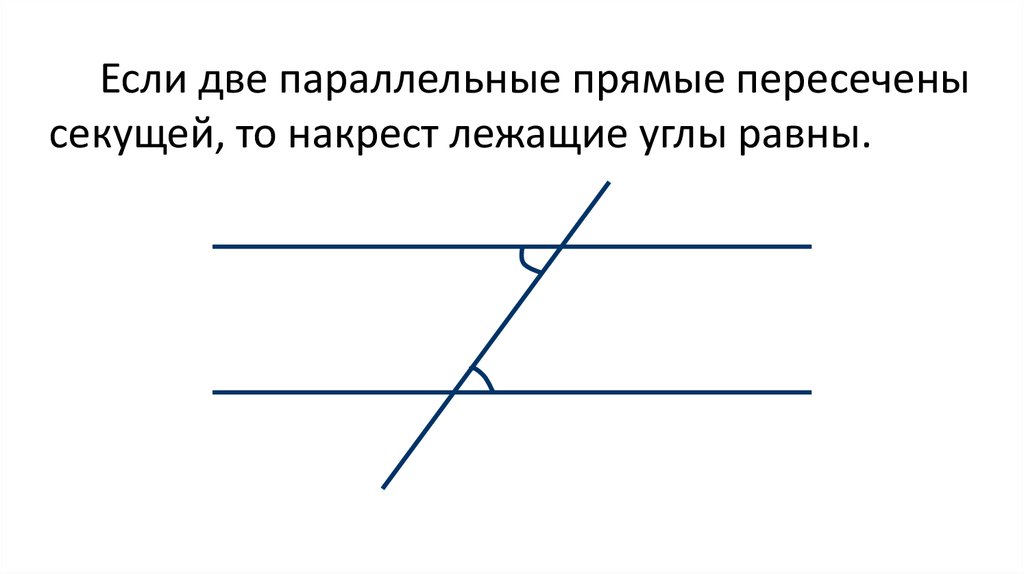
Если две параллельные прямые пересечены
секущей, то накрест лежащие углы равны.

3.

Теорема. Если две параллельные прямые пересечены
секущей, то соответственные углы равны.
Доказательство.
Так как а || b,
то ∠ 2 = ∠ 3 (как накрест лежащие).
∠ 1 = ∠ 3 (как вертикальные).
Следует, что ∠ 1 = ∠ 2.
Теорема доказана.
c
a
1
3
b
2

4.

В
D
N
А
M
С
∠ NMC = ∠ DAC (как соответственные),
∠ DAC = ∠ BAD (AD – биссектриса).

5.

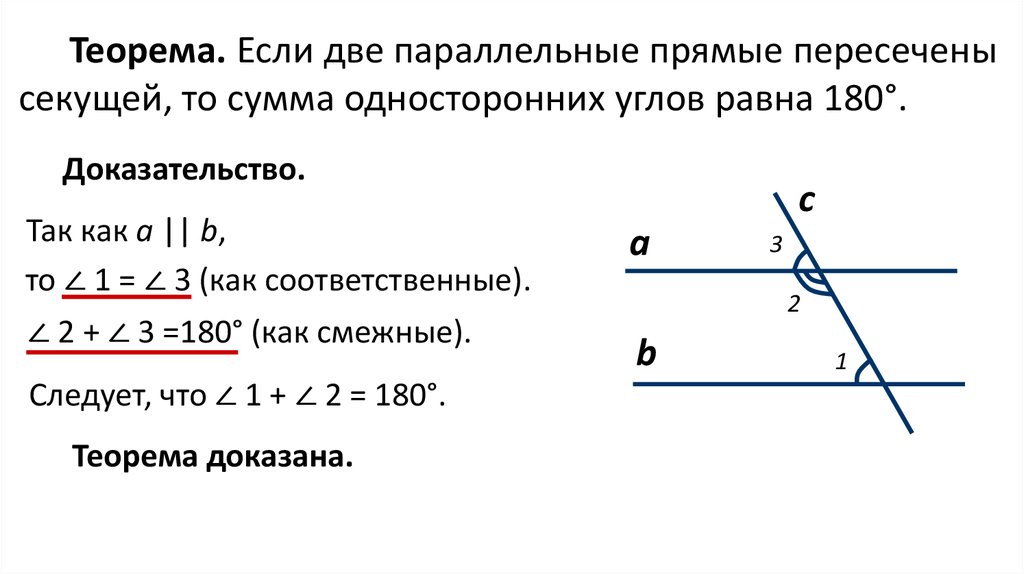
Теорема. Если две параллельные прямые пересечены
секущей, то сумма односторонних углов равна 180°.
Доказательство.
Так как а || b,
то ∠ 1 = ∠ 3 (как соответственные).
∠ 2 + ∠ 3 =180° (как смежные).
Следует, что ∠ 1 + ∠ 2 = 180°.
Теорема доказана.
c
a
3
2
b
1

6.

С
D
E
А
В
∠ BAD + ∠ ADE = 180°

7.

Задача. Луч BD – биссектриса ∠ АВС, прямая DE
параллельна прямой АВ, а градусная мера ∠ ЕDB
равна 32°. Чему равен ∠ CED?
Решение.
С
∠ BDE = ∠ ABD
D
(как внутр. накрест лежащие ),
то есть ∠ ABD = 32°.
∠ ABС = 64°, так как BD – биссектриса.
∠ ABC, ∠ CED – соответственные,
А
значит, ∠ ABC = ∠ CED.
Следовательно, ∠ CED = 64°.
Ответ: 64°.
E
32°
В

8.

Задача. Градусная мера одного из внутренних
односторонних углов, образованных при пересечении
двух параллельных прямых секущей, меньше градусной
меры другого на 26°. Вычислите градусные меры этих
c
углов.
a
Решение.
Пусть ∠ 1 =