Статические и астатические системы автоматического регулирования. (Тема 6)

1. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР

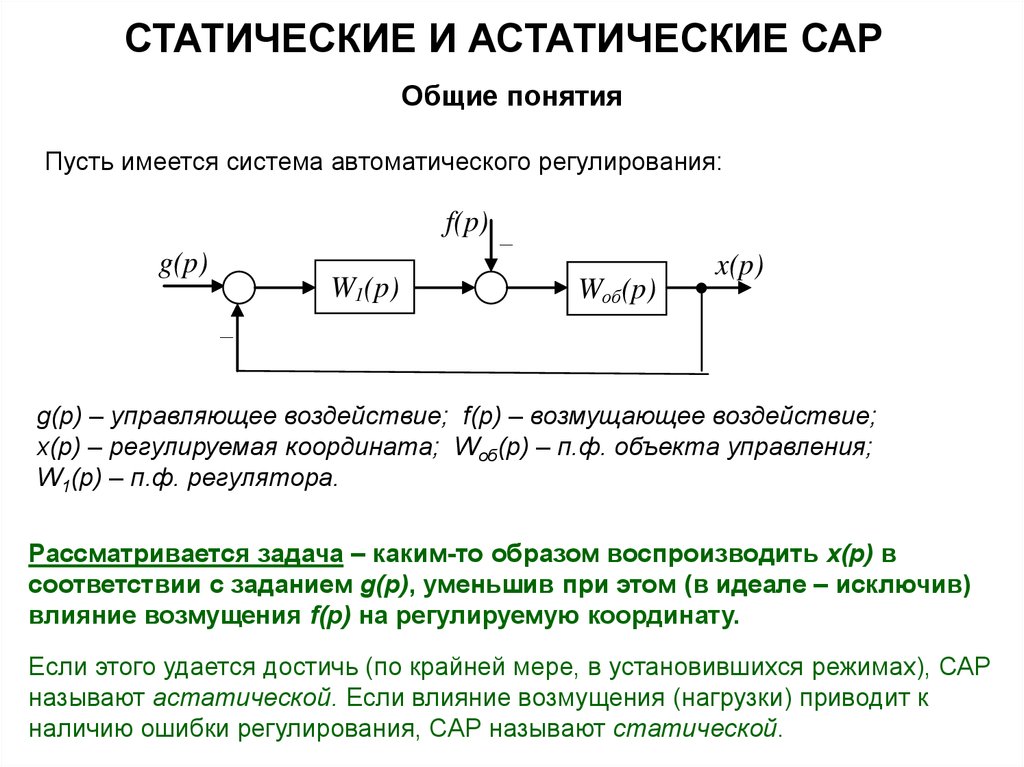
Общие понятия
Пусть имеется система автоматического регулирования:
f(p)
g(p)
W1(p)
–
Wоб(p)
x(p)
–
g(p) – управляющее воздействие; f(p) – возмущающее воздействие;
x(p) – регулируемая координата; Wоб(p) – п.ф. объекта управления;
W1(p) – п.ф. регулятора.
Рассматривается задача – каким-то образом воспроизводить x(p) в
соответствии с заданием g(p), уменьшив при этом (в идеале – исключив)
влияние возмущения f(p) на регулируемую координату.
Если этого удается достичь (по крайней мере, в установившихся режимах), САР
называют астатической. Если влияние возмущения (нагрузки) приводит к
наличию ошибки регулирования, САР называют статической.

2.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
В более узком смысле понятия статизм и астатизм системы
рассматриваются раздельно применительно к управляющему g(p) и
возмущающему f(p) воздействиям.
Эти понятия важны при рассмотрении показателей точности систем точного
воспроизведения и систем автоматической стабилизации.
Для систем точного воспроизведения представляет интерес вопрос,
является ли САР статической или астатической по управляющему
воздействию.
Если ошибка воспроизведения управляющего воздействия
t g t x t
в установившемся режиме (при t ) равна нулю, то САР называется
астатической по управляющему воздействию. В противном случае
САР называется статической по управляющему воздействию.

3.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
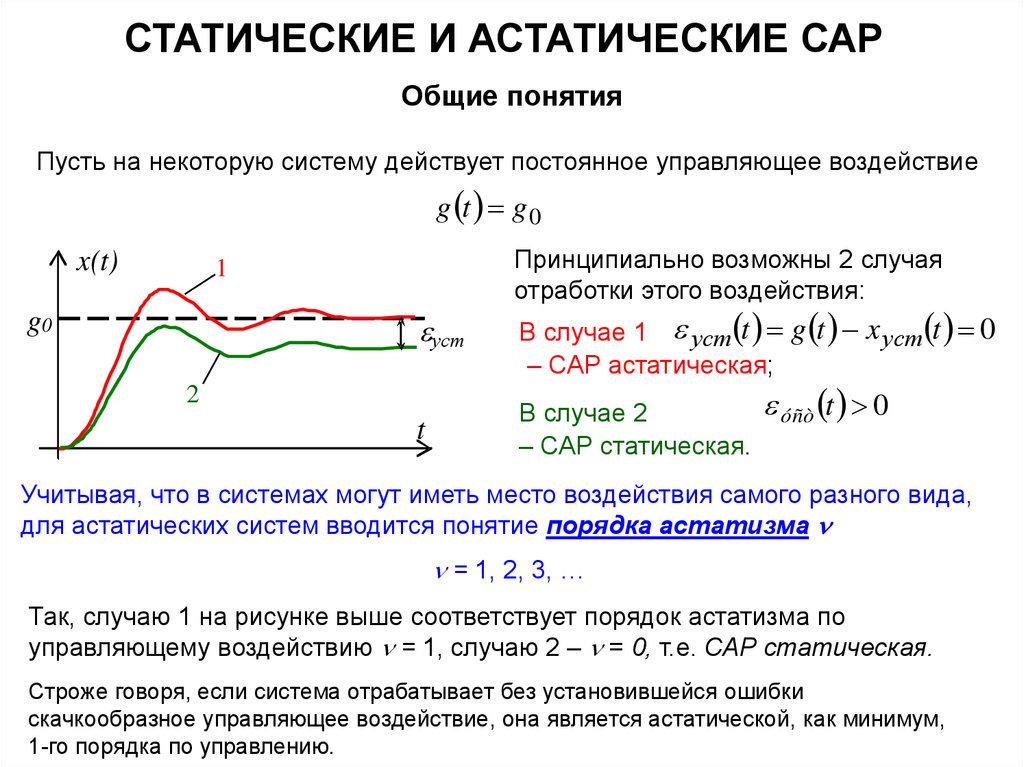
Пусть на некоторую систему действует постоянное управляющее воздействие
g t g 0
x(t)
Принципиально возможны 2 случая
отработки этого воздействия:
1
g0
уст
В случае 1 уст t g t x уст t 0
– САР астатическая;
t
В случае 2
– САР статическая.
2
óñò t 0
Учитывая, что в системах могут иметь место воздействия самого разного вида,
для астатических систем вводится понятие порядка астатизма
= 1, 2, 3, …
Так, случаю 1 на рисунке выше соответствует порядок астатизма по
управляющему воздействию = 1, случаю 2 – = 0, т.е. САР статическая.
Строже говоря, если система отрабатывает без установившейся ошибки
скачкообразное управляющее воздействие, она является астатической, как минимум,
1-го порядка по управлению.

4.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
Пусть на систему действует линейное управляющее воздействие
g t Vt
Принципиально возможны 3 случая отработки этого воздействия:
По аналогичному принципу считают, что
если система отрабатывает без
установившейся ошибки линейное
управляющее воздействие, она является
астатической, как минимум, 2-го порядка по
управлению.
x(t)
2 уст
1
0
t
Если
óñò t const 0
Если
óñò t
Если óñò t 0 – говорят, что порядок
астатизма САР по управлению 2
– порядок астатизма САР по управлению
– порядок астатизма САР по управлению
1
0 (статическая)

5.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
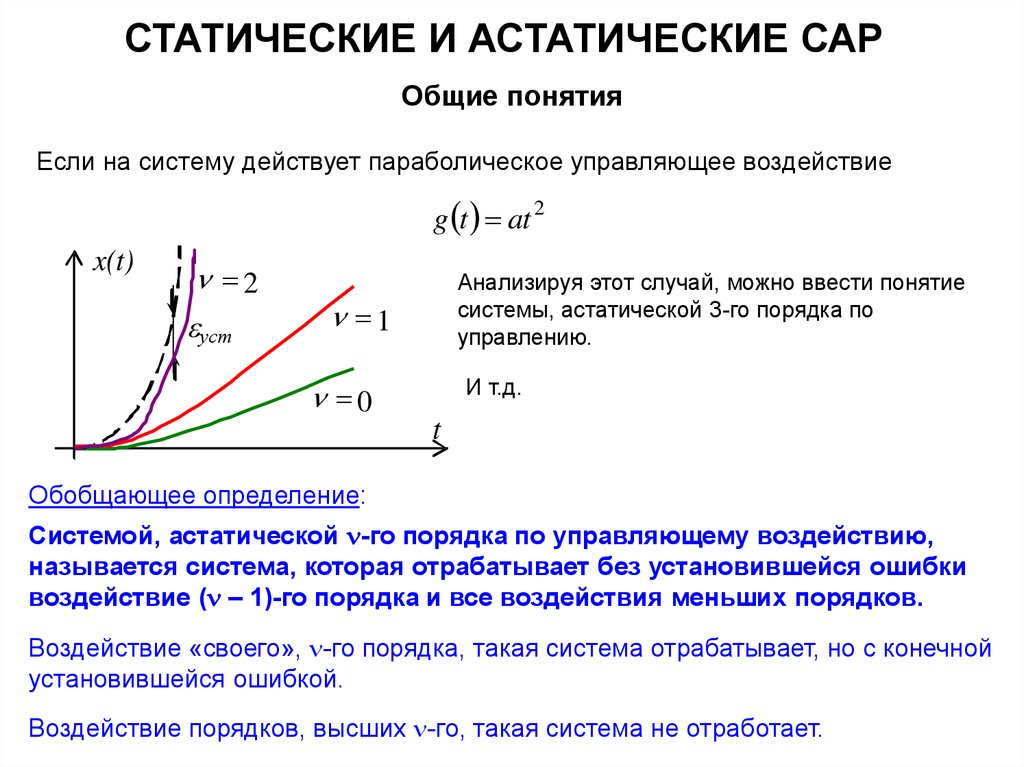
Если на систему действует параболическое управляющее воздействие
g t at 2
x(t)
2
уст
Анализируя этот случай, можно ввести понятие
системы, астатической 3-го порядка по
управлению.
1
И т.д.
0
t
Обобщающее определение:
Системой, астатической -го порядка по управляющему воздействию,
называется система, которая отрабатывает без установившейся ошибки
воздействие ( – 1)-го порядка и все воздействия меньших порядков.
Воздействие «своего», -го порядка, такая система отрабатывает, но с конечной
установившейся ошибкой.
Воздействие порядков, высших -го, такая система не отработает.

6.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
Для систем стабилизации представляет интерес вопрос, является ли САР
статической или астатической по возмущающему воздействию.
Если возмущающее воздействие оказывает влияние на регулируемую
координату в установившемся режиме (т.е., появляется дополнительная
составляющая ошибки регулирования, вызванная наличием возмущения), то
система называется статической по возмущающему воздействию, в
противном случае – астатической.
x
xзад
Под статической характеристикой
системы понимают зависимость
Астатическая САР
x уст f
Статическая САР
f
при постоянном управляющем
воздействии
g t g 0
Если система астатическая по возмущению, ошибка регулирования равна нулю при
любом (приемлемом) значении возмущения, и статическая характеристика представляет
собой прямую линию, параллельную оси абсцисс.
Если система статическая по возмущению, с ростом величины возмущения ошибка
регулирования будет увеличиваться.

7.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Общие понятия
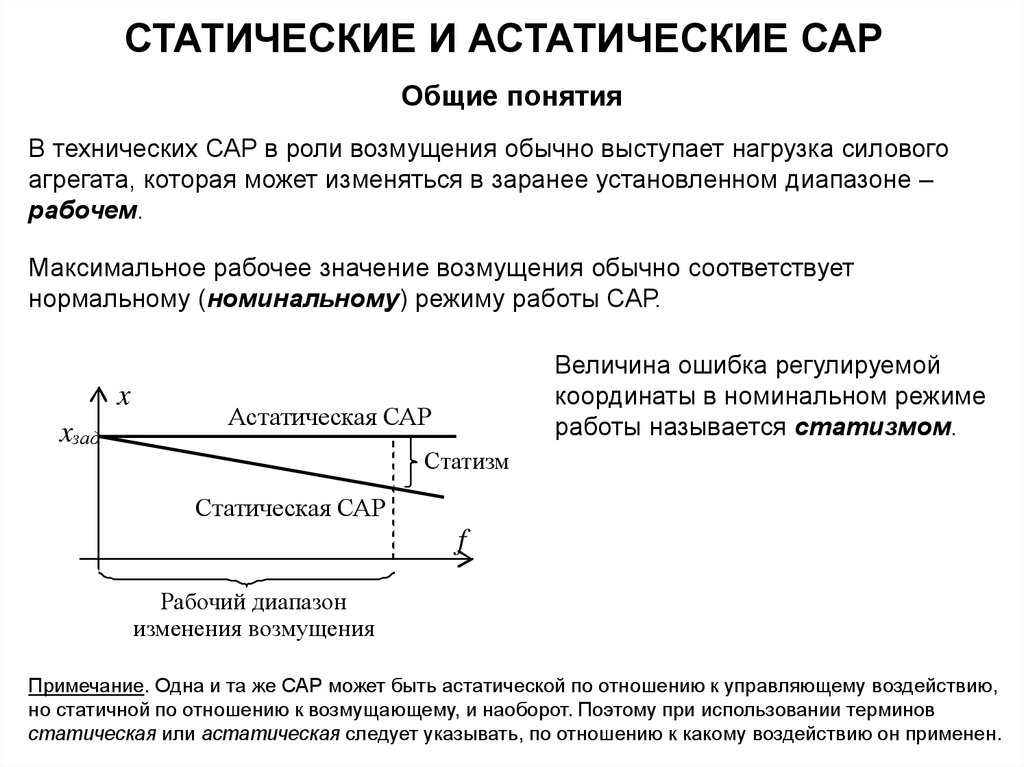
В технических САР в роли возмущения обычно выступает нагрузка силового
агрегата, которая может изменяться в заранее установленном диапазоне –
рабочем.
Максимальное рабочее значение возмущения обычно соответствует
нормальному (номинальному) режиму работы САР.
x
xзад
Величина ошибка регулируемой
координаты в номинальном режиме
работы называется статизмом.
Астатическая САР
Статизм
Статическая САР
f
Рабочий диапазон
изменения возмущения
Примечание. Одна и та же САР может быть астатической по отношению к управляющему воздействию,
но статичной по отношению к возмущающему, и наоборот. Поэтому при использовании терминов
статическая или астатическая следует указывать, по отношению к какому воздействию он применен.

8.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
Системы точного воспроизведения удобно рассматривать, принимая п.ф.
обратной связи, равную 1. Акцент делаем на точности отработки
управляющего воздействия.
(p)
g(p)
W(p)
Обобщенная структурная схема
системы точного воспроизведения
x(p)
–
Представим п.ф. разомкнутой САР в виде:
W p
где W p
k
p
W p
P p
– нормированная ПФ разомкнутой САР, в которой
Q p
P 0 Q 0 1
– количество чистых интеграторов в п.ф. разомкнутой системы
(порядок астатизма п.ф. разомкнутой системы)

9.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
(p)
g(p)
W(p)
Обобщенная структурная схема
системы точного воспроизведения
x(p)
–
Для определения установившейся ошибки может быть использована теорема о
конечном значении
уст lim t lim p p
(*)
t
p 0
Если окажется, что уст 0 , САР является астатической, в противном случае –
статической.
Вводя в рассмотрение передаточную функцию системы по ошибке
K p
p
g p
выражение (*) для установившейся ошибки перепишется в виде:
уст lim pK p g p
p 0
(**)

10.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
(p)
g(p)
W(p)
Обобщенная структурная схема
системы точного воспроизведения
x(p)
–
П.ф. системы по ошибке можно вычислить следующим образом:
p
1
K p
g p 1 W p
p
k
1 W p p k W p
p
1
(1)
Тогда установившаяся ошибка может быть вычислена следующим образом:
pg p
k
p 0
1 W p
p
уст lim p p lim
p 0
(2)

11.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
Частный случай.
(p)
g(p)
–
W(p)
x(p)
Пусть система должна отрабатывать
постоянное управляющее воздействие:
g t g 0
или
g p g0 p
Установившаяся ошибка будет равна:
уст lim pK p
p 0
g0
K 0 g0
p
(3)
Из (3) видно, что САР будет астатической, если K 0 0
Анализируя (1), можно показать, что K 0 0 , если
В противном случае САР будет статической. При
1
0 будет
K 0
1
1 k
Таким образом, если =0, то САР будет статической, и установившаяся ошибка, как
видно из (3), будет обратно пропорциональна коэффициенту усиления k разомкнутой
САР, сложенному с единицей.
Замечание. Теоретически ошибку можно приблизить к нулю, устремляя k к бесконечности. Это
положение реализуется в релейных САР, релейные элементы которых работают в скользящем
режиме.

12.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
Система будет астатической (по крайней мере, 1-го порядка), если порядок астатизма
п.ф. разомкнутой системы > 0. В астатической САР всегда должны присутствовать
интегрирующие звенья в чистом виде (хотя бы одно) – то есть, не должны
компенсироваться дифференцирующими звеньями и не должны быть замкнутыми
жесткими о.с.
Теорема.
Порядок астатизма замкнутой САР по управляющему воздействию
совпадает с порядком астатизма п.ф. разомкнутой САР.
Доказательство. Пусть к системе приложено управляющее воздействие n-го порядка
g t g 0t n
Вычисляем установившуюся ошибку по (2):
g p g0
n!
p n 1
g 0 n!
pg p
p
p n
уст lim
lim
n 1 lim
g 0 n!
k
k
p 0
p 0
p 0 p k W p
1 W p
1 W p p
(4)
p
p
Из последнего выражения следует, что уст 0, если n 1
т.е. если порядок астатизма системы по крайней мере на 1 превышает порядок кривой.
Теорема доказана.

13.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
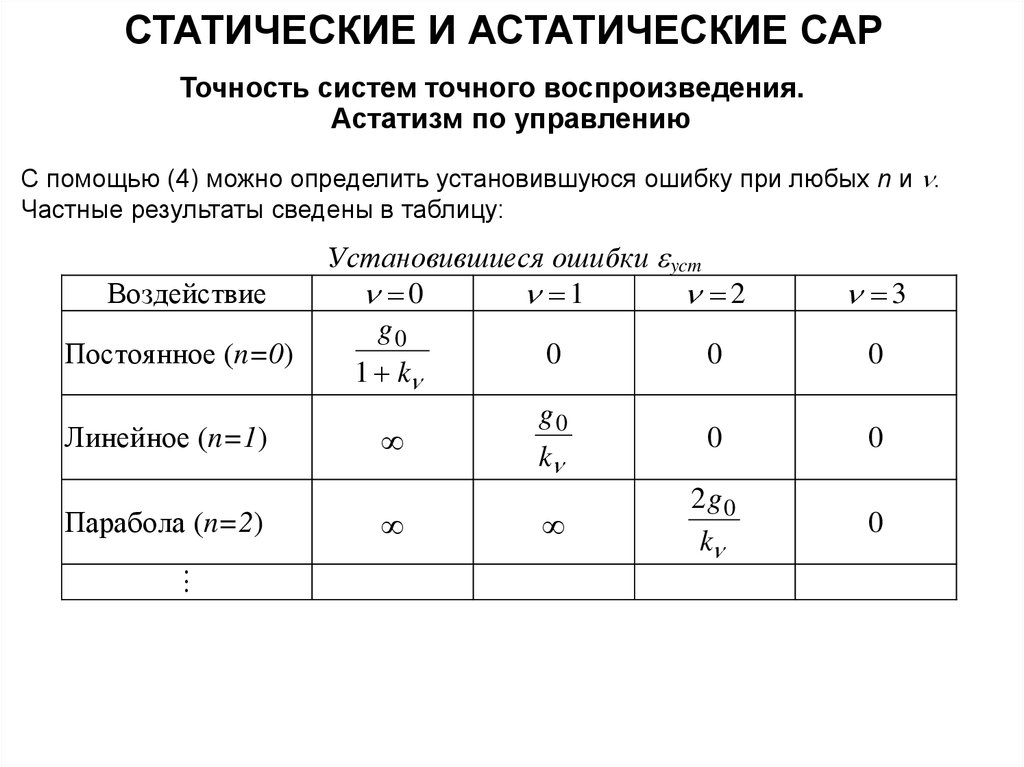
С помощью (4) можно определить установившуюся ошибку при любых n и .
Частные результаты сведены в таблицу:
Воздействие
Постоянное (n=0)
Линейное (n=1)
Парабола (n=2)
Установившиеся ошибки ycm
0
1
2
g0
0
0
1 k
g0
0
k
2g0
k
3
0
0
0

14.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем точного воспроизведения.
Астатизм по управлению
Для астатических систем часто применяют термин добротность системы.
Астатическая система 1-го порядка ( =1) отрабатывает
x(t)
линейно (n=1) изменяющийся сигнал (сигнал, изменяющийся с
V
уст=
постоянной скоростью) с постоянной ошибкой (см. таблицу)
g(t)=Vt
qV
Величина, показывающая отношение скорости изменения
1
x(t)
регулируемой координаты к ошибке в установившемся
t
режиме, называется добротностью САР по скорости,
Отработка астатической
которая численно равна коэффициенту усиления k
системой 1-го порядка линейного
разомкнутой САР:
qV k
управляющего воздействия
Астатическая система 2-го порядка ( =2) отрабатывает сигнал,
x(t)
изменяющийся по параболическому закону (n=2) (сигнал,
a
изменяющийся с постоянным ускорением) с постоянной
уст=
2
at
qa
2
ошибкой (см. таблицу)
g(t)=
2
Величина, показывающая отношение ускорения
x(t)
t
регулируемой координаты к ошибке в
Отработка астатической системой 2-го установившемся режиме, называется добротностью
порядка параболического управляющего
САР по ускорению, которая численно равна
воздействия
коэффициенту усиления k разомкнутой САР:
qa k
Говоря вообще, чем выше добротность q, тем меньше установившаяся ошибка ycm, и
тем точнее отработка системой управляющего воздействия.

15.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем стабилизации.
Астатизм по возмущению
f(p)
Обобщенная
x(p)
структурная схема
W1(p)
Wоб(p)
системы
g(p)
стабилизации
–
Wос(p)
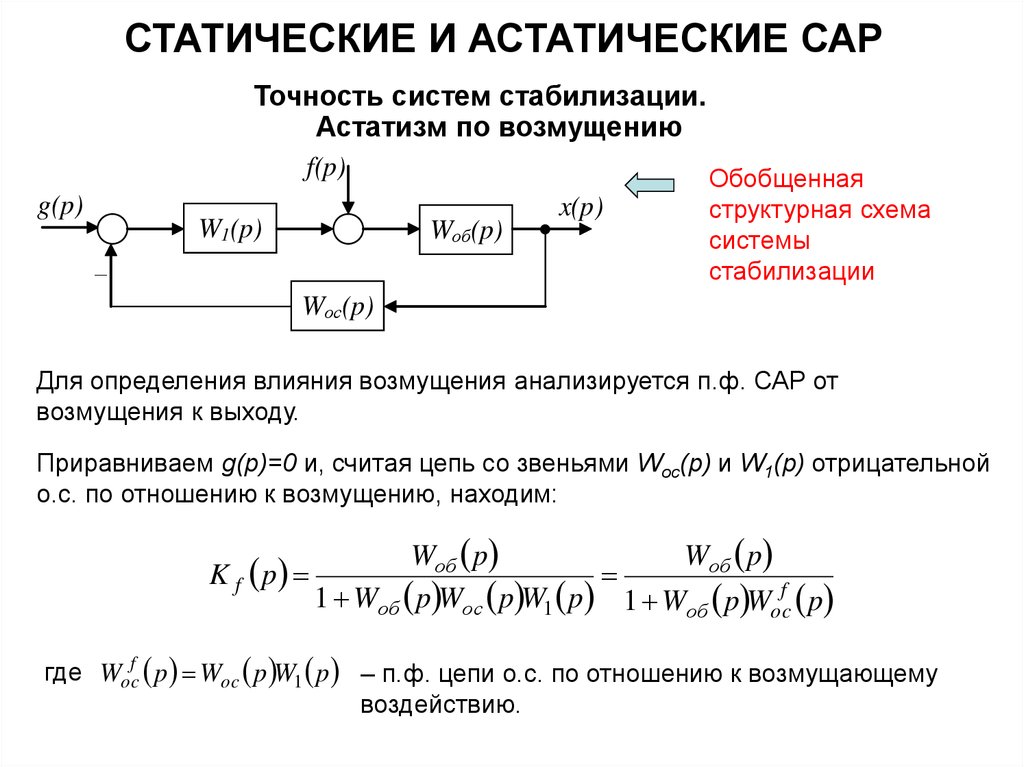
Для определения влияния возмущения анализируется п.ф. САР от
возмущения к выходу.
Приравниваем g(p)=0 и, считая цепь со звеньями Woc(p) и W1(p) отрицательной
о.с. по отношению к возмущению, находим:
K f p
Wоб p
Wоб p
1 Wоб p Wоc p W1 p 1 Wоб p Wocf p
где Wocf p Woc p W1 p – п.ф. цепи о.с. по отношению к возмущающему
воздействию.

16.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем стабилизации.
Астатизм по возмущению
f(p)
Обобщенная
x(p)
структурная схема
W1(p)
Wоб(p)
системы
g(p)
стабилизации
–
Wос(p)
Передаточные функции в знаменателе последнего выражения представим
в виде:
Wоб p
k об
W p ;
об об
p
Wocf
p
k oc
f
p
W
oc oc
p
где об – порядок астатизма п.ф. объекта управления (количество чистых
интеграторов в п.ф. ОУ);
ос – порядок астатизма п.ф. цепи ОС по отношению к возмущению
(количество чистых интеграторов в соответствующей цепи).
Wоб p , Wocf p – соответствующие нормированные п.ф.

17.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Точность систем стабилизации.
Астатизм по возмущению
Тогда искомая п.ф. системы по возмущению
k об
W p
об об
x p
k об p ocWоб p
p
K f p
об oc
k
k
f p 1 об W p oc W f p p
k об k ocWоб p Wocf p
об
oc
p об
p oc
Для исключения влияния возмущения на регулируемую координату (то есть,
для обеспечения астатизма САР по возмущению) необходимо, чтобы
K f 0 0
Из последнего выражения следует, что для этого необходимо, чтобы ос > 0.
Астатизм системы по возмущающему воздействию определяется
порядком астатизма цепи о.с. по отношению к возмущению и не зависит
от порядка астатизма объекта управления.
Говоря иначе, если чистые интеграторы отсутствуют в цепи о.с., то САР
будет статической, независимо от того, есть ли интеграторы в ОУ или нет.

18.

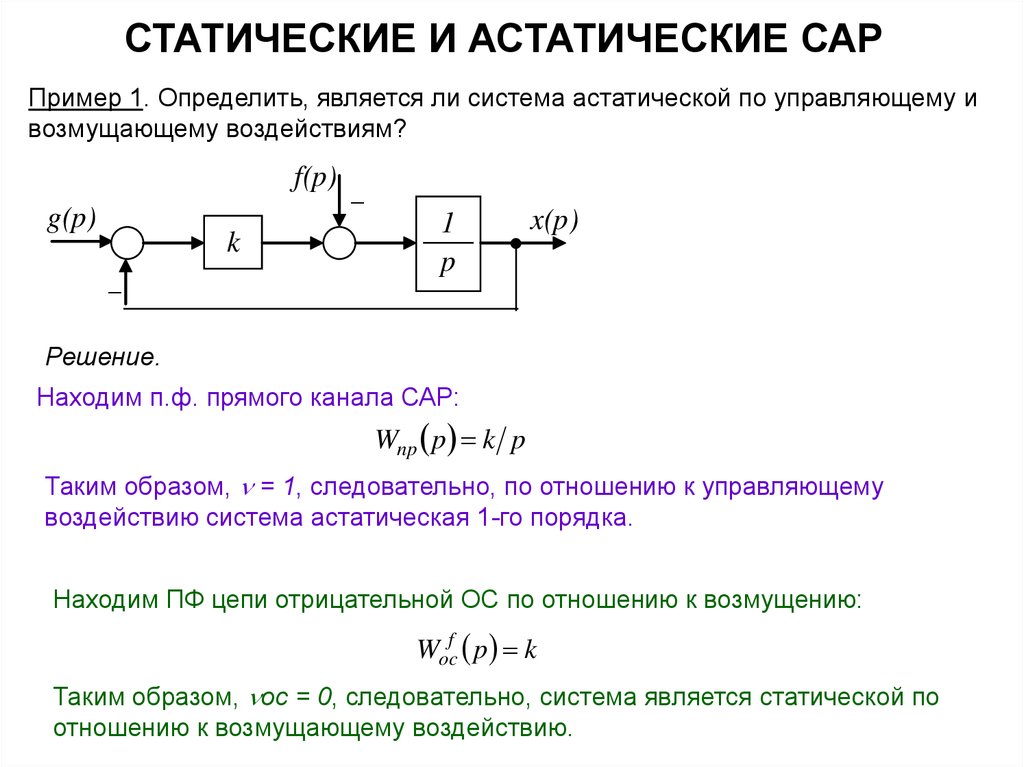
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Пример 1. Определить, является ли система астатической по управляющему и
возмущающему воздействиям?
f(p)
g(p)
k
–
–
1
p
x(p)
Решение.
Находим п.ф. прямого канала САР:
Wnp p k p
Таким образом, = 1, следовательно, по отношению к управляющему
воздействию система астатическая 1-го порядка.
Находим ПФ цепи отрицательной ОС по отношению к возмущению:
Wocf p k
Таким образом, ос = 0, следовательно, система является статической по
отношению к возмущающему воздействию.

19.

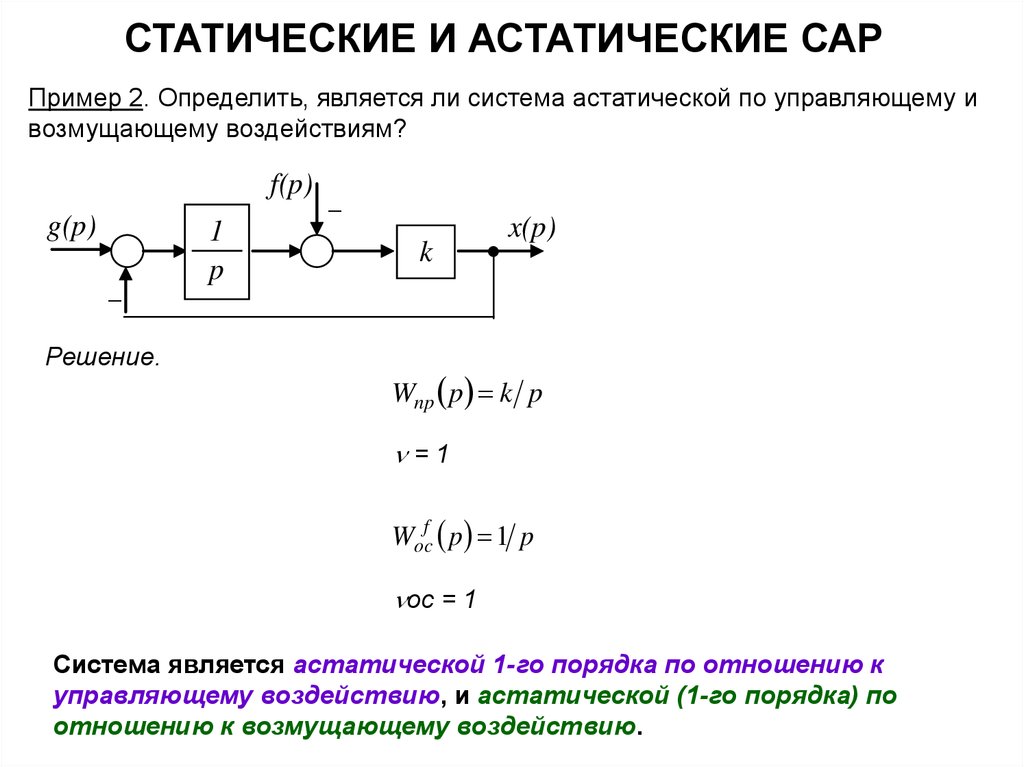
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Пример 2. Определить, является ли система астатической по управляющему и
возмущающему воздействиям?
f(p)
g(p)
–
Решение.
1
p
–
k
x(p)
Wnp p k p
=1
Wocf p 1 p
ос = 1
Система является астатической 1-го порядка по отношению к
управляющему воздействию, и астатической (1-го порядка) по
отношению к возмущающему воздействию.

20.

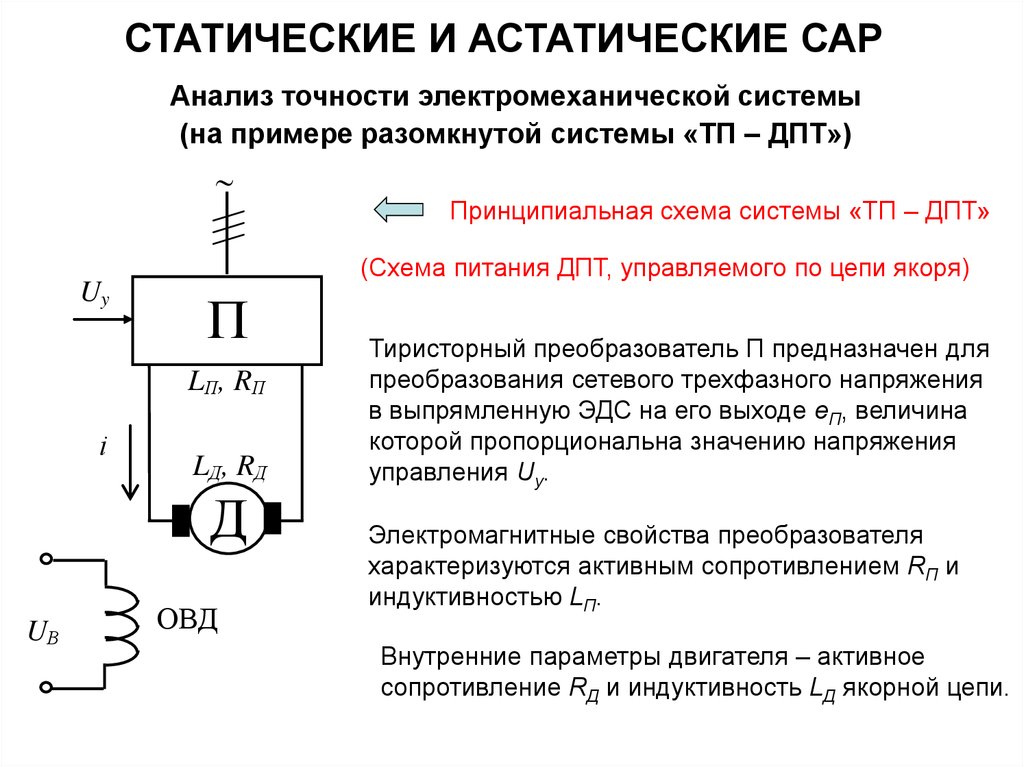
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Uy
(Схема питания ДПТ, управляемого по цепи якоря)
П
LП, RП
і
LД, RД
Д
UВ
Принципиальная схема системы «ТП – ДПТ»
ОВД
Тиристорный преобразователь П предназначен для
преобразования сетевого трехфазного напряжения
в выпрямленную ЭДС на его выходе еП, величина
которой пропорциональна значению напряжения
управления Uy.
Электромагнитные свойства преобразователя
характеризуются активным сопротивлением RП и
индуктивностью LП.
Внутренние параметры двигателя – активное
сопротивление RД и индуктивность LД якорной цепи.

21.

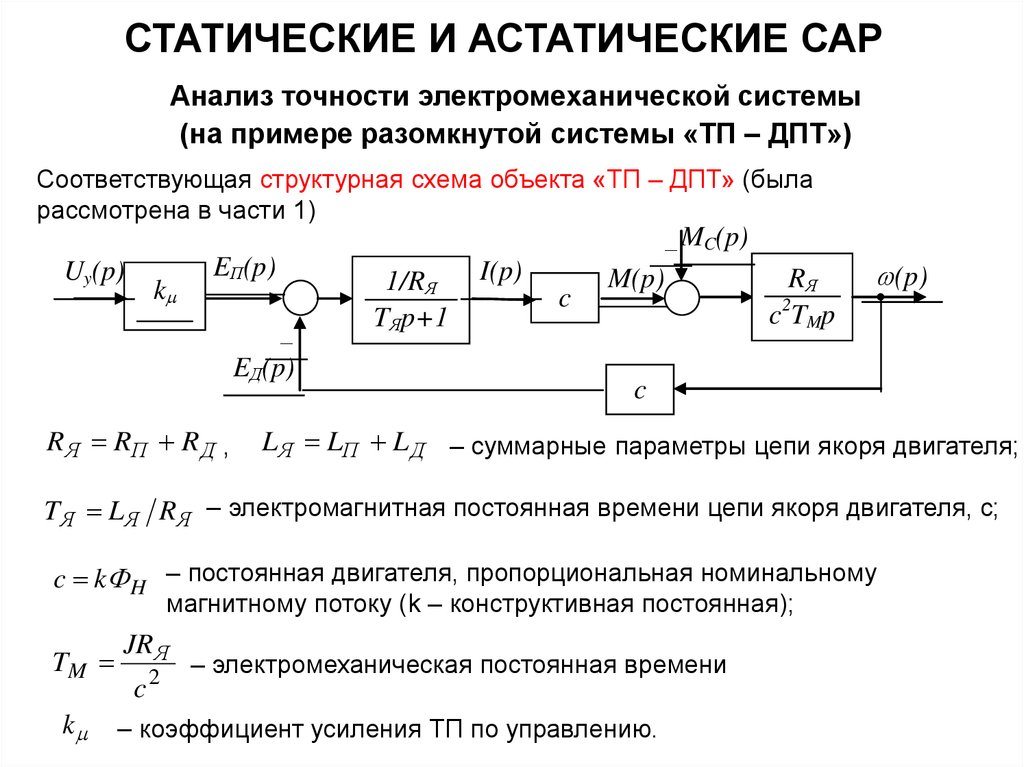
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Соответствующая структурная схема объекта «ТП – ДПТ» (была
рассмотрена в части 1)
Uy(p)
k
EП(p)
–
EД(p)
R Я RП R Д ,
1/RЯ
TЯp+1
– MC(p)
I(p)
c
M(p)
RЯ
c2TMp
(p)
c
LЯ LП L Д – суммарные параметры цепи якоря двигателя;
TЯ LЯ R Я – электромагнитная постоянная времени цепи якоря двигателя, с;
c k H – постоянная двигателя, пропорциональная номинальному
магнитному потоку (k – конструктивная постоянная);
TM
k
JR Я
c
2
– электромеханическая постоянная времени
– коэффициент усиления ТП по управлению.

22.

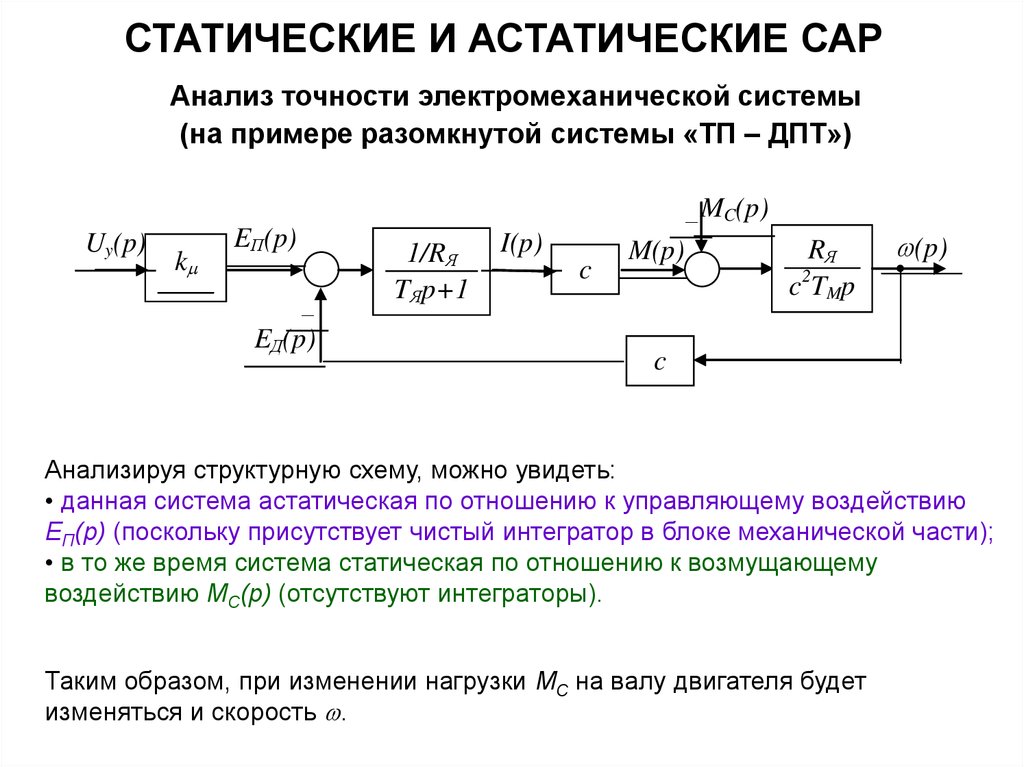
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Uy(p)
k
EП(p)
–
EД(p)
1/RЯ
TЯp+1
– MC(p)
I(p)
c
M(p)
RЯ
c2TMp
(p)
c
Анализируя структурную схему, можно увидеть:
• данная система астатическая по отношению к управляющему воздействию
EП(p) (поскольку присутствует чистый интегратор в блоке механической части);
• в то же время система статическая по отношению к возмущающему
воздействию МC(p) (отсутствуют интеграторы).
Таким образом, при изменении нагрузки МC на валу двигателя будет
изменяться и скорость .

23.

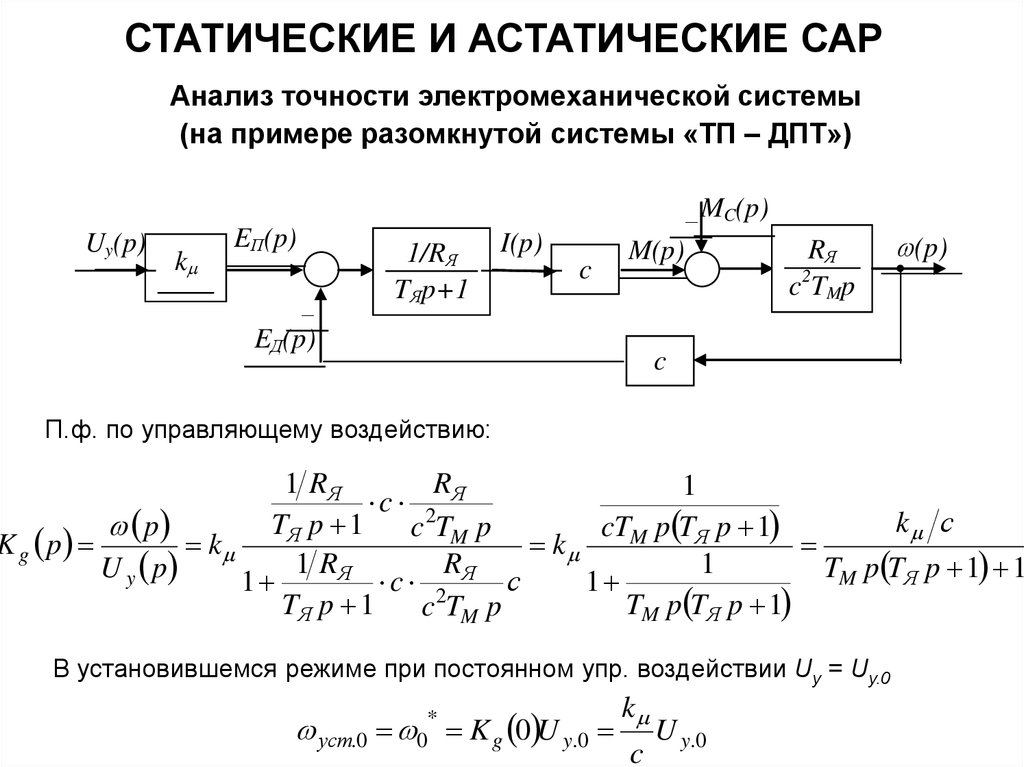
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Uy(p)
k
EП(p)
–
1/RЯ
TЯp+1
– MC(p)
I(p)
c
M(p)
EД(p)
RЯ
c2TMp
(p)
c
П.ф. по управляющему воздействию:
1 RЯ
R
1
c 2 Я
k с
TЯ p 1
p
c TM p
cTM p TЯ p 1
K g p
k
k
1
R
R
1
U y p
TM p TЯ p 1 1
Я
1
c 2 Я с
1
TЯ p 1
TM p TЯ p 1
c TM p
В установившемся режиме при постоянном упр. воздействии Uy = Uy.0
уст.0 0*
K g 0 U y.0
k
c
U y.0

24.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Uy(p)
k
EП(p)
1/RЯ
TЯp+1
–
– MC(p)
I(p)
c
EД(p)
M(p)
RЯ
c2TMp
(p)
c
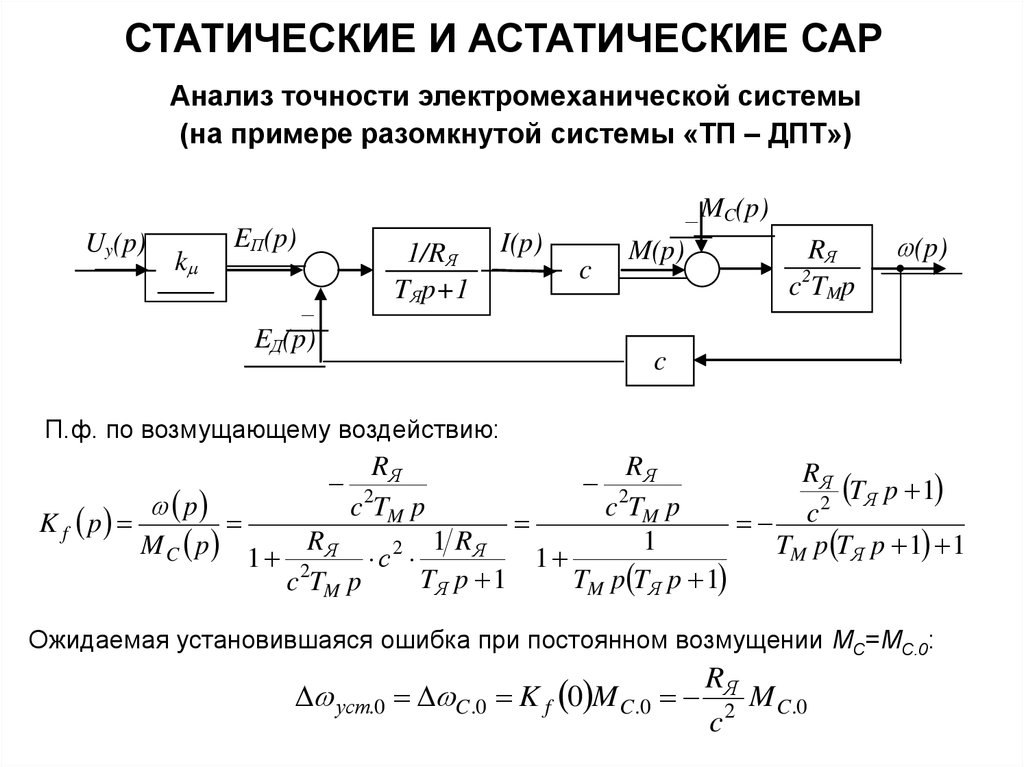
П.ф. по возмущающему воздействию:
RЯ
RЯ
TЯ p 1
2
p
c 2TM p
K f p
c
1
M C p 1 RЯ с 2 1 RЯ
TM p TЯ p 1 1
1
TЯ p 1
TM p TЯ p 1
c 2TM p
RЯ
c 2TM p
Ожидаемая установившаяся ошибка при постоянном возмущении MC=MC.0:
уст.0 C.0 K f 0 M C.0
RЯ
M C.0
2
c

25.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Уравнение статической характеристики при произвольных постоянных
значениях управляющего и возмущающего воздействий:
уст уст C
*
k
c
Uy
Семейство статических
характеристик – прямые,
параллельные друг другу
(т.е. статизм
характеристик одинаков).
Uy>Uy.0
0
*
RЯ
MC
2
c
Uy=Uy.0
C.0
Uy<Uy.0
MC
MC.0

26.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
Характер процессов в динамике
(t)
уст.0
Uy.0
MС.0
Uy(t)
MC(t) t
При подаче на ТП
некоторого
управляющего
воздействия Uy = Uy.0
С.0 двигатель без нагрузки
на валу каким-то
образом разгонится до
заданной скорости
уст.0 k U y.0 c
После скачкообразного приложения возмущающего воздействия (наброса
нагрузки) MC = MC.0 будет иметь место ошибка регулирования, которая после
затухания переходного процесса будет равна
2
C .0 RЯ M C .0 c
Примечания.
1) Характер переходного процесса определяется полюсами системы (двигателя).
2) Сравнивая п.ф. Kg(p) и Kf(p), видно, что знаменатели, т.е., характеристические полиномы
двигателя, остаются одинаковыми вне зависимости от того, что является входом, и что – выходом.
Этот вывод можно распространить на любую замкнутую САР: характеристический полином G(p) не
зависит от того, на основании какой п.ф. он записан.

27.

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Анализ точности электромеханической системы
(на примере разомкнутой системы «ТП – ДПТ»)
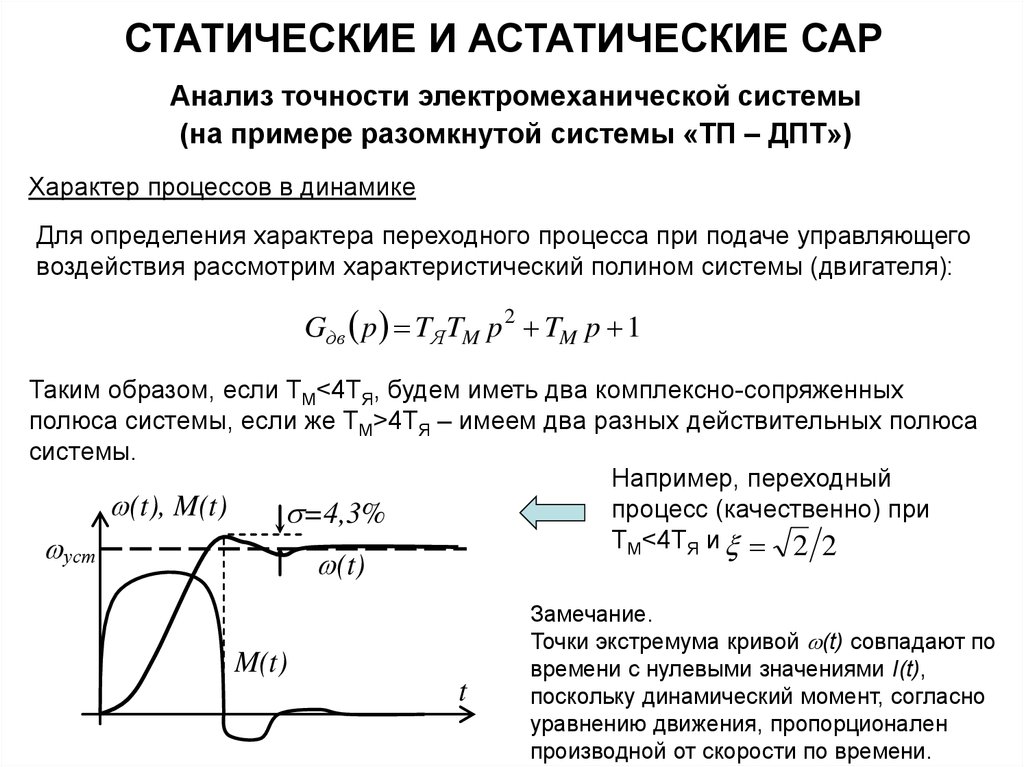
Характер процессов в динамике
Для определения характера переходного процесса при подаче управляющего
воздействия рассмотрим характеристический полином системы (двигателя):
Gдв p TЯ TM p 2 TM p 1
Таким образом, если TM<4TЯ, будем иметь два комплексно-сопряженных
полюса системы, если же TM>4TЯ – имеем два разных действительных полюса
системы.
Например, переходный
(t), M(t)
процесс (качественно) при
=4,3%
TM<4TЯ и 2 2
(t)
уст
M(t)
t
Замечание.
Точки экстремума кривой (t) совпадают по
времени с нулевыми значениями I(t),
поскольку динамический момент, согласно
уравнению движения, пропорционален
производной от скорости по времени.