Похожие презентации:
Probability Concepts
1. Probability Concepts
By Dias Kulzhanov2. Definition of Probability
Probability is a number between 0 and 1 that describes the chance
that a stated event will occur.
An event is a specified set of outcomes of a random variable.
Mutually exclusive events can occur only one at a time. Exhaustive
events cover or contain all possible outcomes.
The two defining properties of a probability are, first, that 0 ≤ P(E) ≤ 1
where P(E) denotes the probability of an event E), and second, that
the sum of the probabilities of any set of mutually exclusive and
exhaustive events equals 1.
A probability estimated from data as a relative frequency of
occurrence is an empirical probability. A probability drawing on
personal or subjective judgment is a subjective probability. A
probability obtained based on logical analysis is an a priori
probability.
3. Probability Stated as Odds
• Odds for E = P(E)/[1 − P(E)]. The odds for E are the probability of Edivided by 1 minus the probability of E. Given odds for E of “a to b,”
the implied probability of E is a/(a + b).
In the example, the statement that the odds for the company’s EPS
for FY2014 beating $0.69 are 1 to 7 means that the speaker believes
the probability of the event is 1/(1 + 7) = 1/8 = 0.125.
• Odds against E = [1 − P(E)]/P(E), the reciprocal of odds for E. Given
odds against E of “a to b,” the implied probability of E is b/(a+ b).
The statement that the odds against the company’s EPS for FY2014
beating $0.69 are 15 to 1 is consistent with a belief that the
probability of the event is 1/(1 + 15) = 1/16 = 0.0625.
4. Unconditional and conditional probability
• The probability in answer to the straightforward question “What isthe probability of this event A?” is an unconditional probability,
denoted P(A). Unconditional probability is also frequently referred to
as marginal probability.
• Contrast the question “What is the probability of A?” with the
question “What is the probability of A, given that B has occurred?”
The probability in answer to this last question is a conditional
probability, denoted P(A | B) (read: “the probability of A given B”).
5. Multiplication and Additional Rules of probability
6. The Total Probability Rule
7. Expected value
Variance of expected valueConditional expected values
8. Portfolio Expected Return
9.
Portfolio variance of return10.
11. Covariance and Correlation
• Covariance is a measure of the co-movement between randomvariables
• The calculation of covariance in a forward-looking sense requires
the specification of a joint probability function, which gives the
probability of joint occurrences of values of the two random
variables.
• Correlation is a number between −1 and +1 that measures the comovement (linear association) between two random variables.









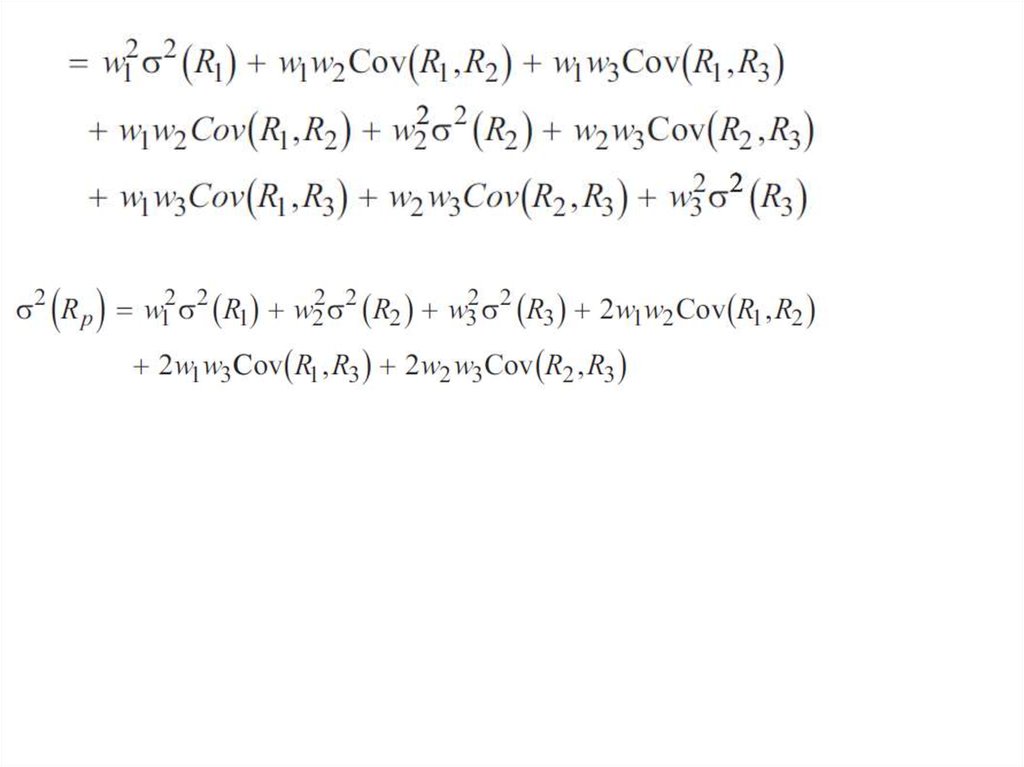




 Математика
Математика








