Похожие презентации:
Потребительское поведение
1. курс: «МИКРОЭКОНОМИКА – 2» Тема 1. Теория потребительского выбора Лекция 1. Потребительское поведение
Доц., к.э.н. Киреев Андрей владимирович2. Предпочтения потребителя
Предпочтения потребителя описываются тройкой бинарныхотношений (≻, ≿,∽), заданных на множестве потребительских
наборов.
Отношения предпочтения связаны между собой следующим
образом:
x ≿ y тогда и только тогда, когда неверно, что y ≻
x
(что эквивалентно, x ≻ y тогда и только тогда, когда неверно,
что y ≿ x)
(1)
x ∽ y тогда и только тогда, когда как x ≻ y,
так и y ≻ x, неверны
(2)
x ∽ y тогда и только тогда, когда x ≿ y и y ≿ x
(3)
3. Аксиоматика ординалистской теории
• Аксиома полной (совершенной)упорядоченности или сравнимости.
Аксиома транзитивности.
• Аксиома непрерывности
• Аксиома рефлексивности
• Аксиома ненасыщения.
• Аксиома предпочтения среднего набора
• Аксиома о независимости потребителя
4. Свойства предпочтений потребителя (рациональные предпочтения)
5. Дополнительные понятия
6. Свойства предпочтений потребителя
Аксиома(Сильная форма)
7. Свойства предпочтений потребителя (cоответствующие экономической и житейской интуиции)
8. Свойства предпочтений потребителя
9. Теорема Дебре (в слабой форме)
10. Доказательство (продолжение)
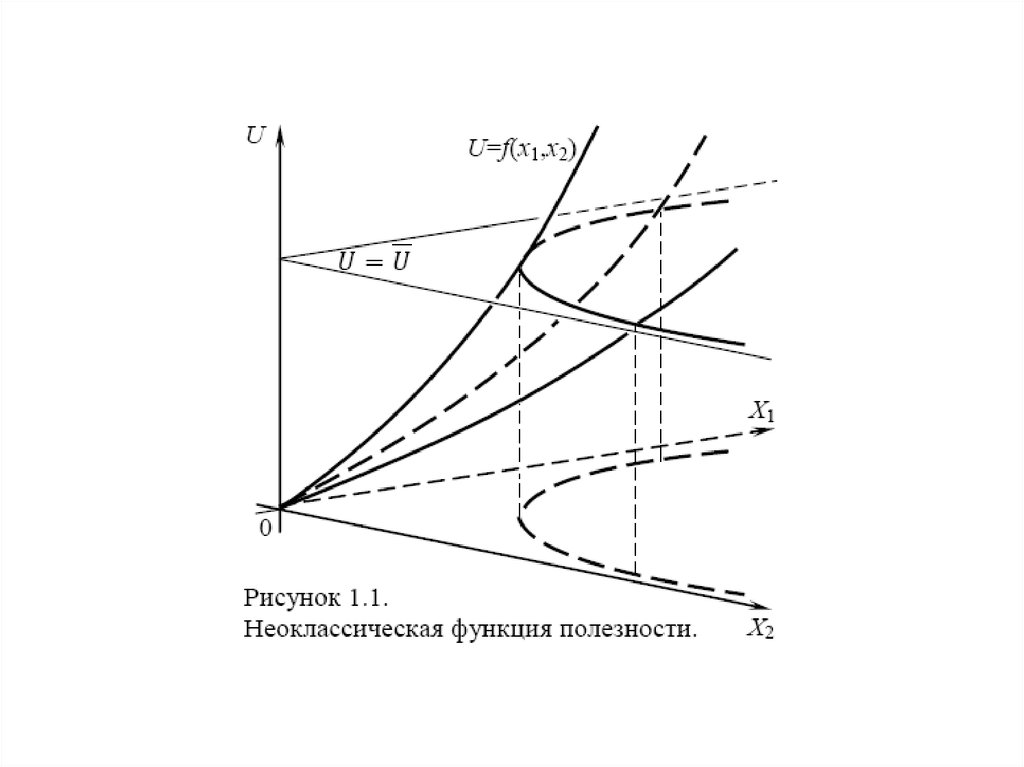
11. Свойства функции полезности
12.
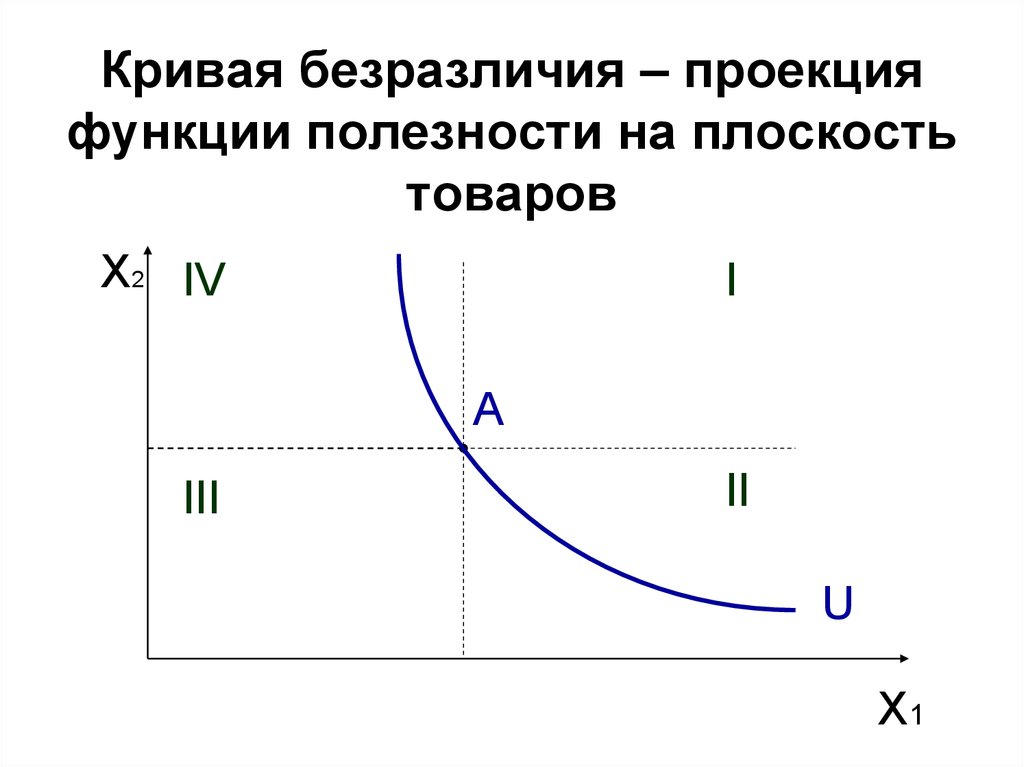
13. Кривая безразличия – проекция функции полезности на плоскость товаров
X2 IVI
A
III
II
U
X1
14. Кривые безразличия
IC (indifference curve) – это множество точек(наборов товаров) одинаково полезных для
потребителя, т.е. потребителю безразлично,
какой из этих наборов выбрать с точки зрения
получаемой полезности.
Совокупность кривых безразличия, т.е. если
заполнить
плоскость
товарных
наборов
кривыми безразличия, получим карту кривых
безразличия.
К.Б. – лежащие выше и правее другой кривой, представляют
предпочтительные для данного потребителя наборы;
- имеют отрицательный наклон;
- никогда не пересекаются;
- может быть проведена через любую точку пространства товаров.
более
15.
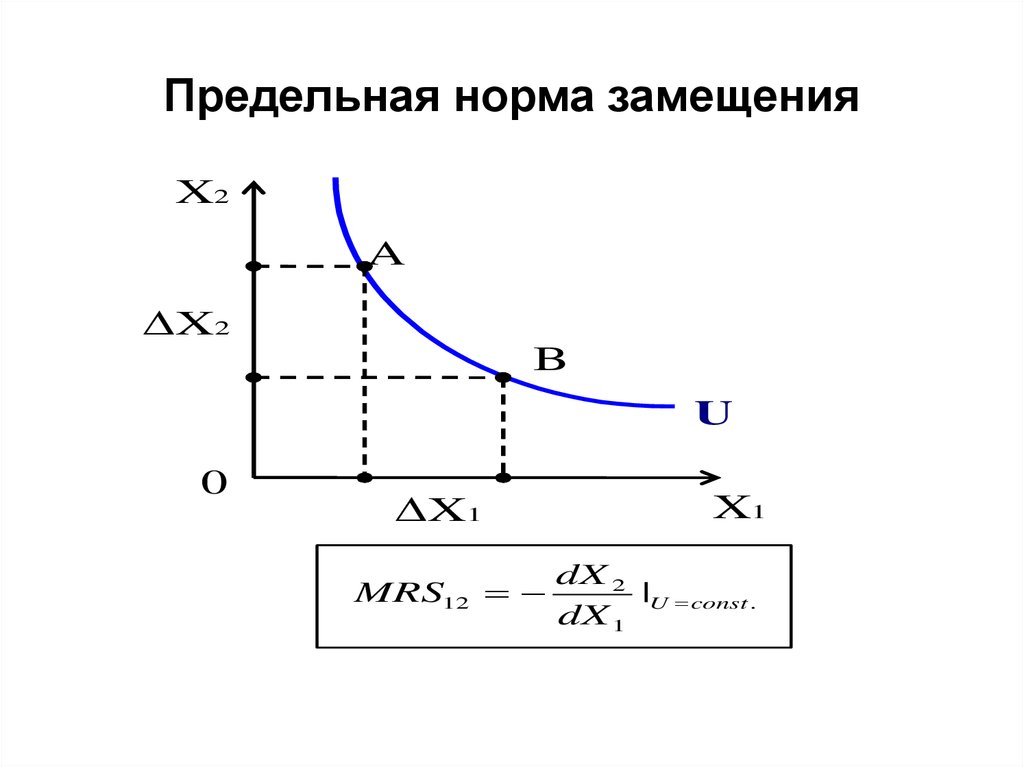
Предельная норма замещенияX2
A
X2
B
U
0
X1
MRS12
X1
dX 2
|U const .
dX 1
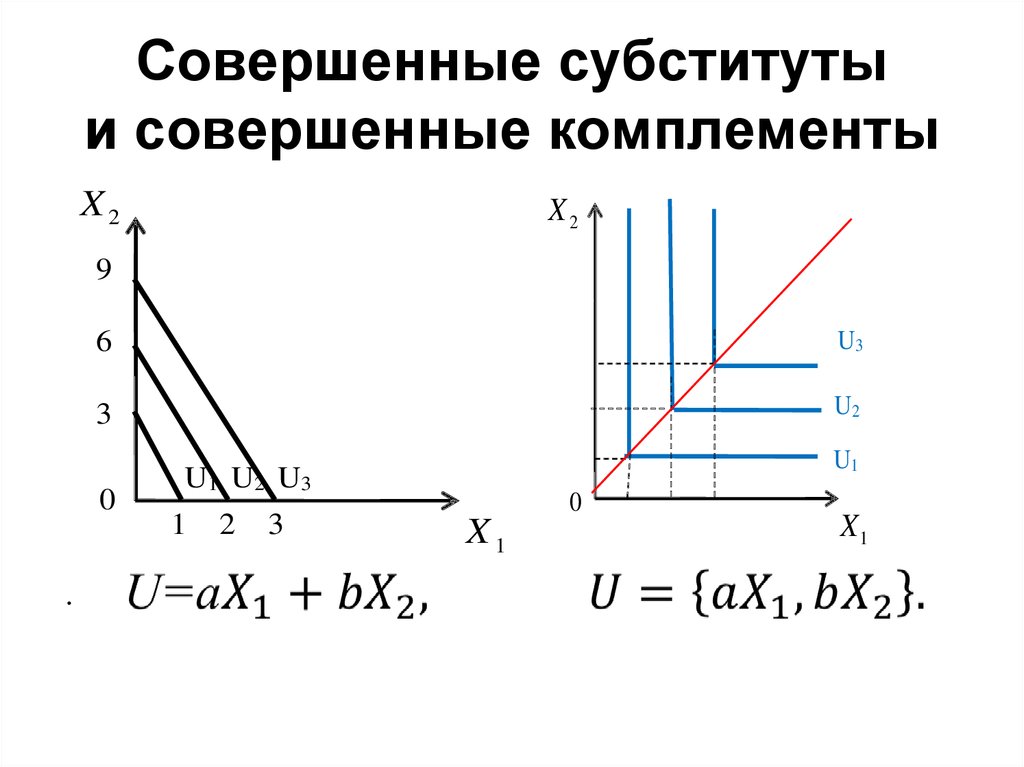
16. Совершенные субституты и совершенные комплементы
X2X2
9
6
U3
3
U2
0
.
U1
U1 U2 U3
1
2
3
0
X1
X1
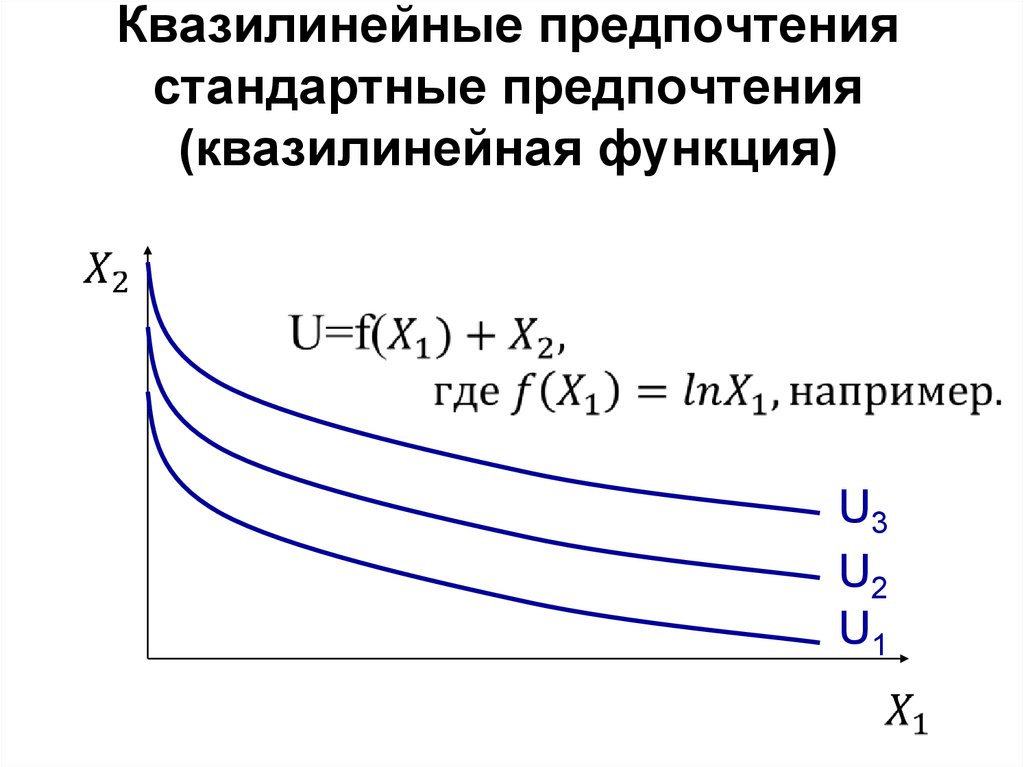
17. Квазилинейные предпочтения стандартные предпочтения (квазилинейная функция)
U3U2
U1
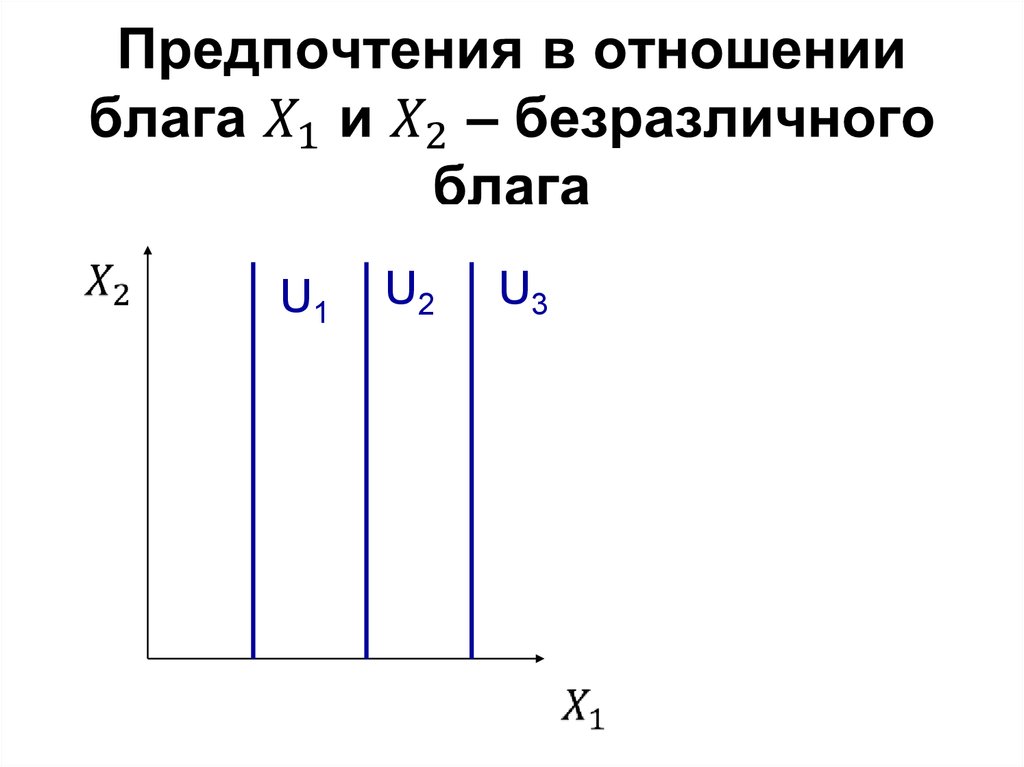
18. Предпочтения в отношении блага X_1 и X_2 – безразличного блага
U1U2
U3
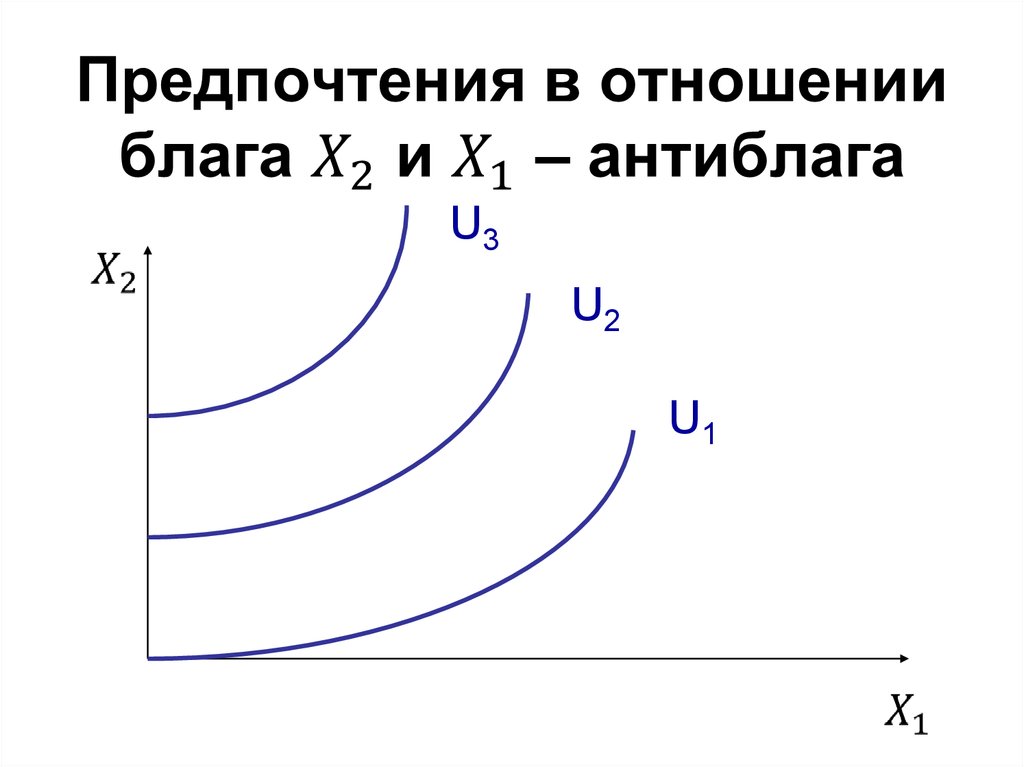
19. Предпочтения в отношении блага X_2 и X_1 – антиблага
U3U2
U1
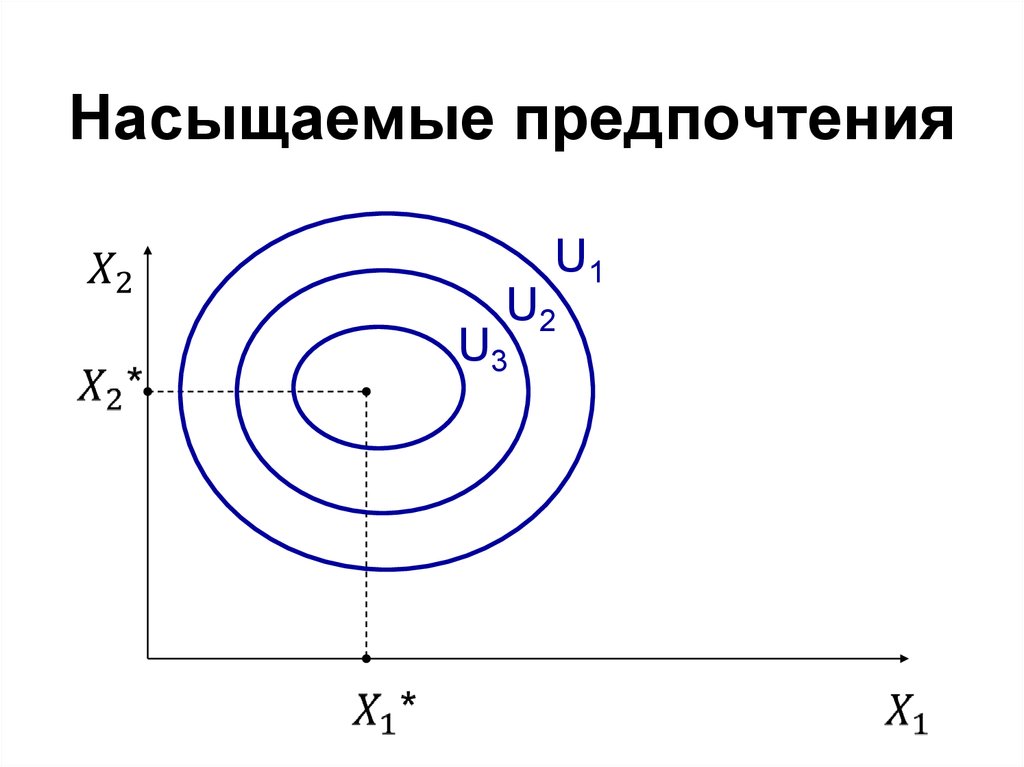
20. Насыщаемые предпочтения
U1U2
U3
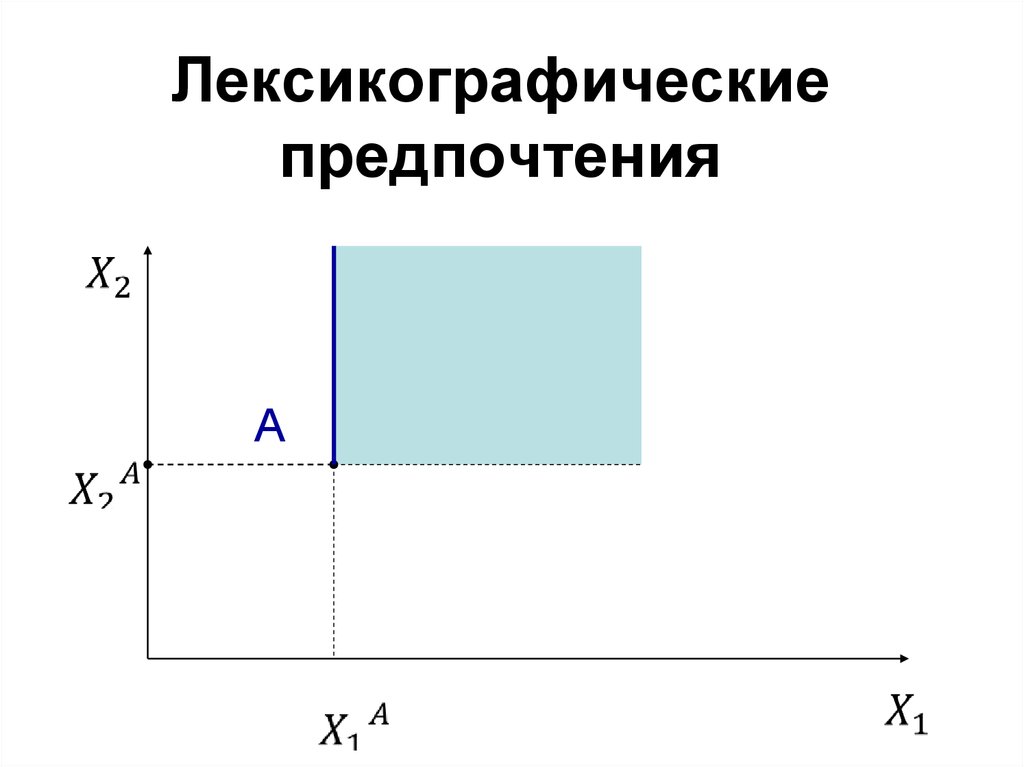
21. Лексикографические предпочтения
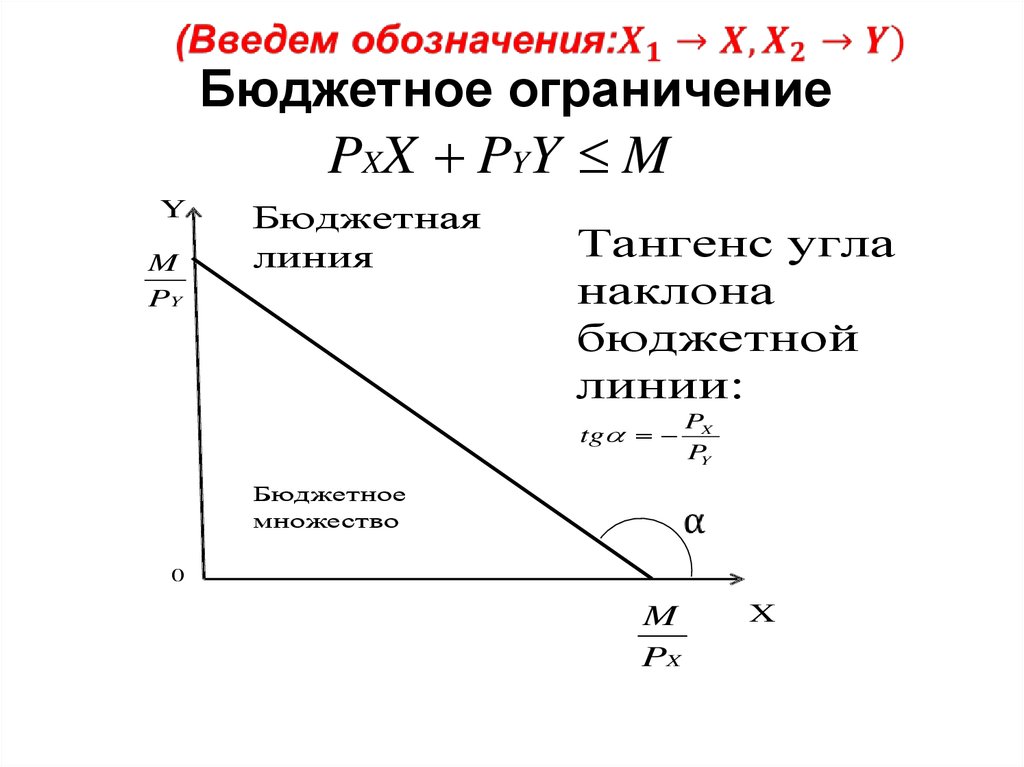
A22. Бюджетное ограничение
PXX PYY MY
M
PY
Бюджетная
линия
Тангенс угла
наклона
бюджетной
линии:
tg
PX
PY
Бюджетное
множество
0
M
PX
X
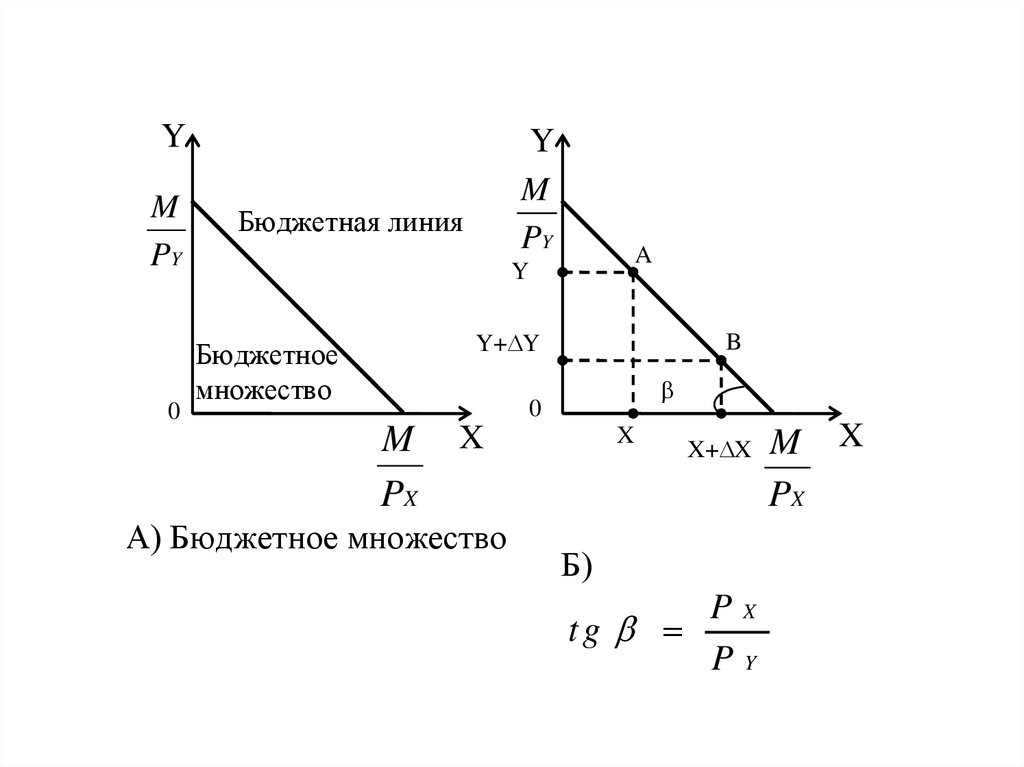
23.
YM
PY
0
Y
M
PY
Бюджетная линия
A
Y
B
Y+ Y
Бюджетное
множество
0
M
PX
X
А) Бюджетное множество
X
X+ X
Б)
PX
tg
PY
M X
PX
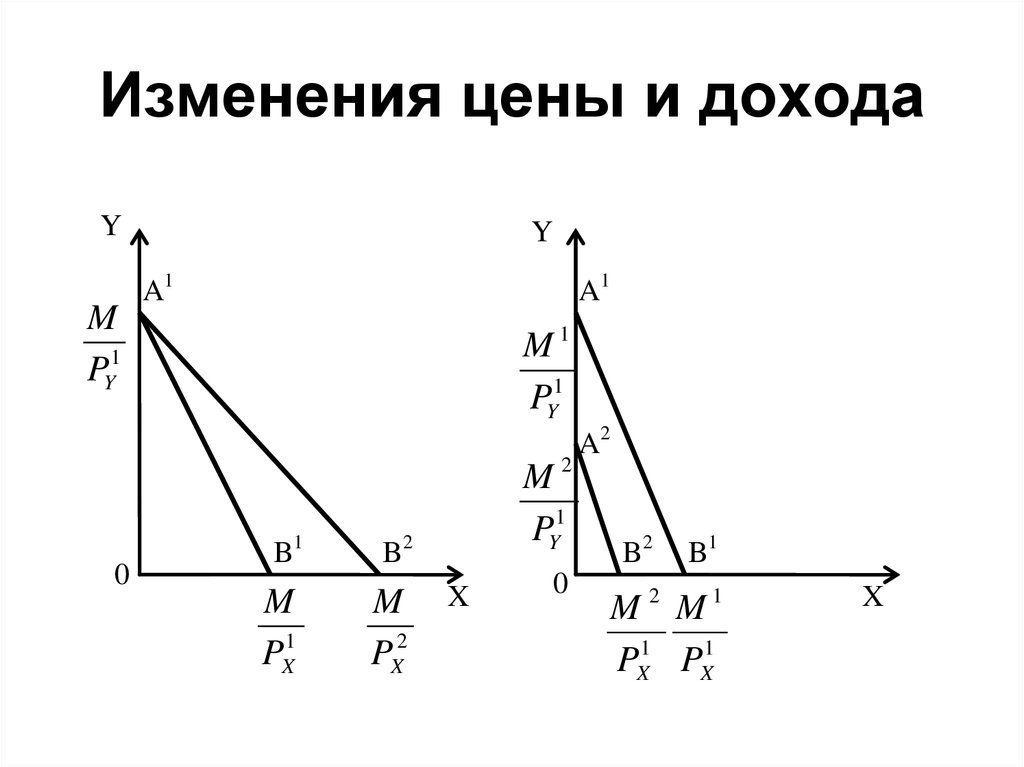
24. Изменения цены и дохода
YM
PY1
0
Y
A1
A1
M1
PY1
B1
B2
M
PX1
M
PX2
M2
PY1
X
0
A2
B2
B1
M 2 M1
PX1 PX1
X
25. Бюджетное ограничение при выборе с начальным запасом
PX X * PY Y * m PX Wx PY W yили :
PX (Wx X *) PY (Wy Y * ) 0
26.
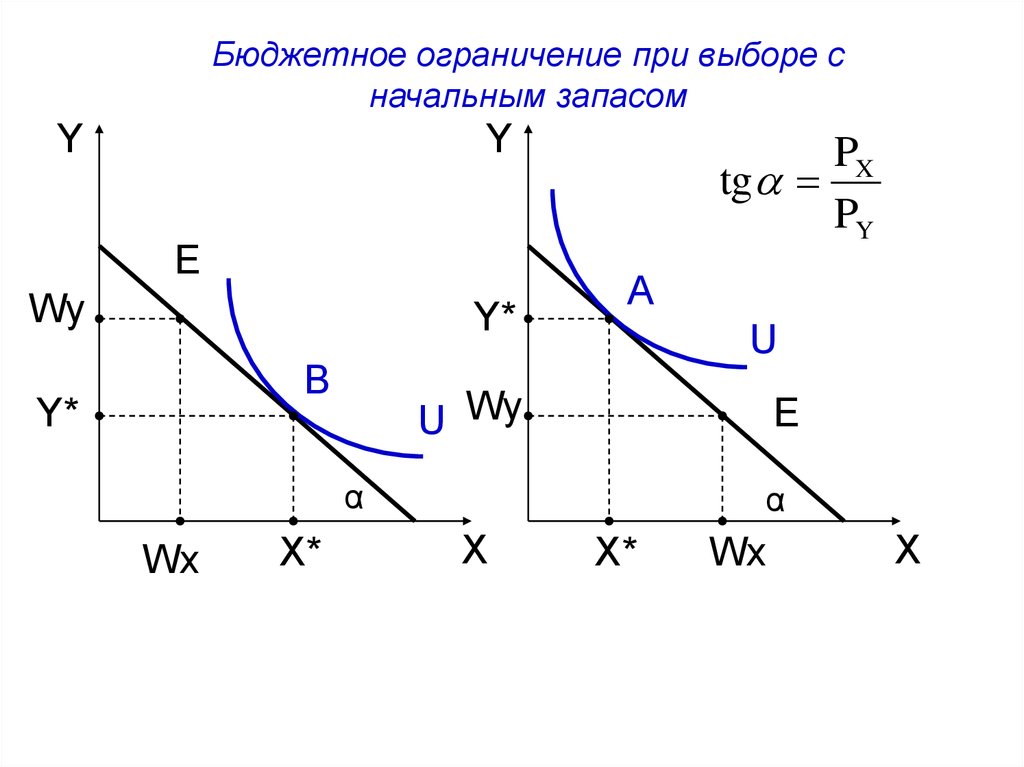
Бюджетное ограничение при выборе сначальным запасом
Y
Y
Е
Wy
Y*
В
Y*
PX
tg
PY
А
U
Е
U Wy
α
Wx
X*
α
X
X*
Wx
X
27.
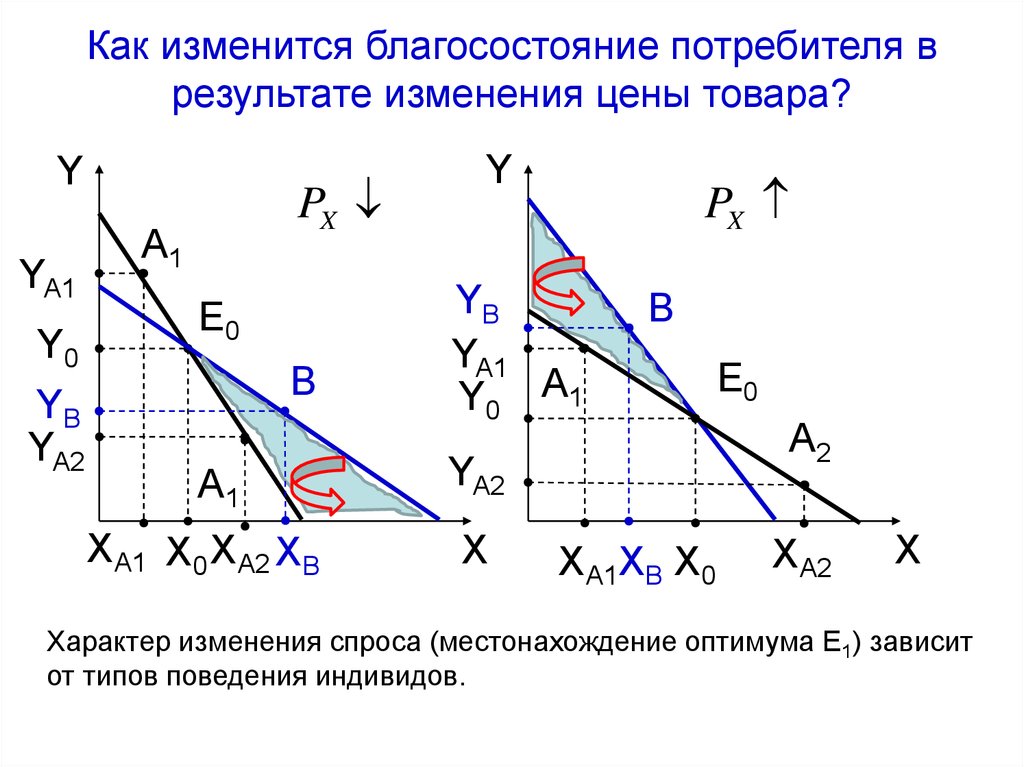
Как изменится благосостояние потребителя врезультате изменения цены товара?
Y
YA1
Y0
YB
YA2
PX
А1
E0
B
А1
XA1 X0 XA2 XB
Y
PX
YB
YA1
Y0 A1
B
YA2
X
XA1XB X0
E0
A2
XA2
X
Характер изменения спроса (местонахождение оптимума E1) зависит
от типов поведения индивидов.
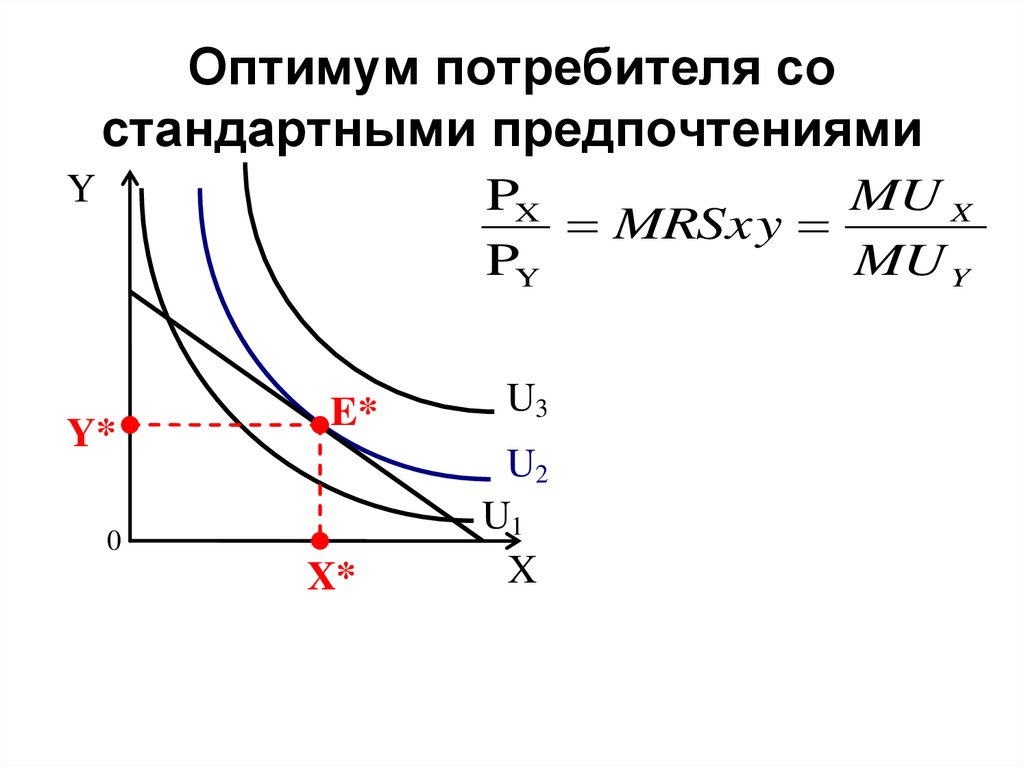
28. Оптимум потребителя со стандартными предпочтениями
YPX
MU X
MRSxy
PY
MU Y
Y*
E*
0
X*
U3
U2
U1
X
29. Двойственная природа потребительского выбора
Оптимальный выбор набора товаров X иY может анализироваться как проблема
максимизации уровня полезности при
заданном бюджетном ограничении
(прямая задача), но и как проблема
минимизации бюджетных расходов при
заданном уровне полезности
(двойственная задача).
D. McFadden, S. Winter
Lecture Notes on Consumer Theory, 1968, California, Berkeley
30.
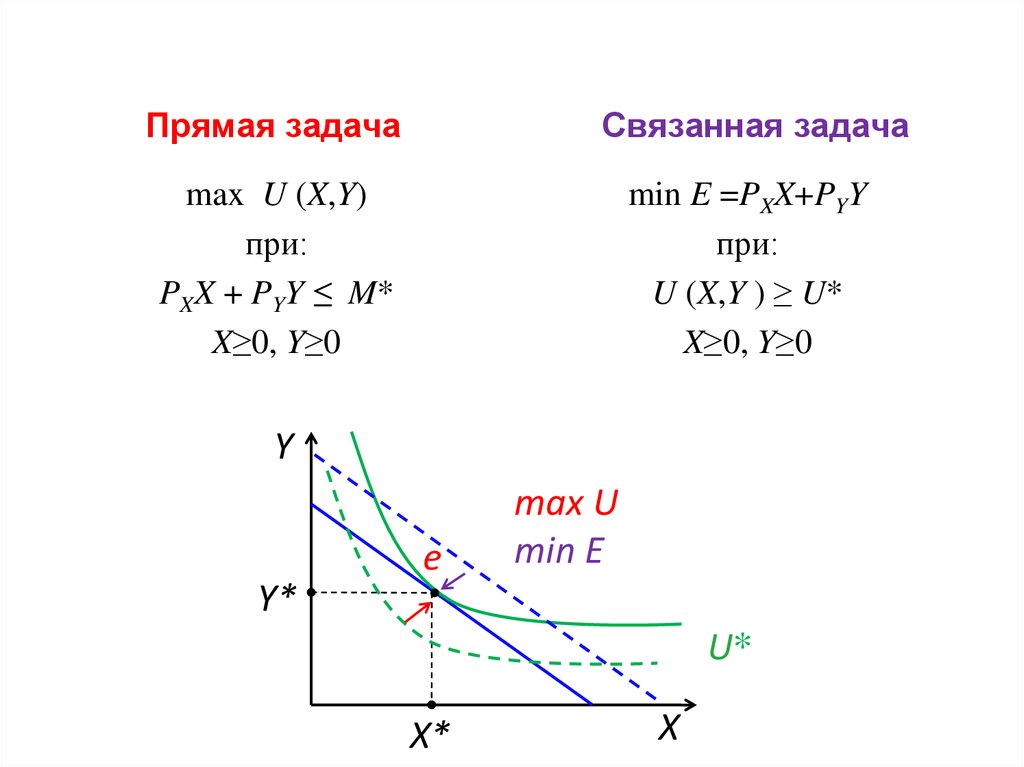
Прямая задачаСвязанная задача
max U (X,Y)
при:
PXX + PYY ≤ M*
X≥0, Y≥0
min E =PXX+PYY
при:
U (X,Y ) ≥ U*
X≥0, Y≥0
Y
е
max U
min E
Y*
U*
X*
X
31. Нахождение внутреннего оптимума методом Лагранжа
U ( X , Y ) maxM PX X PY Y
L U ( X , Y ) ( PX X PY Y M )
U ( X , Y )
L
PX 0
X
X
U ( X , Y )
L
PY 0
Y
Y
L
PX X PY Y M 0
MU X
MU Y
PX
PY
32. Условие Куна-Таккера для функции двух переменных
)33. Неявная (косвенная) функция полезности - это функция максимального значения полезности от цен товаров и дохода. René Roy, De
Неявная (косвенная) функция полезности это функция максимального значения полезности отцен товаров и дохода.
René Roy, De l'utilité: Contribution à la théorie des choix. Hermann, Paris
(1942)
max U (X,Y)
PX X+PYY ≤ M, X ≥ 0, Y ≥0
↓
X = dX (PX ,PY , M)
Y = dY (PX,PY , M)
↓
подстановка X и Y в U (X,Y):
U(X, Y )=V(PX, PY, M)
Прямая задача
↓
Индивидуальные функции
некомпенсированного
(маршаллианского)
спроса
↓
Неявная (косвенная)
функция полезности
34. Применение неявной функции полезности (для изучения влияния налогообложения )
Пусть U(X,Y)=X0,5Y0,5, М=2, РХ=0,25, PY=1, и требуется оценитьпоследствия поштучного (tX=0,25) и аккордного (T=0,5)
налогообложения для потребителя и госбюджета. Тогда:
M
M
X
;Y
2 PX
2 PY
t X 0,25 PX 0,25 0,25 0,5 X
V ( PX , PY , M )
Vt X
2
2 t X 0,25 2 0,5
2 0,5
M
2
2
0,5
0,5
2( PX PY )
2(0,25 1)
2
1,41
0,5
2(0,5 1)
T 0,5 M 2 0,5 1,5 VT
1,5
1,5
0,5
2(0,25 1)
Вывод: при одинаковых поступлениях в бюджет (tX=T=0,5) аккордный
налог в меньшей степени снижает благосостояние потребителя, т.к.
1,5>1,41.
35. Функция расходов – это функция минимальных расходов, которые должен осуществить потребитель, чтобы при заданных ценах достичь
данного уровня полезностиmin E=PX X+PYY
U (X,Y) ≥ U*, X≥0, Y≥0
↓
X*=hX(PX ,PY ,U )
Y*=hY(PX,PY ,U )
↓
подстановка X* и Y* в E(X,Y) :
PX hX(PX,PY,U) +PY hY(PX,PY ,U )=
=E(PX, PY,U)
Обратная задача
↓
Функции
компенсированного
(хиксианского) спроса
↓
Функция расходов



















 Экономика
Экономика








