Электростатика. (Лекция 11)

1.

ЭЛЕКТРОСТАТИКА
ПЛАН ЛЕКЦИИ
1. Проводники в электростатическом поле.
2. Электроемкость уединенного проводника.
3. Конденсаторы.
4. Энергия электрического поля:
энергия взаимодействия системы точечных зарядов;
энергия системы объемно распределенных зарядов;
энергия системы поверхностно распределенных зарядов;
энергия системы линейно распределенных зарядов;
энергия заряженного проводника.
энергия заряженного конденсатора.
1

2.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Электрические свойства среды определяются реакцией заряженных
частиц на внешнее электрическое поле
Под действием внешнего поля возможно
перемещение зарядов в объеме вещества.
неограниченное
Такие заряды называются свободными, в результате их движения
возникает электрический ток
Вещества, у которых под действием электрического поля
преобладающим является процесс неограниченного движения зарядов,
называются проводниками.
Типичные проводники – это металлы.
2

3.

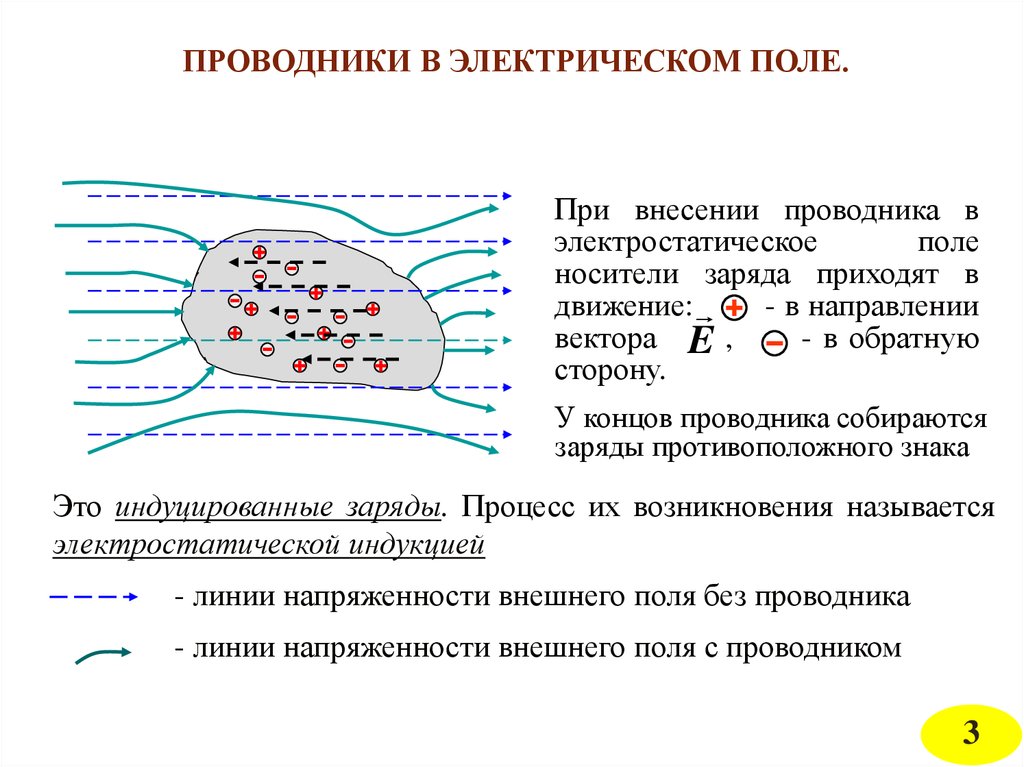
ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
При внесении проводника в
электростатическое
поле
носители заряда приходят в
движение:
- в направлении
вектора E ,
- в обратную
сторону.
У концов проводника собираются
заряды противоположного знака
Это индуцированные заряды. Процесс их возникновения называется
электростатической индукцией
- линии напряженности внешнего поля без проводника
- линии напряженности внешнего поля с проводником
3

4.

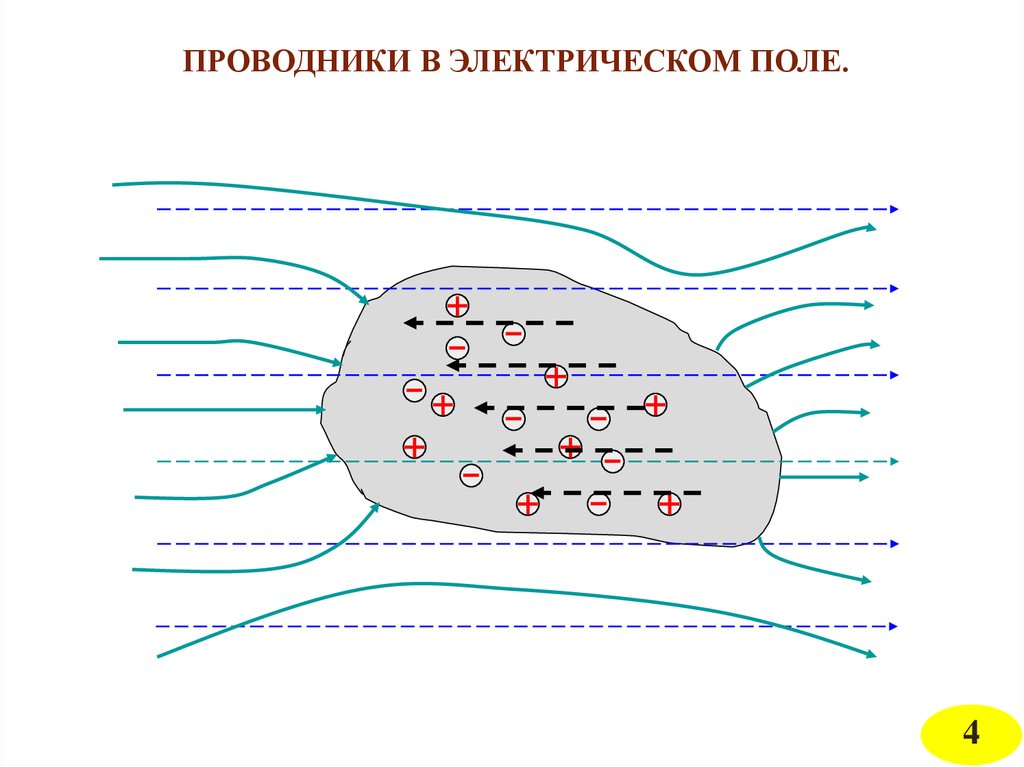
ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
4

5.

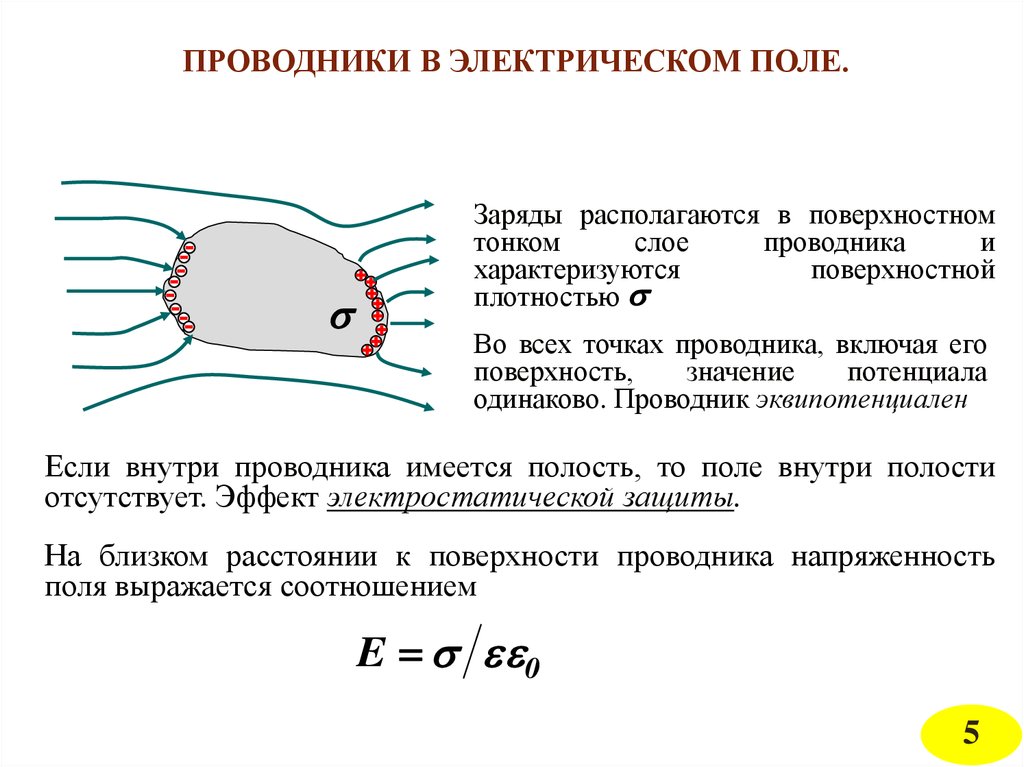
ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Заряды располагаются в поверхностном
тонком
слое
проводника
и
характеризуются
поверхностной
плотностью
Во всех точках проводника, включая его
поверхность,
значение
потенциала
одинаково. Проводник эквипотенциален
Если внутри проводника имеется полость, то поле внутри полости
отсутствует. Эффект электростатической защиты.
На близком расстоянии к поверхности проводника напряженность
поля выражается соотношением
E 0
5

6.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Электроемкость уединенного проводника.
Заряд
распределяется по поверхности проводника так, чтобы
напряженность поля внутри проводника была равна нулю, а потенциал
во всех точках проводника оставался постоянным
Если проводнику сообщить дополнительный заряд, то он
распределяется по его поверхности подобно предыдущему заряду
Это справедливо, если проводник уединенным, т.е. он удален на такое
расстояние от окружающих тел, что эти тела не влияют на
распределение зарядов на поверхности проводника и на его поле
Потенциал уединенного проводника пропорционален заряду
g C
C - электрическая емкость уединенного проводника
Электрическая емкость уединенного проводника является мерой
его способности накапливать электрический заряд.
6

7.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Электроемкость уединенного проводника.
Чем больше емкость проводника, тем больший заряд способен он
удерживать при заданном .
Электрическая емкость численно равна заряду, сообщение которого
проводнику повышает его потенциал на единицу
C g ,
или
C dg d
Единица электроемкости – фарад. В СИ за 1 фарад принимается
емкость такого проводника, потенциал которого изменяется на 1
вольт при сообщении проводнику заряда в 1 Кулон.
Что такое электрическая емкость величиной в 1 фарад?
7

8.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Электроемкость уединенного проводника.
Пример. Вычислим емкость шара с объемной плотностью заряда
помещенного
в
бесконечную
диэлектрическую
среду
проницаемостью . Потенциал на поверхности шара равен:
R
R
g
3 0
g
2
R ,
R
R
2
3 0
g
R
,
4 0 R
C 4 0 R
- радиус шара. Поскольку
3g
R
g
2
3 0 4 R
3
4 0 R
а емкость шара равна
.
C
g
g
4 3
R
3
g,
с
, то
Отсюда
g
g
4 0 R
4 0 R
R
C
4 0
1
9
9
10
м
12
4 3.14 1 8.85 10
8

9.

ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Конденсаторы.
Устройства, имеющие большую, не зависящую от окружающих тел
электроемкость, называются конденсаторами.
Конденсаторы – это два проводника, расположенных близко друг к
другу. Проводники называют обкладками и располагают так, чтобы
их поле было сосредоточено внутри конденсатора
Например, две пластинки, два коаксиальных цилиндра или две
концентрические сферы, расположенные близко друг к другу.
Электроемкость конденсатора определяется соотношением:
g
g
С
U
Пример - две заряженные пластины. Разность
потенциалов определяется соотношением:
d Емкость такого конденсатора равна:
1 2
0
g 0 0 S 0 S
g
0 S
С
С
d
d
d
d
9

10.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Потенциальная энергия пробного
электрическое поле заряда g :
Wp
1
gg пр
4 0
r
заряда,
помещенного
в
Рассмотрим энергию взаимодействия системы точечных зарядов,
непрерывно распределенных зарядов, заряженных проводников.
Энергией взаимодействия электрических зарядов называется такая
энергия, за счет которой совершается работа при взаимных
перемещениях заряженных частиц.
Эта энергия количественно равна работе, которую совершают силы
взаимодействия при разнесении всех частиц системы на
бесконечные расстояния друг от друга.
10

11.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Рассмотрим систему заряженных частиц состоящую из двух частиц
W12 - энергия первой частицы в поле второй
W21 - энергия второй частицы в поле первой
1
( W12 W21 ) W p
Очевидно, что W12 W21 Wp
2
Выражение для энергии взаимодействия многих частиц:
1
Wp Wpi ,
2 i
где
Wpi - потенциальная энергия
остальных частиц системы.
i -ой
частицы в полях всех
Энергия взаимодействия системы зарядов называется электрической
энергией этой системы.
11

12.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия взаимодействия системы точечных зарядов
Потенциал электрического поля - это отношение потенциальной
энергии заряда в электрическом поле, к величине самого заряда:
Wp
g пробн.
Отсюда с учетом выражения W p
1
W pi ,можно получить формулу
2 i
для энергии взаимодействия системы точечных зарядов в виде:
1
W p g i i
2 i
где i - полный потенциал, созданный всеми остальными
зарядами системы в точке, где расположен заряд g i.
12

13.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия системы объемно распределенных зарядов
Рассмотрим заряд, непрерывно распределенный по объему V с
объемной плотностью g x , y , z .
Мысленно разобьем объем V на малые элементы dV, каждый из
которых может быть рассмотрен как точечный заряд величиной
dg g dV
Тогда заряженный объем Vможно рассматривать как совокупность
большого числа бесконечно малых точечных зарядов
1
Применим к такой системе соотношение W p g i i , вместо
2 i
суммы записав интеграл:
1
1
W p dg g dV
2V
2V
13

14.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия системы поверхностно распределенных зарядов
Электрическая энергия системы поверхностно распределенных зарядов
может быть записана в виде формулы, похожей на предыдущую:
1
1
W p dg dS
2S
2S
Энергия системы линейно распределенных зарядов
Для заряда, непрерывно распределенного вдоль кривой l с линейной
плотностью g , электрическая энергия выражается соотношением вида:
1
1
W p dg g dS
2l
2l
14

15.

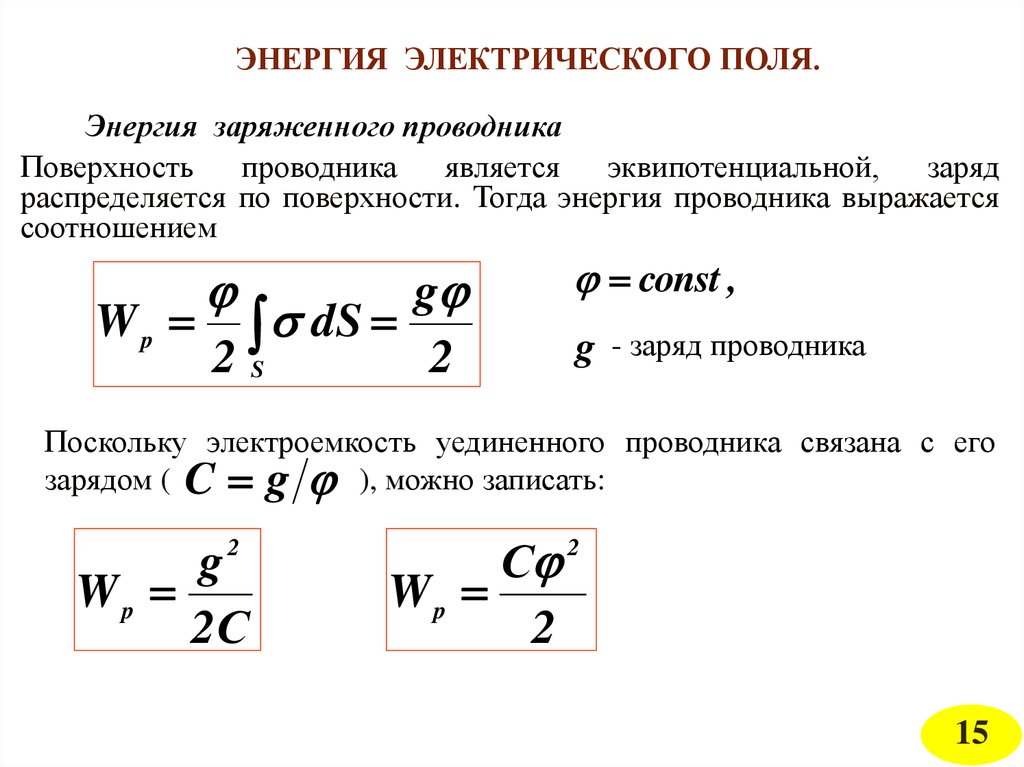
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия заряженного проводника
Поверхность
проводника
является
эквипотенциальной,
заряд
распределяется по поверхности. Тогда энергия проводника выражается
соотношением
g
W p dS
2S
2
const ,
g
- заряд проводника
Поскольку электроемкость уединенного проводника связана с его
зарядом ( C g ), можно записать:
2
g
Wp
2С
С
Wp
2
2
15

16.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия заряженного конденсатора
Рассмотрим плоский заряженный конденсатор. Потенциал
обкладки, несущей заряд g , обозначим
1 , а потенциал
обкладки с зарядом g, обозначим 2 . Полные заряды каждой из
обкладок можно разделить на элементарные заряды g , которые
находятся в точках с потенциалом 1 , либо 2 . Применим формулу
для энергии взаимодействия системы зарядов:
1
W p g i i
2 i
1
1
1
W p g 1 g 2 g 1 2 gU
2
2
2
Поскольку С g U, можно записать полученное выражение иначе:
1
g 2 CU 2
W p gU
2
2C
2
1
W p gU
2
CU 2
Wp
2
16

17.

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
Энергия заряженного конденсатора
Используя выражение для энергии заряженного конденсатора,
найдем силу, с которой обкладки плоского конденсатора
притягивают друг друга.
Введем
координатную
ось
x,
перпендикулярную
плоскости
обкладок.
Емкость плоского конденсатора:
С
0 S
Здесь
d
d
CU 2
g2
Wp
x
2
2 0 S
x - координата второй обкладки.
Будем считать заряд на обкладках постоянным.
Продифференцировав выражение для W p x ,
получим:
Модуль этого выражения и есть сила
W p
g2
притяжения
обкладок
плоского
F x
конденсатора.
x
2 0 S
x
x
17