Похожие презентации:
Векторная алгебра
1. Математика
Часть 1УГТУ-УПИ
2006г.
2.
Лекция 4Векторная алгебра
I. Векторы. Линейные операции над векторами.
Линейная зависимость векторов.
2. Базис и координаты вектора.
3. Линейные операции над векторами, заданными в
координатной форме.
4. Проекция вектора на ось.
5. Скалярное произведение векторов.
6. Векторное произведение векторов.
7. Смешанное произведение векторов.
3.
1. Вектор. Линейные операции над векторами.Определение.
Вектор – направленный отрезок;
его характеристики – длина и направление.
Базовые определения: нулевой вектор,коллинеарные
векторы; компланарные векторы, равные векторы.
Линейные операции над векторами.
I. Сложение векторов
Геометрическое определение –
правило треугольника и правило
параллелограмма:
4.
2. Умножение вектора на число.Произведением
вектора a на число называется
вектор b , удовлетворяющий условиям:
b
1) длина вектора
вектора
a
равна произведению длины
на модуль числа :
b a
2) направление вектора b :
совпадает с a ,если >0, направлен в
противоположную сторону, если < 0.
5.
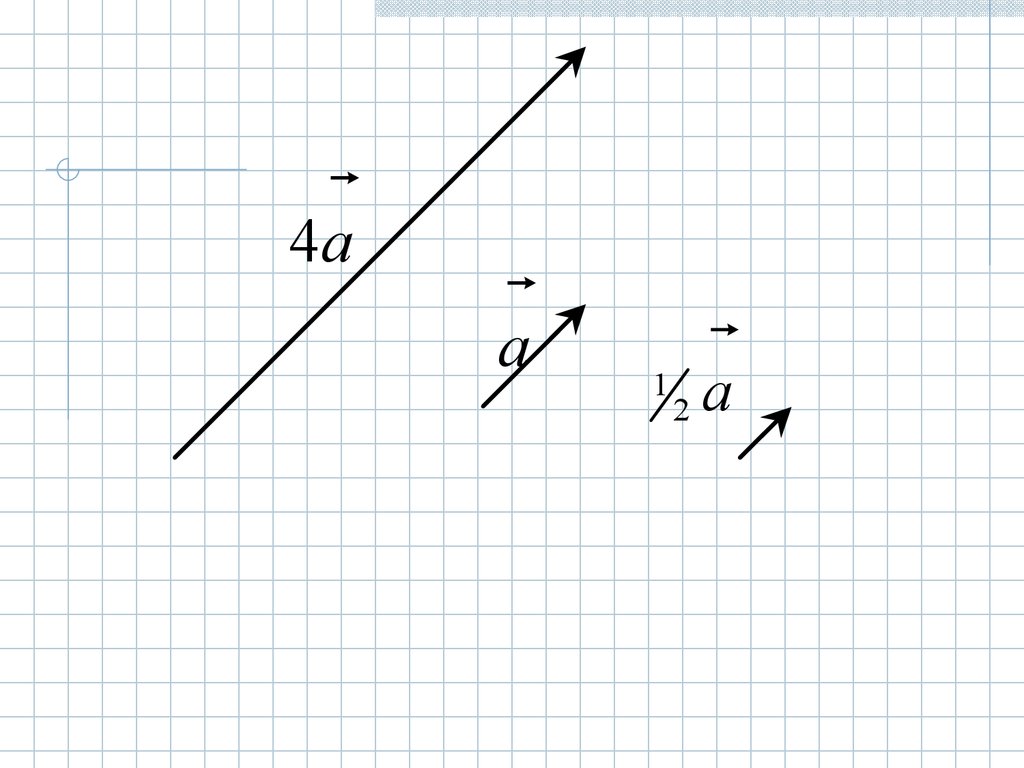
4aa
1 a
2
6.
Свойства линейных операций над векторами.I. Сложение.
1.
a b b a
2. a b c a b c
a a 0 , a
3. a , a a :
-противоположный
4.
a , a 0 a
II. Умножение
вектора
на
число.
1.
2.
3.
4.
a b a b
a a a
a a
1 a a
вектор.
7.
Линейная зависимость (ЛЗ) векторов.Линейной комбинацией (ЛК) векторов называется
сумма их произведений
на произвольные числа:
n
k ak 1a1 ... n an
.
Если
k 1
k ak 0,
n
k 1
и среди коэффициен тов k есть отличные от нуля ,
то векторы называются линейно зависимыми.
Если k ak 0 только когда все 1 2 ... n 0,
n
k 1
то векторы a1 , a2 ,..., an линейно независимы.
8.
2. Базис и координаты вектора.Базисом множества векторов на прямой
называется любой ненулевой вектор этой
прямой.
Базисом множества векторов на плоскости
называются любые два неколлинеарных вектора
этой плоскости.
9.
Базисом множества векторов в пространственазываются любые три некомпланарных
вектора.
Т
(О единственности разложения вектора по
базису).
Любой вектор d может быть разложен по
базису и это разложение единственно.
10.
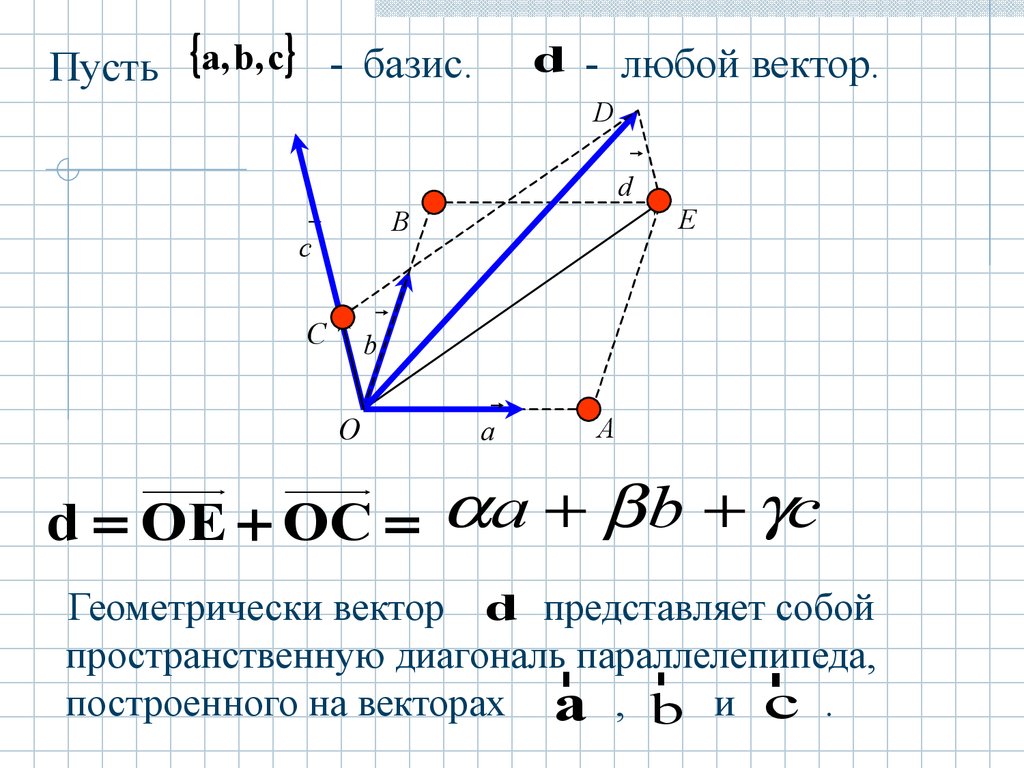
Пусть a, b, c - базис.d - любой вектор.
D
d
E
B
c
b
C
O
a
A
d OE OC a b c
d представляет собой
Геометрически вектор
пространственную диагональrпараллелепипеда,
r
r
построенного на векторах a , b и c .
11.
, ,d по базису
Числа
в
разложении
вектора
a , b , c называются координатами вектора d
в базисе a, b , c .
Можно использовать такую запись:
d { , , }
12.
Следствие.Два вектора, заданные в одном и том же базисе
d1 1 , 1 , 1
d 2 2 , 2 , 2
равны тогда и только тогда, когда равны их
соответствующие координаты:
1 2 , 1 2 , 1 2
13.
3.Линейные операции над векторами,
заданными в координатной форме.
I.Сложение.
Т Если
d1 1 , 1 , 1 и
d 2 2 , 2 , 2
то
d1 d 2 1 2 , 1 2 , 1 2
Доказательство.
Пусть a, b, c - базис.
14.
d 1 1a 1b 1cd a b c
2
2
2
2
d1 d 2 1 2 a ( 1 2 )b ( 1 2 )c
15.
II. Умножение вектора на число.Т
Если
то
d , ,
в базисе
kd {k , k , k }
a , b , c ,
16.
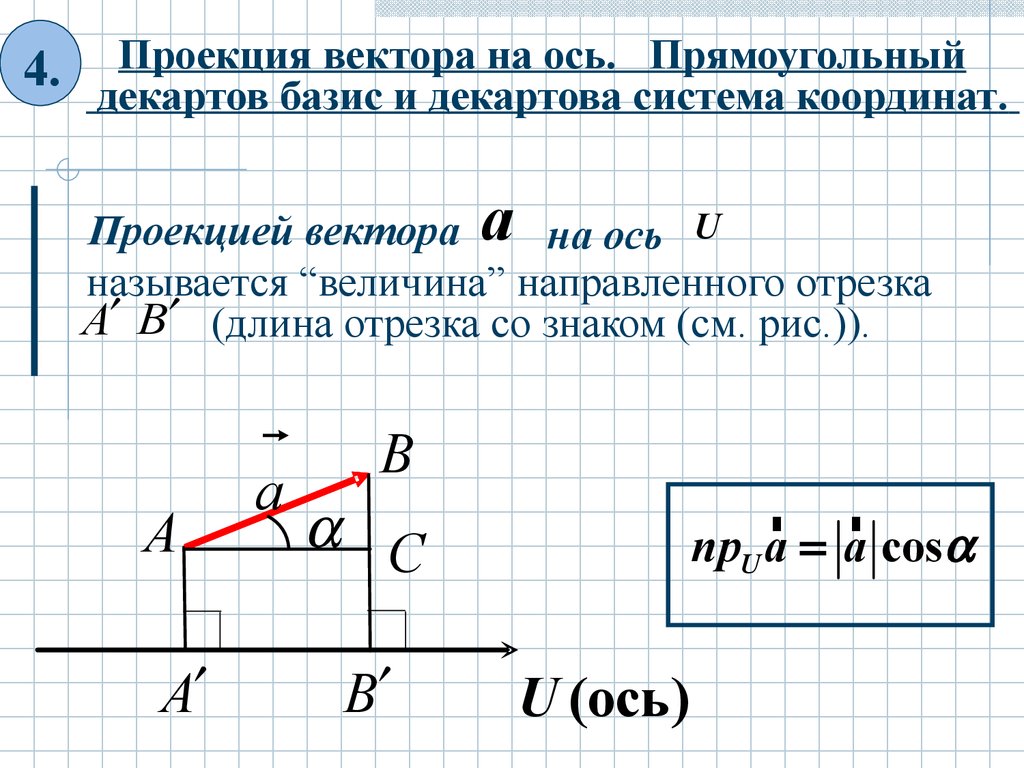
Проекция вектора на ось. Прямоугольный4. декартов
базис и декартова система координат.
a
Проекцией вектора
на ось U
называется “величина” направленного отрезка
A B (длина отрезка со знаком (см. рис.)).
A
A
a
B
C
B
r r
npU a a cos
U (ось)
17.
Системой координат в пространстве называютсовокупность базиса a , b, c и некоторой
точки О, называемой началом координат.
uuuur
OM ,
Вектор
идущий из начала координат в точку M,
называется радиус-вектором точки M .
Координатами точки M называются координаты её
радиус-вектора.
18.
Декартовымпрямоугольным
базисом
в
пространстве называется тройка упорядоченных
взаимно перпендикулярных
векторов единичной
длины: i , j , k
r
r
r
r
d xi yj zk , d x, y , z в базисе i , j, k .
Такой базис называют ещё ортонормированным (ОНБ) ,
а связанную с ним систему координат декартовой.
Прямые линии, проведенные через начало координат по
направлениямr базисных векторов,rназываются осями
u
r
координат: i - порождает OX ; j – OY ; k – OZ .
Координаты точки М в декартовой системе координат
называются соответственно абсциссой, ординатой и
аппликатой .
19.
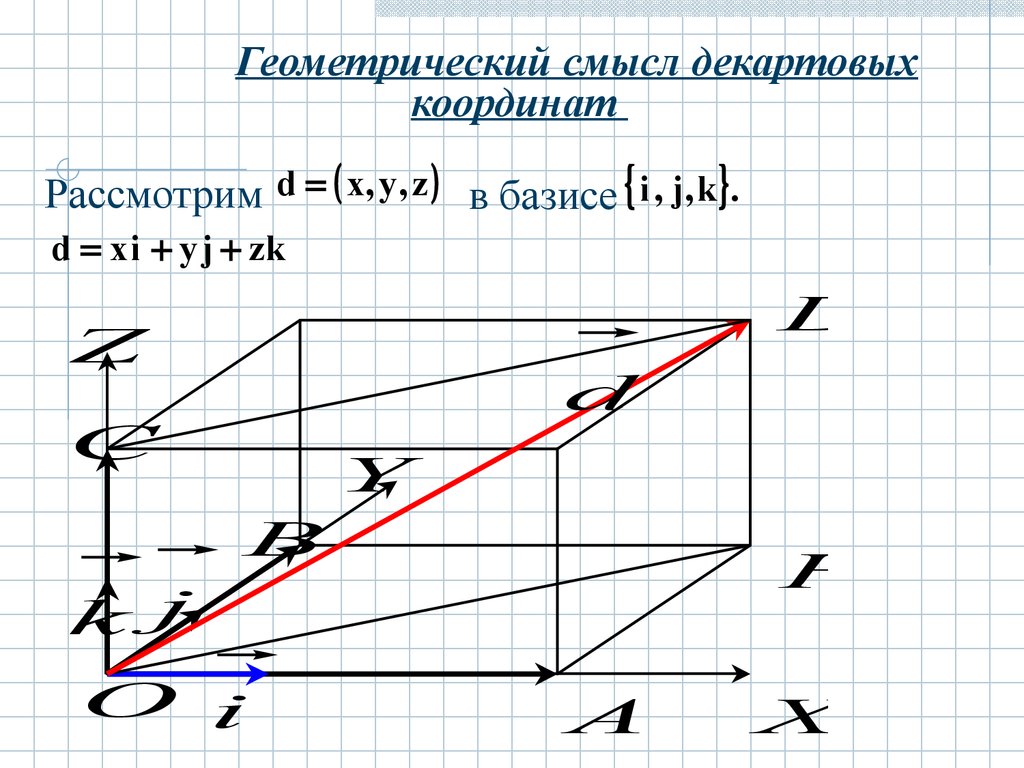
Геометрический смысл декартовыхкоординат
Рассмотрим d x, y , z в базисе i , j, k .
d x i y j zk
Z
d
C
D
Y
B
k j
O i
H
A
X
20.
Zd
C
D
Y
B
k j
O i
r uuu
r
r uuu
H
uuu
r
r rA
r
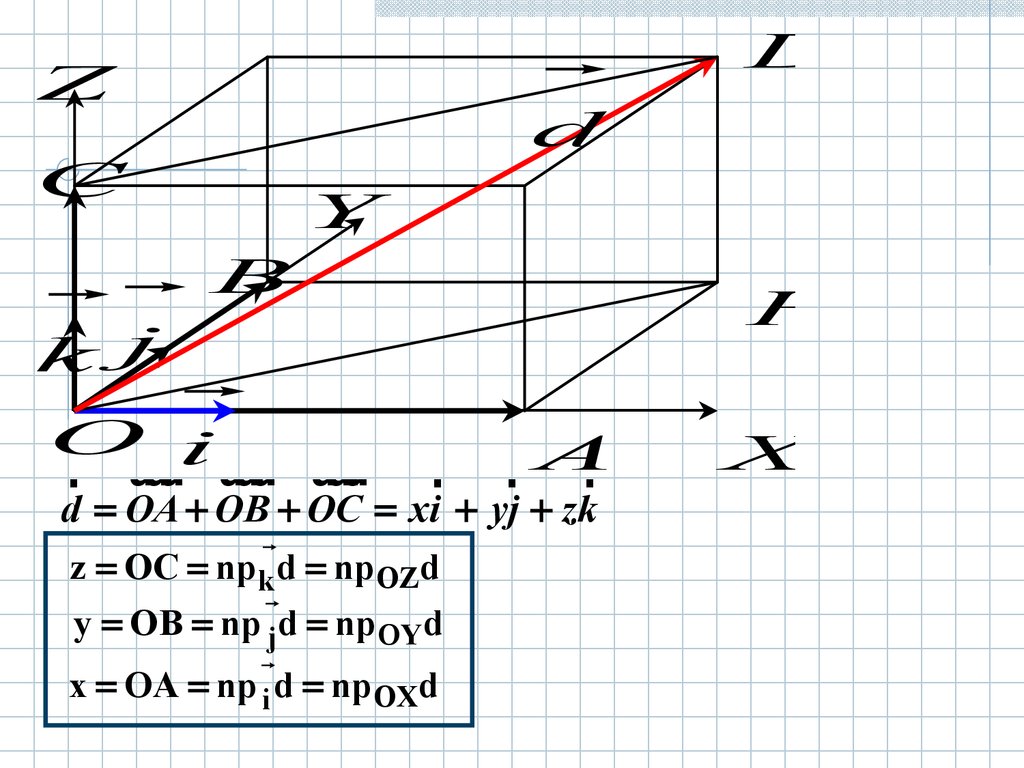
d OA OB OC xi yj zk
z OC npk d np OZd
y OB np jd np OYd
x OA np i d npOXd
X
21.
Вывод.Декартовы координаты вектора совпадают
с его проекциями на соответствующие
координатные оси.
Пусть
d, OX
d, OY
d, OZ
d OD x 2 y 2 z 2
x npOXd d cos
y npOYd d cos
z np OZd d cos
-длина вектора d x, y , z
22.
coscos
cos
x
x2 y 2 z 2
-направляющие косинусы
y
2
2
x y z
2
вектора
z
d x, y , z
x2 y 2 z 2
cos2 cos2 cos2 1
-основное тождество.
23.
Вывод.Декартовы координаты вектора позволяют найти его
длину и направление, то есть все характеристики.
d
:
d
Ортом
вектора
0
называется
вектор
Определение.
d 0 d, d 0 1.
d
d0
d
d 0 cos , cos , cos
24.
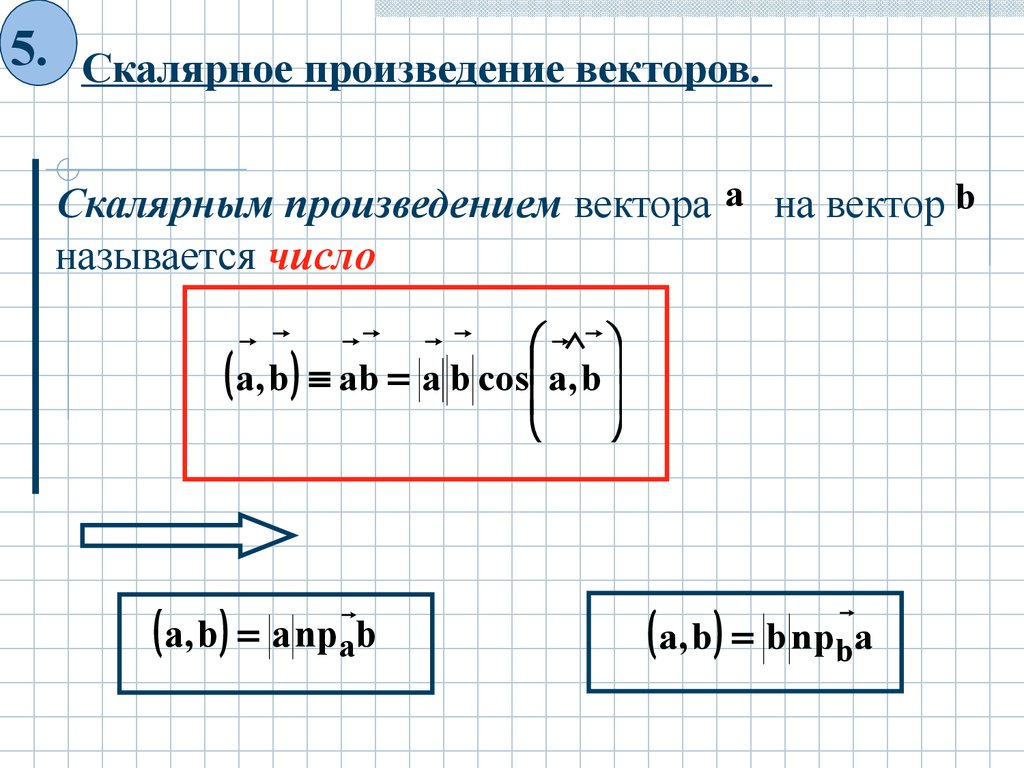
5. Скалярное произведение векторов.Скалярным произведением вектора a на вектор b
называется число
a, b ab a b cos a, b
a, b a npab
a, b b npba
25.
Алгебраические свойства скалярного произведения.r r
r r
1. a , b b , a
r r
r r
r r
2. a , b a , b a , b
rr
r rr
rr
3. a b , c a , c b , c
r
r
2 r
r r
r2
a , a 0
4. a , a a r r
0, a 0
26.
r1. a
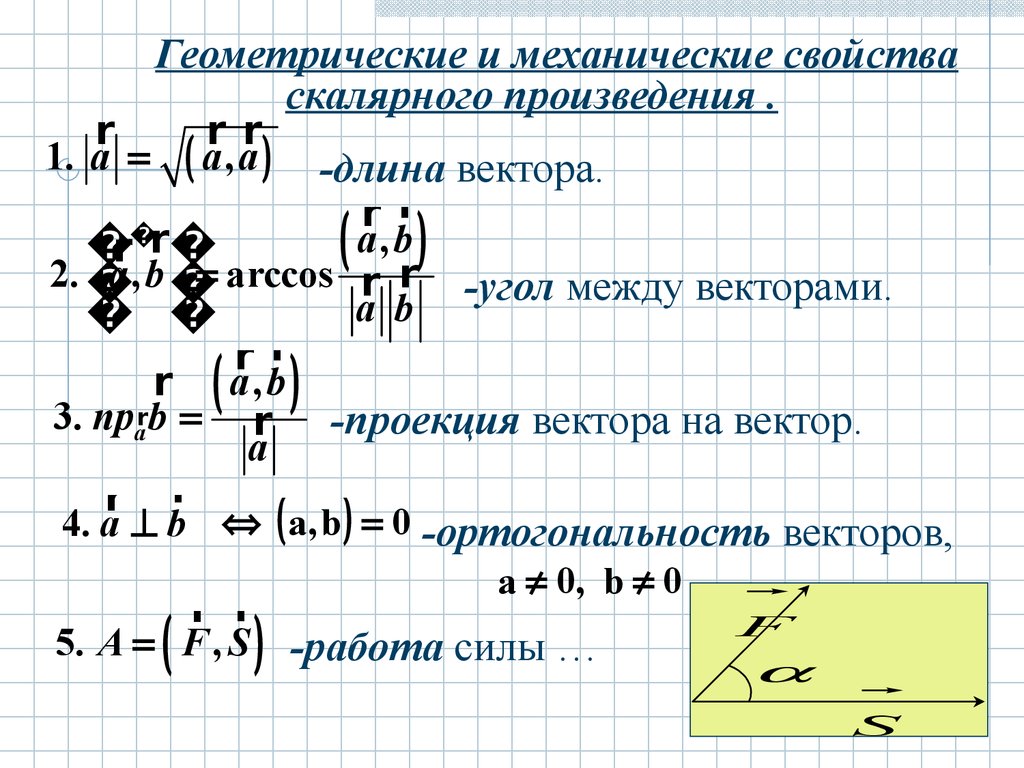
Геометрические и механические свойства
скалярного произведения .
r r
a,a
-длина вектора.
r
r
a,b
r r
2.
a , b arccos r r -угол между векторами.
a b
r r
r a,b
3. nparb r -проекция вектора на вектор.
a
r r
4. a b a, b 0 -ортогональность векторов,
a 0, b 0
r r
F
5. A F , S -работа силы …
S
27.
Формула для вычисления скалярного произведениявекторов, заданных декартовыми координатами.
Т
a x1 , y1 , z1 ,
b x2 , y 2 , z 2
Если
в базисе i , j , k , то
a, b x1x2 y1y 2 z1z 2
28.
6.Векторное произведение векторов.
Определение.
Тройка векторов
называется правой, если
кратчайший поворот от первого
вектора ко
второму вектору виден из конца третьего вектора
осуществляющимся против часовой стрелки.
a,b,c
c
- правая тройка.
b
a
b, a, c - левая тройка.
29.
bc
a
a , b , c - левая тройка.
b , a , c - правая тройка.
Замечание.
Перестановка местами двух соседних
векторов тройки меняет её ориентацию.
Циклическая перестановка векторов тройки
не меняет её ориентации.
a,b,c
b,c,a
30.
Определение.Векторным произведением вектораa на вектор b
называется вектор c :
r r
r r r
1. c a b sin
a,b
;
r r r r
2. c a , c b ;
r r r
3. a , b , c
- правая тройка.
31.
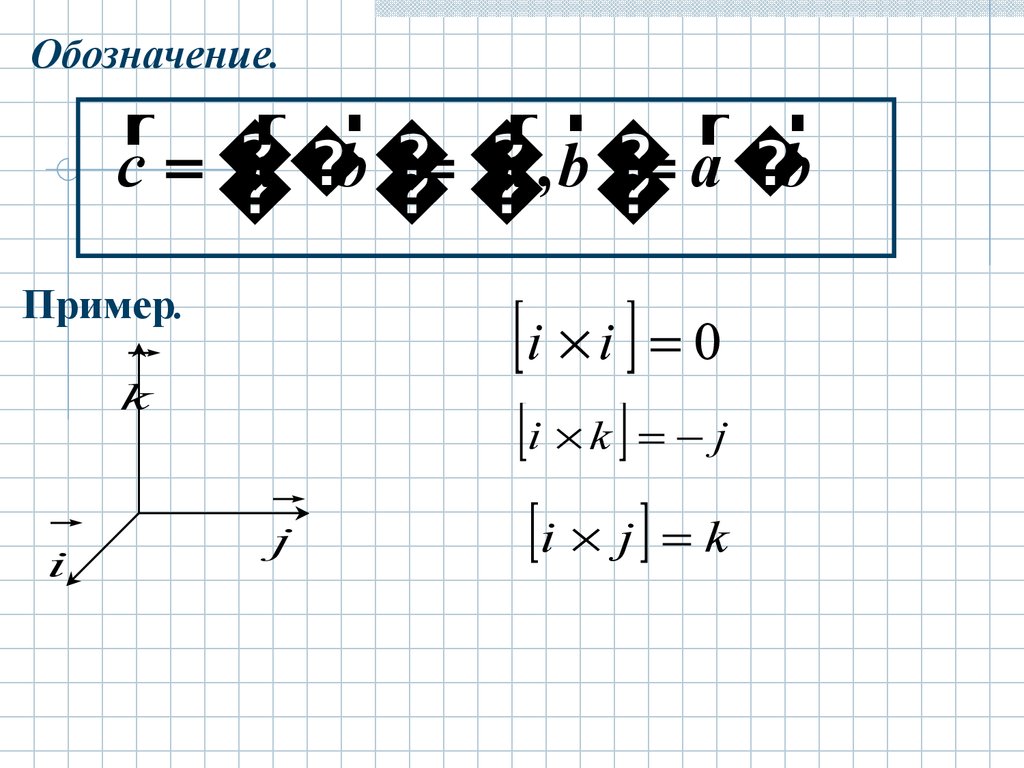
Обозначение.r
r r
r r
r r
a b
c
a
b
a
,
b
Пример.
k
i
i i 0
j
i k j
i j k
32.
Алгебраические свойства векторного произведения.r r
r r
1.
a
b
b
a
r r
r r
r r
2.
a
b
a
b
a
b
r r
r r
r
r
r
3. a b c a c
b
c
r
r r
r
4. a a 0, a .
33.
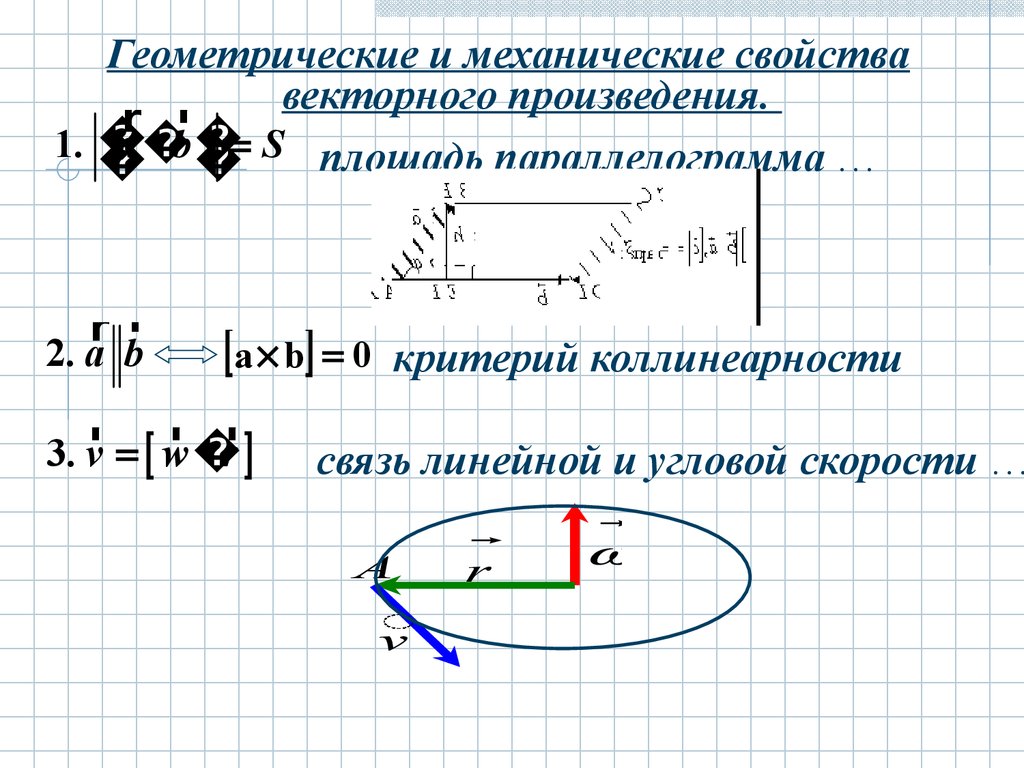
Геометрические и механические свойствавекторного произведения.
r
r
1.
a b
S площадь параллелограмма …
r r
2. a b
a b 0 критерий коллинеарности
r
r r
3. v w r
связь линейной и угловой скорости …
A
v
r
34.
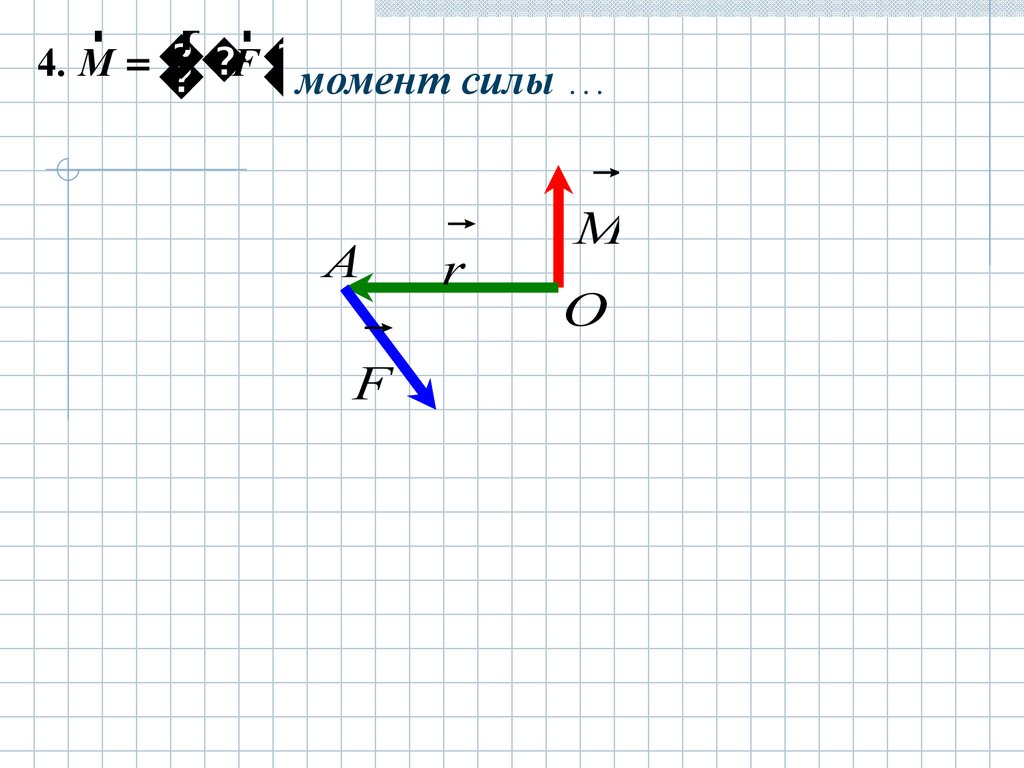
rr r
4. M
r
F
момент силы …
A
F
r
M
O
35.
Вычисление векторного произведения вдекартовых координатах.
Т
a x1 , y1 , z1 , b x 2 , y 2 , z 2
Если
в базисе i , j , k , то
i
a b x1
x2
j
y1
y2
k
z1
z2
36.
7.Смешанное произведение векторов.
Определение.
Смешанным произведением векторов
называется число
ab c ([a , b ], c )
a, b , c
37.
Т(о геометрическом смысле смешанного
произведения).
V - объем параллелепипеда …,
abc 0 - тройка векторов компланарна,
V
- тройка левая.
Доказательство.
Пусть a, b, c - правая тройка.
38.
ab
H
c
b
a
ab c ([a, b ], c ) a b c cos a b H
SОСН
H V
39.
Следствие.Необходимым и достаточным условием компланарности
трёх векторов является равенство нулю их смешанного
произведения.
Вычисление смешанного произведения векторов,
заданных декартовыми координатами .
Т
c
Если a x1 , y1 , z1 , b x 2 , y 2 , z 2 , x 3 , y 3 , z 3
в базисе i , j , k ,
то
x1
ab c x 2
x3
y1
y2
y3
z1
z2
z3
40.
Следствие 1.Необходимым и достаточным условием компланарности
трёх векторов является равенство нулю определителя,
строками которого являются координаты этих векторов .
Следствие 2.
Необходимым и достаточным условием линейной
зависимости трёх векторов, является равенство нулю
того же определителя.
Свойство смешанного произведения.
Перестановка местами двух соседних сомножителей
меняет знак смешанного произведения, а циклическая
перестановка сомножителей знака не меняет.











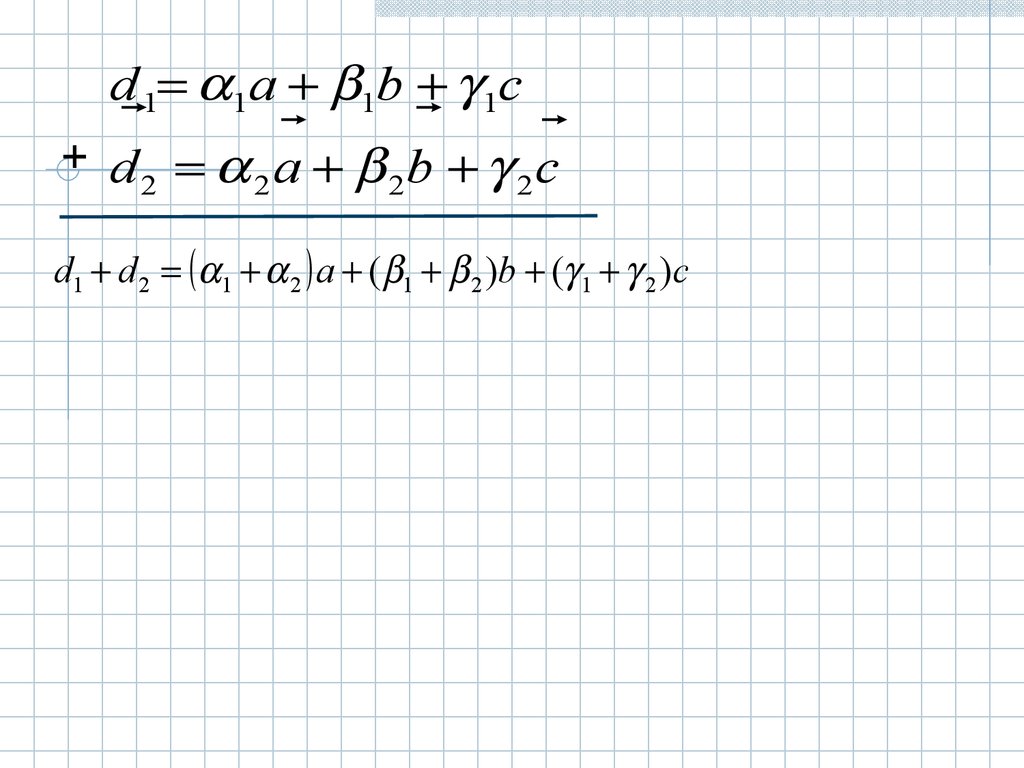















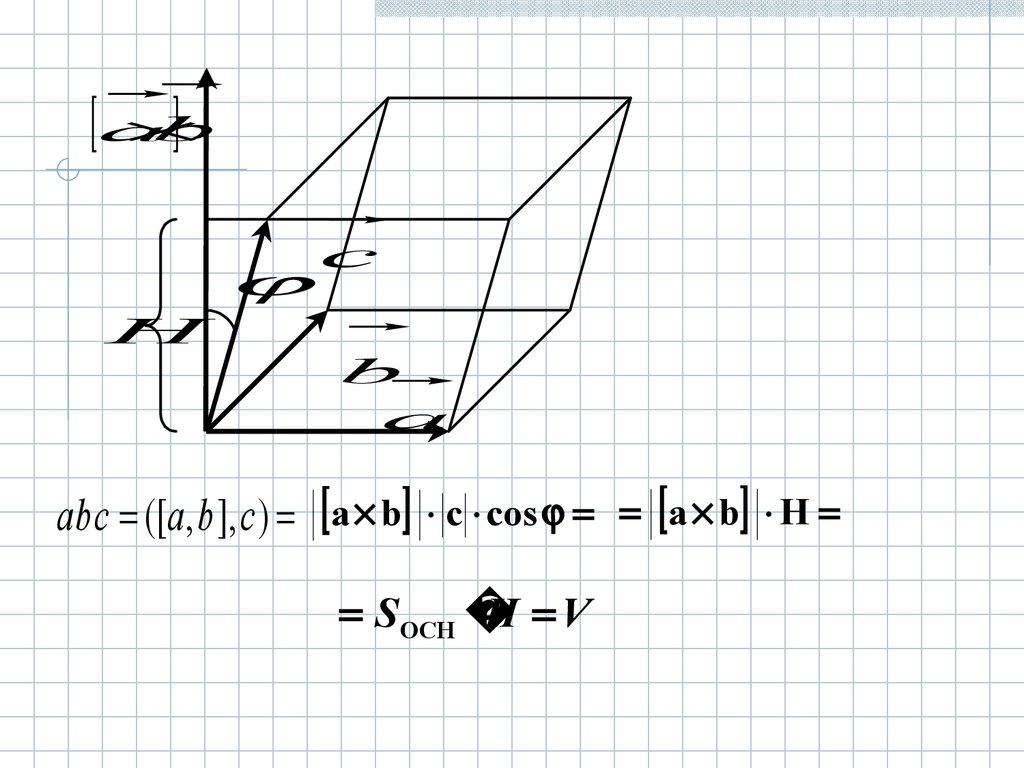


 Математика
Математика








