Похожие презентации:
Некоторые часто встречающиеся дискретные распределения
1.
Некоторые часто встречающиесядискретные распределения
Проводится n испытаний по схеме Бернулли
с вероятностью успеха p.
Х-число успехов.
Тогда говорят, что Х имеет биномиальное
распределение с параметрами n,p
Х принимает значения: 0,1,2,…n
p( X k ) C p (1 p)
k
n
k
n k
2.
Стрелок производит 3 выстрела по мишени.Вероятность попадания при одном выстреле
равна 0,6. Х-число попаданий. Найти
распределение Х.
3.
Найдем MX ираспределения
DX
Введем для каждого
величину Zi .
1, åñëè â i ì
Zi
0, åñëè â i ì
для
биномиального
i=1,2…n
случайную
èñï û ò àí èè óñï åõ
èñï û ò àí èè í åóäà÷à
Тогда
Х= Z1 +Z2 +…+Zn
4.
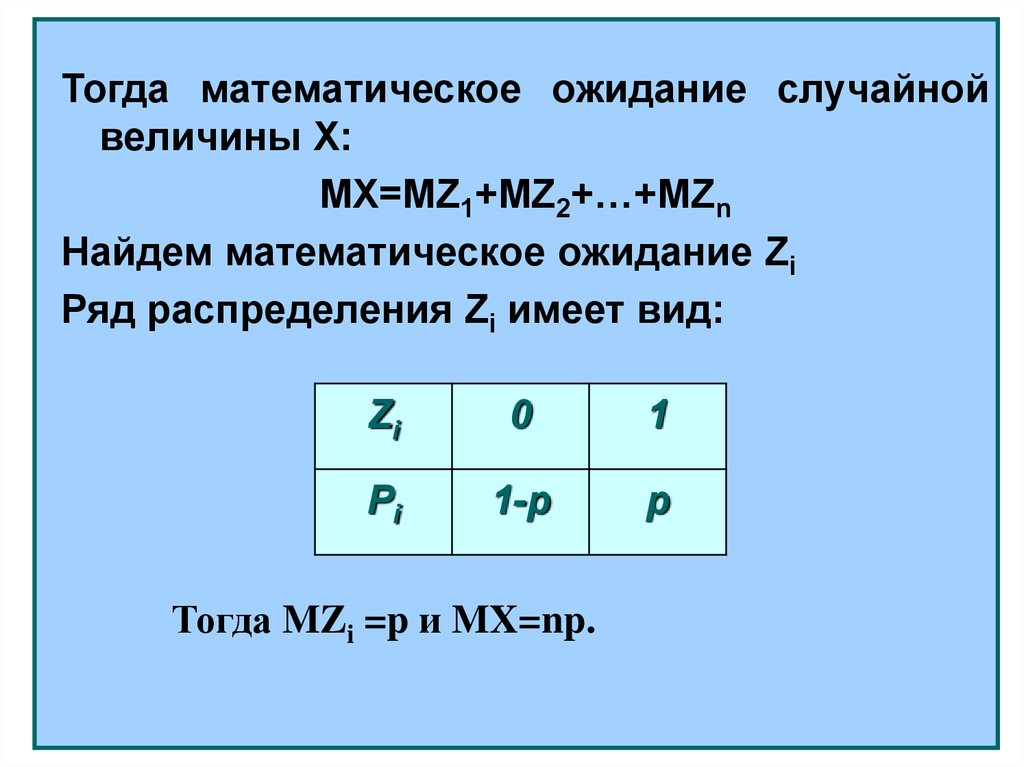
Тогда математическое ожидание случайнойвеличины Х:
MX=MZ1+MZ2+…+MZn
Найдем математическое ожидание Zi
Ряд распределения Zi имеет вид:
Zi
0
1
Pi
1-p
p
Тогда MZi =p и MX=np.
5.
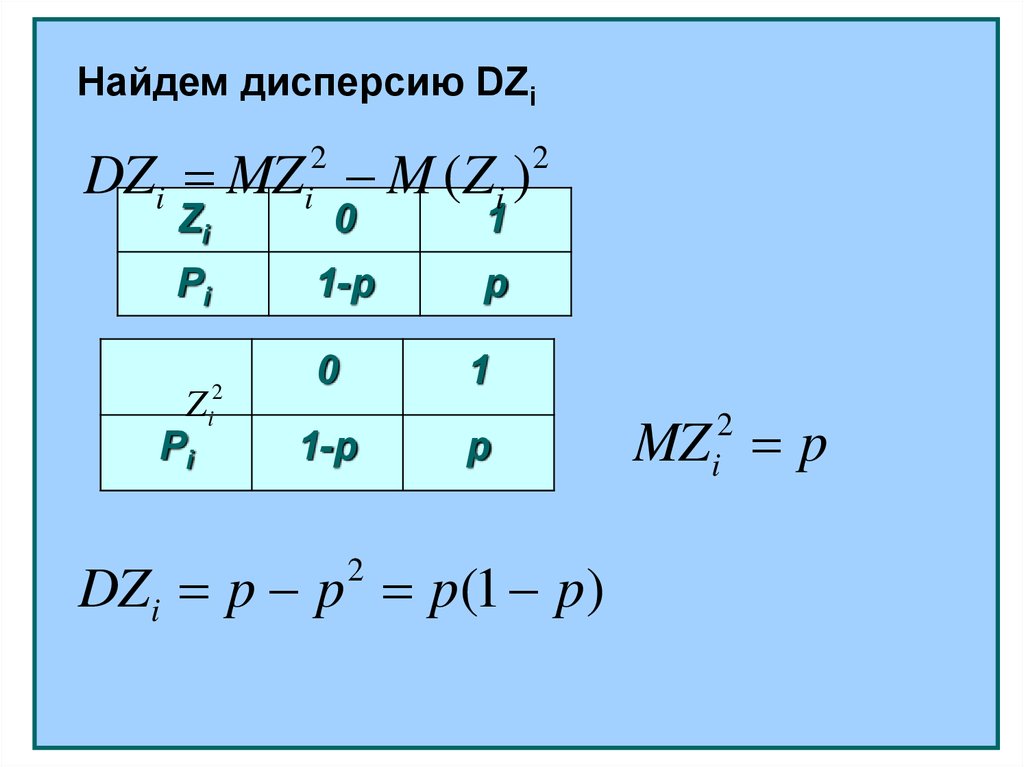
Найдем дисперсию DZiDZi MZ M (Zi )
Zi
Pi
Z
Pi
2
i
2
i
0
1
1-p
p
0
2
1
1-p
p
DZi p p p(1 p)
2
MZ p
2
i
6.
Таккак
случайные
независимы, то
величины
Zi
DX DZ1 DZ 2 ... DZ n
np(1 p) npq
7.
Таким образом, для случайной величины,распределенной по биномиальному закону,
MX n p
DX n p q
8.
Пусть Х – число наступлений редкого события занекоторый промежуток времени.
Известно среднее число наступлений этого
события за этот промежуток времени a
Тогда Х может принимать значения
0, 1, 2,…,k,…
k
a
p( X k ) e
k!
a
Говорят, что Х имеет распределение Пуассона с
параметром a.
9.
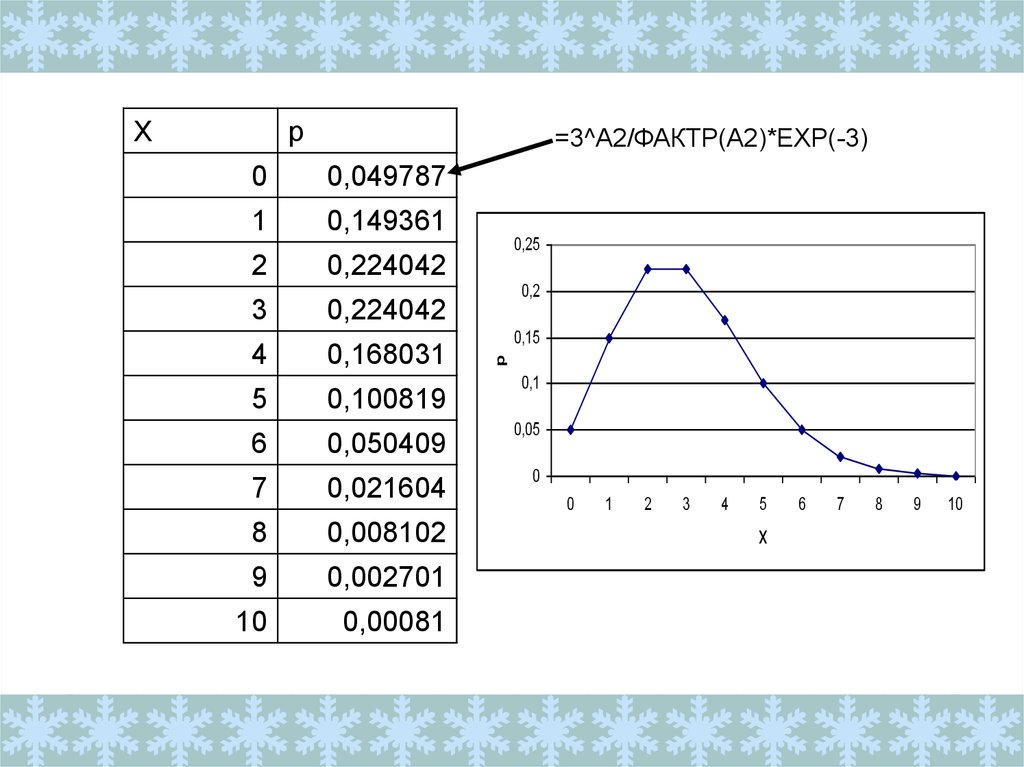
При работе оборудования время от временивозникают сбои. В среднем за месяц возникает
3 сбоя. Пусть Х-число сбоев за месяц. Найти
распределение Х.
Вычислить вероятности событий:
А - за месяц будет не больше 2-х сбоев;
В - в течение месяца произойдет хотя бы один
сбой.
10.
Хp
=3^A2/ФАКТР(A2)*EXP(-3)
0
0,049787
1
0,149361
2
0,224042
3
0,224042
4
0,168031
5
0,100819
6
0,050409
7
0,021604
8
0,008102
9
0,002701
10
0,00081
11.
Хp
=3^A2/ФАКТР(A2)*EXP(-3)
0
0,049787
1
0,149361
2
0,224042
3
0,224042
0,25
0,2
0,15
0,168031
5
0,100819
6
0,050409
0,05
7
0,021604
0
8
0,008102
9
0,002701
10
0,00081
p
4
0,1
0
1
2
3
4
5
Х
6
7
8
9
10
12.
Хp
0
0,049787
1
0,149361
2
0,224042
3
0,224042
4
0,168031
5
0,100819
6
0,050409
7
0,021604
8
0,008102
9
0,002701
10
0,00081
0,42319
13.
Для распределения Пуассона MX=a, DX=a14.
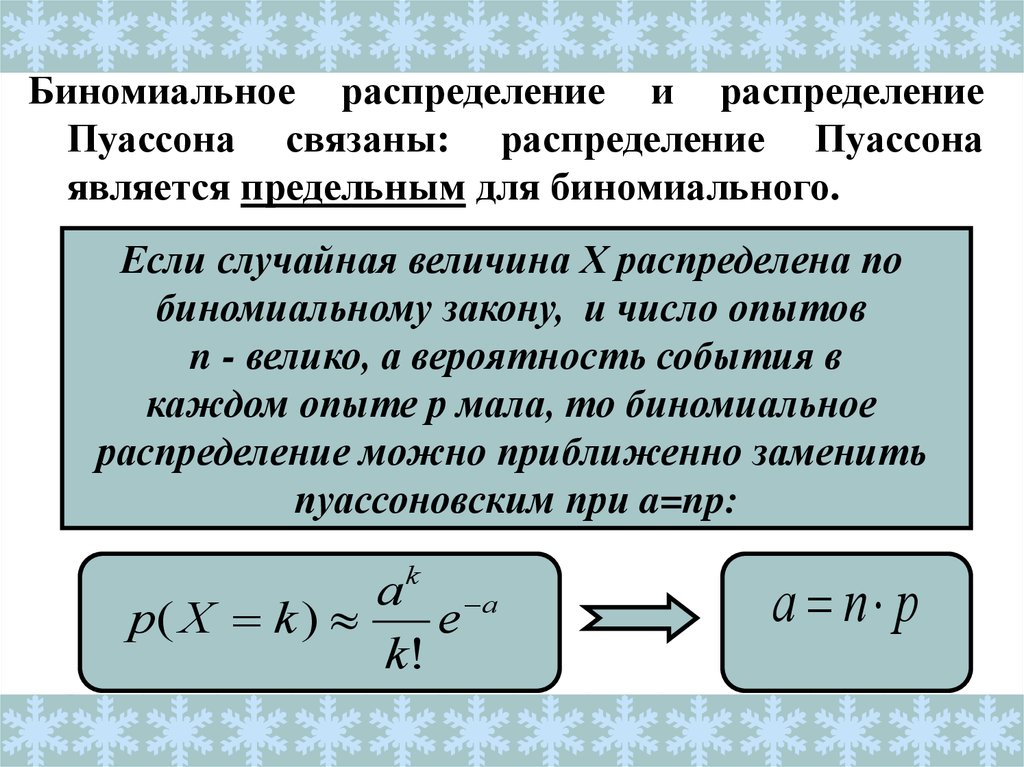
Биномиальное распределение и распределениеПуассона связаны: распределение Пуассона
является предельным для биномиального.
Если случайная величина Х распределена по
биномиальному закону, и число опытов
n - велико, а вероятность события в
каждом опыте р мала, то биномиальное
распределение можно приближенно заменить
пуассоновским при a=np:
k
a a
p( X k )
e
k!
a n p
15.
По цели производится 50 независимыхвыстрелов. Вероятность попадания в цель
при одном выстреле равна 0.04.
Используя предельное свойство
биномиального распределения, найти
вероятность того, что в цель попадет
один снаряд.
16.
Событие А - попадание при одном выстреле.Вероятность р(А)=0.04. Всего производится серия
таких выстрелов: n=50.
Так как р достаточно мало, а n - велико,
биномиальное
распределение
приближенно
можно заменить распределением Пуассона.
Найдем параметр a распределения Пуассона:
a n p 50 0.04 2
17.
Тогда вероятность р50(1) того, что из 50-тивыстрелов будет одно попадание по формуле
Пуассона будет:
1
2 2
p50 (1)
e 0, 271
1!
18.
Проводится n независимых испытаний,в каждом из которых возможны 2 исхода: успех
с вероятностью p и неудача с вероятностью 1-p.
Испытания проводятся до первого успеха. Пусть X –
число проведенных испытаний. Тогда X имеет
геометрическое распределение.
19.
Х принимает значения 1,2,3…,k,…p( X k ) (1 p)
k 1
p
20.
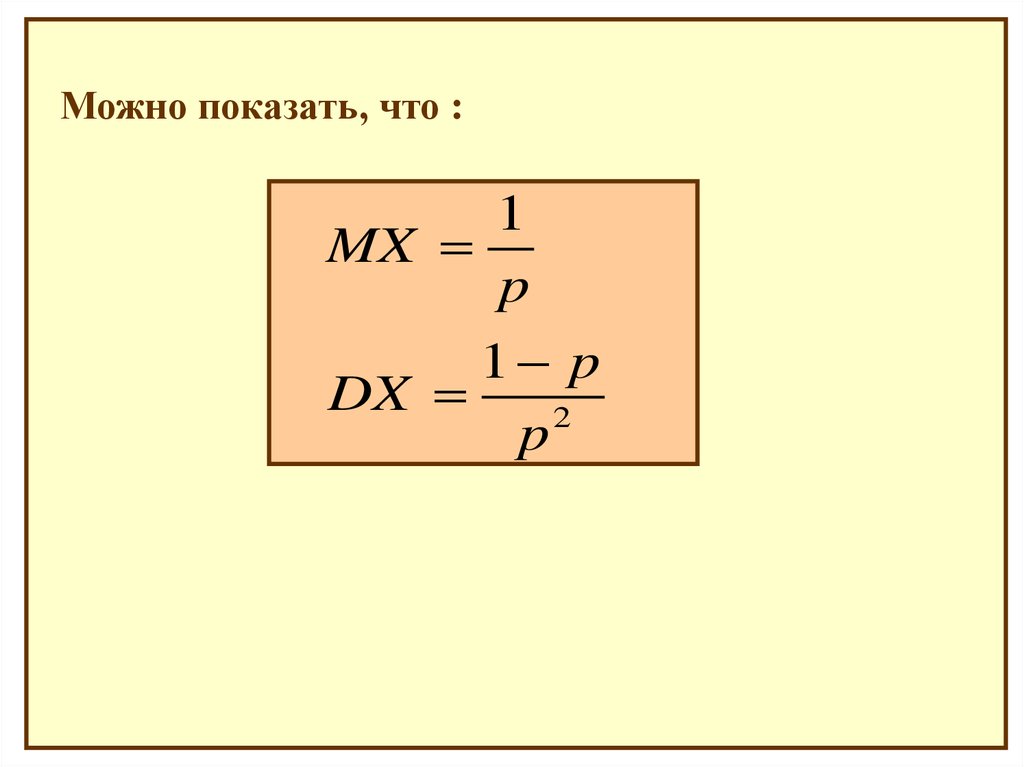
Можно показать, что :1
MX
p
1 p
DX
2
p
21.
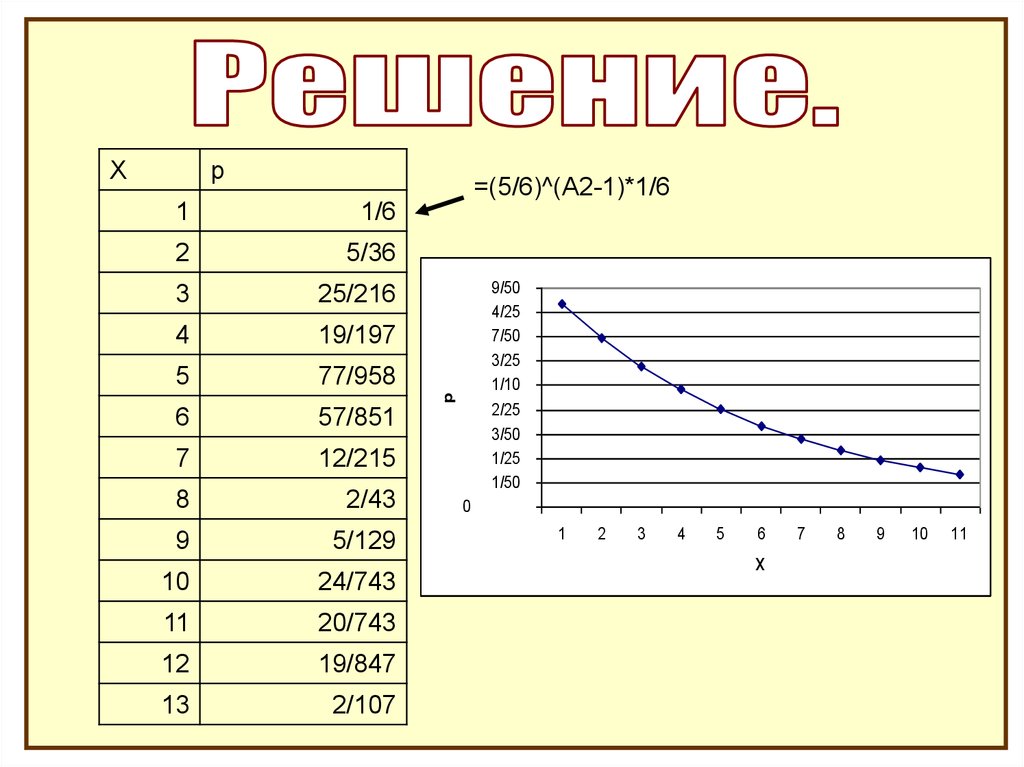
Игральная кость бросается до первого появленияшестерки. Х- число сделанных бросков. Найти
распределение Х, MX, DX
22.
p1
1/6
2
5/36
3
25/216
4
19/197
5
77/958
6
57/851
7
12/215
8
2/43
9
5/129
10
24/743
11
20/743
12
19/847
13
2/107
=(5/6)^(A2-1)*1/6
9/50
4/25
7/50
3/25
1/10
p
Х
2/25
3/50
1/25
1/50
0
1
2
3
4
5
6
Х
7
8
9
10
11
















 Математика
Математика








