Булевы отношения

1.

Булевы отношения
Лектор: Завьялов Олег Геннадьевич
кандидат физико-математических наук, доцент

2. Декартово произведение

Отношением R множества А и В называется произвольное
подмножество А В. Если (a, b) R, записывают aRb.
Говорят, что a и b находятся в отношении R, или a относится к b.
Если А=В, то отношение есть подмножество А А; такое
отношение называется бинарным отношением (или
отношение) на А.

3. Пример

A={1, 2, 3}, B={r, s}
A B= {(1,r), (1,s), (2,r), (2,s), (3,r), (3,s)}
Тогда R={(1,r), (1,s), (3, s)} – отношение множеств А и В.
(3, s) R
3Rs
Множество А B содержит 6 элементов.
2^6=64 подмножеств множества А B
64 различных отношения на А B

4. Примеры

5. Определения

Область определения отношения R на А и В есть
множество всех х А таких, что для некоторых у В
(х,у) R.
Область определения R есть множество всех первых
координат упорядоченных пар из R.
Множество значений отношения R на А и В есть
множество всех у В таких, что (х, у) R для
некоторого х А.
Множество значений R есть множество всех вторых
координат упорядоченных пар из R.

6. С каждым отношением R на A  B связано отношение R -1 на B  A.

С каждым отношением R на A B связано отношение
R -1 на B A.
Пусть R A B есть отношение на A B.
Тогда отношение R -1 на В А определяется следующим
образом:
R -1={(b, a): (a, b) R}.
(b, a) R -1 тогда и только тогда, когда (a, b) R,
что равносильно bR -1a тогда и только тогда, когда aRb.
Отношение R -1 называется обратным отношением к
данному отношению R.

7. Примеры

Пусть R={(1, r), (1, s), (3, s)},
тогда R -1 = {(r, 1), (s,1), (s, 3)}.
Пусть {(x,y): x - является мужем y},
тогда R -1 – отношение {(x,y): у – жена х}.
Пусть R – отношение {(x,y): y является родственником х},
тогда R = R -1.
Пусть R – отношение {(x,y): х2 + y2 =4},
тогда R = R -1.

8. Определение

Пусть R A B – отношение на A B,
а S B C – отношение на B C.
Композицией отношений S и R называется отношение
T A C, определенное таким образом:
Т={(a, c): существует такой элемент b из B,
что (a, b) R и (b, с) S}.
Это множество обозначается Т = S R.

9. Пример

Пусть А={1, 2, 3}, B={x, y}, C=
Пусть отношения R на A B и S на B C заданы в
виде:
тогда

10.

поскольку
……

11. Пример

Пусть R и S – бинарные отношения на множестве
положительных целых чисел, заданные в виде
S = {(x, x+2): x – положительное целое число} и
R = {(x, x2): x –положительное целое число} и
R S = {(x, (x+2)2): x – положительное целое число}

12. Теорема

Композиция отношений ассоциативна: если A, B, C и D –
множества и если R A B, S B C и T C D,
тогда T (S R ) = (T S) R.
Доказательство:
Пусть (a, d) T (S R), тогда существует такое с С,
что (a, c) S R и (c, d) T.
Поскольку (a, c) S R, существует такое b B, что
(a, b) R и (b, c) S.
Поскольку (b, c) S и (c, d) T, (b, d) T S.
Поскольку (b, d) T S и (a, b) R, (a, d) (T S) R.
Таким образом, T (S R) (T S) R.
Вторая часть доказательства, что (T S) R T (S R)
аналогична.

13. Определения

Отношение R на A A называется рефлексивным, если
(a, a) принадлежит R для всех a из А.
Отношение R называется антирефлексивным, если из
(a, b) R следует a b.
Отношение R симметрично, если для всех a и b,
принадлежащих А, из (a, b) R следует, что (b, a) R.
Отношение R транзитивно, если для всех a, b и с из А,
(a, b) R и (b, с) R, следует, что (a, c) R.
Отношение R называется антисимметричным, если для
всех a и b из А, из принадлежности (a, b) и (b, a)
отношению R следует, что a=b.

14. Пример

Пусть А = {1, 2, 3, 4, 5, 6} и пусть отношение R1 A A
есть множество R1 = {(1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6,6),
(1, 2), (1, 4), (2, 1), (2, 4), (3, 5), (5, 3), (4, 1), (4, 2)}.
Отношение R1 рефлексивно, так как для каждого a A,
(a, a) R1.
Отношение R1 является симметричным:

15.

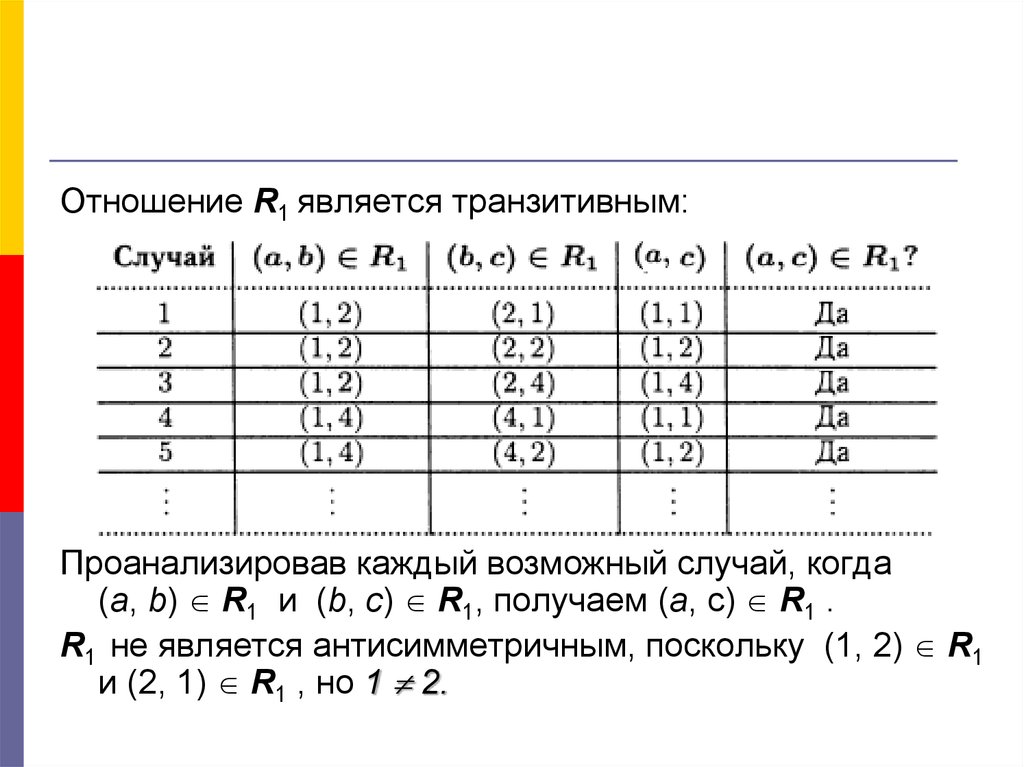
Отношение R1 является транзитивным:
Проанализировав каждый возможный случай, когда
(a, b) R1 и (b, c) R1, получаем (a, с) R1 .
R1 не является антисимметричным, поскольку (1, 2) R1
и (2, 1) R1 , но 1 2.

16. Пример

Пусть А – множество положительных чисел.
Отношение R: (x, y) R, y кратно х.
R рефлексивно, т.к. для каждого положительного числа
n, n=1 n и (n, n) R.
R не является симметричным, так как (2, 4) R, но
(4, 2) R.
R антисимметрично, так как если (m, n) R и (n, m) R,
тогда n кратно m и m кратно n, так что m=n.
R транзитивно, потому что если (m, n) R и (n, p) R,
тогда n кратно m и p кратно n, так что p кратно m
и (m, p) R.

17. Определения

Пусть R – бинарное отношение на множестве А.
Рефлексивное замыкание R есть наименьшее
рефлексивное отношение на А, содержащее R как
подмножество.
Симметричное замыкание R есть наименьшее
симметричное отношение на А, содержащее R как
подмножество.
Транзитивное замыкание R есть наименьшее
транзитивное отношение на А, содержащее R как
подмножество.

18. Теорема

Пусть R – отношение на множестве А и I = {x: x=(a, a) для
некоторого a A}. Тогда:
1) R I есть рефлексивное замыкание R;
2) R R -1 есть симметричное замыкание R;
3) Если А – конечное множество, содержащее n
элементов, то отношение
R R 2 R 3 … R n есть транзитивное замыкание R.

19. Начальные сведения о графах. Подробно в о 2 семестре Граф – наглядное представление конечного антирефлексивного симметричного

отношения
Граф – конечное множество V, называемое
множеством вершин, на котором задано
симметричное антирефлексивное отношение R и
выделено множество Е двухэлементных подмножеств
V, определяемое как {a, b} E тогда и только тогда,
когда (a, b) R и a b.
Множество Е называется множеством ребер. Всякий
элемент Е называется ребром.
Граф обозначается G(V, E).
Элементы a и b графа V соединены или связаны
ребром {a, b}, если {a, b} E.

20. Конечный граф изображается при помощи диаграммы, в котором вершины представлены точками, ребра, соединяющее вершины, линиями

между точками.
Пример
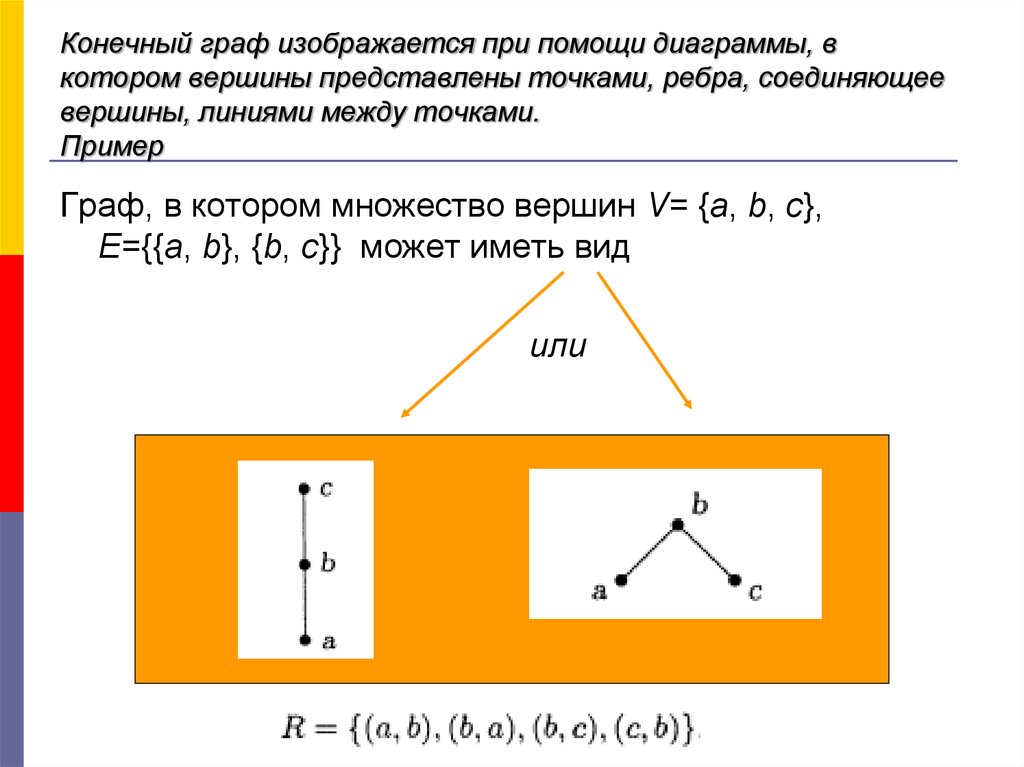
Граф, в котором множество вершин V= {a, b, c},
E={{a, b}, {b, c}} может иметь вид
или

21. Пример

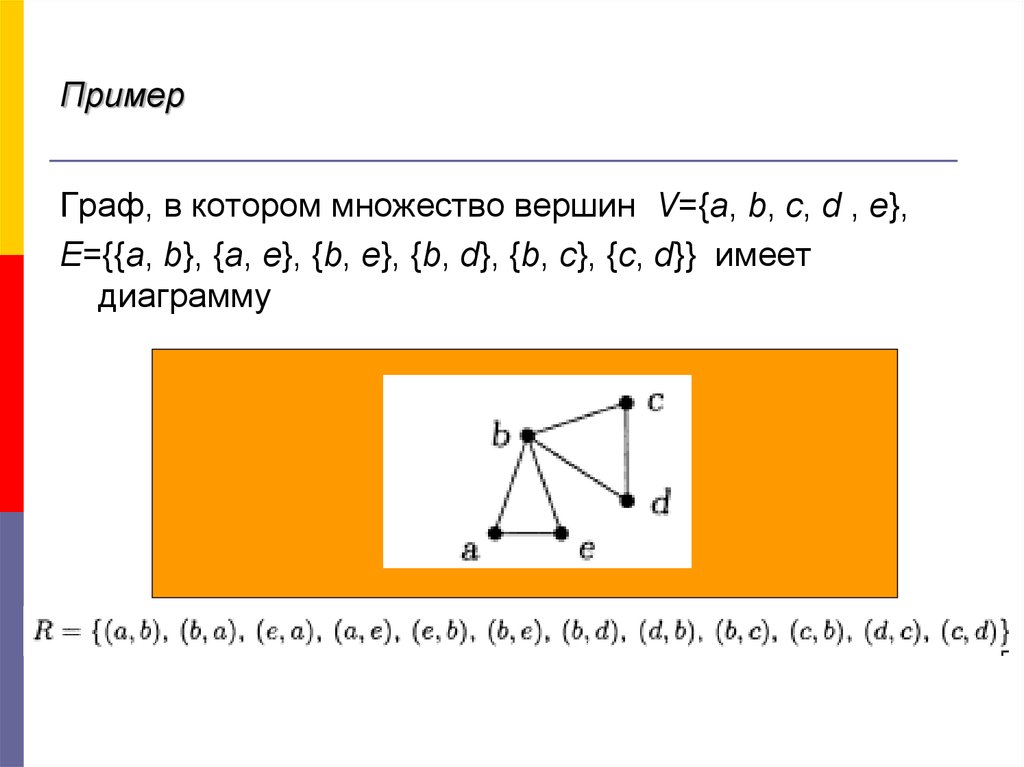
Граф, в котором множество вершин V={a, b, c, d , e},
Е={{a, b}, {a, e}, {b, e}, {b, d}, {b, c}, {c, d}} имеет
диаграмму

22. Определения

Ориентированный граф, или орграф G состоит из
множества V вершин и отношения E на V,
называемого множеством ориентированных ребер
или просто ребер, если понятно, что граф
ориентирован.
Обозначается G(V, E)
Элемент множества Е называется ориентированным
ребром.
Если (a, b) E, тогда a называется начальной
вершиной (a, b), b - его конечной вершиной.

23. В случае ориентированного графа допускается наличие петель. Пример

Орграф с вершинами
V={a, b, c} и ребрами E={(a, b), (b, c), (c, b), (c, a)}
Порядок имеет значение. (a, b) может быть ребром
диаграммы, (b, a) – нет.

24. Пример

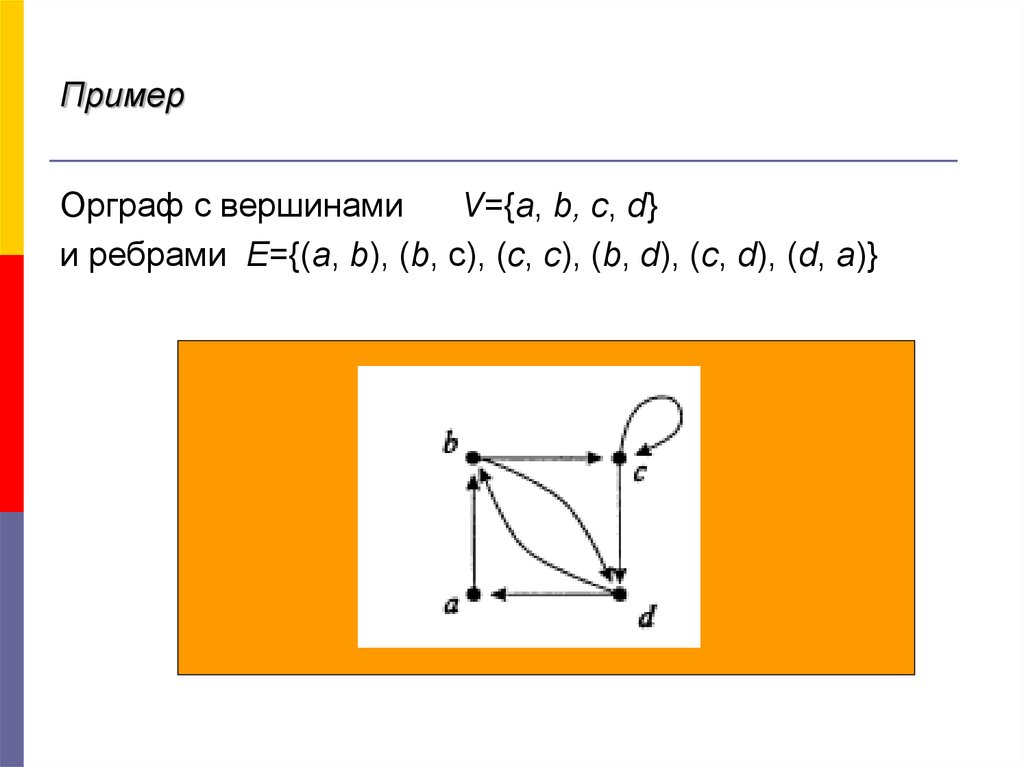
Орграф с вершинами
V={a, b, c, d}
и ребрами E={(a, b), (b, c), (c, c), (b, d), (c, d), (d, a)}

25. Определение

Отношение R на А есть отношение частичного
порядка, если оно рефлексивно, симметрично и
транзитивно.
Если отношение R на А является отношением частичного
порядка, то (А, R) называют частично
упорядоченным множеством (или ЧУ-множеством
с порядком R).
Если отношение порядка R предполагается по
умолчанию, то (А, R) можно обозначить просто через
А.

26. Пример (*)

Пусть С = {1, 2, 3}, Х – множество всех подмножеств
множества С:
Определим отношение R на Х посредством (T, V) R,
если T V.
({2}, {1, 2}) R, поскольку {2} {1, 2} и
({1, 2}, {3}) R, поскольку {2, 3} {3}.
R – отношение частичного порядка,
(A, R) – ЧУ-множество.

27. Пример

Пусть S – множество действительных чисел,
R1 – отношение, определенное условием (x, y) R1,
если х у.
R1 – отношение частичного порядка,
(S, R1) – ЧУ-множество.
Обозначение.
Частично упорядочение принято обозначать через
а ЧУ-множество - через (S, ).
-частичный порядок на множестве S.

28. Определение

Два элемента a и b ЧУ-множества (S, ) сравнимы, если
a b или b a.
Если каждые два элемента ЧУ-множества (S, )
сравнимы, то (S, ) называется вполне
упорядоченным множеством, или цепью.

29. Примеры

Пусть Т – множество положительных делителей числа 30
и 1 есть отношение m 1 n, если m делит n нацело.
Целые числа 5 и 15 сравнимы, поскольку 5 делит 15
нацело, а 5 и 6 – нет.
Пусть А – множество целых чисел и
R= 2 – отношение х 2 у, если х меньшее или равно у.
Упорядоченное множество (А, 2) является цепью.

30. Пример

Пусть S – множество всех подмножеств множества
{a,b,c} 3 есть отношение частичного порядка в
примере (*).
Множества {a, b} и {a,b,c} сравнимы,
однако {a, b} и {b,c} таковыми не являются.
ЧУ-множество (S, 3) цепью не является.

31. Диаграммы Гессе

Для изображения ЧУ-множеств.
Для заданного ЧУ-множества (А, 2) диаграмма Гессе
состоит из совокупности точек и линий, в которой точки
представляют элементы А, и если a c для элементов
a и с множества А, тогда а помещено ниже с, и они
соединены линией, если не существует такое b a, c,
что a b c.
Если рассмотрение отношений ограничено отношениями
частичного порядка, для них диаграммы Гессе –
просто ориентированный граф, в котором петли не
указаны.
Если a b c, тогда линия от a к с не указана.

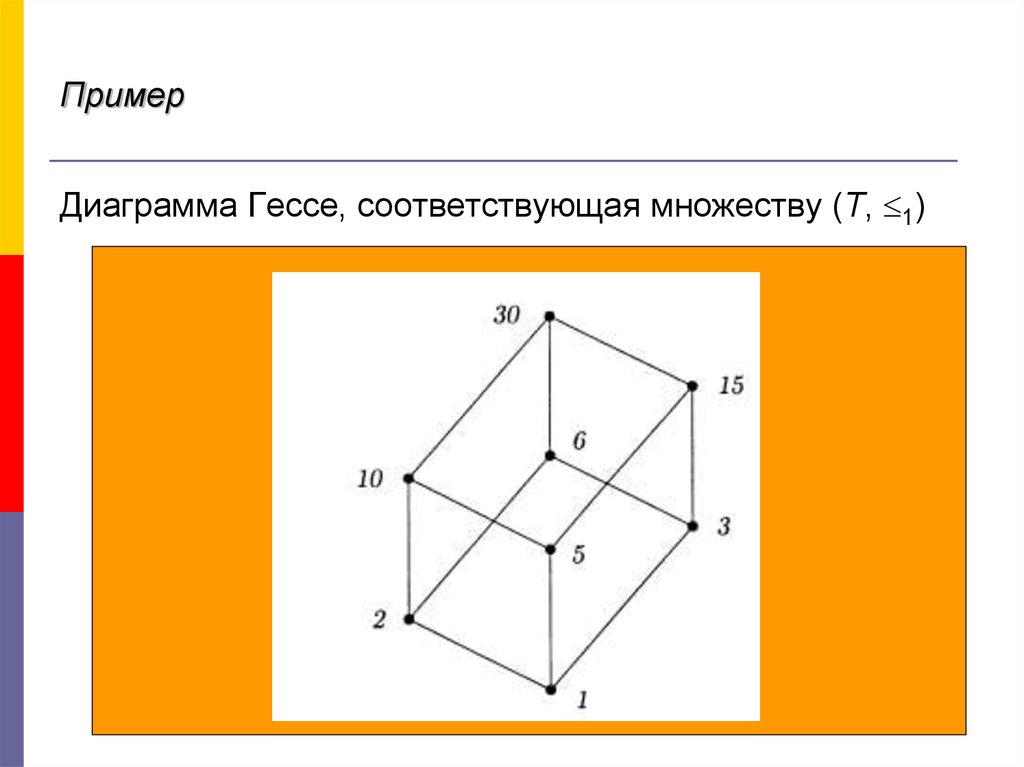
32.

Пример
Диаграмма Гессе, соответствующая множеству (Т, 1)

33.

Пример
Диаграмма Гессе, соответствующая множеству (S, 3)

34. Задания для самостоятельной работы

1.
2.

35.

Отношения эквивалентности

36. Определение

Отношение R на А есть отношение эквивалентности,
если оно рефлексивно, симметрично и транзитивно,
Пример (**).
Пусть А – множество целых чисел.
Отношение R3 А А посредством R3 ={(a, b): a – b = 5 k
для некоторого числа k}.
Например, (7,2) R3 , т.к. 7 – 2 = 5 = 5 1,
(-11, 4) R3 , т.к. (-11) – 4 = -15 = 5 (-3)

37.

Отношение R3 рефлексивно.
Если а – целое число (а А), то a – a = 0 = 5 0 = 5 k
для k = 0. (а, а) R3 .
Отношение R3 симметрично.
(a, b) R3 . Тогда существует целое m, что a – b = 5 m
для m – целого. (b, a) R3

38.

Отношение R3 транзитивно.
Предположим, a, b, c – целые числа,
(a, b) R3 и (b, c) R3 .
Если (a, b) R3 , тогда a – b = 5 k для некоторого
целого числа k,
Если (b, c) R3 , тогда b – c = 5 m для некоторого
целого m.
Суммирование левых и правых частей:
или
для целого числа k + m. (a, c) R3.

39.

Отношение эквивалентности R на множестве А
разбивает его на подмножества, элементы
которых эквивалентны друг другу
и не эквивалентны элементам других множеств.
В контексте отношений эквивалентности эти
подмножества называются классом
эквивалентности по отношению R.

40. Пример

Пусть множество А – набор разноцветных шаров, а
отношение R задается условием:
(a, b) R тогда и только тогда, когда a и b имеют
одинаковый цвет. Поскольку R – отношение
эквивалентности, каждый класс эквивалентности будет
состоять из шаров, имеющих одинаковый цвет.
Если определить отношение R условием:
(a, b) R тогда и только тогда, когда шары a и b имеют
одинаковый диаметр, то каждый класс
эквивалентности будет состоять из шаров одинакового
размерами.

41. Определение

Пусть a A, и R - отношение эквивалентности на А А.
Пусть [а] обозначает множество
{x: xRa} = {x: (x, a) R}, называемое классом
эквивалентности, содержащим а.
Символ [A]R обозначает множество всех классов
эквивалентности множества А по отношению R.

42. Пример

Отношение R1 есть отношение эквивалентности на
множестве А = {1, 2, 3, 4, 5, 6}.
Классы эквивалентности по отношению R1 были
получены путем определения класса эквивалентности
каждого элемента множества А:
где 1 [1], поскольку (1, 1) R1,
2 [1], поскольку (2, 1) R1,
4 [1], поскольку (4, 1) R1, и не существует иного х из
А, что (х, 1) R1. Также:

43.

Также:

44.

Имеется только три различных класса эквивалентности:
поэтому

45.

Из примера видно, что любой элемент класса
эквивалентности порождает класс эквивалентности.
Если b [a], то [a] = [b].
Любой класс эквивалентности представляет класс.
Каждый класс эквивалентности содержит по крайней
мере один элемент.
В силу рефлексивности отношения, множество всех
элементов, эквивалентных элементу а, должно
содержать а.
С другой стороны, никакой элемент не может
принадлежать двум различным классом
эквивалентности.

46. Пример

Рассмотрим отношение эквивалентности R3 и примера
(**). Для множества А всех целых чисел R3 А А
определено посредством R3 = {(a, b): a – b = 5 k для
некоторого целого числа k}.
Поскольку
следует

47.

48.

представляют собой различные классы эквивалентности по
отношению R3 .
Таким образом
Элементы [0] “похожи” в том смысле, что каждый из них кратен пяти.
Элементы другого класса эквивалентности “похожи” том смысле, что
имеют один и тот же остаток при делении на пять.

49. Определения

Совокупность классов эквивалентности разделяет все
множество А на непустые взаимоисключающие, или
непересекающие подмножества, в том смысле, что
никакие два из них не имеют общих элементов.
Такое разделение множества называется его
разбиением.
Пусть A и I – множества и пусть А = {Ai : i I}, где I
непусто, есть множество непустых подмножеств
множества А. Множество А называется разбиением
А, если выполнены условия:

50. Теорема

Непустое множество подмножеств А множества А есть
разбиение А тогда и только тогда, когда А = [A]R по
некоторому отношению эквивалентности R.

51. Пример

Пусть
Рассмотрим разбиение
Необходимо определить R таким образом:
R = {(a, b) : a Ai и b Ai для некоторого i }.
Итак
есть отношение, соответствующее данному разбиению.

52.

Последний слайд лекции