Арифметическая прогрессия

1. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

2. Основные формулы арифметической прогрессии:

Рекуррентный способ задания
арифметической прогрессии
an+1=an+d
Разность прогрессии
Формула n-ого члена
Характеристическое свойство
Сумма п-первых членов
арифметической прогрессии
d=an+1-an
an=a1+d(n-1)
2a1 d п 1
Sn
n
2

3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ

4. Основные формулы геометрической прогрессии:

Рекуррентный способ задания
геометрической прогрессии
b
n 1
q
Знаменатель прогрессии
Формула n-ого члена
Характеристическое свойство
b
n
q
b
b
n 1
n
b
b
b
2
n
n
n
b1 b
n 1
bn 1 bn 1
b b
n 1
n 1

5.

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Число d –
называется
разностью
арифметическо
й прогрессии.
Число q –
называется
знаменателем
геометрической
прогрессии.

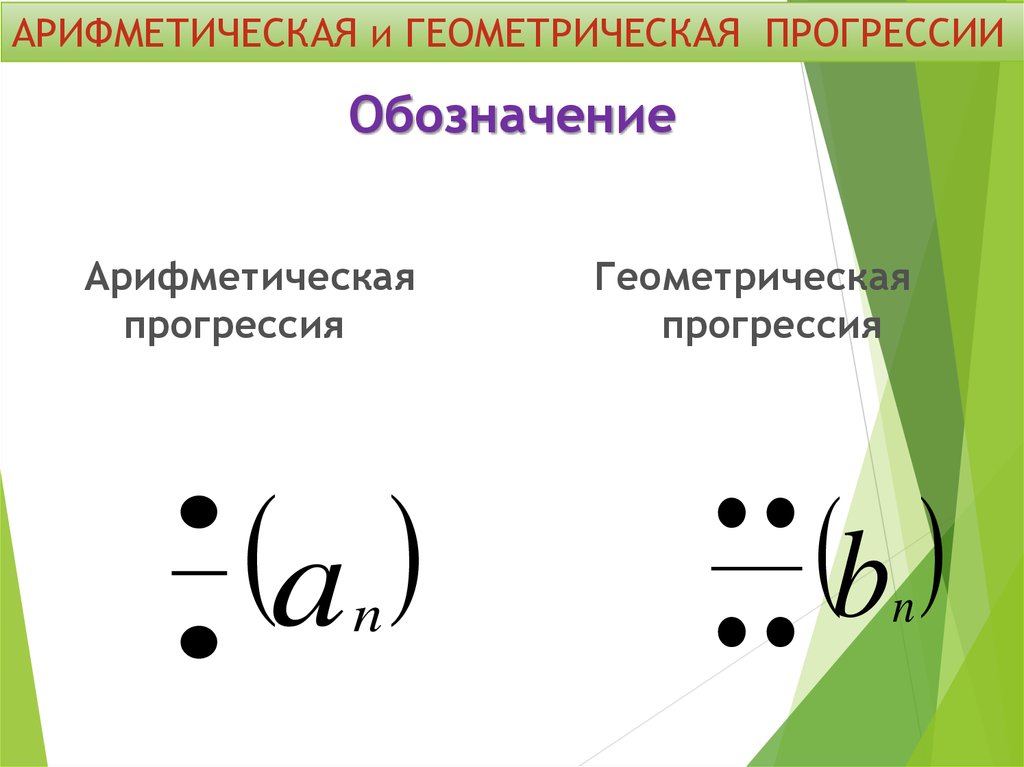
6. Обозначение

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Обозначение
Арифметическая
прогрессия
a
n
Геометрическая
прогрессия
b
n

7. Допустимые значения

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Допустимые значения
Арифметическая
прогрессия
a1 , d
любые числа
Геометрическая
прогрессия
,
b1 q
числа неравные
нулю

8. Рекуррентная формула

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Рекуррентная формула
Арифметическая
Геометрическая
прогрессия
прогрессия
an 1 an d
n N
bn 1 bn q
n N

9. Нахождение

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Нахождение
разность
арифметической
прогрессии
d a n 1 a
n
знаменатель
геометрической
прогрессии
q
b
b
n 1
n
n N
n N

10. Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Используя рекуррентную формулу,
получим формулу общего члена
геометрической
прогрессии.
b b q
b b q b q q b q
b b q b q q b q
b b q b q q b q
2
3
1
2
1
1
2
4
3
1
Итак,
4
1
b
n
3
1
3
5
2
4
1
b1 b
n 1

11. Формула n-го члена

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Формула n-го члена
арифметическая
геометрическая
прогрессия
прогрессия
an a1 d n 1 bn b1 b
n N
n N
n 1

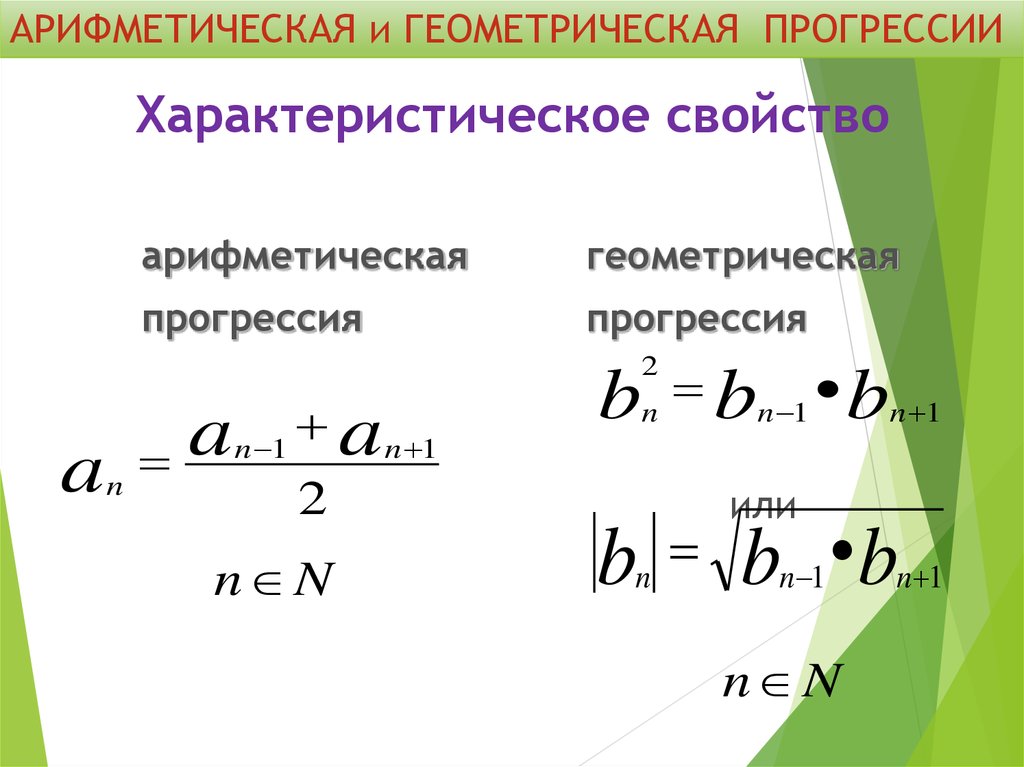
12. Характеристическое свойство

АРИФМЕТИЧЕСКАЯ и ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ
Характеристическое свойство
a
n
арифметическая
геометрическая
прогрессия
прогрессия
a
n 1
a n 1
b
b
n
n 1 bn 1
2
2
n N
b
n
или
b b
n 1
n N
n 1