Похожие презентации:
Схематизация опор. Определение реакций
1. Схематизация опор Определение реакций
12.
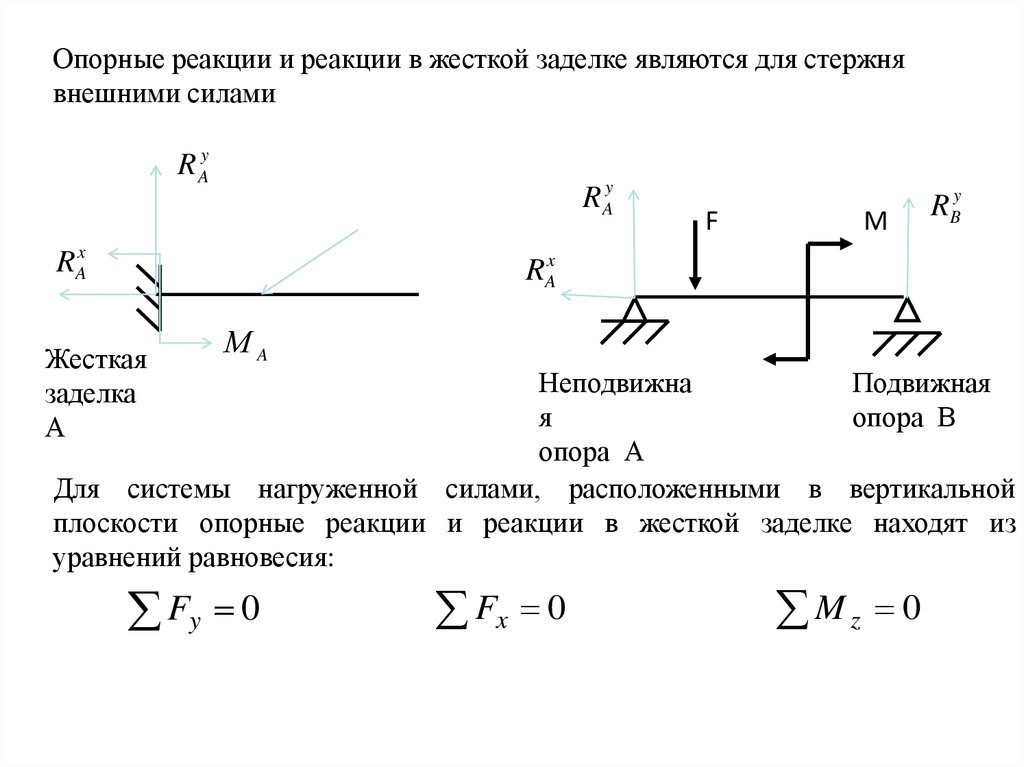
Опорные реакции и реакции в жесткой заделке являются для стержнявнешними силами
R Ay
R Ay
RAx
F
M
RBy
RAx
Жесткая
заделка
А
МA
Неподвижна
Подвижная
я
опора В
опора А
Для системы нагруженной силами, расположенными в вертикальной
плоскости опорные реакции и реакции в жесткой заделке находят из
уравнений равновесия:
Fy 0
Fx 0
Mz 0
3.
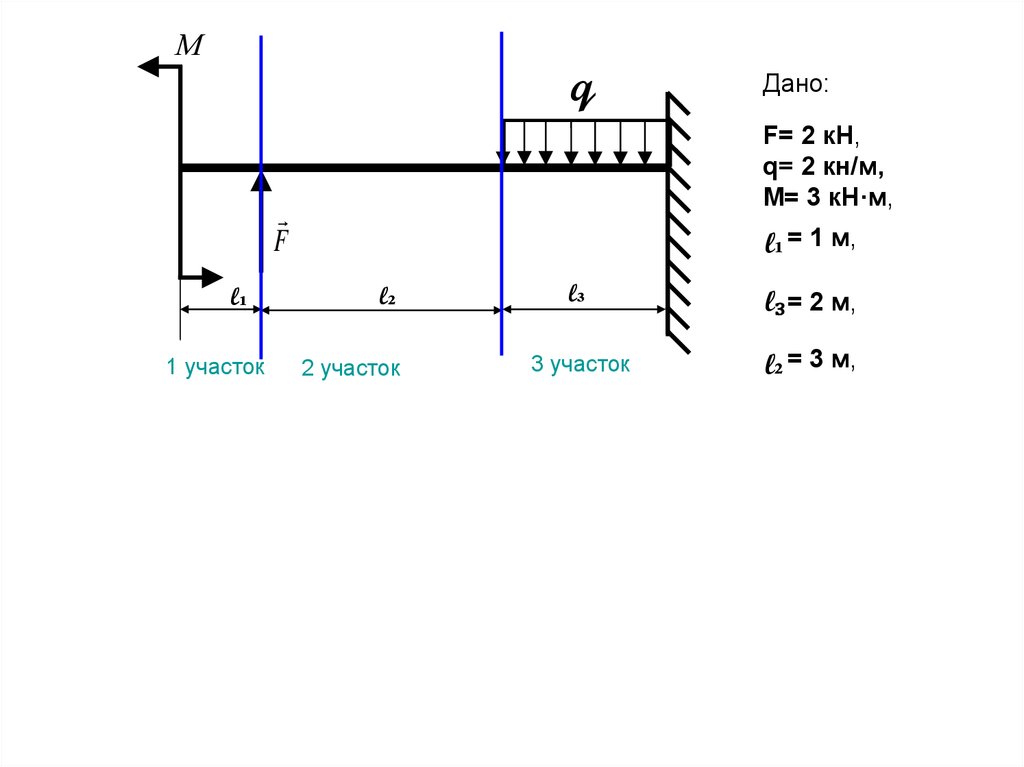
Мq
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
F
l₁
Дано:
l₁ = 1 м,
l₂
l₃
l₃ = 3 м,
l₂ = 2 м,
4.
Мq
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
F
l₁
1 участок
Дано:
l₁ = 1 м,
l₂
2 участок
l₃
l₃ = 2 м,
3 участок
l₂ = 3 м,
5.
М1
2
1 участок
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
1 F
l₁
q
l₁ = 1 м,
2
l₂
2 участок
l₃
l₃ = 3 м,
3 участок
l₂ = 2 м,
6.
М3
1
2
1 участок
Дано:
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
1 F
l₁
q
2
l₂
2 участок
3
l₃
3 участок
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,
7.
М 33
q
2
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
x
F
х
l₁
1 участок
2
3
l₃
l₂
0 Х 1 м
1 участок
2 участок
Дано:
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,
Рассмотрим первый грузовой участок
На первом участке поперечная сила
Q1
Q1 постоянна и равна нулю
= 0,
8.
М 33
q
2
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
x
F
х
2
3
l₃
l₂
l₁
1 участок
0 Х 1 м
2 участок
1 участок
В сечении на первом участке изгибающий момент
М1 = - М ,
М 1 = - 3 кН • м
Дано:
l₁ = 1 м,
l₃ = 3 м,
l₂ = 2 м,
М 1 равен
9.
М 3Дано:
х
x
F 2
l₁ = 1 м,
l₂
l₁
1 участок
l₃ = 3 м,
l₂ = 2 м,
2 участок
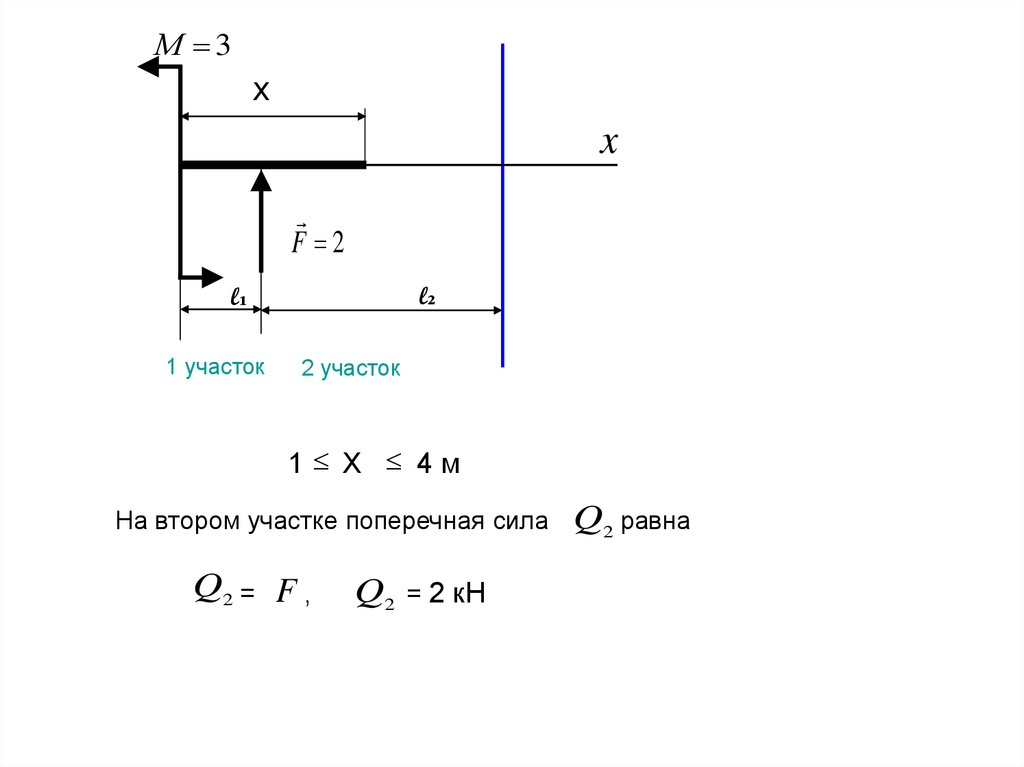
1 Х 4м
На втором участке поперечная сила
Q2 = F ,
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
Q2 = 2 кН
Q2 равна
10.
М 3Дано:
х
x
F 2
l₁ = 1 м,
l₂
l₁
1 участок
l₃ = 3 м,
l₂ = 2 м,
2 участок
1 Х 4м
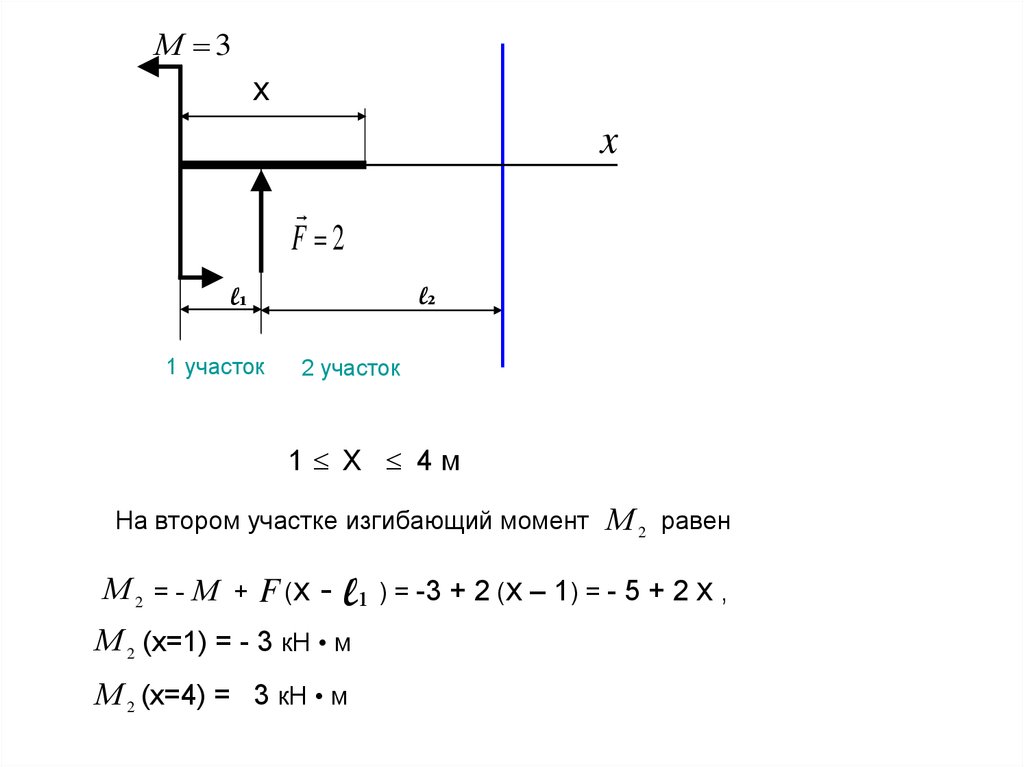
На втором участке изгибающий момент
М 2 = - М + F (х -
F= 2 кН,
q= 2 кн/м,
М= 3 кН·м,
М 2 равен
l₁ ) = -3 + 2 (х – 1) = - 5 + 2 х ,
М 2 (x=1) = - 3 кН • м
М 2 (x=4) = 3 кН • м
11.
М 3q=2
х
x
F 2
l₃
l₂
l₁
1 участок
2 участок
3 участок
4 Х 6м
На третьем участке поперечная сила
Q3 = F
-
Определим
Q3
равна
q [ х – ( l₁ + l₂) ] = F- q [ х – (1 + 3)] = F - q (х – 4)
Q3 на границах третьего участка
Q3(x=4) = 2 – 2(4-4) = 2 кН
Q3(x=6) = 2 – 2(6-4) = - 2 кН
12.
М 3q=2
х
x
F 2
l₁
1 участок
l₃
l₂
2 участок
3 участок
4 Х 6м
На третьем участке изгибающий момент М 3 равен
2
М 3 = - М + F • ( х – l₁ ) – q[х - ( l₁2 + l₂) ] / 2
М 3 = - М + F •( х – 1) – q(х - 4) /2
Определим М 3 на границах третьего участка
2
(x=4)
=
-3
+
2(4-1)
2
0
/2= 3 кН • м
М3
2
М 3(x=6) = -3 + 2(6-1) - 2 • 2 /2 = 3 кН • м
13.
dMЕсли Q =
= 0, то изгибающий момент имеет максимум.
dx
Q3 = F - q (х – 4) = 0
2-2 (х – 4)=0 , х = 5 м
Максимум момента равен 4 кН• м
14.
При построении эпюр следует руководствоватьсяприведенными правилами:
Эпюру моментов строят на сжатом волокне, т. е. положительные
моменты (и положительные поперечные силы) откладывают вверх
от оси, а отрицательные — вниз.
Пользуясь принципом смягченных граничных условий, будем
полагать, что в сечении, где приложена сосредоточенная сила,
значение поперечной силы меняется скачкообразно, причем скачок
равен модулю этой силы.
На том же основании будем полагать, что в сечении, где
приложена пара сил (момент), значение изгибающего момента
меняется скачкообразно, причем скачок равен моменту пары.
Если в каком-либо сечении балки приложена сосредоточенная
сила, то на эпюре поперечных сил в этом сечении будет скачок на
величину силы, а на эпюре изгибающих моментов произойдет
излом эпюры.
Если участок балки загружен равномерно распределенной нагрузкой q, то на эпюра поперечных сил на этом участке ограничена
наклонной прямой, а эпюра моментов – кривой второго порядка.
15.
Правильность построения эпюр Q и М следует проверять спомощью теоремы Журавского:
Между изгибающим моментом, поперечной силой и интенсивностью
распределенной нагрузки существуют дифференциальные
зависимости, основанные на теореме Журавского.
Эта теорема формулируется так: поперечная сила равна
первой производной от изгибающего момента по
абсциссе сечения балки.
dM
d 2M
dQ
q= dx = dx2
Q = dx = tg ,
где — угол, который составляет касательная к эпюре моментов с
положительным направлением оси x.
16.
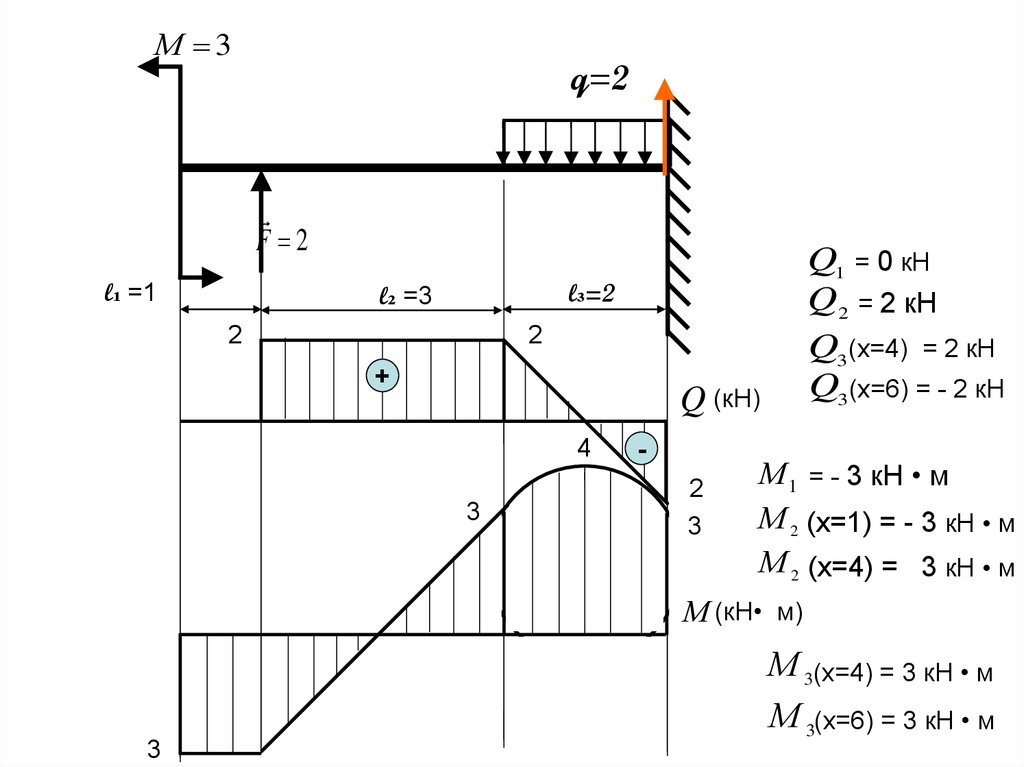
М 3q=2
F 2
l₁ =1
Q1 = 0 кН
Q2 = 2 кН
Q3 (x=4) = 2 кН
Q3(x=6) = - 2 кН
l₃=2
l₂ =3
2
2
+
Q (кН)
4
3
-
2
3
М 1 = - 3 кН • м
М 2 (x=1) = - 3 кН • м
М 2 (x=4) = 3 кН • м
М (кН• м)
3
М 3(x=4) = 3 кН • м
М 3(x=6) = 3 кН • м
17. Определение реакций
АПример 1. Определить реакции.
y
RA= 3 кН
F= 5 кН
H= 0
RB= 2
кН
1. Показываем реакции.
2. Считаем число реакций
х
А
2м
3м
В
3. Из уравнений статики определяем реакции.
∑ МА = 0.
RB · 5 – F · 2 = 0.
RB = (5 · 2) / 5 = 2 кН.
∑ Мв = 0.
RА · 5 – F · 3 = 0.
RА = (5 · 3) / 5 = 3 кН.
∑ Х = 0.
-HA = 0.
Проверка:
∑ Y= 0.
HA = 0.
R А + RB – F = 0.
3 + 2 – 5 = 0. 0 = 0.
Подписываем реакции.
17
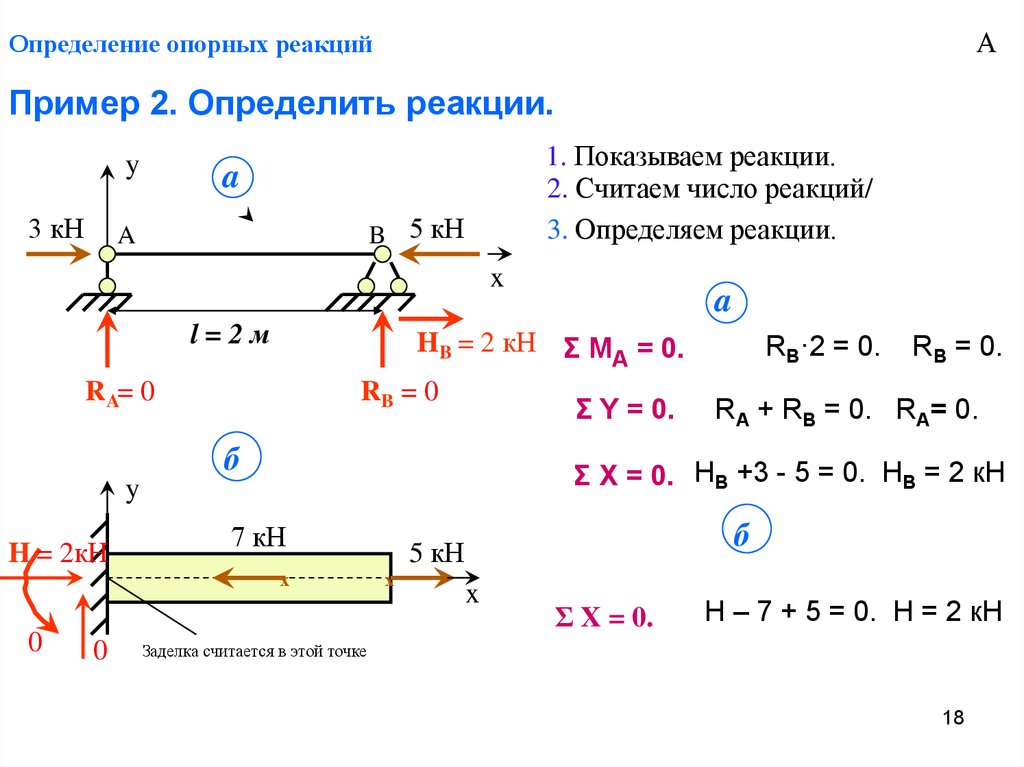
18. Определение опорных реакций
АОпределение опорных реакций
Пример 2. Определить реакции.
y
3 кН
1. Показываем реакции.
2. Считаем число реакций/
3. Определяем реакции.
a
B 5 кН
A
x
l=2м
HB = 2 кН Σ M = 0.
A
RB = 0
Σ Y = 0.
RA= 0
б
7 кН
х
0
0
RB·2 = 0.
RB = 0.
RA + RB = 0. RA= 0.
Σ X = 0. HB +3 - 5 = 0. HB = 2 кН
y
H = 2кН
a
б
5 кН
х
x
Σ X = 0.
Н – 7 + 5 = 0. Н = 2 кН
Заделка считается в этой точке
18
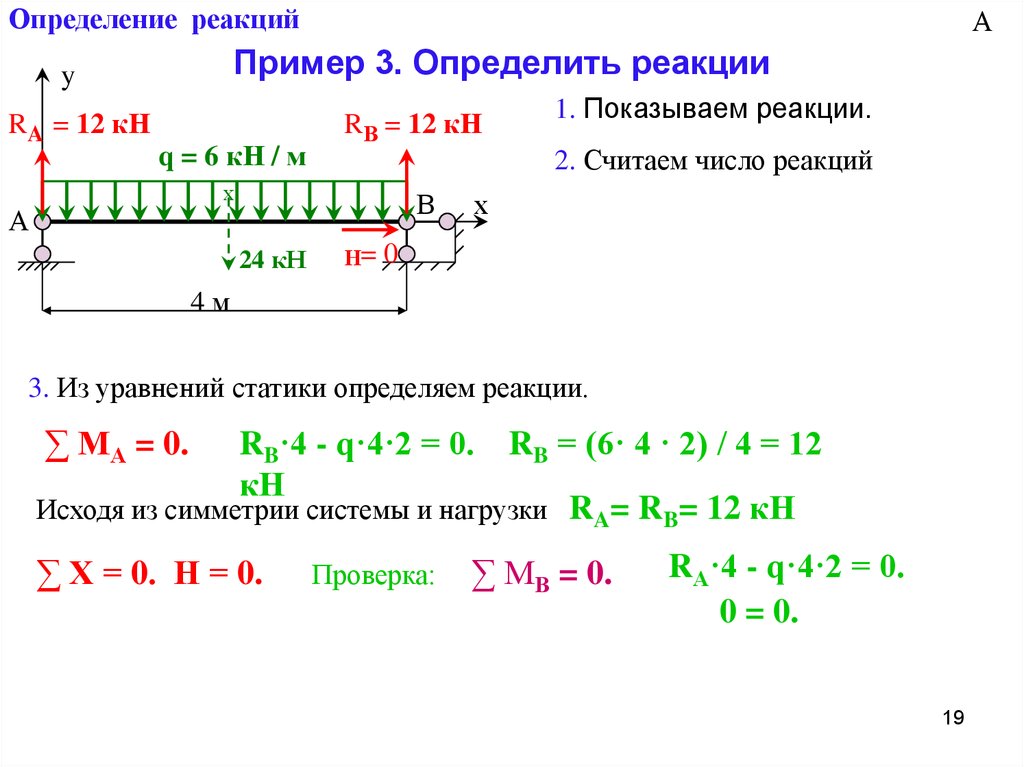
19. Определение реакций
Пример 3. Определить реакцииy
RA = 12 кН
А
q = 6 кН / м
RВ = 12 кН
х
А
В
24 кН
Н=
1. Показываем реакции.
2. Считаем число реакций
х
0
4м
3. Из уравнений статики определяем реакции.
∑ МА = 0.
RB·4 - q·4·2 = 0.
кН
RB = (6· 4 · 2) / 4 = 12
Исходя из симметрии системы и нагрузки RA= RB= 12 кН
∑ Х = 0. Н = 0.
Проверка:
∑ МВ = 0.
RА·4 - q·4·2 = 0.
0 = 0.
19
20. Определение опорных реакций
АОпределение опорных реакций
Пример 4. Определить реакции.
RA = -1 кН
А
RB= 5 кН
H =0
F = 4 кН
1. Показываем реакции.
2. Считаем число реакций
y
В
х
М = 5 кН·м
3м
2м
∑ Х = 0. -Н = 0. Н = 0.
3. Определяем реакции.
∑ МА = 0.
∑ МВ = 0.
RB ·3 - F·5 + М = 0.
-RА ·3 - F·2 + М = 0.
RB = (4 · 5 – 5) / 3 = 5 кН
RА = (- 4 · 2 + 5) / 3 = - 1 кН < 0
Проверка: ∑ Y = 0.
RA + RB – F = 0. -1 + 5 – 4 = 0. 0 = 0.
20
21. Определение реакций
АПример 5. Определить реакции.
При одновременном действии различных видов нагрузки
можно пользоваться принципом суперпозиции и расслаивать
нагрузку по видам:
8 кН
F=4
кН
8 кН
q=3 кН / м
l=4м
2 кН
4 кН
2 кН
6кН
6кН
3 кН / м
4м
4м
21
22. Определение реакций
Пример 6. Определить реакции.RA = 1.33 ql
q
2l
M = ql
2
F = ql
RB
1. Показываем реакции.
= - 0.33 ql
2. Считаем число реакций .
Н= 0
l
3. Определяем реакции.
∑MB = 0.
∑ МА = 0.
– q ∙2l ∙ l + M +F ∙2l + RB∙3l = 0;
– q ∙2l ∙ l + ql 2 + ql ∙2l + RB ∙3l = 0;
RB = - 0.33 ql < 0
– RA∙3l + q∙2l ∙2l + M - F ∙l = 0;
– RA∙3l + q∙2l ∙2l + ql 2 – ql ∙l = 0;
RA = 1.33 ql.
Проверка : ∑ Y = 0.
RA + RB – q∙2l + F = 0;
1.33 ql – 0.33 ql – 2ql + ql = 0.
0 = 0.
22
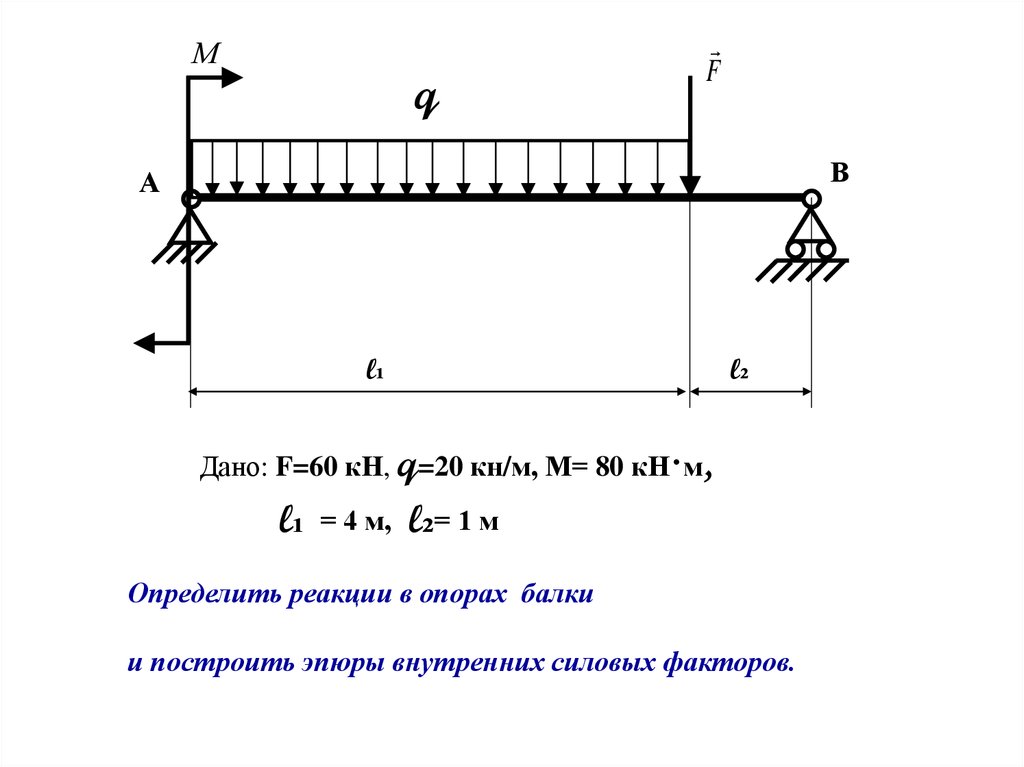
23.
Мq
F
В
А
l₁
l₂
Дано: F=60 кН, q=20 кн/м, М= 80 кН·м,
l₁
= 4 м,
l₂= 1 м
Определить реакции в опорах балки
и построить эпюры внутренних силовых факторов.
24.
Используя принцип освобождаемости от связейпредставляем тело свободным и вместо связей
указываем реакции в точках А и В.
Определяем реакции связей (опорные реакции).
25.
RАМ
F
q
RВ
В
А
Q
l₁
l₂
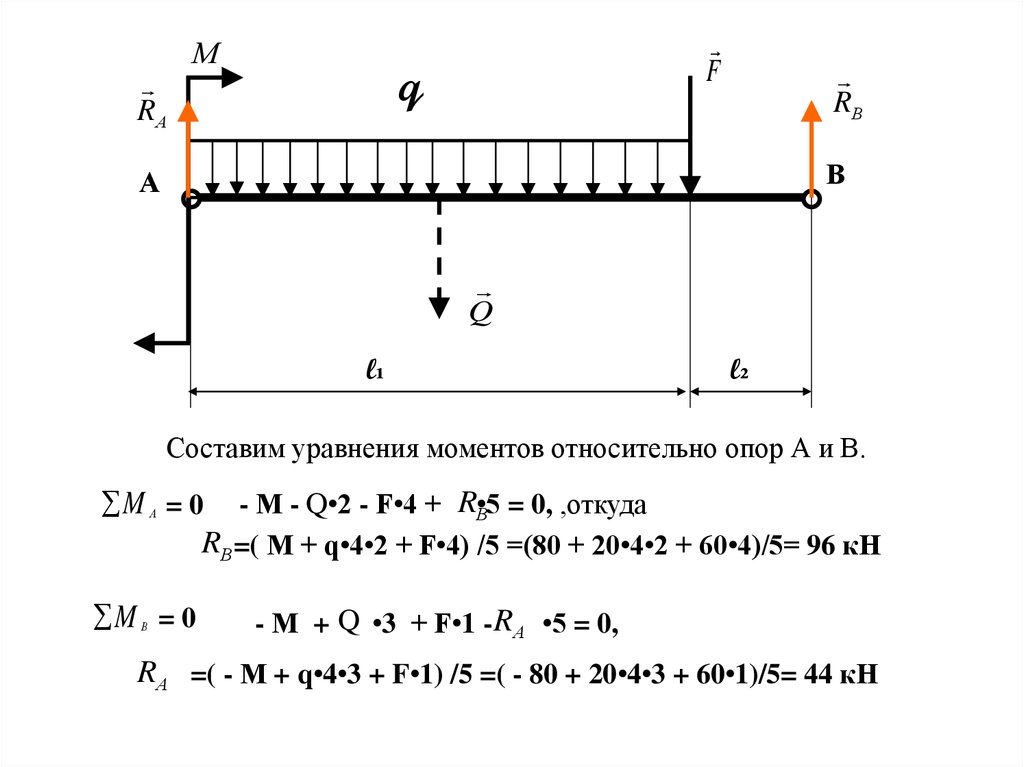
Составим уравнения моментов относительно опор А и В.
M = 0 - М - Q•2 - F•4 + RВ•5 = 0, ,откуда
RВ =( М + q•4•2 + F•4) /5 =(80 + 20•4•2 + 60•4)/5= 96 кН
А
M = 0
В
- М + Q •3 + F•1 - RА •5 = 0,
RА =( - М + q•4•3 + F•1) /5 =( - 80 + 20•4•3 + 60•1)/5= 44 кН
26.
Проверим правильность определения реакций, составив уравнениепроекций на ось у:
Y =0
RА + RВ - 4•q - F = 44 + 96 – 80 – 60 = 0
Полученное тождество 0 = 0 говорит о том, что реакции определены правильно.
Разобьем балку на грузовые участки и применим метод сечений.
Напомним, что в общем случае границами участков балки являются концы
балки, опоры, начало и конец распределенной нагрузки, точки приложения
сосредоточенных сил и внешних моментов.
27.
RАМ
q
F
RВ
В
А
l₁
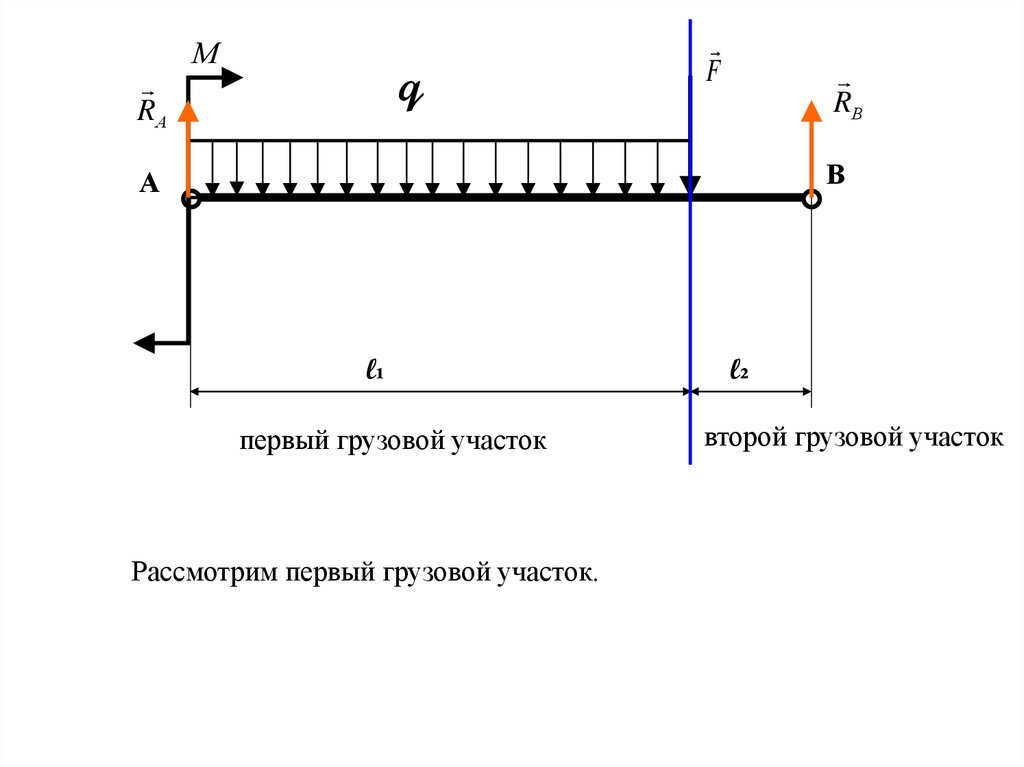
первый грузовой участок
Рассмотрим первый грузовой участок.
l₂
второй грузовой участок
28.
RАМ
q
1
x
А
Х
1
l₁
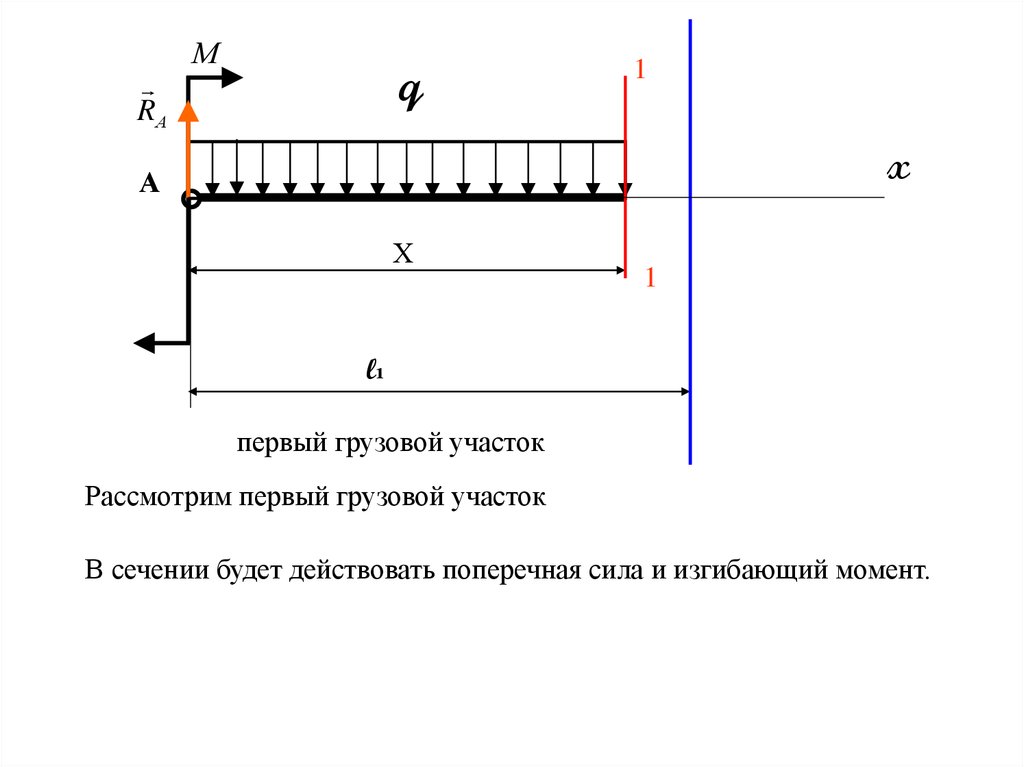
первый грузовой участок
Рассмотрим первый грузовой участок
В сечении будет действовать поперечная сила и изгибающий момент.
29.
RАМ
q
1
А
С
x
Х
0 Х 4 м
l₁
1
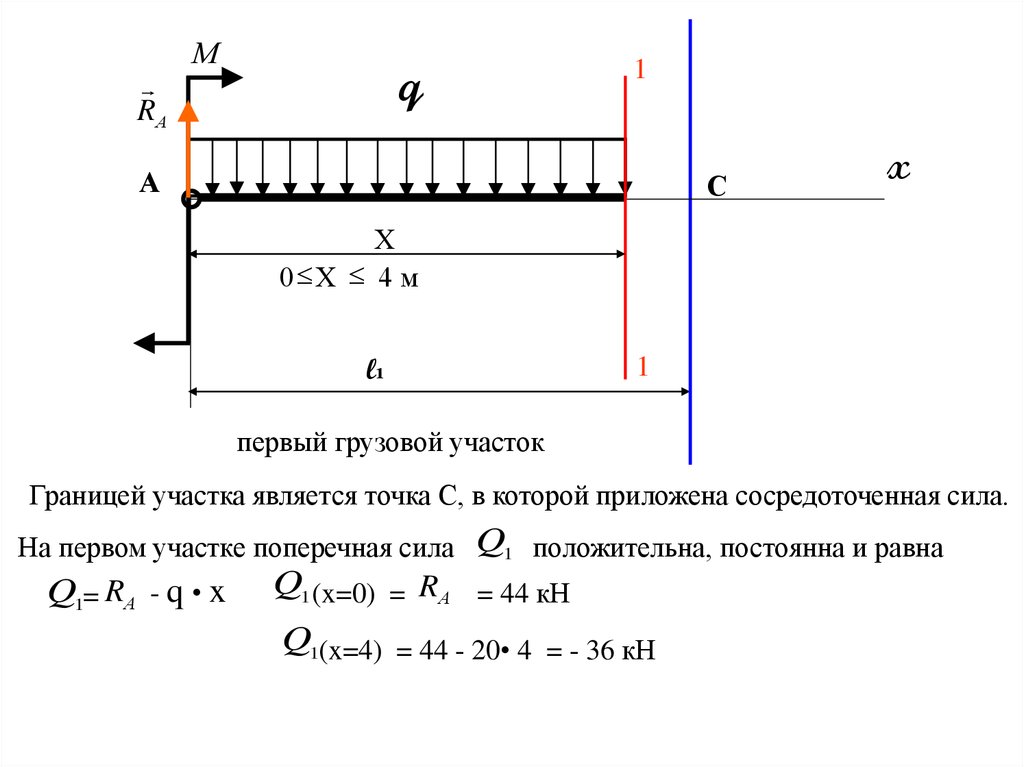
первый грузовой участок
Границей участка является точка С, в которой приложена сосредоточенная сила.
На первом участке поперечная сила Q1 положительна, постоянна и равна
Q1= RА - q • x
Q1 (x=0) = RА = 44 кН
Q1(x=4) = 44 - 20• 4 = - 36 кН
30.
RАМ
q
А
1
С
Х
0 Х 4 м
l₁
1
первый грузовой участок
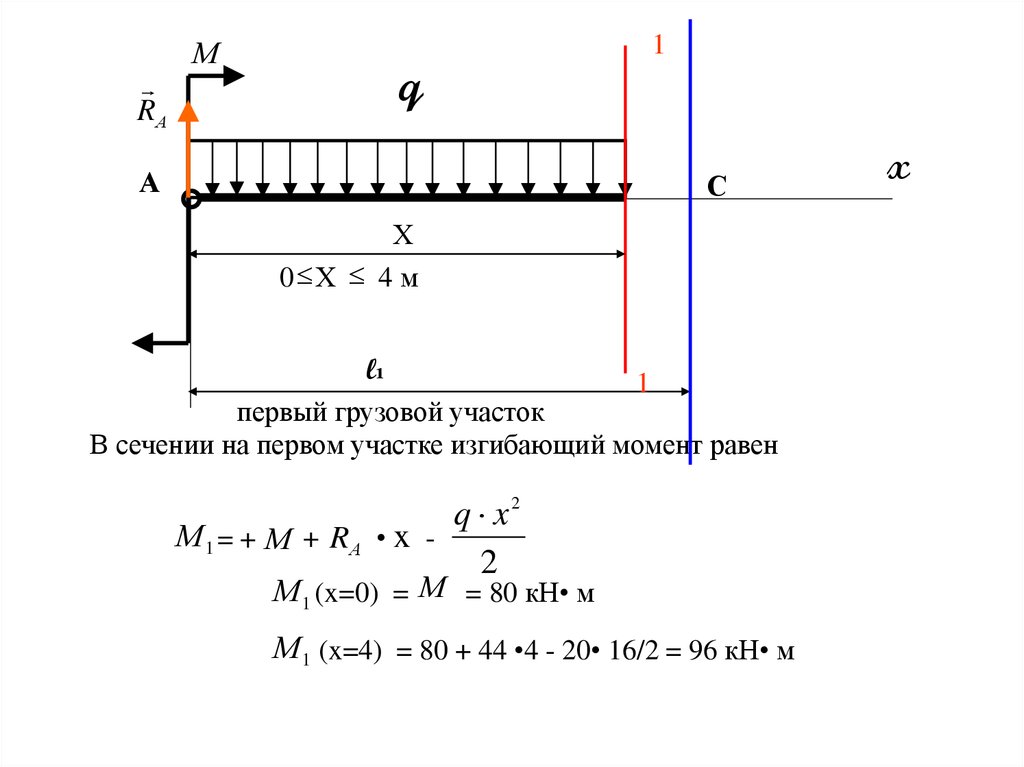
В сечении на первом участке изгибающий момент равен
q x2
М 1 = + М + RА • x 2
М 1 (x=0) = М = 80 кН• м
М 1 (x=4) = 80 + 44 •4 - 20• 16/2 = 96 кН• м
x
31.
Fq
М
В
А
2,2 м
44
+
36
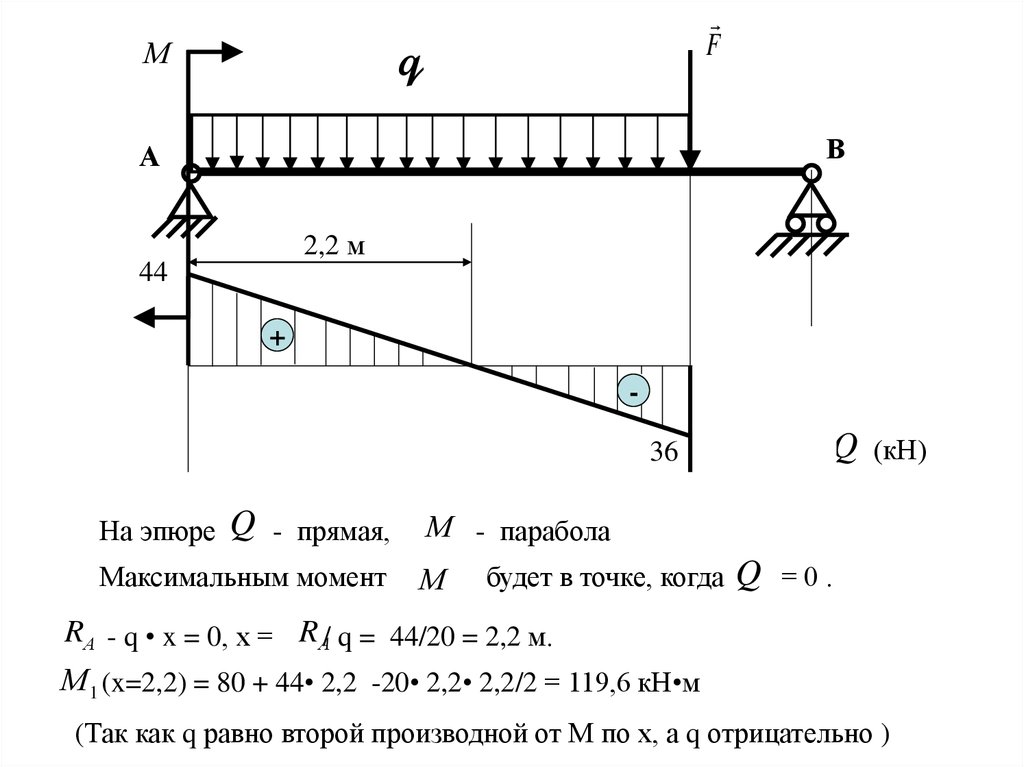
На эпюре
Q
- прямая,
-
Q
(кН)
128,4
М - парабола
Максимальным момент М будет в точке, когда
96Q = 0 .
80
RА - q • x = 0, х = RА/ q = 44/20+= 2,2 м.
М (кН• м)
М 1 (x=2,2) = 80 + 44• 2,2 -20• 2,2• 2,2/2 = 119,6 кН•м
(Так как q равно второй производной от М по х, а q отрицательно )
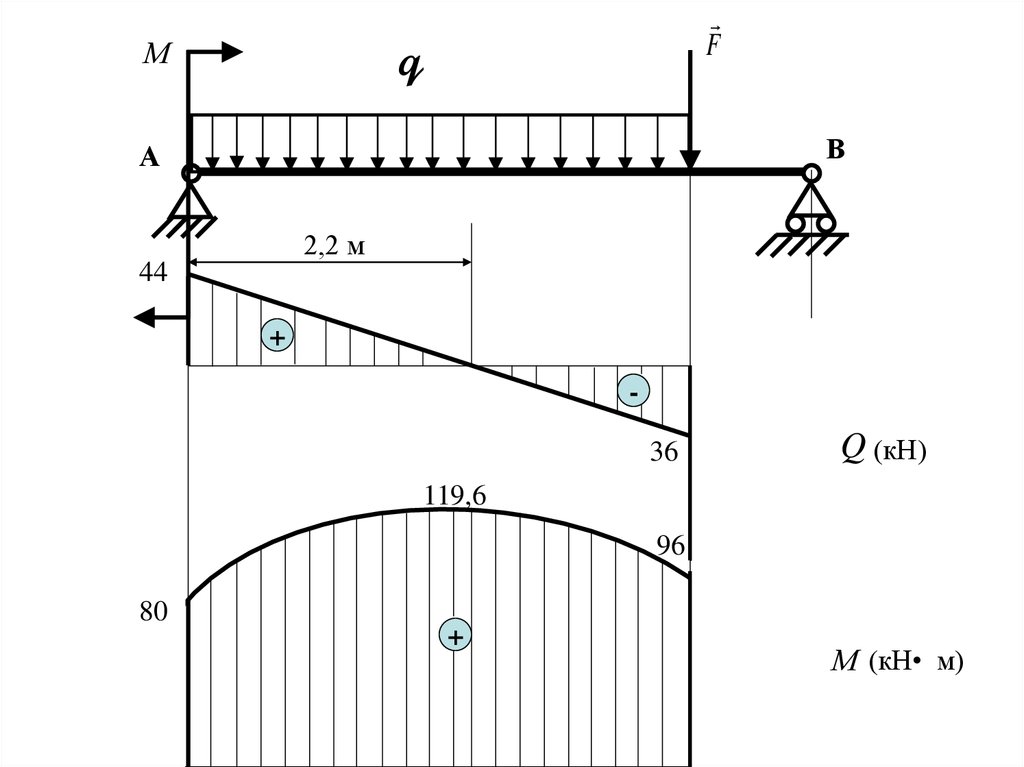
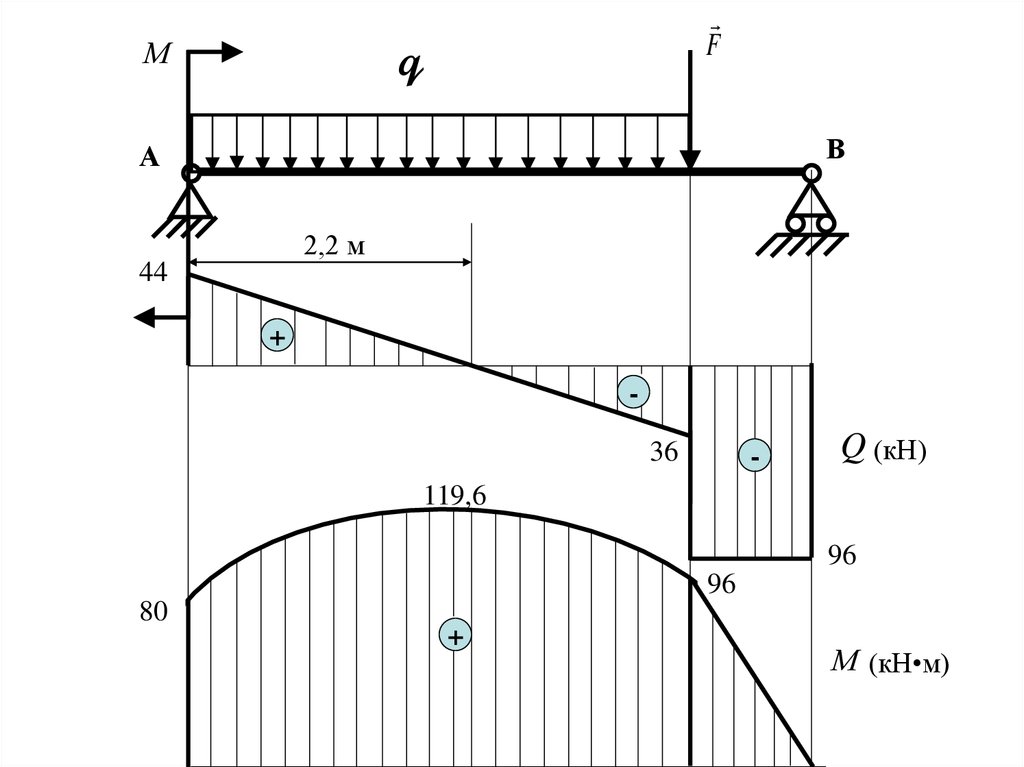
32.
Fq
М
В
А
2,2 м
44
+
36
-
Q (кН)
119,6
96
96
96
80
+
М (кН• м)
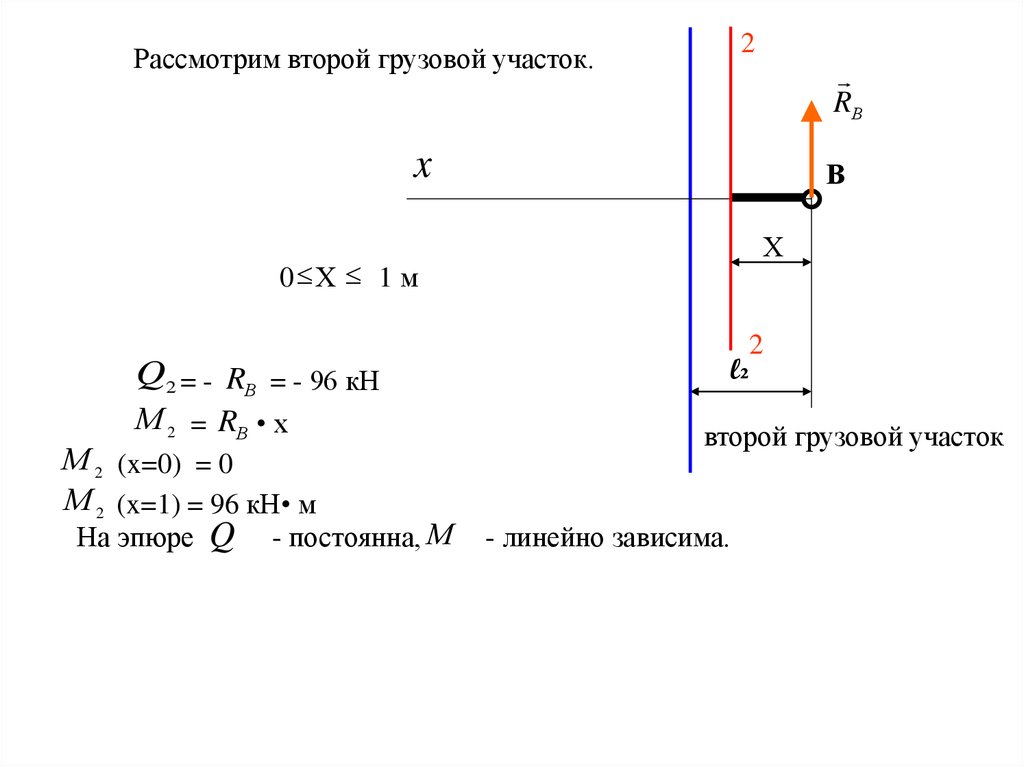
33.
2Рассмотрим второй грузовой участок.
RВ
x
В
Х
0 Х 1 м
l₂
Q2 = - RВ = - 96 кН
М 2 = RВ • х
М 2 (x=0) = 0
М 2 (x=1) = 96 кН• м
На эпюре
Q
- постоянна, М
2
второй грузовой участок
- линейно зависима.
34.
Fq
М
В
А
2,2 м
44
+
36
-
Q (кН)
119,6
96
96
80
+
М (кН•м)
35.
При проверке эпюр следует ось x мысленно всегда направлять слеванаправо.
На участке, где нет распределенной нагрузки, эпюра
моментов,представляет собой наклонную прямую, а эпюра
поперечных сил — прямую, параллельную оси.
На участке, где приложена равномерно распределенная нагрузка, эпюра
моментов представляет собой параболу, а эпюра поперечных сип —
наклонную прямую.
На конце балки изгибающий момент равен нулю, если там не приложена
пара сил.
При построении эпюры для консольных балок начало координат удобно
брать на конце консоли, что нередко дает возможность обойтись без
определения опорных реакций.
В сечении, соответствующем заделке, поперечная сила равна реактивной
силе, а изгибающий момент — реактивному моменту.


















 Физика
Физика








