Похожие презентации:
Определить реакцию опоры балки
1.
2FМ3
q
В
А
а=2 м
2F
q
b=3 м
RA
А
Y
РГЗ №3. Изгиб.
Дано: a = 2 м; b = 3 м; c = 1,5 м; М3 = 45 кН·м;
F=30 кН; q=20 кН/м; [σ] = 100 МПа
Решение:
с=1,5 м
1. Определить реакции опор балки.
M B 0
a
М3
RB
M 3 R A b 2 F ( a b) q a b 0
2
a
M 3 2 F ( a b) q a b
В
2
RA
b
2
45 2 30 (2 3) 20 2 3
2 168 1 168,3 кН
RA
3
3
M A 0
a
M 3 RB b 2 F a q a 0
2
a
M 3 2F a q a
2
RB
b
2
45 2 30 2 20 2
2 68 1 68,3 кН
RB
3
3
Проверка:
Σ Fy =
0 +R –R =
–2F – q·a
A
B
0
–60 – 40 +168,3 – 68,3 = 0
0=0
2.
2FМ3
q
2F
z1
q
I участок 0 ≤ z1 < а = 2 м
В
А
а=2 м
2. Вычислить внутренние силовые
факторы и построить их эпюры.
b=3 м
QY 2 F q z1
с=1,5 м
RA
RB
z3
М3
z2
2F q
z1
при z1 0 QY 2 30 20 0 60 кН
при z1 2 QY 2 30 20 2 100 кН
z1
2
0
при z1 0 M X 2 30 0 20 0 0 кН м
2
2
при z1 2 M X 2 30 2 20 2 160 кН м
2
M X 2 F z1 (q z1 )
II участок 0 ≤ z2 < с = 1,5 м
М3
QY 0 кН
z2
M X М 3 45 кН м
3.
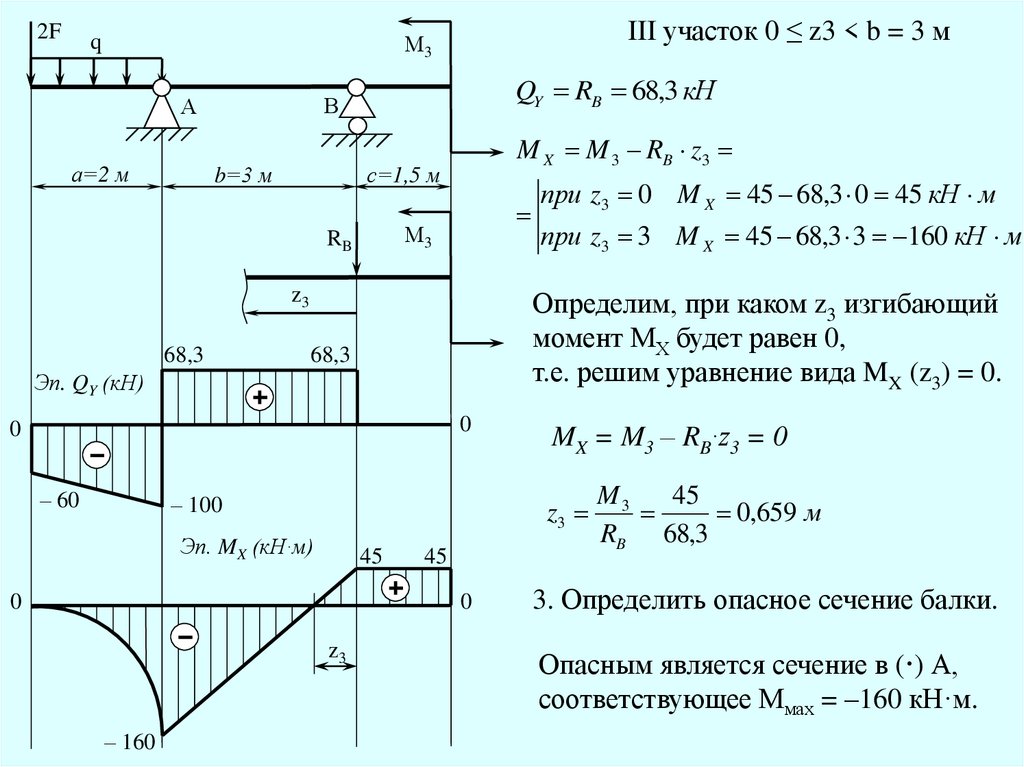
2FIII участок 0 ≤ z3 < b = 3 м
М3
q
а=2 м
QY RB 68,3 кН
В
А
b=3 м
M X M 3 RB z3
с=1,5 м
М3
RB
z3
68,3
68,3
0
0
– 100
MX = M3 – RB·z3 = 0
z3
Эп. MX (кН·м)
45
0
45
0
z3
– 160
при z3 3 M X 45 68,3 3 160 кН м
Определим, при каком z3 изгибающий
момент МХ будет равен 0,
т.е. решим уравнение вида MX (z3) = 0.
Эп. QY (кН)
– 60
при z3 0 M X 45 68,3 0 45 кН м
M3
45
0,659 м
RB 68,3
3. Определить опасное сечение балки.
Опасным является сечение в (·) А,
соответствующее Ммах = –160 кН·м.
4.
4. Определить осевой момент сопротивления и подобрать сечениесоответствующего профиля.
Условие прочности:
МАХ
MХ
WХ
160 103
3
3
0
,
0016
м
1600
см
Осевой момент сопротивления: WХ
100 106
MХ
Подбираем сечение двутавра по сортаменту прокатной стали. Выбираем балку
двутавровую №55 с осевым моментом сопротивления WX = 2035 см3
и выписываем все характеристики выбранного сечения.



 Физика
Физика








