Похожие презентации:
Плоский изгиб
1. Тема 6
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВhttp://www.mech-lab.ru/equipment.html
Тема 6
Плоский изгиб
Тихонкин Игорь Васильевич, доцент, к.т.н.
Кафедра Теоретической и прикладной механики
Инженерного института ФГБОУ ВПО НГАУ
2.
3.
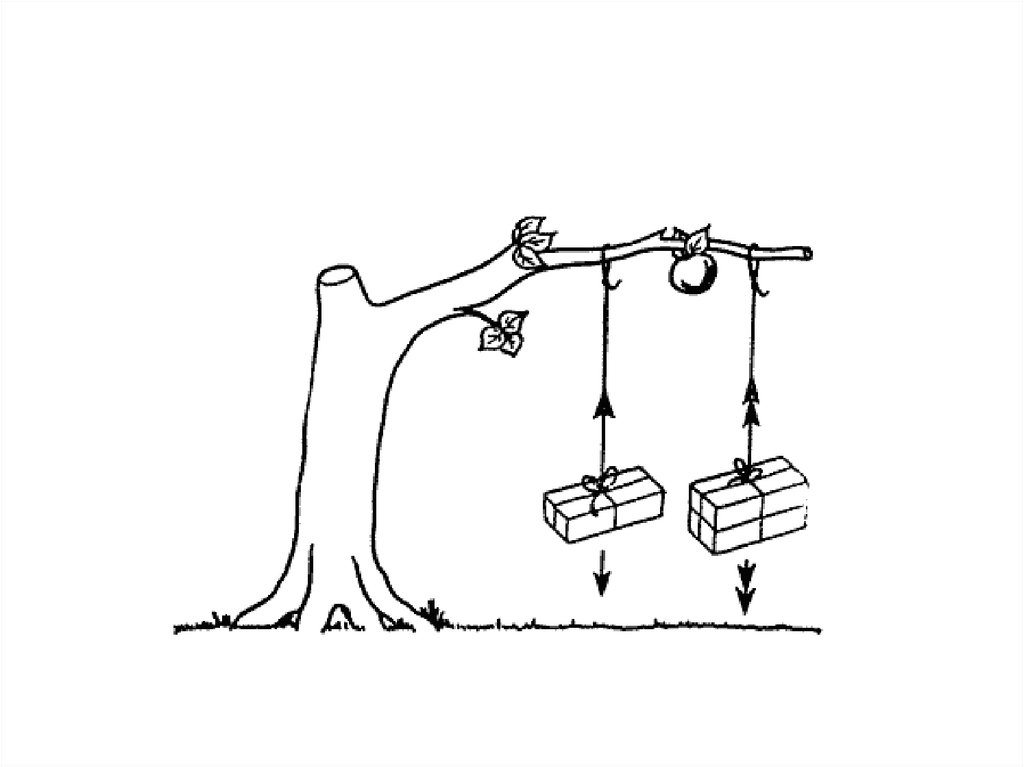
Все материалы иS
конструкции, хотя и в
весьма различной степени,
под действием нагрузки
испытывают смещения.
Теория упругости - это
наука о соотношениях
между нагрузками и
перемещениями в твердых
S
телах.
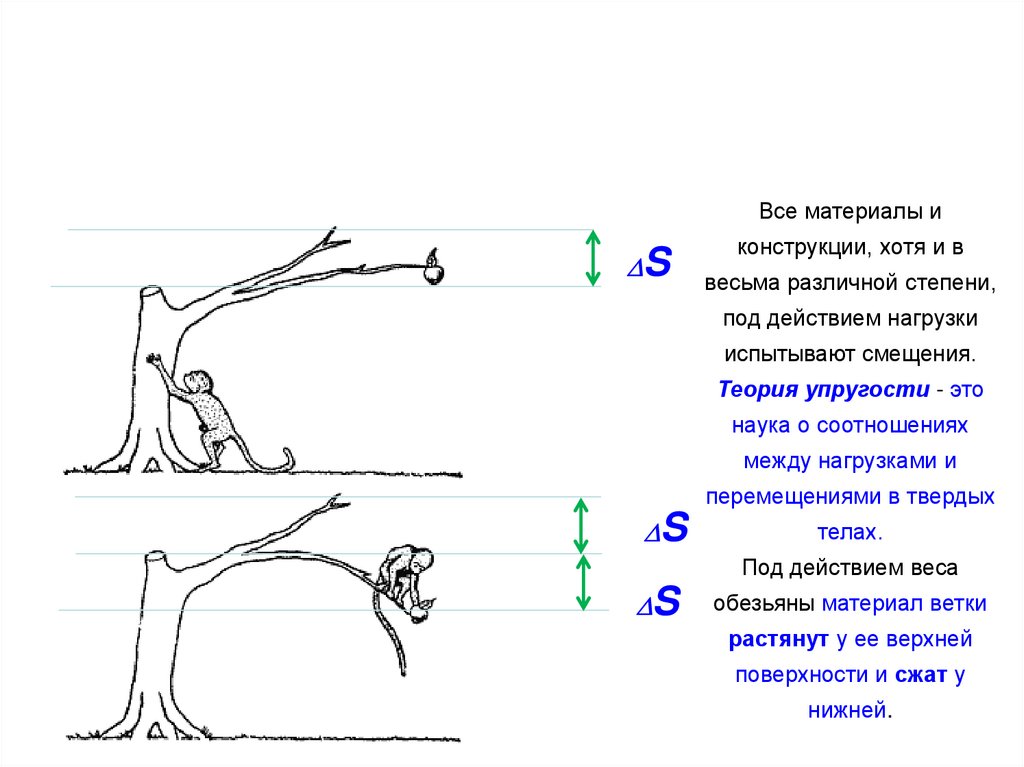
Под действием веса
S
обезьяны материал ветки
растянут у ее верхней
поверхности и сжат у
нижней.
4.
5.
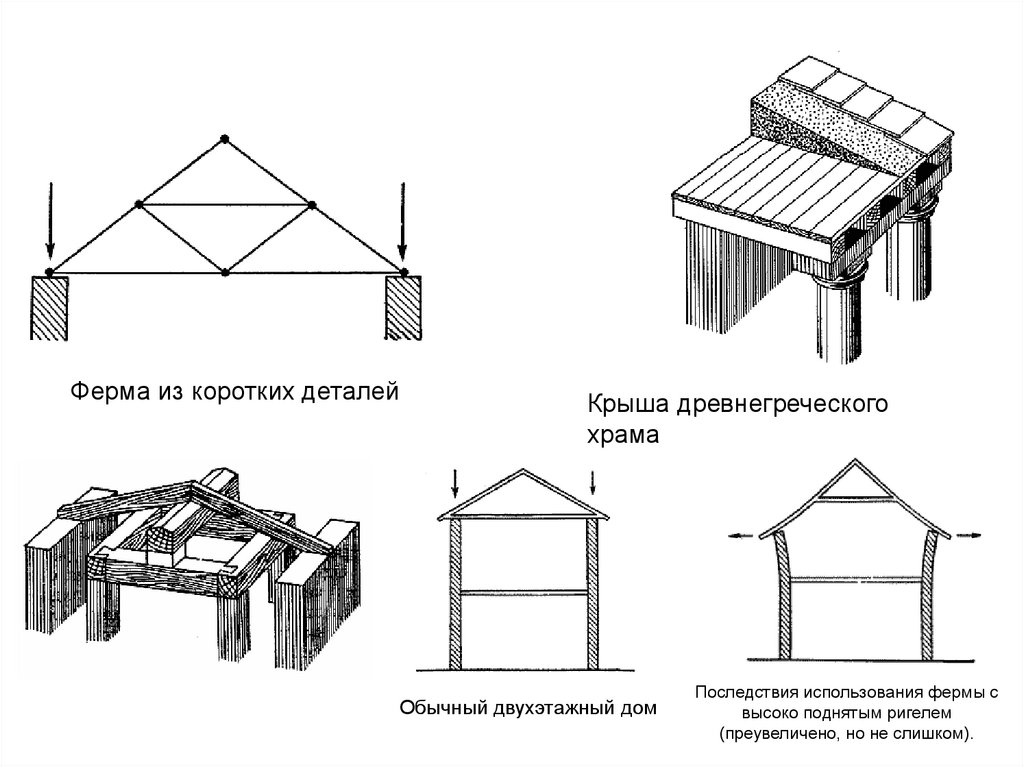
Ферма из коротких деталейКрыша древнегреческого
храма
Обычный двухэтажный дом
Последствия использoвания фермы с
высоко поднятым ригелем
(преувеличено, но не слишком).
6.
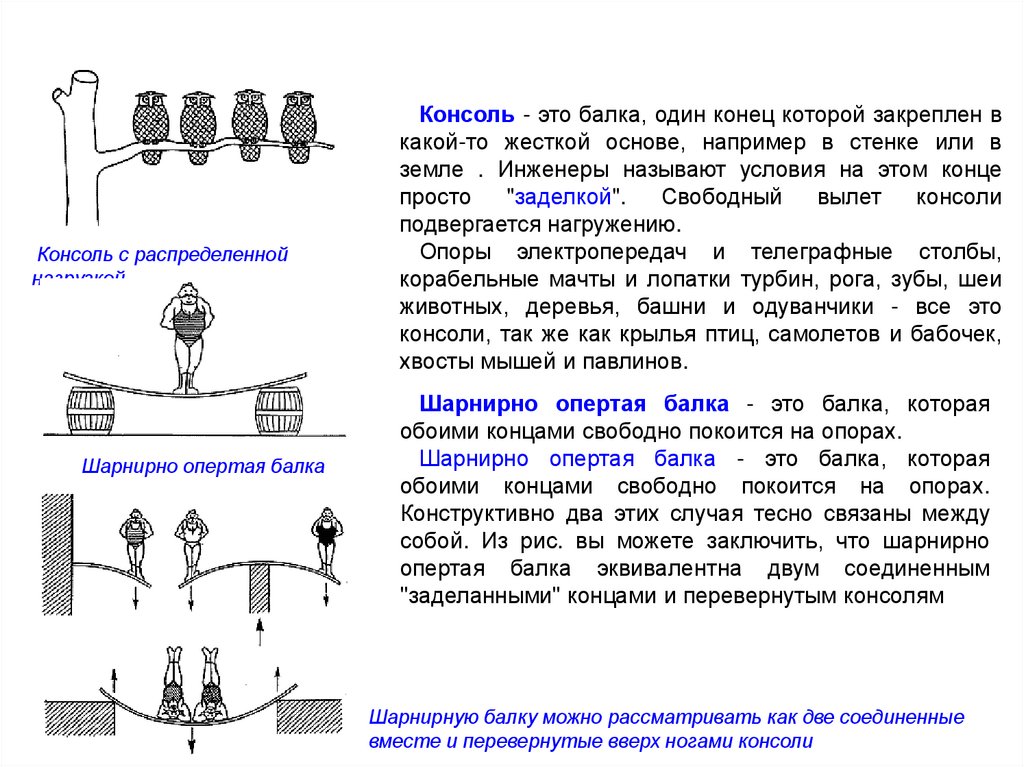
Консоль с распределеннойнагрузкой.
Шарнирно опертая балка
Консоль - это балка, один конец которой закреплен в
какой-то жесткой основе, например в стенке или в
земле . Инженеры называют условия на этом конце
просто
"заделкой".
Свободный
вылет
консоли
подвергается нагружению.
Опоры электропередач и телеграфные столбы,
корабельные мачты и лопатки турбин, рога, зубы, шеи
животных, деревья, башни и одуванчики - все это
консоли, так же как крылья птиц, самолетов и бабочек,
хвосты мышей и павлинов.
Шарнирно опертая балка - это балка, которая
обоими концами свободно покоится на опорах.
Шарнирно опертая балка - это балка, которая
обоими концами свободно покоится на опорах.
Конструктивно два этих случая тесно связаны между
собой. Из рис. вы можете заключить, что шарнирно
опертая балка эквивалентна двум соединенным
"заделанными" концами и перевернутым консолям
Шарнирную балку можно рассматривать как две соединенные
вместе и перевернутые вверх ногами консоли
7.
8.
9.
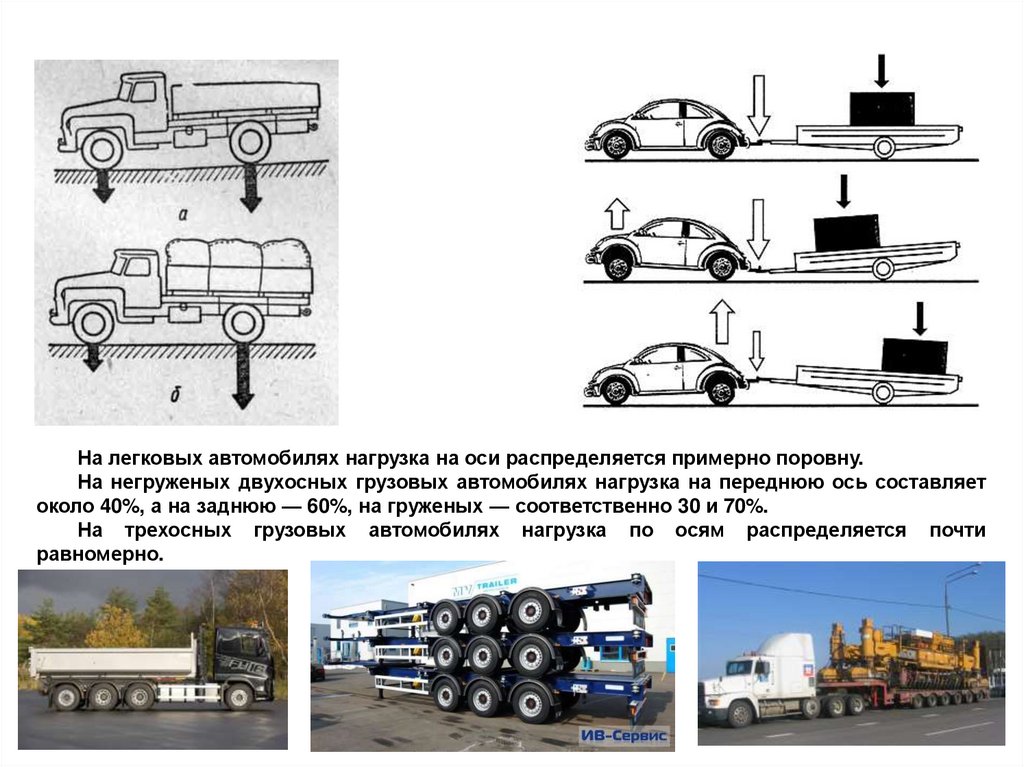
На легковых автомобилях нагрузка на оси распределяется примерно поровну.На негруженых двухосных грузовых автомобилях нагрузка на переднюю ось составляет
около 40%, а на заднюю — 60%, на груженых — соответственно 30 и 70%.
На трехосных грузовых автомобилях нагрузка по осям распределяется почти
равномерно.
10.
11. Грузовые автомобили с несколькими осями
Замещение несколькихреакций
12. Силы, действующие на автомобиль (… … полуприцеп)
• Распределённая нагрузка• собственный вес автомобиля
• реакция опор (колес)
• результирующие (шасси)
• прочие силы (моменты сил)
… их
схематичное
изображение
для
проведения
расчетов…
13.
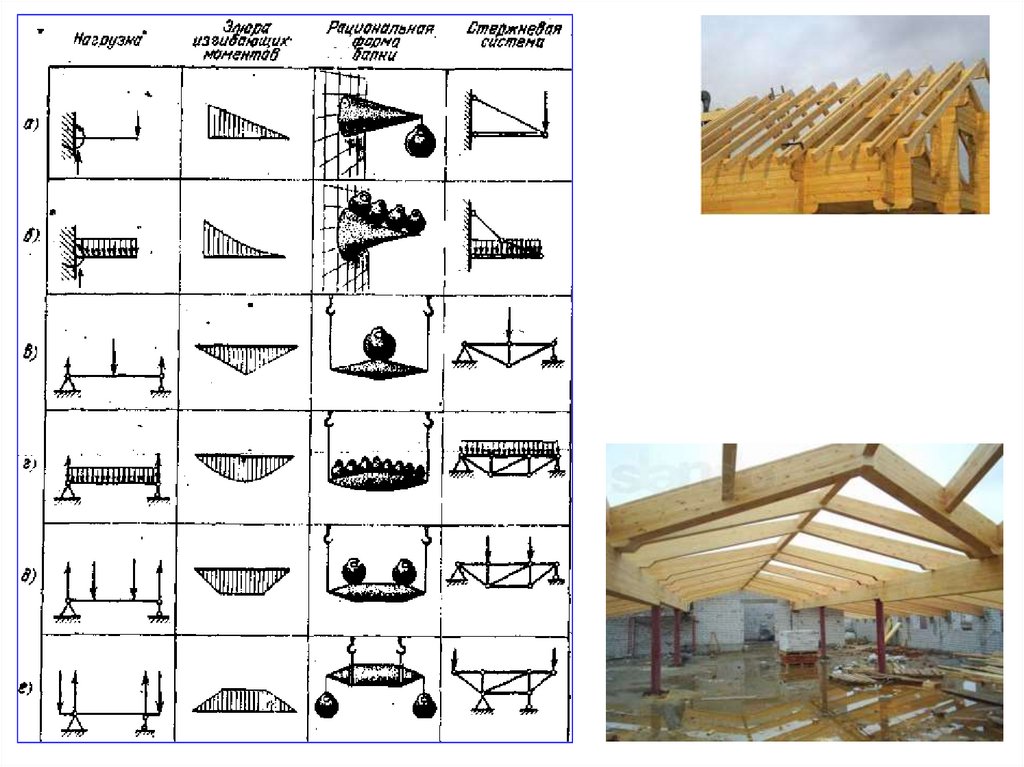
Рис. Изгибающий момент балки.а) Схема сил, б) эпюра (график) изгибающих моментов,
в) рациональные формы балок.
14.
15.
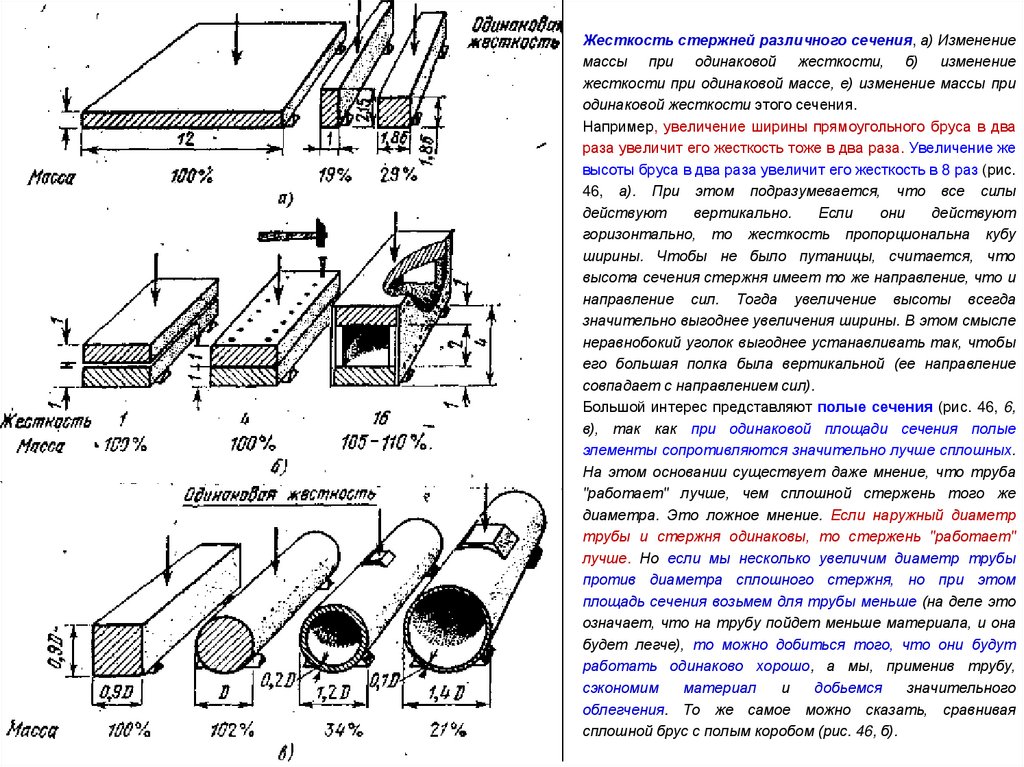
Жесткость стержней различного сечения, а) Изменениемассы при одинаковой жесткости, б) изменение
жесткости при одинаковой массе, е) изменение массы при
одинаковой жесткости этого сечения.
Например, увеличение ширины прямоугольного бруса в два
раза увеличит его жесткость тоже в два раза. Увеличение же
высоты бруса в два раза увеличит его жесткость в 8 раз (рис.
46, а). При этом подразумевается, что все силы
действуют
вертикально.
Если
они
действуют
горизонтально, то жесткость пропорциональна кубу
ширины. Чтобы не было путаницы, считается, что
высота сечения стержня имеет то же направление, что и
направление сил. Тогда увеличение высоты всегда
значительно выгоднее увеличения ширины. В этом смысле
неравнобокий уголок выгоднее устанавливать так, чтобы
его большая полка была вертикальной (ее направление
совпадает с направлением сил).
Большой интерес представляют полые сечения (рис. 46, 6,
в), так как при одинаковой площади сечения полые
элементы сопротивляются значительно лучше сплошных.
На этом основании существует даже мнение, что труба
"работает" лучше, чем сплошной стержень того же
диаметра. Это ложное мнение. Если наружный диаметр
трубы и стержня одинаковы, то стержень "работает"
лучше. Но если мы несколько увеличим диаметр трубы
против диаметра сплошного стержня, но при этом
площадь сечения возьмем для трубы меньше (на деле это
означает, что на трубу пойдет меньше материала, и она
будет легче), то можно добиться того, что они будут
работать одинаково хорошо, а мы, применив трубу,
сэкономим
материал
и
добьемся
значительного
облегчения. То же самое можно сказать, сравнивая
сплошной брус с полым коробом (рис. 46, б).
16.
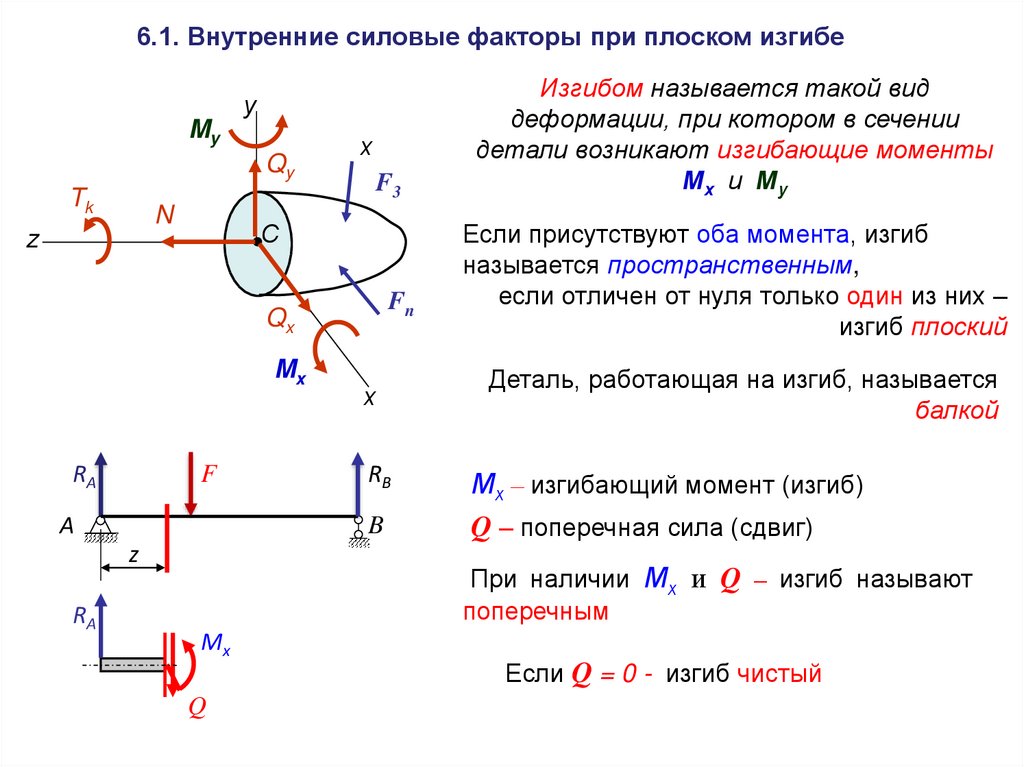
6.1. Внутренние силовые факторы при плоском изгибеу
My
Qy
Tk
N
z
х
F3
С
Fn
Qx
Mx
RA
F
A
RB
B
z
RA
х
Изгибом называется такой вид
деформации, при котором в сечении
детали возникают изгибающие моменты
Мх и М у
Если присутствуют оба момента, изгиб
называется пространственным,
если отличен от нуля только один из них –
изгиб плоский
Деталь, работающая на изгиб, называется
балкой
Мх – изгибающий момент (изгиб)
Q – поперечная сила (сдвиг)
При наличии Мх и Q – изгиб называют
поперечным
Mx
Q
Если Q = 0 - изгиб чистый
17.
ВСМ – внутренние силовые факторы18.
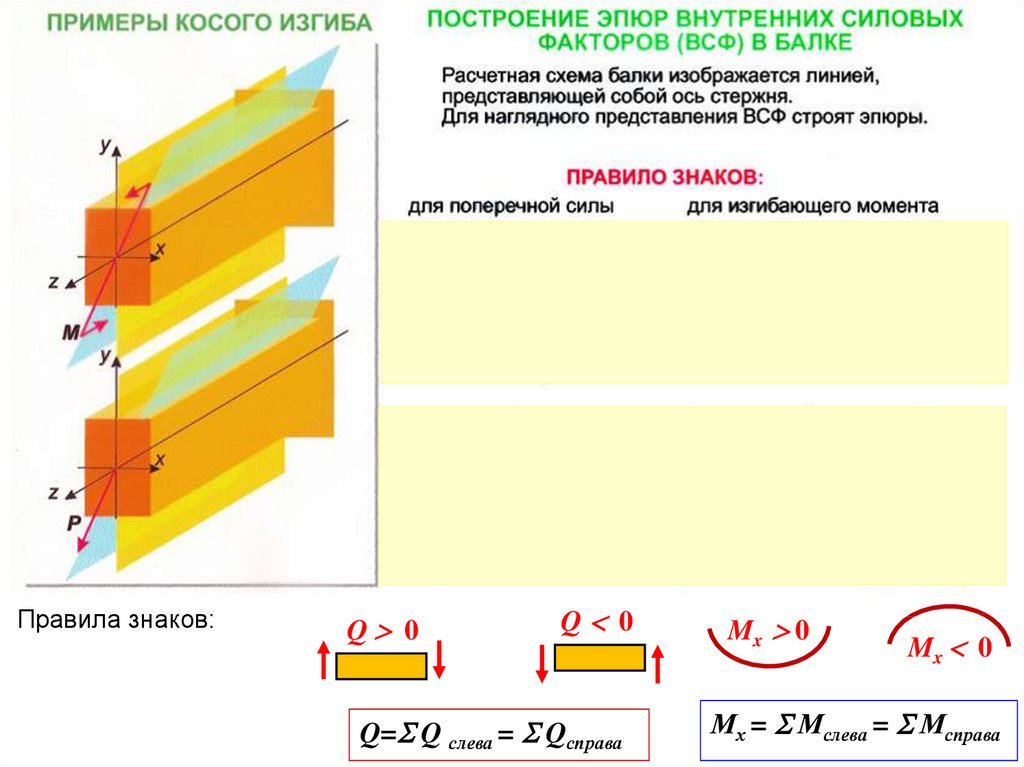
Правила знаков:Q 0
Q 0
Q= Q слева = Qсправа
Mx 0
Mx 0
Мх = Мслева = Мсправа
19.
Примеры практического использования20.
21.
22.
Расчет балки на прочность ведется по опасному сечениюОпасное сечение определяется визуально по графикам (эпюрам) Мх и Q
6.2. Эпюры изгибающего момента и поперечной силы
Метод сечений:
- рассечь балку плоскостью
- отбросить одну часть
- длину оставшейся части обозначить z
- записать уравнение для изгибающего момента в данном сечении
Мх = Мслева = Мсправа
+
-
- по уравнению построить график (эпюру) изменения Мх
- получить уравнение для поперечной силы Q
Q= Q слева = Qсправа
или
+
dM x
Q
dz
-
- по уравнению построить график (эпюру) изменения Q
- по эпюрам определить опасное сечение балки
23.
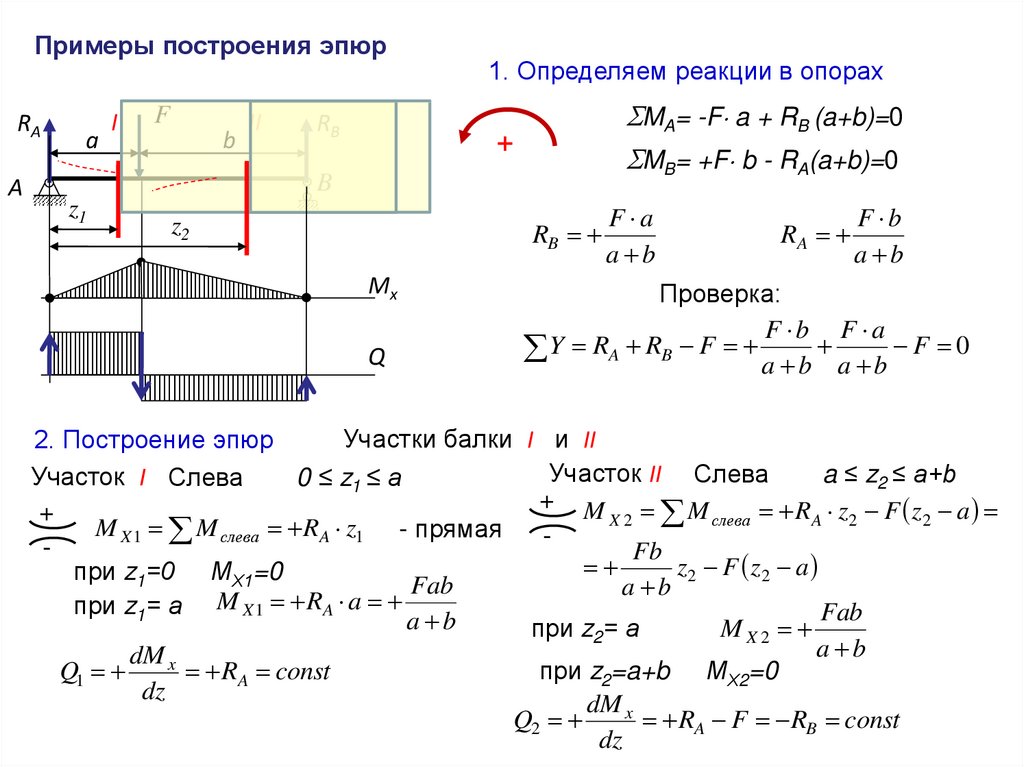
Примеры построения эпюрRA
A
a
I
F
b
II
RB
1. Определяем реакции в опорах
MA= -F a + RB (a+b)=0
MB= +F b - RA(a+b)=0
+
B
z1
z2
RB
Mx
Q
F a
a b
RA
F b
a b
Проверка:
F b F a
Y
R
R
F
F 0
A
B
a b a b
Участки балки I и II
2. Построение эпюр
Участок II Слева
a ≤ z2 ≤ a+b
Участок I Слева
0 ≤ z1 ≤ a
+ M M
+
слева RA z2 F z2 a
X2
M X 1 M слева RA z1 - прямая
Fb
z2 F z2 a
при z1=0 МХ1=0
Fab
a b
при z1= а M X 1 RA a
Fab
a b
при z2= а
MX2
a b
dM x
Q1
RA const
при z2=a+b МХ2=0
dz
dM x
Q2
RA F RB const
dz
24.
RAI
M=30кН·м
II
A
RВ
1. Определяем реакции в опорах
MA= -М+ RB ·3 = 0
+
B
1м
z1
+20
2м
-10
RB=+10кН
z2
Проверка:
Mx
-10
Q
-10
MB= -М - RA·3 = 0
RА=-10кН
Σ Y=RA+RB=+10-10=0
2. Построение эпюр
Участок I Слева
0 ≤ z1 ≤ 1м
+ M M
- прямая
слева RA z1
X1
при z1=0 МХ1=0
при z1=1м МХ1=-10кН·м
dM x
Q1
RA 10кН const
dz
Участок II Справа
0 ≤ z2 ≤ 2м
+
при z2=0
M X 2 M справа RВ z2
dM x
Q2
RВ 10кН const
dz
Опасное сечение – под моментом
МХ2=0
при z2=2м
│M │ max =20кН·м
МХ2=+20кН·м
│Q │ max =10кН
25.
RAqz
A
qL
q
B
L
z
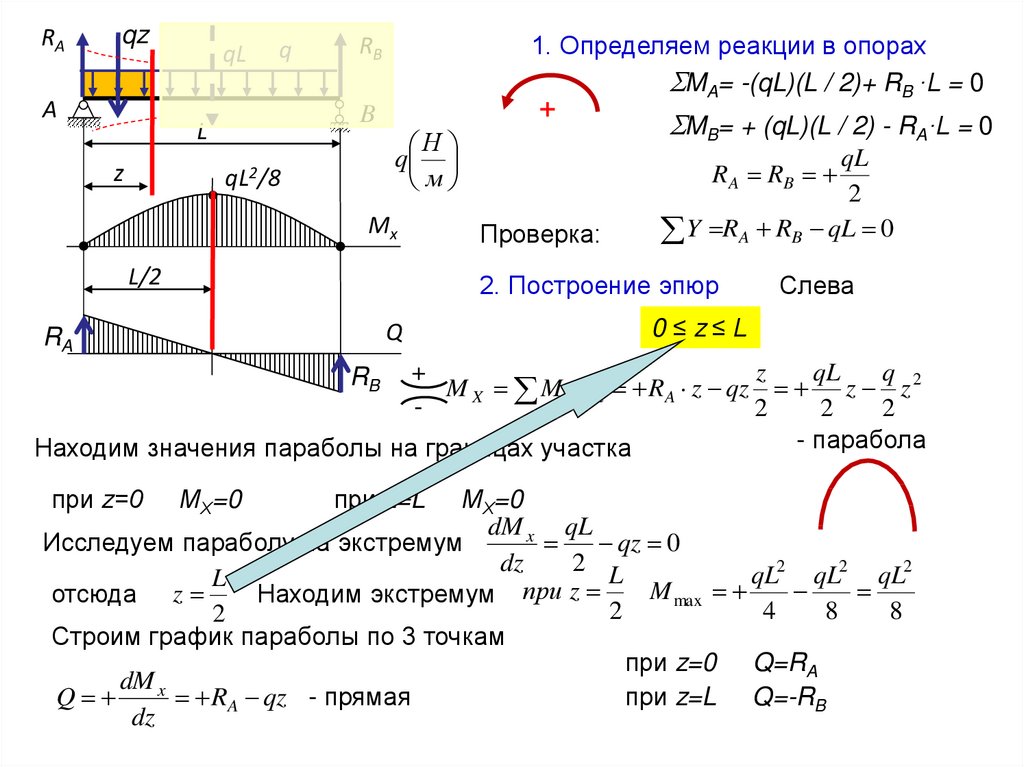
1. Определяем реакции в опорах
MA= -(qL)(L / 2)+ RB ·L = 0
RB
qL2/8
+
Н
q
м
Mx
L/2
MB= + (qL)(L / 2) - RA·L = 0
qL
2
Y RA RB qL 0
RA RB
Проверка:
2. Построение эпюр
Q
RA
Слева
0 ≤ z≤ L
+
z
qL
q
M X M слева RA z qz z z 2
2
2
2
- парабола
Находим значения параболы на границах участка
RB
при z=0
МХ=0
при z=L
МХ=0
dM x qL
Исследуем параболу на экстремум
qz 0
dz
2 L
qL2 qL2 qL2
L
M max
отсюда z
Находим экстремум при z
2
4
8
8
2
Строим график параболы по 3 точкам
при z=0 Q=RA
dM x
Q
RA qz - прямая
при z=L Q=-RB
dz
26.
МКонсольная балка
Mx=-M=const
z
Mx
M=const
Q=0
Чистый изгиб
Q
Q=d Mx / dz =0=const
27.
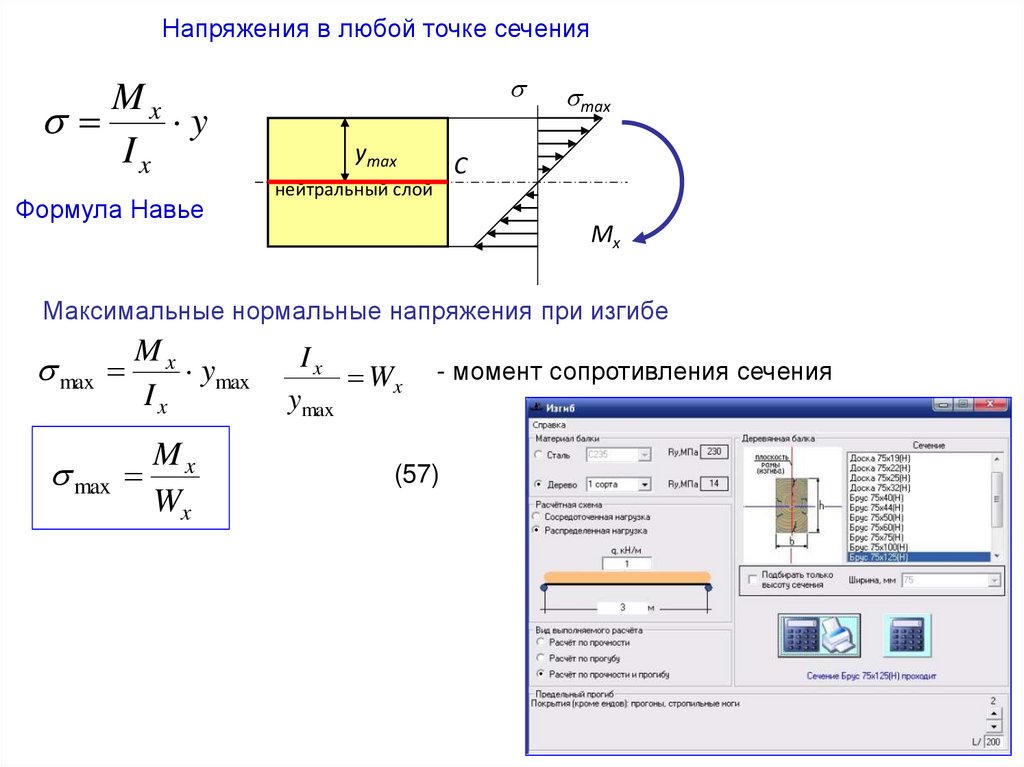
Напряжения в любой точке сеченияMx
y
Ix
Формула Навье
ymax
max
C
нейтральный слой
Mx
Максимальные нормальные напряжения при изгибе
max
max
Mx
ymax
Ix
Mx
Wx
Ix
Wx
ymax
- момент сопротивления сечения
(57)
28.
6.4 Условие прочности при изгибе по нормальным напряжениямУсловие прочности по нормальным напряжениям max
При изгибе
max
Mx
Wx
Условие прочности при изгибе
M x max
Wx
изг
(58)
Условие прочности (58) по нормальным напряжениям является основным и
служит для проектировочного расчета при изгибе
29.
Пример проектировочного расчета балки на прочностьI
RA
2м
A
RВ
II
1м
F
B
z1
z2
Mx
-20
Определить размеры поперечного
сечения балки для четырех вариантов
сечения:
- прямоугольного при h/b=2;
- квадратного;
- круглого;
-стандартного двутавра.
Сравнить экономичность профилей.
Сила F=20кН. Материал – сталь Ст3
20
Q
Расчет
-10
1 Определение реакций в опорах
MA=+RB 2-F 3=0;
MB=-RA 2-F 1=0
RB=(3/2)F=30кН
RА=-(1/2)F=-10кН
Проверка: Y=RA+RB-F=-10+30-20=0
Участок 2
Мх2=-F z2
Справа
при z2=0
2 Построение эпюр
0 z2 1м
МХ2=0
при z2=1м МХ2=-20кН·м
dM x
Q2
F 20кН const
dz
Участок 1
Мх1=+RА z1
Слева
при z1=0
0 z1 2м
МХ1=0
при z1=2м МХ1=-20кН·м
dM x
Q1
RA 10кН const
dz
В опасном сечении В
│M │ max =20кН·м
│Q │ max =20кН
30.
3 Расчет балки на прочность по нормальным напряжениямУсловие прочности
Прямоугольное сечение
h×b
h/b=2
bh 2 b 2b
Wx
0,667b3
6
6
2
Mx
max
Wx
изг
х
h
│M │ max =20кН·м
Из условия прочности
b
изг=150МПа
b 3
M x max
0,667 изг
3
20
10
3
6
0,667 150 10
0,0585 м 58,5 мм
h=2b=58,5 2=117 мм
Округляем до нормальных значений: b=60 мм; h=120 мм
Площадь сечения A= b·h =60 120=7200 мм2=72 см2
Квадратное сечение
a 3
6 M x max
изг
а×а
а3
Wx
6
Из условия прочности
3
6
20
10
3
0,0928 м 92,8 мм
6
150 10
Площадь сечения A=а2=95 95=9025 мм2=90,25 см2
Округляем а=95 мм
31.
Круглое сечение ØdУсловие прочности
M x max
Wx
Wx
изг
d 3
│M │ max =20кН·м
изг=150МПа
Из условия прочности
32
32 M x max
изг
3
32
20
10
3
0,110 м 110 мм
6
150 10
Площадь сечения A= d2/4= (110)2/4=9499мм2=95см2
Стандартный двутавр
х
d 3
Из условия прочности
Wx Мх max/ изг=20 103/(150 106)=0,133 10-3м3=133см3
По таблице сортамента (Wx )табл=143см3 у двутавра
№18
Площадь двутавра A=23,4см2
4 Экономичность сечений
Сечение
двутавр
прямоугольник
квадрат
круг
А, см2
А / Amin
23,4
1
72
3,1
90,25
3,9
95
4,1
При изгибе наиболее
экономичным является
двутавровое сечение
32.
6.5 Касательные напряжения при изгибе. Формула ЖуравскогоQ
А*
C*
уС*
b*
В
х
С
*
Q Sx
*
b Ix
Чтобы найти величину касательных напряжений в
произвольной точке В поперечного сечения, нужно:
- определить значение поперечной силы Q в
данном сечении (с эпюры поперечной силы)
- совместить ось х в сечении с нейтральной линией
- провести через точку В сечение параллельно
нейтральной линии, найти ширину профиля в
этом месте b*
- найти центр отсеченной части сечения С*, ее
площадь А* и вычислить статический момент
отсеченной части сечения относительно
нейтральной линии Sx*=А* yC*
- вычислить касательные напряжения по
формуле Журавского
33.
Касательные напряжения в прямоугольном сечении балкиC*
y
h
A*
Момент инерции сечения Ix= bh3/12
Ширина прямоугольника постоянна
b*=b
Площадь отсеченной части сечения
A*=b (h/2-y)
yC*
B
x
C
max
b
Q S x*
*
b Ix
6Q h
2
3 y
bh 2
Координата центра С* отсеченной
части
yC*=y+[(h/2-y)/2]=(1/2) (h/2+y)
Статический момент отсеченной части сечения
Sx*=А* yC*=b (h/2-y) (1/2) (h/2+y)=(b/2) [(h/2)2-(y)2]
2
max
2
6Q h 3Q 3Q
3
bh 2 2bh 2 A
max
34.
6.6. Условие прочности при изгибе по касательным напряжениямmax
Q max S x*
I x b*
max
max
(60)
Пример расчета на прочность балки при изгибе
5кН
F=10кН 5кН
1м
1м
5
Мх
5
Q
5
Для заданной схемы балки определить
необходимые размеры прямоугольного сечения
деревянного бруса при соотношении сторон h/b=1,5.
Значения допускаемых напряжений принять
следующие (для древесины хвойных пород при 15%
влажности): изг=8МПа; на скалывание вдоль
волокон ск=1МПа.
Расчет
1 Построение эпюр изгибающего момента и поперечной силы
В опасном сечении
│M │ max =5кН·м
│Q │ max =5кН
35.
2 Проектировочный расчет на прочность по нормальным напряжениямM x max
Wx
b 3
изг
M x max
0,375 изг
при h/b=1,5
bh 2 b 1,5b
2,25b3
Wx
0,375b3
6
6
6
2
3
5
10
3
0,119 м 119 мм
6
0,375 8 10
h=1,5b=119 1,5=178,5мм
Округляем до нормальных размеров: b=120мм; h=180мм
3 Поверочный расчет на прочность по касательным напряжениям
max
max
max
A*
h
C*
yC*
0,347 106 Па 0,347 МПа
x
max =0,347МПа
C
max
b
max
3Q
3 5 103
2bh 2 0,120 0,180
<
ск =1 МПа
Вывод:
Условие прочности по касательным
напряжениям выполняется




















 Физика
Физика








