Hierarchies in Systems Biology

1.

Hierarchies in Systems Biology
Organism
Tissue
Organ
Cell
Network
Pathway
RNA
Protein
DNA
(Slide compliments of Joe Nadeau)
Physical Laws of Nature

2.

Systems biology involves
1. Data acquisition;
2. Data organization and integration;
3. Computation (mathematical
modeling).
Mark A. Knepper, MD, PhD
Laboratory of Kidney & Electrolyte Metabolism
National Heart, Lung, and Blood Institute
NIH
Bethesda, Maryland, USA
Johns Hopkins, 2010

3.

Three Stages of Signal Transduction
1. Reception of extracellular signal by cell
2. Transduction of signal from outside of cell
to inside of cell—often multi-stepped
Note not necessarily transduction of ligand
3. Cellular Response
Response is inititiated and/or occurs
entirely within receiving cell

4.

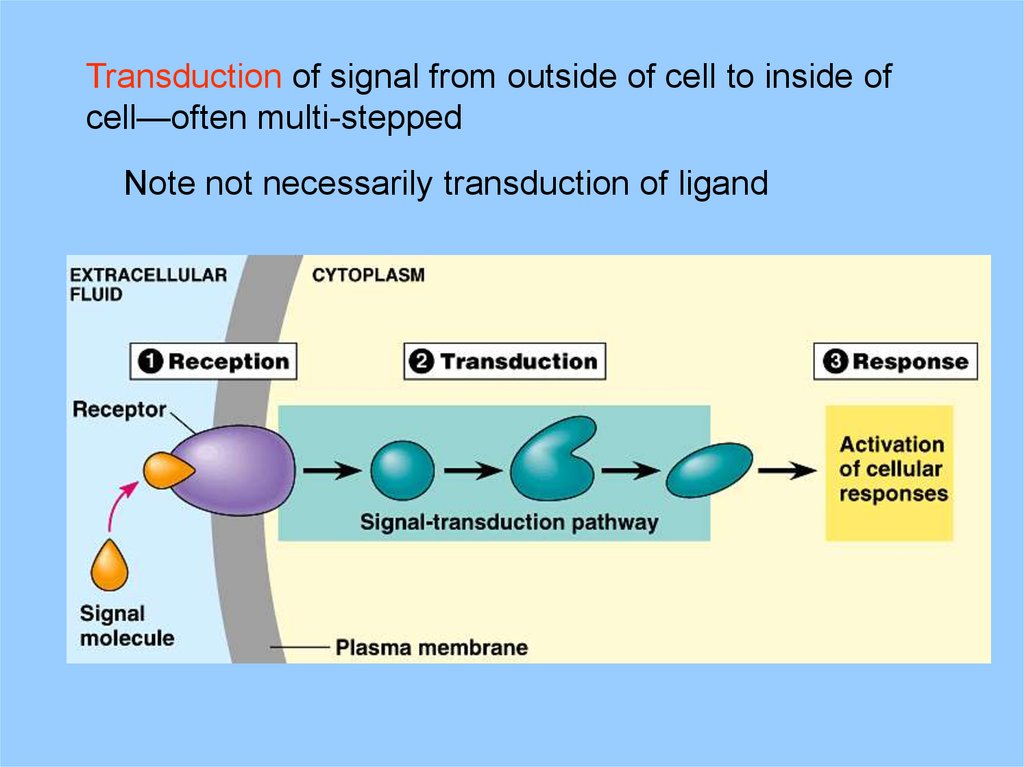
Transduction of signal from outside of cell to inside of
cell—often multi-stepped
Note not necessarily transduction of ligand

5.

6.

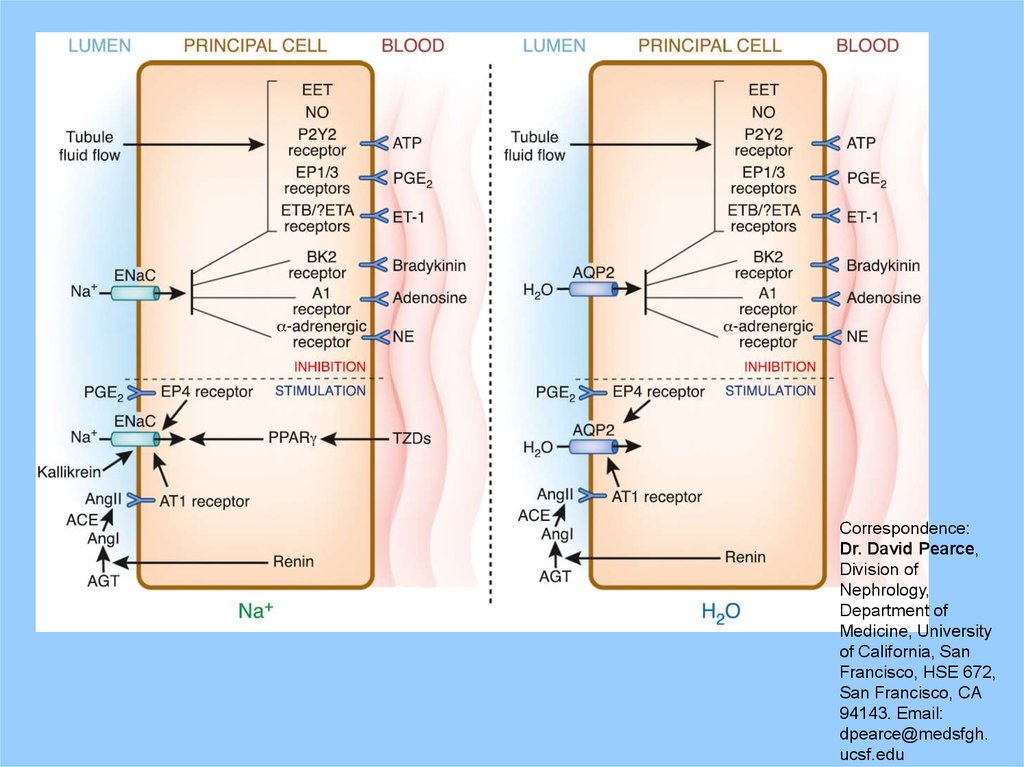
Correspondence:
Dr. David Pearce,
Division of
Nephrology,
Department of
Medicine, University
of California, San
Francisco, HSE 672,
San Francisco, CA
94143. Email:
dpearce@medsfgh.
ucsf.edu

7.

Chemical Signaling Between Cells
Three general categories of chemical signaling:
•Cytoplasmic connections between cells
•Cell-to-cell contact-mediated signaling
•Free diffusion between cells
•Distant cells (hormones)
•Adjacent cells (within interstitial space)

8.

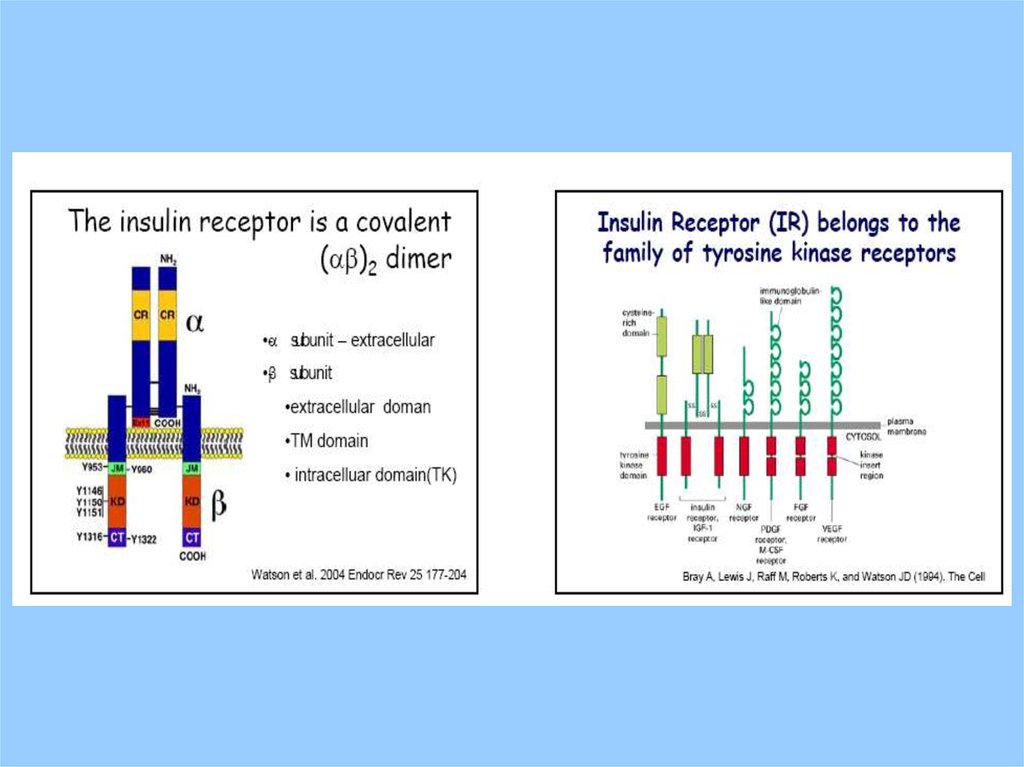
Introduction
Signal Transducing Receptor Classes
Receptor Tyrosine Kinases
Receptor Serine/Threonine Kinases
Phospholipids and Phospholipases
G-Protein Coupled Receptors
G-Proteins
Intracellular Hormone Receptors

9.

Природа биологических сигналов
Chemical Signaling Between Cells

10.

Высокая аффинность рецептора и
лиганда , по-видимому, достигается за
счет конгруэнтности участка молекулы
рецептора, непосредственно входящего в
контакт, с лигандом. Впервые такая
мысль была сформулирована
нобелевскими лауреатами 1908 года
И.М. Мечниковым и П. Эрлихом.
Существование таких
специализированных доменов в
молекулах рецепторов подтверждено
современными исследованиями.

11.

Принципиальный момент:
Передача сигнала происходит в
результате физического контакта
лиганда с рецептором.
All of latter involves the physical movement of
Ligands.
That is, Ligand Reception by a Protein
Note that Reception means Molecule-toMolecule Contact

12.

Константа аффинности отражает
энергию связи лиганд-рецептор.
The equilibrium constant
(association constant):
Keq = KA
Provides a qualitative measure of
the affinity
∆G= -RTlnKeq.

13.

Энтропию термодинамической системы можно определить
через множество возможных равновероятных (микро)
конфигураций (Ω), соответствующих конкретному
состоянию системы:
где kb постоянная Больцмана (имеет размерность
энергия/Т).
S=kb lnΩ
Изменения энтропии в термодинамических обратимых процессах
(ΔS). Макроскопическое определение:
ΔS=∫δQ/T

14.

Энтальпия или энергия расширенной
системы E равна сумме внутренней
энергии газа U
и
потенциальной энергии E = PV
H = U + PV
.

15.

Свободная энергия (функция) Гиббса:
G=H–TS
ΔG = ΔH – T ΔS
Must know this!
изменение энтропии мира в результате изменений в системе:
ΔStotal = ΔSsurr + ΔSsys

16.

Классическим определением энергии
Гиббса является выражение
G =U +PV−TS
Где:
U — внутренняя энергия,
P — давление,
V — объём,
T — абсолютная температура,
S — энтропия.

17.

The free energy enables us to do changes that occur
at a constant temperature and pressure (the Gibbs
free energy) or constant temperature and volume (the
Helmholtz free energy.)
The Helmholtz free energy is of
interest mainly to chemical
engineers

18.

Clark’s Theory
Условия применимости
классической модели
взаимодействия лигандрецептор

19.

1
2
3
4
5
обратимость связывания
все рецепторы эквивалентны и
независимы
биологический ответ пропорционален
количеству занятых рецепторов
параметры связывания и
эффективность определяются в
состоянии равновесия
лиганд не изменяется химически

20.

Signal-Transduction Emphasis
signals that are released from one cell and
allowed to freely diffuse to a second (or more)
recipient cell(s)
We will consider in particular those events
that follow the reception of chemical signals
We will not dwell on the purpose of the
signal

21.

Взаимодействие молекулы лиганда (l) со
связывающей молекулой (b) в условиях
равновесия можно описать таким
уравнением:
k1 [b][l] – k2 [bl] = 0;
k1/ k2 = Ka;
Kd = Ka-1

22.

Ka (B0 - [bl]) = [bl]/ [l] ;
Если: [bl] = B ; [l] = F
То: B/ F = Ka (B0 – B)
получаем уравнение Скетчарда

23.

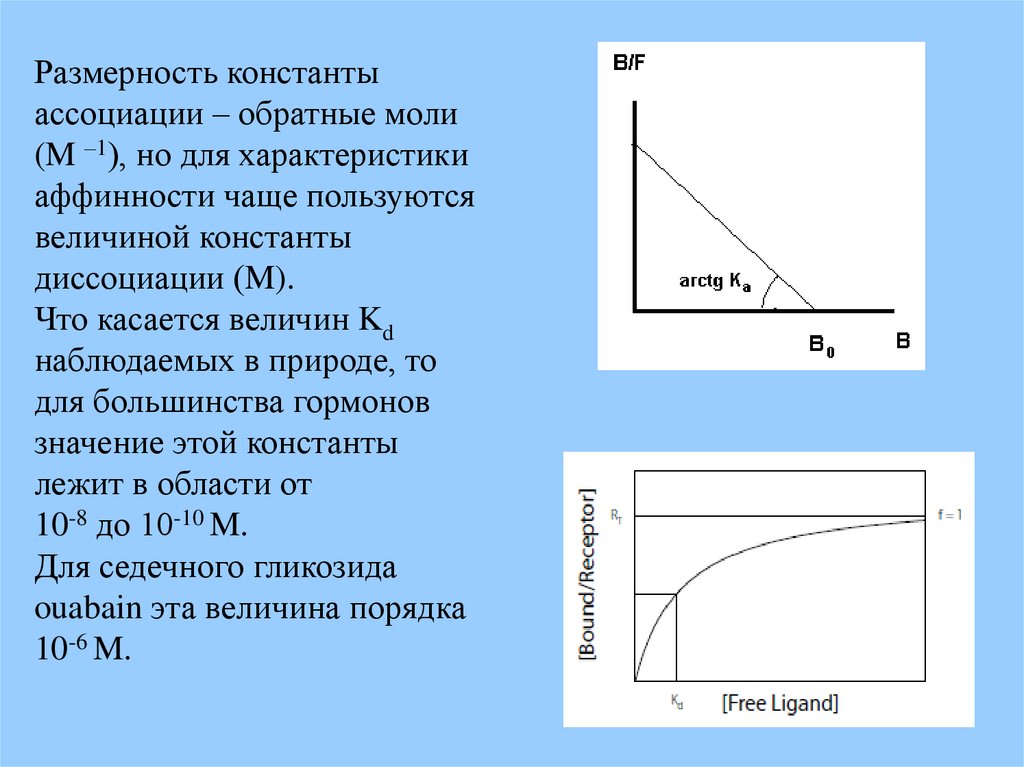
Размерность константы
ассоциации – обратные моли
(M –1), но для характеристики
аффинности чаще пользуются
величиной константы
диссоциации (M).
Что касается величин Kd
наблюдаемых в природе, то
для большинства гормонов
значение этой константы
лежит в области от
10-8 до 10-10 M.
Для седечного гликозида
ouabain эта величина порядка
10-6 M.

24.

The equilibrium constant (association constant): Keq = KA
Provides a qualitative measure of the affinity ∆G= -RTlnKeq.
[M] is the concentration of the protein,
[L] is the concentration of the free ligand
The fractional saturation –Y:
When the protein is half saturated with the ligand the
ligand concentration is equal to KD

25.

Multiple Independent Binding Sites
ν = nY
ν - the moles of bound ligand over the total protein concentration
ν - varies from 0 to n (instead of 0 to 1 for Y)
Scatchard plot

26.

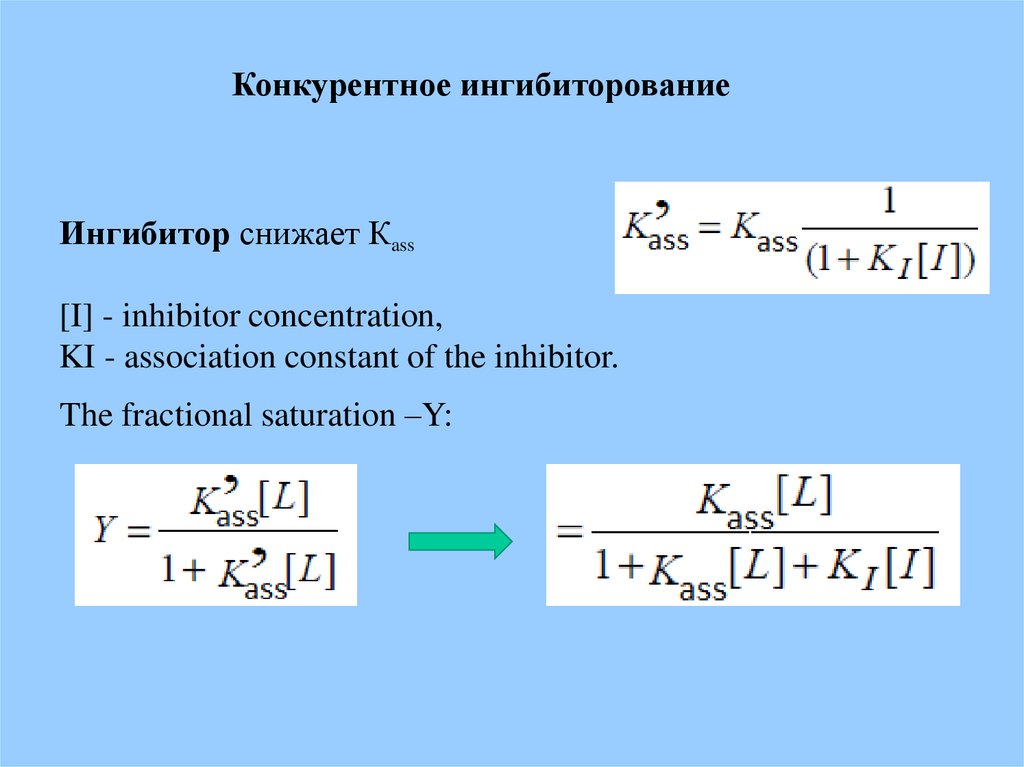
Конкурентное ингибиторование
Ингибитор снижает Кass
[I] - inhibitor concentration,
KI - association constant of the inhibitor.
The fractional saturation –Y:

27.

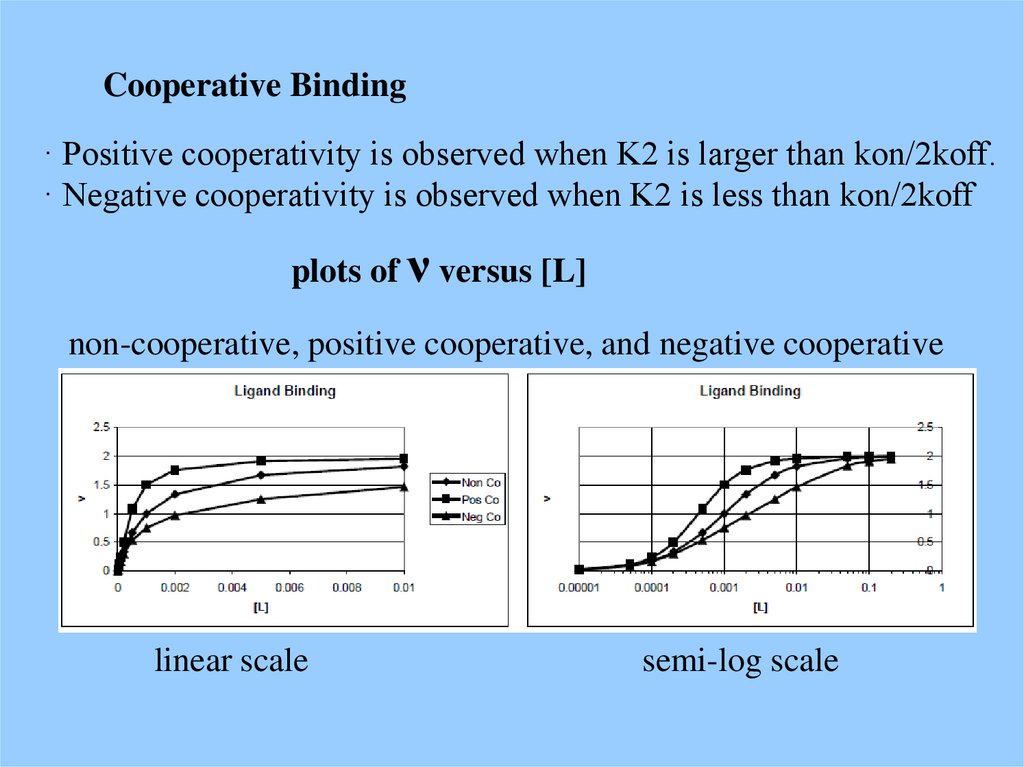
Cooperative Binding
· Positive cooperativity is observed when K2 is larger than kon/2koff.
· Negative cooperativity is observed when K2 is less than kon/2koff
plots of ν versus [L]
non-cooperative, positive cooperative, and negative cooperative
linear scale
semi-log scale

28.

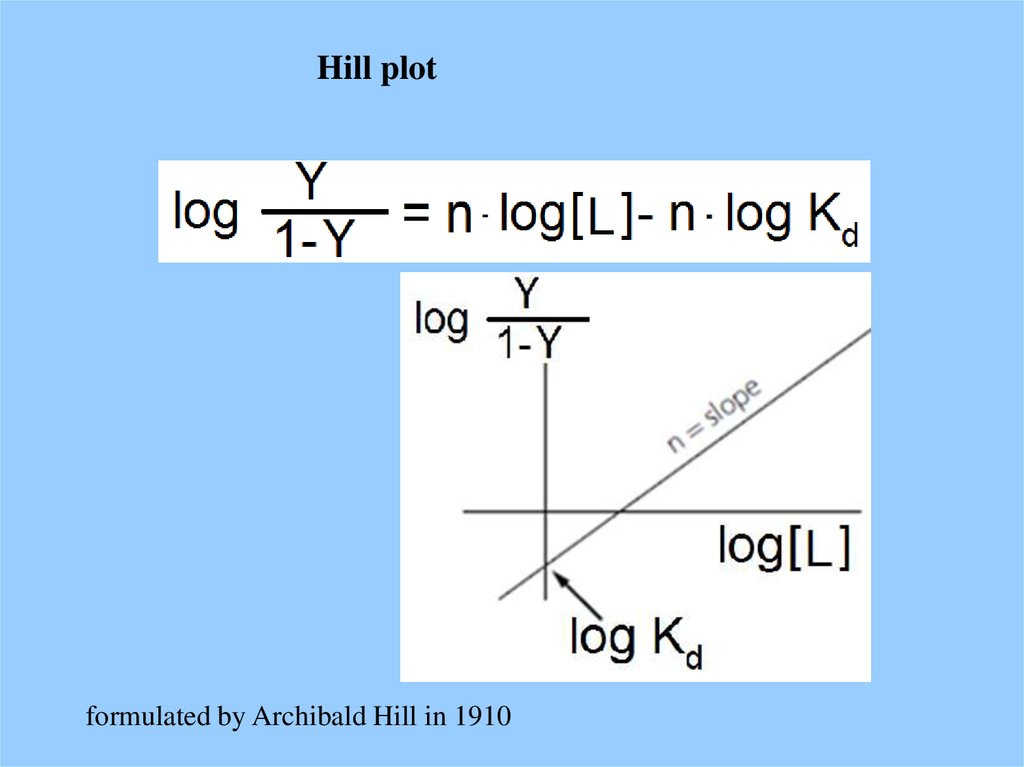
Hill plot
formulated by Archibald Hill in 1910

29.

30.

Independent sites - microscopic and macroscopic binding affinities
(binding of two ligands to an immunoglobulin)
2 -two ways to make [ML].
equilibrium association constants
macroscopic binding constants
microscopic association constant
if only one ligand can bind
kinetic rate constants
for ligand binding is kon
for release of the ligand is koff
2 -two ways of forming [ML]
starting from [ML2].

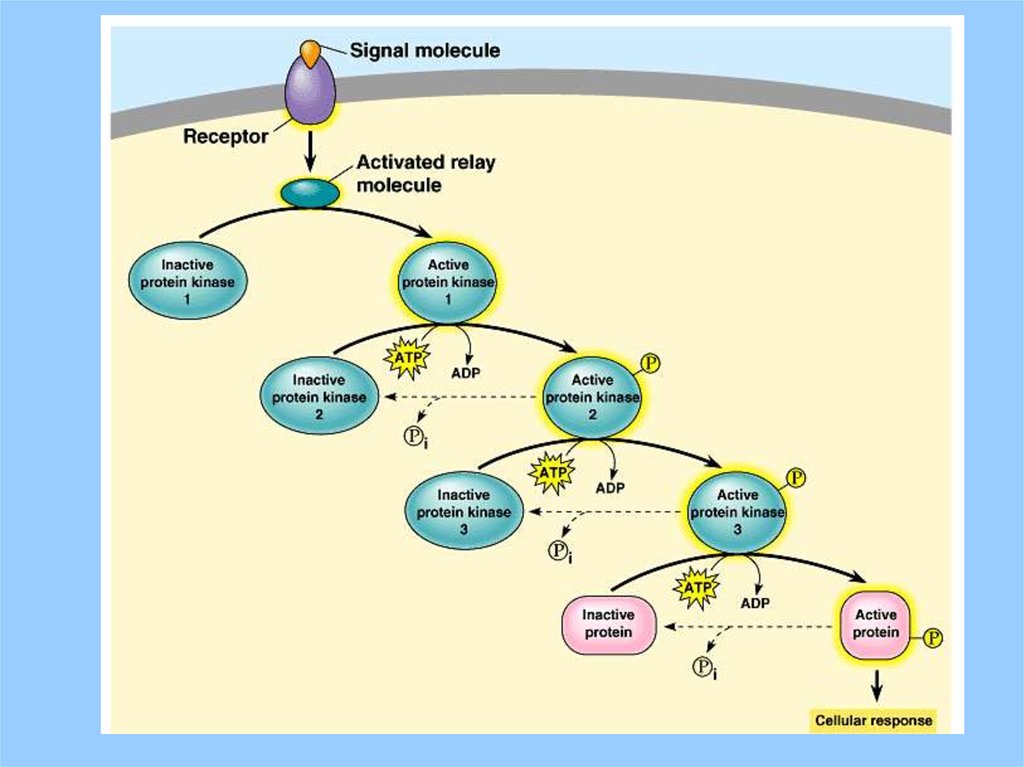
31. Signal Amplification (Cascade)

Note how, via catalysis, one ligand molecule binding
gives rise to many new intracellullar molecules

32.

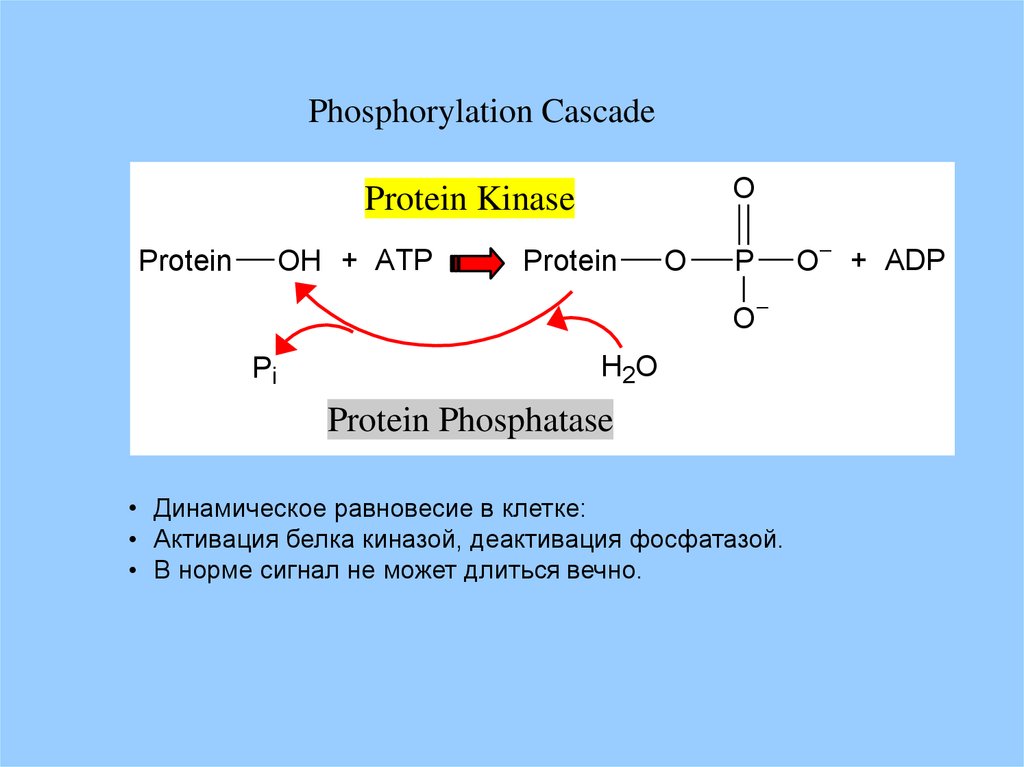
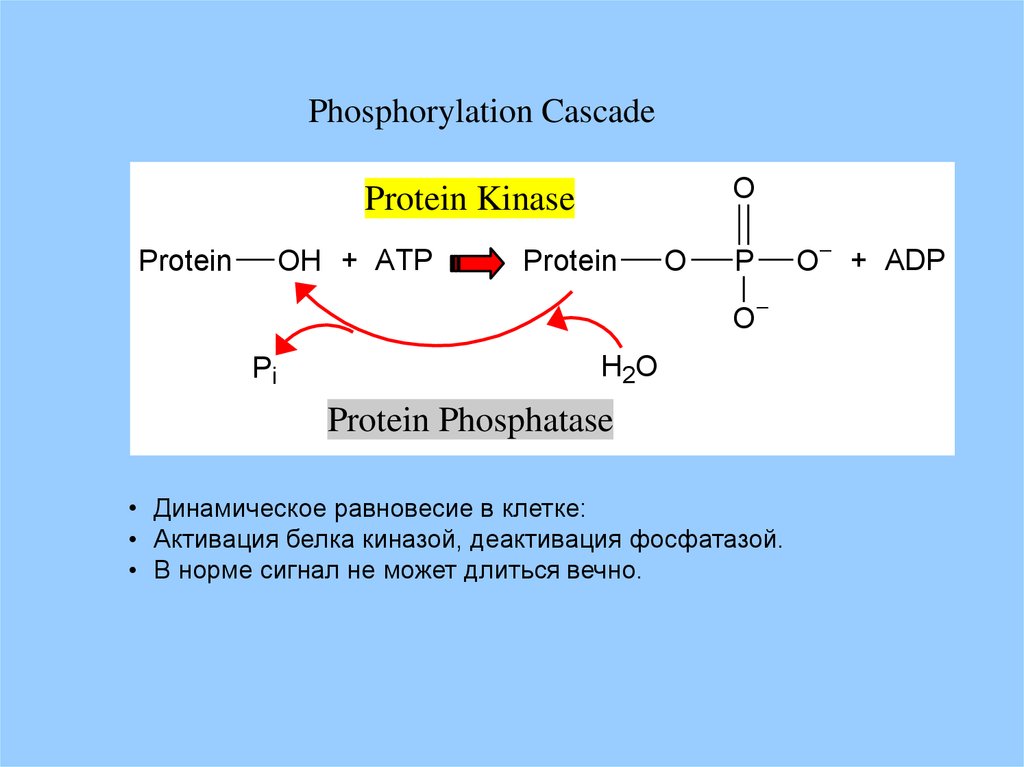
Phosphorylation Cascade
O
Protein Kinase
OH + ATP
Protein
Protein
O
P
O
Pi
H2O
Protein Phosphatase
• Динамическое равновесие в клетке:
• Активация белка киназой, деактивация фосфатазой.
• В норме сигнал не может длиться вечно.
O + ADP

33.

A simple model of enzyme action:
V0 = kcat[ES]
Начальная скорость реакции – концентрация
продукта мала, субстрат в избытке, концентрация
субстрата много больше чем
продукта ([P] << [S]) и
фермента ([E] << [S]).

34.

Скорость образования: [ES] = k1[E][S].
Скорость убывания: [ES] = k-1[ES] + kcat [ES].
Стационарное состояние: k-1[ES] + kcat[ES] = k1[E][S]
Условия ([P] << [S]) и ([E] << [S]).
обычно создаются в эксперименте и тогда согласно
закону сохранения массы:
[S]0 = [S]free + [ES] + [P] ,
тогда приближенно - [S]0 = [S]
для фермента - [E]total = [E]free + [ES]

35.

Цель, определить [ES] через измеряемые величины.
Сгруппируем константы (кинетические) и переменные
(концентрации):
(k-1 + kcat) [ES] = k1 [E][S],
(k-1 + kcat)/k1 = [E][S]/[ES] ;
Km = (k-1 + kcat)/k1

36.

Выразим [E] через [ES] и [E]total:
[E] = [E]total - [ES];

37.

Km = ([E]total - [ES]) [S]/[ES]
[ES] Km = [E]total[S] - [ES][S]
[ES] Km + [ES][S] = [E]total[S]
[ES](Km + [S]) = [E]total[S]
[ES] = [E]total [S]/(Km + [S])
V0 = kcat[E]total [S]/(Km + [S]) (подставляя в V0 = kcat[ES] )

38.

В условиях насыщения субстратом, когда [ES] = [E]total
Vmax = kcat [E]total подставляем в V0 = kcat[E]total [S]/(Km + [S])
V0 = Vmax [S]/(Km + [S])
Это выражение скорости реакции через концентрацию субстрата и Km
Физический смысл Km
При [S] = Km V0 = 1/2 Vmax ; при малых [S]
V0 стремится к Vmax[S] /Km
Vmax /Km (или kcat /Km ) - «каталитическая сила»

39.

40.

41.

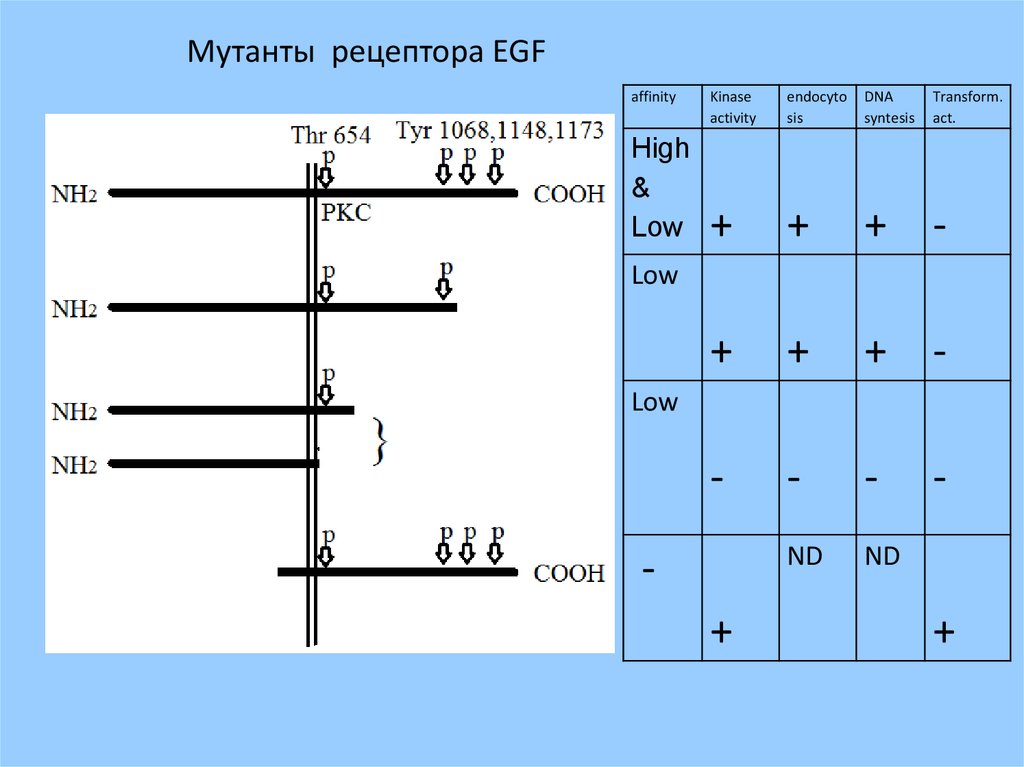
Мутанты рецептора EGF
affinity
High
&
Low
Kinase
activity
endocyto
sis
DNA
syntesis
Transform.
act.
+
+
+ -
+
+
+
-
-
-
-
-
ND
ND
Low
Low
+
+

42.

About 70 to 80 percent breast
precancers have over expression of
Her-2/neu oncogene. Although Her2/neu oncogene was first identified in
breast cancer

43.

One of the fascinating things that
have happened in recent years is that
an antibody to counteract the
Her-2/neu receptor, can be given intravenously.
It has quite a unique mechanism of action. It
attaches only to cells with too much Her-2/neu
receptor, not the normal ones. Unlike
chemotherapy, with which case most dividing
cells are destroyed, it is a targeted therapy.
http://EzineArticles.com/?expert=Michael_Russell

44.

45.

Настоящий инженер
немедленно начнет писать
функцию с 7-ю
переменными и
минимизировать ее с
помощью системы
дифференциальных
уравнений...

46.

Ингибитор снижает Кass
[I] - inhibitor concentration,
KI - association constant of the inhibitor.
The fractional saturation –Y:

47.

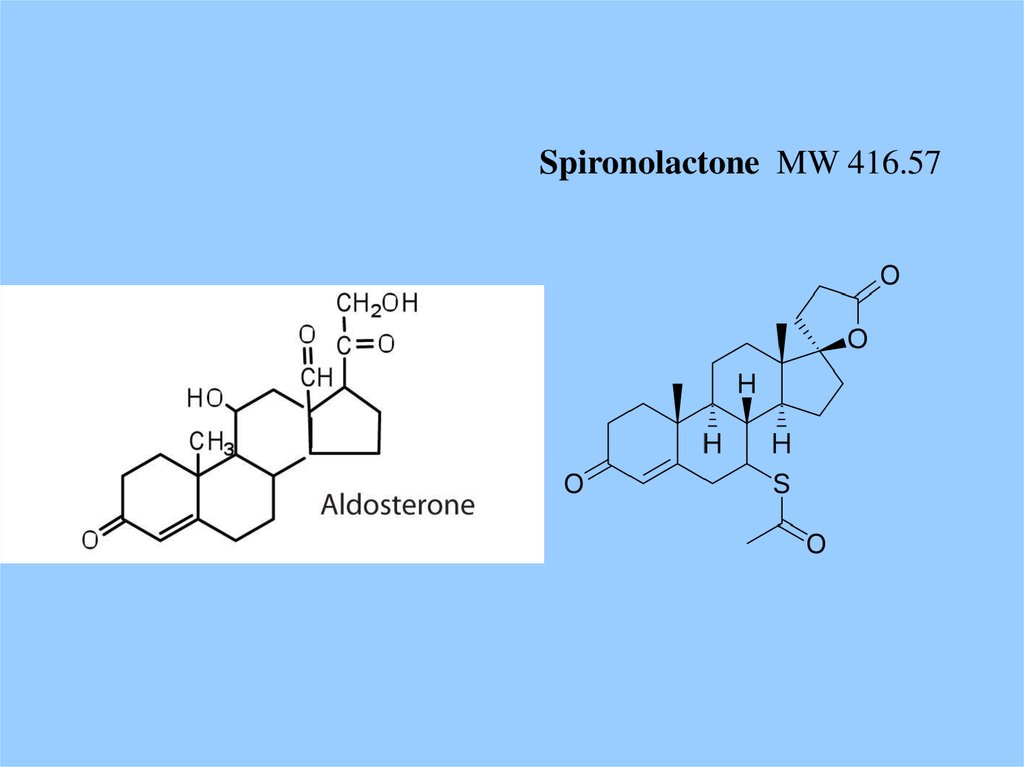
Spironolactone MW 416.57

48.

Spironolactone (верошпирон)
IC50 ~ 2 nM
Aldosterone
Kd ~ 0.14 nM
Aldosterone blood plasma concentration
«норма» ~ 0.2 nM
«отеки, гипертония» ~ 0.5 nM
Доза верошпирона для нормализации - ?

49.

50.

51.

Phosphorylation Cascade
O
Protein Kinase
OH + ATP
Protein
Protein
O
P
O
Pi
H2O
Protein Phosphatase
• Динамическое равновесие в клетке:
• Активация белка киназой, деактивация фосфатазой.
• В норме сигнал не может длиться вечно.
O + ADP

52.

A simple model of enzyme action:
V0 = kcat[ES]
Начальная скорость реакции – концентрация
продукта мала, субстрат в избытке, концентрация
субстрата много больше чем
продукта ([P] << [S]) и
фермента ([E] << [S]).

53.

Скорость образования: [ES] = k1[E][S].
Скорость убывания: [ES] = k-1[ES] + kcat [ES].
Стационарное состояние: k-1[ES] + kcat[ES] = k1[E][S]
Условия ([P] << [S]) и ([E] << [S]).
обычно создаются в эксперименте и тогда согласно
закону сохранения массы:
[S]0 = [S]free + [ES] + [P] ,
тогда приближенно - [S]0 = [S]
для фермента - [E]total = [E]free + [ES]

54.

Цель, определить [ES] через измеряемые величины.
Сгруппируем константы (кинетические) и переменные
(концентрации):
(k-1 + kcat) [ES] = k1 [E][S],
(k-1 + kcat)/k1 = [E][S]/[ES] ;
Km = (k-1 + kcat)/k1

55.

Выразим [E] через [ES] и [E]total:
[E] = [E]total - [ES];

56.

Km = ([E]total - [ES]) [S]/[ES]
[ES] Km = [E]total[S] - [ES][S]
[ES] Km + [ES][S] = [E]total[S]
[ES](Km + [S]) = [E]total[S]
[ES] = [E]total [S]/(Km + [S])
V0 = kcat[E]total [S]/(Km + [S]) (подставляя в V0 = kcat[ES] )

57.

В условиях насыщения субстратом, когда [ES] = [E]total
Vmax = kcat [E]total подставляем в V0 = kcat[E]total [S]/(Km + [S])
V0 = Vmax [S]/(Km + [S])
Это выражение скорости реакциичерез концентрацию субстрата и Km
Физический смысл Km
При [S] = Km V0 = 1/2 Vmax ; при малых [S]
V0 стремится к Vmax[S] /Km
Vmax /Km (или kcat /Km ) - «каталитическая сила»

58.

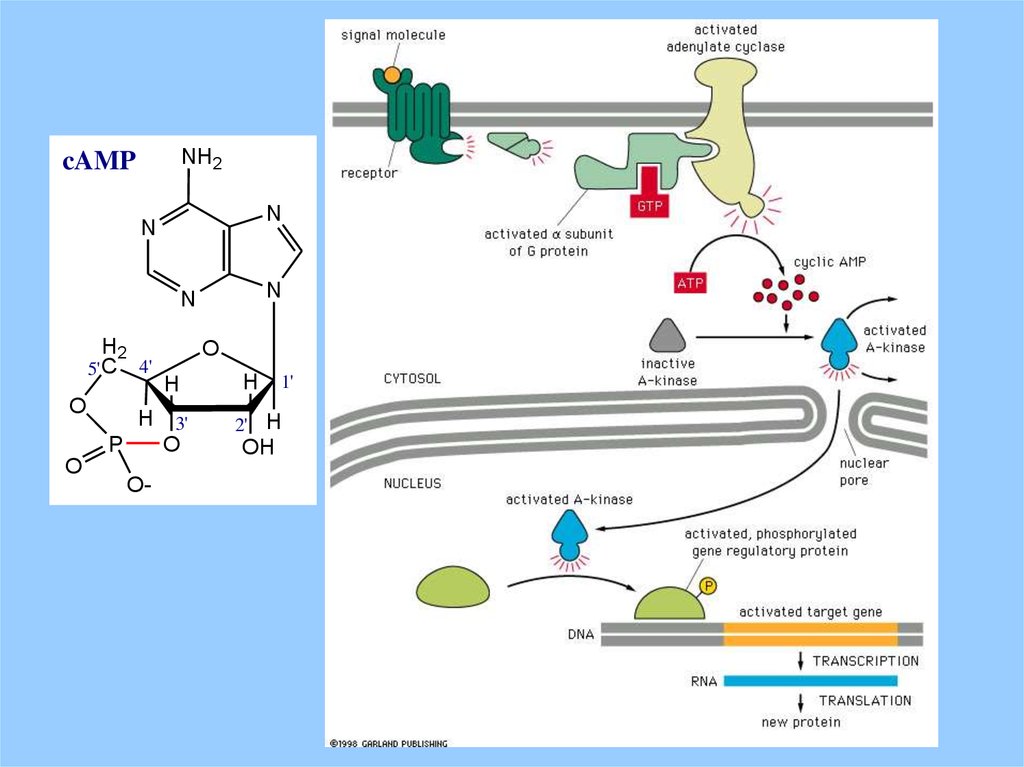
NH2
cAMP
N
N
N
N
H2
5' C
O
O
4'
O
H
H 3'
P
O
O-
H
1'
2' H
OH

59.

60.

61.

62.

63.

64.

Studies of water transport across cell plasma membrane.
Schematic diagram of the experimental setup

65.

Hypotonic medium causes cell swelling and activates
adaptive mechanism of recovery which is termed
Regulatory Volume Decrease (RVD).
H2O
H2O
H2O
H2O
H2O
K+
H2O
H2O
K+
H2O
H2O
H2O
H
O
H2O
Cl- K+ 2
organic
anions
To understand the adaptive reaction better one needs to
use mathematical modeling of osmolytes fluxes.

66.

Following processes were taken into account in the model of the
cell response to the hypotonic shock :
The equations of mathematical model
Cell ion content and ion fluxes
dn Na
A 3J pump J Na J NKCC ,
dt
Sodium
dnK
A 2 J pump J K J KCC J NKCC ,
dt
Potassium
dnCl
A( J Cl J KCC 2 J NKCC ),
dt
Chloride
dn X
AJ X ,
dt
Organic anions (X)
Em F (nNa nK nCl zX) / Cm / A, Transmembrane
potential difference
dV
n n K nCl n X
AVW PW Na
П e .
dt
V
Cell volume
Iliaskin AV, e.a. Biofizika. 2011 May-Jun;56(3):550-60.

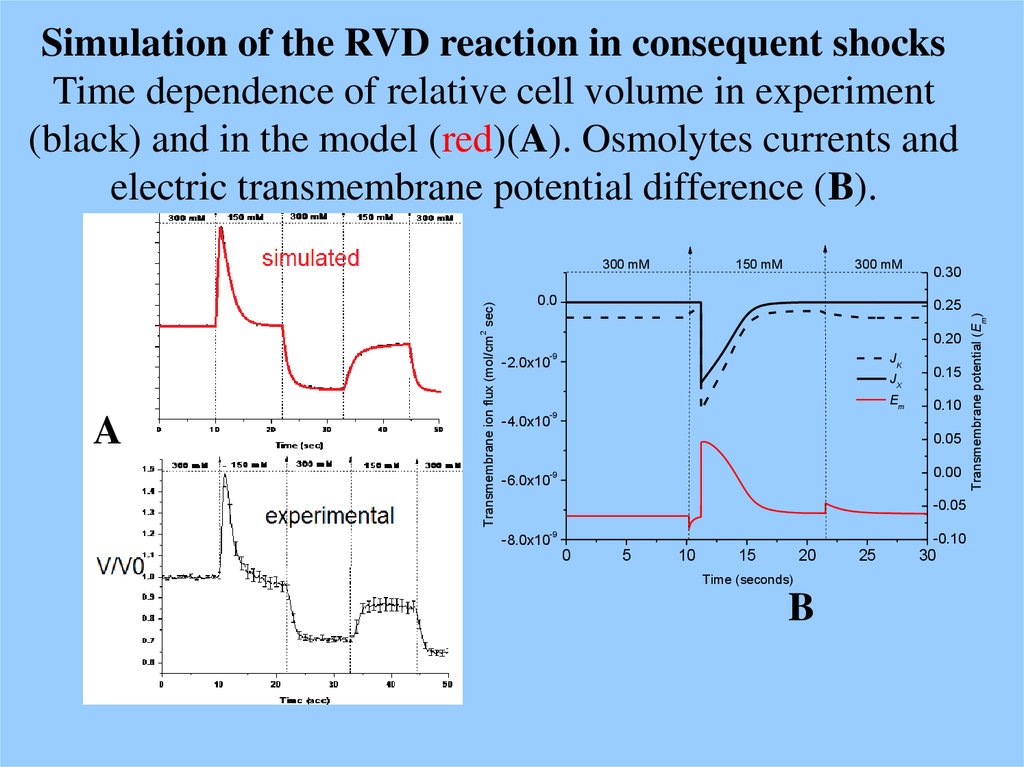
67. Simulation of the RVD reaction in consequent shocks Time dependence of relative cell volume in experiment (black) and in the

model (red)(A). Osmolytes currents and
electric transmembrane potential difference (B).
300 mM
150 mM
0.0
0.20
-9
JK
-2.0x10
JX
Em
-9
0.15
0.10
-4.0x10
0.05
0.00
-9
-6.0x10
-0.05
-9
-0.10
-8.0x10
0
5
10
15
20
Time (seconds)
B
25
30
Transmembrane potential (Em)
A
0.30
0.25
2
Transmembrane ion flux (mol/cm sec)
300 mM

68.

Principal cell
Some key agents
in the mechanism
of antidiuretic
action of
vasopressin