Похожие презентации:
Решение нелинейных уравнений
1. Решение нелинейных уравнений
2. Постановка задачи
Пусть требуется решить уравнениеf x 0
Приближенно решить уравнение или
вычислить корень x с точностью - это
значит найти число x , такое что x x
3. Локализация и отделение корня
Локализация корней - необходимоопределить количество, характер и
расположение корней на числовой прямой
Отделение корня - нужно указать отрезок ,
внутри которого лежит один и только один
корень данного уравнения
4. Локализация и отделение корня
Теорема 1. Если функция непрерывна на отрезке ина его концах принимает значения разного знака, то
на этом отрезке существует хотя бы одна точка, в
которой функция обращается в ноль.
Теорема 2. Для того чтобы дифференцируемая на
интервале функция возрастала (убывала),
необходимо и достаточно, чтобы во всех его точках
производная была неотрицательной
(неположительной)
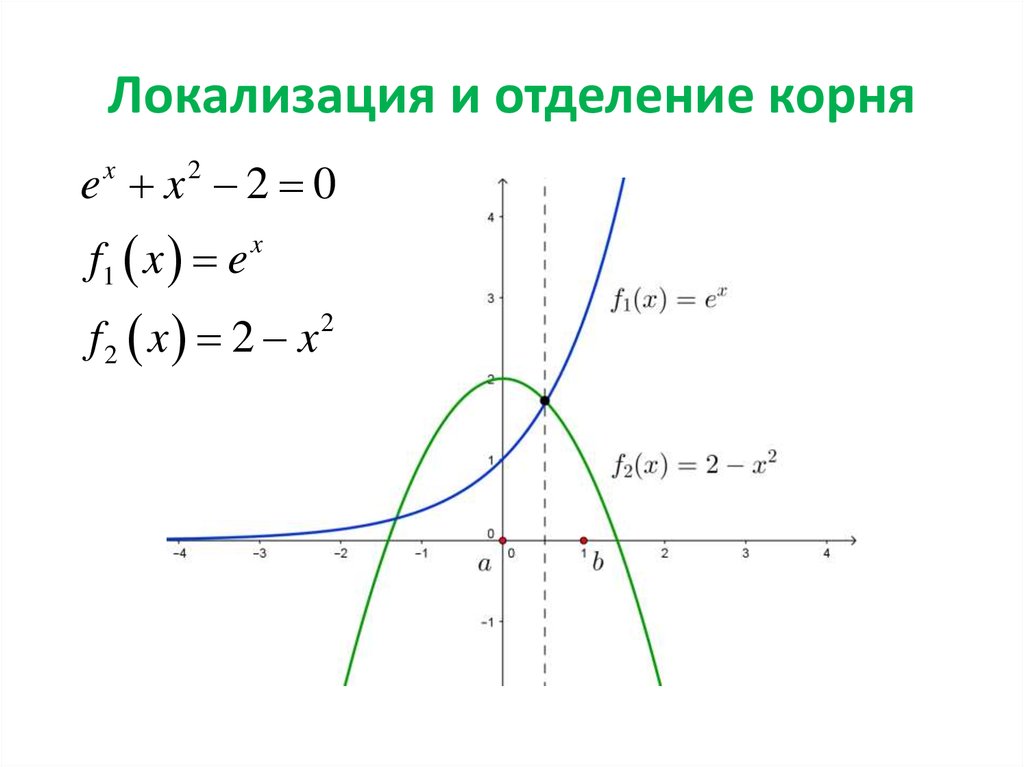
5. Локализация и отделение корня
e x 2 0x
2
f1 x e
x
f2 x 2 x2
6. Локализация и отделение корня
f x ex x2 2непрерывная
f 0 1 0, f 1 1,7 0
значит корень существует
x
f x e 2 x 0 на 0;1
значит функция монотонная, это
обеспечивает единственность корня
7. Схема изучения метода
Ограничения
Алгоритм
Рисунок
Правило остановки
Скорость сходимости
Достоинства и недостатки метода
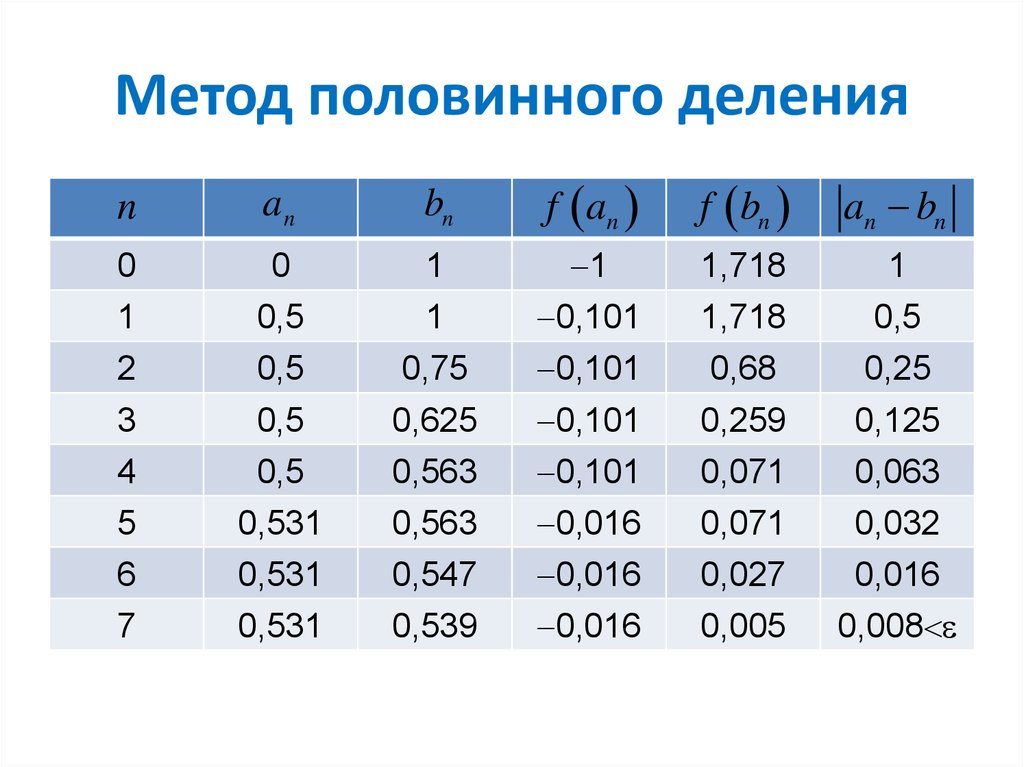
8. Метод половинного деления
Ограничения НетАлгоритм Строим последовательность
вложенных отрезков содержащих корень
a0 , b0 a1, b1 an , bn , где
ai
ai 1 bi i
ci
bi
2
Теорема 3. Для любой последовательности
вложенных отрезков существует единственная
точка, принадлежащая всем отрезкам этой
последовательности
9. Метод половинного деления
10. Метод половинного деления
Правило остановки Процесс деленияпродолжается до тех пор, пока длина отрезка
не станем меньше
Скорость сходимости
Метод сходится со скоростью геометрической
прогрессии со знаменателем q 0,5
Это довольно медленно
11. Метод половинного деления
Достоинства метода• Метод очень прост
• Не имеет ограничений
• Легко программируется
Недостатки метода
• Если есть проблемы с отделением корня и в
отрезке их несколько, то не понятно к какому
сходимся последовательность
• Метод не применим к корням четной кратности
• Не обобщается на системы уравнений
12. Метод половинного деления
nan
bn
f an
f bn
an bn
0
1
2
0
0,5
0,5
1
1
0,75
1
0,101
0,101
1,718
1,718
0,68
1
0,5
0,25
3
4
5
0,5
0,5
0,531
0,625
0,563
0,563
0,101
0,101
0,016
0,259
0,071
0,071
0,125
0,063
0,032
6
0,531
0,547
0,016
0,027
0,016
7
0,531
0,539
0,016
0,005
0,008
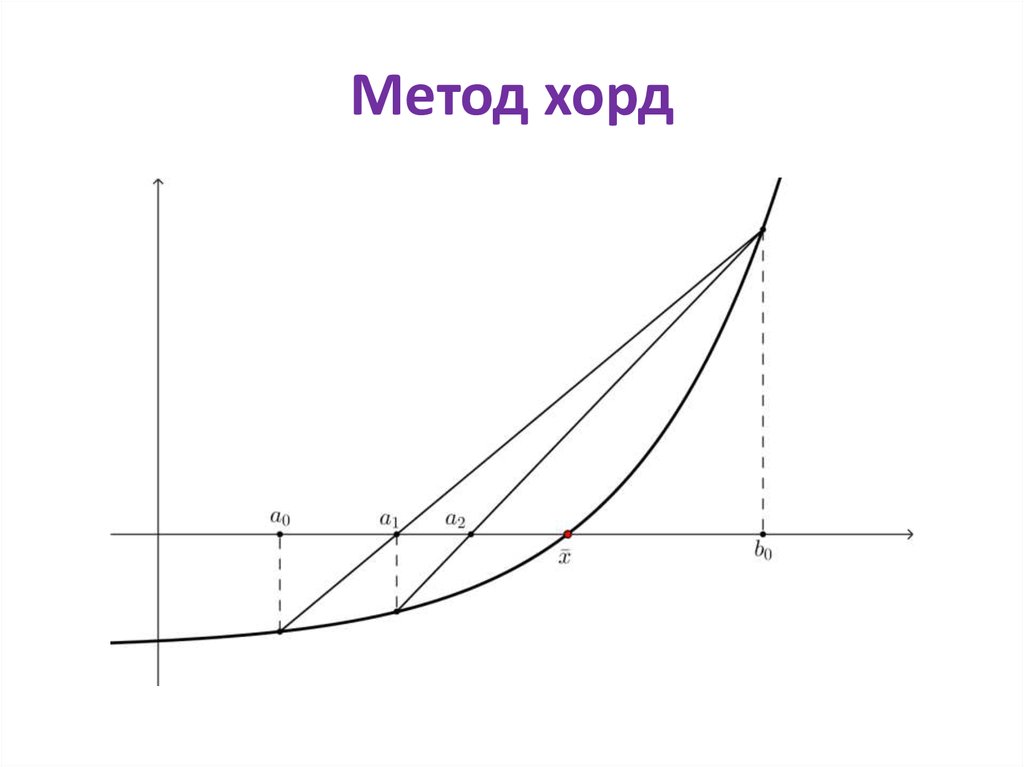
13. Метод хорд
Ограничения. Этот метод может бытьиспользован только в том случае, если
функция на отрезке не имеет точек
перегиба, т.е. постоянна по знаку вторая
производная
Алгоритм.
xn xn 1 f xn 1
если x0 a
b xn 1
f b f xn 1 ,
14. Метод хорд
15. Метод хорд
Алгоритм.xn xn 1 f xn 1
если x0 b
xn 1 a
f xn 1 f a ,
Теорема 4. Если функция непрерывна и выпукла на
отрезке, то уравнение f x 0 имеет на отрезке
единственный корень, и последовательность xn
монотонно сходится к нему.
16. Метод хорд
17. Метод хорд
При выборе нулевого приближения следуетруководствоваться рисунком или следующим
правилом:
a, если f a f a 0
x0
b, если f b f b 0
18. Метод хорд
Правило остановкиЕсли f x m1 ,
a ,b
то вычисления можно прекратить, когда
выполнено условие
f xn m1
В силу выпуклости функции можно
утверждать, что
m1 min f a , f b
a ,b
19. Метод хорд
Скорость сходимостиМожно рассчитывать на его быструю
сходимости только если функция близка к
линейной
Если на функцию не накладывать
ограничений, то метод может проигрывать
даже методу половинного деления
20. Метод хорд
Достоинства метода• При определенных ограничениях имеет неплохую
скорость сходимости
Недостатки метода
• Ограничения на свойства функции
• Сходимость к корню с одной стороны
• Усложненное правило остановки
21. Метод хорд
f x ex x2 2f x ex 2 x
f x e x 2 0
f 0 1 0 f 1 1,72 0
f 0 f 0 0 x0 0
f 0 1 f 1 4,72 m1 min f x 1
0;1
10 2 m1 0,01
22. Метод хорд
nxn
f xn
0
1
0
0,368
1
0,42
2
3
4
0,492
0,526
0,534
0,122
0,032
0,008 m1
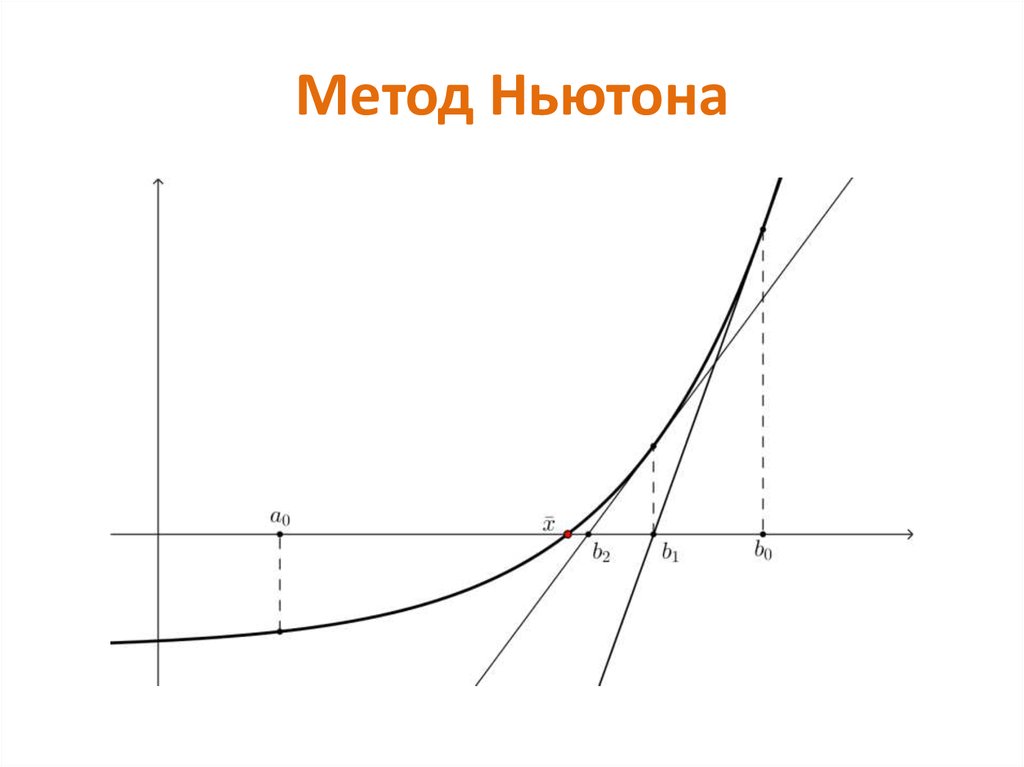
23. Метод Ньютона
Ограничения. Те же что и для метода хордАлгоритм. Выберем
a, если f a f a 0
x0
b, если f b f b 0
далее
f xn 1
xn xn 1
f xn 1
24. Метод Ньютона
25. Метод Ньютона
Правило остановки То же что и для методахорд
Скорость сходимости. При выборе начального
приближения из достаточно малой
окрестности корня метод сходится
квадратично, т.е. скорость сходимости
велика. Для кратного корня скорость
геометрической прогрессии
26. Метод Ньютона
Достоинства метода• Высокая скорость сходимости
Недостатки метода
• Ограничения на свойства функции
• Сходимость к корню с одной стороны
• Усложненное правило остановки
27. Метод Ньютона
f x e x 2x
2
f x ex 2 x
f x e x 2 0
f 0 1 0 f 1 1,72 0
f 1 f 1 0 x0 1
f 0 1 f 1 4,72 m1 min f x 1
0;1
10 2 m1 0,01
28. Метод Ньютона
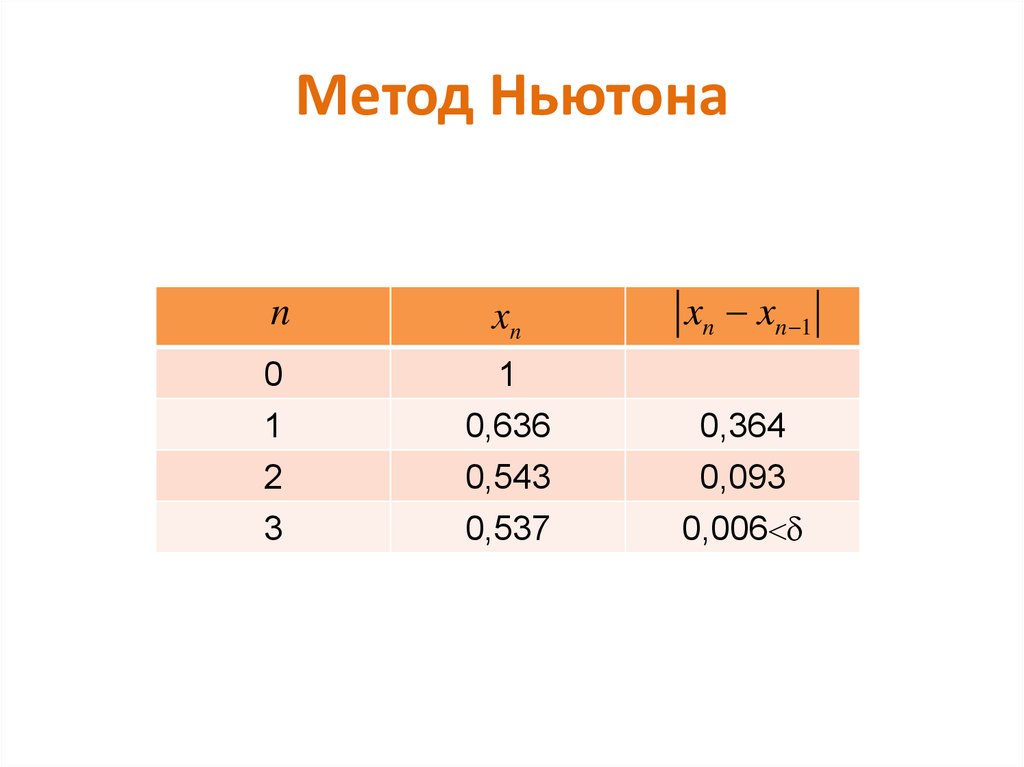
nxn
xn xn 1
0
1
1
0,636
0,364
2
3
0,543
0,537
0,093
0,006
29. Комбинированный метод
Поскольку методы касательных и хорд даютприближения один с избытком, а другой с
недостатком их часто используют совместно комбинированный метод. В этом случае получаем
систему вложенных отрезков
a0 , b0 a1, b1
an , bn
содержащих корень уравнения.
30. Комбинированный метод
В этом случае можно использовать правилоостановки, как в методе половинного деления
bn an
При этом использование метода Ньютона позволяет
повысить скорость сходимости метода хорд
31. Комбинированный метод
32. Комбинированный метод
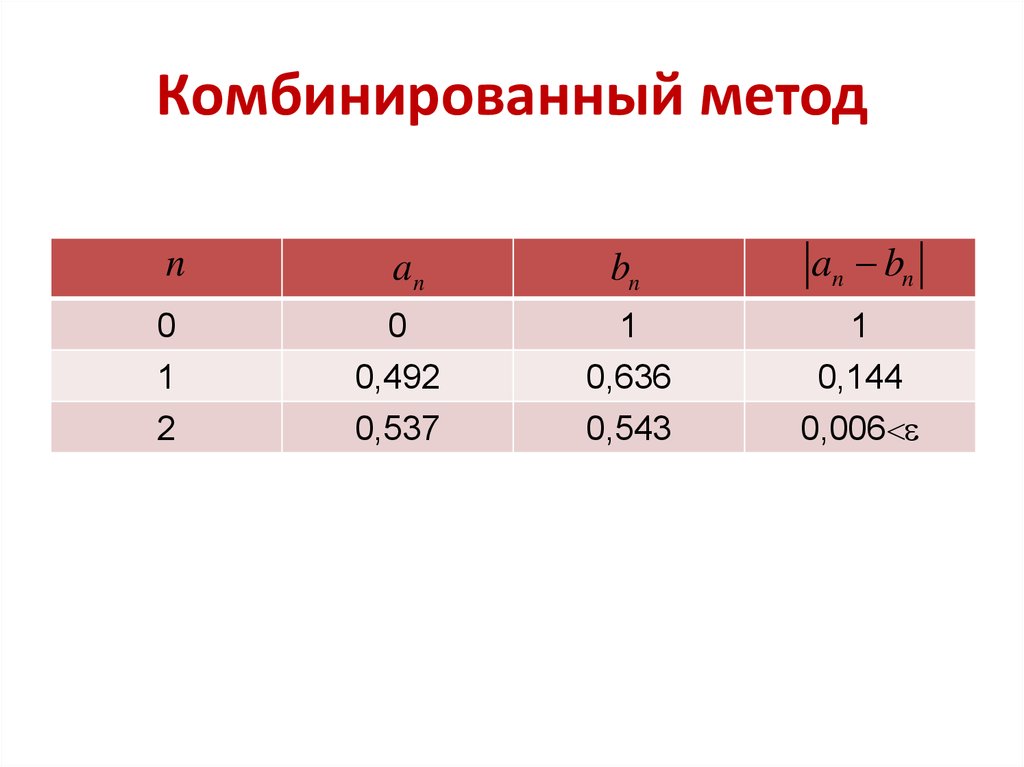
nan
bn
an bn
0
1
0
0,492
1
0,636
1
0,144
2
0,537
0,543
0,006
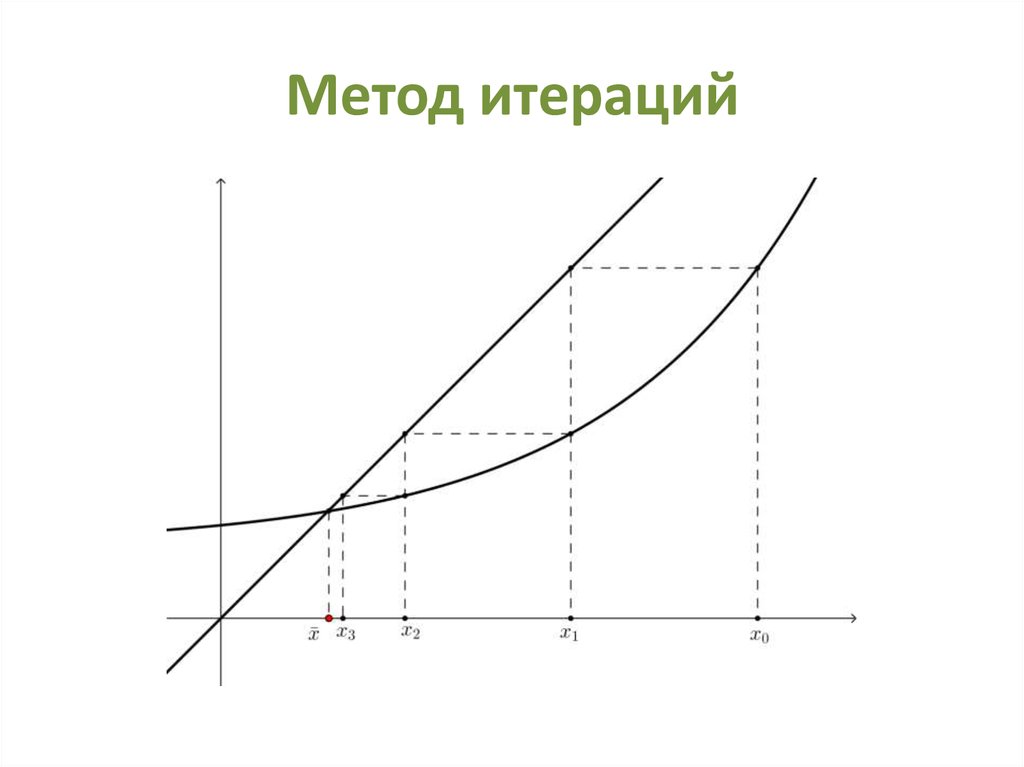
33. Метод итераций
Ограничения. Метод итераций применяетсяпри решении уравнений вида:
x x
Функция x определенная на отрезке a, b
называется сжимающей, если существует
такая положительная постоянная q 1 , что
для любых x1, x2 a, b выполняется
неравенство
x1 x2 q x1 x2
34. Метод итераций
Теорема 5. Если x дифференцируема на отрезке,причем sup x 1 , то она является сжимающей
на этом отрезке, и можно взять q sup x
Теорема 6. Пусть функция является сжимающей на
отрезке и переводит этот отрезок в себя, при всех
x a, b . Тогда уравнение x x на этом отрезке
имеет, и притом, единственное решение.
35. Метод итераций
АлгоритмЛюбое x0 a, b
Далее xn xn 1
36. Метод итераций
37. Метод итераций
38. Метод итераций
Правило остановкиxn xn 1
1 q
q
Скорость сходимости Определяется
значением q
39. Метод итераций
Достоинства метода• Не накапливается ошибка вычислений.
Ухудшение очередного приближения отразится
лишь на числе итераций
• При небольшом значении q высокая скорость
сходимости
Недостатки метода
• Подбор сжимающей функции с небольшим
значением q
• Усложненное правило остановки
40. Метод итераций
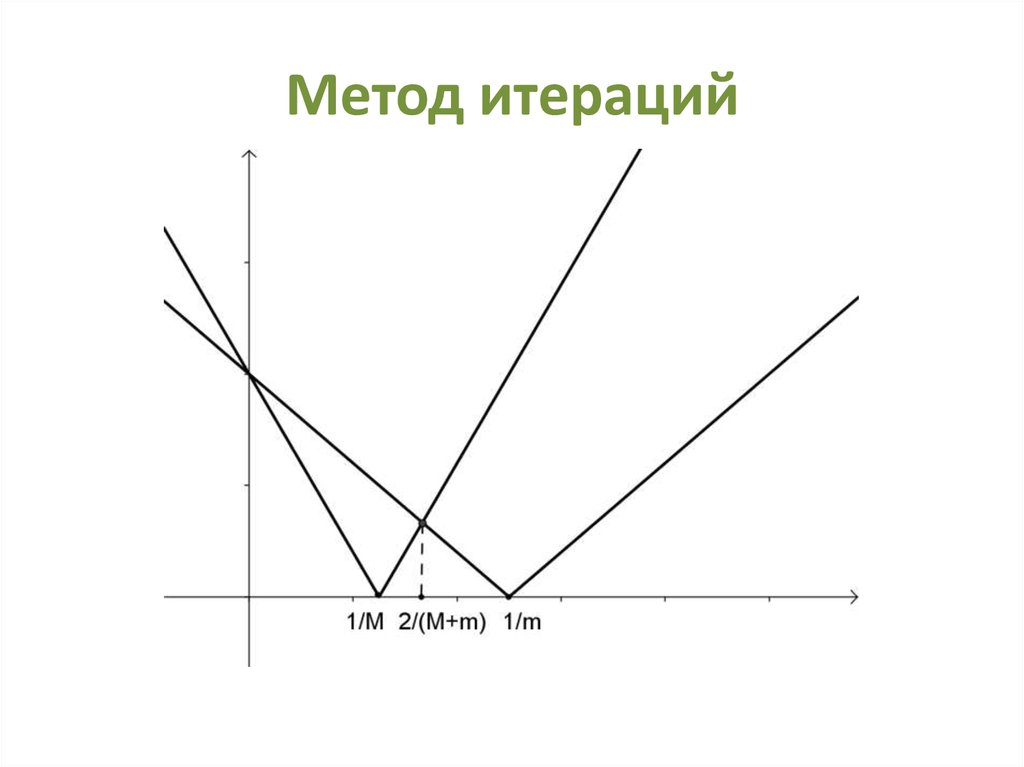
Теорема 7. Пусть дана непрерывнодифференцируема на отрезке функция, причем
m min f x 0, а M max f x ,
2
тогда для любого 0,
M
, функция
x x f x является сжимающей на отрезке,
причем при
2
коэффициент сжатия
M m
принимает минимально возможное значение
M m
q
M m
41. Метод итераций
42. Метод итераций
Воспользуемся предложенным приемомf x ex x2 2
f x ex 2 x
m 1 M 4,72 0,35 q 0,65
x x 0,35 e x x 2 2
10
2
1 q
0,02
q
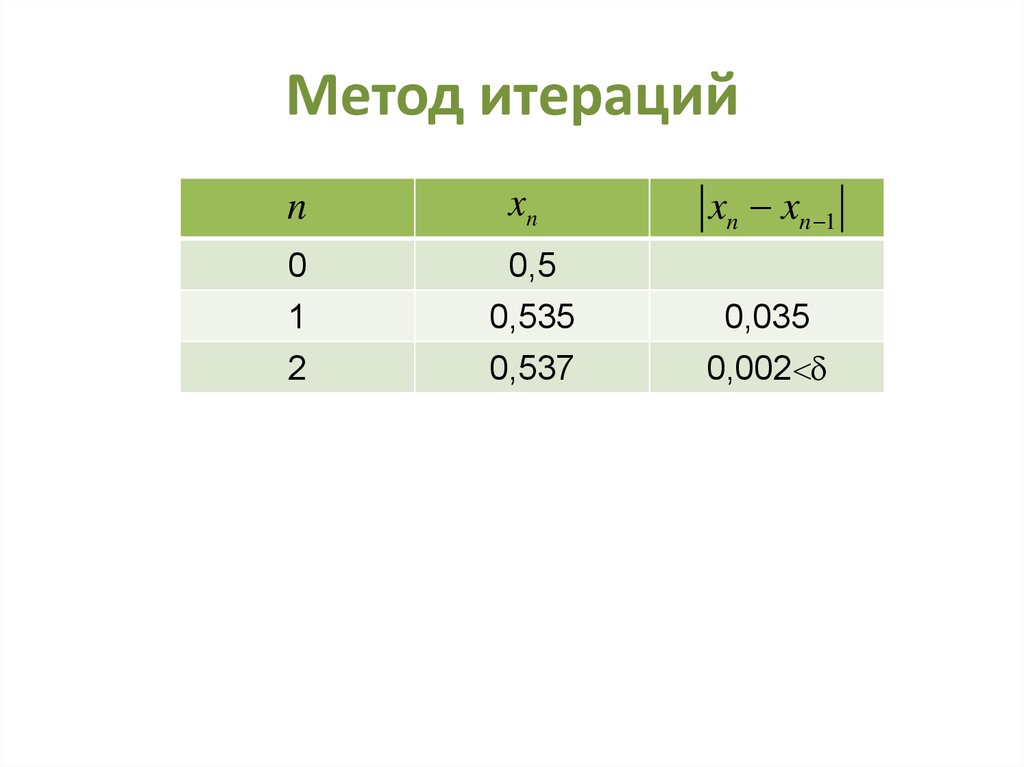
43. Метод итераций
nxn
xn xn 1
0
1
2
0,5
0,535
0,537
0,035
0,002


































 Математика
Математика








