Решение нелинейных уравнений

1. Решение нелинейных уравнений

2.

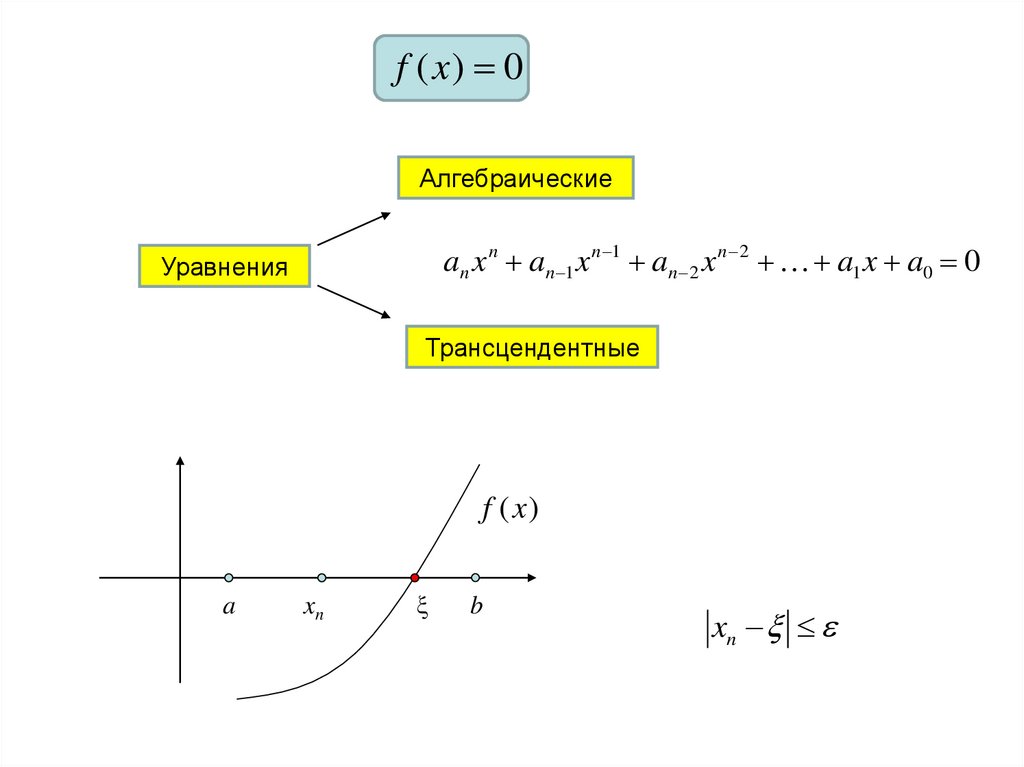
f ( x) 0
Алгебраические
an x n an 1 x n 1 an 2 x n 2 a1 x a0 0
Уравнения
Трансцендентные
f (x )
a
xn
b
xn

3. Метод дихотомии

Метод хорд
Метод дихотомии
f ( x) 0
f (x )
ak
с
c
bk
ak bk
2
if f (ak ) f (c) 0 ak 1 ak , bk 1 c
f f (c) f (bk ) 0 ak 1 c, bk 1 bk
[a, b] [a0 , b0 ] [a1, b1 ] [a2 , b2 ] [ak , bk ]
bk ak

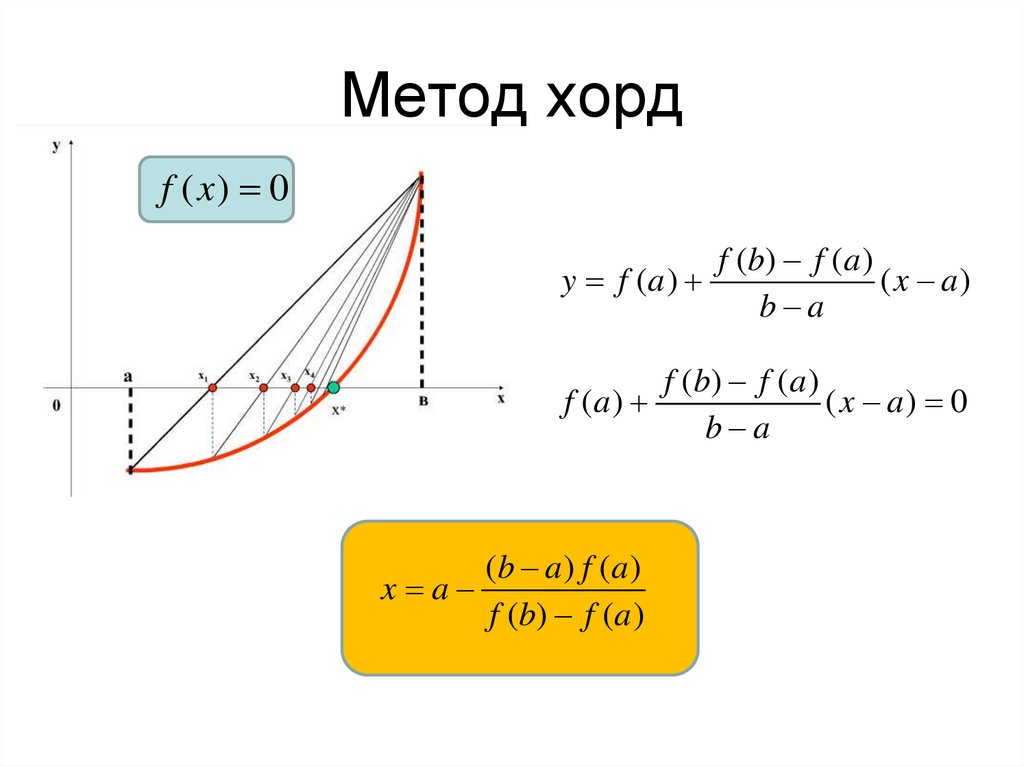
4. Метод хорд

Метод хорд
f ( x) 0
f ( b) f ( a )
y f (a )
( x a)
b a
f ( b) f ( a )
f (a )
( x a) 0
b a
(b a ) f ( a )
x a
f ( b) f ( a )

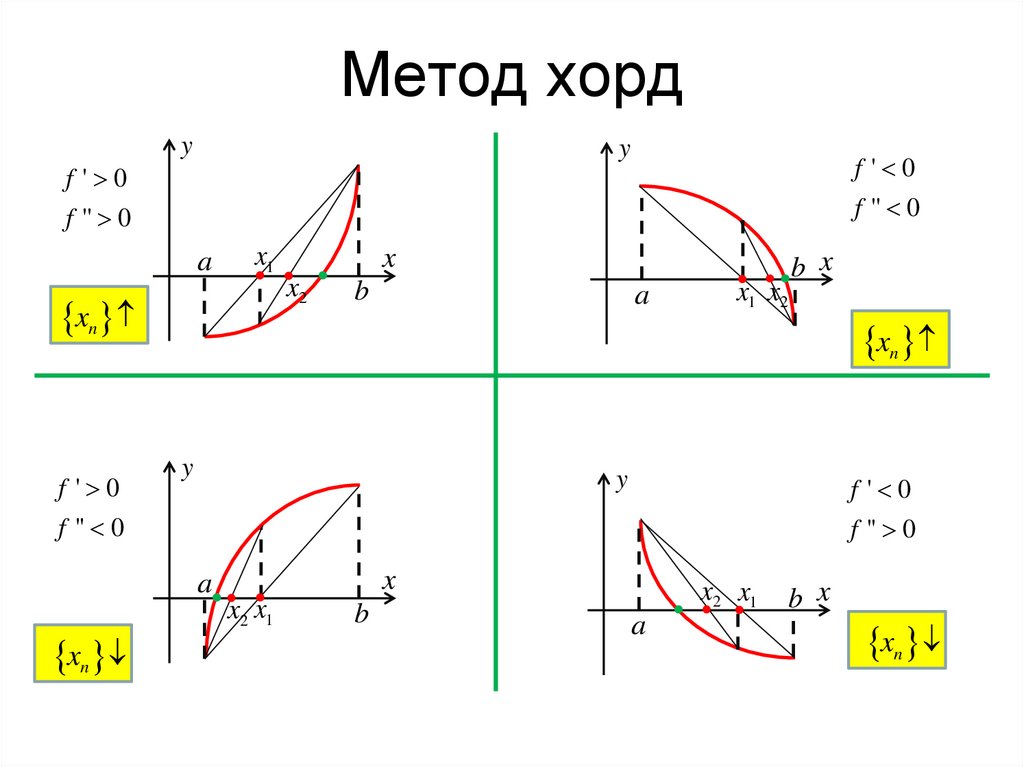
5. Метод хорд

Метод хорд
y
y
f ' 0
f ' 0
f '' 0
f '' 0
a
x1
x2
xn
f ' 0
x
b
a
x1 x2
b x
xn
y
y
f ' 0
f '' 0
f '' 0
a
xn
x
x2 x1
b
x2 x1
a
b x
xn

6.

Метод хорд
Метод хорд
x a
(b a ) f ( a )
(b a )
f ( b) f ( a )
( b xn ) f ( xn )
f ' f '' 0 xn 1 xn
f ( b ) f ( xn )
( xn a ) f ( x n )
f ' f '' 0 xn 1 xn
f ( xn ) f ( a )
Неподвижная точка в методе хорд – это тот конец отрезка (a или b) на
котором совпадают знаки функции и второй производной, т.е.:
f ( x) f ( x) 0

7.

Метод хорд
Метод
хорд
f ' f '' 0
xn 1 xn
( b xn ) f ( xn )
f ( b ) f ( xn )
xn , xn b
x lim xn
n
(b x ) f ( x )
x x
f ( x) 0
f ( b) f ( x )
f ' f '' 0
( xn a ) f ( x n )
xn
xn , xn a x lim
xn 1 xn
n
f ( xn ) f ( a )
( x a) f ( x)
x x
f ( x) 0
f ( x ) f (a )

8.

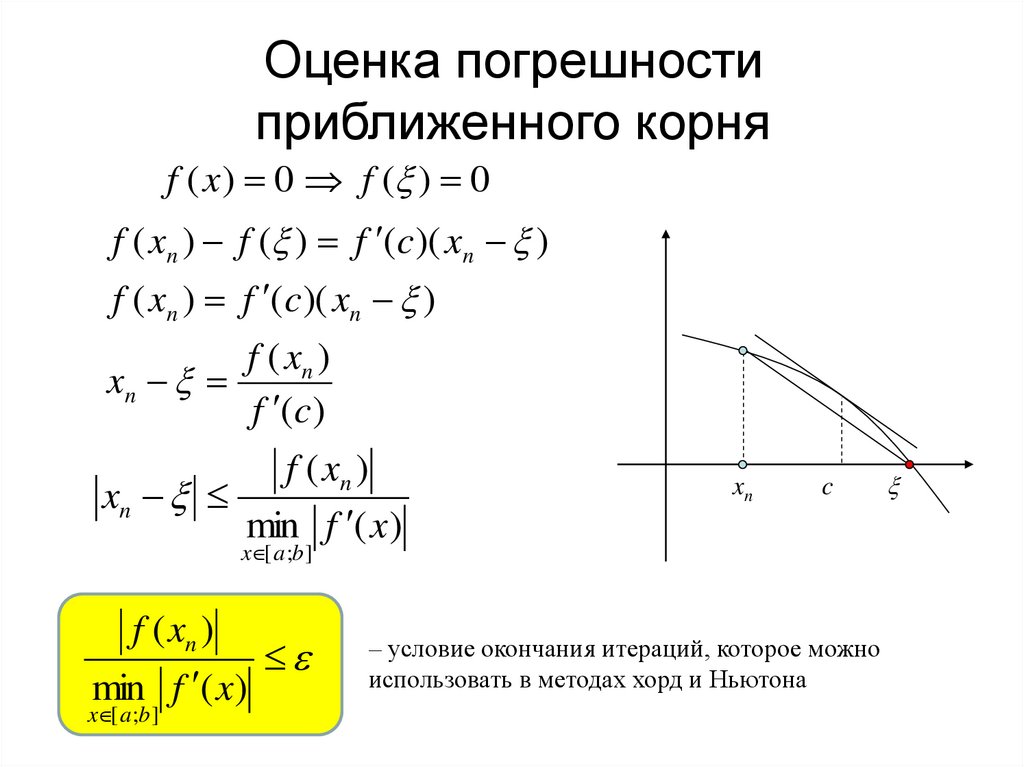
Оценка
погрешности
Оценка
погрешности
приближенного корня
f ( x ) 0 f ( ) 0
f ( xn ) f ( ) f ( c )( xn )
f ( xn ) f ( c )( xn )
f ( xn )
xn
f ( c)
f ( xn )
xn
min f ( x )
xn
c
x [ a ;b ]
f ( xn )
min f ( x)
x [ a ;b ]
– условие окончания итераций, которое можно
использовать в методах хорд и Ньютона

9.

Метод
хорд
Оценка погрешности
оценка погрешности
xn xn xn 1 ,
M 2m, M max f ( x ) , m min f ( x ) .
x [ a ;b ]
xn xn 1
x [ a ;b ]

10.

Метод
хорд (пример)
Метод
хорд
(пример)
x e 0
x
f ( x) x e x
f '( x ) 1 e x
f ''( x ) e
x
Функция строго возрастает и выпукла вниз на
всей числовой прямой.
1
f ( 1) 1 0, f (0) 1 0,
e
a 1, b 0, x0 a 1.
( b xn ) f ( x n )
xn f ( x n )
xn
xn 1 xn
xn
f ( b ) f ( xn )
1 f ( xn ) 1 f ( x n )
f '( x ) 1 e x 1 | xn x | | f ( xn ) |

11.

Метод
хорд (пример)
Метод
хорд
(пример)
f ( x) x e x
xn
xn 1
1 f ( xn )
x0 1
x ex 0
x0 1, d 0,63
x1 0,6126998368, d 0,07
x2 0,5721814121, d 0,008
x3 0,5677032142, d 0,0009
x4 0,5672055526, d 0,0001
| xn x | d
d | f ( xn ) |
x5 0,5671502142, d 0,00001
x6 0,5671440604, d 0,0000012
x 0,56714 с точностью до 10 5

12.

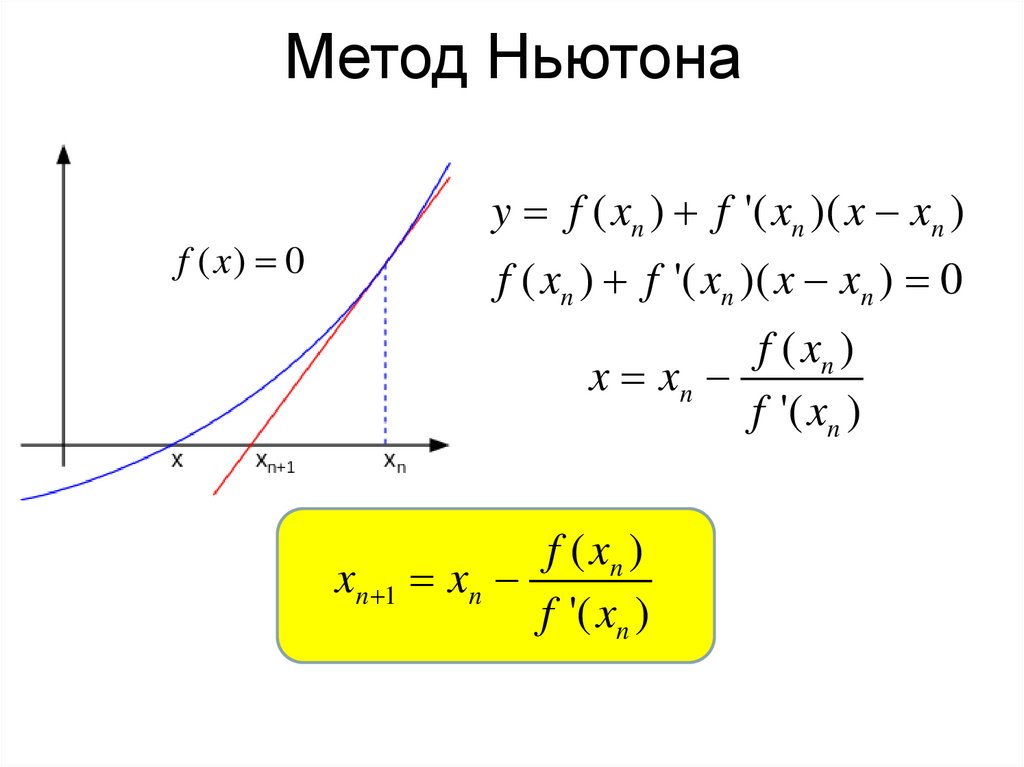
Метод Ньютона
Метод Ньютона (метод касательных)
f ( x) 0
y f ( xn ) f '( xn )( x xn )
f ( xn ) f '( xn )( x xn ) 0
f ( xn )
x xn
f '( xn )
f ( xn )
xn 1 xn
f '( xn )

13.

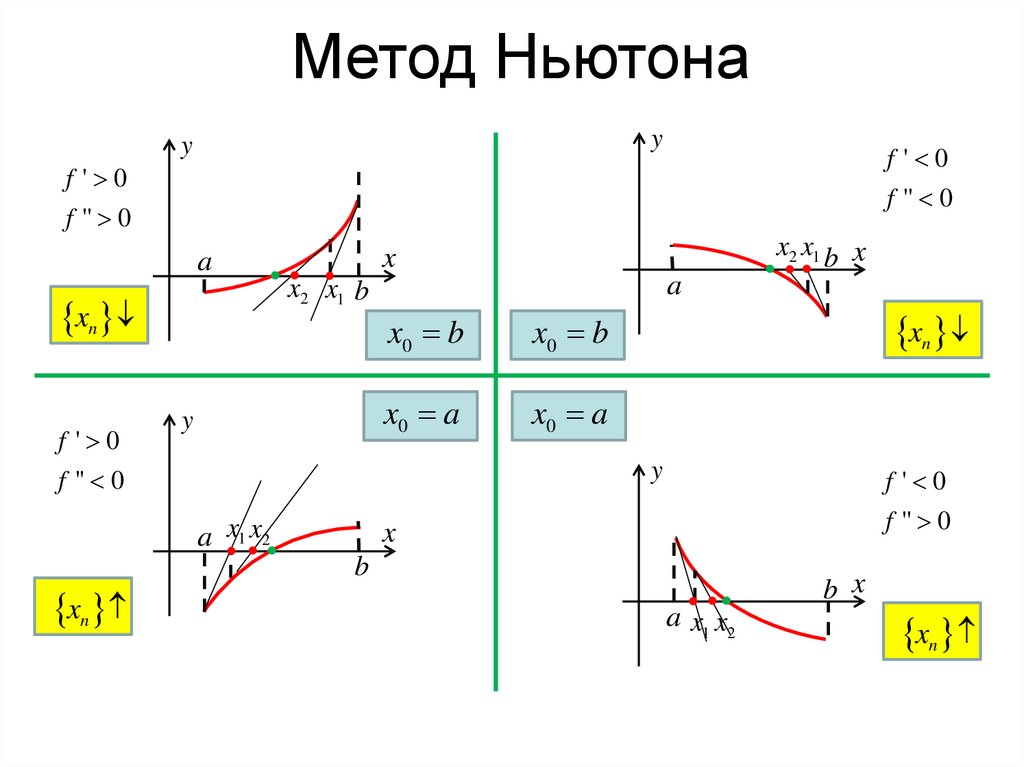
Метод Ньютона
Метод Ньютона (метод касательных)
y
y
f ' 0
f ' 0
f '' 0
f '' 0
a
x2 x1 b
xn
f ' 0
y
x0 b
x0 b
x0 a
x0 a
xn
y
f '' 0
a x1 x2
xn
x2 x1 b x
x
a
f ' 0
f '' 0
x
b
b x
a x1 x2
xn

14.

Метод Ньютона
Метод Ньютона (метод касательных)
f ( xn )
xn 1 xn
f '( xn )
xn
или , a xn b x lim xn
n
f ( x)
x x
f ( x) 0
f '( x )

15.

Оценка погрешности
Метод
Ньютона
M 2 2m1 , M 2 max f ( x) , m1 min f ( x)
x [ a ;b ]
xn xn 1
x [ a ;b ]
xn 2

16.

Метод
Ньютона (пример
1)
Метод
Ньютона
(пример)
x e 0
x
f ( x) x e x
f '( x ) 1 e x
f ''( x ) e x
Функция строго возрастает и выпукла вниз на
всей числовой прямой.
1
f ( 1) 1 0, f (0) 1 0,
e
a 1, b 0, x0 b 0.
f ( xn )
xn 1 xn
f '( xn )
f '( x ) 1 e x 1 | xn x | | f ( xn ) |

17.

Ньютона (пример)
МетодМетод
Ньютона
(пример)
f ( x) x e
f '( x ) 1 e x
x
x e 0
x
x0 0, d 1
xn 1 xn
f ( xn )
f '( xn )
x0 0
x1 0,5, d 0,1
x2 0,5663110032, d 0,0013
x3 0,5671431650, d 0,0000002
| xn x | d
d | f ( xn ) |
x 0,567143 с точностью до 10 6

18.

Недостатки метода Ньютона
Недостатки:
1) Расходится в тех областях,
где
f ' ( x) 0
2) если функция f(x) задана таблично,
то вычисление f ' ( x) затруднено
Пути устранения:
Модифицированный
метод Ньютона
Метод секущих

19.

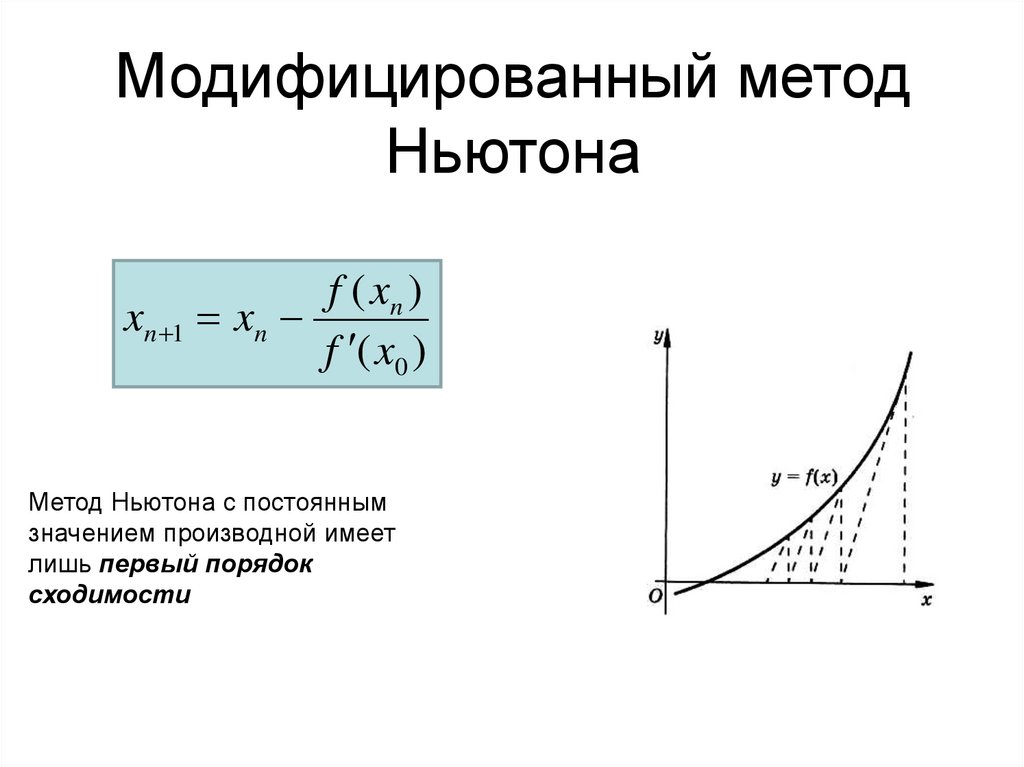
Модифицированный метод
Ньютона
f ( xn )
xn 1 xn
f ( x0 )
Метод Ньютона с постоянным
значением производной имеет
лишь первый порядок
сходимости

20.

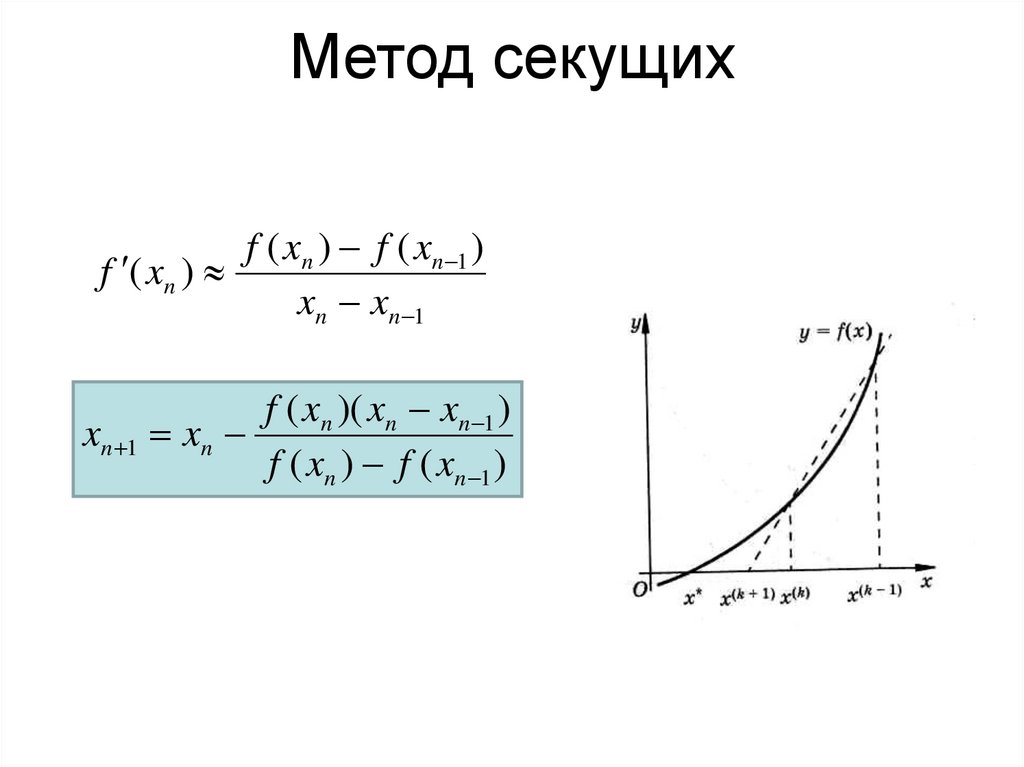
Метод секущих
f ( xn ) f ( xn 1 )
f ( xn )
xn xn 1
f ( xn )( xn xn 1 )
xn 1 xn
f ( xn ) f ( xn 1 )

21.

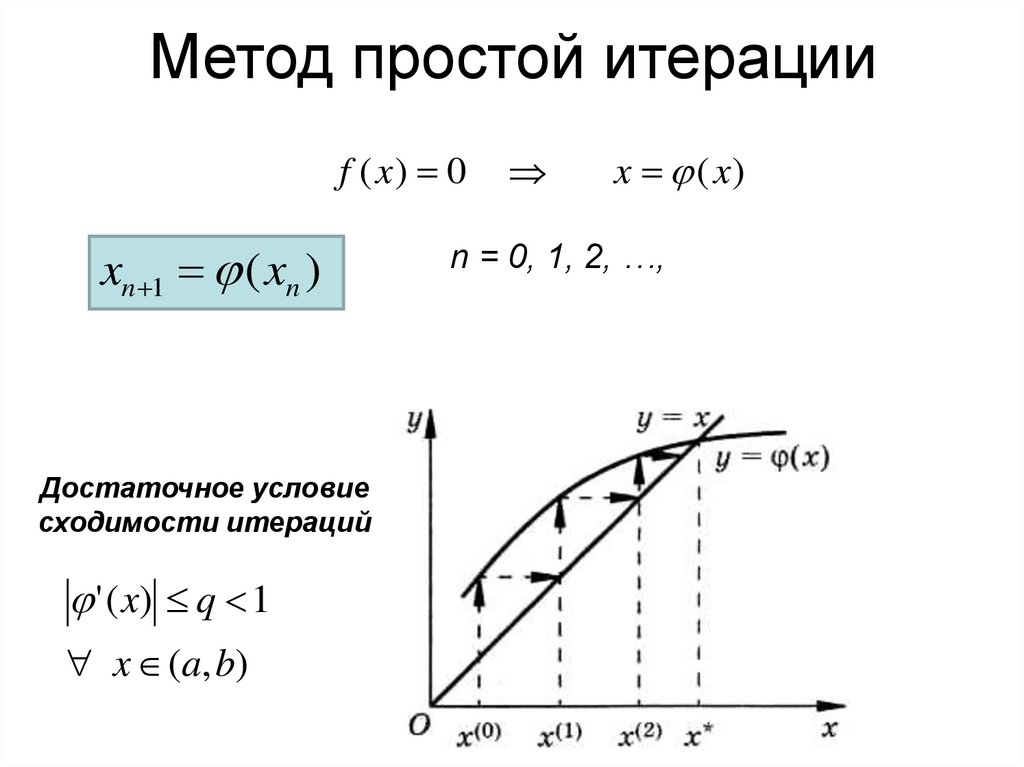
Метод простой итерации
f ( x) 0
xn 1 ( xn )
Достаточное условие
сходимости итераций
' ( x) q 1
x (a, b)
x (x )
n = 0, 1, 2, …,

22.

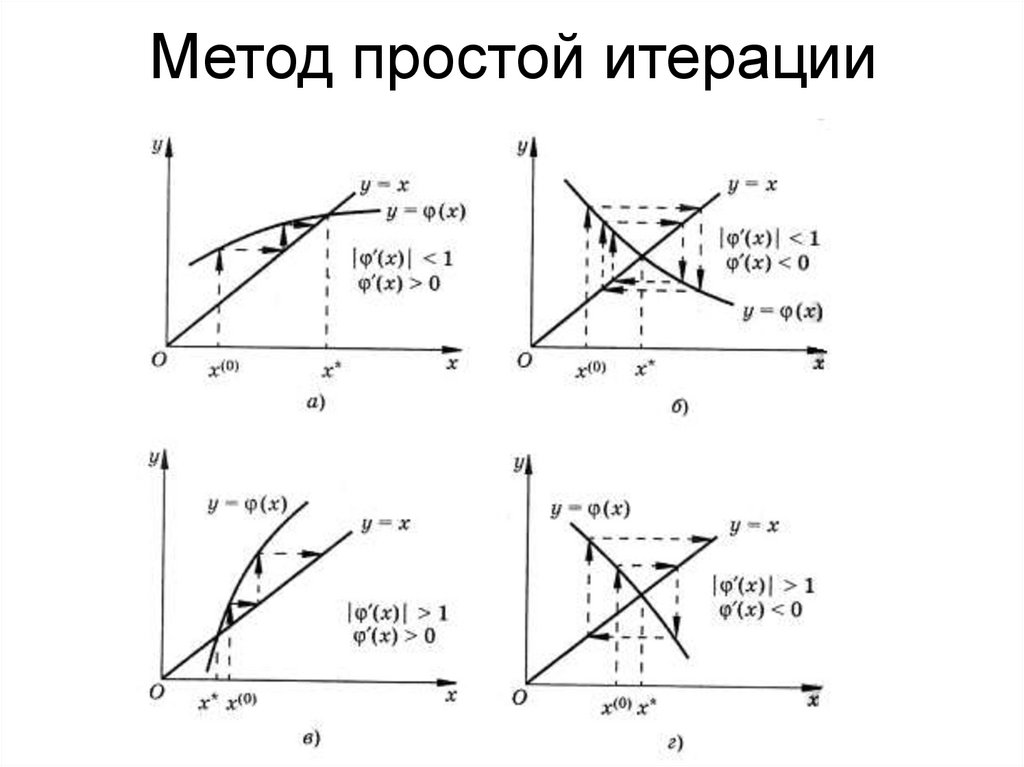
Метод простой итерации
Достаточное условие сходимости итераций
' ( x) q 1
x ( a , b)
q
xn
xn xn 1
1 q
xn xn 1
1 q
q

23.

Метод простой итерации
xk k , xk 1 k 1
( x ) ( ) ( )( x )
x xk
xk 1 ( xk )
k 1 ( ) ( )( xk )
k 1 k ( )
k 1 k
( x) 1

24.

Метод простой итерации