Похожие презентации:
Динамический анализ и синтез в робототехнике
1.
Федеральное государственное бюджетное образовательное учреждениевысшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «Мехатронные системы»
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез
в робототехнике»
Автор Зубкова Ю.В., старший преподаватель
Ижевск
2013
2. Динамический анализ механизмов
Задачи динамики:-
-
прямая задача: по заданным силам и моментам определить обобщенные
ускорения, интегрирование которых позволяет получить значения
обобщенных координат и скоростей;
обратная задача: по заданным обобщенным координатам, скоростям и
ускорениям определить действующие в сочленениях манипулятора силы и
моменты.
Предметом динамики манипулятора как раздела робототехники является
математическое описание действующих на манипулятор сил и моментов в
форме уравнений динамики движения.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
2
3. Основные понятия и определения
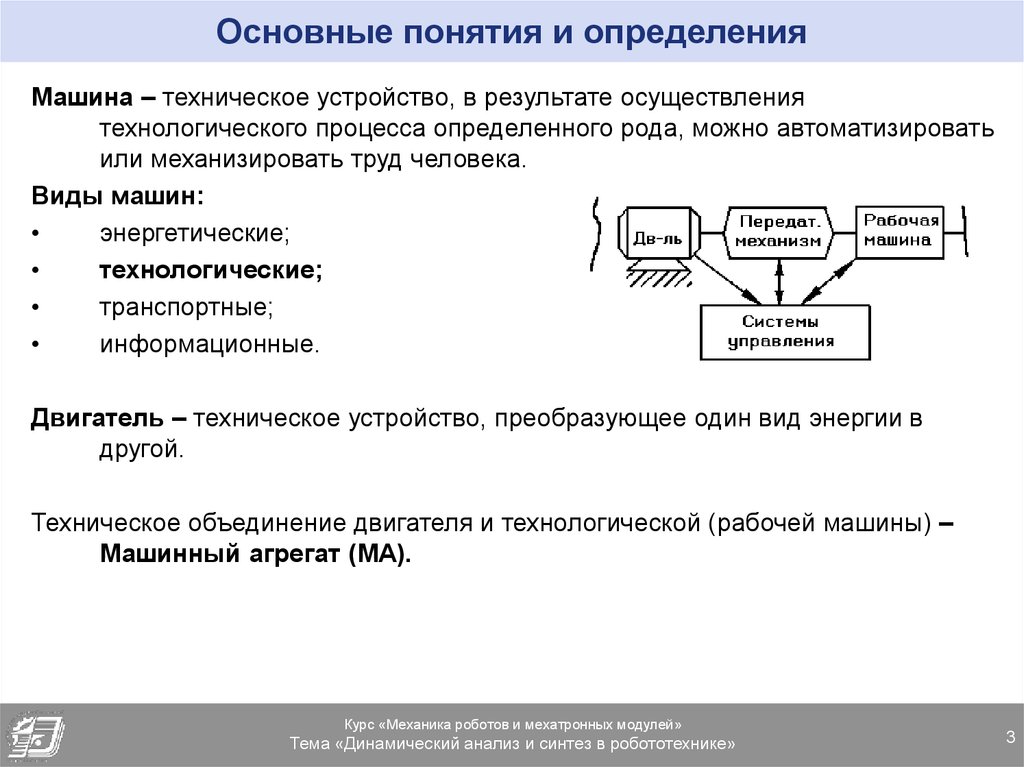
Машина – техническое устройство, в результате осуществлениятехнологического процесса определенного рода, можно автоматизировать
или механизировать труд человека.
Виды машин:
энергетические;
технологические;
транспортные;
информационные.
Двигатель – техническое устройство, преобразующее один вид энергии в
другой.
Техническое объединение двигателя и технологической (рабочей машины) –
Машинный агрегат (МА).
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
3
4. Силы и моменты, действующие в машинном агрегате
1. Движущиеся силы и моменты Fд и МдРабота движущих сил и моментов за цикл
положительна: Ад>0.
Цикл – промежуток времени, по истечению которого все
кинематические параметры принимают первоначальное
значение, а технологический процесс, происходящий в
рабочей машине, начинает повторяться вновь.
2. Силы и моменты сопротивления (Fс,Mс)
Работа сил и моментов сопротивления за цикл отрицательна: Аc<0.
3. Силы тяжести (Gi).
Работа силы тяжести за цикл равна нулю: АGi=0.
4. Расчетные силы и моменты (ФSi,MФi)
ФSi,MФi – Главные векторы сил инерции и главные моменты от сил инерции.
5. Реакции в кинематических парах (Qij).
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
4
5. Понятие о механических характеристиках
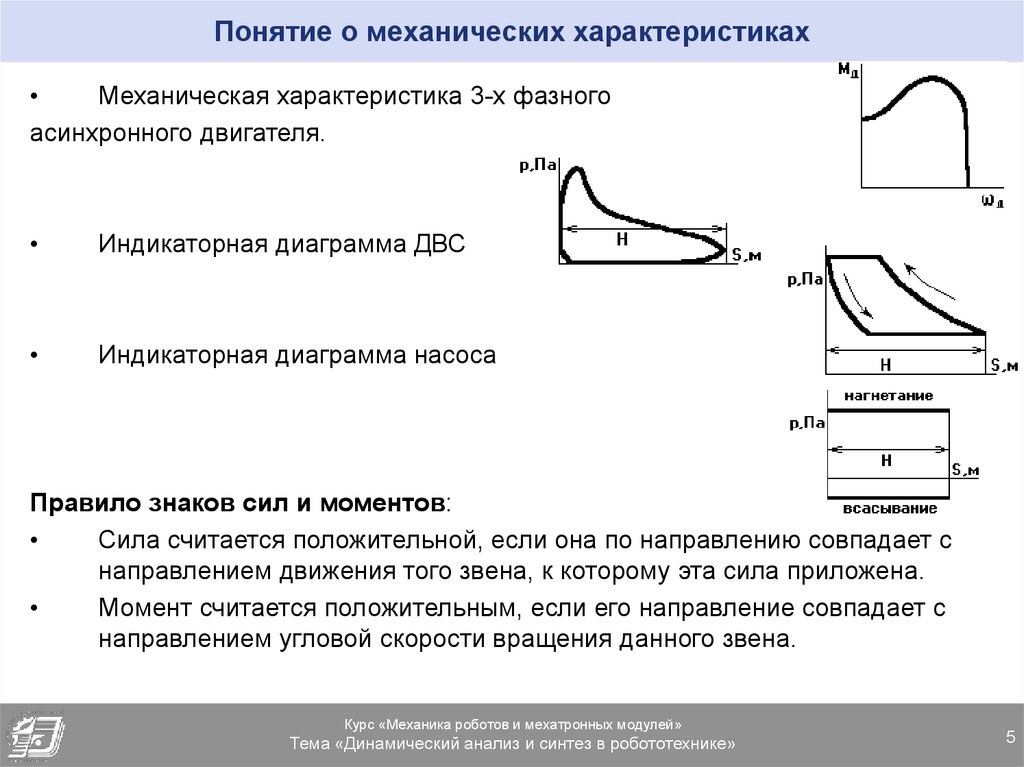
Механическая характеристика 3-х фазного
асинхронного двигателя.
Индикаторная диаграмма ДВС
Индикаторная диаграмма насоса
Правило знаков сил и моментов:
Сила считается положительной, если она по направлению совпадает с
направлением движения того звена, к которому эта сила приложена.
Момент считается положительным, если его направление совпадает с
направлением угловой скорости вращения данного звена.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
5
6. Понятие о расчетной схеме машинного агрегата и переход от неё к динамической модели
Если жесткость с1 , то можно перейти кдвумассовой модели (необходимо 2 диф. уравнения).
Если жесткость с2 , то получим одномассовую
динамическую модель.
Два вида одномассовых динамических моделей:
1. Если звено приведения совершает вращательное
движение, то одномассовая модель имеет вид:
Закон движения должен быть один,
Т Т А
поэтому м = 1 , м = 1
прив
2
нач
I
м
2
М КОН
Тнач
М
М НАЧ
пр
d м
2. Если звено приведения совершает поступательное движение, то
одномассовая модель имеет вид:
прив
m
2
Vм2
sМ КОН
Т нач
F d s
пр
м
sМ НАЧ
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
6
7. Приведение сил и масс к одномассовой динамической модели
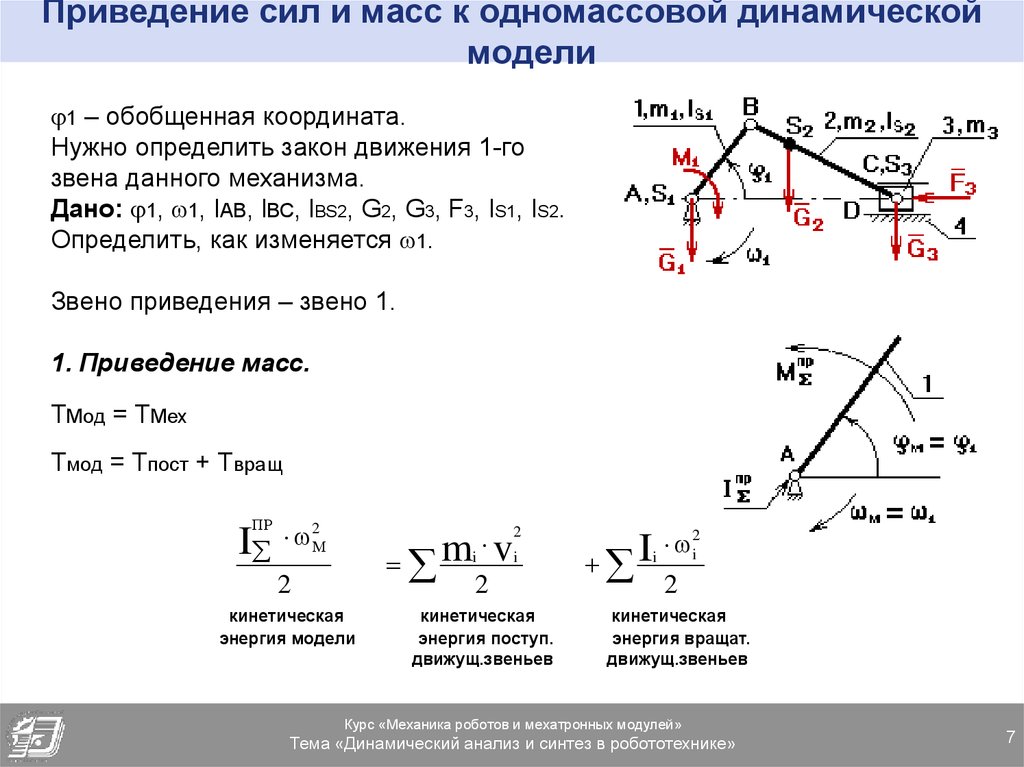
1 – обобщенная координата.Нужно определить закон движения 1-го
звена данного механизма.
Дано: 1, 1, lAB, lBC, lBS2, G2, G3, F3, IS1, IS2.
Определить, как изменяется 1.
Звено приведения – звено 1.
1. Приведение масс.
ТМод = ТМех
Тмод = Тпост + Твращ
ПР
I
2М
2
кинетическая
энергия модели
mi vi
2
2
кинетическая
энергия поступ.
движущ.звеньев
2
Ii i
2
кинетическая
энергия вращат.
движущ.звеньев
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
7
8. Приведение сил и масс к одномассовой динамической модели (продолжение)
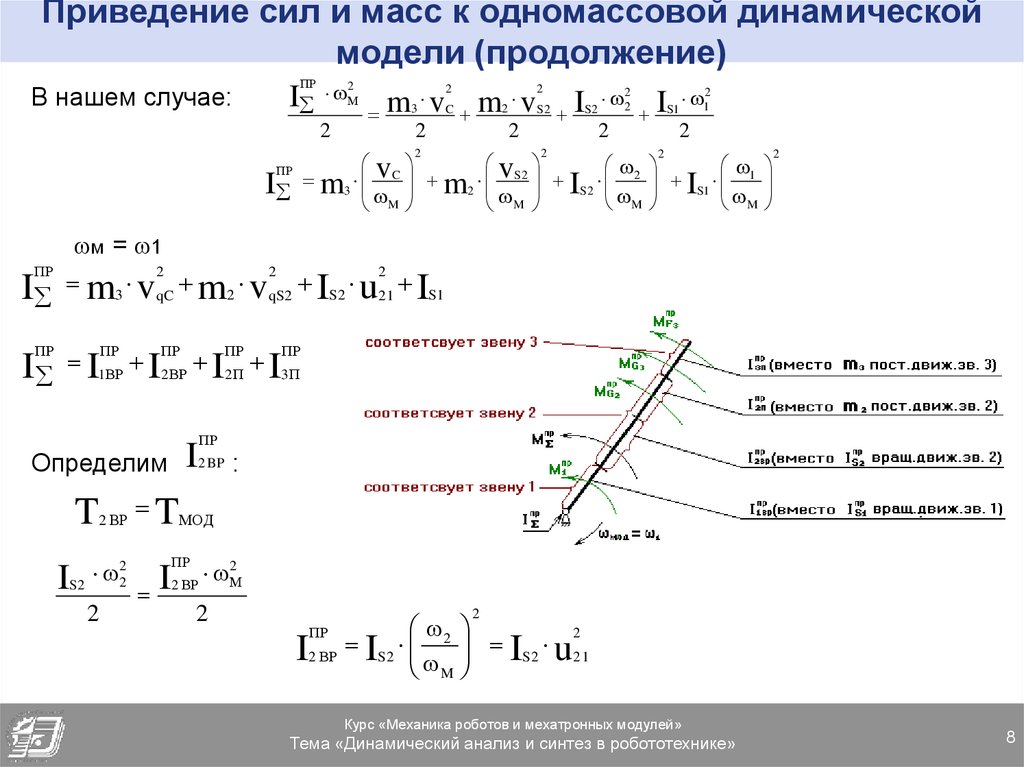
В нашем случае:ПР
I
2М
2
m v
3
2
C
2
m v
2
2
S2
2
2
I
S2
2
22
2
I
vC
vS 2
2
I m3 M m2 M IS2 M
ПР
ПР
I
ПР
I
12
S1
2
2
IS1 1
M
2
м = 1
2
2
2
m3 vqC m2 vqS2 IS2 u21 IS1
ПР
ПР
ПР
ПР
I1ВР I2 ВР I2 П I3П
Определим
T
2 ВР
I
S2
22
2
I
ПР
2 BP
:
TМОД
I
ПР
2 ВР
2М
2
2
ПР
I2 ВР IS2 M
2
2
IS 2 u2 1
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
8
9. Приведение сил и масс к одномассовой динамической модели (продолжение)
2. Приведение сил.АΣ – работа суммарного приведенного момента на его возможное
перемещение.
Т – Тнач = АΣ
ПР
I2 2м
ТНАЧ
2
М
КОН
М2 d
ПР
М
М
(1)
НАЧ
M пр d 1 Fi d s i M i d i
M пр M Fi v i cos( Fi
M пр Fi
vi
cos( Fi
M
передат
функция
M пр Fi v qi cos( Fi
|
1
dt
ˆ v ) M
i
i
i
ˆ v ) M
i
i
i
M
ˆ v ) M u
i
i
передаточ
отношение
i 1
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
9
10. Приведение сил и масс к одномассовой динамической модели (продолжение)
ПРВместо силы F3 – момент M .
F3
ПР
Определим M F3 :
AM
ПР
AF
3
M F v cos( F ˆ v
M F v cos( F ˆ v )
ПР
M
i
C
i
C
)
ПР
i
qC
i
C
Формула для определения закона движения звена приведения в форме
кинетической энергии (определение ωм)
Из выражения (1) получаем, что м равна
ω
M
2 ( A TНАЧ )
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
I ПР
10
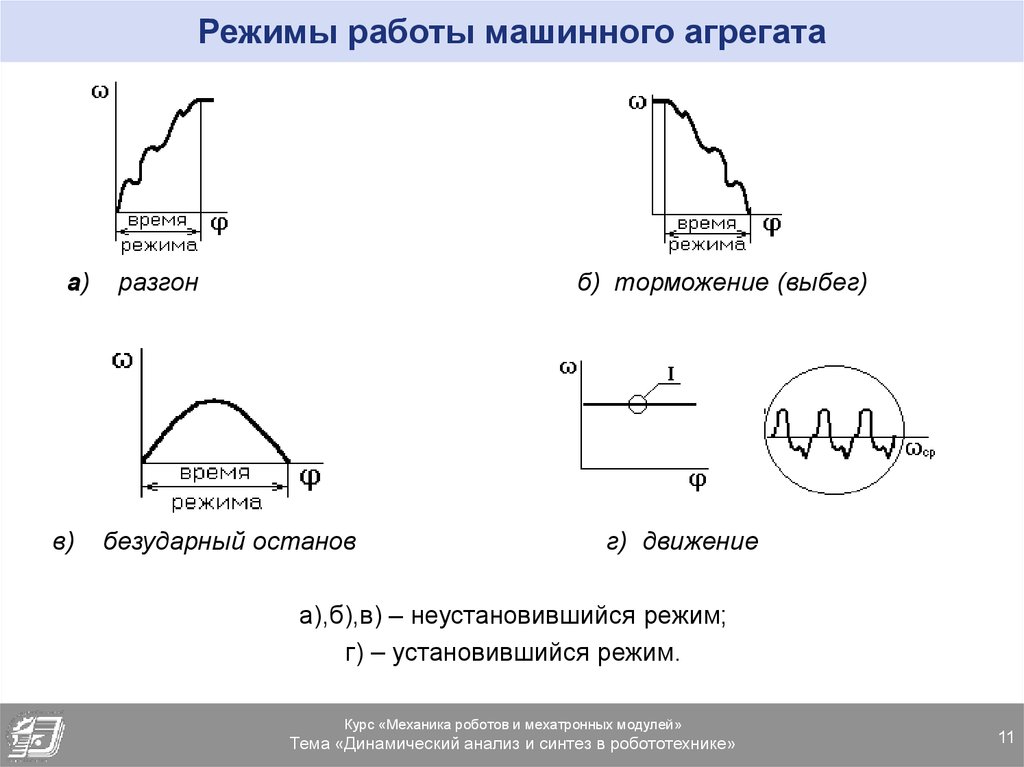
11. Режимы работы машинного агрегата
а)в)
разгон
б) торможение (выбег)
безударный останов
г) движение
а),б),в) – неустановившийся режим;
г) – установившийся режим.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
11
12. Законы движения звена приведения одномассовой динамической модели
1. Для неустановившегося режима работы машинного агрегата.2 (A T )
- угловая скорость: ω
I
НАЧ
ПР
M
ПР
ПР
2
d I
M ПР МПР d
2 I
2 I
M
- угловое ускорение:
Время режима определяется по формуле:
ко н
t
d M
M
нач
2. Для установившегося режима работы машинного агрегата.
М СР
М max М min
2
Отклонения угловой скорости от среднего уровня характеризуется
коэффициентом неравномерности :
М max М min
М СР
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
12
13. Законы движения звена приведения одномассовой динамической модели (продолжение)
Для определения угловой скоростиПР
ПР
ПР
где
I I I
III
const
ω
M
2 ( A TНАЧ )
I
,
ПР
var
Для удержания колебаний угловой скорости м в заданных пределах, первая
ПР
группа звеньев должна иметь (II ) НЕОБХ .
Изменение м от м_max до м_min приводит к изменению кинетической энергии
первой группы звеньев (ΔТI), которое равно:
I
ПР
( T I ) MAX
I
ПР
I
НЕОБХ
2
М СР
М max
ПР
I
2
М min
М max М min
2
I
М max
2
НЕОБХ
I
( TI) M AX
М max
I
I
ПР
I НЕОБХ
ПР
I НЕОБХ
М СР
М min
2
НЕОБХ
2
М min
М max М min
М СР
2М СР
( TI) M AX
2М СР
n
; [рад/с]
30
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
13
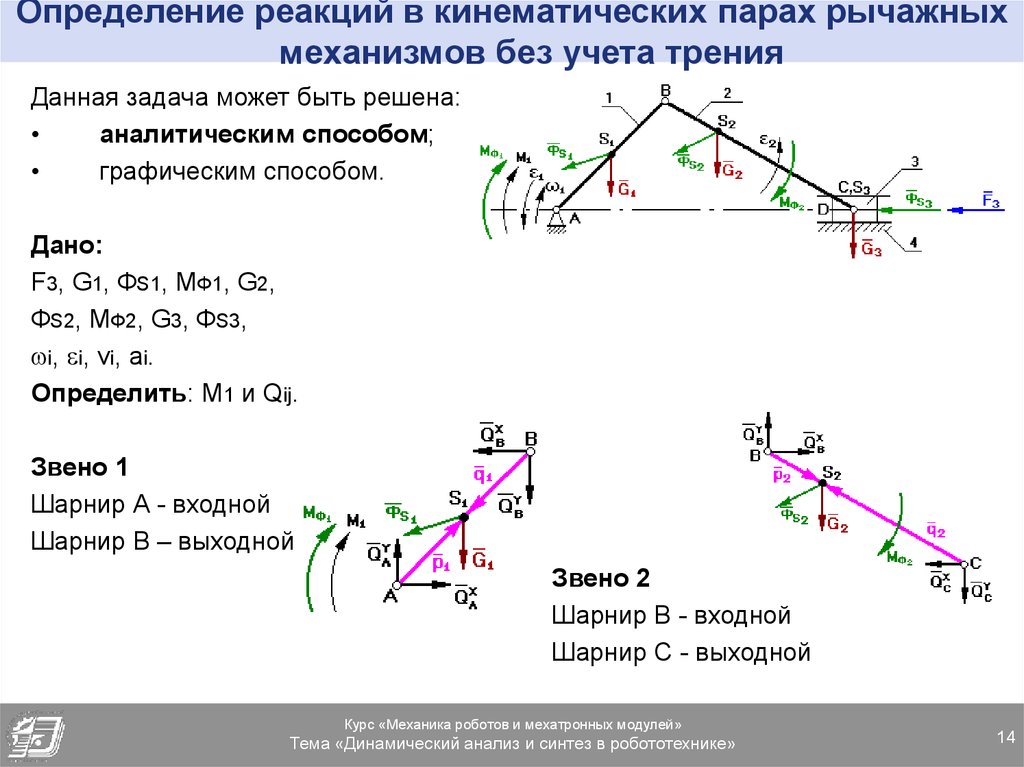
14. Определение реакций в кинематических парах рычажных механизмов без учета трения
Данная задача может быть решена:аналитическим способом;
графическим способом.
Дано:
F3, G1, ФS1, MФ1, G2,
ФS2, МФ2, G3, ФS3,
i, i, vi, ai.
Определить: М1 и Qij.
Звено 1
Шарнир А - входной
Шарнир В – выходной
Звено 2
Шарнир В - входной
Шарнир С - выходной
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
14
15. Определение реакций в кинематических парах рычажных механизмов без учета трения (продолжение)
Звено 3При решении задачи используется принцип Даламбера:
X
3 звено:
F3 ФS3
Q
Q Q
C
Y
34
X
X
X
B
C
S2
Y
Y
Y
C
S2
2 звено: Q Q Ф
Q Q Ф G
Q р Q q М
В
Х
Q
В
1 звено:
Si
mi а Si
Фi
i ISi
G3
C
В
Ф
М
2
2
2
C
Ф2
Y
Y
X
Х
Y
Y
X
2
В
2
C
2
C
2
р Q р Q q Q q МФ 2
X
X
X
A
B
S1
Y
Y
Y
A
B
S1
Q Q Ф
Q Q Ф G
Q р Q q М М
Q р Q р Q q Q q М М
1
A
1
Ф1
1
1
B
Х
Y
Y
X
Х
Y
Y
X
A
1
A
1
B
1
B
1
1
Ф1
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
15
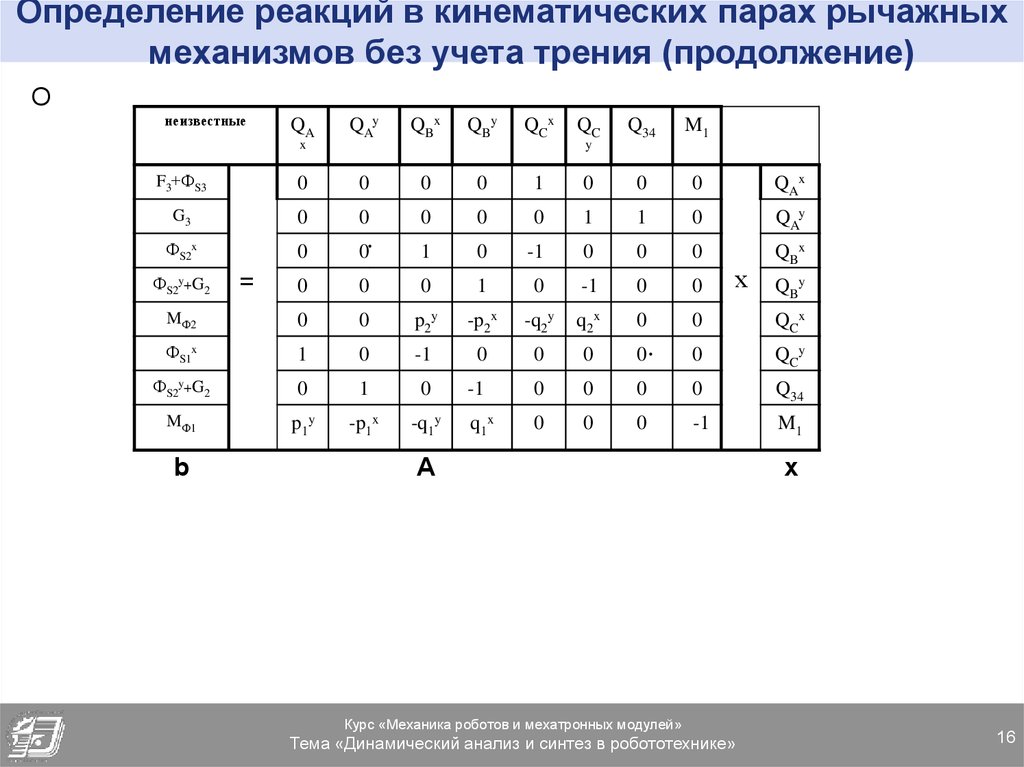
16. Определение реакций в кинематических парах рычажных механизмов без учета трения (продолжение)
Онеизвестные
QA
QAy
QBx
QBy
QCx
x
QC
Q34
M1
y
F3+ФS3
0
0
0
0
1
0
0
0
QAx
G3
0
0
0
0
0
1
1
0
QAy
ФS2x
0
0
1
0
-1
0
0
0
QBx
0
0
0
1
0
-1
0
0
MФ2
0
0
p2y
-p2x
-q2y
q2x
0
0
QCx
ФS1x
1
0
-1
0
0
0
0
0
QCy
ФS2y+G2
0
1
0
-1
0
0
0
0
Q34
MФ1
p 1y
-p1x
-q1y
q 1x
0
0
0
-1
M1
ФS2y+G2
b
=
х
A
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
QBy
x
16
17. Учет трения при определении реакций в кинематических парах
Трение является сложным физико-химическим процессом, сопровождающийсявыделением тепла.
Если суммарная высота микронеровностей взаимодействующих поверхностей:
больше, чем высота слоя смазки, то - сухое трение.
равна высоте слоя смазки, то - граничное трение.
меньше, чем высота слоя смазки, то - жидкостное.
Учет трения в поступательной кинематической паре
При учете трения результирующая реакция Q21 отклоняется от общей нормали
на угол трения в сторону противоположную направлению движения.
Коэффициент трения f определяется экспериментально и зависит от
многих факторов.
без учета трения
с учетом трения
Fтр=Qn12 * tg
tg = f
Fтр=Qn12 * f
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
17
18. Учет трения во вращательной кинематической паре
1 - цапфаrц - радиус цапфы
Δ - зазор
- радиус круга трения;
= О1С
O 1C
Из ΔО1СК
= sin О1С = О1К sin
O1 K
Mc= Q12*О1С = Q12* rц*sin
При малых углах : sin ≈ tg = f .
Тогда :
Mc= Q12* rц*f
При учете трения во вращательной КП результирующая реакция
отклоняется от общей нормали на угол трения и проходит
касательно к кругу трения радиуса .
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
18
19. Динамический анализ механизмов
Предметом динамики манипулятора как раздела робототехники являетсяматематическое описание действующих на манипулятор сил и моментов в
форме уравнений динамики движения.
Задачи динамики:
- прямая задача: по заданным силам и моментам определить обобщенные
ускорения, интегрирование которых позволяет получить значения
обобщенных координат и скоростей;
- обратная задача: по заданным обобщенным координатам, скоростям и
ускорениям определить действующие в сочленениях манипулятора силы и
моменты.
Динамическая модель манипулятора может быть построена на основе
использования известных законов ньютоновой или лагранжевой механики.
Уравнения движения реального манипулятора могут быть получены
традиционными методами Лагранжа – Эйлера, Ньютона – Эйлера или с
помощью принципа Д’Аламбера.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
19
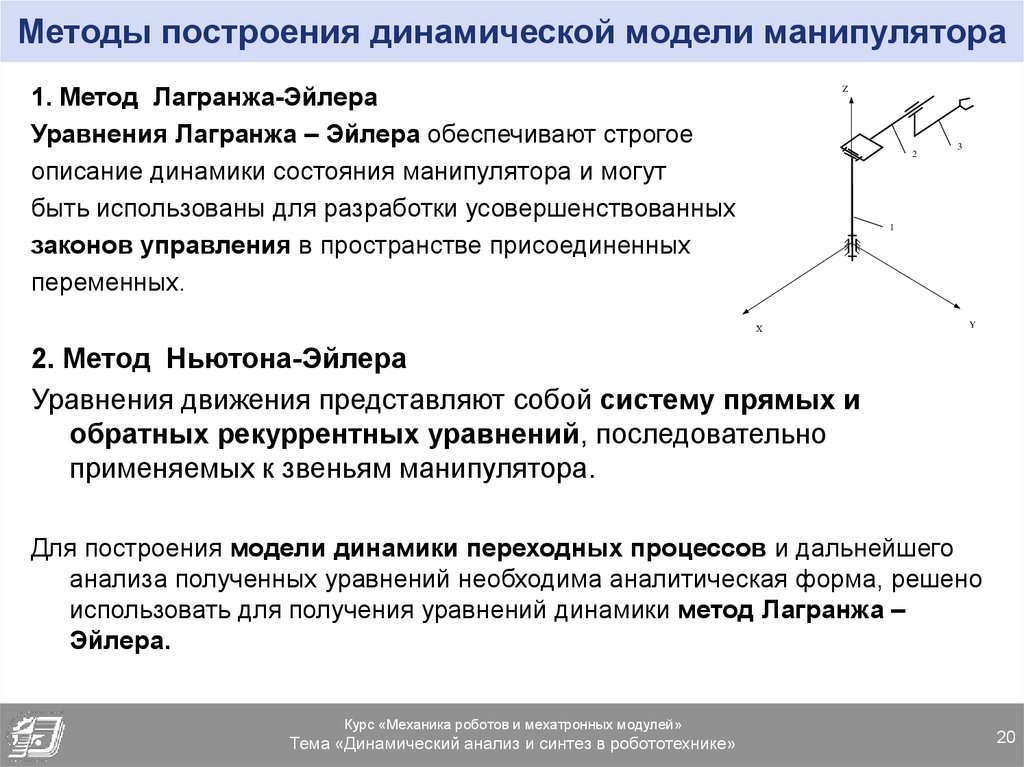
20. Методы построения динамической модели манипулятора
1. Метод Лагранжа-ЭйлераУравнения Лагранжа – Эйлера обеспечивают строгое
описание динамики состояния манипулятора и могут
быть использованы для разработки усовершенствованных
законов управления в пространстве присоединенных
переменных.
Z
2
3
1
Х
Y
2. Метод Ньютона-Эйлера
Уравнения движения представляют собой систему прямых и
обратных рекуррентных уравнений, последовательно
применяемых к звеньям манипулятора.
Для построения модели динамики переходных процессов и дальнейшего
анализа полученных уравнений необходима аналитическая форма, решено
использовать для получения уравнений динамики метод Лагранжа –
Эйлера.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
20
21. Уравнения динамики манипулятора
Уравнения Лагранжа второго рода для голономной системы с n степенямисвободы, которым отвечают обобщенные координаты q i (j = 1,2,…,n)
d L
dt q j
L
q Q jд
j
(j = 1,2,…,n),
(1)
где L T П – функция Лагранжа, разности кинетической Т и потенциальной П
энергий системы.
Учитывая, что L T П и П q j 0 , перепишем уравнение (1) в виде:
d T
dt q j
T
Qj
q
j
Учёт внешнего воздействия – силы
Fв
Q j Q jд
Известно, что
(2)
, приложенной к захватному устройству:
(3)
Q Q
jв
jF
n
T Ti
(4)
i 1
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
21
22. Уравнения динамики манипулятора (продолжение)
Определим Тi по формуле:1
1
Ti mi v02i mi v 0i i riц ιT 0ι i
2
2
(5)
Если за полюс звена принять его центр инерции, величина riц будет равна нулю
и выражение (5) упростится:
1
1
(6)
Ti mi v02i ιT 0ι i
2
2
Тензор вектора Oi0 имеет вид диагональной матрицы: Zo
Θ O0 i
J xi
0
0
i-1
0
0
J zi
0
J yi
0
Oi0 y 0
i
J x y z dmi
2
2
J y x i z i dmi
J z x i2 y i2 dmi
2
i
i+1
zi 0
Oi
моменты инерции относительно осей в которой
определяются выражениями:
2
i
Oi-1 i
xi0
Xo
zi
yi
xi
Yo
O
Связанные системы координат с началом в
центре кинематической пары Oi xi yi zi и в
0 0 0 0
центре инерции Oi xi yi zi
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
22
23. Уравнения динамики манипулятора (продолжение)
Определим вектор скорости центра инерции звена i через проекции на осисвязанной с ним системы координат:
v iц vixц , viyц , vizц
T
Вектор скорости через проекции на оси неподвижной системы осей:
v 0iц v0ixц , v0iyц , v0izц
T
По аналогии с viц введем вектор угловой скорости звена:
i ix , viy , iz T
Запишем уравнение (6) в развернутой форме:
Ti 0,5mi vix2 ц viy2 ц viz2ц 0,5 J xi ix2 J yi iy2 J zi iz2 (7)
С учётом уравнения (4) получим:
1 n
Ti mi v02ixц v02iyц v02izц J xi ix2 J yi iy2 J zi iz2
2 i 1
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
(8)
23
24. Заключение
При решении задач динамики необходимо построить динамическую модельмногозвенного механизма (манипулятора).
В качестве динамической характеристики выбирают кинетическую энергию
механизма.
Динамический анализ заключается в исследовании движения механизма под
действием движущих сил.
Прямая и обратная задачи динамики:
Прямая задача состоит в том, чтобы по заданным силам и моментам
определить обобщенные ускорения, интегрирование которых позволяет
получить значения обобщенных координат и скоростей.
Обратная задача динамики заключается в том, чтобы по заданным
обобщенным координатам, скоростям и ускорениям определить
действующие в сочленениях манипулятора силы и моменты.
На этапе динамического синтеза решается задача выбора параметров
динамической схемы механизма: масс, их расположения, жесткостей
звеньев.
Курс «Механика роботов и мехатронных модулей»
Тема «Динамический анализ и синтез в робототехнике»
24
25.
СПАСИБО ЗА ВНИМАНИЕ© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Зубкова Юлия Валерьевна, 2013

















 Механика
Механика








