Кинематический анализ шарнирно-рычажных механизмов

1. ТЕОРИЯ МЕХАНИЗМОВ И МАШИН

МГГУ – 2008
КАФЕДРА «Теоретическая и прикладная механика»
ТЕОРИЯ МЕХАНИЗМОВ И
МАШИН
Кинематический анализ шарнирнорычажных механизмов
Доктор технических наук, профессор
АЛЮШИН Юрий Алексеевич

2. Основные понятия

• Механизмами называют изолированную часть
некоторой механической системы (без источников и
потребителей энергии), предназначенную для
преобразования движения одного тела в требуемое
движение одного или нескольких других тел.
МЕХАНИЗМ – система тел, предназначенная для
преобразования заданного движения одного или нескольких тел
в требуемое движение других твердых тел
ПЛОСКИЕ МЕХАНИЗМЫ – механизмы, траектории всех частиц
подвижных звеньев которых расположены в плоскостях,
параллельных одной и той же неподвижной плоскости.
Шарнирно- рычажными называют механизмы из абсолютно
твердых тел (АТТ), соединенных между собой цилиндрическими
шарнирами, допускающими их относительное вращение.
2

3. Лихтенхельдт В. Синтез механизмов. – М.: Наука, 1978. – 228 с.

• «Вопрос о том, какие механизмы – кулачковые,
зубчатые или шарнирные – целесообразнее
применять для осуществления рабочего процесса,
чаще всего решается в пользу кулачковых или
зубчатых механизмов, хотя во многих случаях
шарнирные механизмы представляют собой гораздо
более удобную и совершенную конструкцию…
Причиной этого является то обстоятельство, что
методы расчета звеньев шарнирных механизмов
сложны и мало доступны многим конструкторам. Им
кажется, что в каждом отдельном случае проще и
удобнее для заданного закона движения звена
механизма рассчитать кулачковый механизм, чем
шарнирный»
3

4. Звенья шарнирно-рычажных механизмов

•ЗВЕНО = твердое тело (часть механизма), состоящее из одной или
нескольких жестко связанных деталей, участвующих в движении как
одно целое.
Виды звеньев:
СТОЙКА, КРИВОШИП, КОРОМЫСЛО, ШАТУН, ПОЛЗУН,
Стойка – неподвижное звено механизма, на котором закреплены все другие его
звенья.
Кривошип – звено, совершающее полный оборот вокруг неподвижной оси.
Коромысло – звено, совершающее колебательное движение (неполный
оборот) вокруг неподвижной оси.
Шатун – звено, шарнирно соединённое с двумя (или более) другими
подвижными звеньями и совершающее плоскопараллельное движение в виде
вращения вокруг подвижного полюса (ППД).
Ползун – звено, совершающее прямолинейное поступательное движение по
фиксированным направляющим.
Кулисная пара – два подвижных смежных звена с относительным
поступательным движением друг относительно друга.
4

5. Различные варианты определения «кулисы»

Кулиса – звено, вращающееся относительно подвижной оси (с
направляющими для ползуна - камня) и образующее с другим подвижным
звеном скользящую пару.
КУЛИСА = подвижная направляющая для ползуна (в т.ч. и коромысло, если по
нему скользит ползушка) = звено, которое несет подвижные направляющие для
ползуна.
КУЛИСА (СЭС) –звено кулисного механизма, вращающееся вокруг
НЕПОДВИЖНОЙ оси и образующее с другим подвижным звеном (ползуном)
поступательную пару.
КУЛИСА (Политехнический Словарь, фр. – паз, желобок, выемка, скользить) =
подвижное звено кулисного механизма, образующее с другим подвижным
звеном поступательную пару. Ползун, перемещающийся по
направляющим, иногда называют камнем. Кулисы бывают вращающиеся,
качающиеся, прямолинейно движущиеся и пр.
КУЛИСА = подвижное звено кулисной пары, которое несет подвижные
направляющие для ползуна, в т.ч. и коромысло, если по нему скользит ползун (шка), совершающий поступательное или составное (сложное) движение.
Фролов К.В.: «Кулисой обычно называют звено с пазом, по которому
перемещается ползун (кулисный камень)»
В гидроприводах широко применяется разновидность кулисного механизма
(рис. 2.4г, стр. 25, ТММ-87), в котором кулису с камнем заменяет цилиндр с
поршнем
5

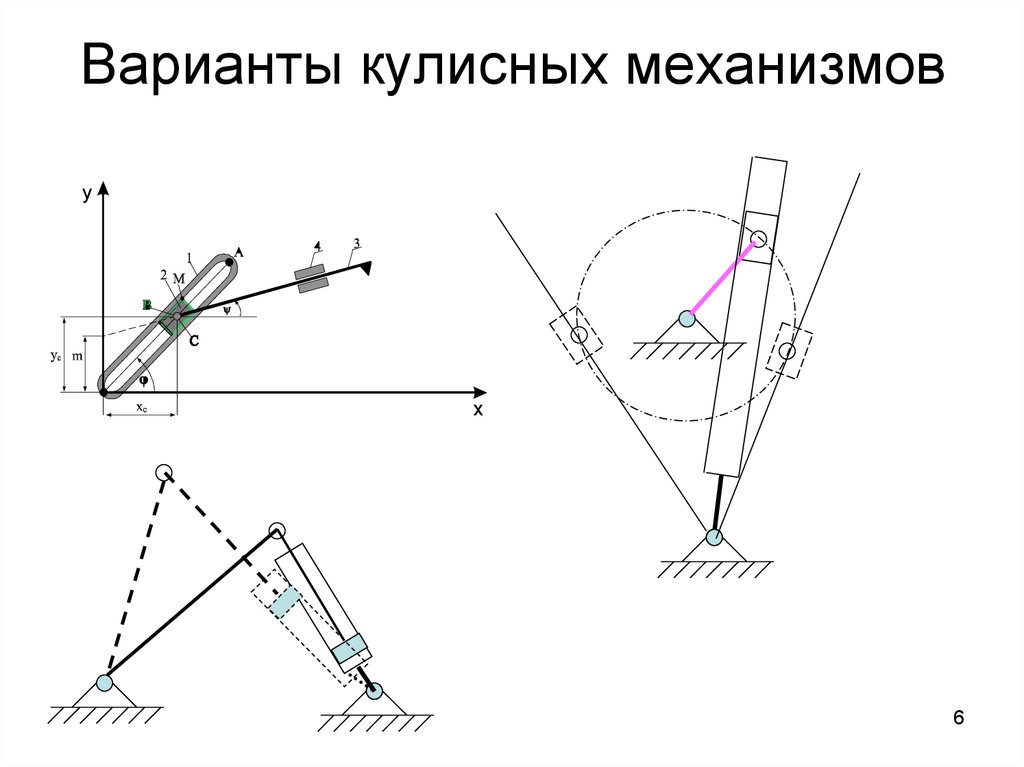
6. Варианты кулисных механизмов

6

7.

Переход от плоскопараллельного движения к
вращательному и поступательному движениям
x x p ( p ) cos( ) ( p ) sin( )
y y p ( p ) sin( ) ( p ) cos( )
Вращательное движение относительно неподвижной оси Р(a,b):
yP P b
xP P a
x a ( a) cos( ) ( b) sin( )
y b ( a) sin( ) ( b) cos( )
Поступательное движение
Sin(0)=0
Cos(0)=1
0
xP P u х (t )
x u x (t ),
у P P u у (t )
y u y (t ),
z
7

8. Координаты, компоненты скорости и ускорения для кривошипа

x cos( ) sin( )
y sin( ) cos( )
y
Компоненты вектора скорости
xt t [ sin( ) cos( )] t y
y t t [ cos( ) sin( )] t x
А
О
x
Компоненты вектора ускорения
xtt tt y t yt
ytt tt x t xt
8

9. Координаты, компоненты скорости и ускорения для коромысла

Координаты
x a ( a) cos( ) ( b) sin( )
y b ( a) sin( ) ( b) cos( )
Компоненты вектора скорости
xt t ( y b)
y
А
yt t ( x a)
Компоненты вектора ускорения
xtt tt ( y b) t yt
уtt tt ( х а) t хt
О
b
x
a
9

10. Координаты, компоненты скорости и ускорения для шатуна

Уравнения движения
в форме Лагранжа
Компоненты
скорости:
в форме
Лагранжа
в форме
Эйлера
x xP ( Р ) cos ( Р ) sin
y yР ( Р ) sin ( Р ) cos
xt ( xt ) P t [( Р ) sin ( Р ) cos ]
yt ( yt ) P t [( Р ) cos ( Р ) sin ]
xt ( xt ) P t ( у уР )
уt ( уt ) P t ( х хР )
Компоненты ускорения
в форме Эйлера
xtt ( xtt ) P tt ( у уР ) t [ уt ( уt ) Р ]
( xtt ) P tt ( у уР ) t2 ( х хР )
уtt ( уtt ) P tt ( х хР ) t [ хt ( хt ) Р ]
( уtt ) P tt ( х хР ) ( у уР )
2
t
10

11. Координаты, компоненты скорости и ускорения для ползуна

• Уравнения движения
x xP P u х (t ),
x ( xP P )
у у P P u у (t ), у ( у P P )
Компоненты вектора перемещения
Компоненты вектора скорости
xt ( xt ) Р
Компоненты вектора ускорения
xtt ( xtt ) Р
ui (t ) xi i [ui (t )]P
ui ,t (t ) xi ,t vi ( xi ,t ) Р
уt ( уt ) Р
ui ,tt (t ) xi ,tt wi ( xi ,tt ) Р
уtt ( уtt ) Р
11

12. Кинематические связи в шарнирно - рычажных механизмах

• Кинематическими связями называют
соотношения между постоянными
(расстояния между осями шарниров) и
переменными (углы наклона линий,
соединяющих оси шарниров)
параметрами механической системы в
произвольный момент времени.
Кинематические связи – это граничные условия, записанные в
виде математических уравнений для произвольного момента
времени
12

13. Кривошипно-ползунный механизм

b L1 sin L2 sin( )
b L1 sin L2 sin
sin( ) (L1 sin b) / L2
L1 sin b
arcsin
L2
L1 cos
t t
L2 cos( )
b
b
sin ( L1 sin b) / L2
L1 sin b
L2
arcsin
L1 cos
t t
L2 cos
2
L1 cos
L
sin
L
cos
2 1
1
tt tt
t
tg
2
L2 cos
L2 cos L2 cos
x tt ( x tt ) A tt ( y y A ) t [ y t ( y t ) A ] y tt ( y tt ) A tt ( x x A ) t [ x t ( x t ) A ]13

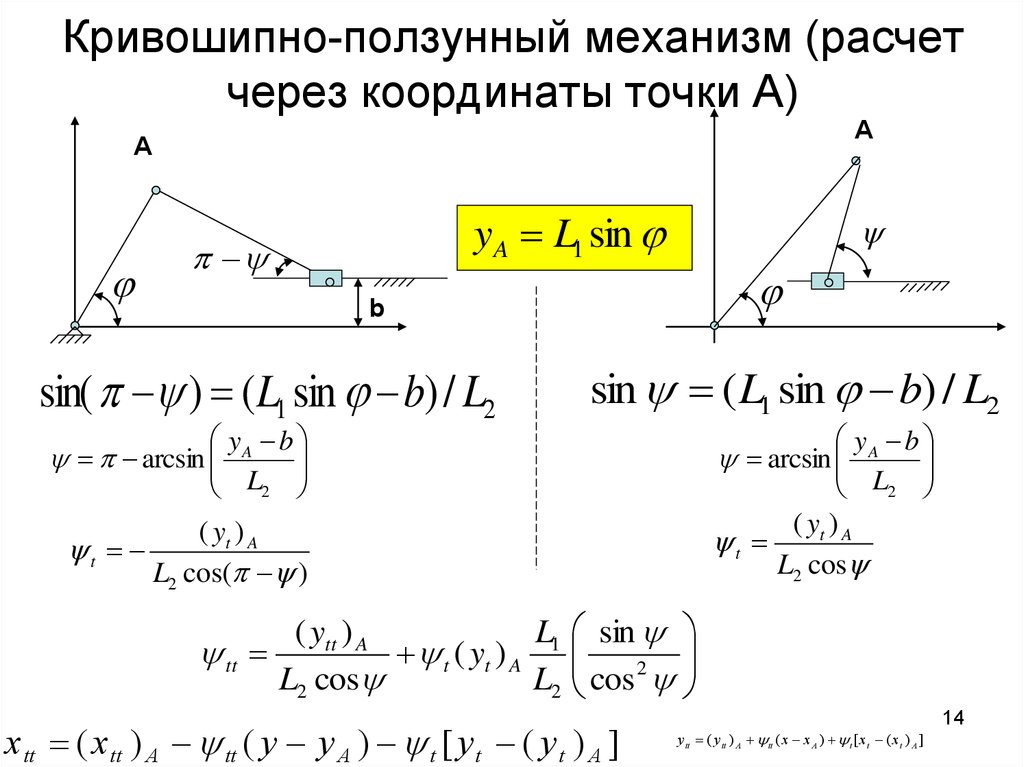
14. Кривошипно-ползунный механизм (расчет через координаты точки А)

А
А
yA L1 sin
b
sin( ) (L1 sin b) / L2
sin ( L1 sin b) / L2
yA b
arcsin
L2
t
yA b
arcsin
L2
( yt ) A
t
L2 cos
( yt ) A
L2 cos( )
( ytt ) A
L1 sin
tt
t ( yt ) A
L2 cos
L2 cos 2
x tt ( x tt ) A tt ( y y A ) t [ y t ( y t ) A ]
14
y tt ( y tt ) A tt ( x x A ) t [ x t ( x t ) A ]

15. Кривошипно-ползунный механизм. Другой вариант записи кинематических связей

L2
L1
Н
L1 sin L2 sin H
=const
15

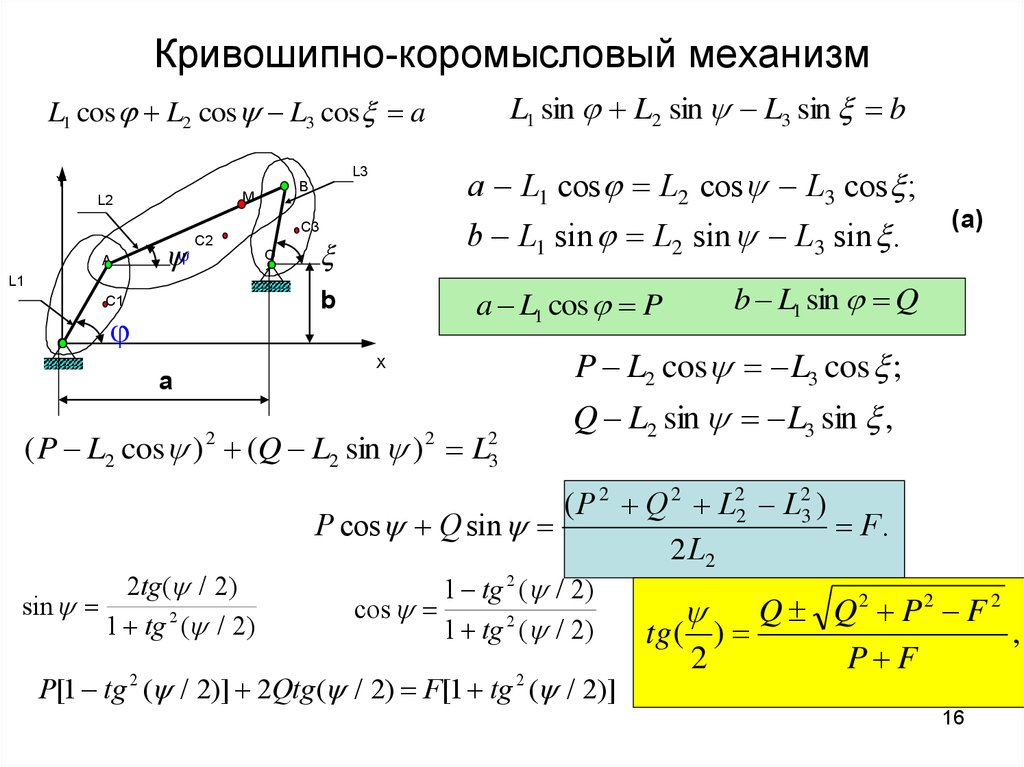
16. Кривошипно-коромысловый механизм

L1 sin L2 sin L3 sin b
L1 cos L2 cos L3 cos a
Y
M
L2
A
C2
L1
b L1 sin L2 sin L3 sin .
P L2 cos L3 cos ;
X
a
Q L2 sin L3 sin ,
( P L2 cos ) (Q L2 sin ) L
2
2tg ( / 2)
sin
1 tg 2 ( / 2)
2
2
3
( P 2 Q 2 L22 L23 )
P cos Q sin
F.
2 L2
1 tg 2 ( / 2)
2
2
2
cos
Q
Q
P
F
1 tg 2 ( / 2)
tg ( )
,
P[1 tg ( / 2)] 2Qtg( / 2) F[1 tg ( / 2)]
2
(a)
b L1 sin Q
a L1 cos P
b
C1
O
C3
O
1
a L1 cos L2 cos L3 cos ;
L3
B
2
2
P F
16

17. Кривошипно-коромысловый механизм

L1 sin L2 sin L3 sin b
L1 cos L2 cos L3 cos a
a L1 cos L2 cos L3 cos ;
b L1 sin L2 sin L3 sin .
(a)
b L1 sin Q
a L1 cos P
P L2 cos L3 cos ;
;
Q L2 sin L3 sin ,
( P L2 cos ) (Q L2 sin ) L
2
2tg ( / 2)
sin
1 tg 2 ( / 2)
2
2
3
( P 2 Q 2 L22 L23 )
P cos Q sin
F.
2 L2
1 tg 2 ( / 2)
2
2
2
cos
Q
Q
P
F
1 tg 2 ( / 2)
tg ( )
,
P[1 tg ( / 2)] 2Qtg( / 2) F[1 tg ( / 2)]
2
2
2
P F
17

18. Кривошипно-коромысловый механизм. Уравнения для углов наклона шатуна и коромысла

a L1 cos L2 cos L3 cos ;
b L1 sin L2 sin L3 sin .
a L1 cos P
(a)
b L1 sin Q
P L2 cos L3 cos ;
;
Q L2 sin L3 sin ,
Q Q2 P2 F 2
tg ( )
,
2
P F
1, 2
Q Q2 P2 F 2
2arctg
,
P F
Из системы (а) получаем 4 варианта значений угла «кси»:
cos ( L1 cos L2 cos a) / L3
L2 cos P
arccos
,
L3
sin ( L1 sin L2 sin b) / L3
L2 sin Q
arcsin
L3
18

19. Соотношения между угловыми скоростями для кривошипно-коромыслового механизма

Дифференцируем систему уравнений (а) (см. сл. 16-18) по времени
t L2 sin t L3 sin t L1 sin ;
t L2 cos t L3 cos t L1 cos ,
(b)
Решаем полученную систему по методу определителей
L2 sin
L3 sin
L2 cos
L3сos
L2 L3 sin( )
t L1 sin
L3 sin
t L1L3 sin( )
t L1 cos L3 cos
L2 sin t L1 sin
t L1L2 sin( )
L2 cos t L1 cos
t
t
L1 sin( )
t t
L2 sin( )
t t
L1 sin( )
L3 sin( )
19

20. Решение системы линейных уравнений по методу Крамера

t L2 cos t L3 cos t L1 cos
t L2 sin t L3 sin t L1 sin
(b)
Исходная система и ее основной определитель
a11 x a12 y b1
a 21 x a 22 y b2
a11
a12
a21 a22
a11a22 a12 a21
«Дополнительные определители»
x
b1
a12
b2
a22
y
b1a22 b2 a12
a11
b1
a21 b2
a11b2 a21b1
Решение системы
x
x
y
y
20

21. Соотношения между угловыми ускорениями для кривошипно-коромыслового механизма

Дифференцируем систему уравнений (b) (см. сл. 19) по времени
tt L2 sin tt L3 sin tt L1 cos t2 L1 cos t2 L2 cos t2 L3 cos ;
tt L2 cos tt L3 cos tt L1 cos t2 L1 sin t2 L2 sin t2 L3 sin
Решаем полученную систему по методу определителей
L2 sin
L3 sin
L2 cos
L3сos
L2 L3 sin( )
f1 tt L1 sin t2 L1 cos t2 L2 cos t2 L3 cos
f 2 tt L1 cos t2 L1 sin t2 L2 sin t2 L3 sin
f 1 cos f 2 sin
tt
L2 sin( )
f 1 cos f 2 sin
tt
L3 sin( )
21

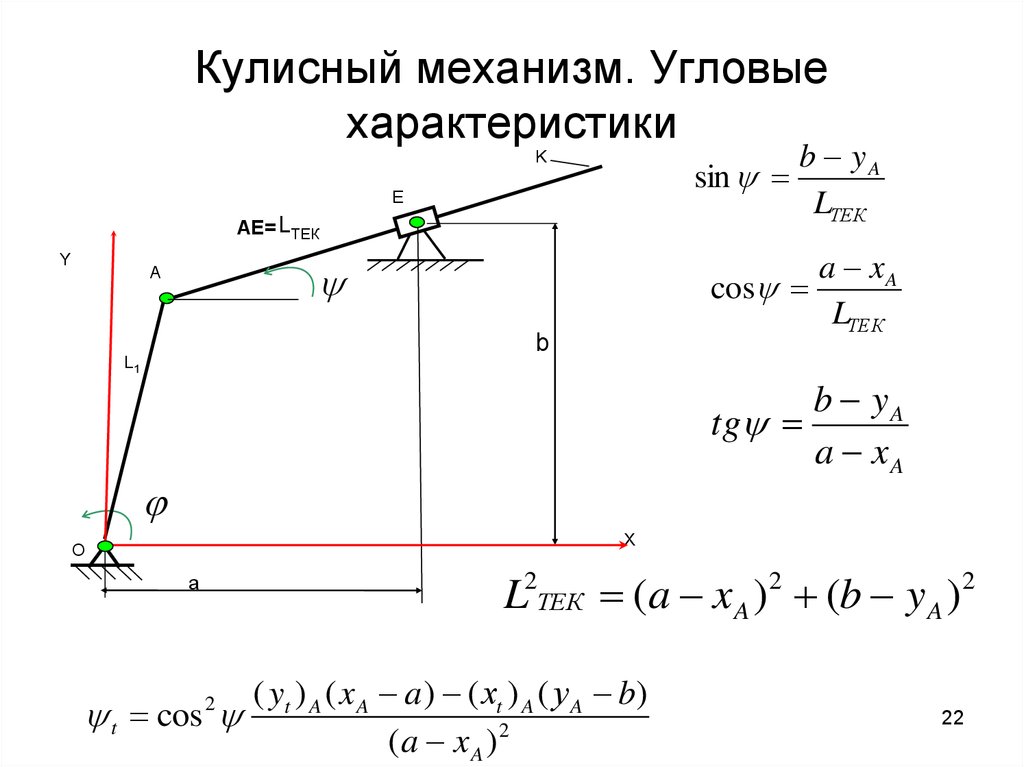
22. Кулисный механизм. Угловые характеристики

b yA
sin
LТЕК
K
E
AE= LТЕК
Y
a xA
cos
LТЕК
A
b
L1
b yA
tg
a xA
X
O
L2ТЕК (a xA )2 (b y A )2
a
( yt ) A ( x A a) ( хt ) A ( у A b)
t cos
(a x A ) 2
2
22

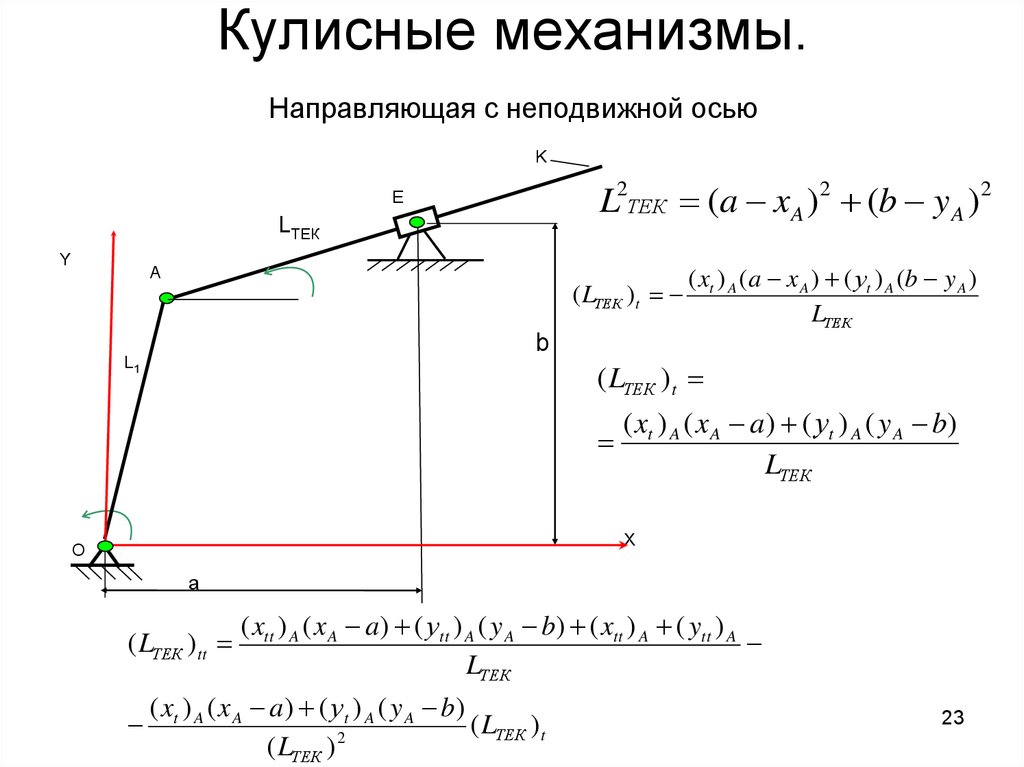
23. Кулисные механизмы. Направляющая с неподвижной осью

K
L2ТЕК (a xA )2 (b y A )2
E
LТЕК
Y
A
( LТЕК )t
( xt ) A (a x A ) ( уt ) A (b y A )
LТЕК
b
L1
( LТЕК ) t
( xt ) A ( x A a ) ( уt ) A ( y A b)
LТЕК
X
O
a
( LТЕК ) tt
( xtt ) A ( x A a ) ( уtt ) A ( y A b) ( xtt ) A ( ytt ) A
LТЕК
( xt ) A ( x A a ) ( уt ) A ( y A b)
( LТЕК ) t
2
( LТЕК )
23

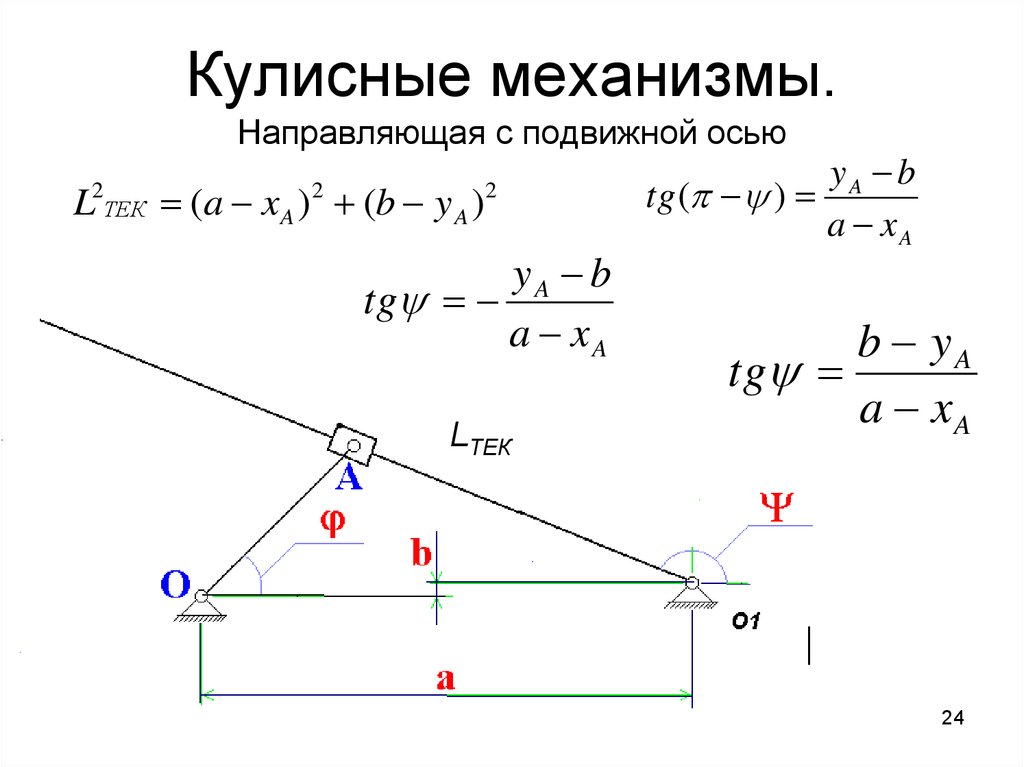
24. Кулисные механизмы. Направляющая с подвижной осью

L ТЕК (a xA ) (b y A )
2
2
2
yA b
tg
a xA
LТЕК
yA b
tg ( )
a xA
b yA
tg
a xA
24

25.

• Все механизмы отличаются
кинематическими связями.
• Число возможных вариантов
механизмов и кинематических связей
бесконечно.
25

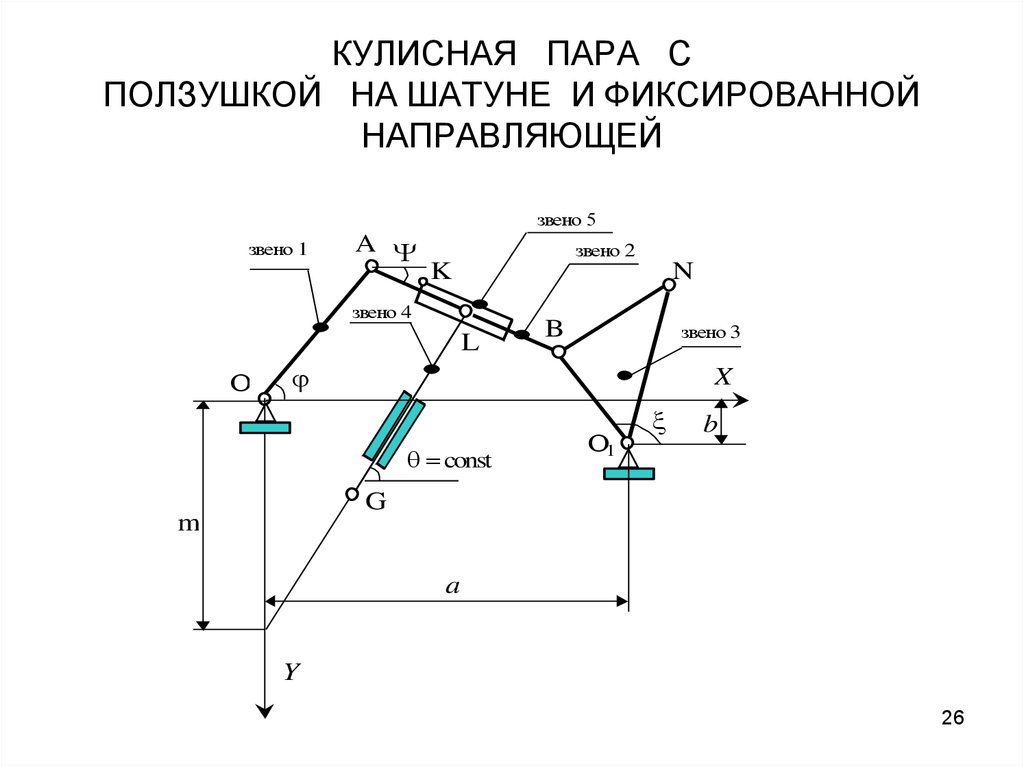
26. КУЛИСНАЯ ПАРА С ПОЛЗУШКОЙ НА ШАТУНЕ И ФИКСИРОВАННОЙ НАПРАВЛЯЮЩЕЙ

звено 5
звено 1
A
звено 2
K
N
звено 4
L
О
B
звено 3
X
const
О1
b
G
m
a
Y
26

27. КУЛИСНАЯ ПАРА С ПОЛЗУШКОЙ НА ШАТУНЕ И ФИКСИРОВАННОЙ НАПРАВЛЯЮЩЕЙ

Пусть уравнение фиксированной направляющей имеет вид
(1)
y m xtg
где m - отрезок, отсекаемый прямой с углом наклона на оси «у».Положение шатуна
определяют оси шарниров А и В. Коэффициенты уравнения
(2)
y n xtg
соединяющей их прямой находим из системы уравнений
(3a)
n x tg
n x tg y
A
B
y y
yB
(3b)
A
откуда
tg B
xB x A
;
(4)
Величину “n” удобно найти из уравнения (3a) или (3b).
Точка пересечения L должна одновременно принадлежать обеим прямым (1) и (2),
тогда ее координаты должна определять система уравнений
(5a)
(5b)
yL xLtg m
y x tg n
L
A
L
Отсюда находим
n m
tg tg
ntg mtg
tg tg
(7)
При программировании на ЭВМ для расчета ординаты точки пересечения удобнее
пользоваться одним из уравнений (5).
xL
6)
yL
27

28. УГОЛ МЕЖДУ ШАТУНОМ И ФИКСИРОВАННЫМ НАПРАВЛЕНИЕМ ДВИЖЕНИЯ ПОЛЗУНА

Уравнение прямой, вдоль которой движется ползун
где m - отрезок, отсекаемый прямой с углом наклона «Тета» на оси «у».Положение шатуна определяют
оси шарниров А и В. Уравнение прямой, ортогональной (1)
y n xtg (2)
y m xtg
(1)
из условия ортогональности должно иметь угловой коэффициент
(3)
y n x / tg
Слагаемое “n” находим из условия прохождения прямой (2) через точку D с координатами xD, yD , т.е.
n yD
y yD
xD
tg
x xD
tg
(4)
Координаты точки пересечения прямых (1) и (2) определяются системой уравнений
и составляют (по любому методу решения системы)
x ( yD m)tg
;
(6)
xN D
1 tg 2
Затем находим расстояние между точками D и N
(7)
h ( xN xD )2 ( yN yD )2
xN
x
y N yD D
tg
tg
xN tg y N m
и искомый угол
sin( )
h
L
m xDtg yDtg 2
yN
1 tg 2
h
L
arcsin( )
28

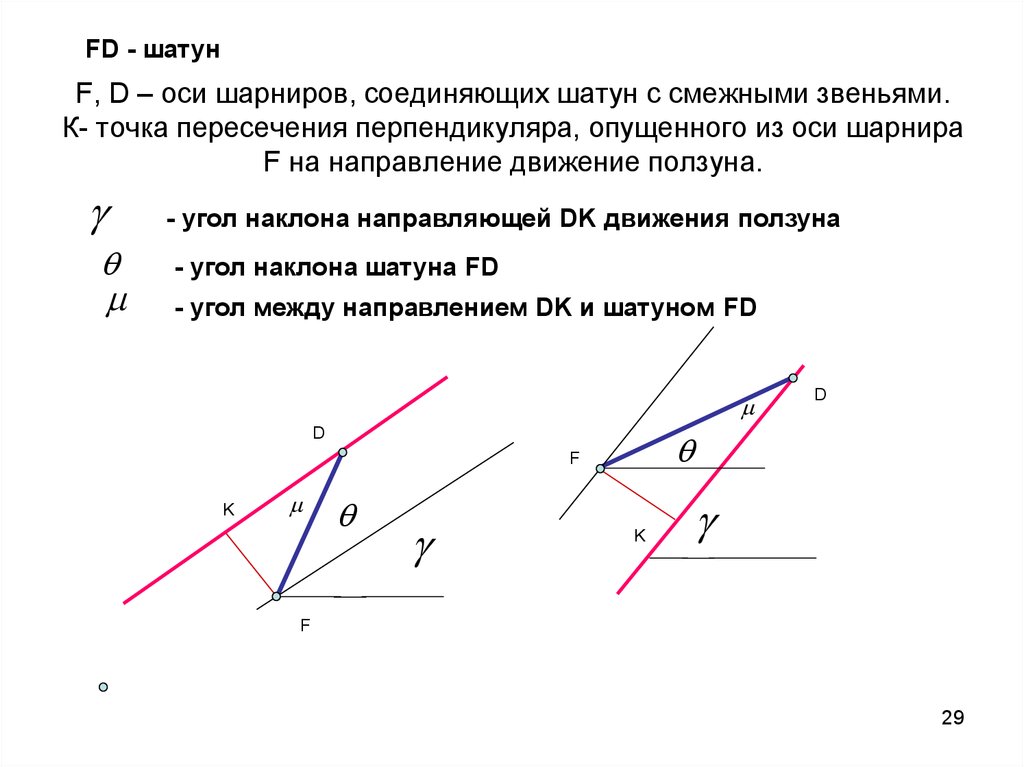
29. F, D – оси шарниров, соединяющих шатун с смежными звеньями. К- точка пересечения перпендикуляра, опущенного из оси шарнира F на

FD - шатун
F, D – оси шарниров, соединяющих шатун с смежными звеньями.
К- точка пересечения перпендикуляра, опущенного из оси шарнира
F на направление движение ползуна.
- угол наклона направляющей DK движения ползуна
- угол наклона шатуна FD
- угол между направлением DK и шатуном FD
D
F
K
D
K
F
29

30.

• Расстояние от точки Р(хР, уР) до прямой А*х + В*у + С = 0
определяет уравнение
h ( sign (C ))
Ax P By P C
A2 B 2
Знак "-" соответствует случаю, когда точка Р и начало координат находятся по одну
сторону от прямой
Знак "+" соответствует случаю, когда точка Р и начало координат находятся по разные
стороны прямой
Этот вариант удобен тем, что легко определить производные ht и htt , а именно:
ht
A( xt ) P B( yt ) P C
A B
2
h
sin
L5
yF yK
yF yK
t t 0
t
ht
L5 cos
htt
2
A( xtt ) P B( ytt ) P C
A2 B 2
tt tt
tt
htt
ht
t sin
L5 cos
L5 cos 2
30

31. Два коромысла с кулисной парой

B
D(x D,yD)
K(x K,yK)
Ltek=O1K
mu
h
L4
Teta
Ksi
O2(m, n)
O1(a,b)
31

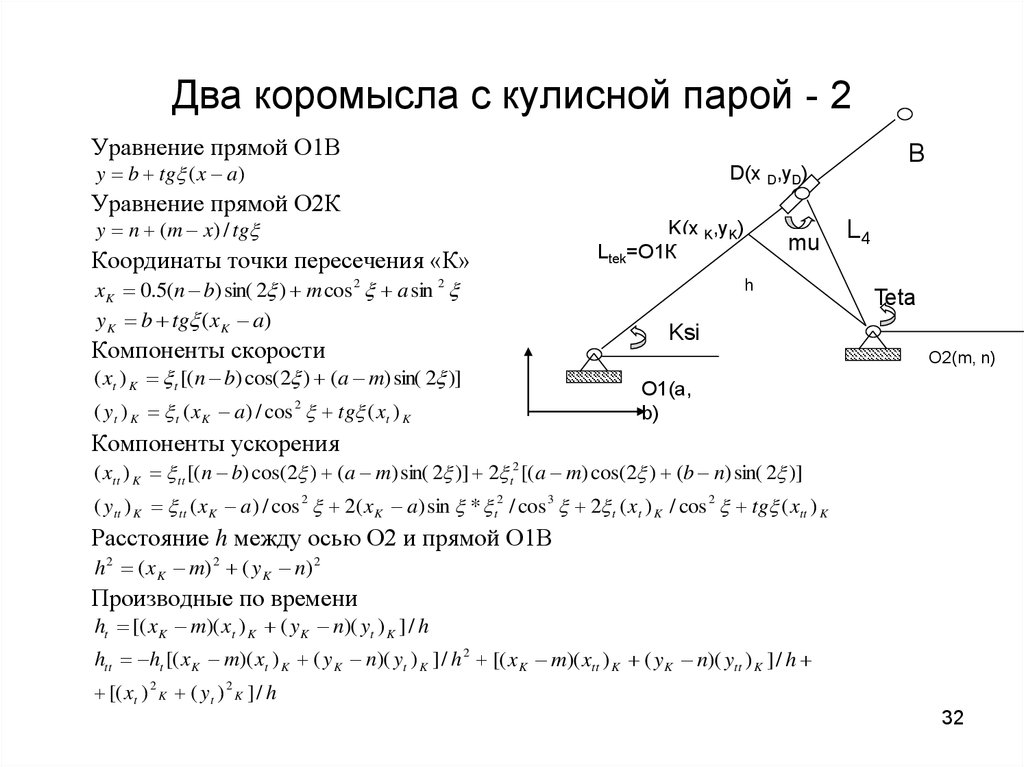
32. Два коромысла с кулисной парой - 2

Уравнение прямой О1В
y b tg ( x a )
B
D(x D,yD)
Уравнение прямой О2К
y n (m x) / tg
Координаты точки пересечения «К»
x K 0.5(n b) sin( 2 ) m cos 2 a sin 2
y K b tg ( xK a)
Компоненты скорости
( xt ) K t [(n b) cos(2 ) (a m) sin( 2 )]
( y t ) K t ( x K a) / cos tg ( xt ) K
2
K(x K,yK)
Ltek=O1К
mu
h
L4
Teta
Ksi
O2(m, n)
O1(a,
b)
Компоненты ускорения
( xtt ) K tt [( n b) cos( 2 ) (a m) sin( 2 )] 2 t2 [( a m) cos( 2 ) (b n) sin( 2 )]
( y tt ) K tt ( x K a) / cos 2 2( x K a) sin * t2 / cos 3 2 t ( xt ) K / cos 2 tg ( xtt ) K
Расстояние h между осью О2 и прямой О1В
h 2 ( x K m) 2 ( y K n) 2
Производные по времени
ht [( x K m)( xt ) K ( y K n)( yt ) K ] / h
htt ht [( x K m)( xt ) K ( y K n)( yt ) K ] / h 2 [( x K m)( xtt ) K ( y K n)( ytt ) K ] / h
[( xt ) 2 K ( y t ) 2 K ] / h
32

33. Два коромысла с кулисной парой - 3

Для расчета текущей длины О1Д находим точку пересечения Д прямых О1ДВ
(уравнение приведено выше) и О2Д
Уравнение прямой О2Д
y n tg ( x m)
Получаем систему
xD tg y D mtg n
xD tg y D atg b
mtg atg b n
xD
tg tg
y D b tg ( xD a)
Производные по времени
(m t / cos 2 a t / cos 2 )(tg tg ) x D ( t / cos 2 t / cos 2 )(tg tg )
( xt ) D
(tg tg ) 2
( yt ) D t ( x D a) / cos 2 tg ( xt ) D
Текущая длина
Ltek ( xD a) 2 ( y D b) 2
( Ltek ) t [( x D a)( xt ) D ( y D b)( yt ) D ] / Ltek
2
( Ltek ) tt ( Ltek ) t [( x D a)( xt ) D ( y D b)( yt ) D ] /( Ltek ) 2
[( x D a)( xtt ) D ( y D b)( ytt ) D ] /( Ltek ) [( xt ) 2D ( yt ) 2D ] /( Ltek )
33

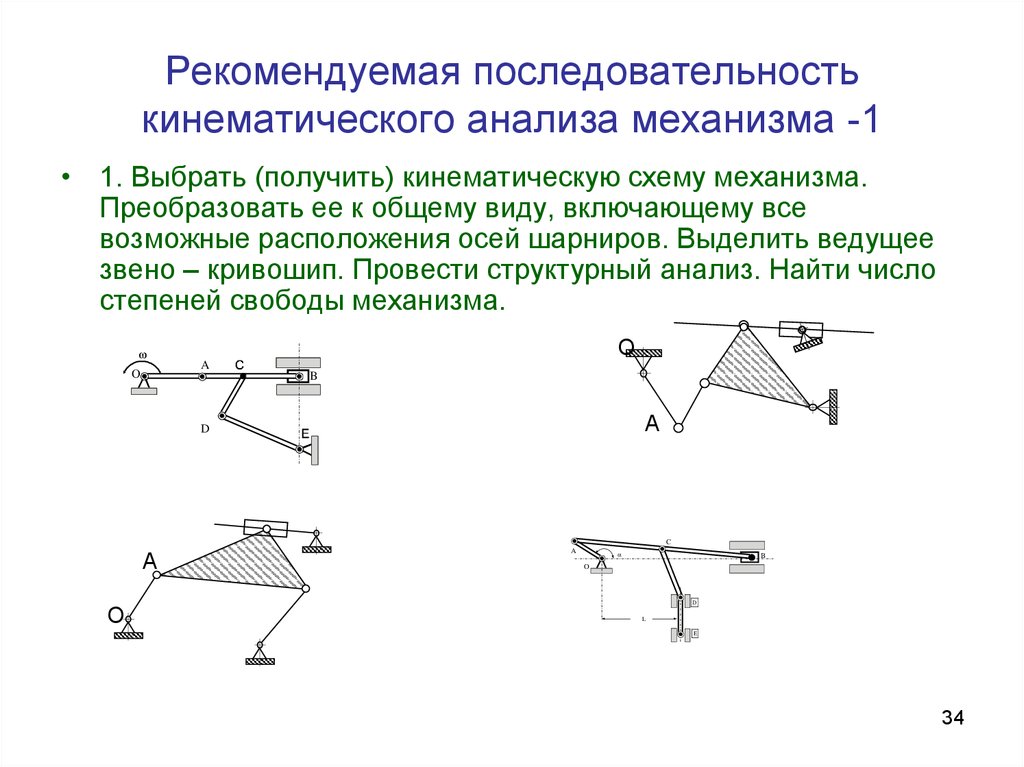
34. Рекомендуемая последовательность кинематического анализа механизма -1

• 1. Выбрать (получить) кинематическую схему механизма.
Преобразовать ее к общему виду, включающему все
возможные расположения осей шарниров. Выделить ведущее
звено – кривошип. Провести структурный анализ. Найти число
степеней свободы механизма.
O
A
O
B
A
D
C
A
A
B
O
D
O
L
E
34

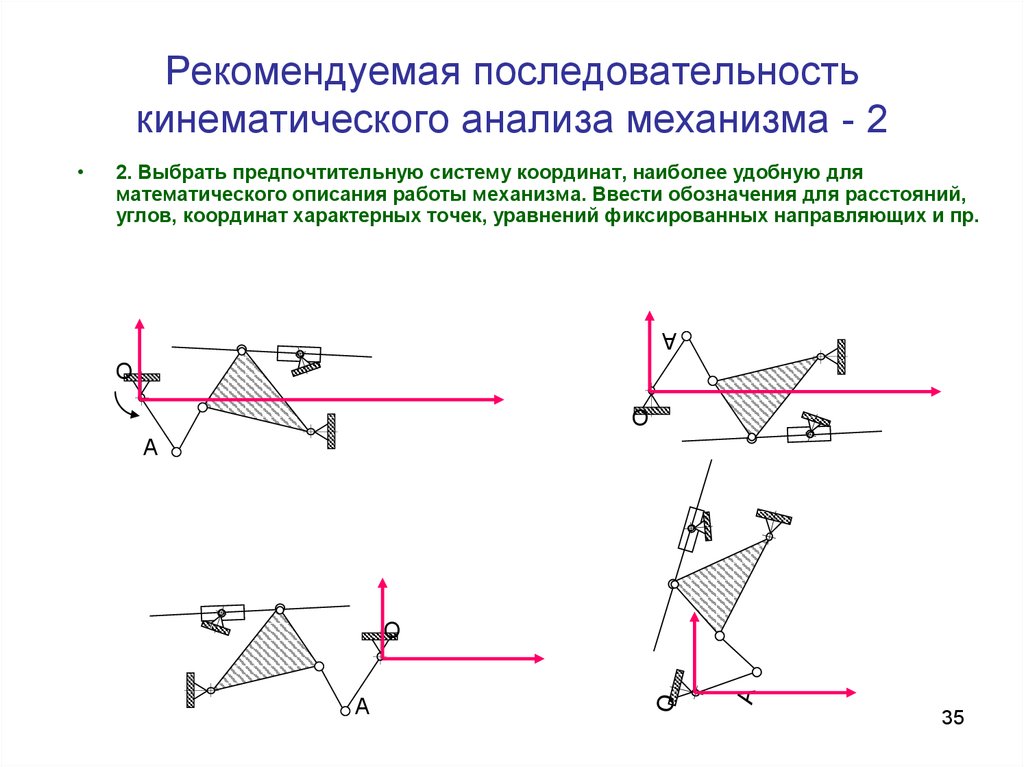
35. Рекомендуемая последовательность кинематического анализа механизма - 2

2. Выбрать предпочтительную систему координат, наиболее удобную для
математического описания работы механизма. Ввести обозначения для расстояний,
углов, координат характерных точек, уравнений фиксированных направляющих и пр.
A
O
O
A
O
A
35

36.

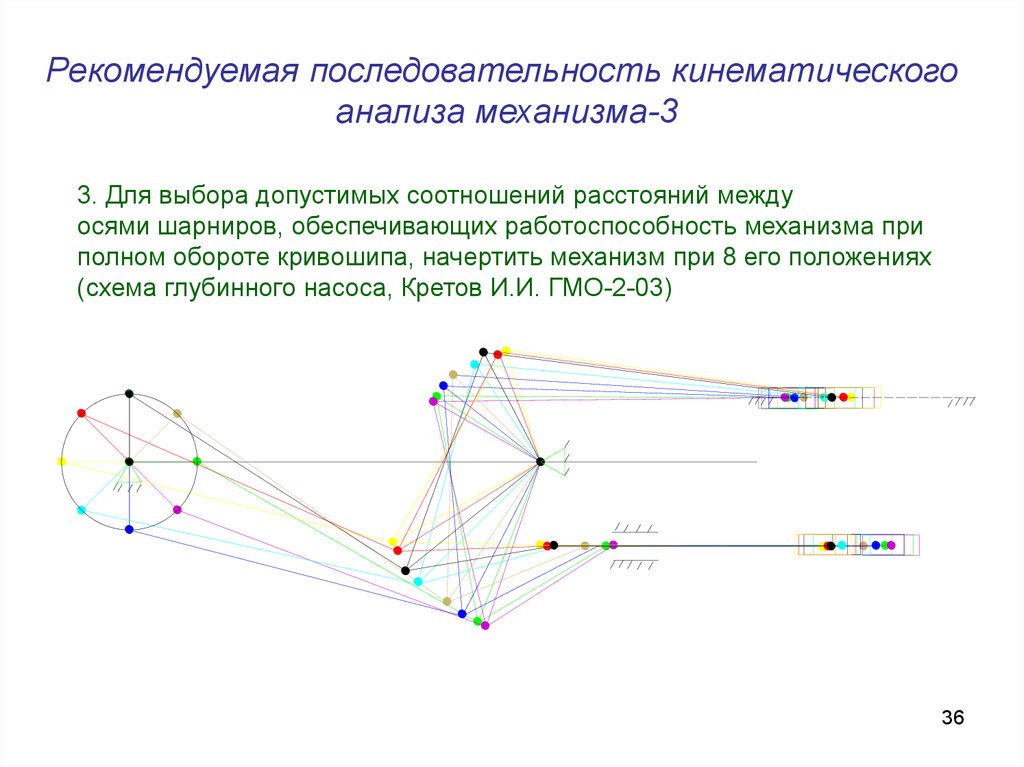
Рекомендуемая последовательность кинематического
анализа механизма-3
3. Для выбора допустимых соотношений расстояний между
осями шарниров, обеспечивающих работоспособность механизма при
полном обороте кривошипа, начертить механизм при 8 его положениях
(схема глубинного насоса, Кретов И.И. ГМО-2-03)
36

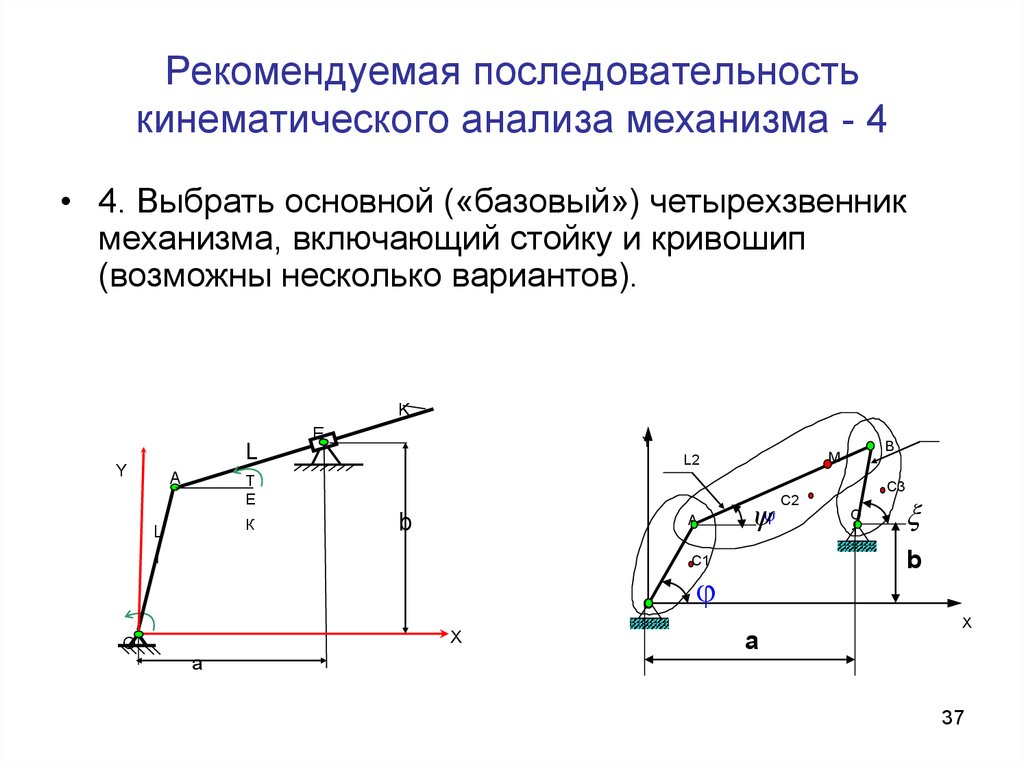
37. Рекомендуемая последовательность кинематического анализа механизма - 4

• 4. Выбрать основной («базовый») четырехзвенник
механизма, включающий стойку и кривошип
(возможны несколько вариантов).
K
L
Y
A
E
Y
Т
Е
К
L
A
b
O
X
O
C2
C3
O
1
b
C1
1
B
M
L2
X
a
a
37

38. Рекомендуемая последовательность кинематического анализа механизма - 5

5. Выписываем (из лекций или учебного пособия) уравнения для
координат, скоростей и ускорений каждого из звеньев
четырехзвенника. Все они могут быть получены из общих
соотношений для шатуна (см. слайд 7).
x x p ( p ) cos( ) ( p ) sin( )
y y p ( p ) sin( ) ( p ) cos( )
xt ( xt ) P t ( у уР )
уt ( уt ) P t ( х хР )
xtt ( xtt ) P tt ( у у Р ) 2 t ( x xР )
уtt ( уtt ) P tt ( х хР ) t ( у у Р )
2
38

39. Рекомендуемая последовательность кинематического анализа механизма - 6

6. Записываем уравнения кинематических связей для рассматриваемого
четырехзвенника, находим соотношения для углов, угловых скоростей и
ускорений.
Кривошипно-коромысловый
механизм (см. слайды 16-21)
t t
L1 sin( )
L2 sin( )
Q Q2 P2 F 2
tg ( )
,
2
P F
L1 sin( )
t t
L3 sin( )
Кривошипно-кулисный механизм (см. слайды 22-24)
b yA
tg
a xA
t cos 2
( yt ) A ( x A a) ( хt ) A ( у A b)
(a x A ) 2
39

40. Рекомендуемая последовательность кинематического анализа механизма - 7

7. Переходим к программированию задачи, например
в электронных таблицах Excel.
7.1. Указываем автора работы, группу, схему (строки 1-2)
7.2. Выделяем блок исходных данных (строки 3-19)
7.3. Вводим стандартный блок «Угловые
характеристики работы кривошипа» (строки 20-30)
4
L1
5
L2
6
L3
7
Alfa_A
8
Betta_A
9
Fi0
10
(Fi_t)0=
11
(Fi_tt)0=
12
+Fi_tt
13
Delta_Fi (градусы)
14
Delta_Fi (радианы)
7.4. Рассчитываем координаты, компоненты скорости и ускорения
шарнира А, принадлежащего кривошипу (строки 32-38). Расчет
кинематических характеристик центра массы кривошипа С1
можно перенести в раздел «Энергетический анализ механизма»
40

41. Рекомендуемая последовательность кинематического анализа механизма - 8

Переходим к программированию блока
«Кинематические связи»
8.1. Вводим промежуточные переменные, чтобы длина
программируемых выражений не превышала 1 строки
8.2. После вычисления искомых угловых функций и их
производных по времени проводим обязательную проверку
исходных уравнений
8.3. Определяем все возможные решения системы уравнений,
описывающей кинематические связи в механизме.
8.4. Вводим обязательные строки «Принятые значения» и
переносим в них адреса результатов, используемых в
последующих расчетах.
41

42. Рекомендуемая последовательность кинематического анализа механизма - 9

Переходим к программированию кинематических
характеристик ведомых звеньев четырехзвенника
9.1. Используя координаты, скорости и ускорения оси
шарнира, связывающего исследуемое звено с ведущим,
определяем координаты, скорости и ускорения других
частиц звена, включая ось шарнира, связывающего его с
последующим ведомым звеном.
9.2. Повторяем п. 9.1 для всех остальных звеньев механизма
42

43. Рекомендуемая последовательность кинематического анализа механизма - 10

Через каждые 5-8 строк программы проводим
проверку результатов кинематических
расчетов:
• для координат – по виду траектории,
• для скоростей и ускорений – по выполнению
свойств производных от рассчитываемых
функций (координат, углов и пр.),
• по сохранению расстояний между осями
шарниров,
• по сравнения результатов с численным
дифференцированием.
43

44. После завершения кинематического анализа переходим к расчету кинематических характеристик центров масс звеньев, их кинетической

ЭНЕРГЕТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
После завершения кинематического анализа
переходим к расчету кинематических
характеристик центров масс звеньев, их
кинетической и потенциальной энергии,
ньютоновых сил инерции и скорости изменения
(мощности) кинетической и потенциальной
энергии.
ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
Используя результаты кинематического и энергетического
анализов, определяем обобщенные силы, приведенные к осям
шарниров, с обязательной проверкой энергетического баланса
при выборе различных комбинаций обобщенных сил.
44