Кручение стержней круглого сечения

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Лекции
по дисциплине «Техническая механика»
270800 - Строительство

2. Кручение стержней круглого сечения

3. Основные понятия деформации кручения

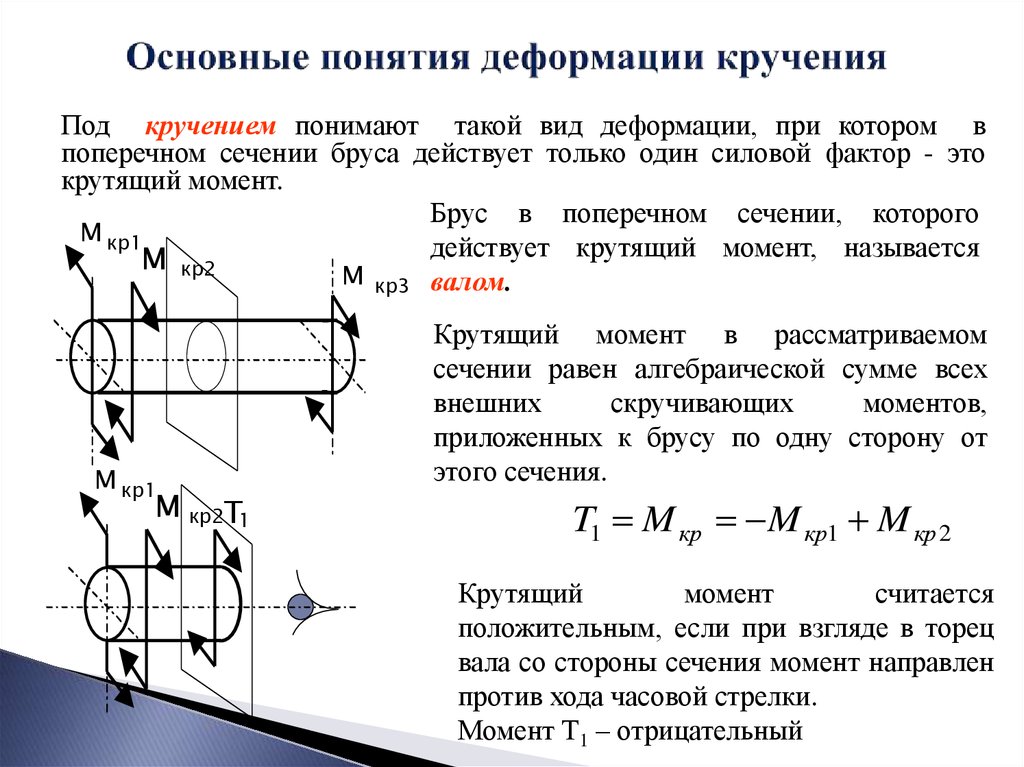
Под кручением понимают такой вид деформации, при котором в
поперечном сечении бруса действует только один силовой фактор - это
крутящий момент.
Брус в поперечном сечении, которого
М кр1
действует крутящий момент, называется
М кр2
М кр3 валом.
М кр1
М кр2Т1
Крутящий момент в рассматриваемом
сечении равен алгебраической сумме всех
внешних
скручивающих
моментов,
приложенных к брусу по одну сторону от
этого сечения.
T1 M кр M кр1 M кр 2
Крутящий
момент
считается
положительным, если при взгляде в торец
вала со стороны сечения момент направлен
против хода часовой стрелки.
Момент Т1 – отрицательный

4. Закон Гука при кручении

Основные допущения:
1.Поперечные сечения вала, плоские и нормальные к его оси до деформации,
остаются плоскими и нормальными к оси, и после деформации.
2.Радиусы поперечных сечений не искривляются и сохраняют свою длину.
3.Расстояния между поперечными сечениями не изменяются.
При кручении наблюдается плоское напряженное состояние чистого
сдвига и соблюдается закон Гука при сдвиге:
G
Т
Т
d
dz d
d
dz
d
dz
G G

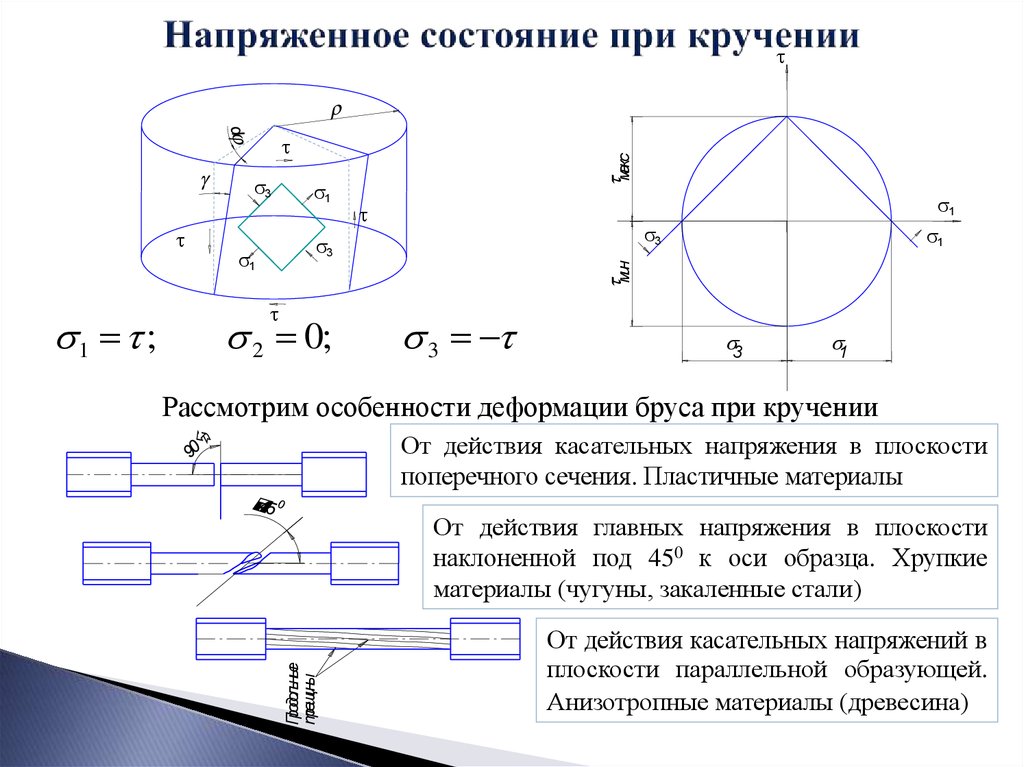
5. Напряженное состояние при кручении

3
1 ;
1
3
3
1
1
мин
1
макс
2 0;
3
3
1
Рассмотрим особенности деформации бруса при кручении
Возможны следующие варианты разрушения образцов
От действия касательных напряжения в плоскости
поперечного сечения. Пластичные материалы
Продольные
трещины
От действия главных напряжения в плоскости
наклоненной под 450 к оси образца. Хрупкие
материалы (чугуны, закаленные стали)
От действия касательных напряжений в
плоскости параллельной образующей.
Анизотропные материалы (древесина)

6. Напряжения при кручении

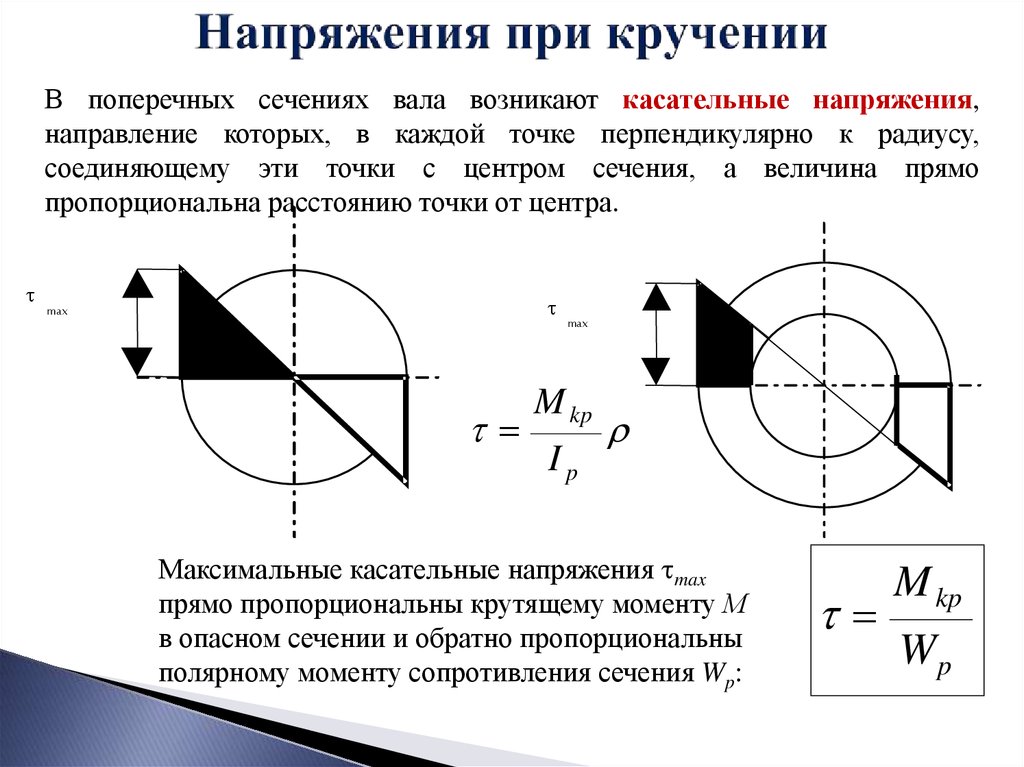
В поперечных сечениях вала возникают касательные напряжения,
направление которых, в каждой точке перпендикулярно к радиусу,
соединяющему эти точки с центром сечения, а величина прямо
пропорциональна расстоянию точки от центра.
max
max
M kp
Ip
Максимальные касательные напряжения max
прямо пропорциональны крутящему моменту М
в опасном сечении и обратно пропорциональны
полярному моменту сопротивления сечения Wp:
M kp
Wp

7.

Полярный момент инерции характеризует, влияние размеров и формы
поперечного сечения вала на его способность сопротивляться угловым
деформациям
d 4
2
Для круглого сечения
d /2
d I
Ip
3
p
0
Для трубчатого сечения
Ip
32
,
d 4 1 4
32
здесь α = d1 /d, d1 –внутренний диаметр трубы, d – наружный диаметр трубы
Полярный момент инерции выражается в м4 (мм4, см4).
Полярный момент сопротивления характеризует влияние геометрических
размеров и формы поперечного сечения вала на его прочность.
Wp
Ip
м акс
Для круглого сечения
Для трубчатого сечения
Wp
Wp
d 3
16
d 3 1 4
16

8. Условие прочности при кручении

Наибольшие касательные напряжения, возникающие в скручиваемом брусе
не должны превышать соответствующих допускаемых значений
Типовые задачи при кручении
max
M kp
Wp
max
1. Проверочный расчет
2. Конструкционный расчет
кр
d 3
max
M kp
max
16M kp
kр
Для круглого сечения
3.Проектный расчет – определение
допускаемого момента
Wp
кр
d 3
max
16M kp
Для трубчатого сечения
M W
кр
1 4 kр
кр
p

9. Деформации при кручении. Условие жесткости при кручении

При кручении различают угол закручивания и относительный угол
закручивания
G G
Закон Гука при кручении
Напряжения при кручении
Угол закручивания
M
Ip
Ml
GI p
Условие жесткости при кручении
Наибольший относительный угол закручивания, возникающий в
скручиваемом брусе не должен превышать соответствующих допускаемых
значений
max
Где [ ] – допускаемы относительный угол закручивания.
[ ]=0,0045….0,02 рад/м

10. Потенциальная энергия деформации

M M Ml
M 2l
U
2
2 GI p 2GI p
Полная потенциальная энергия
деформации
Удельная потенциальная энергия (полная)
1
u
12 22 32 2 1 2 2 3 1 3
2E
1
1 2
2
2
u
2 2
2E
E
Удельная потенциальная
энергия изменения
объема
1 2 2
uV
1 22 32
6E
Удельная потенциальная энергия
изменения формы
1 2
1 22 32 1 2 2 3 3 1
3Е
1
1 2 2 2 3 2 3 1 2
6Е
uф

11.

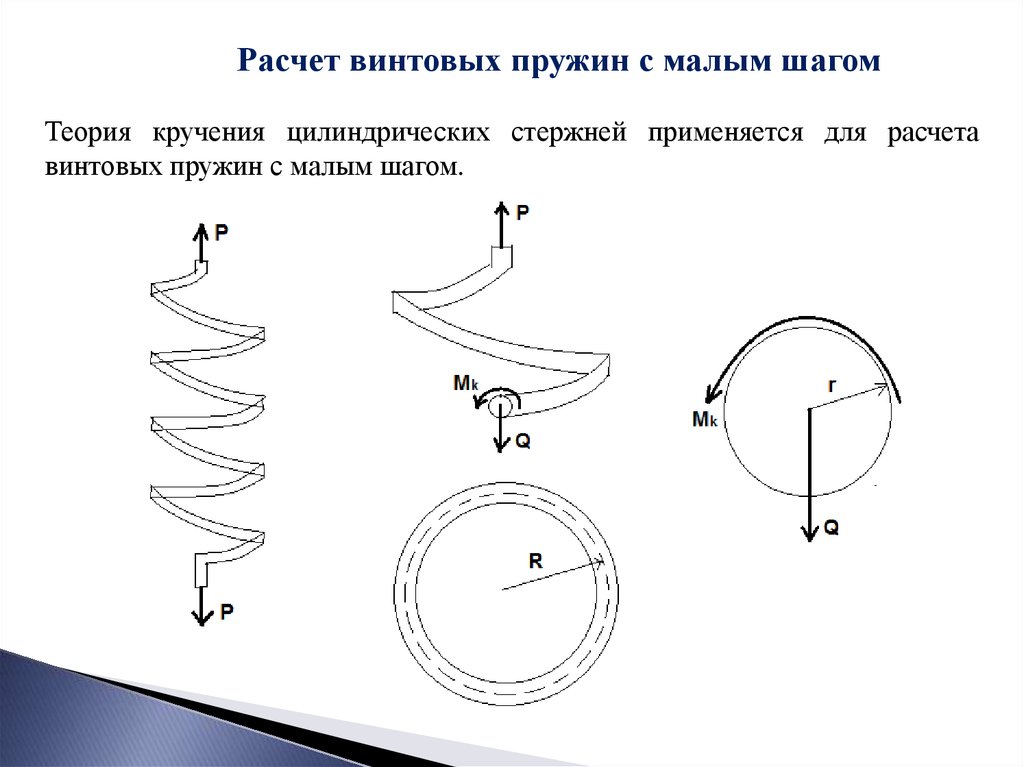
Расчет винтовых пружин с малым шагом
Теория кручения цилиндрических стержней применяется для расчета
винтовых пружин с малым шагом.

12.

Касательные напряжения, возникающие в поперечном сечении
проволоки пружины состоят из двух составляющих, от действия
сдвигающей силы Q=P и крутящего момента Мк =Р*R
Наибольшие значения касательных напряжений возникают в крайних
волокнах проволоки пружины и равны
max
Где:
P 2R
1
2
r
r
r – радиус поперечного сечения проволоки пружины;
R – радиус цилиндра винтовой пружины.

13.

Условие прочности пружины:
max
2 PR
3
r
Для определения осадки пружины рассмотрим деформацию элемента
пружины dS
За счет закручивания этого элемента точка О займет положения точки О1 и
получим

14.

Интегрируя это выражение получим осадку пружины
где
.
C
4 PR 3 n
CP,
4
3
Gr
4R n
Gr
4
– жесткость пружины.
n -- количество витков пружины
Условие жесткости пружины:
4 PR 3 n
4
Gr
из которого вытекают три задачи: проверка условия жесткости пружины,
определение радиуса поперечного сечения проволоки и допускаемой
нагрузки:
4 PR 3 n
.
4
Gr
r
4 PR 3 n
G
Pдоп
Gr 4
4R 3 n