Центральное растяжение-сжатие. Расчет статически определимой стержневой системы

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Решение задач
по дисциплине «Техническая механика»
270800 - Строительство

2. Центральное растяжение-сжатие Расчет статически определимой стержневой системы

3.

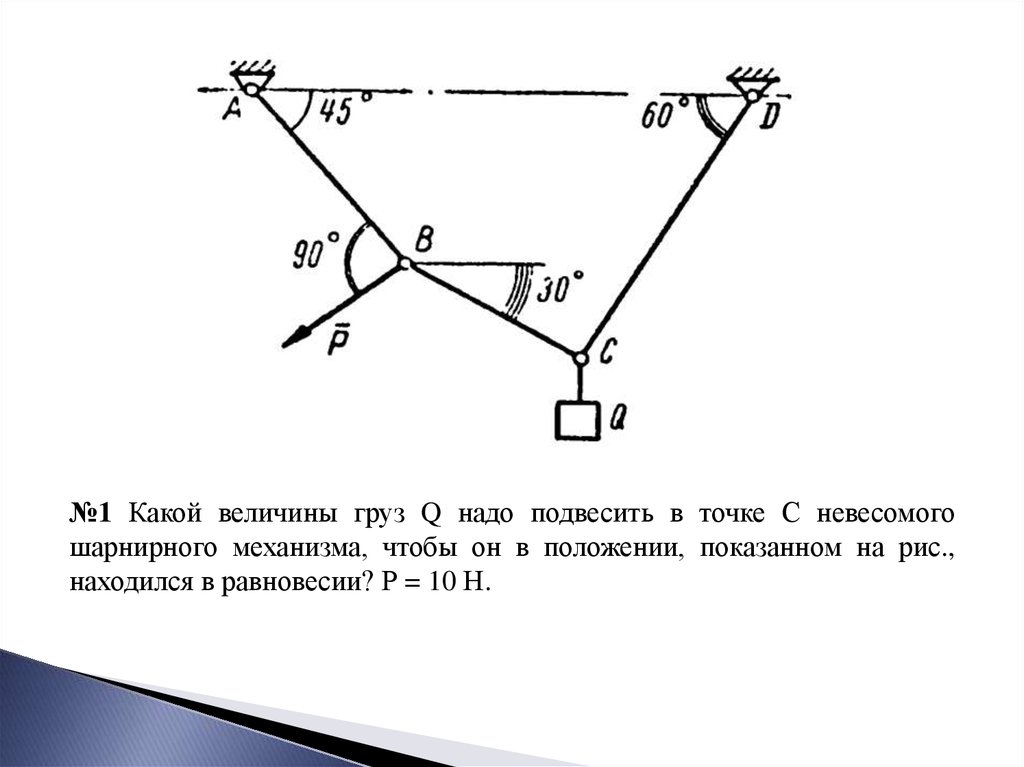
№1 Какой величины груз Q надо подвесить в точке С невесомого
шарнирного механизма, чтобы он в положении, показанном на рис.,
находился в равновесии? Р = 10 Н.

4.

а)
б)
N1
2
Q =100 кН
2м
B
1
A
C
1
C
D1
fc
0,5
1м
B
D
1
3
C
A
B
D
A
1м
1м
1
N2
Q
№2 Жесткая балка, деформацией которой пренебрегаем, закреплена и
нагружена, как показано на рис. Стержень 1 – стальной, сечением 10
см2, стойка 2 – деревянная, сечением 10 10 см2, стержень 3 – медный,
сечением 30 см2. Определить вертикальное перемещение точки С, если
линейные модули упругости материалов стержней равны Ест=2,1 105
МПа, Ем=1 105 МПа, Ед=1 104 Мпа.

5.

Решение
Из условия равновесия жесткой балки АВ определяем внутренние
усилия в стержне 1 и стойке 2.
3
отсюда N1 66,667 кН 66,667 10 МН
m B N1 3 Q 2 0
3
отсюда N 2 33,333 кН 33,33 10 МН
Y N1 Q N 2 0
Примерная деформированная схема системы представлена на рис.б,
CC ' DD ' l3
где
BB' l2
АА' l1
Из закона Гука определяем удлинение стержней 1 и 3 и укорочение
стойки 2.
N1 1
66,667 10 3 1
5
l1
31,75 10 м
E ст A1 2,1 10 5 10 10 4
N 2 2 33,333 10 3 1
5
l 2
33
,
33
10
м
E A2 1 10 4 100 10 4
N3 3
100 10 3 0,5
l3
16,67 10 5 м.
5
4
E м A3 1 10 30 10
Из рис.б определяем:
DD' BB'
AA' BB'
31,75 33,33
2 33,33
2 10 5 32,28 10 5 м.
3
3
Вертикальное перемещение точки С будет:
f C CC' 32,28 10 5 16,67 10 5 48,95 10 5 м.

6.

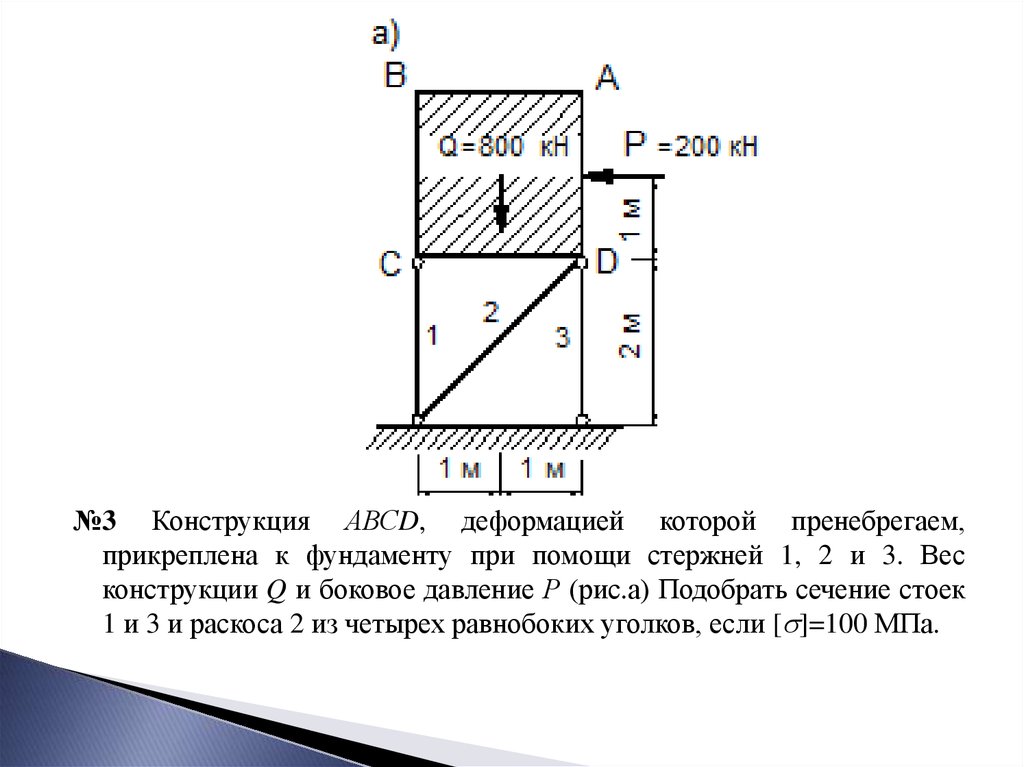
№3 Конструкция АВСD, деформацией которой пренебрегаем,
прикреплена к фундаменту при помощи стержней 1, 2 и 3. Вес
конструкции Q и боковое давление Р (рис.а) Подобрать сечение стоек
1 и 3 и раскоса 2 из четырех равнобоких уголков, если [ ]=100 МПа.

7.

Решение
Из условия равновесия конструкции АВСD
определяем усилия в стержнях 1, 2 и 3 (рис.б):
0
X
P
N
Cos
45
0
2
N 2 282,89 кН.
0
Y
Q
N
N
Sin
45
N3 0
1
2
m
D
Q 1 м P 1 м N1 2 м 0
800 1 200 1
N1
500 кН.
2
N 3 800 500 282,89 0,707 100 кН .

8.

Из условия прочности стоек и раскоса определяем требуемые площади
уголков и из таблицы сортаментов подбираем номер равнобокого
Ni
Ni
уголка:
тр
Ai
,
Ai
;
N1
N1
500 10 3
; A1
125 10 3 м 2 12,5 см 2 .
4 A1
4 4 100
Для 1-го стержня принимаем четыре уголка 100 100 6,5 с площадью
сечения А1=12,8 см2.
N2
282,89 10 3
A2
0,7072 10 3 м 2 7,072 см 2 .
4
4 100
Для 2-го стержня - четыре уголка 63 63 6 с А2=7,28 см2.
N3
100 10 3
A3
0,25 10 3 м 2 2,5 см 2 .
4 4 100
2
Для 3-го стержня - четыре уголка 45 45 3 с A3 2,65 см .

9.

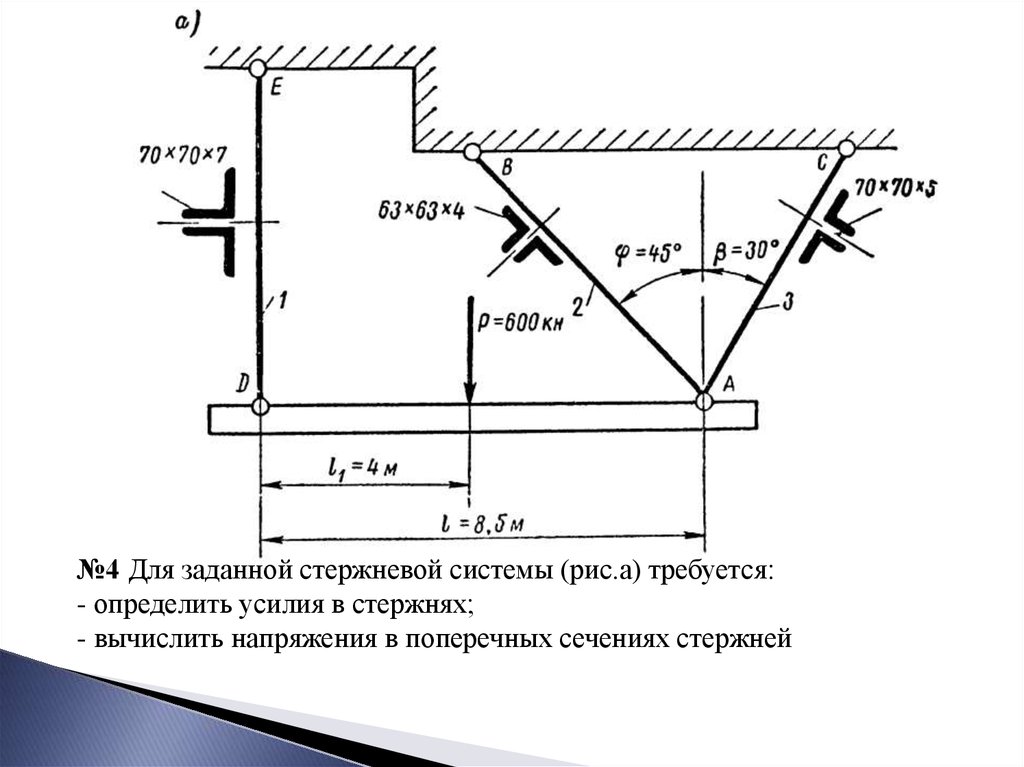
№4 Для заданной стержневой системы (рис.а) требуется:
- определить усилия в стержнях;
- вычислить напряжения в поперечных сечениях стержней

10.

Решение: Применяем метод сечений и рассматриваем равновесие плиты
AD под действием заданных нагрузок и искомых усилий в стержнях
(рис.б)
Из суммы моментов относительно точки А получим:

11.

Из суммы проекций сил на ось Х получим:
Из суммы проекций сил на ось Y получим:
Решая полученную систему уравнений, находим:
Для проверки возьмем сумму моментов относительно точки D:
Следовательно, усилия в стержнях определены верно. Подставляя
числовые данные (Р = 600 кН), получаем:

12.

По таблице сортамента прокатных профилей находим площади
поперечных сечений стержней:
-для стержня АВ – равнополочный уголок – 63*63*4:
А=2*4,96=9,92 см2;
- для стержня АС – 70*70*5: А=2*6,86=13,72 см2;
- для стержня DE – 70*70*7: А=2*9,42=18,84 см2.
Вычисляем напряжения в поперечных сечениях стержней:

13.

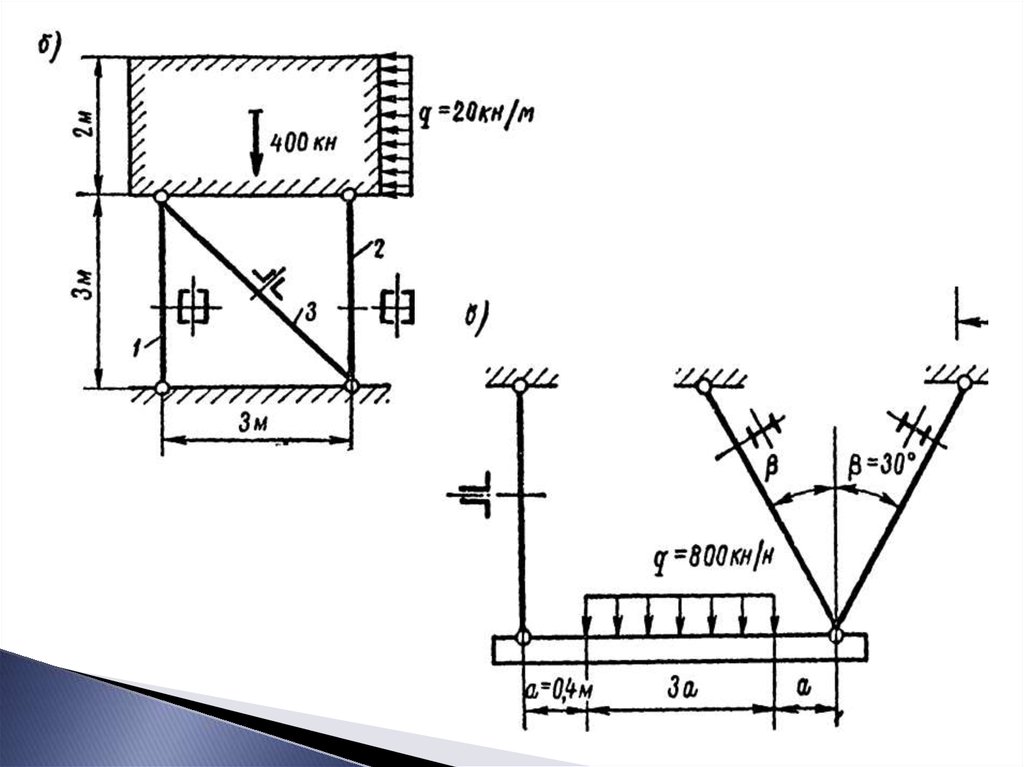
№5 Определить размеры поперечных сечений стальных стержней. Для
стержней работающих на растяжение – [σ]р=160 МПа, работающих на
сжатие - [σ]с=100 МПа.

14.

15.

Ответы:
№1
Q = 77,4 Н.
№5
а) d1 = 27 мм, d2 = 58 мм;
б) 1-й стержень - № 12; 2-й стержень - № 8; 3-й стержень – 32*32*3;
в) 125*80*10; двутавр № 12.