Похожие презентации:
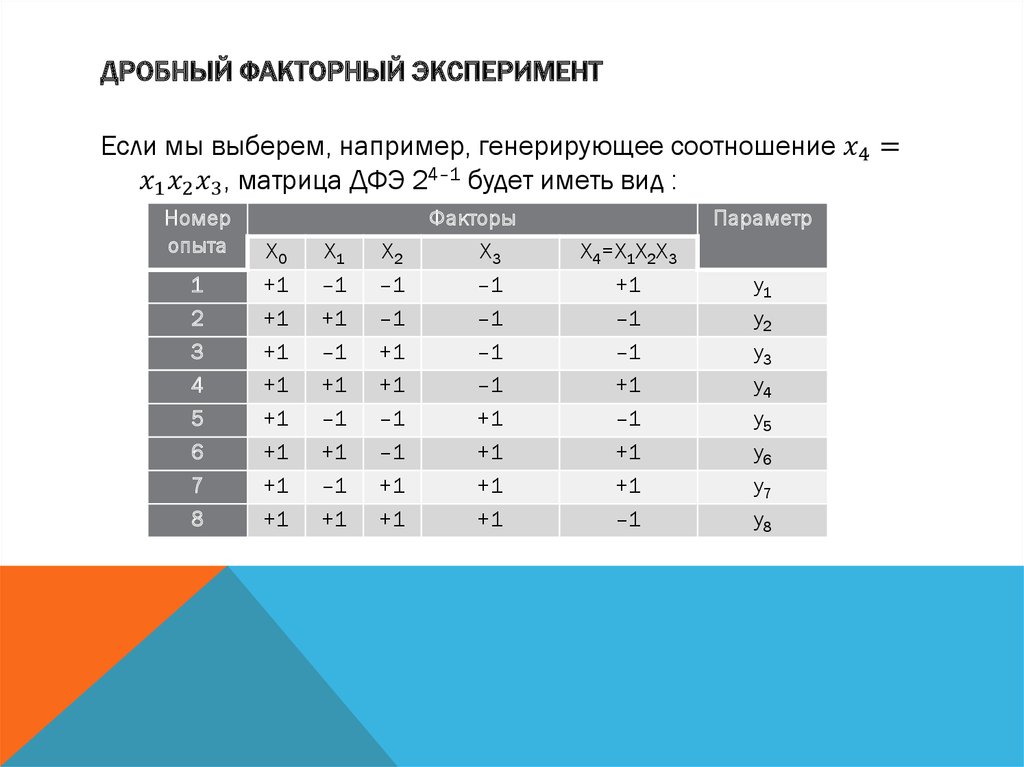
Дробный факторный эксперимент
1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
2. Дробный факторный эксперимент
ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТПри оптимизации мы стремимся сделать эффекты
взаимодействия как можно меньшими. В задачах
интерполяции, напротив, их выявление часто важно и
интересно. С ростом числа факторов число возможных
взаимодействий быстро растет.
С увеличением числа факторов резко возрастает количество
опытов ПФЭ. Так при 5-и факторах оно равно 32, при 6-и — 64
и т.д. Выполнить такое количество опытов технически сложно.
Существует методика уменьшения числа опытов — дробный
факторный эксперимент, план которого представляет собой
некоторую часть (½, ¼ и т.д.) плана ПФЭ.
3. Учет эффектов взаимодействия факторов ПФЭ 23
УЧЕТ ЭФФЕКТОВ ВЗАИМОДЕЙСТВИЯ ФАКТОРОВ ПФЭ 23Рассмотрим матрицу 22 с учетом взаимодействия факторов с
уравнением регрессии y = b0X0+b1X1+b2X2+b12X1X2.
Если есть основания считать, что процесс
описывается линейной моделью,
достаточно определить b0, b1, b2. При
линейном приближении эффект
взаимодействия стремится к нулю (b12 0)
и этот вектор-столбец можно использовать
для нового фактора X3. Матрица
планирования запишется в виде
следующей таблицы
Заменим эффект взаимодействия новым
фактором, уравнение регрессии примет
вид y = b0X0+b1X1+b2X2+b3X3.
Номер
опыта
1
2
3
4
Номер
опыта
1
2
3
4
X0
X1
X2
X1X2
y
+1
+1
+1
+1
–1
+1
–1
+1
–1
–1
+1
+1
+1
–1
–1
+1
y1
y2
y3
y4
X0
X1
X2
X3
y
+1
+1
+1
+1
–1
+1
–1
+1
–1
–1
+1
+1
+1
–1
–1
+1
y1
y2
y3
y4
4. Учет эффектов взаимодействия факторов ПФЭ 23
УЧЕТ ЭФФЕКТОВ ВЗАИМОДЕЙСТВИЯ ФАКТОРОВ ПФЭ 23Для матрицы 23 (табл. ) существует четыре взаимодействия факторов
Номер X0 X1 X2 X3 X1X2 X1X3 X2X3 X1X2X3 y
опыта
1
+1 –1 –1 –1 +1
+1
+1
–1
y1
2
+1 +1 –1 –1 –1
–1
+1
+1
y2
3
+1 –1 +1 –1 –1
+1
–1
+1
y3
4
+1 +1 +1 –1 +1
–1
–1
–1
y4
5
+1 –1 –1 +1 +1
–1
–1
+1
y5
6
+1 +1 –1 +1 –1
+1
–1
–1
y6
7
+1 –1 +1 +1 –1
–1
+1
–1
y7
8
+1 +1 +1 +1 +1
+1
+1
+1
y8
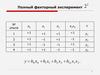
Уравнение регрессии:
y = b0X0+b1X1+b2X2+b3X3+b12X1X2+b23X2X3+b13X1X3+b123X1X2X3 .
5. Дробный факторный эксперимент
ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТДля того, чтобы сократить число опытов, нужно новому фактору
присвоить вектор-столбец матрицы, принадлежащий
взаимодействию, которым можно пренебречь.
Следует подчеркнуть, что формальное приравнивание произведения
факторов фактору, не входящему в это произведение, является
основополагающей идеей метода ДФЭ. В данном случае используется
только половина ПФЭ 23, поэтому этот план называется полурепликой
от ПФЭ 23. Например, матрица из 8 опытов для четырехфакторного
планирования будет полурепликой от ПФЭ 24, а для пятифакторного
планирования – четвертьрепликой от 25.
Для того, чтобы дробная реплика представляла собой ортогональный
план, в качестве реплика следует брать ближайший полный
факторный эксперимент.
6. Дробный факторный эксперимент
ДРОБНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТПоскольку в линейной модели эффекты взаимодействия между
несколькими факторами не учитываются, уровни оставшихся
факторов получаются с использованием некоторых
генерирующих соотношений между факторами первой группы.
Генерирующее соотношение – произведение факторов,
заменяемое в матрице новой независимой переменной.
Например, для случая четырех факторов, когда факторы х1, х2 и
х3 являются свободными, для получения значений фактора х4
можем использовать такие генерирующие соотношения:







 Математика
Математика