Похожие презентации:
Коэффициент размножения нейтронов в цепном процессе
1. Коэффициент размножения нейтронов в цепном процессе
кафедра«Теоретическая и
эксперимент а льная физика
ядерн ых ре акторов»
доцент
Савандер В. И .
2. Цепной процесс деления ядер
• Превышение f 1 над единицей создаетвозможность развития цепной реакции
деления.
3. Цепной процесс деления ядер
• Наряду со средним числом нейтронов на один актделения используют величину, равную числу
нейтронов деления в расчете на один
поглощенный делящимся нуклидом
eff
f (E) f (E)
f (E)
f (E) c (E) 1 (E)
• Условие осуществимости цепного процесса
eff 1
4. Цепной процесс деления ядер
• При рассмотрении цепных процессов всенейтроны в размножающей среде в любой момент
времени можно разделить на отдельные
поколения. Нейтрон каждого поколения проходит
следующий жизненный цикл:
• рождается в реакции деления;
• некоторое время движется в активной зоне,
рассеиваясь на ядрах среды (замедляется и
диффундирует);
• затем либо порождает нейтроны следующего
поколения, либо теряется, например в реакции
радиационного захвата, либо покидает пределы
размножающей среды.
5. Цепной процесс деления ядер
упрощенная модель цепного процесса1. размножающая среда представляется бесконечной,
однородной и изотропной.
2. всем нейтронам в среде приписывается одна и та
же энергия (так называемая, односкоростная
модель)
3. все нейтроны каждого поколения рождаются
одновременно, живут определенное время
(время жизни одного поколения), и одновременно
заканчивают свой жизненный цикл, порождая
нейтроны следующего поколения.
6. Цепной процесс деления ядер
Определение коэффициента размножениякоэффициента размножения нейтронов есть
отношение числа нейтронов последующего
поколения в единичном объеме среды , к
числу нейтронов предыдущего поколения в
том же объеме
n ( i 1)
K (i ) ;
n
7. Цепной процесс деления ядер
• Для выбранной модели изменение во времениплотности нейтронов будет описываться
кусочно-постоянной функцией
n(t ) K n(0) m τ t ( m 1)
m
• Однако, если время жизни поколения мало, а
коэффициент
размножения
не
сильно
отличается от единицы, временное поведение
плотности
нейтронов
можно
описать
непрерывной функцией времени
8. Цепной процесс деления ядер
n(t τ) K n(t);Δn n(t τ) n(t) (K 1 ) n(t);
dn(t)
n(t τ) n(t)
τ;
dt
dn (t ) K 1
n (t )
dt
9. Цепной процесс деления ядер
• Решение этого уравненияK 1
n(t ) n(0) exp
t
• Очевидно, что при K=1 получим n(t)=const, то есть,
в такой размножающей среде будет осуществляться
стационарный процесс (критическая среда)
• При К>1 – рост числа нейтронов (надкритическая
среда),
• при К<1-затухание процесса (подкритическая
среда)
10. Цепной процесс деления ядер
• Величинаназывается периодом
K 1
разгона или затухания.
Задача с источником
1. в среде присутствует внешний источник
нейтронов постоянной мощности q, не
связанный с реакцией деления в среде
2. источник распределен равномерно по
объему среды
T
11. Цепной процесс деления ядер
dn (t ) K 1n(t ) q;
dt
K 1
t
q
A(t ) A0 e
1 K
12. Цепной процесс деления ядер
В критической среде K=1n(t ) n(0) qt
Для подкритической среды
q
n (t )
1 K
то есть в подкритической среде с источником
возможен стационарный процесс.
13. Цепной процесс деления ядер
Газокинетическое уравнение для бесконечнойоднородной среды
n t
tot t dE s ( E E ) (t , E )
t
0
( E ) dE f ( E ) f ( E ) (t , E );
0
(t , E , ) V ( E ) n (t , E , )
14. Цепной процесс деления ядер
• Будем искать решение нестационарной задачи вразделенных переменных
n(t , E ) A(t ) n( E )
• проинтегрируем по энергетической переменной , получим
уравнение
dA
n( E )dE A(t ) t ( E ) V ( E ) n( E )dE
dt 0
0
0
0
A(t ) dE dE s ( E E ) V ( E ) n ( E )
0
0
A(t ) dE ( E ) dE f ( E ) f ( E ) V ( E ) n ( E )
15. Цепной процесс деления ядер
• Введем следующую нормировку по энергетическойпеременной
( E ) V ( E ) n( E )dE
t
0
V ( E ) n( E )dE
t ;
( E E )dE ( E );
s
0
0
( E ) V ( E ) n( E )dE
s
0
V ( E ) n( E )dE
s
V ( E ) n( E )dE V
0
0
0
f
( E ) f ( E ) V ( E ) n( E )dE
V ( E ) n( E )dE
0
f t
s
n( E ) dE 1
0
16. Цепной процесс деления ядер
• С учетом введенных обозначений, получимнестационарное уравнение
1 dA(t )
f f a A(t )
V dt
A(t ) A(0) e t
1 f f
1
1 ,
a
V a
• коэффициент размножения для однородной бесконечной
среды
K
f f
a
;
a
V
,
a
1
a
17. Цепной процесс деления ядер
• Таким образом, в среде, где одновременноприсутствуют нейтроны разных поколений,
коэффициент
размножения
можно
определить как отношение скорости
рождениях нейтронов в размножающей
среде в данный момент нейтронов, к
скорости поглощения нейтронов в тот же
момент времени нейтронов. Обычно, для
бесконечной
среды
коэффициент
размножения обозначается K
18. Последовательные поколения
1. В общем случае в размножающей среде в любой моментвремени присутствуют нейтроны разных поколений
2. Предположим, что в момент времени
t=0 в
размножающую среду одномоментно впустили Q0
нейтронов в каждый элементарный объем.
3. Рассмотрим развитие цепного процесса во времени от
поколения к поколению.
4. Будем рассматривать нейтроны всех энергий,
принадлежащих к данному поколению
n(t ) n( E , t )dE
0
19. Последовательные поколения
Нейтроны нулевого поколенияdn ( 0) (t )
a V n ( 0) (t ),
dt
n ( 0) (0) Q0 ,
lim n ( 0) ( t ) 0
t
Нейтроны первого поколения
dn (1) (t )
a V n (1) (t ) f f V n (0) (t ),
dt
n (1) (0) 0, lim n (1) (t ) 0
t
dn ( i ) (t )
a V n ( i ) (t ) f f V n ( i 1) (t ),
dt
n ( i ) (0) 0; lim n ( i ) (t ) 0, i 0,1,..
t
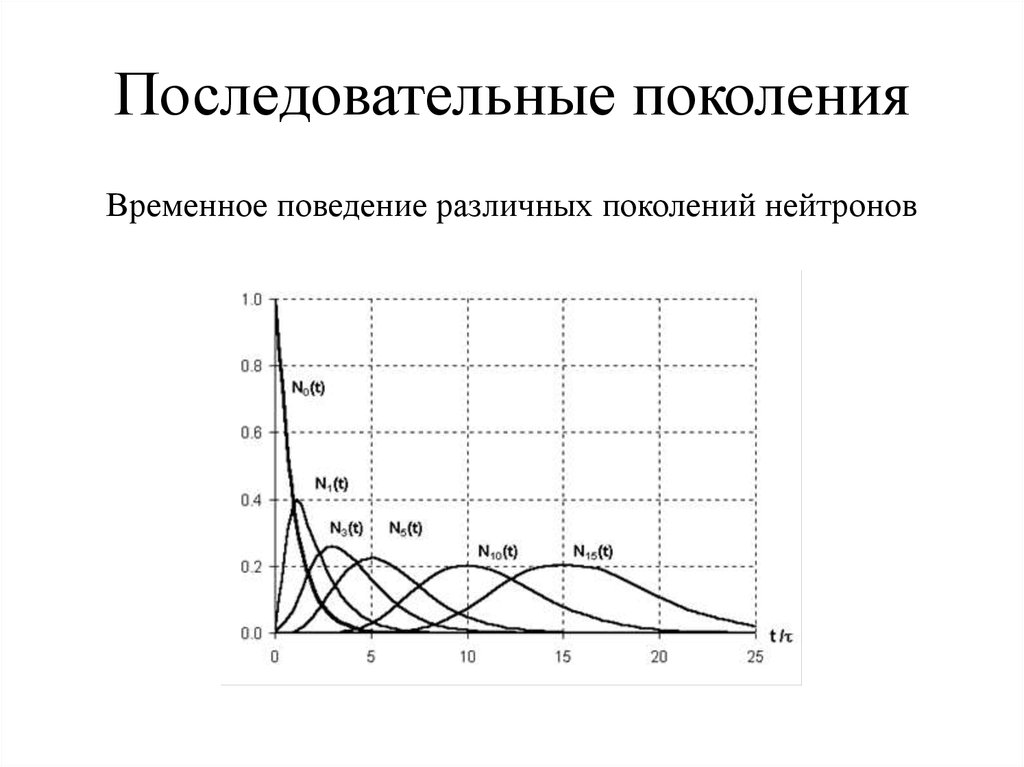
20. Последовательные поколения
Временное поведение различных поколений нейтронов21. Последовательные поколения
Полное число нейтронов в каждом поколенииQ
(i )
f f V N ( i 1) (t )dt
0
Проинтегрируем уравнения для плотности нейтронов в
каждом поколении по времени в интервале (0, )
(i )
(i )
dt
n
(
t
)
N
;
0
dn (0) (t )
(0)
(0)
(0)
(0)
dt
N
(
t
)
N
(
)
N
(0)
N
(0) Q0 ,
0
0
dt
dn ( i ) (t )
(i )
(i )
dt
N
(
)
N
(0) 0;
0
dt
22. Последовательные поколения
соотношения для последовательных поколенийнейтронов
a Ф (1) f f Ф (0) =0,
a Ф (1) f f Ф (0) , Q (1) f f Ф (0) ,
...,
a Ф ( i ) f f Ф ( i 1) , Q ( i ) f f Ф ( i 1) a Ф ( i ) ,
коэффициент размножения есть отношения общего
числа нейтронов в двух последовательных
поколениях
Q (i )
K ( i 1)
Q
23. Последовательные поколения
Учитывая соотношенияQ ( i ) f f Ф ( i 1) ,
Q ( i 1) f f Ф ( i 2) a Ф ( i 1)
Получим
K
f f Ф ( i 1)
a Ф
( i 1)
f f
a
Таким образом, в итоге получили эквивалентность
обоих выражений для коэффициента размножения в
бесконечной размножающей среде.
24. Последовательные поколения
Отметим два важных следствия изполученных соотношений.
Ф(i )
Q (i )
( i 1) K ;
( i 1)
Ф
Q
a
(i )
f
K
(i )
0;
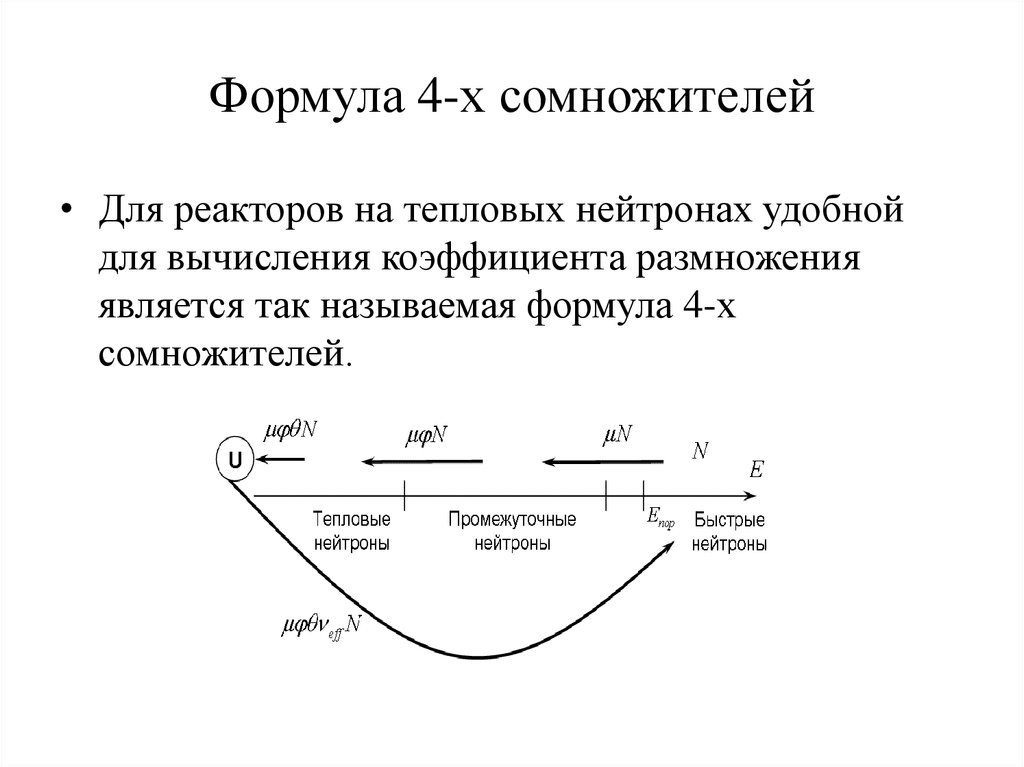
25. Формула 4-х сомножителей
• Для реакторов на тепловых нейтронах удобнойдля вычисления коэффициента размножения
является так называемая формула 4-х
сомножителей.
26. Формула 4-х сомножителей
• Рассматривается однородная бесконечнаяразмножающая среда, состоящая из смеси
урана-235 , урана-238 и замедлителя.
• Рассмотрим жизненный цикл одного
поколения нейтронов при их движении по
энергетической шкале.
• Пусть в единице объема среды появился один
быстрый нейтрон в результате деления ядра
урана-235 тепловым нейтроном.
27. Формула 4-х сомножителей
• Нейтроны с энергией E>Eпор могут вызыватьделение ядер урана-238. Эти вновь родившиеся
нейтроны отнесем к этому же поколению.
• Это увеличение числа нейтронов в результате
размножения на быстрых нейтронах
характеризуется коэффициентом µ, равным числу
быстрых нейтронов, которые замедлились до
энергии ниже порога деления , отнесённому к
одному быстрому нейтрону, появившемуся при
делении U-235 тепловыми нейтронами.
28. Формула 4-х сомножителей
• В результате размножения на U-238 за порог деленияуйдет µ быстрых нейтронов.
• Эти нейтроны, сталкиваясь с ядрами замедлителя,
будут замедлятся.
• В процессе замедления часть нейтронов будет
потеряно в результате резонансного поглощения на
ядрах U-238.
• Резонансное поглощение нейтронов в процессе
замедления характеризуется коэффициентом φвероятностью того, что быстрый нейтрон в процессе
замедления избежит радиационного захвата.
• до тепловой энергии замедляются µφ нейтронов
29. Формула 4-х сомножителей
• Не все тепловые нейтроны поглотятся в топливе. Часть ихбудет захвачена ядрами замедлителя.
• Введем коэффициент θ, определив его как вероятность
захвата теплового нейтрона ураном .
• В результате ядрами урана будет поглощено µφθ
нейтронов.
• Часть этих нейтронов будет поглощено ядрами U-235, в
результате чего появятся быстрые нейтроны нового
поколения .
• Их число, приходящееся на один нейтрон, поглощенный в
топливе, обозначим через νef – среднее число нейтронов
деления на один захваченный тепловой нейтрон в топливе.
30. Формула 4-х сомножителей
• Очевидно, что Peff
f
f
а
Pf
x 5f
x a5 (1 x ) a8
- вероятность того, что при захвате теплового
нейтрона топливом произойдет реакция деления.
- Таким образом во втором поколении число
быстрых нейтронов деления изменится до
значения µφθνef
K eff




























 Физика
Физика








