Похожие презентации:
Степени и корни
1.
Степени и корни2. Корень n-ой степени
n –ой степени из числа «а» называется такоечисло, n –ая степень которого равна «а».
Корнем
27 3 так
3
как 3 3 3 3 27
3
Примеры:
3
4
27 3
81 3
16 2
4
6
625
1
1
64 2
5
7
128 2
5
1
1
2
32
3.
Свойства корней n-й степени4.
Нахождение знаний выражений5
8 4
5
4
1
5
16
3 5
21
7
128
8 4
5
5
32
4
4
81
81
4
16
16
15
7
21
2
7
3
2
5
2
5
3
1,5
2
2
5.
Иррациональным уравнениемназывается уравнение, содержащее
неизвестную под знаком корня, а
также под знаком возведения в
дробную степень.
2x 3 x 1
3
x 5 12 x 4 5
4
7
3x x 8 15
6.
Метод возведения в степеньобеих частей уравнения:
1) Если иррациональное уравнение содержит
только один радикал, то нужно записать
так, чтобы в одной части знака равенства
оказался только этот радикал. Затем обе
части уравнения возводят в одну и ту же
степень, чтобы получилась рациональное
уравнение.
7.
Метод возведения в степеньобеих частей уравнения:
2)
Если в иррациональном уравнении
содержится два или более радикала, то
сначала изолируется один из радикалов,
затем обе части уравнения возводят в одну и
ту же степень, и повторяют операцию
возведения в степень до тех пор, пока не
получится рациональное уравнение.
8.
Решение уравнений с проверкой:9.
Решение уравнений с проверкой:10.
Решение уравнений с переходом ксистеме уравнения и неравенств
f ( x) g ( x)
f ( x) g ( x)
f ( x) g 2 ( x)
g ( x) 0
f ( x) g ( x)
f ( x) 0...или....g ( x) 0














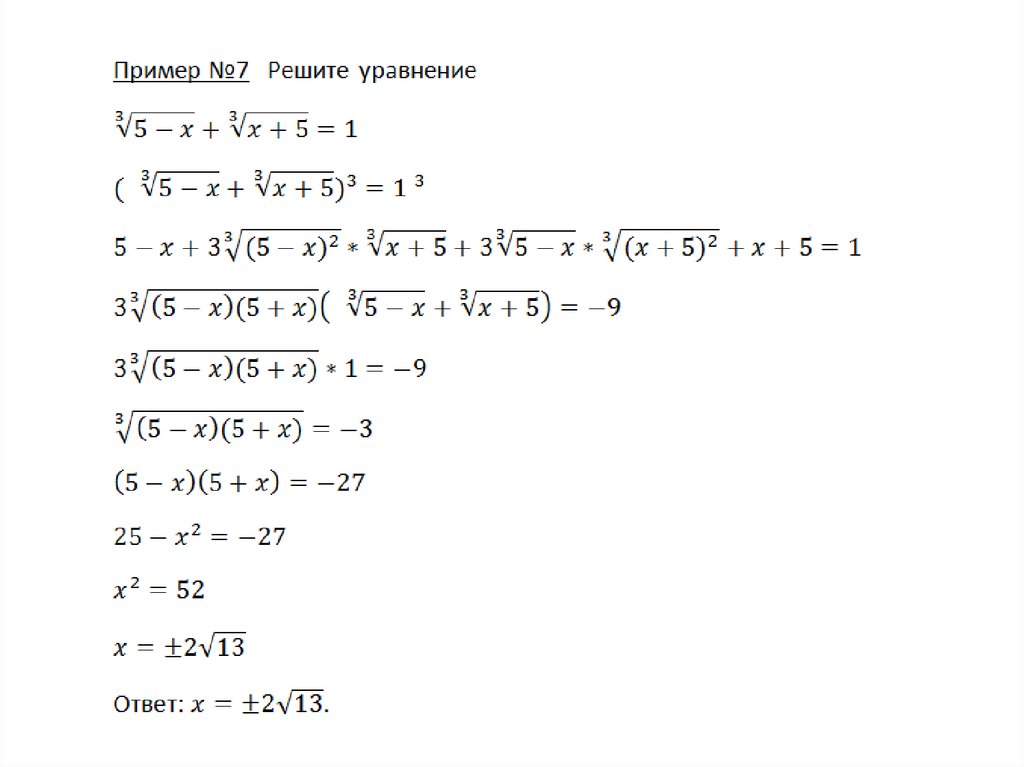




 Математика
Математика








